线性分组码
合集下载
第3章线性分组码

8
第3章 线性分组码
3.2 码的一致校验矩阵与生成矩阵
码的生成矩阵( k 维线性子空间)
由于[n,k,d]线性分组码是一个k维线性空间。因此必 可找到k个线性无关的矢量,能张成该线性空间。设 C1 , C 2 , C k 是k个线性无关的矢量,则对任意 C ,可有:
C m1C1 m2 C 2 mk C k C1 C2 m1 , m2 , mk C k G称为该分组码的生成矩阵 mG
4
第3章 线性分组码
3.1 线性分组码的基本概念
线性空间的性质
零元素是唯一的 负元素是唯一的, V 关于0元素有 0 0, k 0 0, ( 1) ,
- 唯一
k ( ) k k
如果
如果 k =0,那么k=0或 =0.
9
第3章 线性分组码
3.2 码的一致校验矩阵与生成矩阵
例:一个[7, 3 ]码,m2 m1 m0 → c6 c5 c4 c3 c2 c1 c0 ,如 果码字的生成规则为:
若用矩阵形式表示这些线性方程 组, 则:
C m2 m1
1 0 0 1 1 1 0 m0 0 1 0 0 1 1 1 0 0 1 1 1 0 1
0 ;(β 称为 的负元素)
3
第3章 线性分组码
3.1 线性分组码的基本概念
数量乘法满足下列两条规则 : ⑤ 1 ⑥ k ( l ) ( kl ) 数量乘法与加法满足下列两条规则: ⑦ (k l ) k l ⑧ k ( ) k k
[ n –i, k -i]缩短码的纠错能力至少与原[n, k ]码 相同。 [n –i, k -i]缩短码是[n , k ]码缩短i位得到的, 因而码率R 比原码要小, 但纠错能力不一定比原码 强。
线性分组码

系统码的校验矩阵和生成矩阵可以转换。
13
线性分组码的性质
线性分组码中任意两个码字的模2加仍为一个码字,这个性 质称为码的封闭性。 零矢量必须是任一线性分组码中的一个码字,称为零码字。 生成矩阵中各行都是一个码字,且生成矩阵的各行是线性 无关的(任意两行相加不为零)。任意码字C是生成矩阵中 各行的某一线性组合。 校验矩阵的各行应该是线性无关的,否则将得不到r个线性 无关的监督关系式,从而得不到r个独立的监督位。
23
汉明码
汉明码实际上是(2m-1, 2m-m-1)线性分组码,其校验行有m行,共有 n=2m-1列,任一列都不为零且两两互不相等,因此能纠正任何单 个错误。 汉明码的校验矩阵一般有两种构造方式: 一是校验矩阵的标准形式,即H=[PI] 式中P为m×(n-m)维矩阵,I为m×m维单位阵。按这种校验矩阵编 出的码是系统码。 二是校验矩阵的列是按二进制数的自然顺序从左到右排列的非零 列,例如,当n=7,k=4时,H中的第一列为[0 0 1],第二列为[0 1 0],…,第七列为[1 1 1],按这种校验矩阵编出的码是非系统码。 发生单个错误时,伴随式是H中与错误位置对应的列,所以汉明码 伴随式二进制数的值就是错误位置的序号。
14
例题-由生成矩阵生成码字
由生成矩阵 所有码字为
m 000
1 0 0 1 1 1 0 G 0 1 0 0 1 1 1 0 0 1 1 1 0 1
生成的(7,3)码的
C 0000000
0 0 0 1 1 1 1
0 1 1 0 0 1 1
1 0 1 0 1 0 1
在校验方程的矩阵形式中,令
1 1 则校验方程可以写成 H 1 0
HCT=0 或CHT=0
信息论与编码_第7章线性分组码

1 1 1 0 1 1 [000]. 0 0 1 0 0 1
17
线性分组码的校验矩阵
例7-2(续2):求对偶码C
1 1 0 1 0 0 对偶码的生成矩阵=校验矩阵H 1 1 1 0 1 0 . 1 0 1 0 0 1
c mH , c1 m1 m2 m3 c m m 1 2 2 c3 m2 m3 c4 m1 c5 m2 c6 m3
例7-3 设一个(6,3)线性分组码C的校验矩阵为
1 1 0 1 0 0 H 1 1 1 0 1 0 0 0 1 0 0 1
任何1列线性无关, 第1、2列线性相关, C的最小汉明距离 =2
23
线性分组码
线性分组码概念 线性分组码的生成矩阵 线性分组码的校验矩阵 线性分组码的最小汉明重量 线性分组码的译码 完备码 汉明码
21
线性分组码的最小汉明重量
定理7-4 线性分组码C的最小汉明距离等于该码中非零 码字的最小 汉明重量 。 例7-2(续3) 全体码字为:
码字 000000 011101 110001 101100 111010 100111 001011 010110
C的最小汉明距离=3, 可以纠1个错,检2个错
对偶码C 000 000 101 001 111 010 010 011 110 100 011 101 001 110 100 111
18
线性分组码的校验矩阵
课堂练习:已知(5, 3)线性分组码的生成矩阵为G
1 0 1 1 0 G 0 1 0 1 1 1 1 0 1 0
信息元
000 001 010 011 100 101 110 111
第二章 线性分组码(zhb)
1
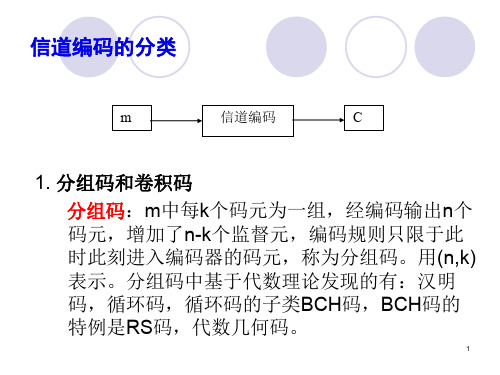
卷积码:m中每k0个码元为一组,经编码输出n0个
码元,增加了n0-k0个监督元,编码规则不仅于此
时此刻进入编码器的码元有关,还与此刻相邻的
m时刻有关,称为卷积码。用(n0,k0,m) 表示。 目前常见的几种码:
级联码:将分组码和卷积码结合起来的码,一般用RS码为外码,卷
积码作为内码。
Turbo码:是并行结构的级联码系统码,将卷积码和随机交织器相结 合。被IS-2000标准作为第三代移动通信手机中的纠错抗干扰方案。 LDPC码:是一种线性分组码,Low-Density-Parity-CheckCodes, 它 能比其它码带来更高的编码增益。被通信公司作为第四代移动通信中
h11Cn 1 h12Cn 2 h1k Cn k Cn k 1 0 h C h C h C C 21 n 1 22 n 2 2k n k n k 2 0 h r1Cn 1 h r2Cn 2 h rk C n k C0 0
Wmin minWV, V C, V 0
线性分组码的最小距离等于它的最小重量
d min Wmin
线性分组码纠t个错误的充要条件是码的最小距离为:
d
2t 1
10
三、(n,k)码的监督矩阵H和生成矩阵G 1. 监督矩阵(也称校验矩阵)
h11 h12 h h 22 21 H h r1 h r2 h1k h 2k h rk 1 0 0 0 0 1
23
伴随式计算电路
R0 R1 R2 R3 R4 R5 R6
输入
输出
+
S0
+
S1
卷积码:m中每k0个码元为一组,经编码输出n0个
码元,增加了n0-k0个监督元,编码规则不仅于此
时此刻进入编码器的码元有关,还与此刻相邻的
m时刻有关,称为卷积码。用(n0,k0,m) 表示。 目前常见的几种码:
级联码:将分组码和卷积码结合起来的码,一般用RS码为外码,卷
积码作为内码。
Turbo码:是并行结构的级联码系统码,将卷积码和随机交织器相结 合。被IS-2000标准作为第三代移动通信手机中的纠错抗干扰方案。 LDPC码:是一种线性分组码,Low-Density-Parity-CheckCodes, 它 能比其它码带来更高的编码增益。被通信公司作为第四代移动通信中
h11Cn 1 h12Cn 2 h1k Cn k Cn k 1 0 h C h C h C C 21 n 1 22 n 2 2k n k n k 2 0 h r1Cn 1 h r2Cn 2 h rk C n k C0 0
Wmin minWV, V C, V 0
线性分组码的最小距离等于它的最小重量
d min Wmin
线性分组码纠t个错误的充要条件是码的最小距离为:
d
2t 1
10
三、(n,k)码的监督矩阵H和生成矩阵G 1. 监督矩阵(也称校验矩阵)
h11 h12 h h 22 21 H h r1 h r2 h1k h 2k h rk 1 0 0 0 0 1
23
伴随式计算电路
R0 R1 R2 R3 R4 R5 R6
输入
输出
+
S0
+
S1
线性分组码

二、线性分组码的严格数学定义2
2. 定理1 (码的封闭性)
设CH为由监督矩阵H定义的分组码,则c1,c2CH : c1+c2CH 证明: 由c1CH,得Hc1T=0T;
由c2CH,得Hc2T=0T;
所以 H(c1+c2)T=H(c1T+c2T) =Hc1T+Hc2T=0T c1+c2满足HcT=0T,所以c1+c2 CH
+
+
考虑如何用串行方式?
三、G与H的关系4
0 1 2 3 4 5 6 7 8 9 10 11 12 13
D0
D1
+
D2
+
D3
+
D0
D1
+
D2
+
D3
+
m4m5m6
m6
m6
D0
D1
m6+m5 m6
D0
D1
m6
m6
+
D2
+
D3
+
m4m5
m6+m5
m6+m5
+
D2
m6+m5+m6
=m5
+
D3
+
m4
m5+m4
互为对偶码,若CH=CG, 则称为自对偶码(P62)
[Q In-k] [IkP]T= [QIn-k] [IkT PT]T= Q + PT = 0
所以 P= - QT 或 Q = -PT
由此得 G=[Ik P] = [ Ik –QT] H=[Q In-k]= [ -PT In-k]
三、G与H的关系2
8.2 线性分组码 线性分组码编码

第八章 差错控制编码
8.2 线性分组码
线性分组码的编码
1
引言
• 信道编码,目的是提高数字通信的可靠性
– 差错率是信噪比的函数
• 信道编码,差错控制编码,抗干扰编码
• 信道编码过程:
– 信息码元序列+监督码元→编码码组
• 信道译码过程:
– 编码码组→检错或纠错→信息码元序列
2
1. 线性分组码的概念
1 0 0
G=0 1 0 0 1 1
1 0 1
0 0 1 1 1 0
1 1 0
1 1 1
7
由式
,得码组矩阵为:
0 0 0 0 0 1
0 0 0 0 0 0 0 0 1 1 1 0
0 C=0
1
1 1 0
0 1
0
1 0 0
0 1 0
0 0 1
1 0 1
0 1 1
110=100
1 1 0
0 1 0
0 1 1
6
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
例8-1 已知(6,3)码的生成矩阵为G,试求:(1) 编码码组 和各码组的码重;(2) 最小码距 d及min其差错控制能力。
解
(1) 由3位码组成的信息码组矩阵为D:
0 0
0 0
0 1
0 1 0
1 0 0 1 0 1
0 1 1
D=
ck = dk
ck +1 ck+2
= =
h11d1 h12d2 h1k dk h21d1 h22d2 h2k dk
G生成矩阵
cn = hm1d1 hm2d2 hmk dk
5
写成矩阵形式,有 C = D G ,G为生成矩阵(k*n),且:
8.2 线性分组码
线性分组码的编码
1
引言
• 信道编码,目的是提高数字通信的可靠性
– 差错率是信噪比的函数
• 信道编码,差错控制编码,抗干扰编码
• 信道编码过程:
– 信息码元序列+监督码元→编码码组
• 信道译码过程:
– 编码码组→检错或纠错→信息码元序列
2
1. 线性分组码的概念
1 0 0
G=0 1 0 0 1 1
1 0 1
0 0 1 1 1 0
1 1 0
1 1 1
7
由式
,得码组矩阵为:
0 0 0 0 0 1
0 0 0 0 0 0 0 0 1 1 1 0
0 C=0
1
1 1 0
0 1
0
1 0 0
0 1 0
0 0 1
1 0 1
0 1 1
110=100
1 1 0
0 1 0
0 1 1
6
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
例8-1 已知(6,3)码的生成矩阵为G,试求:(1) 编码码组 和各码组的码重;(2) 最小码距 d及min其差错控制能力。
解
(1) 由3位码组成的信息码组矩阵为D:
0 0
0 0
0 1
0 1 0
1 0 0 1 0 1
0 1 1
D=
ck = dk
ck +1 ck+2
= =
h11d1 h12d2 h1k dk h21d1 h22d2 h2k dk
G生成矩阵
cn = hm1d1 hm2d2 hmk dk
5
写成矩阵形式,有 C = D G ,G为生成矩阵(k*n),且:
6.2线性分组码

线性特性:码字c的各位码元是消息m各位的线性组 合
一个( 一个(n,k)线性分组码的码字 c可以表示为 ) 可以表示为
c=mG
其中m:长度为 的消息或 的消息或k维的消息向量 其中 :长度为k的消息或 维的消息向量 Gk*n:k行n列的生成矩阵 列的生成矩阵 行 列的 矩阵运算采用模二加和模二乘。 矩阵运算采用模二加和模二乘。
1 0 1 1 0 1 0 1 1 0 0 0 1 1 1 G = 0 1 0 1 1 R2 + R3 → R3 →0 1 0 1 1 R1 + R3 → R1 → 0 1 0 1 1 1 1 0 1 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 R1 ← → R 3 →0 1 0 1 1 = G S 0 0 1 1 1
线性分组码的性质
(1)零向量一定是一个码字,记作 θ = (0,0,L ,0) )零向量一定是一个码字, (2)任意两码字的和仍是一个码字。 )任意两码字的和仍是一个码字。 都可以表示为G的行向量的线性组合 (3)任意码字 都可以表示为 的行向量的线性组合。 )任意码字c都可以表示为 的行向量的线性组合。
G的行向量是码集合中的码字(它们线性无关) 的行向量是码集合中的码字(它们线性无关) 的行向量是码集合中的码字
(4)线性分组码的最小距离等于最小非 码的码重: 码的码重: )线性分组码的最小距离等于最小非0码的码重 码重:码字中的非0符号个数。
d min = min w(c)
c ≠θ
例:c = (0101) d = w(c)
系统码。 (1)则该码称为系统码。 )则该码称为系统码
容易发现,若系统线性分组码的生成矩阵G 的左(右) 半部分是Ik*K的单位阵,则线性分组码的前(后)k位是 信息位,后n-k位是校验位。 若不是系统码,则可以通过简单行变换得到系统码生成 矩阵。
信息论基础——线性分组码
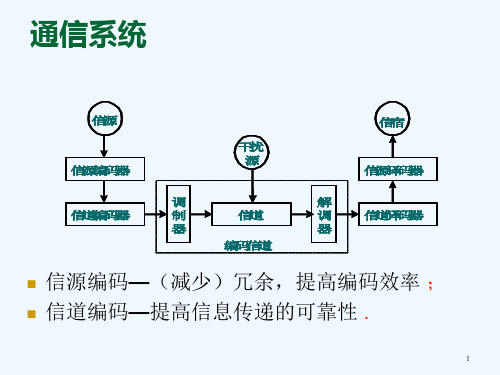
即校验位是由信息位线性组合得到.
17
线性分组码的基本概念
信息位 00 01 10 11 x2 x0 x1 00000 x3 x0 x x x 01101 0 1 4 码字 10111 11010
信息位k=2 码字数M=4
可见,码字的三个校验元都由其前两位线 性组合得到,即可由的线性方程组求得;
18
线性分组码的基本概念
f1 : GF (2) 2 GF (2)5
信息位 00 01 10 11 码字 00000 01101 10111 11010
1 ( 0 1 ) 1 ( 1 0 ) 1 1
f( 1 1 ) 1 1 0 1 0
1 ( 0 1 1 0 1 )1 ( 1 0 1 1 1 ) 1 1 0 1 0
30
线性分组码的基本概念
汉明距离: 指(n,k)分组码中两个码字xn 、 yn对应位取 值不同的个数;记为d(xn , yn).
5 5 ( 1 0 1 0 1 ) , y ( 0 1 1 1 1 ) 例: x
d(x ,y ) 3
5 5
31
线性分组码的基本概念
线性分组码的最小距离: 称(n,k)分组码中任两个码字汉明距离的最小 值,为该分组码的最小距离d.
f ( 1 ( 0 1 ) 1 ( 1 0 ) ) 1 ( 0 1 1 0 1 ) 1 ( 1 0 1 1 1 ) 线性编码
19
线性分组码的基本概念
例题1: 下面是某个(n,k)线性二元码的全部码字
x16=000000 x26=100011 x36=010101 x46=001111 x56=110110 x66=101100 x76=011010 x86=111001 求n、k的值;
17
线性分组码的基本概念
信息位 00 01 10 11 x2 x0 x1 00000 x3 x0 x x x 01101 0 1 4 码字 10111 11010
信息位k=2 码字数M=4
可见,码字的三个校验元都由其前两位线 性组合得到,即可由的线性方程组求得;
18
线性分组码的基本概念
f1 : GF (2) 2 GF (2)5
信息位 00 01 10 11 码字 00000 01101 10111 11010
1 ( 0 1 ) 1 ( 1 0 ) 1 1
f( 1 1 ) 1 1 0 1 0
1 ( 0 1 1 0 1 )1 ( 1 0 1 1 1 ) 1 1 0 1 0
30
线性分组码的基本概念
汉明距离: 指(n,k)分组码中两个码字xn 、 yn对应位取 值不同的个数;记为d(xn , yn).
5 5 ( 1 0 1 0 1 ) , y ( 0 1 1 1 1 ) 例: x
d(x ,y ) 3
5 5
31
线性分组码的基本概念
线性分组码的最小距离: 称(n,k)分组码中任两个码字汉明距离的最小 值,为该分组码的最小距离d.
f ( 1 ( 0 1 ) 1 ( 1 0 ) ) 1 ( 0 1 1 0 1 ) 1 ( 1 0 1 1 1 ) 线性编码
19
线性分组码的基本概念
例题1: 下面是某个(n,k)线性二元码的全部码字
x16=000000 x26=100011 x36=010101 x46=001111 x56=110110 x66=101100 x76=011010 x86=111001 求n、k的值;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c =(1010011) e =(0100000) r =(1110011)
s = r HT = e HT = (0100000) c =(1010011) e =(1001000) r = (0011011)
101 | 1000 111 | 0100 110 | 0010 011 | 0001
T
=
G=
gk,n-1 gk,n-2
… gk,0
秩是多少?
G称为[n,k]码的生成矩阵。
G的标准形式[IkP], 称为典型生成矩阵。
三、G与H的关系
G的行矢量是码字, HgiT=0T, 有HGT= 0T, H与G所张成的空间互为零空间。 CH: H校验,G生成。 CG: G校验,H生成。 互为对偶码,若CH=CG, 则称为自对偶码(P62)
五、线性分组码的译码5
构造办法: a.按H的二进制数的顺序排列。 例GF(2)上的[7,4,3]的汉明码,m=3, 23-1=7个非零列,3维矢量按 0~7的二进制数排列 H= 1111000 1100110 1010101
b. 系统码 1110100 H= 1 1 0 1 0 1 0 1011001
+ + + +
考虑如何用串行方式?
三、G与H的关系4
0 1 2 3 4 5 6 7 8 9 10 11 12 13
D0
D1
+
D2
+
D3
+
D0
D1
+
D2
+
D3
+
m4 m5 m6
0 1 2 3 4 5 6 7 8 9 10 11 12 13
m6
m6
D0 D1 +
m6
D2 +
m6
D3 +
m6
m4 m5 m6+m5 m6+m5
..........
cn-1 cn-2 =0 c0
HcT=0T
hn-k,n-1hn-k,n-2 … hn-k,n-k00…1
二、线性分组码的严格数学定义
1.定义
GF(q)中的元素(q为素数幂)组成的(n-k)n矩阵,其秩为n-k。满足方程 HcT=0T的矢量c=(cn-1, cn-2, …ci,… ,c0) ( ciGF(q) )的集合称为[n,k]线性分组 码。H称为监督(检验)矩阵。 HcT=0T称为(一致)监督矩阵。
d min w(c)
c[ n, k ]
c1 d(c1,c2) d(c1,c3)
定理5:GF(2)上的[n,k,d]分组码中任何码字c1,c2满足: c2 w(c1+c2) = w(c1)+w(c2)- 2(c1c2) 内积 或 d(c1,c2) w(c1)+w(c2)
d(c2,c3)
r(x) - m(x)xn-k (mod g3(x))
除法电路
(见168页)
四、线性分组码的最小距离、检错和纠错能力
1. 检、纠错的必要条件:码字在一些码元发生错误后,还没有变成其它码字。 为使码具有强的检错、纠错能力,各码字的距离差别(汉明距离)足够大。 2. 线性分组码的最小距离d(最小汉明距离) 若[n,k]线性分组码的最小距离为d, 记为[n,k,d] 定理4:[n,k]分组码的最小距离d满足 d(c1,c2)=w(c1+c2)=w(c3)
D0 D1 + D2 +
m6+m4
D3 +
m4 m 5 m6
三、G与H的关系5
x6 x5x4 100| G= 0 1 0 | 001| x3 x2x 1110 0111 1101 g1(x)=x6+x3+x2+x=x(x5+x2+x+1) 写成多项式
=x(x+1)(x4+x3+x2+1) g2(x)=x5+x2+x+1=(x+1)(x4+x3+x2+1) 4+x3+x2+1 g (x)= x 6 3 2 4 3 2 3 g1(x)=x +x +x +x= x(x+1)(x +x +x +1) =x(x+1)g3(x) g2(x)=x5+x2+x+1=(x+1)(x4+x3+x2+1) =(x+1)g3(x)
[Q In-k] [IkP]T= [QIn-k] [IkT PT]T= Q + PT = 0
所以 P= - QT 或 Q = -PT
由此得 G=[Ik P] = [ Ik –QT] H=[Q In-k]= [ -PT In-k]
三、G与H的关系2
例: 已知[7,3]码(p52, 例3.1)
101 111 110 011 |1000 |0100 |0010 |0001
第三章 线性分组码
陆以勤
2005年3月
一、线性分组码的一般性定义
定义:通过预定的线性运算将k维q元(q为素数幂)信息数组变换成n维 (n>k)码数组(称码字),由qk个码字所成的集合,称为[n,k]线性分组码, 简称分组码。 码字用 (cn-1, cn-2, … , cn-k, cn-k-1, … , c1, c0)表示。 码率(传信率,信道利用率)R=k/n表示信息位所占的比重。 最简单的情况:在后面添加n-k个监督元,叫系统码(定义3.2.2)。
r2 r3
T
s = r HT = ( r 6 r5 r4 r3 r2 r1 r0 )
r6 + r 4 + r3 r6 + r 5 + r4 + r2 = r +r +r 6 5 1 r5 + r 4 + r0
r4 r5
T
= (s3 s2 s1 s0)
#43;
S1
+
S2
+
S3
五、线性分组码的译码3
二、线性分组码的严格数学定义4
由第2章定理3可知,必存在k个线性独立的码字g1, g2, … , gk, 使cCH:
c=mn-1g1+mn-2g2+… + mn-kgk =m G g1,n-1 g1,n-2 … g1,0 g2,n-1 g2,n-2 … g2,0
..........
基不同,G不同,但 生成的空间是一样的, 不同的G的意义是什 么?
0 T 1 1 1
s = r HT = e HT = (1001000)
101 | 1000 111 | 0100 110 | 0010 011 | 0001
T
=
1 1 1 0
T
+
1 0 0 0
T
=
(0110)
五、线性分组码的译码4
若e = (0, …,0, ei, 0, … 0) s= ei hi T 若为二进制,则s =hiT 若要各列彼此区分,各列互不相同,即任意两列线性无关 H(n-k)×n
H=
c=(c6c5c4c3c2c1c0) 由HcT=0T得 c3=c6+c4 c2=c6+c5+c4 c1=c6+c5 c0=c5+c4
P= -QT= 1110 0111 1101 G=[Ik P] = 100| 1110 010| 0111 001| 1101
三、G与H的关系3
设信息组m = (m6m5m4) c6=m6 c5=m5 c4=m4 c3=m6+m4=c6+c4 c2=m6+m5+m4=c6+c5+c4 c1=m6+m5=c6+c5 c0=m5+m4=c5+c4
(3) 纠正t个错误,或检测e(t) 个错误,则要求d t+e+1 (4) 纠正t个错误和个删除,则要求d 2t+ +1 e t
e
t
t
e
1
t
1
t
t
1
e
t
t
t
t
五、线性分组码的译码
1. 伴随式
c H cT = 0 T HrT= H(c+e)T= HcT+HeT= HeT 定义s rHT 称为接收字r 的伴随式(校正子)
2.再证维数为k 设cCH, 则HcT=0T. c与H的每一行矢量正交, 故c在由H的行矢量张成的n-k维线 性子空间Vn,n-k的零空间中(第2章定理17, 定理2.6.9), CH中每个码字和H张成的子 空间的矢量正交, 所以CH为H张成的子空间的零空间(第2章定理16, 定理2.6.8), 维 数为k (第2章定理18, 定理2.6.10)。
h1T h0T hn-1T hn-2T
= ei1 hi1T+ …+ei2 hi2T+…+ eit hi tT 发生错误的位所对应的列 向量的线性组合
五、线性分组码的译码2
101 | 1000 111 | 0100 例:[7,3]码, H= 110 | 0010 011 | 0001 101 | 1000 111 | 0100 110 | 0010 011 | 0001
最多可构成2n-k-1个互不相同的非零列,即必须保证 2n-k-1 n
取下限,得2n-k-1 = n,即为汉明码。
2. 汉明码
定义(定义3.3.1):GF(2)上的线性分组码[n,k,d]称为汉明码,若满足下列条件: (1) n = 2m-1 (mN,且m3); (2) k=2m-m-1 (3)n-k = m; (4) d=3。
二、线性分组码的严格数学定义2
s = r HT = e HT = (0100000) c =(1010011) e =(1001000) r = (0011011)
101 | 1000 111 | 0100 110 | 0010 011 | 0001
T
=
G=
gk,n-1 gk,n-2
… gk,0
秩是多少?
G称为[n,k]码的生成矩阵。
G的标准形式[IkP], 称为典型生成矩阵。
三、G与H的关系
G的行矢量是码字, HgiT=0T, 有HGT= 0T, H与G所张成的空间互为零空间。 CH: H校验,G生成。 CG: G校验,H生成。 互为对偶码,若CH=CG, 则称为自对偶码(P62)
五、线性分组码的译码5
构造办法: a.按H的二进制数的顺序排列。 例GF(2)上的[7,4,3]的汉明码,m=3, 23-1=7个非零列,3维矢量按 0~7的二进制数排列 H= 1111000 1100110 1010101
b. 系统码 1110100 H= 1 1 0 1 0 1 0 1011001
+ + + +
考虑如何用串行方式?
三、G与H的关系4
0 1 2 3 4 5 6 7 8 9 10 11 12 13
D0
D1
+
D2
+
D3
+
D0
D1
+
D2
+
D3
+
m4 m5 m6
0 1 2 3 4 5 6 7 8 9 10 11 12 13
m6
m6
D0 D1 +
m6
D2 +
m6
D3 +
m6
m4 m5 m6+m5 m6+m5
..........
cn-1 cn-2 =0 c0
HcT=0T
hn-k,n-1hn-k,n-2 … hn-k,n-k00…1
二、线性分组码的严格数学定义
1.定义
GF(q)中的元素(q为素数幂)组成的(n-k)n矩阵,其秩为n-k。满足方程 HcT=0T的矢量c=(cn-1, cn-2, …ci,… ,c0) ( ciGF(q) )的集合称为[n,k]线性分组 码。H称为监督(检验)矩阵。 HcT=0T称为(一致)监督矩阵。
d min w(c)
c[ n, k ]
c1 d(c1,c2) d(c1,c3)
定理5:GF(2)上的[n,k,d]分组码中任何码字c1,c2满足: c2 w(c1+c2) = w(c1)+w(c2)- 2(c1c2) 内积 或 d(c1,c2) w(c1)+w(c2)
d(c2,c3)
r(x) - m(x)xn-k (mod g3(x))
除法电路
(见168页)
四、线性分组码的最小距离、检错和纠错能力
1. 检、纠错的必要条件:码字在一些码元发生错误后,还没有变成其它码字。 为使码具有强的检错、纠错能力,各码字的距离差别(汉明距离)足够大。 2. 线性分组码的最小距离d(最小汉明距离) 若[n,k]线性分组码的最小距离为d, 记为[n,k,d] 定理4:[n,k]分组码的最小距离d满足 d(c1,c2)=w(c1+c2)=w(c3)
D0 D1 + D2 +
m6+m4
D3 +
m4 m 5 m6
三、G与H的关系5
x6 x5x4 100| G= 0 1 0 | 001| x3 x2x 1110 0111 1101 g1(x)=x6+x3+x2+x=x(x5+x2+x+1) 写成多项式
=x(x+1)(x4+x3+x2+1) g2(x)=x5+x2+x+1=(x+1)(x4+x3+x2+1) 4+x3+x2+1 g (x)= x 6 3 2 4 3 2 3 g1(x)=x +x +x +x= x(x+1)(x +x +x +1) =x(x+1)g3(x) g2(x)=x5+x2+x+1=(x+1)(x4+x3+x2+1) =(x+1)g3(x)
[Q In-k] [IkP]T= [QIn-k] [IkT PT]T= Q + PT = 0
所以 P= - QT 或 Q = -PT
由此得 G=[Ik P] = [ Ik –QT] H=[Q In-k]= [ -PT In-k]
三、G与H的关系2
例: 已知[7,3]码(p52, 例3.1)
101 111 110 011 |1000 |0100 |0010 |0001
第三章 线性分组码
陆以勤
2005年3月
一、线性分组码的一般性定义
定义:通过预定的线性运算将k维q元(q为素数幂)信息数组变换成n维 (n>k)码数组(称码字),由qk个码字所成的集合,称为[n,k]线性分组码, 简称分组码。 码字用 (cn-1, cn-2, … , cn-k, cn-k-1, … , c1, c0)表示。 码率(传信率,信道利用率)R=k/n表示信息位所占的比重。 最简单的情况:在后面添加n-k个监督元,叫系统码(定义3.2.2)。
r2 r3
T
s = r HT = ( r 6 r5 r4 r3 r2 r1 r0 )
r6 + r 4 + r3 r6 + r 5 + r4 + r2 = r +r +r 6 5 1 r5 + r 4 + r0
r4 r5
T
= (s3 s2 s1 s0)
#43;
S1
+
S2
+
S3
五、线性分组码的译码3
二、线性分组码的严格数学定义4
由第2章定理3可知,必存在k个线性独立的码字g1, g2, … , gk, 使cCH:
c=mn-1g1+mn-2g2+… + mn-kgk =m G g1,n-1 g1,n-2 … g1,0 g2,n-1 g2,n-2 … g2,0
..........
基不同,G不同,但 生成的空间是一样的, 不同的G的意义是什 么?
0 T 1 1 1
s = r HT = e HT = (1001000)
101 | 1000 111 | 0100 110 | 0010 011 | 0001
T
=
1 1 1 0
T
+
1 0 0 0
T
=
(0110)
五、线性分组码的译码4
若e = (0, …,0, ei, 0, … 0) s= ei hi T 若为二进制,则s =hiT 若要各列彼此区分,各列互不相同,即任意两列线性无关 H(n-k)×n
H=
c=(c6c5c4c3c2c1c0) 由HcT=0T得 c3=c6+c4 c2=c6+c5+c4 c1=c6+c5 c0=c5+c4
P= -QT= 1110 0111 1101 G=[Ik P] = 100| 1110 010| 0111 001| 1101
三、G与H的关系3
设信息组m = (m6m5m4) c6=m6 c5=m5 c4=m4 c3=m6+m4=c6+c4 c2=m6+m5+m4=c6+c5+c4 c1=m6+m5=c6+c5 c0=m5+m4=c5+c4
(3) 纠正t个错误,或检测e(t) 个错误,则要求d t+e+1 (4) 纠正t个错误和个删除,则要求d 2t+ +1 e t
e
t
t
e
1
t
1
t
t
1
e
t
t
t
t
五、线性分组码的译码
1. 伴随式
c H cT = 0 T HrT= H(c+e)T= HcT+HeT= HeT 定义s rHT 称为接收字r 的伴随式(校正子)
2.再证维数为k 设cCH, 则HcT=0T. c与H的每一行矢量正交, 故c在由H的行矢量张成的n-k维线 性子空间Vn,n-k的零空间中(第2章定理17, 定理2.6.9), CH中每个码字和H张成的子 空间的矢量正交, 所以CH为H张成的子空间的零空间(第2章定理16, 定理2.6.8), 维 数为k (第2章定理18, 定理2.6.10)。
h1T h0T hn-1T hn-2T
= ei1 hi1T+ …+ei2 hi2T+…+ eit hi tT 发生错误的位所对应的列 向量的线性组合
五、线性分组码的译码2
101 | 1000 111 | 0100 例:[7,3]码, H= 110 | 0010 011 | 0001 101 | 1000 111 | 0100 110 | 0010 011 | 0001
最多可构成2n-k-1个互不相同的非零列,即必须保证 2n-k-1 n
取下限,得2n-k-1 = n,即为汉明码。
2. 汉明码
定义(定义3.3.1):GF(2)上的线性分组码[n,k,d]称为汉明码,若满足下列条件: (1) n = 2m-1 (mN,且m3); (2) k=2m-m-1 (3)n-k = m; (4) d=3。
二、线性分组码的严格数学定义2
