(完整版)线性分组码编码的分析与实现
8.2 线性分组码 线性分组码编码

◼ k位信息码用 d1,d2 ,,dk 表示
n=k+m, n:编码以后的位数 k:编码以前的位数,即 信息码 m=n-k:监督位或校验位
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
4
2. 线性分组码的编码
c1 = d1
c2 = d2
1 0 0
G=0 1 0 0 1 1
1 0 1
0 0 1 1 1 0
1 1 0
1 1 1
7
由式
,得码组矩阵为:
0 0 0 0 0 1
0 0 0 0 0 0 0 0 1 1 1 0
0 C=0
1
1 1 0
0 1
0
1 0 0
0 1 0
0 0 1
1 0 1
0 1 1
110=100
1 1 0
0 1 0
0 1 1
➢在编码前先把信息序列分为k 位一组(称为信息码), 然后附加m 位监督码,形成n = k + m 位的码组。
线性
分组
• 监督码是信息码元的 线性组合。
• 监督码仅与本码组的
信息码有关。
➢ 线性码具有封闭性,即任意两个许用码组之和(模2 加),结果仍为一许用码组。
3
1. 线性分组码的概念
➢ 线性分组码:记作 (n , k)码
第八章 差错控制编码
8.2 线性分组码
线性分组码的编码
1
引言
• 信道编码,目的是提高数字通信的可靠性
– 差错率是信噪比的函数
• 信道编码,差错控制编码,抗干扰编码
• 信道编码过程:
– 信息码元序列+监督码元→编码码组
线性分组码编码的分析与实现

吉林建筑大学电气与电子信息工程学院信息理论与编码课程设计报告设计题目:线性分组码编码的分析与实现专业班级:电子信息工程 111学生姓名:学号:指导教师:设计时间: 2014.11.24-2014.12.5 教师评语:成绩评阅教师日期第1章 概述1.1设计的作用、目的随着计算机、卫星通信及高速数据网的飞速发展,数据的交换、处理和存储技术得到了广泛的应用,人们对数据传输和存储系统的可靠性提出了越来越高的要求。
因此,如何控制差错、提高数据传输和存储的可靠性,成为现代数字通信系统设计的重要课题。
目前,绝大多数的数字计算机和数字通信系统中广泛采用二进制形式的码。
而线性分组码具有编译码简单,封闭性好等特点,采用差错控制编码技术是提高数字通信可靠性的有效方法,是目前较为流行的差错控制编码技术。
对线性分组码的讨论都在有限域GF(2)上进行,域中元素为{0,1},域中元素计算为模二加法和模二乘法。
分组码是一组固定长度的码组,可表示为(n , k),通常它用于前向纠错。
在分组码中,监督位被加到信息位之后,形成新的码。
在编码时,k个信息位被编为n位码组长度,而n-k个监督位的作用就是实现检错与纠错。
对于长度为n的二进制线性分组码,它有种2n 可能的码组,从2n 种码组中,可以选择M=2k 个码组(k<n)组成一种码。
这样,一个k比特信息的线性分组码可以映射到一个长度为n码组上,该码组是从M=2k 个码组构成的码集中选出来的,这样剩下的码组就可以对这个分组码进行检错或纠错。
1.2设计任务及要求设计一个(7,3)线性分组码的编译码程序,完成对任意序列的编码,根据生成矩阵形成监督矩阵,得到伴随式,并根据其进行译码,同时验证工作的正确性,最基本的是要具备对输入的信息码进行编码,让它具有抗干扰的能力。
1. 理解无失真信源编码的理论基础,掌握无失真信源编码的基本方法;2. 掌握哈夫曼编码/费诺编码方法的基本步骤及优缺点;3. 深刻理解信道编码的基本思想与目的,理解线性分组码的基本原理与编码过程4. 能够使用MATLAB或其他语言进行编程,编写的函数要有通用性。
线性分组码 实验报告

线性分组码实验报告《线性分组码实验报告》摘要:本实验旨在研究线性分组码在通信系统中的应用。
通过对线性分组码的理论知识进行学习和探讨,结合实际通信系统的应用场景,设计了一系列实验方案,并进行了实验验证。
实验结果表明,线性分组码在通信系统中具有较高的纠错能力和可靠性,能够有效提高数据传输的质量和稳定性。
引言:线性分组码是一种常用的纠错编码技术,广泛应用于通信系统中。
它通过在数据传输过程中添加冗余信息,以实现对传输数据的纠错和恢复。
在实际通信系统中,线性分组码可以有效提高数据传输的可靠性和稳定性,对于提高通信系统的性能具有重要意义。
因此,对线性分组码的研究和应用具有重要的理论和实际意义。
实验目的:1. 了解线性分组码的基本原理和编码、解码过程;2. 掌握线性分组码在通信系统中的应用方法;3. 验证线性分组码在通信系统中的纠错能力和可靠性。
实验方法:1. 学习线性分组码的基本原理和编码、解码过程;2. 设计实验方案,包括构建通信系统模型、选择适当的编码方式和参数等;3. 进行实验验证,对比不同编码方式和参数下的通信系统性能。
实验结果和分析:通过实验验证,我们发现线性分组码在通信系统中具有较高的纠错能力和可靠性。
在不同的编码方式和参数下,线性分组码都能有效提高通信系统的数据传输质量和稳定性。
这表明线性分组码在通信系统中具有重要的应用价值,能够有效提高通信系统的性能。
结论:线性分组码是一种有效的纠错编码技术,在通信系统中具有重要的应用价值。
通过本实验的研究和验证,我们对线性分组码的原理和应用有了更深入的理解,为通信系统的性能优化提供了重要的参考和支持。
希望本实验结果能够对相关领域的研究和应用提供有益的参考和借鉴。
线性分组码
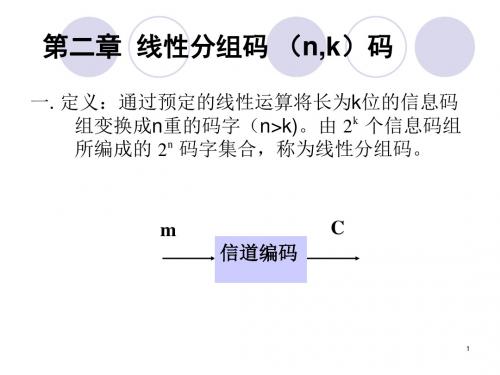
C mG
G是一个k*n阶矩阵,称为(n,k)码的生成矩阵。
7
1 0 G 0
0 0 1 0 0 1
p11 p 21 p k1
p12 p 22 pk 2
p1( n k ) p 2( nk ) I P k pk ( nk )
n 1
u和v之间的距离表示2个码字对应位不同的数目。
如(7,3)码的两个码字:u=0011101
v=0100111
它们之间的距离d=4
4
码的最小距离的dmin :在(n,k)线性码字集合中, 任意两个码字间的距离最小值,是衡量抗干扰能力的 重要参数,dmin越大,抗干扰能力越强。 码字的重量W:码字中非零码元符号的个数;在二元 线性码中,码字的重量是码字中含“1”的个数。 码的最小重量Wmin:线性分组码中,非零码字重量的 最小值,称为码的最小重量,表示为:
限, 性能界限,即码的译码错误概率的上、下 限。 对码距限而言,最重要的限是汉明限,普 洛特金限和吉尔伯特-瓦尔沙莫夫限,汉 明码和普洛特金限告诉我们,在给定码长n 和码的传输速率R=k/n下,最小距离可以达 到的最大值,故它们都是上限,而吉尔伯 特一瓦尔沙莫夫限给出了码的最小距离的 下限。
HC 0
T
T
r=n-k
H
阵是n列,(n-k)行的矩阵;
为了得到确定的码,r个监督方程必须是线性
无关的,即要求H阵的秩为r。
6
2. 生成矩阵G
把方程组写成矩阵的形式为
h11 h 21 h r1
h12 h1k h 22 h 2k h r2 h rk
m 信道编码
C
8.2 线性分组码 线性分组码编码

8.2 线性分组码
线性分组码的编码
1
引言
• 信道编码,目的是提高数字通信的可靠性
– 差错率是信噪比的函数
• 信道编码,差错控制编码,抗干扰编码
• 信道编码过程:
– 信息码元序列+监督码元→编码码组
• 信道译码过程:
– 编码码组→检错或纠错→信息码元序列
2
1. 线性分组码的概念
1 0 0
G=0 1 0 0 1 1
1 0 1
0 0 1 1 1 0
1 1 0
1 1 1
7
由式
,得码组矩阵为:
0 0 0 0 0 1
0 0 0 0 0 0 0 0 1 1 1 0
0 C=0
1
1 1 0
0 1
0
1 0 0
0 1 0
0 0 1
1 0 1
0 1 1
110=100
1 1 0
0 1 0
0 1 1
6
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
例8-1 已知(6,3)码的生成矩阵为G,试求:(1) 编码码组 和各码组的码重;(2) 最小码距 d及min其差错控制能力。
解
(1) 由3位码组成的信息码组矩阵为D:
0 0
0 0
0 1
0 1 0
1 0 0 1 0 1
0 1 1
D=
ck = dk
ck +1 ck+2
= =
h11d1 h12d2 h1k dk h21d1 h22d2 h2k dk
G生成矩阵
cn = hm1d1 hm2d2 hmk dk
5
写成矩阵形式,有 C = D G ,G为生成矩阵(k*n),且:
6.2线性分组码

线性特性:码字c的各位码元是消息m各位的线性组 合
一个( 一个(n,k)线性分组码的码字 c可以表示为 ) 可以表示为
c=mG
其中m:长度为 的消息或 的消息或k维的消息向量 其中 :长度为k的消息或 维的消息向量 Gk*n:k行n列的生成矩阵 列的生成矩阵 行 列的 矩阵运算采用模二加和模二乘。 矩阵运算采用模二加和模二乘。
1 0 1 1 0 1 0 1 1 0 0 0 1 1 1 G = 0 1 0 1 1 R2 + R3 → R3 →0 1 0 1 1 R1 + R3 → R1 → 0 1 0 1 1 1 1 0 1 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 R1 ← → R 3 →0 1 0 1 1 = G S 0 0 1 1 1
线性分组码的性质
(1)零向量一定是一个码字,记作 θ = (0,0,L ,0) )零向量一定是一个码字, (2)任意两码字的和仍是一个码字。 )任意两码字的和仍是一个码字。 都可以表示为G的行向量的线性组合 (3)任意码字 都可以表示为 的行向量的线性组合。 )任意码字c都可以表示为 的行向量的线性组合。
G的行向量是码集合中的码字(它们线性无关) 的行向量是码集合中的码字(它们线性无关) 的行向量是码集合中的码字
(4)线性分组码的最小距离等于最小非 码的码重: 码的码重: )线性分组码的最小距离等于最小非0码的码重 码重:码字中的非0符号个数。
d min = min w(c)
c ≠θ
例:c = (0101) d = w(c)
系统码。 (1)则该码称为系统码。 )则该码称为系统码
容易发现,若系统线性分组码的生成矩阵G 的左(右) 半部分是Ik*K的单位阵,则线性分组码的前(后)k位是 信息位,后n-k位是校验位。 若不是系统码,则可以通过简单行变换得到系统码生成 矩阵。
信息论基础——线性分组码
17
线性分组码的基本概念
信息位 00 01 10 11 x2 x0 x1 00000 x3 x0 x x x 01101 0 1 4 码字 10111 11010
信息位k=2 码字数M=4
可见,码字的三个校验元都由其前两位线 性组合得到,即可由的线性方程组求得;
18
线性分组码的基本概念
f1 : GF (2) 2 GF (2)5
信息位 00 01 10 11 码字 00000 01101 10111 11010
1 ( 0 1 ) 1 ( 1 0 ) 1 1
f( 1 1 ) 1 1 0 1 0
1 ( 0 1 1 0 1 )1 ( 1 0 1 1 1 ) 1 1 0 1 0
30
线性分组码的基本概念
汉明距离: 指(n,k)分组码中两个码字xn 、 yn对应位取 值不同的个数;记为d(xn , yn).
5 5 ( 1 0 1 0 1 ) , y ( 0 1 1 1 1 ) 例: x
d(x ,y ) 3
5 5
31
线性分组码的基本概念
线性分组码的最小距离: 称(n,k)分组码中任两个码字汉明距离的最小 值,为该分组码的最小距离d.
f ( 1 ( 0 1 ) 1 ( 1 0 ) ) 1 ( 0 1 1 0 1 ) 1 ( 1 0 1 1 1 ) 线性编码
19
线性分组码的基本概念
例题1: 下面是某个(n,k)线性二元码的全部码字
x16=000000 x26=100011 x36=010101 x46=001111 x56=110110 x66=101100 x76=011010 x86=111001 求n、k的值;
线性分组码实验报告

线性分组码实验报告综合性设计性实验报告专业:学号:姓名:实验所属课程:信息论与编码实验室(中心):信息技术软件实验室指导教师:2一、题目线性分组码编译码实验二、仿真要求1.分别用不同的生成矩阵进行(7,4)线性分组码的编码,经调制解调后译码,并比较两种线性分组码的纠错能力。
2.掌握线性分组码的编码原理、编码步骤和译码方法。
3.熟悉matlab软件的基本操作,学会用matlab软件进行线性分组码的编码和译码。
三、仿真方案详细设计编码:本实验采用的是(7,4)线性分组码,线性分组码的编码由监督矩阵和生成矩阵实现,监督矩阵H为(3×4)的矩阵,由监督方程和(4×4)的单位矩阵构成,生成矩阵G为(4×7)的矩阵,由(4×4)的单位矩阵和监督矩阵的转置矩阵构成。
实现过程为:1、将要编码的序列先整形,整为4列2、如果序列不能被4整除在后边补0使其能被4整除3、将整形后的序列与生成矩阵G相乘即得到编码后的码字在本实验中,分别生成两种生成矩阵,在产生了生成矩阵后根据输入的四位信息位和生成矩阵相乘即可得到编码矩阵。
译码:在译码过程中,我们利用错误图样和伴随式来进行纠错。
1、设一个接收码字矩阵为R,R*H'=S(模2乘),则S为码字对应的伴随式矩阵如果S=0则说明接受码字无差错;2、如果S不为0,查看矩阵S中不为0的那行所在行数,该行即收码字错误所在行i;3、将S转置,将不为0的一列与H每一列进行比较,找到H中相同列,该列的列数即为错误所在列;4、由步骤2和3得到错误具体位置,模2加对应的错误图样就可得到正确码字。
BPSK调制:BPSK调制利用载波的相位变化来传递数字信息,振幅和频率保持不变。
双极性的全占空矩形脉冲序列与正弦载波相乘就得到调制信号。
因此进行调制时首先进行码形变换变为双极性的,再经乘法器与载波相乘得到调制信号。
其具体实现方法如下:1、将0、1序列变为-1、1序列;2、将序列与载波相乘,为‘1’时与载波相位相同,为‘-1’时与载波相位相反。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计任务书2011—2012学年第一学期专业:通信工程学号:080110501 姓名:李琼课程设计名称:信息论与编码课程设计设计题目:线性分组码编码的分析与实现完成期限:自2011 年12 月19 日至2011 年12 月25 日共 1 周一.设计目的1、深刻理解信道编码的基本思想与目的;2、理解线性分组码的基本原理与编码过程;3、提高综合运用所学理论知识独立分析和解决问题的能力;4、使用MATLAB或其他语言进行编程。
二.设计内容给定消息组M及生成矩阵G,编程求解其线性分组码码字。
三.设计要求编写的函数要有通用性。
四.设计条件计算机、MATLAB或其他语言环境五.参考资料[1]曹雪虹,张宗橙.信息论与编码.北京:清华大学出版社,2007.[2]王慧琴.数字图像处理.北京:北京邮电大学出版社,2007.指导教师(签字):教研室主任(签字):批准日期:年月日该系统是(6,3)线性分组码的编码的实现,它可以对输入的三位的信息码进行线性分组码编码。
当接收到的六位码字中有一位发生错误时,可以纠正这一位错码;当接收到的码字有两位发生错误时,只能纠正一位错误,但同时能检测出另一位错误不能纠正。
只有特定位有两位错误时,才能纠正两位错误。
这样就译出正确的信息码组,整个过程是用MATLAB语言实现的。
关键词:编码;MA TLAB;纠错1课程描述 02 设计原理 (1)2.1 线性分组码的编码 (1)2.1.1 生成矩阵 (1)2.1.2 校验矩阵 (3)2.2 伴随式与译码 (4)2.2.1 码的距离及纠检错能力 (4)2.2.2 伴随式与译码 (4)3 设计过程 (5)3.1 编码过程 (5)3.2 仿真程序 (7)3.4 结果分析 (11)总结 (13)致谢 (14)参考文献 (15)1课程描述线性分组码具有编译码简单,封闭性好等特点,采用差错控制编码技术是提高数字通信可靠性的有效方法,是目前较为流行的差错控制编码技术。
对线性分组码的讨论都在有限域GF(2)上进行,域中元素为{0,1},域中元素计算为模二加法和模二乘法。
分组码是一组固定长度的码组,可表示为(n , k ),通常它用于前向纠错。
在分组码中,监督位被加到信息位之后,形成新的码。
在编码时,k 个信息位被编为n 位码组长度,而n-k 个监督位的作用就是实现检错与纠错。
对于长度为n 的二进制线性分组码,它有种2n 可能的码组,从2n 种码组中,可以选择M=2k 个码组(k<n )组成一种码。
这样,一个k 比特信息的线性分组码可以映射到一个长度为n 码组上,该码组是从M=2k 个码组构成的码集中选出来的,这样剩下的码组就可以对这个分组码进行检错或纠错。
要设计一个(6,3)线性分组码的编译码程序,最基本的是要具备对输入的信息码进行编码,让它具有抗干扰的能力。
同时,还要让它具有对接收到的整个码组中提取信息码组的功能。
但是,在实际的通信系统中,由于信道传输特性不理想以及加性噪声的影响,接收到的信息中不可避免地会发生错误,影响通信系统的传输可靠性,因而,本设计还要让该程序具有纠正错误的能力,当接收到的码组中有一位码,发生错误时可以检测到这一位错码,并且可以纠正这一位错码,并且让系统从纠正后的码组中提取正确的信息码组。
针对给定的矩阵Q=完成如下的工作:1 完成对任意信息序列的编码2 根据生成矩阵,形成监督矩阵;3 根据得到的监督矩阵,得到伴随式,并根据它进行译码;4 验证工作的正确性。
2 设计原理2.1 线性分组码的编码2.1.1 生成矩阵线性分组码(n,k)中许用码字(组)为2k个。
定义线性分组码的加法为模二加法,乘法为二进制乘法。
即1+1=0、1+0=1、0+1=1、0+0=0;1×1=1、1×0=0、0×0=0、0×1=0。
且码字与码字的运算在各个相应比特位上符合上述二进制加法运算规则。
线性分组码具有如下性质(n,k)的性质:1、封闭性。
任意两个码组的和还是许用的码组。
2、码的最小距离等于非零码的最小码重。
对于码组长度为n、信息码元为k位、监督码元为r=n-k位的分组码,常记作(n,k)码,如果满足2r-1≥n,则有可能构造出纠正一位或一位以上错误的线性码。
下面我们通过(7,3)分组码的例子来说明如何具体构造这种线性码。
设分组码(n,k)中,k = 3,为能纠正一位误码,要求r≥3。
现取r=4,则n=k+r =7。
该例子中,信息组为(c6c5c4),码字为(c6c5c4c3c2c1c0).当已知信息组时,按以下规则得到四个校验元,即c3=c6+c4c2=c6+c5+c4 (2-1)c1=c6+c5c0=c5+c4这组方程称为校验方程。
(7,3)线性分组码有23(8)个许用码字或合法码字,另有27-23个禁用码字。
发送方发送的是许用码字,若接收方收到的是禁用码字,则说明传输中发生了错误。
为了深化对线性分组码的理论分析,可将其与线性空间联系起来。
由于每个码字都是一个二进制的n重,及二进制n维线性空间Vn中的一个矢量,因此码字又称为码矢。
线性分组码的一个重要参数是码率r=k/n,它说明在一个码字中信息位所占的比重,r 越大,说明信息位所占比重越大,码的传输信息的有效性越高。
由于(n,k)线性分组,线性分组码的2k 个码字组成了n 维线性空间Vn 的一个K 维子空间。
因此这2k 个码字完全可由k 个线性无关的矢量所组成。
设此k 个矢量为c 1,c 2,…,c k ,有生成矩阵形式为(2-2)(n,k)码字中的任一码字c i ,均可由这组基底的线性组合生成,即 c i =m i ·G=[m n-1 m n-2 … m n-k ]·G式中,mi =[m n-1 m n-2 …m n-k ]是k 个信息元组成的信息组。
表2-1 (7,3)线性分组码对于表2-1给出的(7,3)线性分组码,可将写成矩阵形式[c 6 c 5 c 4 c 3 c 2 c 1 c 0]=[c 6 c 5 c 4]·101110011100100111001故(7,3)码的生成矩阵为G= 101110011100100111001可以看到,从(7,3)码的8个码字中,挑选出k=3个线性无关的码字(1001110)(0100111),(00111101)作为码的一组基底,用c=m ·G 计算得码字。
一个系统码的生成矩阵G ,其左边k 行k 列应是一个k 阶单位方阵I k ,因此生成矩阵G 表示为G=[I k P] (2-3) 式中,P 是一个k ×(n-k)阶矩阵。
2.1.2 校验矩阵表2-1所示的(7,3)线性分组码的四个校验元由式(2-1)所示的线性方程组决定的。
把(2-1)移相,有c6+c4+c3=0c6+c5+c4+c2=0 c6+c1+c5=0 (2-4) c5+c4+c0=0上式的矩阵形式为1000110110001100101110001101 · 0123456c c c c c c c =000这里的四行七列矩阵称为(7,3)码的一致校验矩阵,用H 表示,即1000110110001100101110001101H= (2-5)由H 矩阵得到(n,k)线性分组码的每一码字c i,(i=1,2,…,2k ),都必须满足由H 矩阵各行所确定的线性方程组,即 c i ·H T =0.(7,3)码的生成矩阵G 中每一行及其线性组合都是(n,k )码的码字,所以有G ·H T =0。
由G 和H 构成的行生成的空间互为零空间,即G 和H 彼此正交。
H=[P T I r ]其右边r 行r 列组成一个单位方阵。
2.2 伴随式与译码2.2.1 码的距离及纠检错能力 1.码的距离两个码字之间,对应位取之不同的个数,称为汉明距离,用d 表示。
一个吗的最小距离d min 定义为d min =min{d(c i ,c j ),i ≠j,c i ,c j ∈(n,k)},两个码字之间的距离表示了它们之间差别的大小。
距离越大,两个码字的差别越大,则传送时从一个码字错成另一码字的可能性越小。
码的最小距离愈大,其抗干扰能力愈强。
2. 线性码的纠检错能力对于任一个(n,k )线性分组码,若要在码字内(1) 检测出e 个错误,则要求码的最小距离d ≥e+1;(2) 纠正t 个错误,则要求码的最小距离d ≥2t+1;(3)纠正t 个错误同时检测e(≥t)个错误,则要求 d ≥t+e+1; 2.2.2 伴随式与译码假设接收端收到的码字为B ,那么它和原来发送端发送的码字A 之间就有可能存在着误差。
即在码组A={a 6 a 5 a 4 a 3 a 2 a 1 a 0 }中的任意一位就有可能出错。
这样我们在接收端接收到一个码组是就有可能判断错发送端原来应该要表达的意思。
为了描述数据在传输信道中出现错误的情况,引入了错误图样E ,在错误图样中,0代表对应位没有传错,1代表传输错误。
实际上错误图样E就是收序列与发送序列的差。
所以在译码中用接收到的码字B模尔加错误图样E就可以得到发送端的正确码字A。
因此译码的过程就是要找到错误图样E。
定义:校正子SS = B * H T= ( A + E ) * H T= A * H T+ E * H T= E * H T因为A是编得的正确码字。
根据前面所叙述,它和监督矩阵的转置相乘为0。
显然,S仅与错误图样有关,它们之间是一一对应的关系。
找到了校正子S,也就可以找到E。
而与发送的码字无关。
若E=0,则S=0;因此根据S是否为0可进行码字的检错。
如果接收码字B中只有一位码元发生错误,又设错误在第i位。
即E i-1=1,其他的E i均为0。
在后面的译码程序中,建立了一个校正子S与错误图样E对应的表。
也就是收到一个B序列,就可以通过计算得到一个校正子,而每一个校正子都对应着一个错误图样E,再通过B模尔加上E,就可以得到正确的码字A。
因为在不同的错误序列B中,同一位码元错误时对应的E是一样的,所以可以利用0000000这个正确的码字让它每位依次错误,来求得它的八个校正子。
而这时的矩阵B就是错误图样E。
这样就算得了8个校正子S。
而这时的错误序列B,就是错误图样E,所以有:E与S都已经得到,这时就可以建立一个表来将它们一一对应起来。
3 设计过程3.1 编码过程监督矩阵H与生成矩阵G的关系:由H与G的分块表示的矩阵形式H =[P In-kG=[IkP=Q T则有G ·H T =0 (3-4) 或 H ·G T =0 (3-5) 已知给出的(6,3)码的Q 矩阵(3-6)则可以根据G=[I k Q]求出生成矩阵(3-7)由 P=Q T 和 H =[P I n-k ] 即 MATLAB 函数为:C=rem(I*G ,2); (3-8)其中C 为编码后的结果,I 为信息矩阵,G 为生成矩阵。
