(北京专用)2018年高考数学总复习专题13算法分项练习理!
2016-2018年高考数学分类汇编:专题13极坐标与参数方程 学生版

目录全国1 (2)全国2 (3)全国3 (4)北京 (5)天津 (5)上海 (6)浙江............................................................................................................错误!未定义书签。
江苏 (6)全国1【2018全国1卷理22文22】在直角坐标系xOy 中,曲线C 1的方程为2+=x k y .以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为03cos 22=-+θρρ.(1)求C 2的直角坐标方程;(2)若C 1与C 2有且仅有三个公共点,求C 1的方程.【2017全国1卷理22文22】在直角坐标系xOy 中,曲线C 的参数方程为3cos sin x y θθ=⎧⎨=⎩,(θ为参数),直线l 的参数方程为41x a ty t=+⎧⎨=-⎩(t 为参数).(1)若1-=a ,求C 与l 的交点坐标; (2)若C 上的点到l a .【2016全国1卷理22文22】在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎨⎧+==ta y t a x sin 1cos (t 为参数,0>a )。
在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:θρcos 4=.(I )说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程;(II )直线C 3的极坐标方程为0a =θ,其中0a 满足2tan 0=a ,若曲线C 1与C 2的公共点都在C 3上,求a 。
全国21、【2018全国2卷理22】在直角坐标系xOy 中,曲线C 的参数方程为{x =2cosθy =4sinθ(θ为参数),直线l 的参数方程为{x =1+tcosαy =2+tsinα(t 为参数)(1)求C 和l 的直角坐标方程;(2)若曲线C 截直线l 所得线段的中点坐标为(1,2),求l 的斜率。
2018年北京高考卷数学(理科)试题附详细标准答案

2018年北京高考卷数学(理科)试题附详细标准答案一、选择题(本大题共8小题,每小题5分,共40分)1. 设集合A={x|2<x<3},集合B={x|x²3x+2=0},则A∩B=()A. {1}B. {2}C. {1, 2}D. ∅2. 若复数z满足|z|=1,则|z1|的最大值为()A. 0B. 1C. √2D. 23. 在等差数列{an}中,若a1=3,a3+a5=18,则数列的前5项和为()A. 25B. 35C. 45D. 554. 已知函数f(x)=x²+2ax+a²+2(a为常数),若f(x)在区间(∞,1)上单调递减,则a的取值范围为()A. a≤0C. a≤1D. a≥15. 设平面直角坐标系xOy中,点A(2,3),点B在直线y=3上,则线段AB的中点轨迹方程为()A. y=3B. x=2C. y=3xD. x=3y6. 若sinθ+cosθ=1/2,则sinθ·cosθ的值为()A. 3/4B. 1/4C. 1/4D. 3/47. 在三角形ABC中,a=3,b=4,cosB=3/5,则三角形ABC的面积为()A. 2√6B. 3√6C. 4√6D. 5√68. 设函数f(x)=x²2ax+a²+1(a为常数),若f(x)在区间[1,+∞)上单调递增,则a的取值范围为()A. a≤1B. a≥1D. a≥0二、填空题(本大题共6小题,每小题5分,共30分)9. 已知数列{an}是等差数列,若a1=1,a3+a5=10,则a4的值为______。
10. 若复数z满足|z|=1,则|z1|+|z+1|的最大值为______。
11. 在等比数列{bn}中,b1=2,b3=16,则数列的公比为______。
12. 已知函数f(x)=x²+2x+a(a为常数),若f(x)在区间(∞,1)上单调递减,则a的取值范围为______。
(新课标Ⅱ)2018年高考数学总复习专题13算法分项练习(含解析)理
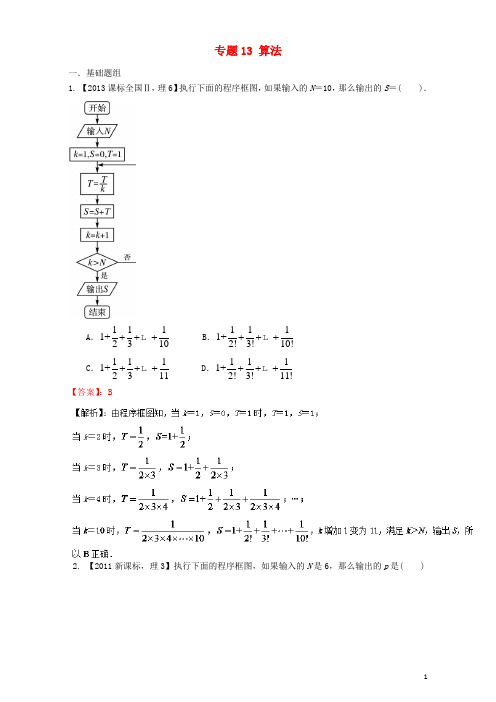
专题13 算法一.基础题组1. 【2013课标全国Ⅱ,理6】执行下面的程序框图,如果输入的N =10,那么输出的S =( ).A .1111+2310+++B .1111+2!3!10!+++C .1111+2311+++D .1111+2!3!11!+++ 【答案】:B2. 【2011新课标,理3】执行下面的程序框图,如果输入的N 是6,那么输出的p 是( )A.120B.720C.1 440D.5 040【答案】B【解析】3. 【2016高考新课标2理数】中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的为2,2,5,则输出的s =(A)7(B)12(C)17(D)34【答案】C【考点】程序框图,直到型循环结构【名师点睛】直到型循环结构:在执行了一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.当型循环结构:在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.二.能力题组1. 【2014新课标,理7】执行右图程序框图,如果输入的x,t均为2,则输出的S= ()A. 4B. 5C. 6D. 7【答案】D2. 【2015高考新课标2,理8】右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入,a b 分别为14,18,则输出的a =( )A .0B .2C .4D .14 【答案】B【解析】程序在执行过程中,,的值依次为14a =,18b =;4b =;10a =;6a =;2a =;2b =,此时2a b ==程序结束,输出的值为2,故选B .【考点定位】程序框图.3. 【2017课标II ,理8】执行右面的程序框图,如果输入的1a =-,则输出的S =A .2B .3C .4D .5【答案】B【考点】程序框图【名师点睛】识别、运行程序框图和完善程序框图的思路:①要明确程序框图的顺序结构、条件结构和循环结构;②要识别、运行程序框图,理解框图所解决的实际问题;③按照题目的要求完成解答并验证.。
高考数学总复习考点知识专题讲解13 二项分布与超几何分布

高考数学总复习考点知识专题讲解 专题13 二项分布与超几何分布知识点一 n 重伯努利试验及其特征 1.n 重伯努利试验的概念将一个伯努利试验独立地重复进行n 次所组成的随机试验称为n 重伯努利试验. 2.n 重伯努利试验的共同特征 (1)同一个伯努利试验重复做n 次. (2)各次试验的结果相互独立.思考在相同条件下,有放回地抽样试验是n 重伯努利试验吗? 答案 是.其满足n 重伯努利试验的共同特征. 知识点二 二项分布一般地,在n 重伯努利试验中,设每次试验中事件A 发生的概率为p (0<p <1),用X 表示事件A 发生的次数,则X 的分布列为P (X =k )=C k n p k (1-p )n -k,k =0,1,2,…,n . 称随机变量X 服从二项分布,记作X ~B (n ,p ). 知识点三 二项分布的均值与方差若X ~B (n ,p ),则E (X )=np ,D (X )=np (1-p ).【例1】(2023•大埔县月考)设随机变量~(,)B n p ξ,若() 2.4E ξ=,() 1.44D ξ=,则参数n ,p 的值分别为()A .12,0.4B .12,0.6C .6,0.4D .6,0.6【例2】(2023•永春县月考)设随机变量~(2,)B p ξ,~(3,)B p η,5(1)9P ξ=…,则(2)(P η=…)A .19B .727C .59D .89【例3】(2023•海门市期末)A 、B 两组各3人独立的破译某密码,A 组每个人译出该密码的概率均为1p ,B 组每个人译出该密码的概率均为2p ,记A 、B 两组中译出密码的人数分别为X 、Y ,且12112p p <<<,则()A .()()E X E Y <,()()D X D Y <B .()()E X E Y <,()()D X D Y >C .()()E X E Y >,()()D X D Y < D .()()E X E Y >,()()D X D Y >【例4】(2018•新课标Ⅲ)某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立.设X 为该群体的10位成员中使用移动支付的人数,() 2.4D X =,(4)(6)P X P X =<=,则(p =)A .0.7B .0.6C .0.4D .0.3【例5】(2023•多选•琼中县模拟)若袋子中有2个白球,3个黑球,现从袋子中有放回地随机取球4次,每次取一个球,取到白球记1分,取到黑球记0分,记4次取球的总分数为X ,则()A .3~(4,)5X B B .4(3)25P X ==C .X 的期望8()5E X =D .X 的方差24()25D X =【例6】(2023•武汉模拟)已知离散型随机变量X 服从二项分布(,)B n p ,其中*n N ∈,01p <<,记X 为奇数的概率为a ,X 为偶数的概率为b ,则下列说法中正确的有()A .1a b +=B .12p =时,a b =C .102p <<时,a 随着n 的增大而增大 D .112p <<时,a 随着n 的增大而减小知识点四 超几何分布1.定义:一般地,假设一批产品共有N 件,其中有M 件次品,从N 件产品中随机抽取n 件(不放回),用X 表示抽取的n 件产品中的次品数,则X 的分布列为P (X =k )=C k M C n -k N -MC n N,k =m ,m +1,m +2,…,r .其中n ,N ,M ∈N *,M ≤N ,n ≤N ,m =max{0,n -N +M },r =min{n ,M }. 如果随机变量X 的分布列具有上式的形式,那么称随机变量X 服从超几何分布. 2.均值:E (X )=nM N. 3.超几何分布是不放回抽样,且超几何分布与二项分布的均值相同. 二项分布与超几何分布的关系在n 次试验中,某事件A 发生的次数X 可能服从超几何分布或二项分布.l 联系:在不放回n 次试验中,如果总体数量N 很大,而试验次数n 很小,此时超几何分布可近似转化成二项分布区别:①当这n 次试验是n 重伯努利试验时(如有放回摸球),X 服从二项分布;②当n 次试验不是n 重伯努利试验时(如不放回摸球),X 服从超几何分布。
最新-2018年高考数学总复习 18-6数学归纳法课后作业

【走向高考】2018年高考数学总复习 12-6数学归纳法(理)课后作业北师大版一、选择题1.若命题p(n)对n=k成立,则它对n=k+2也成立,又已知命题p(1)成立,则下列结论正确的是( )A.p(n)对所有自然数n都成立B.p(n)对所有正偶数n成立C.p(n)对所有正奇数n都成立D.p(n)对所有大于1的自然数n成立[答案] C2.下列代数式(其中k∈N+)能被9整除的是( )A.6+6·7k B.2+7k-1C.2(2+7k+1) D.3(2+7k)[答案] D[解析]对于选项D3(2+7k),(1)当k=1时,显然只有3(2+7k)能被9整除.(2)假设当k=n时,命题成立,即3(2+7n)能被9整除,那么3(2+7n+1)=21(2+7n)-36.这就是说,k=n+1时命题也成立.由(1)(2)可知,命题对任何k∈N+都成立.3.用数学归纳法证明“1+2+…+n+…+2+1=n2(n∈N+)”,从n=k到n=k+1时,左边添加的代数式为( )A.k+1 B.k+2C.k+1+k D.2(k+1)[答案] C[解析]在由n=k到n=k+1时,左边式子为1+2+3+…+k+k+1+k+…+2+1,因此,左边添加的式子为k+1+k.4.在用数学归纳法证明多边形内角和定理时,第一步应验证( )A.n=1成立B.n=2成立C.n=3成立D.n=4成立[答案] C[解析]凸n边形的内角和为(n-2)π,最少边的凸n边形为三角形,所以应验证n =3时成立.5.某学生在证明等差数列前n项和公式时,证法如下:(1)当n=1时,S1=a1显然成立.(2)假设n=k时,公式成立,即S k=ka1+-2d.当n=k+1时,S k+1=a1+a2+…+a k+a k+1=a1+(a1+d)+(a1+2d)+…+a1+(k-1)k+a1+kd =(k+1)a1+(d+2d+…+kd)=(k+1)a1+k k+12d=(k+1)a1+k+1[k+1-1]2d.∴n=k+1时公式成立.∴由(1)(2)知,对n∈N+,公式都成立.以上证明错误的原因是( )A.当n取第一个值1时,证明不对B.归纳假设的写法不对C.从n=k到n=k+1的推理中未用归纳假设D.从n=k到n=k+1的推理有错误[答案] C[解析]由数学归纳法的原理易知选C.6.用数学归纳法证明“当n为正奇数时,x n+y n能被x+y整除”,第二步归纳假设应该写成( )A.假设当n=k(k∈N+)时,x n+y n能被x+y整除B.假设当n=2k(k∈N+)时,x n+y n能被x+y整除C.假设当n=2k+1(k∈N+)时,x n+y n能被x+y整除D.假设当n=2k-1(k∈N+)时,x n+y n能被x+y整除[答案] D[解析]①显然,当n=1时,命题成立,即x1+y1能被x+y整除②假设当n=2k-1(k∈N+)时命题成立,即(x+y)能整除x2k-1+y2k-1则当n=2k+1时,x2k+1+y2k+1=x2x2k-1+x2y2k-1-x2y2k-1+y2y2k-1=x2(x2k-1+y2k-1)-(x+y)(x-y)y2k-1∵x+y能整除(x2k-1+y2k-1)又x+y能整除(x+y)(x-y)y2k-1∴(x+y)能整除(x2k+1+y2k+1)由(1)(2)可知当n为正奇数时x n+y n能被x+y整除.二、填空题7.用数学归纳法证明(n+1)(n+2)…(n+n)=2n×1×3×…×(2n-1)(n∈N+)时,从k到k+1,左边需要增加的代数式为________.[答案]2(2k+1)[解析]当n=k时左边的最后一项是2k,n=k+1时左边的最后一项是2k+2,而左边各项都是连续的,所以n=k+1时比n=k时左边少了(k+1),而多了(2k+1)(2k+2).因此增加的代数式是++k+1=2(2k+1).8.(改编题)用数学归纳法证明“n3+5n能被6整除”的过程中,当n=k+1时,对式子(k+1)3+5(k+1)应变形为:________.[答案](k3+5k)+3k(k+1)+6[解析]首先必须应用归纳假设,然后采用配凑法.三、解答题9.证明凸n边形的对角线的条数为f(n)=12n(n-3)(n≥4).[证明]①n=4时,f(4)=12×4×(4-3)=2.四边形有两条对角线,命题成立.②假设n=k时命题成立,即凸k边形的对角线的条数f(k)=12k(k-3)(k≥4),当n=k+1时凸k+1边形是在k边形基础上增加了一边,增加了一个顶点A k+1,增加的对角线条数是顶点A k+1与不相邻顶点连线再加上原k边形的一边A1A k,共增加了对角线条数(k+1-3)+1=k-1,f(k+1)=12k(k-3)+k-1=12(k2-k-2)=12(k+1)(k-2)=12(k+1)[(k+1)-3].故n=k+1时,命题成立,由①,②可知,对于n≥4,n∈N+命题成立.一、选择题1.用数学归纳法证明1+2+3+…+n2=n4+n22,则当n=k+1时左端应在n=k的基础上加上( )A.k2+1B.(k+1)2C.+4++22D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2[答案] D[解析]∵当n=k时,左侧=1+2+3+…+k2,当n=k+1时,左侧=1+2+3+…+k2+(k2+1)+…+(k+1)2,∴当n=k+1时,左端应在n=k的基础上加上(k2+1)+(k2+2)+(k2+3)+…+(k+1)2.2.在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是1颗珠宝,第二件首饰由6颗珠宝(图中圆圈表示珠宝)构成如图1所示的正六边形,第三件首饰由15颗珠宝构成如图2所示的正六边形,第四件首饰是由28颗珠宝构成如图3所示的正六边形,第五件首饰是由45颗珠宝构成如图4所示的正六边形,以后每件首饰都在前一件上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断前10件首饰所用珠宝总颗数为( )A .190B .715C .725D .385[答案] B[解析] 由条件可知前5件首饰的珠宝数依次为:1,1+5,1+5+9,1+5+9+13,1+5+9+13+17,即每件首饰的珠宝数为一个以1为首项,4为公差的等差数列的前n 项和,通项a n =4n -3.由此可归纳出第n 件首饰的珠宝数为n[1+-2=2n 2-n.则前n 件首饰所用的珠宝总数为2(12+22+…+n 2)-(1+2+…+n)=4n 3+3n 2-n 6.当n =10时,总数为715.二、填空题3.数列{a n }中,已知a 1=2,a n +1=a n3a n +1(n∈N +),依次计算出a 2,a 3,a 4后,归纳、猜测得出a n 的表达式为________.[答案] a n =26n -5[解析] a 1=2,a 2=27,a 3=213,a 4=219,猜测a n =26n -5. 4.(2018·青岛二模)利用数学归纳法证明不等式1+12+13+…+12n -1<f (n)(n≥2,n∈N +)的过程,由n =k 到n =k +1时,左边增加了________项.[答案] 2k[解析] 当n =k 时为1+12+13+…+12k -1,当n =k +1时为1+12+…+12k -1+12k +…+12·2k-1, 所以从n =k 到n =k +1增加了2k项.三、解答题5.数列{a n }满足a 1=1且a n +1=⎝ ⎛⎭⎪⎫1+1n 2+n a n +12n (n≥1).用数学归纳法证明:a n ≥2(n≥2).[解析] 证明:(1)①当n =1时,a 2=2≥2,不等式成立.②假设当n =k(k≥2)时不等式成立,即a k ≥2(k≥2),那么,当n =k +1时,a k +1=(1+1+)a k +12k ≥(1+1+)×2+12k=2+2++12k >2, 这就是说,当n =k +1时不等式成立.根据①②可知a n ≥2对所有n≥2成立.6.(2018·江苏卷)已知△ABC 的三边长都为有理数(1)求证:cosA 是有理数;(2)对任意正整数n ,求证cosnA 是有理数.[解析] 本题主要考查余弦定理、数学归纳法等础知识,考查推理论证的能力与分析问题、解决问题的能力.解:(1)由AB 、BC 、AC 为有理数及余弦定理知cosA =AB 2+AC 2-BC22AB·AC是有理数.(2)用数学归纳法证明cosnA和sinA·sinnA都是有理数.①当n=1时,由(1)知cosA是有理数,从而有sinA·sinA=1-cos2A也是有理数.②假设当n=k(k≥1)时,coskA和sinA·sinkA都是有理数.当n=k+1时,由cos(k+1)A=cosA·coskA-sinA·sinkA,sinA·sin(k+1)A=sinA·(sinA·coskA+cosA·sinkA)=(sinA·sinA)·coskA+(sinA·sinkA)·cosA,及①和归纳假设,知cos(k+1)A与sinA·sin(k+1)A都是有理数.即当n=k+1时,结论成立.综合①、②可知,对任意正整数n,cosnA是有理数.7.在数列{a n}、{b n}中,a1=2,b1=4,且a n,b n,a n+1成等差数列,b n,a n+1,b n+1成等比数列(n∈N+).(1)求a2,a3,a4及b2,b3,b4,由此猜测{a n}、{b n}的通项公式,并证明你的结论;(2)证明:1a1+b1+1a2+b2+…+1a n+b n<512.[解析]考查等差数列、等比数列、数学归纳法、不等式等基础知识,考查综合运用数学知识进行归纳、总结、推理、论证的能力.(1)由条件得2b n=a n+a n+1,a2n+1=b n b n+1,由此可得a2=6,b2=9,a3=12,b3=16,a4=20,b4=25.猜测a n=n(n+1),b n=(n+1)2.用数学归纳法证明:①当n=1时,由上可得结论成立.②假设当n=k时,结论成立,即a k=k(k+1),b k=(k+1)2,那么当n=k+1时,a k+1=2b k-a k=2(k+1)2-k(k+1)=(k+1)(k+2),b k+1=a2k+1b k=(k+2)2,∴当n=k+1时,结论也成立.由①②可知,a n=n(n+1),b n=(n+1)2对一切正整数都成立.(2)1a1+b1=16<512,n≥2时,由①知a n+b n=(n+1)(2n+1)>2(n+1)n,故1a1+b1+1a2+b2+…+1a n+b n<16+12[12×3+13×4+…+1+]=16+12[(12-13)+(13-14)+…+(1n-1n+1)]=16+12(12-1n+1)<16+14=512.综上,原不等式成立.。
五年(2018-22)全国高考数学真题分类汇编(全国卷新高考卷卷等)专题13 计数原理(解析版)

12.(2020年浙江省高考数学试卷·第12题)设 ,则a5=________;a1+a2+a3=________.
【答案】(1).80(2).122
解析: 的通项为 ,令 ,则 , ;
【题目栏目】计数原理\二项式定理\二项展开式通项公式的应用
【题目来源】2020年浙江省高考数学试卷·第12题
2018-2022五年全国各省份高考数学真题分类汇编
专题13计数原理
一、选择题
1.(2022高考北京卷·第8题)若 ,则 ( )
A.40B.41C. D.
【答案】B
解析:令 ,则 ,
令 ,则 ,
故 ,
故选,B.
【题目栏目】计数原理\二项式定理\二项展开式通项公式的应用
【题目来源】2022高考北京卷·第8题
13.(2020天津高考·第11题)在 的展开式中, 的系数是_________.
【答案】【答案】10【解析】因为 的展开式的通项公式为 ,令 ,解得 .所以 的系数为 .故答案为: .
【题目栏目】计数原理\二项式定理\二项展开式通项公式的应用
【题目来源】2020天津高考·第11题
14.(2019年高考浙江文理·第13题)在二项式 的展开式中,常数项是,系数为有理数的项的个数是.
A.5B.8C.10D.15
【答案】C
【解析】根据题意可知,原位大三和弦满足: .
∴ ; ; ; ; .
原位小三和弦满足: .
∴ ; ; ; ; .
故个数之和为10.
故选:C.
【点睛】本题主要考查列举法的应用,以及对新定义的理解和应用,属于基础题.
【题目栏目】计数原理\分类加法计数原理的应用
2018年北京市高考数学试卷(理科)解析
2018年北京市高考数学试卷(理科)参考答案与试题解析一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知集合A={x||x|<2},B={﹣2,0,1,2},则A∩B=()A.{0,1} B.{﹣1,0,1} C.{﹣2,0,1,2}D.{﹣1,0,1,2}【分析】根据集合的基本运算进行计算即可.【解答】解:A={x||x|<2}={x|﹣2<x<2},B={﹣2,0,1,2},则A∩B={0,1},故选:A.【点评】本题主要考查集合的基本运算,根据集合交集的定义是解决本题的关键.比较基础.2.(5分)在复平面内,复数的共轭复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【分析】利用复数的除法运算法则,化简求解即可.【解答】解:复数==,共轭复数对应点的坐标(,﹣)在第四象限.故选:D.【点评】本题考查复数的代数形式的乘除运算,复数的几何意义,是基本知识的考查.3.(5分)执行如图所示的程序框图,输出的s值为()A.B.C.D.【分析】直接利用程序框图的应用求出结果.【解答】解:执行循环前:k=1,S=1.在执行第一次循环时,S=1﹣=.由于k=2≤3,所以执行下一次循环.S=,k=3,直接输出S=,故选:B.【点评】本题考查的知识要点:程序框图和循环结构的应用.4.(5分)“十二平均律"是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献,十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于.若第一个单音的频率为f,则第八个单音的频率为()A. f B. f C. f D.f【分析】利用等比数列的通项公式,转化求解即可.【解答】解:从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于.若第一个单音的频率为f,则第八个单音的频率为:=.故选:D.【点评】本题考查等比数列的通项公式的求法,考查计算能力.5.(5分)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1 B.2 C.3 D.4【分析】画出三视图的直观图,判断各个面的三角形的情况,即可推出结果.【解答】解:四棱锥的三视图对应的直观图为:PA⊥底面ABCD,AC=,CD=,PC=3,PD=2,可得三角形PCD不是直角三角形.所以侧面中有3个直角三角形,分别为:△PAB,△PBC,△PAD.故选:C.【点评】本题考查简单几何体的三视图的应用,是基本知识的考查.6.(5分)设,均为单位向量,则“|﹣3|=|3+|”是“⊥”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【分析】根据向量数量积的应用,结合充分条件和必要条件的对应进行判断即可.【解答】解:∵“|﹣3|=|3+|"∴平方得||2+9||2﹣6•=9||2+||2+6•,即1+9﹣6•=9+1+6•,即12•=0,则•=0,即⊥,则“|﹣3|=|3+|"是“⊥”的充要条件,故选:C.【点评】本题主要考查充分条件和必要条件的判断,结合向量数量积的公式进行转化是解决本题的关键.7.(5分)在平面直角坐标系中,记d为点P(cosθ,sinθ)到直线x﹣my﹣2=0的距离.当θ、m变化时,d的最大值为()A.1 B.2 C.3 D.4【分析】由题意d==,当sin(θ+α)=﹣1时,d max=1+≤3.由此能求出d的最大值.【解答】解:由题意d==,tanα==,∴当sin(θ+α)=﹣1时,d max=1+≤3.∴d的最大值为3.故选:C.【点评】本题考查点到直线的距离的最大值的求法,考查点到直线的距离公式、三角函数性质等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.8.(5分)设集合A={(x,y)|x﹣y≥1,ax+y>4,x﹣ay≤2},则()A.对任意实数a,(2,1)∈A B.对任意实数a,(2,1)∉AC.当且仅当a<0时,(2,1)∈A D.当且仅当a≤时,(2,1)∉A【分析】利用a的取值,反例判断(2,1)∈A是否成立即可.【解答】解:当a=﹣1时,集合A={(x,y)|x﹣y≥1,ax+y>4,x﹣ay≤2}={(x,y)|x﹣y≥1,﹣x+y>4,x+y≤2},显然(2,1)不满足,﹣x+y>4,x+y≤2,所以A,C不正确;当a=4,集合A={(x,y)|x﹣y≥1,ax+y>4,x﹣ay≤2}={(x,y)|x﹣y≥1,4x+y >4,x﹣4y≤2},显然(2,1)在可行域内,满足不等式,所以B不正确;故选:D.【点评】本题考查线性规划的解答应用,利用特殊点以及特殊值转化求解,避免可行域的画法,简洁明了.二、填空题共6小题,每小题5分,共30分.9.(5分)设{a n}是等差数列,且a1=3,a2+a5=36,则{a n}的通项公式为a n=6n ﹣3.【分析】利用等差数列通项公式列出方程组,求出a1=3,d=6,由此能求出{a n}的通项公式.【解答】解:∵{a n}是等差数列,且a1=3,a2+a5=36,∴,解得a1=3,d=6,∴a n=a1+(n﹣1)d=3+(n﹣1)×6=6n﹣3.∴{a n}的通项公式为a n=6n﹣3.故答案为:a n=6n﹣3.【点评】本题考查等差数列的通项公式的求法,考查等差数列的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.10.(5分)在极坐标系中,直线ρcosθ+ρsinθ=a(a>0)与圆ρ=2cosθ相切,则a= 1+.【分析】首先把曲线和直线的极坐标方程转化成直角坐标方程,进一步利用圆心到直线的距离等于半径求出结果.【解答】解:圆ρ=2cosθ,转化成:ρ2=2ρcosθ,进一步转化成直角坐标方程为:(x﹣1)2+y2=1,把直线ρ(cosθ+sinθ)=a的方程转化成直角坐标方程为:x+y﹣a=0.由于直线和圆相切,所以:利用圆心到直线的距离等于半径.则:=1,解得:a=1±.a>0则负值舍去.故:a=1+.故答案为:1+.【点评】本题考查的知识要点:极坐标方程与直角坐标方程的互化,直线与圆相切的充要条件的应用.11.(5分)设函数f(x)=c os(ωx﹣)(ω>0),若f(x)≤f()对任意的实数x都成立,则ω的最小值为.【分析】利用已知条件推出函数的最大值,然后列出关系式求解即可.【解答】解:函数f(x)=cos(ωx﹣)(ω>0),若f(x)≤f()对任意的实数x都成立,可得:,k∈Z,解得ω=,k∈Z,ω>0则ω的最小值为:.故答案为:.【点评】本题考查三角函数的最值的求法与应用,考查转化思想以及计算能力.12.(5分)若x,y满足x+1≤y≤2x,则2y﹣x的最小值是3.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义进行求解即可.【解答】解:作出不等式组对应的平面区域如图:设z=2y﹣x,则y=x+z,平移y=x+z,由图象知当直线y=x+z经过点A时,直线的截距最小,此时z最小,由得,即A(1,2),此时z=2×2﹣1=3,故答案为:3【点评】本题主要考查线性规划的应用,利用目标函数的几何意义以及数形结合是解决本题的关键.13.(5分)能说明“若f(x)>f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是f(x)=sinx.【分析】本题答案不唯一,符合要求即可.【解答】解:例如f(x)=sinx,尽管f(x)>f(0)对任意的x∈(0,2]都成立,当x∈[0,)上为增函数,在(,2]为减函数,故答案为:f(x)=sinx.【点评】本题考查了函数的单调性,属于基础题.14.(5分)已知椭圆M:+=1(a>b>0),双曲线N:﹣=1.若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,则椭圆M的离心率为;双曲线N的离心率为2.【分析】利用已知条件求出正六边形的顶点坐标,代入椭圆方程,求出椭圆的离心率;利用渐近线的夹角求解双曲线的离心率即可.【解答】解:椭圆M:+=1(a>b>0),双曲线N:﹣=1.若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,可得椭圆的焦点坐标(c,0),正六边形的一个顶点(,),可得:,可得,可得e4﹣8e2+4=0,e∈(0,1),解得e=.同时,双曲线的渐近线的斜率为,即,可得:,即,可得双曲线的离心率为e==2.故答案为:;2.【点评】本题考查椭圆以及双曲线的简单性质的应用,考查计算能力.三、解答题共6小题,共80分。
【真题】2018年北京市高考数学(理)试题含答案解析
2018年普通高等学校招生全国统一考试(北京卷)数学(理工类)第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.若集合{}2A x x =<,{}2,0,1,2B x =-,则A B =I (A ){}01, (B ){}-101,,(C ){}-201,,(D ){}-1012,,, 2.在复平面内,复数i1i-的共轭复数对应的点位于 (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限3.执行如图所示的程序框图,输出的s 值为( ). A .12B .56C .76D .7124.“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要的贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于f ,则第八个单音的频率为( ).ABC .D .5.某四棱锥的三视图如图所示,在此三棱锥的侧面中,直角三角形的个数为( ). A .1 B .2 C .3 D .46.设a b ,均为单位向量,则“33a b a b -=+”是“a b ⊥”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件7. 在平面直角坐标系中,记d 为点()P cos ,sin θθ到直线20x my --=的距离.当,mθ变化时,d 的最大值为 (A )1 (B )2 (C )3(D )48. 设集合(){},|1,4,2A x y x y ax y x ay =-≥+>-≤,则()A 对任意实数a ,()2,1A ∈ ()B 对任意实数a ,()2,1A ∉()C 当且仅当0a <时,()2,1A ∉ ()D 当且仅当32a ≤时,()2,1A ∉ 二.填空(9)设{}n a 是等差数列,且13a =,2536a a +=,则{}n a 的通项公式为 。
北京版高考数学分项汇编专题13算法含解析理
专题13 算法 1. 【2020高考北京理第4题】执行如下图的程序框图,输出的s 的值为( )
A. 3-
B. 12-
C. 1
3 D. 2
【答案】D
2. 【2021高考北京理第4题】执行如下图的程序框图,输出的S 值为(
)
A. 2 B .4 C.8 D. 16
【答案】C
【解析】
试题分析:0=k ,11=⇒=k s ,21=⇒=k s ,22=⇒=k s ,8=s ,循环终止,输出的s 为8,应选C 。
考点:算法.
3. 【2021高考北京理第4题】执行如下图的程序框图,输出的S 值为( ).
A .1
B .2
3 C .1321 D .610
987
【答案】C
考点:算法.
4. 【2021高考北京理第4题】当7,3m n ==时,执行如下图的程序框图,输出的S 值为(
)
A .7
B .42
C .210
D .840
【答案】 C 考点:程序框图,容易题.
5. 【2021高考北京,理3】执行如下图的程序框图,输出的结果为( )
A .()22-,
B .()40-,
C .()44--,
D .()08-,
开始x =1,y =1,k =0
s =x -y ,t =x +y
x =s ,y =t
k =k +1
k ≥3
输出(x ,y )
结束是
否
【答案】B
考点定位:此题考点为程序框图,要求会准确运行程序。
【精品】2018年全国高考数学试题及解答分类★★★★★(14 算法初步、框图)
【精品】2018年全国高考数学试题及解答分类★★★★★( 14 算法初步、框图 )一、选择题1.(2018北京文、理)执行如图所示的程序框图,输出的s 值为( )A .12B .56C .76D .7121.【答案】B【解析】初始化数值1k =,1s = 循环结果执行如下:第一次:()1111122s =+-⋅=,2k =,23k =≥不成立;第二次:()21151236s =+-⋅=,3k =,33k =≥成立,循环结束,输出56s =,故选B .2 (2018天津文、理)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为( )(A )1 (B )2 (C )3 (D )4 4.【答案】B【解析】结合流程图运行程序如下:首先初始化数据:20N =,2i =,0T =, 20102N i ==,结果为整数,执行11T T =+=,13i i =+=, 此时不满足5i ≥; 203N i =,结果不为整数,执行14i i =+=,此时不满足5i ≥; 2054N i ==,结果为整数,执行12T T =+=,15i i =+=, 此时满足5i ≥;跳出循环,输出2T =.故选B .3.(2018全国新课标Ⅱ文、理)为计算11111123499100S =-+-++-,设计了如图的程序框图, 则在空白框中应填入( )A .1i i =+B .2i i =+C .3i i =+D .4i i =+ 3.【答案】B【解析】由11111123499100S =-+-+⋯+-得程序框图先对奇数项累加,偶数项累加,最后再相减. 因此在空白框中应填入2i i =+,选B .二、填空1.(2018江苏)一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为 ▲ .1.【答案】8【解析】由伪代码可得3I =,2S =;5I =,4S =;7I =,8S =;因为76>,所以结束循环,输出8S =.三、解答题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题13 算法
1. 【2011高考北京理第4题】执行如图所示的程序框图,输出的s 的值为( )
A. 3-
B. 12-
C. 1
3 D. 2
【答案】D
2. 【2012高考北京理第4题】执行如图所示的程序框图,输出的S 值为( )
A. 2 B .4 C.8 D. 16
【答案】C
【解析】
试题分析:0=k ,11=⇒=k s ,21=⇒=k s ,22=⇒=k s ,8=s ,循环结束,输出的s 为8,故选C 。
考点:算法.
3. 【2013高考北京理第4题】执行如图所示的程序框图,输出的S 值为( ).
A .1
B .23
C .1321
D .610987
【答案】C
考点:算法.
4. 【2014高考北京理第4题】当7,3m n ==时,执行如图所示的程序框图,输出的S 值为
( )
A .7
B .42
C .210
D .840
【答案】C
考点:程序框图,容易题.
5. 【2015高考北京,理3】执行如图所示的程序框图,输出的结果为( )
A .()22-,
B .()40-,
C .()44--,
D . ()08-,
B
【答案】
6.【2016高考北京理数】执行如图所示的程序框图,若输入的a值为1,则输出的k值为()
A.1
B.2
C.3
D.4
【答案】B
【解析】 试题分析:输入1=a ,则0=k ,1=b ;
进入循环体,2
1-
=a ,否,1=k ,2-=a ,否,2=k ,1=a ,此时1==b a ,输出k ,则2=k ,选B.
考点:算法与程序框图
【名师点睛】解决循环结构框图问题,要先找出控制循环的变量的初值、步长、终值(或控制循环的条件),然后看循环体,循环次数比较少时,可依次列出,循环次数较多时,可先循环几次,找出规律,要特别注意最后输出的是什么,不要出现多一次或少一次循环的错误.
7.【2017高考北京理数第3题】执行如图所示的程序框图,输出的s 值为
(A)2 (B)3
2
(C)
5
3(D)
8
5
【答案】C
【考点】循环结构
【名师点睛】解决此类型问题时要注意:第一,要明确是当型循环结构,还是直到型循环结构,并根据各自的特点执行循环体;第二,要明确图中的累计变量,明确每一次执行循环体前和执行循环体后,变量的值发生的变化;第三,要明确循环体终止的条件是什么,会判断什么时候终止循环体,争取写出每一个循环,这样避免出错.。
