固体物理第五章习题
固体物理学:第五章 习 题

第五章 习 题 P3051. 解:一维部洛赫电子的能带具有如下性质,)()(αsk E k E +=,⋅⋅⋅±±=210、、s于是有:αs k kE kk E+∂∂∂∂= ……①和kkE kk E -∂∂∂∂-= ……②而布里渊区在边界上,α2s k±=,取α2sk -=代入①、②两式,可得:αα22s kE s k E-∂∂∂∂=, αα22s kEs k E -∂∂∂∂-= 由上两式相容的条件立即得到:02=±∂∂αsk E ,即能量取极值。
(可参看附加题1、2,课本P288例1、P290例3) 2. 解:对面心立方格子,原胞的三个基矢为:)(21a +=α,)(22a +=α,)(23a +=α,倒格子基矢为:)(11b ++-=α)(12b +-=α ,)(13b -+=α倒格矢:332211n b n b n K n ++=])()()[(3213213211n n n n n n n n n -+++-+++-=α面心立方格子是一个边长为α2的体心立方格子,离原点最近的八个倒格点的坐标是:)111(1,,α ,)111(1,,α,)111(1,,α,)111(1,,α)111(1,,α,)111(1,,α,)111(1,,α,)111(1,,αα3=六个次近邻倒格点的坐标是:)002(1,,±α,)02,0(1,±α,)2,00(1±,α,α2= 由最近邻和次近邻倒格矢的中垂面围成的多面体——截角八面体(它是一个十四面体)便是面心立方格子的第一布里渊区。
如课本P261图5-3。
3. 解:(参考徐习P259~260,教材P191,4-19式)(1)按照定义,空间中E=E F的等能面称为费米面,由mk h E F 222=知道,这是半径为F k 的球面。
在绝对零度下,电子全部位于费米球内,T=0K 时,费米能级的能量32223220)3(2)83(2ππn mn m h E F ==式中n 为电子浓度,令3222)83(22πn m h k m h F =得,31)83(πn k F = 设晶体的电子总数为N ,体积为V,对于具有简单立方结构的单价金属,V=N α3,因此,所求费米球半径:m V N k F /10147.010345.3492.0492.0)183()83(101031331⨯=⨯====-ααππ(2)因简单立方边界为α,其第一布里渊区是空间中边长为1/α的立方体,体积为1/α3,故费米球刚好被包含在其内部。
阎守胜版固体物理习题解答--第五章

5.1证明:长波下单原子链运动方程为 )2(11n n n n u u u um -+=-+β (1)可化为连续介质弹性波动方程 )()(22222tu v tu ∂∂=∂∂(2)证明:在长波极限下位移n u 随n 的变化是非常缓慢的,即可看作是连续变化的∴(1)式可改写为 )},(2),(),({),(22t x u t a x u t a x u tt x u m --++=∂∂β=}),(21),(),(21),({22222xt x u a xt x u axt x u a xt x u ∂∂+∙∂∂-∙∂∂+∙∂∂β222),(a xt x u ∙∂∂=β∴22222222),(),(),(xt x u vxt x u matt x u ∂∂=∂∂=∂∂β其中:a mv ∙=2/1)(β为声速。
5.2从有关一维双原子链晶格振动的结果,从5.1.2式出发,说明当两原子的质量M m =时结果回到一维单原子链的情形解:从一维双原子链格波的色散关系有;})]21(sin)(41[1{2/1222qa m M Mm Mmm M w+-±+=±β当m M =时有: )21c o s1(22qa mw ±=±β∴有qa m w 41cos 422β=+ (1) qa mw 41sin422β=-a q m'=21s i n42β (2) 其中q 为一维双原子链的波失aa q ππ42/2==,q '为一维单原子链的波失aq π2='5.3 设有一维双原子链,链上最近邻原子间的恢复力常数交错的等于β和β10,若两种原子的质量相等,并最近邻间距为2a ,试求在波失0=q 和aq π=处的)(q w ,并画处其色散关系曲线。
解:设n u 和n v 分别代表两种 原子的相对平衡位置的位移,M 代表每个原子的质量,则相邻两种原子的运动方程为)1110()()(1011n n n n n n n n u v v v u u v uM -+=---=--βββ (1) )11()(10)(11n n n n n n n n v u u u v v u vM -+=---=++βββ (2)设试探解为)(0nqa wt i n e u u --=,)(0nqa wt i n e v v --= 将试探波解代入方程中可得)1110(2u vev Mu w iqa-+=--β,)1110(2v ueu Mv w iqa-+=-β)10()11(0)11()10(22=++-=-++∴-u e v Mwu Mwv e iqaiqaββββ要想v u ,有解则须系数行列式为零可得:})]cos 1(20121[11{2/12qa mw--+=±β±w 分别对应于光学支与声学支当0=q 时有)22(2/1==-+w Mw β当aq π=时有2/1)20(M w β=+2/1)2(Mw β=-所以其色散关系如图:5.5 对于金属Al 计算在什么温度下晶格比热和电子比热相等 解:由德拜理论晶格比热为3411)(512DB T k n CvΘ=π,其中1n 为晶体的原子浓度,DΘ为德拜温度,Al 的德拜温度为385K 电子比热为2Cv FBT T k n 222π=其中2n 为晶体的电子浓度因为一个Al 原子可提供3个电子,所以晶体的电子浓度为329323232)(108.1)(108.11002.6277.23--⨯=⨯=⨯⨯⨯==m cm mZ n m ρKk T J mk mn k BFF F FF 518221103/12210357.1,10873.12,1075.1)3(⨯==⨯==⨯==--εεπ由21Cv Cv=可得:5.16K)8T 5(T 2/12F 3D=Θ=π5.7 考虑一个全同原子组成的平面方格子,用m l u ,记第l 列,第m 行的原子垂直于格平面的 位移,每个原子的质量为M ,最近邻原子的力常数为β (1) 证明运动方程为: )}2()2{()(,1,1,,,1,12,2m l m l m l m l m l m l m l u u u u u u dtu d M -++-+=-+-+β证明:系统总的势能为: })(){(212,1,21,,,m l m l m l ml m l u u u u v ++-+-=∑β(1)由运动方程ml m l u v uM ,,∂∂-= 若只考虑最近邻的原子则有)}2()2{(,1,1,,,1,1,m l m l m l m l m l m l m l u u u u u u uM -++-+=-+-+β (2) (2) 设解的形式为)](exp[)0(,wt b mq a q i u u y x m l -+=这里a 是最近邻原子的间距,证明运动方程是可以满足的。
固体物理习题课第五章可打印

式中a为晶格常数。计速度;3)能带底部和能带顶部电子的有效质量 1)能带的宽度 能带底部
能带顶部 能带宽度
电子在波矢k的状态时的速度
电子的有效质量
能带底部
能带顶部
有效质量
有效质量
5.5 设电子等能面为椭球
外加磁场B相对于椭球主轴方向余弦为
1) 写出电子的准经典运动方程 2) 证明电子绕磁场回转频率为
其中
恒定磁场中电子运动的基本方程
电子的速度
电子能量
电子的速度
磁感应强度
代入电子运动方程 应用关系
电子运动方程
令
有非零解,系数行列式为零
无意义 旋转频率
其中
固体物理第五章习题及答案

.
从上式可以看出,当电子从外场力获得的能量又都输送给了晶格时, 电子的有效质量 m* 变 为 . 此时电子的加速度
a= 1 F =0
m*
,
即电子的平均速度是一常量. 或者说, 此时外场力与晶格作用力大小相等, 方向相反. 11. 万尼尔函数可用孤立原子波函数来近似的根据是什么?
[解答] 由本教科书的(5.53)式可知, 万尼尔函数可表示为
m* = 1 m 1 + 2Tn
Vn <1.
10. 电子的有效质量 m* 变为 的物理意义是什么?
[解答] 仍然从能量的角度讨论之. 电子能量的变化
(dE)外场力对电子作的功 = (dE)外场力对电子作的功 + (dE)晶格对电子作的功
m*
m
m
=
1 m
(dE ) 外场力对电子作的功
− (dE)电子对晶格作的功
i 2 nx
V (x) = Vne a
n
中, 指数函数的形式是由什么条件决定的?
[解答] 周期势函数 V(x) 付里叶级数的通式为
上式必须满足势场的周期性, 即
V (x) = Vneinx
n
显然
V (x + a) = Vnein (x+a) = Vneinx (eina ) = V (x) = Vneinx
Es (k)
=
E
at s
− Cs
−
Js
e ik Rn
n
即是例证. 其中孤立原子中电子的能量 Esat 是主项, 是一负值, − Cs和 − J s 是小量, 也是负 值. 13. 紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 哪一个宽? 为什么?
固体物理题库-zzk-第一至第五章
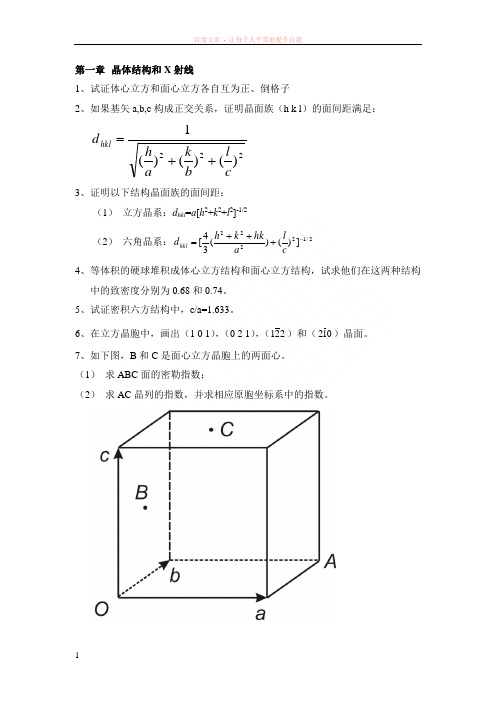
第一章 晶体结构和X 射线1、试证体心立方和面心立方各自互为正、倒格子2、如果基矢a,b,c 构成正交关系,证明晶面族(h k l )的面间距满足:222)()()(1c l b k a hd hkl ++=3、证明以下结构晶面族的面间距:(1) 立方晶系:d hkl =a [h 2+k 2+l 2]-1/2(2) 六角晶系:2/12222])()(34[-+++=c l ahk k h d hkl 4、等体积的硬球堆积成体心立方结构和面心立方结构,试求他们在这两种结构中的致密度分别为0.68和0.74。
5、试证密积六方结构中,c/a=1.633。
6、在立方晶胞中,画出(1 0 1),(0 2 1),(221)和(012)晶面。
7、如下图,B 和C 是面心立方晶胞上的两面心。
(1) 求ABC 面的密勒指数;(2) 求AC 晶列的指数,并求相应原胞坐标系中的指数。
8、六角晶胞的基矢为.,223,223k c c j a i a b j a i a a =+-=+=求其倒格子基矢。
9、求晶格常数为a 的面心立方和体心立方晶体晶面族(h 1 h 2 h 3)之间的面间距(指导p30,10)。
10、讨论六角密积结构,X 光衍射的消光条件。
11、求出体心立方、面心立方的几何因子和消光条件。
12、原胞和晶胞的区别?13、倒空间的物理意义?14、布拉格衍射方程,原子和几何结构因子在确定晶格结构上分别起何作用?15、什么是布拉格简单格子,什么是复式格子?第二章 自由电子气1、设有一个长度为L 的一维金属线,它有N 个导电电子,若把这些导电电子看成自由电子气,试求:(1) 电子的状态密度(2) 绝对零度下的电子费米能级,以及费米能级随温度的变化关系。
(3) 电子的平均能量。
(4) 电子的比热。
2、二维电子气的能态密度2)( πm E N =,证明费米能 ]1ln[/2-=T mk n B F b eT k E π 3、求出一维金属中自由电子的能态密度、费米能级、电子的平均动能以及一个电子对于比热的贡献。
固体物理习题答案(5-7)章

固体物理习题一、 固体电子论基础1. 已知金属铯的E F =1.55eV ,求每立方厘米的铯晶体中所含的平均电子数。
(提示:常温下F E 与0F E 相差不大,可以令0F F E E ≈)解:因为常温下费米能级E F 与绝对零度时的费米能级E F 0相差不大,可令E F ≈E F 0。
金属中的电子可近似地按自由电子气处理,在E ~E+dE 能量区间内的电子态数(计及自旋)为:()dE CE dE E hm VdZ 212132324==π其中:()2132324E hm VC π=, V 为金属的体积,m 为电子的质量。
由于电子遵循费米分布,于是在能量区间E ~E+dE 中的电子数为: dE E E Cf dZ E f dN )()(==式中)(E f 是费米分布函数。
由于在绝对零度时有:⎪⎩⎪⎨⎧><=)E (E 0)E (E 1)(0F 0FE f因此电子总数为:2332300)2(38)(32)(0F FE mE h VE C dEE C dE E E Cf N Fπ====⎰⎰∞单位体积内的电子数为: 233)2(38F mE hV Nn π==代入有关数据得到: )(108.7 )106.155.1101.92()1063.6(314.38321231228327----⨯≈⨯⨯⨯⨯⨯⨯⨯⨯⨯=cm n2. 证明:在T=0K 时,费米能级0F E 处的能态密度为:0023)(FF EN E N =,式中N为金属中的自由电子数。
证明:在K 空间中,在周期性边界条件下,以K K =为半径的球内,电子的数目为(记及自旋):3342K V n π⋅=因此:dK K V dn 28π⋅= (1) 已知自由电子的能量为:mK h E 222=,代入(1)式得:d E E hm Vd n 21323)2(4π= (2)因此电子按照能量分布的状态密度:21323)2(4)(E hm Vd E d nE N π==(3)当T=0K 时,全部电子处于费米球内。
固体物理课后习题与答案

第一章 金属自由电子气体模型习题及答案1. 你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的?[解答] 自由电子论只考虑电子的动能。
在绝对零度时,金属中的自由(价)电子,分布在费米能级及其以下的能级上,即分布在一个费米球内。
在常温下,费米球内部离费米面远的状态全被电子占据,这些电子从格波获取的能量不足以使其跃迁到费米面附近或以外的空状态上,能够发生能态跃迁的仅是费米面附近的少数电子,而绝大多数电子的能态不会改变。
也就是说,常温下电子的平均动能与绝对零度时的平均动能十分相近。
2. 晶体膨胀时,费米能级如何变化?[解答] 费米能级3/222)3(2πn mE o F= , 其中n 单位体积内的价电子数目。
晶体膨胀时,体积变大,电子数目不变,n 变小,费密能级降低。
3. 为什么温度升高,费米能反而降低?[解答] 当K T 0≠时,有一半量子态被电子所占据的能级即是费米能级。
除了晶体膨胀引起费米能级降低外,温度升高,费米面附近的电子从格波获取的能量就越大,跃迁到费米面以外的电子就越多,原来有一半量子态被电子所占据的能级上的电子就少于一半,有一半量子态被电子所占据的能级必定降低,也就是说,温度生高,费米能反而降低。
4. 为什么价电子的浓度越大,价电子的平均动能就越大?[解答] 由于绝对零度时和常温下电子的平均动能十分相近,我们讨论绝对零度时电子的平均动能与电子的浓度的关系。
价电子的浓度越大,价电子的平均动能就越大,这是金属中的价电子遵从费米—狄拉克统计分布的必然结果。
在绝对零度时,电子不可能都处于最低能级上,而是在费米球中均匀分布。
由式3/120)3(πn k F =可知,价电子的浓度越大费米球的半径就越大,高能量的电子就越多,价电子的平均动能就越大。
这一点从3/2220)3(2πn m E F=和3/222)3(10353πn mE E oF ==式看得更清楚。
电子的平均动能E 正比于费米能o F E ,而费米能又正比于电子浓度32l n。
固体物理第5章_能带理论_习题参考答案

第六章 能带理论 (习题参考答案)1. 一矩形晶格,原胞长10a 210m-=⨯,10b410m-=⨯(1)画出倒格子图(2)以广延图和简约图两种形式,画出第一布里渊区和第二布里渊区(3)画出自由电子的费米面(设每个原胞有2个电子)解:(1)因为a =a i=20A i b =b j=40A j倒格子基矢为12a iA*=, 014bj A*=以a *b *为基矢构成的倒格子如图。
由图可见,矩形晶格的倒格子也是矩形格子。
(2)取任一倒格子点O作为原点,由原点以及最近邻点A i,次近邻点B i的连线的中垂线可以围成第一,第二布里渊区,上图这就是布里渊区的广延图。
如采用简约形式,将第二区移入第一区,我们得到下图。
(3) 设晶体中共有N个原胞,计及自旋后,在简约布里渊区中便有2N个状态。
简约布里渊区的面积21()8A a bA ***-=⨯=而状态密度22()16()N g K N A A*==当每个原胞中有2个电子时,晶体电子总数为 22()216Fk FN g k kdk N k ππ=⨯=⎰所以1/211111()0.2()210()8F k A m π---=≈=⨯这就是费米圆的半径。
费米圆如下图所示2. 已知一维晶体的电子能带可写成()2271cos cos 2,88E k ka ka m a ⎛⎫=-+⎪⎝⎭式中a 是晶格常数。
试求: (i )能带的宽度;(ii )电子在波矢k 状态时的速度; (iii )能带底部和顶部电子的有效质量。
()()()()()()()()22222m in 2m ax 22m ax m in 22222m in 71cos cos 2,8811cos 24400,2;221sin 24sin 404k i E k ka ka m a ka m a k E k E am a E E E m am aii v E kv ka ka m aiii E k kk E E mπ⎛⎫=-+⎪⎝⎭⎡⎤=--⎢⎥⎣⎦====∆=-=∴=∇∴=--==+解:当时,当时,能带的宽度为:在能带底部,将在附近用泰勒级数展开,可得:()()()22m in 22m ax 22m ax 220342203k E mm m E k k E E k mk E mm m ππδδδ****=+∴===-=+∴=-在能带顶部,将在附近用泰勒级数展开,令k=+k 可得:aa3. 试证明:如果只计及最近邻的相互作用,用紧束缚方法导出的简单立方晶体中S 态电子的能带为()2cos 2cos 2cos 2s x y z E k E A J ak ak ak πππ⎡⎤=--++⎣⎦并求能带的宽度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)用紧束缚方法处理晶格的s态电子,当只计及最
近邻格点的相互作用时,其能带的表示式为
r
ru r
E s(k)E s a tC SJs eik•R n,
n
ur R
n
是最近邻格矢.
对体心立方晶格,取参考格点的坐标为(0, 0, 0) 则8个最近邻格点的坐标为
a 2
,
a 2
,
a 2
18
将上述8组坐标代入能带的表示式,得
l
l
令
l' l 1
得
k(x a ) f(x l'a )k(x) eikak(x)
l
由上式知
eika 1
所以有
k0,2,4,6,K
aaa
由此得在布里渊区内的值为k=0。
4
2. 一维周期势场为
V(x) 1 2m W 2[b2(xna)2], nabxnab
0, (n1)abxnab
第五章 习题
1
1. 晶格常数为a的一维晶体中,电子的波函数为
(1)
k
(x)
icos3
a
x
(2)
k
(x)
f
(xla),f是某一函数,求电子在以
l
上状态中的波矢。
2
[求解]
由《固体物理教程》(5.14)式
k(r v R v n ) e ik v R v n k(r v )
可知,在一维周期势场中运动的电子波函数满足
9
第二禁带宽度为
Eg2
2V2
21 a
a2V(x)ei4axdx
a 2
2 1 b 1mW2(b2x2)eibxdx 4b b2
21 b1m W 2(b2x2)cos(x)dx
4bb2
b
m W 2b2 2
10
5. 对简立方结构晶体,其晶格常数为a。 (1)用紧束缚方法求出对应非简并s态电子能带; (2)分别画出第一布里渊区[110]方向的能带、电 子的平均速度、有效质量以及沿[110]方向有恒定电 场时的加速度曲线。
带如图所示
13
电子的平均速度 v1E22JSasin( 2ka)
hk h
2
平均速度曲线
14
电子的有效质量
m
h2 2E k2
2JSa2
h2 cos(
2ka ) 2
有效质量曲线
15
在[110]方向上有恒定电场情况下,电子受的力
Fe
电子的加速度
F e2JSa2cos(
am
h2
2ka) 2
设电场方向与[110]方向相反,加速度曲线则如图
11
[求解]
非简并s态电子的能带
v
vv
E s(k) E sa t C S J S e ikR n
n
式中Rn是晶格参考格点的最近邻格矢。
对于简单立方晶体,任一格点有6个最近邻,取
参考格点的坐标为(0, 0, 0), 6个最近邻坐标为
(a,0,0) (0, a,0) (0,0, a)
简单立方晶体非简并s态电子的能带则为
16
7.用紧束缚方法处理体心立方晶体,求出 (1) s态电子的能带为
E s(k r) E s a t C S 8 J sc o sk 2 x a c o sk 2 y a c o sk 2 za ;
(2) 画出第一布里渊区[111]方向的能带曲线; (3) 求出带底和带顶电子的有效质量.
17
[解答]
其中a=4b,W为常数,试画出此势能曲线,并求
出势能的平均值。
5
[求解] 图:一维周期势场
V(x) 1 2m W 2[b2(xna)2], nabxnab
0, (n1)abxnab
6
由图所示,由于势能有周期性。因此只有一个周 期内求平均即可,于是得
V1a2V(x)dx1
b
V(x)dx
aa2
Cs
8Js
cos
kxa 2
cos
kya 2
cos
kza 2
19
(2) 在[111]方向上
kx ky kz
3 k, 3
且第一布里渊区边界在
kx
ky
kz
a
于是能带化成
EE0
8Js
cos3
3ka 6
其中 E0 Esat CS
第一布里渊区[111]方向的能带曲线
20
(3) 由能带的表示式及余弦函数的性质可知,当
kx=ky=kz=0时,Es取最小值,即kx=ky=kz=0是能带 底,电子有效质量为
i a
2
kx ky kz
Esat
Cs
2
J
s
[e
i
a 2
k
x
k
y
cos
kza 2
e i a 2
kx ky
cos
kza 2
e
i
a 2
k
x
k
y
cos
kza
e i a 2
kx ky
cos
kza]
2
2
Esat
Cs
4Js
e
i
a 2
k
x
e
ia 2kx来自cos kya 2
cos
kza 2
Esat
v E s ( k ) E s a t C S J S ( c o s k x a c o s k y a c o s k z a )
12
(2)在[110]方向上
kz
0,
ky
kx
2k 2
能带变成
v
2ka
Es(k)E04JS(cos 2 )
其中
E0Esat CS2JS
在[110]方向上,在第一布里渊区内,电子的能
Eg=2|Vn|,其中Vn是周期势场V(x)付里叶级数的系 数,该系数可由《固体物理教程》(5.22)式
求得 Vn
1 a
a 2
i2nx
V(x)e a dx
a
2
第一个禁带宽度为
Eg12V1
21 a
a2V(x)ei2axdx
a 2
2 1 b 1mW2(b2x2)ei2bxdx
4b b2
24 1 b b b1 2m W 2(b 2 x2)c o s(2 bx )d x 8 m W 3 2 b 2
由此得 (1)
于是
k(xa)eikak(x)
k(xa)icos[3a(xa)]icos(3ax)
icos(3x)
a eika 1
k,3,5,K
aa a
因此得 k,3,5,K
aa a
3
若只取布里渊区内的值: k
a
a
则有
k
a
(2)
k(x a ) f(x a la ) f[x (l 1 )a ]
r
r ur
Es (k )
E
at s
Cs
Js
eik•Rn
n
Esat
Cs
J
s
[e
i
a 2
k
x
k
y
k
z
i a e2
kx ky kz
i a e2
kx ky kz
i a e2
kx ky kz
i a e2
kx ky kz
e e e ] i a 2
kx ky kz
i a
2
kx ky kz
4bb
1 b 1mW2[b2x2]dx
4b b2
mW 2 [b2 x
b
1 x3]
8b
3
b
1 mW 2b2 6
V(x) 1 2m W 2[b2(xna)2], nabxnab
0, (n1)abxnab
7
3. 用近自由电子模型求解上题,确定晶体的第 一及第二个禁带宽度。
8
[求解]
根据教科书(5.35)式知禁带宽度的表达式为
