第6讲 一元二次函数的图象和性质
二次函数图像与性质ppt课件

D.f(1)>25
答案:A
三基能力强化
2.若函数f(x)=ax2+bx+c满足 f(4)=f(1),那么( )
A.f(2)>f(3) B.f(3)>f(2) C.f(3)=f(2) D.f(3)与f(2)的大小关系不确定 答案:C
三基能力强化
3.已知函数y=x2-2x+3在闭区
间[0,m]上有最大值3,最小值2,则
课堂互动讲练
【思路点拨】 (1)待定系数法.(2) 二次函数的单调性.
【解】 (1)依题意,方程f(x)=ax2 +bx=x有等根,
则有Δ=(b-1)2=0,∴b=1. 2分 又f(-x+5)=f(x-3), 故f(x)的图象关于直线x=1对称, ∴-2ba=1,解得 a=-12,
∴f(x)=-21x2+x. 5 分
基础知识梳理
2.二次函数的图象及其性质
基础知识梳理
基础知识梳理
基础知识梳理
二次函数可以为奇函数吗? 【思考·提示】 不会为奇 函数.
三基能力强化
1.已知函数f(x)=4x2-mx+5在
区间[-2,+∞)上是增函数,则f(1)的
范围是( )
A.f(1)≥25
B.f(1)=25
C.f(1)≤2+2=(x+a)2+2 -a2的对称轴为x=-a,
∵f(x)在[-5,5]上是单调函数, ∴-a≤-5,或-a≥5, 解得a≤-5,或a≥5. 10分
规律方法总结
1.二次函数f(x)=ax2+bx+c(a >0)在区间[m,n]上的最值.
当-2ba<m 时,函数在区间[m, n]上单调递增,最小值为 f(m),最大 值为 f(n);
基础知识梳理
1.二次函数的解析式有三种常用表 达形式
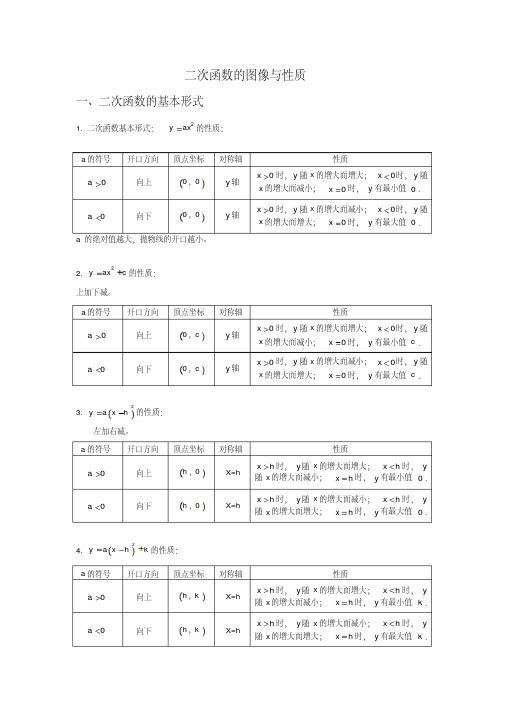
二次函数图象和性质总结表格

二次函数图象和性质总结表格二次函数知识点总结一、二次函数的图像和性质二次函数的图像开口方向、对称轴、顶点坐标、增减性和最值与函数的参数有关。
当参数a大于0时,图像开口向上,对称轴是y轴,顶点坐标为(0,0),在对称轴左侧y随x增大而减小,在对称轴右侧y随x增大而增大。
参数a越大,开口越小。
当参数a小于0时,图像开口向下,对称轴是y轴,顶点坐标为(0,0),在对称轴左侧y随x增大而增大,在对称轴右侧y随x增大而减小。
参数a越小,开口越小。
当二次函数带有平移时,对称轴的位置会发生变化,顶点坐标变为(h,k)。
当参数a大于0时,图像开口向上,对称轴是直线x=h,顶点坐标为(h,k),在对称轴左侧y随x增大而减小,在对称轴右侧y随x增大而增大。
当参数a小于0时,图像开口向下,对称轴是直线x=h,顶点坐标为(h,k),在对称轴左侧y随x增大而增大,在对称轴右侧y随x增大而减小。
二、二次函数的解析式二次函数的解析式为y=ax²+bx+c,其中a、b、c均为实数且a≠0.当二次函数带有平移时,解析式为y=a(x-h)²+k,其中a、h、k均为实数且a≠0.三、二次函数的应用二次函数在数学和现实生活中都有广泛的应用。
例如,二次函数可以用来描述物体的运动轨迹、建筑物的结构、金融市场的波动等等。
在应用中,我们需要根据实际情况确定二次函数的参数,并利用二次函数的性质进行分析和计算。
总之,二次函数是数学中非常重要的一个概念,掌握二次函数的图像、解析式和应用是我们研究数学的基础。
当x>h时,随着x的增大,y会减小。
函数a的符号决定了开口的方向,当a>0时,开口向上,当a<0时,开口向下。
对称轴为直线x=-b/2a,顶点坐标为(-b/2a。
c-b^2/4a)。
当a的绝对值越大时,开口越小;b的符号决定了对称轴在y轴的位置,当b>0时,对称轴在y轴左侧,当b<0时,对称轴在y轴右侧;c的符号决定了抛物线与y轴的交点在哪个象限,当c>0时,抛物线与y轴正半轴相交,当c<0时,抛物线与y轴负半轴相交。
二次函数图像与性质完整归纳
3 2 -2
3 2 0 5…
2
【例 2】 求作函数 y x 2 4 x 3 的图象。
【解】 y x 2 4x 3 ( x2 4x 3)
[( x 2) 2 7] [( x 2) 2 7 先画出图角在对称轴 x 2 的右边部分,列表
x -2 -1 0 1 2 y 76 5 4 3
【点评】 画二次函数图象步骤: (1) 配方; (2) 列表; (3) 描点成图; 也可利用图象的对称性,先画出函数的左(右)边部分图象,再利 用对称性描出右(左)部分就可。
, 3 ] 上是增函数,在区间 [ 3, 10
29 ymaz 20 ) 上是减函数。
【点评】 要研究二次函数顶点、对称轴、最值、单调区间等性质时,方法有两个:
(1) 配方法;如例 3
(2) 公式法:适用于不容易配方题目 ( 二次项系数为负数或分数 ) 如例 4,可避免出错。
任何一个函数都可配方成如下形式:
b 时, y 随 x 的增大而增大; 当 x b
2a
2a
b ,顶点坐标为 2a
b ,4ac b2 .当 2a 4a
x b 时, y 随 x 的增大而增大;当 x 2a
2
有最大值 4ac b . 4a
b 时, y 随 x 的增大而减小;当 x 2a
b 时, y 2a
六、二次函数解析式的表示方法
1. 一般式: y ax 2 bx c ( a , b , c 为常数, a 0 ); 2. 顶点式: y a ( x h)2 k ( a , h , k 为常数, a 0 );
向下
h ,k
x h 时, y 随 x 的增大而减小; x h 时, y X=h
随 x 的增大而增大; x h 时, y 有最大值 k .
《一元二次函数》示范公开课教案【高中数学必修第一册北师大】

《一元二次函数》教学设计1. 熟悉配方法,理解a,b,c (或a,h,k )对二次函数图象的作用.2.理解由y =ax 2到y =a(x −ℎ)2+k 的图象变换方法.3. 掌握二次函数的性质.4. 体会抽象概括的过程,加强直观想象素养的培养.重点:掌握一元二次函数的图象和性质.难点:体会用平移的方法研究一元二次函数的图象,并能迁移到对其他函数的图象的研究之中. 一、新课导入 回顾旧知:初中阶段,我们学习了一元二次函数y =ax²+bx +c (a ≠0),请回顾认识这个函数的过程.答案:认识这个函数的过程是从y =x²开始的,是由简到繁的过程.如图所示:思考:对于二次函数y =a(x −ℎ)2+k (a ≠0)的图象,可以由函数y =ax²的图象,经过怎样的变换得到?师揭示本节课题:《一元二次函数》.设计意图:通过对旧知识的回顾,激发学生对一元二次函数的探究,从而引出今天的课题,激发学生的学习兴趣,让学生在对新问题的挑战中,进一步深化数形结合思想.二、新知探究探究一:一元二次函数.分析:一元二次函数的三种形式:(1)一般式:y =ax²+bx +c (a ≠0)(2)顶点式:y =a(x −ℎ)2+k(a ≠0)◆教学目标 ◆教学重难点 ◆ ◆教学过程◆(3)两根式:y =a(x −x 1)(x −x 2)(a ≠0)思考:如何把一元二次函数的一般式化为顶点式?答案:配方法.一元二次函数y =ax²+bx +c (a ≠0)都可以通过配方化为y =a (x +b 2a )2+4ac−b 24a ,若设 ℎ=−b 2a ,k =4ac−b 24a ,则有y =a(x 一ℎ)2+k (顶点式)通常把一元二次函数的图象叫作抛物线.例如:一元二次函数y =2x 2+3x +5,通过配方可化为y =2(x +34)2+318,其图象为开口向上,以x =−34为对称轴,(−34,318)为顶点的抛物线.探究二:一元二次函数的图象变换规律.分析:如图所示,一元二次函数y =2(x −2)2的图象可以由y =2x 2的图象右移2个单位长度得到;y =2(x −2)2−1的图象可以由由y =2x 2的图象右移2个单位长度,下移1个单位长度得到.知识点:一元二次函数y =a(x −ℎ)2+k 的图象可以由y =ax 2的图象经过向左(或向右)平移|ℎ|个单位长度,再向上(或向下)平移|k|个单位长度而得到.探究三:一元二次函数y =a(x 一ℎ)2+k(a ≠0)的性质.知识点:(1) 函数y =a(x −ℎ)2+k 的图象是一条抛物线,顶点坐标是(ℎ,k ),对称轴是直线x =ℎ.(2)当a >0时,抛物线开口向上;在区间(−∞,ℎ]上,函数值y 随自变量x 的增大而减小;在区间[ℎ,+∞)上,函数值y 随自变量x 的增大而增大;函数在x =ℎ处有最小值,记作y min =k .(3)当a <0时,抛物线开口向下;在区间(−∞,ℎ]上,函数值y 随自变量x 的增大而增大;在区间[ℎ,+∞)上,函数值y 随自变量x 的增大而减小;函数在x =ℎ处有最大值,记作y max =k .小结:二次函数y =a(x −ℎ)2+k(a ≠0),a 决定了二次函数图象的开口大小及方向(a >0,图象开口向上,a 值越大,开口越小;a <0,图象开口向下,a 值越大,开口越大)﹔h 决定了二次函数图象的左、右平移,而且“h 正左移,h 负右移”﹔k 决定了二次函数图象的上、下平移,而且“k 正上移,k 负下移”.图象变换口诀:“上加下减,左加右减”.设计意图:从一元二次函数的三种形式进行探究,从简到繁,唤醒旧知,联系新知,从形式到图象变换,再到性质分析,循序渐进对一元二次函数的变换以及性质进行理解.三、应用举例例1: 已知一元二次函数y =12x ²+2x +5.(1)指出它的图象可以由y =12x ²的图象经过怎样的变换才能得到;(2)指出它的对称轴,试述函数的变化趋势及函数的最大值或最小值.分析:因为题中给出了一元二次函数的一般形式y =12x ²+2x +5,所以我们直接利用配方,将它变成y =a (x +b 2a )2+4ac−b 24a的形式,然后通过结合图形,即可得出答案. 解:(1)配方,可得,y =12x 2+2x +5y =12(x 2+4x)+5y =12(x 2+4x +4−4)+5 y =12(x +2)²+3.所以,y =12x 2+2x +5的图象可以由y =12x ²的图象向左平移2个单位长度,再向上平移3个单位长度而得到.(2) 由(1)可知:该函数的图象开口向上,对称轴为直线x =-2;在区间(−∞,−2]上,函数值y 随自变量x 的增大而减小,在区间[−2,+∞)上,函数值y 随自变量x 的增大而增大;函数在x =−2处取得最小值3,y min =3.例2:若函数y =(a −1)x 2+2x +5的图象恒在x 轴的上方,求实数a 的取值范围. 解:当a −1=0时,函数解析式为y =2x +5,此时函数图象为一条直线,不是恒在x 轴的上方,故a ≠1;当a −1≠0时,若函数图象恒在x 轴上方,则有{a -1>0,Δ=4-20(a -1)<0,解得a >65. 综上所述,实数a 的取值范围为a >65. 四、课堂练习1. 判断下列说法是否正确,正确的在它后面的括号里画“√”,错误的画“×”.(1)二次函数y =3x 2的开口比y =x 2的开口要大.(2)要得到y =—(x—2)2的图象,需要将y =—x 2向左平移2个单位长度.(3)二次函数y =ax 2+bx +c(a ≠0)一定有最小值.(4)二次函数y =x 2−2x +1的对称轴为x =—1.2.若抛物线y=x2−(m−2)x+m+3的顶点在y轴上,求m的值.3. 若函数y=x2+2(2a−1)x+2在区间(−∞,7]上y随x的增大而减小,求实数a的取值范围.4. 求函数y=3+2x−x2(0≤x≤3)的最小值.参考答案:1. (1)×(2)×(3)×(4)×解析:由一元二次函数的图象和性质得知.2. m的值为2.解析:因为抛物线y=x2−(m−2)x+m+3的顶点在y轴上,所以顶点的横坐标为−−(m−2)2×1=m−22=0,故m=2.3. (−∞,−3]解析:由一元二次函数的性质知,抛物线y在区间(−∞,7]上y随x的增大而减小,可得−(2a−1)≥7,所以a的取值范围为(−∞,−3].4. 0解析:将一元二次函数y=3+2x−x2配方得y=−(x−1)2+4,因为(0≤x≤3),所以当x=3时,y min=3+6−9=0.故y的最小值为0.五、课堂小结1.一元二次函数的图象变换规律:h决定了二次函数图象的左、右平移,而且“h正左移,h负右移”﹔k决定了二次函数图象的上、下平移,而且“k正上移,k负下移”.图象变换口诀:“上加下减,左加右减”.2. 一元二次函数图象的性质:(1)函数y=a(x−ℎ)2+k的图象是一条抛物线,顶点坐标是(ℎ,k),对称轴是直线x=ℎ.a决定了二次函数图象的开口大小及方向(a>0,图象开口向上,a值越大,开口越小;a<0,图象开口向下,a值越大,开口越大)﹔(2)当a>0,抛物线开口向上;在区间(−∞,ℎ]上,函数值y随自变量的增大而减小;在区间[ℎ,+∞)上,函数值y随自变量的增大而增大;函数在x=ℎ处有最小值,记作y min=k.(3)当a<0,抛物线开口向下;在区间(−∞,ℎ]上,函数值y随自变量的增大而增大;在区间[ℎ,+∞)上,函数值y随自变量的增大而减小;函数在x=ℎ处有最大值,记作y max=k.六、布置作业教材第33页练习第1、2题.。
3.4 一元二次函数的图象与性质课件-2023届广东省高职高考数学第一轮复习第三章函数

知识点1 知识点2 知识点3 知识点4 知识点5
1.一元二次函数的定义 形如y=ax2+bx+c(a≠0)的函数叫做一元二次函数.它的定义域是 R,图象是一条抛物线.
知识点1 知识点2 知识点3 知识点4 知识点5
2.二次函数y=ax2+bx+c(a≠0)的性质
y=ax2+bx+c
【解析】
(1) 依 题 意 : 抛 物 线 开 口 向 下 , 对 称 轴 为
x
=
m+n 2
=
-2+t2-2-t=-2,如图观察得知:f(-1)>f(1).
(2)依题意得对称轴为 x=m+2 n=-12+7=3,则x1+2 x2=3,从而求得
两根之和为 6.
例5 分别求满足下列条件的二次函数y=f(x)的解析式. (1)图象过点(-1,-22),(0,-8),(2,8); (2)顶点为(-1,-8),且过点(0,-6); (3)过点(1,-8),函数与x轴的两个交点坐标分别为(5,0),(-1, 0). 【分析】 本题考查一元二次函数的三种解析式的求法.一般式:y
=ax2+bx+c;顶点式:y=a(x-m)2+n;交点式:y=a(x-x1)(x-x2).
【解】 (1)设二次函数 f(x)=ax2+bx+c,将点(-1,-22),(0,-
8),(2,8)代入解析式:
a-b+c=-22
c=-8
,解得 a=-2,b=12,c=-8,
4a+2b+c=8
所以函数解析式为 f(x)=-2x2+12x-8.
例4 (1)如果函数f(x)=x2+bx+c对任意实数t,都有f(3+t)=f(3
-t),则(
)
A.f(3)<f(1)<f(4) B.f(1)<f(3)<f(4)
二次函数的图象和性质课件

二次函数的解析试.
解:设所求的二次函数 为y ax2 bx c,由题意得:
{a b c 10 abc 4
4a 2b c 7
待定系数法
解得,a 2,b 3, c 5
所求的二次函数是 y 2x2 3x 5
对自己说,你有什么收获? 对老师说,你有什么疑惑? 对同学说,你有什么温馨提示?
x
y 1 x 22
3
y 1 x2
3
5.二次函数y=ax2 的图象和性质
抛物线 y=ax2(a>0)
y=ax2(a<0)
开口方向
对称轴
向上 直线x=0
向下 直线x=0
顶点坐标 (0,0)
(0,0)
增减性
在对称轴的左侧,y随着x的增大 在对称轴的左侧,y随着x的增大
而减小. 在对称轴的右侧, y随 而增大. 在对称轴的右侧, y随
问题3:多边形的对角线数d与边数n有什么关系?
由图可以想出,如果多边形有n
条边,那么它有 n 个顶点,从一
个顶点出发,连接与这点不相邻
M
N 的各顶点,可以作(n-3)条对角线.
此式表示了多边形
的对角线数d与边
数n之间的关系,对
于n的每一值,d都
即
有唯一的对应值,
即d是n的函数。
问题4:某工厂一种产品现在的年产量是20件,计划今后两年 增加产量。如果每年都比上一年的产量增加x倍,那么两年后 这种产品的产量y将随计划所定的x的值而确定,y与x之间的 关系怎样表示?
返回
在同一坐标系内画出y=2x2、y=2(x-1)2、 y=2(x-1)2+1 的图象
x
-3 -2 -1
0
1
一元二次函数的图像与性质.docx

一元二次函数的图象和性质(-)二次函数基本知识1.二次函数的定义:形如y = 加+ C(QH O且为常数)的函数叫关于X的二次函数。
2.二次函数的解析式的三种形式(1)-般式(三点式):y = ax2+bx + c(a^O)f配方后为_____________________________ 。
其中顶点坐标为___________ ,对称轴为__________ 0(2)顶点式(配方式):y = a(x-h)2+k(a^o)f其中顶点坐标为_______________ ,对称轴为_______(3)两根式(零点式):y = a(x-x])(x-x2)(a^o),其中西‘吃是方程+Z?x + c = 0的两个根,同时也是二次函数的图像与兀轴交点(召,0),(花,0)的横坐标。
求函数解析式时,一般采用待定系数法3 •二次函数的图像和性质(1)二次函数y = ax2+bx + c(a^0)的图像是一条___________ ,其对称轴为_________ ,顶点坐标为 ________ ,开口方向由_____ 决定。
(2)二次函数y = ox? + bx + C(G H 0)的单调性以对称轴为分界。
在作二次函数草图时,往往抓住:开口方向,对称轴,与X轴交点,与『轴交点,顶点等。
(3)二次幣数y二处2+b兀+C(QH0),当△ = /?? _4QC>0时,图像与兀轴有两个交点M}(x,,0),,0),则\M^\=\X2-X\= J(血 + 西)2一4无內=J(--)2-4 -=血—仏_ _ \ a a \a\(4)关于二次函数y = /(x)的对称轴的判断方法:①若二次函数对定义域内所有兀,都有/(Xj) = /(X2),则其对称轴为兀二西[尢2②若二次函数对定义域内所有无,都有f(m+x) = f(m-x)1则其对称轴为x=m.4ac-b 24a(2)在闭区I 可n ]上的最值“轴变区间定” w + n③ 若二次函数对定义域内所有x,都有f(m+x) = f(n-x),则对称轴为% =——④.若二次函数对应方程为/(X)= 0两根为知兀2,则对称轴方程为:x =—---------二24.二次函数y = ax 2+bx+c(a^O)的最值 (1) 在(Y0,+00)上的最值二次函数加+C @H O)在闭区间[弘切上的最值问题,一般情况下,需要分三种情况讨论,依据对称轴与区间的位置关系:唸5,心存〃冷九再结合图像分析。
二次函数的图象与性质

例3:某工厂生产的某种产品按质量分为10个档次,第1档次 (最低档次)的产品一天能生产95件,每件利润6元.每提高一个 档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数, 且1≤x≤10),求出y关于x的函数关系式;
解:∵第一档次的产品一天能生产95件,每件利润6元, 每提高一个档次,每件利润加2元,但一天产量减少5件,
k 1 0,
解得 k=2;
(2)当k=2时,
将x=0.5代入函数关系式 y x2 2x 1
.
y 0.52 2 0.5 1 0.25
归纳总结
此类型题考查二次函数的概念,要抓住二次 项系数不为0及自变量指数为2这两个关键条件, 求出字母参数的值,得到函数解析式,再用代入 法将x的值代入其中,求出y的值.
∴第x档次,提高了(x-1)档,利润增加了2(x-1)元. ∴y=[6+2(x-1)][95-5(x-1)], 即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
(2)若生产第x档次的产品一天的总利润为1120元,求
该产品的质量档次.
解:由题意可得 -10x2+180x+400=1120,
分析:这种产品的原产量是20件, 一年后的产量是 20(1+x) 件,再经过一年后的产量是 20(1+x)2 件,
即两年后的产量y=_2_0_(_1_+_x_)_2 . 答:y=20x2+40x+20;
此式表示了两年后的产量y与计划增产的倍数x之间的关系, 对于x的每一个值,y都有唯一的一个对应值,即y是x的函数.
一般形式
右边是整式; 自变量的指数是2; 二次项系数a ≠0.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六讲二次函数的图象和性质【趣题引路】例生产某商品xt需费用1000+5x+110x2元,出售该商品xt时的价格是每吨a+xb元,其中a,b是常数,如果生产出的商品都能卖掉,并且当产量是150t时利润最大,•这时的价格是每吨40元,求a,b的值.解析设卖出xt的利润是y元,则y=x(a+xb)-(1000+5x+110x2)=(1b-110)x2+(a-5)x-1000.又由题设知,当x=150时,y最大,因此5150,112()1015040.abab-⎧-=⎪-⎪⎨⎪+=⎪⎩即30035,15040. abab⎧+=⎪⎪⎨⎪+=⎪⎩解得 a=45,b=-30.当b=-30时, 1b-110<0,∴函数有最大值.∴a=45,b=-30为所求.点评这是一个关于商品的利润问题,解决此类问题的关键是函数建模,使之转变为函数问题,利用一元二次函数的性质求解.二次函数的研究通常和一元二次方程、一元二次不等式等联系起来.【知识延伸】例1 已知二次函数y=ax2+bx+c的图象与x轴的一个交点坐标是(8,0),顶点坐标是(6,-12),求这个二次函数的解析式.解析 方法一:由题意可列方程组 22880,6,212.4a b c b a b c a⎧⎪⨯+⨯+=⎪⎪-=⎨⎪⎪-=-⎪⎩ 解得a=3,b=-3b,c=96.故函数解析式为y=3x 2-36x+96;方法二:设所求解析式为y=a(x-6)2-12.又图象过(8,0),∴a(8-6)2-12=0,∴a=3,故函数解析式为y=3x 2-36x+96;方法三:函数图象关于直线x=6对称,因此图象一定通过点(8,0)和点(4,0),即4,8是方程ax 2+bx+c=0的两个根,因而二次函数可以写成y=a(x-4)(x-8).又函数图象过(6,-12),∴a(6-4)(6-8)=-12.∴a=3.故函数解析式为y=3x 2-36x+96.点评在求二次函数解析式时,若已知抛物线上任意三点,常设一般式:y=a x 2+bx+c(•a ≠0);若已知顶点或对称轴,常设顶点式:y=a(x+m)2+n,其中(-m,n)为顶点;若已知抛物线与x 轴交点的坐标时,常设交点式:y=a(x-x 1)(x-x 2)(a ≠0).例2 已知抛物线y=x 2+px+q 上有一点M(x 0,y 0)位于x 轴下方,(1)求证:已知抛物线与x 轴有两个交点A(x 1,0),B(x 2,0),其中x 1<x 2;(2)求证:x 1<x 0<x 2;(3)当点M•为(1,-1999)时,求整数x 1,x 2.解析 (1)由已知,得022200000,4().24y p p q y x px q x <⎧⎪⎨-=++=+-⎪⎩ △=p 2-4q=4(x 0+2p )2-4y 0>0,即△>0, ∴方程x 2+px+q=0有两个实根,且不相等.不妨设x 1<x 2,抛物线与x 轴有两个交点A(x 1,0),B(x 2,0);(2)由韦达定理1212,.x x p x x q +=-⎧⎨=⎩又y0=x02+px0+q<0,即x02-(x1+x2)x0+x1x2<0,(x0-x1)(x0-x2)<0,即x1<x0<x2;(3)当点M为(1,-1999)时有x0=1,y0=-1999,则由x1,x2为整数,(x1-1)(x2-1)也为整数,且x1-1>x2-1,得1211999, 11,x x -=⎧⎨-=-⎩或1211,11999.xx-=⎧⎨-=-⎩解得122000, 0,x x =⎧⎨=⎩或122,1998.xx=⎧⎨=-⎩点评此题“△”的求值较新颖,值得借鉴;第(3)•问利用二次三项式的因式分解过渡自然.【好题妙解】佳题新题品味例设抛物线y=a x2+bx+c开口向下,与x轴交于-1与3处,试判断下列关系式哪些是正确的?(1)abc>0;(2)a+b+c=0;(3)a=-12b;(4)3b=2c;(5)a-b+c>0;(6)5a+b+c>0;(7)•c>2b;(8)9a+3b+c=0.解析由开口向下知,a<0.由于抛物线与x轴交于x1=-1与x2=3处.∴y=a(x-x1)(x-x2)=a(x+1)(x-3)=ax2-2ax-3a.即b=-2a,c=-3a.由此可知abc=6a3<0表明(1)错;a+b+c=-4a>0表示(2)错;b=-2a表明(3)对;3b=-6a,•2c=•-6a表示(4)对;a-b+c=0表明(5)错;5a+b+c=0表明(6)错;c-2b=a<0,(7)错;9a+3b+•c=0,(8)对.中考真题欣赏例(2003年北京市中考题)已知抛物线y=ax2+4ax+t与x轴一个交点为A(-1,0).(1)求抛物线与x轴另一个交点B的坐标;(2)D是抛物线与y轴交点,C是抛物线上一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线解析式;(3)E是第二象限内到x轴,y轴的距离之比为5:2的点,如果点E在(2)•中的抛物线上,且它与点A在抛物线对称轴同侧,问:在抛物线的对称轴上是否存在点P,•使△APE的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.解析(1)由已知,-1为方程ax2+4ax+t=0的一根,设另一根为x2,则-1+x2=-4aa=-4∴x2=-3,即抛物线与x轴另一交点为(-3,0);(2)由(1)知(-1)·x2=t a∴ t=3a.则抛物线解析式为y=ax2+4ax+3a,∴D为(0,3a).又AB∥CD ∴C为(-4,3a),∴│AB│=2,│CD│=4,梯形高为│3a│.∴9=242.3│a│,求得a=±1.故所求抛物线为y=x2+4x+3或y=-x2-4x-3;(3)设E(x0,y0)则y0= -52x0(x0<0).(i)若a=-1,则y0=-x02-4x0-3即-52x0=-x02-4x0-3,而此方程无实根;(ii)若a=1,则y0=x02+4x0+3,解方程-52x0=x02+4x0+3,得x01=-12,x02=-6(舍去).∴E(-12,54)∵AE长度一定,只须PA+AE最小.又点A关于x=-2的对称点为B(-3,0),∴PA+PE=PB+PE≥BE.∴P为BE与x=-2的交点时满足题设要求.不难求得BE解析式为y=12x+32,令x=-2,得y=1 2 ,∴P(-2, 1 2 ).即存在这样的点P(-2, 12)满足(3)要求.点评本题难点在(3),关键是将△APE周长最小的条件转化为B、P、E三点共线,•从而求点P.竞赛样题展示例1 (1997年陕西数学竞赛题)若二次函数y=ax 2+bx+c(a≠0)•的图象的顶点在第一象限,且过点(0,1)和(-1,0),则S=a+b+c 的值的变化范围是( )A.0<S<1B.0<S<2C.1<S<2D.-1<S<1解析 将(0,1),(-1,0)代入y=ax 2+bx+c 得1,0.c a b c =⎧⎨-+=⎩即1, 1.c a b =⎧⎨=-⎩ ∴S=a+b+c=2b.∵二次函数y=ax 2+bx+c 顶点在第一象限,∴-2b a>0,又a=b-1, ∴-2(1)b b ->0,即2b(b -1)<0. ∴0<b<1,即0<S<2.选B.点评本题只给出两点,不能求出a 、b 、c 具体的值,只能求出a 、b 、c 之间的关系,•据此再求S的取值范围.例2 (1993年江苏初中数学竞赛试题)已知mn 是两位数,二次函数y=x 2+mx+n •的图象与x 轴交于不同的两点,这两点间距离不超过2.(1)求证:0<m 2-4n≤4;(2)求出所有这样的两位数mn .解析 (1)设y=x 2+mx+n 的图象与x 轴的两交点为A(x 1,0),B(x 2,0),x 1•≠x 2,•则x 1,x 2为方程x 2+mx+n=0的两个不同实根.∴x 1+x 2=-m,x 1·x 2=n.又0<│x 1-x 2│≤2 即0<(x 1+x 2)2-4x 1x 2≤4,也即0<m 2-4n≤4;(2)∵m,n 为整数(m≠0),∴m 2-4n=1,2,3,4,而m 2被4除余0或1,故m 2-4n 被4除也余0或1,从而只能有m 2-•4n=1或m 2-4n=4.解这两个不定方程,得:1,0,m n =⎧⎨=⎩ 3,2,m n =⎧⎨=⎩ 5,6,m n =⎧⎨=⎩ 2,0,m n =⎧⎨=⎩ 4,3,m n =⎧⎨=⎩ 6,8.m n =⎧⎨=⎩ ∴所求两位数为10,32,56,20,43,68.点评一元二次函数y=ax 2+bx+c 与x 轴两交点的横坐标即是方程ax 2+bx+c=0的两根,利用韦达定理即可求解.全能训练A 卷1.已知函数y=(m 2+m)x 2+mx+4,(1)m 是何值时,y 是x 的一次函数?(2)m •是何值时,y 是x 的二次函数?2.已知抛物线y=23x 2与直线y=x+k 有交点,求k 的取值范围.3.已知二次函数的图象经过点(1,0)和(-1,8),且与抛物线y=2x2•的开口方向及形状相同.(1)求此二次函数解析式;(2)求其顶点坐标和与x轴交点坐标;(3)若将此抛物线绕顶点旋转180°后,求旋转后的抛物线的解析式.4.二次函数y=x2+bx+c的图象向左平移两个单位,再向上平移三个单位,•得到二次函数y=x2-2x+1,求b,c的值.5.已知抛物线y=x2+2x+(m-2),问:当m取何值时,抛物线与y轴的交点在x•轴的上方,在x轴的下方,抛物线过原点?6. 如图,抛物线y=ax2+bx+c的对称轴是x=1,则下列关系成立的是( )A.abc>0B.a+b+c<0C.a2<ab-acD.以上均不对A卷答案1.(1)m=-1时,y是x的一次函数;(2)m≠0,且m≠1时,y是x的二次函数.2.k≥-3 83.(1)y=2x2-4x+2. (2)(1,0),(1,0) (3)y=-2x2+4x-24.b=-6,c=6.5.在y=x2+2x+(m-2)中,令x=0,则y=m-2.当m-2>0,即m>2时,抛物线与y轴交于x轴上方;当m-2<0,即m<2时,抛物线与y轴交于x轴下方;当m-2=0,即m=2时,抛物线过原点.6.DB 卷1.设一元二次方程x 2+bx+c=0的两根为98,99,在二次函数y=x 2+bx+c 中,若x 取0,1,2,…,100,曲 则y 的值能被6整除的个数是( )A.33B.34C.65D.672.二次函数y=a 2x 2-4x+1有最小值-1,则a 的值是( ).A. B.D.±2 3.如图,已知抛物线y=12x 2+(k+12)x+(k+1)(k 为常数),与x 轴交于A(x 1,0),•B(x 2,0)(x 1<0<x 2)两点,与y 轴交于C 点,且满足(OA+OB)2=OC 2+16.(1)求此抛物线解析式;(2)设M 、N 是抛物线在x 轴上方的两点,且与x 轴的距离均为1,点P •是抛物线顶点,问:过M 、N 、C 三点的圆与直线CP 是否只有一个公共点C?试证明你的结论.PN M y x O CB A4.已知抛物线y=13x2+bx+c与x轴交于A(-3,0),与y轴交于点E(0,-1).(1)求此二次函数的解析式;(2)若点Q(m,n)在此抛物线上,且-3≤m≤3,求n的取值范围;(3)设点B是此抛物线与x轴的另一个交点,P是抛物线上异于点B的一个动点,•连结BP交y轴于点N(点N在点E的上方),若△AOE∽△BON,求点P的坐标.5.已知二次函数y=ax2+bx+c的图象的顶点是C,它与x轴有两个不相同的交点A和B.(1)若点C的横坐标是3,A,B两点的距离是8,求方程ax2-(6a-b)x+9a-3b+c=0的根;(2)若点C到x轴的距离等于A、B两点距离的k倍,求证:b2-4ac=16k2.B卷答案1.D 由已知可得b=-197,c=98×99,则y=x2-197x+98×99=x(x+1)-198x+98×99.要使6|y,则6|x(x+1).又2|x(x+1),只须3|x(x+1),则3|x或3|x+1.当3|x时,共有[1013]+1=34个,当3|x+1时,共有[1003]=33个。
