第6章含有耦合电感的电路例题
耦合电感_精品文档

线圈电流产生的磁通全部与耦合线圈交链Mmax =
;
K 近于1时称为紧耦合;K 值较小时称为松耦合;K=0 称
为无耦合。
上一页 返回
第二节 有耦合电感的正弦电路
含有耦合电感电路(简称互感电路)的正弦稳态计算可采用 相量法。分析时要注意耦合电感上的电压是由自感电压和互 感电压叠加而成的。根据电压、电流的参考方向及耦合电感 的同名端确定互感电压的方向是互感电路分析计算的难点。 由于耦合电感支路的电压不仅与本支路电流有关,还和与之 有耦合支路的电流有关,列写节点电压方程较困难,所以互 感电路的分析计算一般采用支路电流法(网孔法)。
第六章 耦 合 电 路
第一节 耦合电感 第二节 有耦合电感的正弦电路 第三节 空心变压器 第四节 理想变压器
第一节 耦合电感
一、互感
1. 互感现象 我们先观察下面这个实验。图6−1 所示的实验电路中,线
圈2 两端接一灵敏检流计。当开关S 闭合瞬间,可以观察到 检流计指针偏转一下之后又回到零位。发生这种现象的原因 是由于开关S 闭合的瞬间,线圈1 产生变化的磁通Φ 11,其 中的一部分磁通Φ 12与线圈2 交链,使线圈2 产生感应电动 势,因而产生感应电流使检流计指针偏转。S 闭合后,线圈 1 的电流不再发生变化,虽然仍有磁通与线圈2 交链,但该 磁通是不变化的,所以不产生感应电动势,没有电流流过检 流计,因而检流计的指针回到零位。
上一页 下一页 返回
第一节 耦合电感
在同频正弦稳态电路中,耦合电感的伏安关系可以用相量形 式表示,式(6−5)可表示为
(6−8)
例6−3 电路如图6−8 所示,已知R1=1 Ω,L1=L2=1 H, M=0.5 H,uS=10sin 4t。试求u2。
电路设计--含有耦合电感电路的计算

I 1 I2 I 3
异侧T型连接
U 13 j ( L1 M ) I 1 jM I 3 U 23 j ( L2 M ) I 2 jM I 3
L L +M M 11-
L L +M M 22-
M -M
小结: 同侧T型
L1 - M
L2 - M M
T型连接
同侧T型连接
异侧T型连接
去耦等效电路 同侧T型连接
U 13 jL1 I 1 jM I 2
İ1 İ3
İ2
j ( L1 M ) I 1 jM I 3 U 23 jL2 I 2 2 jM I 3
i º +
u _ º
M
i1 L1 * * i2 L2
di 1 di 2 u L1 M dt dt
di 1 ( L1 M ) M di dt dt
i2 = i - i1
di 2 di 1 u L2 M dt dt
di 2 ( L2 M ) M di dt dt M
i1 = i - i2
无互感时的阻抗小(电抗变小),这是由于互感的削弱作用, 它类似于串联电容的作用,常称为互感的“容性”效应。
思考题1
一个耦合电感,如何通过测量 电感值确定其同名端及互感值M?
L顺 L1 L2 2 M
L反 L1 L2 2 M
L顺 L反 M 4
2、耦合电感的并联电路
(1)同侧并联
i = i1 +i2
解得u, i的关系:
( L1 L2 M ) di u L1 L2 2 M dt
2
( L1 L2 M 2 ) Leq 0 L1 L2 2 M
10.2 含有耦合电感电路的计算
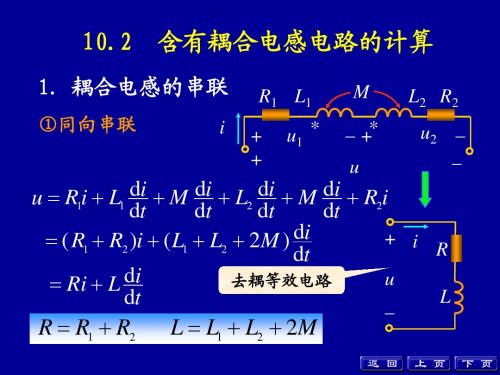
+ u –
L2
( L1L2 M ) Leq 0 L1 L2 2M
2
返 回 上 页 下 页
在正弦稳态电路中
i + u – i1 * L1
M i2
jMI U jL1 I 1 2 jMI U jL I
2 2
1
I I I 1 2
上式变形为:
+ u2 _
u1 N1 -n u2 N2
返 回 上 页 下 页
②变流关系
1 i1 (t ) i2 (t ) n
n:1 + i1 u1 _ *
*
i2 + u2 _
1 i1 (t ) i2 (t ) n
n:1 + i1 u1 _ * * i2
+ u2 _
返 回
上 页
下 页
R1 L1 i + + u1 * M – + u L2 R2 *u – 2 –
+ i R u – L
u R1i L1 di M di L2 di M di R2i dt dt dt dt ( R1 R2 )i ( L1 L2 2M ) di Ri L di dt dt
*
L2
i U jL1 I1 jM ( I - I1 ) jMI + j ( L1 M ) I 1 u U jL2 I 2 jM ( I - I 2 ) – jMI j ( L M ) I
2 2
-M
M
i2
i1 * * L1+M
R R1 R2
L L1 L2 2M
电路知识-20

电路知识-20(总分:100.00,做题时间:90分钟)一、计算题(总题数:11,分数:100.00)1.在下图所示含耦合电感的正弦交流电路中,已知i 1(t)=5cos40tA,i 2(t)=2cos40tA。
试求i(t)和u(t)。
(分数:5.00)__________________________________________________________________________________________ 正确答案:()解析:解:由题可知需要先计算电路的互感,分别为M 1 =7H,M 2 =12H。
再利用相量法计算i(t)和u(t)分别为:其瞬态为:i (t) =2.11cos40tAu(t)=285.7cos(40t-90°)V2.下图所示正弦交流电路,已知,L=0.1H,R=10Ω,C=10 -3 F。
求负载Z L为何值时它可以获得最大功率?最大功率为多少?并求此时电流i 2的瞬时值。
(分数:10.00)__________________________________________________________________________________________ 正确答案:()解析:解:根据理想变压器的原副边电压电流之间的关系,副边电阻Z L变化到原边中有等效阻抗4Z L。
原边等效电路如下图所示。
设。
可知从4Z L电阻两端的戴维南等效电路可得等效电阻为:开路电压为:根据最大功率传输定理,要计算电阻4Z L的最大功率,只要计算出电阻4Z L两端的戴维南等效电路,使电阻4Z L共轭的值等于戴维南等效电路的电阻值,此时电阻4Z L可获得最大功率。
代入已知条件,可得:则其最大功率为:则此时电流i 2的瞬时值为:3.下图所示电路,,求3Ω电阻吸收的功率。
(分数:10.00)__________________________________________________________________________________________ 正确答案:()解析:解:分析上图所示电路,可画出其去耦等效电路如下图所示。
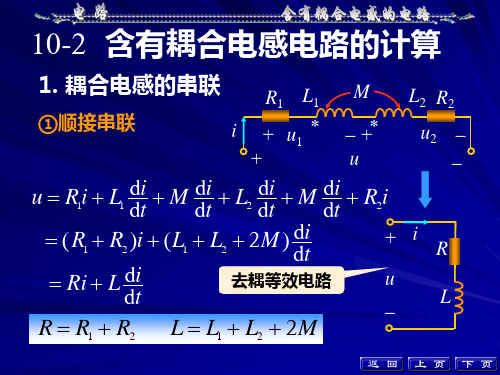
含有耦合电感电路的计算
返回 上页 下页
例2-3
求图示电路的开路电压。
I1 R1 • L1
M12
L2
•
Us +
解法1
_
M31 L3 *
*+
M23 U oc
_
•
I1
R1
U s
j(L1 L3
2M )31
Uoc jM12I1 jM 23I1 jM I 31` 1 jL3I1
j(L3 M12 M 23 M 31)Us R1 j(L1 L3 2M31)
M31 L3+M12 –M23
返回 上页 下页
L1–M12 +M23 –M13 L2–M12–M23 +M13
Us + I1 R1
_
+
L3+M12–M23 –M13
U
_
oc
I1
R1
U s
j(L1 L3
2M31)
U oc
j(L3 M12 M 23 M 31)Us R1 j(L1 L3 2M31)
C
返回 上页 下页
解
R1
+ + R2
i1 1uS - -ki12
* L1
M3
* L2
(R1 jL1)I1 CjL1I3 jM (I2 I3) US
(R2 jL2 )I2 jL2I3 jM (I1 I3) kI1
(
jL1
jL2
j1
C
)I3
jL1I1
jL2 I2
jM (I3 I1) jM (I3 I2 ) 0
R1 jL1
I + U 1 *•
+
jM
– *+
第六章含耦合电感电路的计算

结论:表示两个线圈相互作用,不再考虑实际绕向和相 对位置,只画出同名端及参考方向即可。
耦合电感的相量模型
i1 + u1 _ M i2 * L2
电路理论基础
* L1
u2 _
(1)施感电流均由同名端流入, 电压在同名端为“+‖,耦合电感的 + VCR时域形式: di1 di 2
M dt dt di 1 di 2 u2 M L2 dt dt u1 L1
L1:线圈1的自感系数;M21:线圈1对线圈2的互感系 数。(self-inductance coefficient) (mutual inductance coefficient) 单位:H 同理,当线圈2中通电流i2时会产生磁通22,12 。 i2 为时变时,线圈2和线圈1两端分别产生感应电压 u22 , u12 。
可以证明:M12= M21= M。
电路理论基础
当两个线圈同时通以电流时,每个线圈两端的电 压均包含自感电压和互感电压:
di1 di2 u1 u11 u12 L1 M dt dt di1 di2 u2 u21 u22 M L2 dt dt
理想耦合线圈 的伏安关系
上式体现了线圈间的耦合作用,每个线圈的端电压 是自感电压与互感电压的叠加。 互感的性质 ①从能量角度可以证明,对于线性电感 M12=M21=M ②互感系数 M 只与两个线圈的几何尺寸、匝数 、 相 互位置和周围的介质磁导率有关,如其他条件不变时, 有 M N1N2 (L N2)
电路理论基础
第六章 含耦合电感电路的计算
第六章
含耦合电感电路的计算
电路理论基础
6. 1 耦合电感 6. 2 含有耦合电感电路的计算 6. 3 空心变压器 6. 4 理想变压器
耦合电感的计算

在1≤t≤2s时 所以
i1 t (10t 20)
uab t R1i1 t 10 (10t 20) (100t 200)V di d ubc t L1 5 (10t 20) 50V dt dt uac t uab t ubc (t ) (100t 150)V d 10t 20 di1 ude t M 1 10V dt dt
①若两电流均从同名端流入(或流出),则磁通相助,互感 压降与自感压降同号,即自感压降取正号时互感压降亦取正 号,自感压降取负号时互感压降亦取负号。 ②若一个电流从互感线圈的同名端流入,另一个电流从互 感线圈的同名端流出,磁通相消,互感压降与自感压降异号, 即自感压降取正号时互感压降取负号,自感压降取负号时互 感压降取正号。只要按照上述方法书写,不管互感线圈给出 的是什么样的同名端位置,也不管两线圈上的电压、电流参 考方是否关联,都能正确书写出两线圈的电压、电流之间关 系式。
以u2中的互感压降部分为
M di1 dt
L2
di2 dt
。考
虑磁通相助情况,互感压降部分与自感压降部分同号,所 。将L2上自感压降部分与互
感压降部分代数和相加,即得L2上电压
di2 di1 u2 L2 M dt dt
此例是为了给读者起示范作用,所以列写的过程 较详细。以后再遇到写互感线圈上电压、电流微分关 系,线圈上电压、电流参考方向是否关联、磁通相助 或是相消的判别过程均不必写出,直接可写(对本互感
(6-6b)
图6.3 磁通相助的耦合电感
如果自感磁通与互感磁通的方向相反,即磁通相消, 如图6.3所示,耦合电感的电压、电流关系方程式为:
d 1 di 1 di 2 u1 L1 M dt dt dt d 2 di2 di1 u2 L2 M dt dt dt
含有耦合电感的电路学生用2
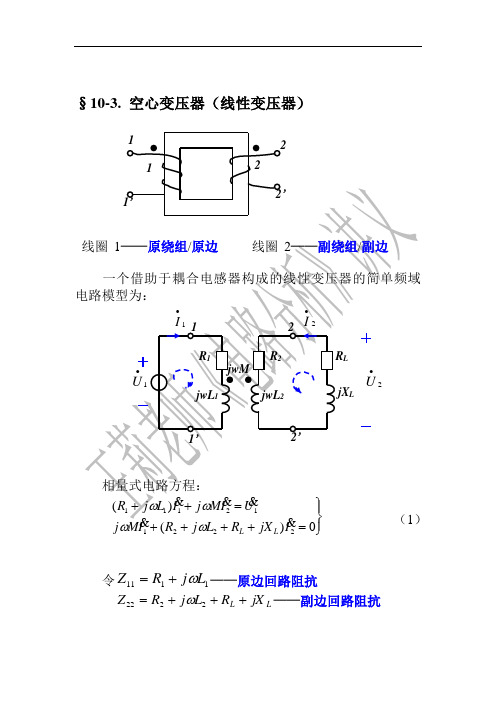
§10-3. 空心变压器(线性变压器)⎭2221L L令1111L j R Z ω+=──原边回路阻抗L L jX R L j R Z +++=2222ω──副边回路阻抗M j Z M ω= 则电路方程为:⎪⎭⎪⎬⎫=+=+022*******I Z I Z U I Z I Z M M (2)解方程(2)得22Z ──引入阻抗/反射阻抗(reflected impedance )即副边的回路阻抗通过互感反映到原边的等效阻抗。
注意:反射阻抗的性质与Z22相反; 由(4)得变压器副边的等效电路:2Z eq 11∙U Z M j ω∙LL jX222)(MLjRZeqωω++=L1SU∙22)(LjMωω︒∠=++︒∠=++=∙01011010)(222111j j L j M L j R U I sωωω A2112)(M U L j R M j I sωωω+-=∙Cj L j L j R ωωω1211+++ S U ∙112)(L j R M ωω++A jj j 01110102=+++︒∠=2112U L j R M j I s ωω+-=∙采用戴维南定理与最大功率传输定理。
解法1: 副边的去耦合等效电路其开路电压2M 最大功率(传输)为505.015.24142222max ==+⨯==S s M ocL U jU jX R U P∴ VU s 10=耦合系数Z L111S L M U jX R jX ∙+222ML X jX R ++2221121=⨯==L L M X X X k解法2:直接用受控源解 (1)移去L Z 后的电路如图示:等效阻抗 1122L L out jX R +j X j R M +++=1)(222)22(2222MMX j X R -++=R 1R 2当电路实现最大功率传输时5.15.2j Z Z L out +== 由实部、虚部分别相等,得⎪⎪⎪⎨⎧+=-=+5.125.22222M M X X R原边匝数N 1副边匝数N 2电路模型:1将(3)代入(2)得:221212∙∙∙∙+-=I L j L j I M j U M j U ωωωω 1 2i i22122112∙∙∙∙+-=I L j L I M j L U M U ωω由于理想变压器是全耦合变压器,耦合因数k=1,即21L L M =铁芯变压器是近似的理想变压器,广泛用于电力和电子工业中。
