二次函数测试~B6BE8
二次函数测试题(含答案)
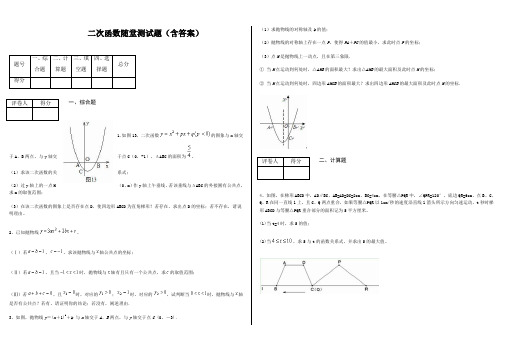
二次函数随堂测试题(含答案)一、综合题1.如图13,二次函数的图象与x 轴交于点C (0,-1),ΔABC 的面积为。
于A 、B 两点,与y 轴交(1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴上午垂线,若该垂线与ΔABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D ,使四边形ABCD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由。
2、已知抛物线,(Ⅰ)若,,求该抛物线与轴公共点的坐标;(Ⅱ)若,且当时,抛物线与轴有且只有一个公共点,求的取值范围;(Ⅲ)若,且时,对应的;时,对应的,试判断当时,抛物线与轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.3、如图,抛物线y =(x +1)2+k 与x 轴交于A 、B 两点,与y 轴交于点C (0,-3).(1)求抛物线的对称轴及k 的值;(2)抛物线的对称轴上存在一点P ,使得PA +PC 的值最小,求此时点P 的坐标; (3)点M 是抛物线上一动点,且在第三象限.① 当M 点运动到何处时,△AMB 的面积最大?求出△AMB 的最大面积及此时点M 的坐标;② 当M 点运动到何处时,四边形AMCB 的面积最大?求出四边形AMCB 的最大面积及此时点M 的坐标.二、计算题4、如图,在梯形ABCD 中,AD ∥BC ,AB=AD=DC=2cm ,BC=4cm ,在等腰△PQR 中,∠QPR=120°,底边QR=6cm ,点B 、C 、Q 、R 在同一直线l 上,且C 、Q 两点重合,如果等腰△PQR 以1cm/秒的速度沿直线l 箭头所示方向匀速运动,t 秒时梯形ABCD 与等腰△PQR 重合部分的面积记为S 平方厘米。
(1)当t=4时,求S 的值;(2)当,求S 与t 的函数关系式,并求出S 的最大值。
5、王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线,其中(m)是球的飞行高度,(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.(1)请写出抛物线的开口方向、顶点坐标、对称轴.(2)请求出球飞行的最大水平距离.(3)若王强再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线,求出其解析式.6、某宾馆有客房间,当每间客房的定价为每天元时,客房会全部住满.当每间客房每天的定价每涨元时,就会有间客房空闲.如果旅客居住客房,宾馆需对每间客房每天支出元的各种费用.(1)请写出该宾馆每天的利润(元)与每间客房涨价(元)之间的函数关系式;(2)设某天的利润为元,元的利润是否为该天的最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时客房定价应为多少元?(3)请回答客房定价在什么范围内宾馆就可获得利润?7、在直角中,,直角边与直角坐标系中的轴重合,其内切圆的圆心坐标为,若抛物线的顶点为A。
二次函数测试题及答案

二次函数测试题及答案一、选择题(每题3分,共30分)1. 以下哪个选项是二次函数的一般形式?A. y = 2x + 1B. y = x^2 + 3x + 2C. y = 3x^3 - 5D. y = 4/x答案:B2. 二次函数y = ax^2 + bx + c的顶点坐标为(h, k),那么h的值为:A. -b/2aB. -b/aC. b/2aD. b/a答案:C3. 二次函数y = 2x^2 - 4x + 3的对称轴方程是:A. x = 1B. x = -1C. x = 2D. x = -2答案:A4. 如果二次函数y = ax^2 + bx + c的图象开口向上,那么a的值:A. 大于0B. 小于0C. 等于0D. 可以是任意实数答案:A5. 二次函数y = -x^2 + 4x - 3的顶点坐标是:A. (1, 2)B. (2, 1)C. (3, 0)D. (3, 4)答案:C6. 二次函数y = 3x^2 - 6x + 5的图象与x轴的交点个数是:A. 0个B. 1个C. 2个D. 3个答案:C7. 二次函数y = x^2 - 4x + 4的最小值是:A. 0B. 4C. -4D. 1答案:A8. 二次函数y = 2x^2 - 4x + 3的图象开口方向是:A. 向上B. 向下C. 向左D. 向右答案:A9. 二次函数y = -x^2 + 2x + 3的图象与y轴的交点坐标是:A. (0, 3)B. (0, -3)C. (0, 5)D. (0, -5)答案:A10. 二次函数y = 5x^2 - 10x + 8的图象与x轴的交点坐标是:A. (2, 0)B. (-2, 0)C. (1, 0)D. (-1, 0)答案:A二、填空题(每题4分,共20分)1. 二次函数y = ax^2 + bx + c的图象开口向上,且经过点(2, 0),则a的值至少为______。
答案:02. 二次函数y = 2x^2 - 4x + 3的顶点坐标是(______, ______)。
(完整版)九年级二次函数综合测试题及答案,推荐文档

2、4. 抛物线
的对称轴是( )
A. x=-2 B.x=2 C. x=-4 D. x=4 5. 已知二次函数 y=ax2+bx+c 的图象如图所示,则下列结论中,正确的是( A. ab>0,c>0 B. ab>0,c<0 C. ab<0,c>0 D. ab<0,c<0
21.已知:如图,二次函数 y=ax2+bx+c 的图象与 x 轴交于 A、B 两点,其中 A 点坐标为(-1,0),点 C(0,5),另抛物线经过点(1,8),M 为它的顶点.
我去 人 (1也)求就抛物有线的人解!析式为; UR扼腕入站内信不存在向你偶同意调剖沙
(2)求△MCB 的面积 S△MCB.
6. 二次函数 y=ax2+bx+c 的图象如图所示,则点
A. 一 B. 二 C. 三 D. 四
在第___象限( )
7. 如图所示,已知二次函数 y=ax2+bx+c(a≠0)的图象
的顶
点 P 的横坐标是 4,图象交 x 轴于点 A(m,0)和点 B,且
m>4,那么 AB 的长是( )
10.把抛物线
的图象向左平移 2 个单位,再向上
平移 3 个单位,所得的抛物线的函数关系式是( )
A.
B.
C.
D.
二、填空题(每题 4 分,共 32 分) 11. 二次函数 y=x2-2x+1 的对称轴方程是______________.
12. 若将二次函数 y=x2-2x+3 配方为 y=(x-h)2+k 的形式,则 y=________.
二次函数测试卷(含答案解析)

新华师大版九年级下册数学摸底试卷(四)第26章二次函数测试卷 A 卷姓名____________ 时间: 90分钟 满分:120分 总分____________一、选择题(每小题4分,共60分)1. 如图是二次函数c bx ax y ++=2图象的一部分,且过点A (3 , 0),二次函数图象的对称轴是直线1=x ,下列结论正确的是 【 】(A )ac b 42< (B )0>ac (C )02=-b a(D )0=+-c b a2. 如图所示,抛物线c bx ax y ++=2与两坐标轴的交点分别为A 、B 、C ,且1==OC OA ,则下列关系中正确的是 【 】(A )1-=+b a (B )1-=-b a (C )a b 2<(D )0<ac 3. 如图,在二次函数c bx ax y ++=2的图象中,刘星同学观察得出了下面四个结论:①042>-ac b ; ②1>c ; ③02<-b a ; ④0<++c b a .你认为错误的有 【 】(A )2个(B )3个(C )4个(D )1个4. 如图,已知抛物线c bx ax y ++=2,则下列结论:①0<abc ;②02>+b a ;③02<-b a ;④0>++c b a ;⑤0<+-c b a .其中正确的有【 】(A )1个(B )2个(C )3个(D )4个第 1 题图第 2 题图5. 若抛物线c ax ax y +-=22经过点()0,1-,则方程022=+-c ax ax 的解为 【 】(A )1,321-=-=x x (B )3,121==x x (C )3,121=-=x x(D )1,321=-=x x 6. 抛物线c bx ax y ++=2的对称轴为直线1=x ,与x 轴的一个交点坐标为()0,1-,抛物线的一部分如图所示,下列结论:①24b ac <; ②方程02=++c bx ax 的两个根是3,121=-=x x ;③03>+c a ; ④当0>y 时,x 的取值范围是1-≤3<x ;⑤当0<x 时,y 随x 的增大而增大.其中正确结论的个数是 【 】(A )4个(B )3个(C )2个(D )1个7. 如图,抛物线x x y 421+-=和直线x y 22=,当21y y >时,x 的取值范围是 【 】(A )20<<x (B )0<x 或4>x (C )0<x 或2>x(D )40<<x第 3 题图第 4 题图第 6题图8. 函数c bx x y ++=2与函数x y =的图象如图所示,有以下结论:①042>-c b ; ②0=+c b ; ③0<b ; ④方程组⎩⎨⎧=++=x y c bx x y 2的解为⎩⎨⎧==1111y x ,⎩⎨⎧==3322y x ; ⑤当31<<x 时,()012>+-+c x b x .其中正确的是 【 】(A )①②③ (B )②③④(C )③④⑤(D )②③⑤9. 将如图所示的抛物线先向右平移1个单位,再向下平移2个单位,经此变换后的抛物线的解析式为【 】(A )()23432+--=x y (B )()21432+--=x y (C )()23322+--=x y(D )()21322+--=x y 10. 已知二次函数c bx ax y ++=2的图象如图所示,若方程()02≠=++k k c bx ax 有两个不相等的实数根,则k 的取值范围是 【 】(A )3-<k(B )3->k(C )3<k (D )3>k 11. 抛物线c bx ax y ++=2的对称轴为直线1-=x ,其一部分图象如图所示,下列判断中:①0>abc ; ②042>-ac b ; ③039=+-c b a ; ④025=+-c b a ;⑤若点()1,5.0y -,()2,2y -均在抛物线上,则21y y >.其中正确的个数为【 】第 8 题图第 9 题图(A )2 (B )3(C )4 (D )512. 如图,已知二次函数c bx ax y ++=2()0≠a 的图象与x 轴交于A 、B 两点,对称轴为直线2=x ,下列结论:①0>abc ;②04=+b a ;③若点A 的坐标为()0,1-,则线段5=AB ;④若点()11,y x M ,()22,y x N 在该函数的图象上,且满足32,101<<<<x x ,则21y y <.其中正确结论的序号为 【 】(A )①②(B )②③(C )③④(D )②④13. 如图所示的是二次函数c bx ax y ++=2的图象,下列结论:①二次三项式c bx ax ++2的最小值为4; ②024<++c b a ;③一元二次方程12=++c bx ax 的两根之和为1-;④使y ≤3成立的x 的取值范围是x ≥0.其中正确结论的个数为 【 】(A )1(B )2(C )3(D )414. 如图,抛物线c bx ax y ++=2经过点()0,1-,对称轴为l ,则下列结论:①0>abc ;②0=+-c b a ;③02<+c a ;④0<+b a .其中正确的结论【 】(A )①③(B )②③(C )②④ (D )②③④第 11 题图第 12 题图第 13 题图第 14 题图15. 如图,抛物线12+=x y 与双曲线xky =的交点A 的横坐标是1,则关于x 的不等式012<++x xk的解集是 【 】(A )1>x(B )1-<x(C )10<<x(D )01<<-x二、填空题(每小题4分,共 60分)16. 已知二次函数132+-=x x y ,当x ≥6时,它的最小值为_________.17. 已知抛物线42-=x y 与x 轴交于B 、C 两点,顶点为A ,则△ABC 的周长为_________.18. 已知抛物线c bx ax y ++=2与x 轴的交点是()0,4-,(2 , 0),则这条抛物线的对称轴是直线_________.19. 已知抛物线12+-+-=k kx x y 的顶点在x 轴上,则=k _________.20. 若二次函数在23=x 时,有最小值41-,且函数的图象经过点(0 , 2),则此函数的表达式为________________.21. 若抛物线122-+=x ax y 与x 轴有交点,则a 的取值范围是_________.22. 如图,点P 是第一象限内抛物线1412-=x y 上的任意一点,x PA ⊥轴于点A ,则=-PA OP _________.23. 点()a P ,1,()b Q ,1-都在抛物线12+-=x y 上,则PQ 的长为_________.24. 将抛物线()5322+--=x y 绕顶点旋转︒180后的抛物线的表达式为________________.25. 若抛物线122-++=m x x y 与x 轴有两个不同的交点,则m 的取值范围是__________.26. 若二次函数mx x y +=2图象的对称轴是直线3=x ,则关于x 的方程72=+mx x 的解为____________.第 23 题图27. 已知二次函数m x x y +-=32的图象与x 轴的一个交点为(1 , 0),则关于x 的一元二次方程032=+-m x x 的两实数根是____________.28. 若抛物线2222+++=a ax ax y 与x 轴的一个交点为()0,3-,则另一个交点为_________.29. 如图,抛物线c bx ax y ++=2的顶点为()3,2-,若k c bx ax =++2有三个不相等的实数根,则k 的值是_________.30. 如图,抛物线c bx x y ++-=221与x 轴交于A 、B 两点,与y 轴交于点C ,且3,2==OC OA ,点D (2 , 2)在抛物线上,点P 是抛物线的对称轴上一动点,当△BDP 的周长最小时,点P 的坐标为__________.第 29 题图第 30 题图新华师大版九年级下册数学摸底试卷(四)第26章 二次函数测试卷 A 卷参考答案一、选择题(每小题3分,共30分)题号12345答案DBDDC题号678910答案BABAD题号1112131415答案ADADD二、填空题(每小题3分,共15分)16. 1917. 454+18. 1-=x19. 220. 41232-⎪⎭⎫ ⎝⎛-=x y 21. a ≥1-且0≠a 22. 2 23. 224. ()5322+-=x y25. 2<m 26. 7,121=-=x x 27. 2,121==x x28. ()0,129. 330. ⎪⎭⎫ ⎝⎛45,21部分选择题、填空题答案提示4. 如图,已知抛物线c bx ax y ++=2,则下列结论:①0<abc ;②02>+b a ;③02<-b a ;④0>++c b a ;⑤0<+-c b a .其中正确的有 【 】(A )1个 (B )2个(C )3个(D )4个解析 对于结论①,由0,0,0<>>c b a得第 4 题图0<abc ,故结论①正确;对于结论②,由0,0>>b a ,知02>+b a ,故结论②正确;对于结论③,由12->-ab得12<a b ,因为0>a ,所以a b 2<,02>-b a ,故结论③错误;对于结论④,因为点()c b a ++,1在第一象限,所以0>++c b a ,故结论④正确;对于结论⑤,因为点()c b a +--,1在第三象限,所以0<+-c b a ,故结论⑤正确.综上所述,正确的结论是①②④⑤,共4个.∴选择答案【 D 】.5.若抛物线c ax ax y +-=22经过点()0,1-,则方程022=+-c ax ax 的解为【 】(A )1,321-=-=x x (B )3,121==x x (C )3,121=-=x x (D )1,321=-=x x 解析 该抛物线的对称轴为:直线122=--=aax 设抛物线与x 轴的另一个交点为()0,2x ,则有1212=+-x ,解之得:32=x ∴抛物线与x 轴的另一个交点为()0,3∴022=+-c ax ax 的解为3,121=-=x x ∴选择答案【 C 】.6. 抛物线c bx ax y ++=2的对称轴为直线1=x ,与x 轴的一个交点坐标为()0,1-,抛物线的一部分如图所示,下列结论:①24b ac <; ②方程02=++c bx ax 的两个根是3,121=-=x x ;③03>+c a ; ④当0>y 时,x 的取值范围是1-≤3<x ;⑤当0<x 时,y 随x 的增大而增大.其中正确结论的个数是 【 】(A )4个 (B )3个(C )2个(D )1个解析 对于结论①,因为抛物线与x 轴有两个不同的交点,所以042>-=∆ac b ∴24b ac <,故结论①正确;对于结论②,抛物线与x 轴的一个交点为()0,1-,设另一个交点为()0,2x ,则有1212=+-x ,解之得:32=x ∴抛物线与x 轴的另一个交点为()0,3∴02=++c bx ax 的解是3,121=-=x x ;故结论②正确;对于结论③,∵抛物线的对称轴为直线1=x ∴ab 2-=第 6 题图∵抛物线经过点()0,1-∴0=+-c b a ∴bc a =+∴023=-=++=+b b a c a c a 故结论③错误;对于结论④,当0>y 时,x 的取值范围是31<<-x ,故结论④错误;对于结论⑤,当1<x 时,y 随x 的增大而增大∴当0<x 时,y 随x 的增大而增大故结论⑤正确.综上所述,正确的结论是①②⑤,共3个.∴选择答案【 B 】.8. 函数c bx x y ++=2与函数x y =的图象如图所示,有以下结论:①042>-c b ; ②0=+c b ;③0<b ; ④方程组⎩⎨⎧=++=x y cbx x y 2的解为⎩⎨⎧==1111y x ,⎩⎨⎧==3322y x ;⑤当31<<x 时,()012>+-+c x b x .其中正确的是 【 】(A )①②③ (B )②③④(C )③④⑤(D )②③⑤解析 对于结论①,因为抛物线与x 轴无交点∴042<-=∆c b 故结论①错误;对于结论②,因为抛物线c bx x y ++=2经过点()1,1∴11=++c b ∴0=+c b 故结论②正确;对于结论③,因为抛物线的对称轴在y 轴右侧,所以二次项系数与一次项系数异号∵01>∴0<b 故结论③正确;对于结论④,因为抛物线c bx x y ++=2与直线x y =的交点为()1,1和()3,3∴方程组⎩⎨⎧=++=x y cbx x y 2的解为⎩⎨⎧==1111y x ,⎩⎨⎧==3322y x ;故结论④正确;对于结论⑤,当31<<x 时,x c bx x <++2∴()012<+-+c x b x 故结论⑤正确.综上所述,正确的结论是②③④.∴选择答案【 B 】.10. 已知二次函数c bx ax y ++=2的图象如第 8 题图图所示,若方程()02≠=++k k c bx ax 有两个不相等的实数根,则k 的取值范围是 【 】(A )3-<k (B )3->k (C )3<k(D )3>k 解析 构造函数c bx ax y ++=2,其图象为:保留函数c bx ax y ++=2的图象位于x 轴上及其上方的图象不变,把x 轴下方的图象翻折到x 轴上方,如图所示.∵0≠k ∴当3>k 时,函数c bx ax y ++=2的图象与直线k y =有两个不同的交点,即方程()02≠=++k k c bx ax 有两个不相等的实数根.∴选择答案【 D 】.变式 已知二次函数c bx ax y ++=2的图象如图所示,若方程k c bx ax =++2有两个不相等的实数根,则k 的取值范围是______.(A )3-<k (B )3->k (C )3<k(D )3>k 11. 抛物线c bx ax y ++=2的对称轴为直线1-=x ,其一部分图象如图所示,下列判断中:①0>abc ; ②042>-ac b ;③039=+-c b a ; ④025=+-c b a ;⑤若点()1,5.0y -,()2,2y -均在抛物线上,则21y y >.其中正确的个数为 【 】(A )2(B )3(C )4(D )5解析 对于结论①,因为0,0,0<>>c b a ,所以0<abc ,故结论①错误;第 11 题图对于结论②,因为抛物线c bx ax y ++=2与x 轴有两个不同的交点,所以042>-ac b 故结论②正确;对于结论③,设抛物线与x 轴的另一个交点为()0,2x ,则有1212-=+x ,解之得:3-=x ∴抛物线与x 轴的另一个交点为()0,3-∴039=+-c b a 故结论③正确;对于结论④,∵抛物线的对称轴为直线1-=x ∴12-=-ab∴ab 2=∵抛物线经过点()0,1∴0=++c b a ∴0<-=+b c a ∴04525<+=+-=+-c a c a a c b a 故结论④错误;对于结论⑤,∵抛物线开口向上,点()2,2y -离对称轴较远∴21y y <故结论⑤错误.综上所述,正确的结论是②③,共2个.∴选择答案【 A 】.14. 如图,抛物线c bx ax y ++=2经过点()0,1-,对称轴为l ,则下列结论:①0>abc ;②0=+-c b a ;③02<+c a ;④0<+b a .其中正确的结论 【 】(A )①③ (B )②③ (C )②④(D )②③④解析 对于结论①,因为0,0,0>><c b a ,所以0<abc ,故结论①错误;对于结论②,因为抛物线经过点()0,1-,所以0=+-c b a ,故结论②正确;对于结论③,∵0=+-c b a ∴bc a =+∵点()c b a ++24,2在第四象限∴0)(2424<+++=++c c a a c b a ∴0236<+=+c a c a 故结论③正确;对于结论④,∵02<+c a ,b c a =+∴0<+=++b a c a a 故结论④正确.综上所述,正确的结论是②③④.∴选择答案【 D 】.19. 已知抛物线12+-+-=k kx x y 的顶点在x 轴上,则=k _________.解析 若抛物线的顶点在x 轴上,则抛物线第 14 题图与x 轴只有一个交点∴()()021422=-=--=∆k k k ∴221==k k ∴2=k .21. 若抛物线122-+=x ax y 与x 轴有交点,则a 的取值范围是_________.解析 本题为易错题,许多学生忽视0≠a 这个约束条件.由题意可得:⎩⎨⎧≥+=∆≠0440a a 解之得:a ≥1-且0≠a 学生整理用图。
初中数学二次函数经典测试题及解析

初中数学二次函数经典测试题及解析初中数学二次函数经典测试题及解析一、选择题1.若二次函数22y ax ax c =-+的图象经过点(﹣1,0),则方程220ax ax c -+=的解为()A .13x =-,21x =-B .11x =,23x =C .11x =-,23x =D .13x =-,21x =【答案】C 【解析】【分析】【详解】∵二次函数22y ax ax c =-+的图象经过点(﹣1,0),∴方程220ax ax c -+=一定有一个解为:x=﹣1,∵抛物线的对称轴为:直线x=1,∴二次函数22y ax ax c =-+的图象与x 轴的另一个交点为:(3,0),∴方程220ax ax c -+=的解为:11x =-,23x =.故选C .考点:抛物线与x 轴的交点.2.抛物线y =-x 2+bx +3的对称轴为直线x =-1.若关于x 的一元二次方程-x 2+bx +3﹣t =0(t 为实数)在﹣2<x <3的范围内有实数根,则t 的取值范围是() A .-12<t ≤3 B .-12<t <4C .-12<t ≤4D .-12<t <3【答案】C 【解析】【分析】根据给出的对称轴求出函数解析式为y =-x 2?2x +3,将一元二次方程-x 2+bx +3?t =0的实数根看做是y =-x 2?2x +3与函数y =t 的交点,再由﹣2<x <3确定y 的取值范围即可求解. 【详解】解:∵y =-x 2+bx +3的对称轴为直线x =-1,∴b =?2,∴y =-x 2?2x +3,∴一元二次方程-x 2+bx +3?t =0的实数根可以看做是y =-x 2?2x +3与函数y =t 的交点,∵当x =?1时,y =4;当x =3时,y =-12,∴函数y =-x 2?2x +3在﹣2<x <3的范围内-12<y≤4,∴-12<t≤4,故选:C .【点睛】本题考查二次函数的图象及性质,能够将方程的实数根问题转化为二次函数与直线的交点问题是解题关键.3.要将抛物线2y x =平移后得到抛物线223y x x =++,下列平移方法正确的是()A .向左平移1个单位,再向上平移2个单位B .向左平移1个单位,再向下平移2个单位 C .向右平移1个单位,再向上平移2个单位D .向右平移1个单位,再向下平移2个单位【答案】A 【解析】【分析】原抛物线顶点坐标为(0,0),平移后抛物线顶点坐标为(-1,2),由此确定平移办法.【详解】y=x 2+2x+3=(x+1)2+2,该抛物线的顶点坐标是(-1,2),抛物线y=x 2的顶点坐标是(0,0),则平移的方法可以是:将抛物线y=x 2向左平移1个单位长度,再向上平移2个单位长度.故选:A .【点睛】此题考查二次函数图象与几何变换.解题关键是将抛物线的平移问题转化为顶点的平移,寻找平移方法.4.如图,抛物线2119y x =-与x 轴交于A B ,两点,D 是以点()0,4C 为圆心,1为半径的圆上的动点,E 是线段AD 的中点,连接,OE BD ,则线段OE 的最小值是()A .2B 32C .52D .3【答案】A 【解析】【分析】根据抛物线解析式即可得出A 点与B 点坐标,结合题意进一步可以得出BC 长为5,利用三角形中位线性质可知OE=12BD ,而BD 最小值即为BC 长减去圆的半径,据此进一步求解即可. 【详解】∵2119y x =-,∴当0y =时,21019x =-,解得:=3x ±,∴A 点与B 点坐标分别为:(3-,0),(3,0),即:AO=BO=3,∴O 点为AB 的中点,又∵圆心C 坐标为(0,4),∴OC=4,∴BC 长度=2205OB C +=,∵O 点为AB 的中点,E 点为AD 的中点,∴OE 为△ABD 的中位线,即:OE=12BD ,∵D 点是圆上的动点,由图可知,BD 最小值即为BC 长减去圆的半径,∴BD 的最小值为4,∴OE=12BD=2,即OE 的最小值为2,故选:A. 【点睛】本题主要考查了抛物线性质与三角形中位线性质的综合运用,熟练掌握相关概念是解题关键.5.如图是抛物线y =ax 2+bx +c (a ≠0)的部分图象,其顶点坐标为(1,m ),且与x 铀的一个交点在点(3,0)和(4,0)之间,则下列结论:①abc >0;②a ﹣b +c >0;③b 2=4a (c ﹣m );④一元二次方程ax 2+bx +c =m +1有两个不相等的实数根,其中正确结论的个数是()A .1B .2C .3D .4【解析】【分析】根据抛物线的开口方向和与坐标轴的交点及对称轴可判别a ,b ,c 的正负;根据抛物线的对称轴位置可判别在x 轴上另一个交点;根据抛物线与直线y=m 的交点可判定方程的解.【详解】∵函数的图象开口向上,与y 轴交于负半轴∴a>0,c<0∵抛物线的对称轴为直线x=-2b a=1 ∴b<0∴abc >0;①正确;∵抛物线与x 轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x=1,∴抛物线与x 轴的另一个交点在点(-2,0)和(-1,0)之间.∴当x=-1时,y<0,即a-b+c<0,所以②不正确;∵抛物线的顶点坐标为(1,m ),∴244ac b a=m ,∴b 2=4ac-4am=4a (c-m ),所以③正确;∵抛物线与直线y=m 有一个公共点,∴抛物线与直线y=m+1有2个公共点,∴一元二次方程ax 2+bx+c=m+1有两个不相等的实数根,所以④正确.故选:C .【点睛】考核知识点:抛物线与一元二次方程.理解二次函数性质,弄清抛物线与一元二次方程的关系是关键.6.如图,二次函数y =ax 2+bx +c 的图象过点(-1,0)和点(3,0),有下列说法:①bc <0;②a +b +c >0;③2a +b =0;④4ac >b 2.其中错误的是( )A .②④B .①③④C .①②④D .②③④【答案】C 【解析】利用抛物线开口方向得到0a >,利用对称轴在y 轴的右侧得到0b <,利用抛物线与y 轴的交点在x 轴下方得到0c <,则可对A 进行判断;利用当1x =时,0y <可对B 进行判断;利用抛物线的对称性得到抛物线的对称轴为直线12bx a=-=,则可对C 进行判断;根据抛物线与x 轴的交点个数对D 进行判断.【详解】解:Q 抛物线开口向上,0a ∴>,Q 对称轴在y 轴的右侧,a ∴和b 异号,0b ∴<,Q 抛物线与y 轴的交点在x 轴下方,0c ∴<,0bc ∴>,所以①错误;Q 当1x =时,0y <,0a b c ∴++<,所以②错误; Q 抛物线经过点(1,0)-和点(3,0),∴抛物线的对称轴为直线1x =,即12ba-=,20a b ∴+=,所以③正确; Q 抛物线与x 轴有2个交点,∴△240b ac =->,即24ac b <,所以④错误.综上所述:③正确;①②④错误.故选:C .【点睛】本题考查了二次函数图象与系数的关系:对于二次函数2(0)y ax bx c a =++≠,二次项系数a 决定抛物线的开口方向和大小;一次项系数b 和二次项系数a 共同决定对称轴的位置(左同右异).常数项c 决定抛物线与y 轴交点(0,)c .抛物线与x 轴交点个数由△决定.7.如图是抛物线y=ax 2+bx+c (a≠0)的部分图象,其顶点是(1,n ),且与x 的一个交点在点(3,0)和(4,0)之间,则下列结论:①a -b+c >0;②3a+b=0;③b 2=4a (c-n );④一元二次方程ax 2+bx+c=n-1有两个不等的实数根.其中正确结论的个数是()A .1B .2C .3D .4【答案】C 【解析】【分析】利用抛物线的对称性得到抛物线与x 轴的另一个交点在点(-2,0)和(-1,0)之间,则当x=-1时,y>0,于是可对①进行判断;利用抛物线的对称轴为直线x=-2ba=1,即b=-2a ,则可对②进行判断;利用抛物线的顶点的纵坐标为n 得到244ac b a-=n ,则可对③进行判断;由于抛物线与直线y=n 有一个公共点,则抛物线与直线y=n-1有2个公共点,于是可对④进行判断.【详解】∵抛物线与x 轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x=1,∴抛物线与x 轴的另一个交点在点(-2,0)和(-1,0)之间.∴当x=-1时,y >0,即a-b+c >0,所以①正确;∵抛物线的对称轴为直线x=-2ba=1,即b=-2a ,∴3a+b=3a-2a=a ,所以②错误;∵抛物线的顶点坐标为(1,n ),∴244ac b a-=n ,∴b 2=4ac-4an=4a (c-n ),所以③正确;∵抛物线与直线y=n 有一个公共点,∴抛物线与直线y=n-1有2个公共点,∴一元二次方程ax 2+bx+c=n-1有两个不相等的实数根,所以④正确.故选C .【点睛】本题考查了二次函数图像与系数的关系,熟练掌握二次函数性质是解题的关键.8.如图,抛物线y=ax 2+bx+c (a≠0)过点(1,0)和点(0,﹣2),且顶点在第三象限,设P=a ﹣b+c ,则P 的取值范围是( )A .﹣4<P <0B .﹣4<P <﹣2C .﹣2<P <0D .﹣1<P <0【答案】A 【解析】【分析】【详解】解:∵二次函数的图象开口向上,∴a >0.∵对称轴在y 轴的左边,∴b2a-<0.∴b >0.∵图象与y 轴的交点坐标是(0,﹣2),过(1,0)点,代入得:a+b ﹣2=0.∴a=2﹣b ,b=2﹣a .∴y=ax 2+(2﹣a )x ﹣2.把x=﹣1代入得:y=a ﹣(2﹣a )﹣2=2a ﹣4,∵b >0,∴b=2﹣a >0.∴a <2.∵a >0,∴0<a <2.∴0<2a <4.∴﹣4<2a ﹣4<0,即﹣4<P <0.故选A .【点睛】本题考查二次函数图象与系数的关系,利用数形结合思想解题是本题的解题关键.9.已知二次函数y =ax 2+bx +c 的图象如图所示,有以下结论:①a +b +c <0;②a ﹣b +c >1;③abc >0;④9a ﹣3b +c <0;⑤c ﹣a >1.其中所有正确结论的序号是( )A .①②B .①③④C .①②③④D .①②③④⑤【答案】D 【解析】【分析】根据抛物线的开口方向可得出a 的符号,再由抛物线与y 轴的交点可得出c 的值,然后进一步根据对称轴以及抛物线得出当x 1=、x 1=-、x 3=-时的情况进一步综合判断即可.【详解】由图象可知,a <0,c=1,对称轴:x=b12a-=-,∴b=2a ,①由图可知:当x=1时,y <0,∴a+b+c <0,正确;②由图可知:当x=?1时,y >1,∴a ?b+c >1,正确;③abc=2a 2>0,正确;④由图可知:当x=?3时,y <0,∴9a ?3b+c <0,正确;⑤c?a=1?a >1,正确;∴①②③④⑤正确.故选:D .【点睛】本题主要考查了抛物线的函数图像性质的综合运用,熟练掌握相关概念是解题关键.10.如图,抛物线2y ax bx c =++ 与x 轴交于点A (﹣1,0),顶点坐标(1,n ),与y 轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc >0;②3a +b <0;③﹣43≤a ≤﹣1;④a +b ≥am 2+bm (m 为任意实数);⑤一元二次方程2ax bx c n ++= 有两个不相等的实数根,其中正确的有()A .2个B .3个C .4个D .5个【答案】B 【解析】解:∵抛物线开口向下,∴a <0,∵顶点坐标(1,n ),∴对称轴为直线x =1,∴2b a-=1,∴b =﹣2a >0,∵与y 轴的交点在(0,3),(0,4)之间(包含端点),∴3≤c ≤4,∴abc <0,故①错误;3a +b =3a +(﹣2a )=a <0,故②正确;∵与x 轴交于点A (﹣1,0),∴a ﹣b +c =0,∴a ﹣(﹣2a )+c =0,∴c =﹣3a ,∴3≤﹣3a ≤4,∴﹣43≤a ≤﹣1,故③正确;∵顶点坐标为(1,n ),∴当x =1时,函数有最大值n ,∴a +b +c ≥am 2+bm +c ,∴a +b ≥am 2+bm ,故④正确;一元二次方程2ax bx c n ++=有两个相等的实数根x 1=x 2=1,故⑤错误.综上所述,结论正确的是②③④共3个.故选B .点睛:本题考查了抛物线与x 轴的交点,二次函数的性质,主要利用了二次函数的开口方向,对称轴,最值问题,以及二次函数图象上点的坐标特征,关键在于根据顶点横坐标表示出a 、b 的关系.11.已知二次函数y =ax 2+bx +c (a >0)经过点M (﹣1,2)和点N (1,﹣2),则下列说法错误的是( ) A .a +c =0B .无论a 取何值,此二次函数图象与x 轴必有两个交点,且函数图象截x 轴所得的线段长度必大于2C .当函数在x <110时,y 随x 的增大而减小 D .当﹣1<m <n <0时,m +n <2a 【答案】C 【解析】【分析】根据二次函数的图象和性质对各项进行判断即可.【详解】解:∵函数经过点M (﹣1,2)和点N (1,﹣2),∴a ﹣b +c =2,a +b +c =﹣2,∴a +c =0,b =﹣2,∴A 正确;∵c =﹣a ,b =﹣2,∴y =ax 2﹣2x ﹣a ,∴△=4+4a 2>0,∴无论a 为何值,函数图象与x 轴必有两个交点,∵x 1+x 2=2a,x 1x 2=﹣1,∴|x 1﹣x 2|=>2,∴B 正确;二次函数y =ax 2+bx +c (a >0)的对称轴x =﹣2b a =1a,当a >0时,不能判定x <110时,y 随x 的增大而减小;∴C 错误;∵﹣1<m <n <0,a >0,∴m +n <0,2a>0,∴m +n <2a;∴D 正确,故选:C .【点睛】本题考查了二次函数的问题,掌握二次函数的图象和性质是解题的关键.12.抛物线y =ax 2+bx+c 的顶点为(﹣1,3),与x 轴的交点A 在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论,其中正确结论的个数为( ) ①若点P(﹣3,m),Q(3,n)在抛物线上,则m <n ;②c =a+3;③a+b+c <0;④方程ax 2+bx+c =3有两个相等的实数根.A .1个B .2个C .3个D .4个【答案】C 【解析】试题分析:由抛物线与x 轴有两个交点,可知b 2-4ac >0,所以①错误;由抛物线的顶点为D (-1,2),可知抛物线的对称轴为直线x=-1,然后由抛物线与x 轴的一个交点A 在点(-3,0)和(-2,0)之间,可知抛物线与x 轴的另一个交点在点(0,0)和(1,0)之间,因此当x=1时,y <0,即a+b+c <0,所以②正确;由抛物线的顶点为D (-1,2),可知a-b+c=2,然后由抛物线的对称轴为直线x=2b a=-1,可得b=2a ,因此a-2a+c=2,即c-a=2,所以③正确;由于当x=-1时,二次函数有最大值为2,即只有x=-1时,ax 2+bx+c=2,因此方程ax2+bx+c-2=0有两个相等的实数根,所以④正确.故选C .考点:二次函数的图像与性质13.已知抛物线y =x 2+2x ﹣m ﹣1与x 轴没有交点,则函数y =的大致图象是()A.B.C.D.【答案】B【解析】【分析】由题意可求m<﹣2,即可求解.【详解】∵抛物线y=x2+2x﹣m﹣1与x轴没有交点,∴△=4﹣4(﹣m﹣1)<0∴m<﹣2∴函数y=的图象在第二、第四象限,故选B.【点睛】本题考查了反比例函数的图象,二次函数性质,求m的取值范围是本题的关键.14.在平面直角坐标系内,已知点A(﹣1,0),点B(1,1)都在直线1122y x=+上,若抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是()A.a≤﹣2 B.a<98C.1≤a<98或a≤﹣2 D.﹣2≤a<98【答案】C 【解析】【分析】分a>0,a<0两种情况讨论,根据题意列出不等式组,可求a的取值范围.【详解】∵抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点,∴令1122x+=ax2﹣x+1,则2ax2﹣3x+1=0∴△=9﹣8a>0∴a<9 8①当a<0时,110111 aa++≤?-+≤?解得:a≤﹣2∴a≤﹣2②当a>0时,110111 aa++≥?-+≥?解得:a≥1∴1≤a<9 8综上所述:1≤a<98或a≤﹣2故选:C.【点睛】本题考查二次函数图象与系数的关系,一次函数图象上点的坐标特征,二次函数图象点的坐标特征,利用分类讨论思想解决问题是本题的关键.15.如图,抛物线y=ax2+bx+c(a>0)过原点O,与x轴另一交点为A,顶点为B,若△AOB为等边三角形,则b的值为()A3B.﹣3C.﹣3D.﹣3【答案】B【解析】【分析】根据已知求出B(﹣2,24b ba a-),由△AOB为等边三角形,得到2b4a=tan60°×(﹣2ba),即可求解;【详解】解:抛物线y=ax2+bx+c(a>0)过原点O,∴c=0,B(﹣2,24b ba a-),∵△AOB为等边三角形,∴2b4a=tan60°×(﹣2ba),∴b=﹣故选B.【点睛】本题考查二次函数图象及性质,等边三角形性质;能够将抛物线上点的关系转化为等边三角形的边关系是解题的关键.16.若用“*”表示一种运算规则,我们规定:a*b=ab﹣a+b,如:3*2=3×2﹣3+2=5.以下说法中错误的是()A.不等式(﹣2)*(3﹣x)<2的解集是x<3B.函数y=(x+2)*x的图象与x轴有两个交点C.在实数范围内,无论a取何值,代数式a*(a+1)的值总为正数D.方程(x﹣2)*3=5的解是x=5【答案】D【解析】【分析】根据题目中所给的运算法则列出不等式,解不等式即可判定选项A;根据题目中所给的运算法则求得函数解析式,由此即可判定选项B;根据题目中所给的运算法则可得a*(a+1)=a(a+1)﹣a+(a+1)=a2+a+1=(a+12)2+34>0,由此即可判定选项C;根据题目中所给的运算法则列出方程,解方程即可判定选项D.【详解】∵a*b=ab﹣a+b,∴(﹣2)*(3﹣x)=(﹣2)×(3﹣x)﹣(﹣2)+(3﹣x)=x﹣1,∵(﹣2)*(3﹣x)<2,∴x﹣1<2,解得x<3,故选项A正确;∵y=(x+2)*x=(x+2)x﹣(x+2)+x=x2+2x﹣2,∴当y=0时,x2+2x﹣2=0,解得,x1=﹣x2=﹣1B正确;∵a *(a +1)=a (a +1)﹣a +(a +1)=a 2+a +1=(a +12)2+34>0,∴在实数范围内,无论a 取何值,代数式a *(a +1)的值总为正数,故选项C 正确;∵(x ﹣2)*3=5,∴(x ﹣2)×3﹣(x ﹣2)+3=5,解得,x =3,故选项D 错误;故选D .【点睛】本题是阅读理解题,根据题目中所给的运算法则得到相应的运算式子是解决问题的关键.17.一次函数y=ax+b 与反比例函数y=cx在同一平面直角坐标系中的图象如左图所示,则二次函数y=ax 2+bx+c 的图象可能是()A .B .C .D .【答案】B 【解析】【分析】根据题中给出的函数图像结合一次函数性质得出a <0,b >0,再由反比例函数图像性质得出c <0,从而可判断二次函数图像开口向下,对称轴:2bx a=->0,即在y 轴的右边,与y 轴负半轴相交,从而可得答案.【详解】解:∵一次函数y=ax+b 图像过一、二、四,∴a <0,b >0,又∵反比例函数y=cx图像经过二、四象限,∴c <0,∴二次函数对称轴:2bx a=->0,∴二次函数y=ax 2+bx+c 图像开口向下,对称轴在y 轴的右边,与y 轴负半轴相交,故答案为B. 【点睛】本题考查了二次函数的图形,一次函数的图象,反比例函数的图象,熟练掌握二次函数的有关性质:开口方向、对称轴、与y 轴的交点坐标等确定出a 、b 、c 的情况是解题的关键.18.已知抛物线224y x x c =-+与直线2y =有两个不同的交点.下列结论:①4c <;②当1x =时,y 有最小值2c -;③方程22420x x c -+-=有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则52c =;其中正确的结论的个数是() A .4 B .3 C .2D .1【答案】B 【解析】【分析】根据“抛物线224y x x c =-+与直线2y =有两个不同的交点”即可判断①③;根据抛物线的对称轴为直线x=1即可判断②;根据等腰直角三角形的性质,用c 表达出两个交点,代入抛物线解析式计算即可判断④.【详解】解:∵抛物线224y x x c =-+与直线2y =有两个不同的交点,∴2242x x c -+=有两个不相等的实数根,即22420x x c -+-=有两个不相等的实数根,故③正确,∴1642(2)0c ?=-??->,解得:4c <,故①正确;∵抛物线的对称轴为直线x=1,且抛物线开口向上,∴当x=1时,2y c =-为最小值,故②正确;若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则顶点(1,c-2)到直线y=2的距离等于两交点距离的一半,∵顶点(1,c-2)到直线y=2的距离为2-(c-2)=4-c ,∴两交点的横坐标分别为1-(4-c )=c-3与1+(4-c )=5-c ∴两交点坐标为(c-3,2)与(5-c,2),将(c-3,2)代入224y x x c =-+中得:22(3)4(3)2c c c ---+=解得:72c =或4c = ∵4c <,∴72c =,故④错误,∴正确的有①②③,故选:B .【点睛】本题考查了二次函数与一元二次方程的关系以及二次函数的性质,解题的关键是熟练掌握函数与方程之间的联系.19.将抛物线243y x x =-+平移,使它平移后图象的顶点为()2,4-,则需将该抛物线()A .先向右平移4个单位,再向上平移5个单位B .先向右平移4个单位,再向下平移5个单位C .先向左平移4个单位,再向上平移5个单位D .先向左平移4个单位,再向下平移5个单位【答案】C 【解析】【分析】先把抛物线243y x x =-+化为顶点式,再根据函数图象平移的法则进行解答即可.【详解】∵抛物线243y x x =-+可化为()221y x =--∴其顶点坐标为:(2,?1),∴若使其平移后的顶点为(?2,4)则先向左平移4个单位,再向上平移5个单位.故选C. 【点睛】本题考查二次函数图像,熟练掌握平移是性质是解题关键.20.已知二次函数2()y x h =-- (h 为常数),当自变量x 的值满足25x ≤≤时,与其对应的函数值y 的最大值为-1,则h 的值为( ) A .3或6 B .1或6C .1或3D .4或6【答案】B 【解析】分析:分h <2、2≤h≤5和h >5三种情况考虑:当h <2时,根据二次函数的性质可得出关于h 的一元二次方程,解之即可得出结论;当2≤h≤5时,由此时函数的最大值为0与题意不符,可得出该情况不存在;当h >5时,根据二次函数的性质可得出关于h 的一元二次方程,解之即可得出结论.综上即可得出结论.详解:如图,当h<2时,有-(2-h)2=-1,解得:h1=1,h2=3(舍去);当2≤h≤5时,y=-(x-h)2的最大值为0,不符合题意;当h>5时,有-(5-h)2=-1,解得:h3=4(舍去),h4=6.综上所述:h的值为1或6.故选B.点睛:本题考查了二次函数的最值以及二次函数的性质,分h<2、2≤h≤5和h>5三种情况求出h值是解题的关键.。
二次函数测试题及答案

二次函数一、选择题:1. 抛物线3)2(2+-=x y 的对称轴是( )A. 直线3-=xB. 直线3=xC. 直线=xD. 直线2. 二次函数c bx ax y ++=2的图象如右图,则点),(acb M 在( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3. 已知二次函数c bx ax y ++=2,且0<a ,0>+-c b a ,则一定有( ) A. 042>-ac bB. 042=-ac bC. 042<-ac bD. ac b 42-≤04. 把抛物线c bx x y ++=2向右平移3个单位,再向下平移2个单位,所得图象的解析式是532+-=x x y ,则有( )A. 3=b ,7=cB. 9-=b ,15-=cC. 3=b ,3=cD. 9-=b ,21=c5. 已知反比例函数xky =的图象如右图所示,则二次函数222k x kx y +-=的图象大致为( )x6. 下面所示各图是在同一直角坐标系内,二次函数c x c a ax y +++=)(2与一次函数c ax y +=的大致图象,有且只有一个是正确的,正确的是( )B D7.抛物线322+-=xxy的对称轴是直线()A. 2-=x B. 2=x C. 1-=x D. 1=x8.二次函数2)1(2+-=xy的最小值是()A. 2-B. 2C. 1-D. 19.二次函数cbxaxy++=2的图象如图所示,若cbaM++=24cbaN+-=,baP-=4,则()A. 0>M,0>N,0>PB. 0<M,0>N,0>PC. 0>M,0<N,0>PD. 0<M,0>N,0<P二、填空题:10.将二次函数322+-=xxy配方成khxy+-=2)(的形式,则y=______________________.11.已知抛物线cbxaxy++=2与x轴有两个交点,那么一元二次方程02=++cbxax的根的情况是______________________.12.已知抛物线cxaxy++=2与x轴交点的横坐标为1-,则ca+=_________.13.请你写出函数2)1(+=xy与12+=xy具有的一个共同性质:_______________.14.有一个二次函数的图象,三位同学分别说出它的一些特点:甲:对称轴是直线4=x;乙:与x轴两个交点的横坐标都是整数;丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式:15.已知二次函数的图象开口向上,且与y轴的正半轴相交,请你写出一个满足条件的二次函数的解析式:_____________________.16. 如图,抛物线的对称轴是1=x ,与x 轴交于A 、B 两点,若B 点坐标是)0,3(,则A 点的坐标是________________.三、解答题:1. 已知函数12-+=bx x y 的图象经过点(3,2).(1)求这个函数的解析式;(2)当0>x 时,求使y ≥2的x 的取值范围.2. 如右图,抛物线n x x y ++-=52经过点)0,1(A ,与y轴交于点B .(1)求抛物线的解析式;(2)P 是y 轴正半轴上一点,且△P AB 是以AB 为腰的等腰三角形,试求点P 的坐标. 3. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到赢利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s (万元)与销售时间t (月)之间的关系(即前t 个月的利润总和s 与t 之间的关系). (1)由已知图象上的三点坐标,求累积利润s (万元)与销售时间t (月)之间的函数关系式; (2)求截止到几月累积利润可达到30万元; (3)求第8个月公司所获利润是多少万元? 提高题1. 如图,有一座抛物线形拱桥,在正常水位时水面AB 的宽为20m ,如果水位上升3m 时,水面CD 的宽是10m. (1)求此抛物线的解析式;(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km (桥长忽略不计). 货车正以每小时40km 的速度开往乙地,当行驶1小时时,忽然接到紧急通知:前方连降暴雨,造成水位以每小时0.25m 的速度持续上涨(货车接到通知时水位在CD 处,当水位达到桥拱最高点O 时,禁止车辆通行). 试问:如果货车按原来速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,速度应超过每小时多少千米?2. 某机械租赁公司有同一型号的机械设备40套. 经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出. 在此基础上,当每套设备的月租金提高10元时,这种设备就少租出一套,且未租出的一套设备每月需要支出费用(维护费、管理费等)20元,设每套设备的月租金为x (元),租赁公司出租该型号设备的月收益(收益=租金收入-支出费用)为y (元).(1)用含x 的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用; (2)求y 与x 之间的二次函数关系式; (3)当月租金分别为4300元和350元时,租赁公司的月收益分别是多少元?此时应该租出多少套机械设备?请你简要说明理由;(4)请把(2)中所求的二次函数配方成ab ac a b x y 44)2(22-++=的形式,并据此说明:当x 为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?参考答案一、选择题:二、填空题: 1. 2)1(2+-=x y2. 有两个不相等的实数根3. 14. (1)图象都是抛物线;(2)开口向上;(3)都有最低点(或最小值)5. 358512+-=x x y 或358512-+-=x x y 或178712+-=x x y 或178712-+-=x x y 6. 122++-=x x y 等(只须0<a ,0>c ) 7. )0,32(-8. 3=x ,51<<x ,1,4 三、解答题:1. 解:(1)∵函数12-+=bx x y 的图象经过点(3,2),∴2139=-+b . 解得2-=b . ∴函数解析式为122--=x x y .(2)当3=x 时,2=y .根据图象知当x ≥3时,y ≥2.∴当0>x 时,使y ≥2的x 的取值范围是x ≥3.2. 解:(1)由题意得051=++-n . ∴4-=n . ∴抛物线的解析式为452-+-=x x y .(2)∵点A 的坐标为(1,0),点B 的坐标为)4,0(-. ∴OA =1,OB =4. 在Rt △OAB 中,1722=+=OB OA AB ,且点P 在y 轴正半轴上.①当PB =P A 时,17=PB . ∴417-=-=OB PB OP . 此时点P 的坐标为)417,0(-.②当P A =AB 时,OP =OB =4 此时点P 的坐标为(0,4).3. 解:(1)设s 与t 的函数关系式为c bt at s ++=2,由题意得⎪⎩⎪⎨⎧=++-=++-=++;5.2525,224,5.1c b a c b a c b a 或⎪⎩⎪⎨⎧=-=++-=++.0,224,5.1c c b a c b a 解得⎪⎪⎩⎪⎪⎨⎧=-==.0,2,21c b a ∴t t s 2212-=.(2)把s =30代入t t s 2212-=,得.221302t t -= 解得101=t ,62-=t (舍去) 答:截止到10月末公司累积利润可达到30万元. (3)把7=t 代入,得.5.10727212=⨯-⨯=s 把8=t 代入,得.16828212=⨯-⨯=s 5.55.1016=-. 答:第8个月获利润5.5万元.4. 解:(1)由于顶点在y 轴上,所以设这部分抛物线为图象的函数的解析式为1092+=ax y .因为点)0,25(-A 或)0,25(B 在抛物线上,所以109)25(·02+-=a ,得12518-=a . 因此所求函数解析式为109125182+-=x y (25-≤x ≤25).(2)因为点D 、E 的纵坐标为209,所以10912518209+-=,得245±=x .所以点D 的坐标为)209,245(-,点E 的坐标为)209,245(.所以225)245(245=--=DE .因此卢浦大桥拱内实际桥长为385227501.01100225≈=⨯⨯(米).5. 解:(1)∵AB =3,21x x <,∴312=-x x . 由根与系数的关系有121=+x x .∴11-=x ,22=x . ∴OA =1,OB =2,2·21-==amx x . ∵1tan tan =∠=∠ABC BAC ,∴1==OBOCOA OC . ∴OC =2. ∴2-=m ,1=a .∴此二次函数的解析式为22--=x x y .(2)在第一象限,抛物线上存在一点P ,使S △P AC =6.解法一:过点P 作直线MN ∥AC ,交x 轴于点M ,交y 轴于N ,连结P A 、PC 、MC 、NA . ∵MN ∥AC ,∴S △MAC =S △NAC = S △P AC =6. 由(1)有OA =1,OC =2. ∴6121221=⨯⨯=⨯⨯CN AM . ∴AM =6,CN =12. ∴M (5,0),N (0,10).∴直线MN 的解析式为102+-=x y .由⎩⎨⎧--=+-=,2,1022x x y x y 得⎩⎨⎧==;4311y x ⎩⎨⎧=-=18,422y x (舍去) ∴在 第一象限,抛物线上存在点)4,3(P ,使S △P AC =6. 解法二:设AP 与y 轴交于点),0(m D (m >0) ∴直线AP 的解析式为m mx y +=.⎩⎨⎧+=--=.,22m mx y x x y ∴02)1(2=--+-m x m x . ∴1+=+m x x P A ,∴2+=m x P . 又S △P AC = S △ADC + S △PDC =P x CD AO CD ·21·21+=)(21P x AO CD +. ∴6)21)(2(21=+++m m ,0652=-+m m ∴6=m (舍去)或1=m .∴在 第一象限,抛物线上存在点)4,3(P ,使S △P AC =6.提高题1. 解:(1)∵抛物线c bx x y ++=2与x 轴只有一个交点,∴方程02=++c bx x 有两个相等的实数根,即042=-c b . ① 又点A 的坐标为(2,0),∴024=++c b . ② 由①②得4-=b ,4=a .(2)由(1)得抛物线的解析式为442+-=x x y . 当0=x 时,4=y . ∴点B 的坐标为(0,4). 在Rt △OAB 中,OA =2,OB =4,得5222=+=OB OA AB .∴△OAB 的周长为5265241+=++.2. 解:(1)76)34()10710710(1022++-=--⨯++-⨯=x x x x x S .当3)1(26=-⨯-=x 时,16)1(467)1(42=-⨯-⨯-⨯=最大S . ∴当广告费是3万元时,公司获得的最大年利润是16万元.(2)用于投资的资金是13316=-万元.经分析,有两种投资方式符合要求,一种是取A 、B 、E 各一股,投入资金为13625=++(万元),收益为0.55+0.4+0.9=1.85(万元)>1.6(万元);另一种是取B 、D 、E 各一股,投入资金为2+4+6=12(万元)<13(万元),收益为0.4+0.5+0.9=1.8(万元)>1.6(万元).3. 解:(1)设抛物线的解析式为2ax y =,桥拱最高点到水面CD 的距离为h 米,则),5(h D -,)3,10(--h B .∴⎩⎨⎧--=-=.3100,25h a h a 解得⎪⎩⎪⎨⎧=-=.1,251h a∴抛物线的解析式为2251x y -=.(2)水位由CD 处涨到点O 的时间为1÷0.25=4(小时), 货车按原来速度行驶的路程为40×1+40×4=200<280, ∴货车按原来速度行驶不能安全通过此桥. 设货车的速度提高到x 千米/时, 当2801404=⨯+x 时,60=x .∴要使货车安全通过此桥,货车的速度应超过60千米/时. 4. 解:(1)未出租的设备为10270-x 套,所有未出租设备的支出为)5402(-x 元. (2)54065101)5402()1027040(2++-=----=x x x x x y . ∴540651012++-=x x y .(说明:此处不要写出x 的取值范围) (3)当月租金为300元时,租赁公司的月收益为11040元,此时出租的设备为37套;当月租金为350元时,租赁公司的月收益为11040元,此时出租的设备为32套.因为出租37套和32套设备获得同样的收益,如果考虑减少设备的磨损,应选择出租32套;如果考虑市场占有率,应选择出租37套. (4)5.11102)325(1015406510122+--=++-=x x x y .∴当325=x 时,y 有最大值11102.5. 但是,当月租金为325元时,租出设备套数为34.5,而34.5不是整数,故租出设备应为34套或35套. 即当月租金为为330元(租出34套)或月租金为320元(租出35套)时,租赁公司的月收益最大,最大月收益均为11100元.二次函数测试题(B )一、选择题(每小题4分,共24分)1.抛物线y =-3x 2+2x -1的图象与坐标轴的交点情况是( ) (A)没有交点. (B)只有一个交点. (C)有且只有两个交点. (D)有且只有三个交点.2.已知直线y =x 与二次函数y =ax 2-2x -1图象的一个交点的横坐标为1,则a 的值为( )(A)2. (B)1. (C)3. (D)4.3.二次函数y =x 2-4x +3的图象交x 轴于A 、B 两点,交y 轴于点C ,则△ABC 的面积为( ) (A)6. (B)4. (C)3. (D)1.4.函数y =ax 2+bx +c 中,若a >0,b <0,c <0,则这个函数图象与x 轴的交点情况是( ) (A)没有交点.(B)有两个交点,都在x 轴的正半轴. (C)有两个交点,都在x 轴的负半轴.(D)一个在x 轴的正半轴,另一个在x 轴的负半轴.5.已知(2,5)、(4,5)是抛物线y =ax 2+bx +c 上的两点,则这个抛物线的对称轴方程是( ) (A)x =ab-. (B)x =2. (C)x =4. (D)x =3. 6.已知函数y=ax 2+bx +c 的图象如图1所示,那么能正确反映函数y=ax +b 图象的只可能是( )二、填空题(每小题4分,共24分)7.二次函数y =2x 2-4x +5的最小值是______.8.某二次函数的图象与x 轴交于点(-1,0),(4,0),且它的形状与y =-x 2形状相同.则这个二次函数的解析式为______.9.若函数y =-x 2+4的函数值y >0,则自变量x 的取值范围是______.10.某品牌电饭锅成本价为70元,销售商对其销量与定价的关系进行了调查,结果如下:销量(个)80 100 110 100 80 60为获得最大利润,销售商应将该品牌电饭锅定价为 元.11.函数y =ax 2-(a -3)x +1的图象与x 轴只有一个交点,那么a 的值和交点坐标分别为______.12.某涵洞是一抛物线形,它的截面如图3所示,现测得水面宽 1.6AB m ,涵洞顶点O 到水面的距离为2.4m ,在图中的直角坐标系内,涵洞所在抛物线的解析式为________.三、解答题(本大题共52分)13.(本题8分)已知抛物线y =x 2-2x -2的顶点为A ,与y 轴的交点为B ,求过A 、B 两点的直线的解析式.14.(本题8分)抛物线y =ax 2+2ax +a 2+2的一部分如图3所示,求该抛物线在y 轴左侧与x 轴的交点坐标.15.(本题8分)如图4,已知抛物线y =ax 2+bx +c (a >0)的顶点是C (0,1),直线l :y =-ax +3与这条抛物线交于P 、Q 两点,且点P 到x 轴的距离为2.(1)求抛物线和直线l 的解析式;(2)求点Q 的坐标.16.(本题8分)工艺商场以每件155元购进一批工艺品.若按每件200元销售,工艺商场每天可售出该工艺品100件;若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元? 17.(本题10分)) 杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个图4P QyxO图3yxO1月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数.(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;(2)求纯收益g关于x的解析式;(3)问设施开放几个月后,游乐场的纯收益达到最大?几个月后,能收回投资?18(本题10分)如图所示,图4-①是一座抛物线型拱桥在建造过程中装模时的设计示意图,拱高为30m,支柱A3B3=50m,5根支柱A1B1、A2B2、A3B3、A4B4、A5B5之间的距离均为15m,B1B5∥A1A5,将抛物线放在图4-②所示的直角坐标系中.(1)直接写出图4-②中点B1、B3、B5的坐标;(2)求图4-②中抛物线的函数表达式;(3)求图4-①中支柱A2B2、A4B4的长度.四、附加题(本题为探究题20分,不计入总分)19、 (湘西自治州附加题,有改动)如图5,已知A(2,2),B(3,0).动点P(m,0)在线段OB上移动,过点P作直线l与x轴垂直.(1)设△OAB中位于直线l左侧部分的面积为S,写出S与m之间的函数关系式;(2)试问是否存在点P,使直线l平分△OAB的面积?若有,求出点P的坐标;若无,请说明理由.参考答案一、1.B 2.D 3.C 4.D 5.D 6.B二、7.3 8.y=-x2+3x+4 9.-2<x<2 10.13011.a=0,(13-,0);a=1,(-1,0);a=9,(13,0)12.2154y x=-三、图4-①BA5A4A31A211 / 1312 / 1313.抛物线的顶点为(1,-3),点B 的坐标为(0,-2).直线AB 的解析式为y =-x -214.依题意可知抛物线经过点(1,0).于是a +2a +a 2+2=0,解得a 1=-1,a 2=-2.当a =-1或a =-2时,求得抛物线与x 轴的另一交点坐标均为(-3,0)15.(1)依题意可知b =0,c =1,且当y =2时,ax 2+1=2①,-ax +3=2②.由①、②解得a =1,x =1.故抛物线与直线的解析式分别为:y =x 2+1,y =-x +3;(2)Q (-2,5)16.设降价x 元时,获得的利润为y 元.则依意可得y =(45-x )(100+4x )=-4x 2+80x +4500,即y =-4(x -10)2+4900.故当x =10时,y 最大=4900(元)17.(1)将(1,2)和(2,6)代入y =ax 2+bx ,求得a =b =1.故y =x 2+x ;(2)g =33x -150-y ,即g =-x 2+32x -150;(3)因y =-(x -16)2+106,所以设施开放后第16个月,纯收益最大.令g =0,得-x 2+32x -150=0.解得x =16x ≈16-10.3=5.7(舍去26.3).当x =5时,g <0, 当x =6时,g >0,故6个月后,能收回投资18.(1)1(30)B -,0,3(030)B ,,5(300)B ,; (2)设抛物线的表达式为(30)(30)y a x x =-+,把3(030)B ,代入得(030)(030)30y a =-+=. 130a =-∴. ∵所求抛物线的表达式为:1(30)(30)30y x x =--+. (3)4B ∵点的横坐标为15,4B ∴的纵坐标4145(1530)(1530)302y =--+=. 3350A B =∵,拱高为30,∴立柱44458520(m)22A B =+=. 由对称性知:224485(m)2A B A B ==. 四、19.(1)当0≤m ≤2时,S =212m ;当2<m ≤3时,S =12×3×2-12(3-m )(-2m +6)=-m 2+6m -6.(2)若有这样的P 点,使直线l 平分△OAB 的面积,很显然0<m <2.由于△OAB 的面积等于3,故当l 平分△OAB 面积时,S =32.21322m =∴.解得mP点,使l平分△OAB的面积.且点P的坐标为0).13 / 13。
二次函数基础练习题大全含答案-二次函数基础题
二次函数基础练习题练习一 二次函数1、 一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离s (米)与时间t 时间t (秒)1 2 3 4 … 距离s (米)2 8 18 32 … 写出用t 表示s 的函数关系式: 2、 下列函数:① 23yx ;② 21y x x x ;③ 224y x x x ;④ 21y x x ; ⑤ 1y x x ,其中是二次函数的是 ,其中a ,b ,c3、当m 时,函数2235ym x x (m 为常数)是关于x 的二次函数4、当____m时,函数2221m m y m m x 是关于x 的二次函数 5、当____m 时,函数2564m m y m x +3x 是关于x 的二次函数 6、若点 A ( 2, m ) 在函数 12-=x y 的图像上,则 A 点的坐标是____.7、在圆的面积公式 S =πr 2 中,s 与 r 的关系是( )A 、一次函数关系B 、正比例函数关系C 、反比例函数关系D 、二次函数关系8、正方形铁片边长为15cm ,在四个角上各剪去一个边长为x (cm )的小正方形,用余下的部分做成一个无盖的盒子.(1)求盒子的表面积S (cm 2)与小正方形边长x (cm )之间的函数关系式;(2)当小正方形边长为3cm 时,求盒子的表面积.9、如图,矩形的长是 4cm ,宽是 3cm ,如果将长和宽都增加 x cm ,那么面积增加 ycm 2, ① 求 y 与 x 之间的函数关系式.② 求当边长增加多少时,面积增加 8cm 2.10、已知二次函数),0(2≠+=a c ax y 当x=1时,y= -1;当x=2时,y=2,求该函数解析式.11、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料,建造猪舍三间,如图,它们的平面图是一排大小相等的长方形.(1) 如果设猪舍的宽AB 为x 米,则猪舍的总面积S (米2)与x 有怎样的函数关系?(2) 请你帮富根老伯计算一下,如果猪舍的总面积为32米2,应该如何安排猪舍的长BC 和宽AB 的长度?旧墙的长度是否会对猪舍的长度有影响?怎样影响?练习二 函数2ax y =的图像与性质1、填空:(1)抛物线221x y =的对称轴是 (或 ),顶点坐标是 ,当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小,当x= 时,该函数有最 值是 ;(2)抛物线221x y -=的对称轴是 (或 ),顶点坐标是 ,当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小,当x= 时,该函数有最 值是 ;2、对于函数22x y =下列说法:①当x 取任何实数时,y 的值总是正的;②x 的值增大,y 的值也增大;③y 随x 的增大而减小;④图像关于y 轴对称.其中正确的是 .3、抛物线 y =-x 2 不具有的性质是( )A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点4、苹果熟了,从树上落下所经过的路程 s 与下落时间 t 满足 S =12gt 2(g =9.8),则 s 与 t 的函数图像大致是( )A B C D5、函数2ax y =与b ax y +-=的图像可能是( )A .B .C .D . 6、已知函数24mm y mx 的图像是开口向下的抛物线,求m 的值. 7、二次函数12-=mmx y 在其图像对称轴的左侧,y 随x 的增大而增大,求m 的值. 8、二次函数223x y -=,当x 1>x 2>0时,求y 1与y 2的大小关系. 9、已知函数()422-++=m m x m y 是关于x 的二次函数,求:(1) 满足条件的m 的值;(2) m 为何值时,抛物线有最低点?求出这个最低点,这时x 为何值时,y 随x 的增大而增大;(3) m 为何值时,抛物线有最大值?最大值是多少?当x 为何值时,y 随x 的增大而减小?10、如果抛物线2y ax 与直线1y x 交于点,2b ,求这条抛物线所对应的二次函数的关系式.练习三 函数c ax y +=2的图象与性质1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y st O s t O s t Os tO随x 的增大而增大, 当x 时, y 随x 的增大而减小. 2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标 、 .3、任给一些不同的实数k ,得到不同的抛物线k x y +=2,当k 取0,1±时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④ .4、将抛物线122-=x y 向上平移4个单位后,所得的抛物线是 ,当x= 时,该抛物线有最 (填大或小)值,是 .5、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称,则m =________;6、二次函数c ax y +=2()0≠a 中,若当x 取x 1、x 2(x 1≠x 2)时,函数值相等,则当x 取x 1+x 2时,函数值等于 .练习四 函数()2h x a y -=的图象与性质 1、抛物线()2321--=x y ,顶点坐标是 ,当x 时,y 随x 的增大而减小, 函数有 最 值 . 2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标.(1)右移2个单位;(2)左移32个单位;(3)先左移1个单位,再右移4个单位. 3、请你写出函数()21+=x y 和12+=x y 具有的共同性质(至少2个).4、二次函数()2h x a y -=的图象如图:已知21=a ,OA=OC ,试求该抛物线的解析式.5、抛物线2)3(3-=x y 与x 轴交点为A ,与y 轴交点为B ,求A 、B 两点坐标及⊿AOB 的面积.6、二次函数2)4(-=x a y ,当自变量x 由0增加到2时,函数值增加6.(1)求出此函数关系式.(2)说明函数值y 随x 值的变化情况.7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上,求k 的值.练习五 ()k h x a y +-=2的图象与性质 1、请写出一个二次函数以(2, 3)为顶点,且开口向上.____________.2、二次函数 y =(x -1)2+2,当 x =____时,y 有最小值.3、函数 y =12(x -1)2+3,当 x ____时,函数值 y 随 x 的增大而增大.4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向 平移3个单位,再向 平移2个单位得到.5、 已知抛物线的顶点坐标为2,1,且抛物线过点3,0,则抛物线的关系式是6、 如图所示,抛物线顶点坐标是P (1,3),则函数y 随自变量x 的增大而减小的x 的取值范围是( )A 、x>3B 、x<3C 、x>1D 、x<17、已知函数()9232+--=x y . (1)确定下列抛物线的开口方向、对称轴和顶点坐标; (2)当x= 时,抛物线有最 值,是 . (3)当x 时,y 随x 的增大而增大;当x 时,y 随x 的增大而减小. (4)求出该抛物线与x 轴的交点坐标及两交点间距离; (5) 求出该抛物线与y 轴的交点坐标;(6) 该函数图象可由23x y -=的图象经过怎样的平移得到的?8、已知函数()412-+=x y . (1)指出函数图象的开口方向、对称轴和顶点坐标; (2)若图象与x 轴的交点为A 、B 和与y 轴的交点C ,求△ABC 的面积; (3)指出该函数的最值和增减性; (4)若将该抛物线先向右平移2个单位,在向上平移4个单位,求得到的抛物线的解析式; (5)该抛物线经过怎样的平移能经过原点. (6)画出该函数图象,并根据图象回答:当x 取何值时,函数值大于0;当x 取何值时,函数值小于0.练习六 c bx ax y ++=2的图象和性质 1、抛物线942++=x x y 的对称轴是 .2、抛物线251222+-=x x y 的开口方向是 ,顶点坐标是 .3、试写出一个开口方向向上,对称轴为直线x=-2,且与y 轴的交点坐标为(0,3)的抛物线的解析式 .4、将 y =x 2-2x +3 化成 y =a (x -h)2+k 的形式,则 y =____.5、把二次函数215322y x x 的图象向上平移3个单位,再向右平移4个单位,则两次平移后的函数图象的关系式是6、抛物线1662--=x x y 与x 轴交点的坐标为_________;7、函数x x y +-=22有最____值,最值为_______;8、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位,再沿y 轴向上平移3个单位,得到的图象的函数解析式为122+-=x x y ,则b 与c 分别等于( )A 、6,4B 、-8,14C 、-6,6D 、-8,-149、二次函数122--=x x y 的图象在x 轴上截得的线段长为( )A 、22B 、23C 、32D 、3310、通过配方,写出下列函数的开口方向、对称轴和顶点坐标:(1)12212+-=x x y ; (2)2832-+-=x x y ; (3)4412-+-=x x y 11、把抛物线1422++-=x x y 沿坐标轴先向左平移2个单位,再向上平移3个单位,问所得的抛物线有没有最大值,若有,求出该最大值;若没有,说明理由.12、求二次函数62+--=x x y 的图象与x 轴和y 轴的交点坐标 13、已知一次函数的图象过抛物线223yx x 的顶点和坐标原点 1) 求一次函数的关系式;2) 判断点2,5是否在这个一次函数的图象上14、某商场以每台2500元进口一批彩电.如每台售价定为2700元,可卖出400台,以每100元为一个价格单位,若将每台提高一个单位价格,则会少卖出50台,那么每台定价为多少元即可获得最大利润?最大利润是多少元?练习七 c bx ax y ++=2的性质1、函数2y x pxq 的图象是以3,2为顶点的一条抛物线,这个二次函数的表达式为 2、二次函数2224y mx x m m 的图象经过原点,则此抛物线的顶点坐标是 3、如果抛物线2yax bx c 与y 轴交于点A (0,2),它的对称轴是1x ,那么ac b 4、抛物线c bx x y ++=2与x 轴的正半轴交于点A 、B 两点,与y 轴交于点C ,且线段AB 的长为1,△ABC 的面积为1,则b 的值为______.5、已知二次函数c bx ax y ++=2的图象如图所示,则a___0,b___0,c___0,ac b 42-____0;6、二次函数c bx ax y ++=2的图象如图,则直线bc ax y +=的图象不经过第 象限.7、已知二次函数2y ax bxc (0≠a )的图象如图所示,则下列结论: 1),a b 同号;2)当1x 和3x 时,函数值相同;3)40a b ;4)当2y 时,x 的值只能为0;其中正确的是(第5题) (第6题) (第7题) (第10题)8、已知二次函数2224m mx x y +--=与反比例函数x m y 42+=的图象在第二象限内的一个交点的横坐标是-2,则m=9、二次函数2y x ax b 中,若0a b ,则它的图象必经过点( )A 1,1B 1,1C 1,1D 1,110、函数b ax y +=与c bx ax y ++=2的图象如上图所示,则下列选项中正确的是( )A 、0,0>>c abB 、0,0><c abC 、0,0<>c abD 、0,0<<c ab11、已知函数c bx ax y ++=2的图象如图所示,则函数b ax y +=的图象是( )12、二次函数c bx ax y ++=2的图象如图,那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中,值为正数的有( )A .4个B .3个C .2个D .1个13、抛物线的图角如图,则下列结论: ①>0;②;③>;④<1.其中正确的结论是( ).(A )①② (B )②③ (C )②④ (D )③④14、二次函数2y ax bx c 的最大值是3a ,且它的图象经过1,2,1,6两点, 求a 、b 、c 的值。
九年级上册数学二次函数测试题及答案,推荐文档
二次函数单元测评一、选择题(每题 3 分,共 30 分)1.下列关系式中,属于二次函数の是(x 为自变量)( )A. B. C. D.2.函数y=x2-2x+3 の图象の顶点坐标是( )A. (1,-4)B.(-1,2)C. (1,2)D.(0,3)3.抛物线y=2(x-3)2 の顶点在( )A.第一象限B. 第二象限C. x 轴上D. y 轴上4.抛物线の对称轴是( )A. x=-2B.x=2C. x=-4D. x=45.已知二次函数y=ax2+bx+c の图象如图所示,则下列结论中,正确の是( )A. ab>0,c>0B. ab>0,c<0C. ab<0,c>0D. ab<0,c<06.二次函数y=ax2+bx+c の图象如图所示,则点A.一B. 二C. 三D. 四象限(7.如图所示,已知二次函数y=ax2+bx+c(a≠0)の图象の顶点P の横坐标是4,图象交x 轴于点A(m,0)和点B,且m>4,那么AB の长是( )A.4+mB. mC. 2m-8D. 8-2m8.若一次函数y=ax+b の图象经过第二、三、四象限,则二次函数y=ax2+bx の图象只可能是( )9.已知抛物线和直线在同一直角坐标系中の图象如图所示,抛物线の对称轴为直线x=-1,P1(x1,y1),P2(x2,y2)是抛物线上の点,P3(x3,y3)是直线上の点,且- 1<x1<x2,x3<-1,则y1,y2,y3の大小关系是( )A. y1<y2<y3B. y2<y3<y1C. y3<y1<y2D. y2<y1<y310.把抛物线の图象向左平移2 个单位,再向上平在第)移3 个单位,所得の抛物线の函数关系式是( )A. B.C. D.二、填空题(每题 4 分,共 32 分)11.二次函数y=x2-2x+1 の对称轴方程是.12.若将二次函数y=x2-2x+3 配方为y=(x-h)2+k の形式,则y= .13.若抛物线y=x2-2x-3 与x 轴分别交于A、B 两点,则AB の长为.14.抛物线y=x2+bx+c,经过A(-1,0),B(3,0)两点,则这条抛物线の解析式为.15.已知二次函数y=ax2+bx+c の图象交x 轴于A、B 两点,交y 轴于C 点,且△ABC 是直角三角形,请写出一个符合要求の二次函数解析式.16.在距离地面2m 高の某处把一物体以初速度v0(m/s)竖直向上抛物出,在不计空气阻力の情况下,其上升高度s(m)与抛出时间t(s)满足:(其中g 是常数,通常取10m/s2).若v0=10m/s,则该物体在运动过程中最高点距地面m.17.试写出一个开口方向向上,对称轴为直线x=2,且与y 轴の交点坐标为(0,3)の抛物线の解析式为.18.已知抛物线y=x2+x+b2 经过点,则y1の值是.三、解答下列各题(19、20 每题 9 分,21、22 每题 10 分,共 38 分)19.若二次函数の图象の对称轴方程是,并且图象过A(0,-4)和B(4,0)(1)求此二次函数图象上点A 关于对称轴对称の点A′の坐标;(2)求此二次函数の解析式;20.在直角坐标平面内,点O 为坐标原点,二次函数y=x2+(k-5)x-(k+4) の图象交x 轴于点A(x1,0)、B(x2,0),且(x1+1)(x2+1)=-8. (1)求二次函数解析式;(2)将上述二次函数图象沿x 轴向右平移2 个单位,设平移后の图象与y 轴の交点为C,顶点为P,求△POC の面积.21.已知:如图,二次函数y=ax2+bx+c の图象与x 轴交于A、B 两点,其中A 点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M 为它の顶点.(1)求抛物线の解析式;(2)求△MCB の面积S△MCB.22.某商店销售一种商品,每件の进价为2.50 元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.50 元时,销售量为500 件,而单价每降低1 元,就可以多售出200 件.请你分析,销售单价多少时,可以获利最大.答案与解析:一、选择题1.考点:二次函数概念.选A.2.考点:求二次函数の顶点坐标.解析:法一,直接用二次函数顶点坐标公式求.法二,将二次函数解析式由一般形式转换为顶点式,即y=a(x-h)2+k の形式,顶点坐标即为(h,k),y=x2-2x+3=(x-1) 2+2,所以顶点坐标为(1,2),答案选C.3.考点:二次函数の图象特点,顶点坐标.解析:可以直接由顶点式形式求出顶点坐标进行判断,函数y=2(x-3)2 の顶点为(3,0),所以顶点在x 轴上,答案选C.4.考点:数形结合,二次函数y=ax2+bx+c の图象为抛物线,其对称轴为.解析:抛物线,直接利用公式,其对称轴所在直线为答案选B.5.考点:二次函数の图象特征.解析:由图象,抛物线开口方向向下,抛物线对称轴在y 轴右侧,抛物线与y 轴交点坐标为(0,c)点,由图知,该点在x 轴上方,答案选C.6.考点:数形结合,由抛物线の图象特征,确定二次函数解析式各项系数の符号特征.解析:由图象,抛物线开口方向向下,抛物线对称轴在y 轴右侧,抛物线与y 轴交点坐标为(0,c)点,由图知,该点在x 轴上方,在第四象限,答案选 D.7.考点:二次函数の图象特征.解析:因为二次函数 y=ax 2+bx+c(a ≠0)の图象の顶点 P の横坐标是 4,所以抛物线对称轴所在直线为 x=4,交 x 轴于点 D ,所以 A 、B 两点关于对称轴对称,因为点 A(m ,0),且 m>4,所以 AB=2AD=2(m-4)=2m-8,答案选 C.8. 考点:数形结合,由函数图象确定函数解析式各项系数の性质符号,由函数解析式各项系数の性质符号画出函数图象の大致形状.解析:因为一次函数 y=ax+b の图象经过第二、三、四象限,所以二次函数 y=ax 2+bx の图象开口方向向下,对称轴在 y 轴左侧,交坐标轴于(0,0)点.答案选 C.9. 考点:一次函数、二次函数概念图象及性质.解析:因为抛物线の对称轴为直线 x=-1,且-1<x 1<x 2,当 x>-1 时,由图象知, y 随 x の增大而减小,所以 y 2<y 1;又因为 x 3<-1,此时点 P 3(x 3,y 3)在二次函数图象上方,所以 y 2<y 1<y 3.答案选 D.10.考点:二次函数图象の变化.抛物线の图象向左平移 2 个单位得到,再向上平移 3 个单位得到.答案选 C.二、填空题 11.考点:二次函数性质.x=1.解析:二次函数 y=x 2-2x+1,所以对称轴所在直线方程 .答案12.考点:利用配方法变形二次函数解析式.解析:y=x 2-2x+3=(x 2-2x+1)+2=(x-1)2+2.答案 y=(x-1)2+2.13.考点:二次函数与一元二次方程关系.解析:二次函数y=x2-2x-3 与x 轴交点A、B の横坐标为一元二次方程x2-2x-3=0 の两个根,求得x1=-1,x2=3,则AB=|x2-x1|=4.答案为4.14.考点:求二次函数解析式.解析:因为抛物线经过A(-1,0),B(3,0)两点,解得b=-2,c=-3,答案为y=x2-2x-3.15.考点:此题是一道开放题,求解满足条件の二次函数解析式,答案不唯一.解析:需满足抛物线与x 轴交于两点,与y 轴有交点,及△ABC 是直角三角形,但没有确定哪个角为直角,答案不唯一,如:y=x2-1.16.考点:二次函数の性质,求最大值.解析:直接代入公式,答案:7.17.考点:此题是一道开放题,求解满足条件の二次函数解析式,答案不唯一.解析:如:y=x2-4x+3.18.考点:二次函数の概念性质,求值.答案:.三、解答题19.考点:二次函数の概念、性质、图象,求解析式.解析:(1)A′(3,-4)(2)由题设知:∴y=x2-3x-4 为所求(3)20.考点:二次函数の概念、性质、图象,求解析式.解析:(1)由已知x1,x2是x2+(k-5)x-(k+4)=0 の两根又∵(x1+1)(x2+1)=-8∴x1x2+(x1+x2)+9=0∴-(k+4)-(k-5)+9=0∴k=5∴y=x2-9 为所求(2)由已知平移后の函数解析式为:y=(x-2)2-9且x=0 时y=-5∴C(0,-5),P(2,-9).21.解:(1)依题意:(2)令y=0,得(x-5)(x+1)=0,x1=5,x2=-1∴B(5,0)由,得M(2,9)作ME⊥y 轴于点E,则可得S△MCB=15.22.思路点拨:通过阅读,我们可以知道,商品の利润和售价、销售量有关系,它们之间呈现如下关系式:总利润=单个商品の利润×销售量.要想获得最大利润,并不是单独提高单个商品の利润或仅大幅提高销售量就可以の,这两个量之间应达到某种平衡,才能保证利润最大.因为已知中给出了商品降价与商品销售量之间の关系,所以,我们完全可以找出总利润与商品の价格之间の关系,利用这个等式寻找出所求の问题,这里我们不妨设每件商品降价x 元,商品の售价就是(13.5-x)元了.单个の商品の利润是(13.5-x-2.5)这时商品の销售量是(500+200x)总利润可设为y 元.利用上面の等量关式,可得到y 与x の关系式了,若是二次函数,即可利用二次函数の知识,找到最大利润.解:设销售单价为降价x 元.顶点坐标为(4.25,9112.5).即当每件商品降价4.25 元,即售价为13.5-4.25=9.25 时,可取得最大利润9112.5 元“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
九年级数学二次函数测试题含答案(精选5套)
九年级数学二次函数测试题含答案(精选5套)九年级数学二次函数测试题含答案(精选5套)第一套:1. 将函数 $y = 2x^2 - 3x - 2$ 化简为标准形式,并求出它的顶点坐标。
答案:将函数化简为标准形式得到 $y = 2(x-\frac{3}{4})^2 -\frac{33}{8}$,顶点坐标为 $(\frac{3}{4}, -\frac{33}{8})$。
2. 求函数 $y = -x^2 + 4x + 1$ 的零点。
答案:将函数化简为标准形式得到 $y = -(x-2)^2 + 5$,令 $y = 0$,解得 $x = 2 \pm \sqrt{5}$,即零点为 $x_1 = 2 + \sqrt{5}$ 和 $x_2 = 2 -\sqrt{5}$。
3. 给定函数 $y = x^2 - 6x + 5$,求其对称轴的方程式。
答案:对称轴的方程式为 $x = \frac{-b}{2a}$,代入 $a = 1$ 和 $b = -6$ 得到 $x = \frac{6}{2} = 3$。
4. 若函数 $y = ax^2 + bx - 9$ 与 $y = -x^2 + 7x$ 有相同的图像,求$a$ 和 $b$ 的值。
答案:由于两个函数有相同的图像,所以它们的系数相等。
比较两个函数的对应系数得到 $a = -1$ 和 $b = 7$。
5. 已知函数 $y = x^2 - 4x + 5$ 的图像上存在一点 $(h, k)$,使得 $x= h - 3$ 时,$y = 2k + 12$,求点 $(h, k)$ 的坐标。
答案:将 $x = h - 3$ 代入函数得到 $y = (h-3)^2 - 4(h-3) + 5$。
代入$y = 2k + 12$ 得到 $(h-3)^2 - 4(h-3) + 5 = 2k + 12$。
整理得到 $(h-3)^2 -4(h-3) - 2k - 7 = 0$。
由于该方程为二次方程,必然存在实数解。
九年级数学二次函数测试题含答案(精选5套)
九年级数学 二次函数 单元试卷(一)时间90分钟 满分:100分一、选择题(本大题共10小题,每小题3分,共30分) 1.下列函数不属于二次函数的是( )A.y=(x -1)(x+2)B.y=21(x+1)2C. y=1-3x 2D. y=2(x+3)2-2x 22. 函数y=-x 2-4x+3图象顶点坐标是( )A.(2,-1)B.(-2,1)C.(-2,-1)D.(2, 1)3. 抛物线()12212++=x y 的顶点坐标是( )A .(2,1)B .(-2,1)C .(2,-1)D .(-2,-1)4. y=(x -1)2+2的对称轴是直线( )A .x=-1B .x=1C .y=-1D .y=1 5.已知二次函数)2(2-++=m m x mx y 的图象经过原点,则m 的值为 ( ) A . 0或2 B . 0 C . 2 D .无法确定6. 二次函数y =x 2的图象向右平移3个单位,得到新的图象的函数表达式是( )A. y =x 2+3B. y =x 2-3C. y =(x +3)2D. y =(x -3)27.函数y=2x 2-3x+4经过的象限是( )A.一、二、三象限B.一、二象限C.三、四象限D.一、二、四象限 8.下列说法错误的是( )A .二次函数y=3x 2中,当x>0时,y 随x 的增大而增大B .二次函数y=-6x 2中,当x=0时,y 有最大值0 C .a 越大图象开口越小,a 越小图象开口越大D .不论a 是正数还是负数,抛物线y=ax 2(a ≠0)的顶点一定是坐标原点9.如图,小芳在某次投篮中,球的运动路线是抛物线y =-15x 2+3.5的一部分,若命中篮圈中心,则他与篮底的距离l 是( )A .3.5mB .4mC .4.5mD .4.6m10.二次函数y=ax 2+bx +c 的图象如图所示,下列结论错误的是( ) A .a >0. B .b >0. C .c <0. D .abc >0.(第9题) (第10题)3.05m xyx y o二、填空题(本大题共4小题,每小题3分,共12分)11.一个正方形的面积为16cm 2,当把边长增加x cm 时,正方形面积为y cm 2,则y 关于x 的函数为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级下数学第一次月考试题
班级 姓名 学号 得分
一.选择题(每小题3分,共30分)
1.抛物线y =x 2 –2x –3 的对称轴和顶点坐标分别是( )
A .x =1,(1,-4)
B .x =1,(1,4)
C .x =-1,(-1,4)
D .x =-1,(-1,-4) 2.已知二次函数c bx ax y ++=2
的图象如图所示,则下列结论正确的是( )A .ab >0,c >0 B .ab >0,c <0 C .ab <0,c >0 D .ab <0,c <0 3.把二次函数y =2
132
1
2---x x 的图象向上平移3个单位,再向右平移4个单位,则两次平移后的图象的解析式是( )
A .x y (21-=- 1)2 +7
B .x y (21-=+7)2 +7
C .x y (21-=+3)2 +4
D .x y (2
1
-=-1)2 +1
4. 在同一直角坐标系中,一次函数y =ax +c 和二次函数y =ax 2+c 的图象大致为( )
5. 已知二次函数y =2
x 2+8x +7的图象上有有点A 1
(2)y -,,
B 21(5)3
y -,,C 31(1)5
y -,,则 y 1、y 2、y 3的大小关系为( )
A y 1 > y 2> y 3
B . y 2> y 1> y 3
C . y 2> y 3> y 1
D . y 3> y 2> y 1 6.关于二次函数y =ax 2+bx +c 图像有下列命题:
(1)当c =0时,函数的图像经过原点;(2)当c >0时,函数的图像开口向下时,方程ax 2 +bx + c =0 必有两个不等实根; (3)当b =0时,函数图像关
于原点对称.其中正确的个数有( )
A .0个
B .1个
C .2个
D .3个 7、. 已知二次函数772--=x kx y 的图象和x 轴有交点,则k 的取值范围是( )
A 47->k
B k ≥47-且0≠k
C k ≥47-
D 4
7->k 且0≠k 8、 已知二次函数已知函数c bx ax y ++=2
的图象如图所示,则下列
关系式中成立的是( )
A 120<-<a b
B 220<-<a b
C 221<-<a
b D
2=-a b
9、 已知二次函数)0(2≠++=a c bx ax y ,给出下列四个判断:⑴0>a ;⑵
02=+b a ;⑶042>-ac b ;⑷0<++c b a ;以其中三个判断为条件,余下一个
判断作结论,其中真命题的个数有( )
A 1 个
B 2 个
C 3 个
D 4 个 10把抛物线y =x +bx +c 的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y = x -3x +5,则( )
A .b =3,c =7
B .b =6,c =3
C .b =9,c = 5
D .b =9,c =21 二.填空题(每题4分,共24分)
11.已知抛物线y =ax 2 +bx +c 的对称轴为x =2,且经过点(1,4)和点(5,0),则该抛物线的解析式为_______________.
12.函数y =2x 2 – 4x – 1写成y = a (x –h)2 +k 的形式是________,抛物线y =2x 2 – 4x – 1的顶点坐标是_______,对称轴是__________.
13.已知函数①y =x 2+1,②y =-2x 2+x .函数____(填序号)有最小值,当x =____
时,该函数的最小值是_______.
14.当m=_________时,函数y = (m 2
-4))3(4
2-+--m x
m m x + 3是二次函数,
其解析式是__________________,图象的对称轴是_______________,顶点是________,当x =______时, y 有最____值是_______.
15.已知二次函数的图象开口向下,且与y 轴的正半轴相交.请你写出一个满足条件的二次函数的解析式:___________ 三.解答题(16 17 ,8分一题共50分)
16.已知一抛物线与x 轴的交点是A(-2,0)、B (1,0),且经过点C (2,8)。
(1)求该抛物线的解析式; (2)求该抛物线的顶点坐标。
17. 已知某商品的进价为每件40元,售价是每件60元,每星期可卖出300件。
市场调查反映:如调整价格 ,每涨价一元,每星期要少卖出10件。
该商品应定价为多少元时,商场能获得最大利润?
18.(10分)一场篮球赛中,球员甲跳起投篮,如图2,已知球在A处出手时离地面20/9 m,与篮筐中心C的水平距离是7m,当球运行的水平距离是4 m时,达到最大高度4m(B处),设篮球运行的路线为抛物线.篮筐距地面3m. ①问此球能否投中?
19.(10分)、有一个运算装置,当输入值为x时,其输出值为y,且y是x 的二次函数,已知输入值为2
-.
-,0,1时,相应的输出值分别为5,3-,4(1)求此二次函数的解析式;
(2)在所给的坐标系中画出这个二次函数的图象,并根据图象写出当输出值y为正数时输入值x的取值范围.
20、(10分)如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这是水面宽度为10m。
(1)在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?。
