清华大学工业工程系运筹学课件
合集下载
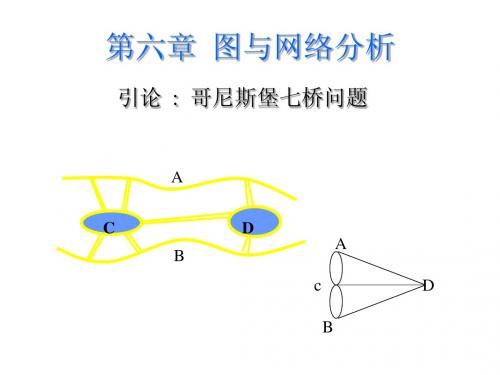
运筹学课件 第六章图与网络分析(清华大学出版社)
w(P ) = min w(P) 0
P
路P0的权称为从vs到vt的距离,记为:d( vs,vt )
OR3 12
– 最短路算法
Dijkstra算法 :有向图 ,wij≥0 一般结论:
vs到 j的 短 v 最 路
vs ,...,vi ,...,vj ⇒ vs ,...,vi
vs到 i的 短 v 最 路
OR3 17
4 )
标号的点,考察弧( v 4 为刚得到 P 标号的点,考察弧( v 4 , v 6),( v 4 , v 7)的端点 v 6,v 7: T ( v ) = min [T ( v ), P ( v ) + l ] = min [13 , 9 + 9 ] = 13 46 6 6 4 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 , 9 + 7 ] = 14 47 7 7 4 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 13 。 6 6 此时 P 标号的点集 S = { , , , v , v , v } v1 v 2 v 3 5 4 6 。 6 7)v 为刚得到 P 标号的点,考察弧( 标号的点,考察弧( v 6 , v 7),( v 6 , v 8)的端点 v 7, 8: v 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 ,13 + 5 ] = 14 67 7 7 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [+ ∞ ,13 + 4 ] = 17 68 8 8 6 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 14 。 7 7 此时 P 标号的点集 S = { , , , v , v , v , v } v1 v 2 v 3 5 4 6 7 。 7
P
路P0的权称为从vs到vt的距离,记为:d( vs,vt )
OR3 12
– 最短路算法
Dijkstra算法 :有向图 ,wij≥0 一般结论:
vs到 j的 短 v 最 路
vs ,...,vi ,...,vj ⇒ vs ,...,vi
vs到 i的 短 v 最 路
OR3 17
4 )
标号的点,考察弧( v 4 为刚得到 P 标号的点,考察弧( v 4 , v 6),( v 4 , v 7)的端点 v 6,v 7: T ( v ) = min [T ( v ), P ( v ) + l ] = min [13 , 9 + 9 ] = 13 46 6 6 4 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 , 9 + 7 ] = 14 47 7 7 4 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 13 。 6 6 此时 P 标号的点集 S = { , , , v , v , v } v1 v 2 v 3 5 4 6 。 6 7)v 为刚得到 P 标号的点,考察弧( 标号的点,考察弧( v 6 , v 7),( v 6 , v 8)的端点 v 7, 8: v 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 ,13 + 5 ] = 14 67 7 7 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [+ ∞ ,13 + 4 ] = 17 68 8 8 6 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 14 。 7 7 此时 P 标号的点集 S = { , , , v , v , v , v } v1 v 2 v 3 5 4 6 7 。 7
运筹学(第四版)清华大学出版社《运筹学》教材编写组-第1章 绪论课件PPT

❖ 在运筹学中除常用的数学方法以外,还引入 一些非数学方法和理论。
❖ 美国运筹学家沙旦(T.L.Saaty),在20世纪70 年代末提出了层次分析法(AHP)。
❖ 切克兰特(P.B.Checkland)把传统的运筹学方 法称为硬系统思考,它适用于解决那种结构 明确的系统以及战术和技术性问题,而对于 结构不明确的,有人参与活动的系统就不太 胜任了。这就应采用软系统思考方法。
(例如投入产出方法)。在当时这些先遣者中,越民义先
生、刘源张院士、朱永津教授、桂湘云教授、陈锡康教授、
徐光煇教授、韩继业教授、李秉全教授、郭绍僖教授等。
2021/3/10
2
第2节 运筹学的性质和特点
❖ 运筹学是一门应用科学,至今还没有统一且 确切的定义。
❖ 莫斯(P.M.Morse)和金博尔(G.E.Kimball)曾对 运筹学下的定义是:“为决策机构在对其控 制下业务活动进行决策时,提供以数量化为 基础的科学方法。”
❖ 以上过程应反复进行。
2021/3/10
6
第4节 运筹学的模型
模型有三种基本形式: ❖ ①形象模型; ❖ ②模拟模型; ❖ ③符号或数学模型。
2021/3/10
7
构模的方法和思路有以下五种:
❖ (1) 直接分析法 ❖ (2) 类比法 ❖ (3) 数据分析法 ❖ (4) 试验分析法 ❖ (5) 想定(构想)法(scenario)
2021/3/10
12
近几年来出现一种新的批评
❖ 指出有些人只迷恋于数学模型的精巧、 复杂化,使用高深的数学工具,而不善 于处理面临大量新的不易解决的实际问 题。现代运筹学工作者面临的大量新问 题是经济、技术、社会、生态和政治等 因素交叉在一起的复杂系统。
运筹学第四版·清华大学出版社·运筹学教材组·2.1线性规划PPT课件

约束条件: am1 x1 am2 x2 L L amn xn bm x1 0L L xn 0
简写为:
max Z
n
cjxj
j1
s.t
n
aij x j
j1
bi
i 1,2, , m
x j 0, j 1,2, , n
§2.1 线性规划问题及其数学模型Page 26
x2
2 4
x1
z 4
表示一簇平行n
max z 2x1 4x2
x1 2x2 2
4 x1
16 4x2 12
x1, x2 0
§2.1 线性规划问题及其数学模型Page 21
(3)无界解
max z x1 x2
2x1 x 4
max z 2x1 3x2 max z 2x1 3x2 0x3 0x4 0x5
x1 2x2 8
4
x1
16
4x2 12
x1, x2 0
x1 2x2 x3
8
4
x1
4 x2
x4 16 x5 12
据环保要求,河流中工业污水的含量应不大于0.2%。 因此两个工厂都需处理一部分工业污水。化工厂1处理污水 的成本是1000元/万立方米,化工厂2处理污水的成本是800元 /万立方米。问:在满足环保要求的条件下,每厂各应处理多 少工业污水,使两个工厂处理工业污水的总费用最小?
§2.1 线性规划问题及其数学模型 Page 11
得到本问题的数学模型为:
min z 1000x1 800x2
简写为:
max Z
n
cjxj
j1
s.t
n
aij x j
j1
bi
i 1,2, , m
x j 0, j 1,2, , n
§2.1 线性规划问题及其数学模型Page 26
x2
2 4
x1
z 4
表示一簇平行n
max z 2x1 4x2
x1 2x2 2
4 x1
16 4x2 12
x1, x2 0
§2.1 线性规划问题及其数学模型Page 21
(3)无界解
max z x1 x2
2x1 x 4
max z 2x1 3x2 max z 2x1 3x2 0x3 0x4 0x5
x1 2x2 8
4
x1
16
4x2 12
x1, x2 0
x1 2x2 x3
8
4
x1
4 x2
x4 16 x5 12
据环保要求,河流中工业污水的含量应不大于0.2%。 因此两个工厂都需处理一部分工业污水。化工厂1处理污水 的成本是1000元/万立方米,化工厂2处理污水的成本是800元 /万立方米。问:在满足环保要求的条件下,每厂各应处理多 少工业污水,使两个工厂处理工业污水的总费用最小?
§2.1 线性规划问题及其数学模型 Page 11
得到本问题的数学模型为:
min z 1000x1 800x2
清华大学运筹学课件(完整课件)
2、定理2
线性规划的基可行解对应于可行域的顶点。
3、定理3 若线性规划有解,则一定存在基可行解 为最优解。
20
§3 单纯形法 基本思路:从可行域的一个顶点到另一个顶点迭代求最优解。
3.1 初始基可行解的确定 1、松弛基(松弛变量对应的B) max z = x1 + 3x2 + 0x3 + 0x4 [eg.8]max z = x1 + 3x2 x1 + 2x2 + x3 =3 x1 + 2x2 ≤ 3 化标准型 2x1 + 3x2 + x4 = 4 2x1 + 3x2 ≤ 4 x1,x2,x3,x4 ≥ 0 x1,x2 ≥ 0
O(0,0)
Q3(2,3)
Q5(4,3) Q2(4,2)
Q1(4,0)
6、可行基 基可行解对应的B为可行基。
基可行解 非可行解
可行解
基解
17
§2 线性规划问题的几何意义 2.1 基本概念 1、凸集:设K为En(n维欧式空间)的一点集,X(1)∈K,X(2)∈K。 若α X(1)+(1-α )X(2)∈K,则称K为凸集。(0<α <1)
15
4、基解:取B = (p1,p2,·,pm) · · a11,·,a1m x1 · · a1m+1,·,a1n xm+1 · · b1 ┆ ┆ ┆ + ┆ ┆ ┆ =┆ am1,·,amm xm · · amm+1,·,amn xn · · bm ↑ ↑ ↑ ↑ 基 基变量 非基 非基变量 令 xm+1 = · = xn = 0 (非基变量为0) · · 则 BXB = b 1 (0) (0) (0) T ∴
运筹学课件PPT课件

整数规划的解法
总结词
整数规划的解法可以分为精确解法和近似解法两大类。
详细描述
整数规划的解法可以分为两大类,一类是精确解法,另一类是近似解法。精确解法包括割平面法、分支定界法等, 这些方法可以找到整数规划的精确最优解。而近似解法包括启发式算法、元启发式算法等,这些方法可以找到整 数规划的近似最优解,但不一定能保证找到最优解。
模拟退火算法采用Metropolis准则来 判断是否接受一个较差解,即如果新 解的能量比当前解的能量低,或者新 解的能量虽然较高但接受的概率足够 小,则接受新解。
模拟退火算法的应用
01
模拟退火算法在旅行商问题中得到了广泛应用。通过模拟退火算 法,可以求解旅行商问题的最优解,即在给定一组城市和每对城 市之间的距离后,求解访问每个城市恰好一次并返回出发城市的 最短路径。
动态规划的解法
确定问题的阶段和状态
首先需要确定问题的阶段和状态,以便将问 题分解为子问题。
建立状态转移方程
根据问题的特性,建立状态转移方程,描述 状态之间的转移关系。
求解子问题
求解每个子问题,并存储其解以供将来使用。
递推求解
从最后一个阶段开始,通过递推方式向前求 解每个阶段的最优解。
动态规划的应用
线性规划的解法
单纯形法
01
单纯形法是求解线性规划问题的经典方法,通过迭代过程逐步
找到最优解。
对偶理论
02
对偶理论是线性规划的一个重要概念,它通过引入对偶问题来
简化求解过程。
分解算法
03
分解算法是将大规模线性规划问题分解为若干个小问题,分别
求解后再综合得到最优解。
线性规划的应用
生产计划
线性规划可以用于生产计划问题, 通过优化资源配置和生产流程, 提高生产效率和利润。
清华大学运筹学课件(完整课件)
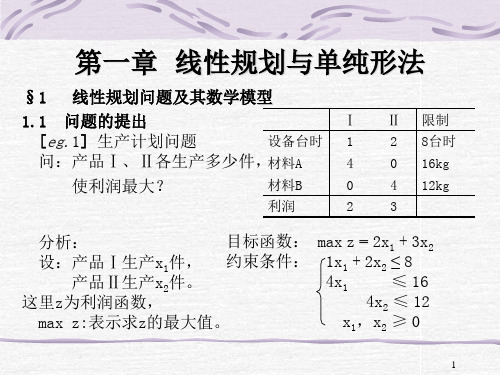
2x1 + 3x2 ≤ 4 x1,x2 ≥ 0
化标准型
max z = x1 + 3x2 + 0x3 + 0x4
x1 + 2x2 + x3 = 3
2x1 + 3x2
+ x4 = 4
x1,x2,x3,x4 ≥ 0
系数矩阵
1 A 2
2 3
1 0
0 1
p1
p2
p3 p4 , 则 B p3 p4
取x3、x4为基变量,令非基变量x1= x2=0 ∴ 初始基可行解:X(0) = (0 0 3 4)T
③
3
z = 2x1 + 4x2,此时表示 目标函数的直线与表示
Q2(4,2)
① *
条件①的直线平行,
o
最优点在线段Q3Q2上。
即存在无穷多最优解。
4 Q1
x1
7
(3)无界解
[eg.5]
max z = 2x1 + 3x2 4x1 ≤ 16 x1,x2 ≥ 0
则x2 → ∞,z → ∞。 即存在无界解。
对于
n
m
max z c j x j cni xni
j 1
i 1
n
aij x j xni bi
i 1, , m
j1
x
j
0
j 1, , n m
设 xni 为基变量可行,i 1,, m
x j为非基变量, j 1,, n
n
xni bi aij x j j 1
代入目标函数
产品Ⅱ生产x2件。
4x1
≤ 16
这里z为利润函数,
4x2 ≤ 12
max z:表示求z的最大值。
化标准型
max z = x1 + 3x2 + 0x3 + 0x4
x1 + 2x2 + x3 = 3
2x1 + 3x2
+ x4 = 4
x1,x2,x3,x4 ≥ 0
系数矩阵
1 A 2
2 3
1 0
0 1
p1
p2
p3 p4 , 则 B p3 p4
取x3、x4为基变量,令非基变量x1= x2=0 ∴ 初始基可行解:X(0) = (0 0 3 4)T
③
3
z = 2x1 + 4x2,此时表示 目标函数的直线与表示
Q2(4,2)
① *
条件①的直线平行,
o
最优点在线段Q3Q2上。
即存在无穷多最优解。
4 Q1
x1
7
(3)无界解
[eg.5]
max z = 2x1 + 3x2 4x1 ≤ 16 x1,x2 ≥ 0
则x2 → ∞,z → ∞。 即存在无界解。
对于
n
m
max z c j x j cni xni
j 1
i 1
n
aij x j xni bi
i 1, , m
j1
x
j
0
j 1, , n m
设 xni 为基变量可行,i 1,, m
x j为非基变量, j 1,, n
n
xni bi aij x j j 1
代入目标函数
产品Ⅱ生产x2件。
4x1
≤ 16
这里z为利润函数,
4x2 ≤ 12
max z:表示求z的最大值。
运筹学教学课件(全)

实用举例
某公司通过市场调研,决定生产高中档新型拉杆箱。 某分销商决定买进该公司3个月内的全部产品。拉杆箱生 产需经过原材料剪裁、缝合、定型、检验和包装4过程。
通过分析生产过程,得出:生产中档拉杆箱需要用 7/10小时剪裁、5/10小时缝合、1小时定型、1/10小时检 验包装;生产高档拉杆箱则需用1小时剪裁、5/6小时缝合、 2/3小时定型、1/4小时检验包装。由于公司生产能力有限, 3月内各部的最大生产时间为剪裁部630小时、缝合部600 小时、定型部708小时、检验包装部135小时。
D {x | Ax b, x (x1,, xi ,, xn ) 0}
是凸集(凸多面体)。
引理2.1:线性规划的可行解 x (x1 ,, xn )T 为基本可行解的 充分必要条件是x的正分量所对应的系数列向量是线性无关的, 即每个正分量都是一个基变量。
定理2.2:线性规划问题的基本可行解x对应于可行域的顶点
通过分析生产过程,得出:生产中档拉杆箱需要用
7/10小时可剪裁以、通5/1过0小线时性缝合规、划1小求时定解型!、1/10小时
检验包装;生产高档拉杆箱则需用1小时剪裁、5/6小时 缝合、2/3小时定型、1/4小时检验包装。由于公司生产 能力有限,3月内各部的最大生产时间为剪裁部630小时、 缝合部600小时、定型部708小时、检验包装部135小时。
x2
L1:x1=6 L3:2x1+3x2=18
B 可行域
L2:x2=4 最优解
x1
4x1+3x2
解的特殊情况——解的特殊情况——无界解
线性规划的基本性质
若线性规划有最 优解,则最优解必在可 行域的顶点上达到。
X
可行域内部的点 • 可行解? 是 • 最优解? 不
工业工程导论之运筹学简介ppt课件

8. 应用数学(运筹学、 16. 安全 9. 管数组理 学 织经 应 规济 用 划学 等 与、 ) 理统论计和----美17国. 国职家业标卫准生A与N医SI学--Z94(82年)
工业工程技术人员的知识结构
工程技术知识 :如机械工程、电气工程、等专业的理论和应用技
术。
通用的数学知识
数学与统计知识:包括应用数学、概率论与数理统计、统计学等
Hydroelectrica Espanol(1-2/1990,$200万) 应用统计预测管理水力发电的水库系统
施乐公司(11/1975,生产率提高50%以上) 缩短反应时间和改进维修人员生产率的维修战略修正
运筹学应用获奖(1990 ~ )
宝洁公司(1-2/1997,$2亿) 重新设计生产和分销系统以降低成本和改进市场进入速度
工业工程导论之
运筹学简介
Introduction of Operations Research
吴小东
什么是工业工程?
美国质量管理权威朱兰博士说:美国值 得 向全世界夸耀的东西就是IE,美国之 所以 打胜第一次世界大战,又有打胜第 二次世 界的力量,就是美国有IE。
工业工程
IE----INDUSTRIAL ENGINEERING 工业工程,简称IE,是世界上公认的能杜绝
approach)进行辅助管理决策制定(aid managerial decision making)的一门学科
(discipline)。
管理者 制定决策 管理科学 运用合理的分析来改善决策的制定
学科应用介绍
OR/MS 的应用
IE应用
生产管理 交通网络 存储管理 市场营销 项目评价 军事方面 等等
管理者管理者制定决策制定决策管理科学管理科学运用合理的分析来改善决策的制定运用合理的分析来改善决策的制定学科介绍安防系统指以搭建安全防范管理平台为目的利用综合布线技术通信技术网络互联技术多媒体应用技术安全防范技术网络安全技术等生产管理生产管理交通网络交通网络存储管理存储管理市场营销市场营销项目评价项目评价军事方面军事方面等等等等学科应用介绍产品组合生产资源分配产品组合生产资源分配设施选址与供应链网络设计设施选址与供应链网络设计生产计划采购生产库存销售生产计划采购生产库存销售设备更新设备更新系统可靠性优化系统可靠性优化人机数量确定问题人机数量确定问题项目优化管理项目优化管理制造工艺优化制造工艺优化等等等等ie应用ie应用安防系统指以搭建安全防范管理平台为目的利用综合布线技术通信技术网络互联技术多媒体应用技术安全防范技术网络安全技术等经典运筹学应用获奖联合航空公司121986600万满足乘客需求以最低成本进行订票处和机场工作班次排程citgo石油公司1219877000万优化炼油运作以及产品的供应配送和营销旧金山警署1219891100万用计算机系统最优排程和巡警设置荷玛特发展公司1219874000万商业区和办公楼销售的最优化安排att121990406亿更多的销售为公司商业用户的电话销售中心的优化选址安防系统指以搭建安全防范管理平台为目的利用综合布线技术通信技术网络互联技术多媒体应用技术安全防范技术网络安全技术等美国石油公司1219821000万确定和评价公司产品商业化的新战略美国邮政服务公司3419871219922亿邮件自动化方案的技术经济分析标准品牌公司121981380万控制100种成品的库存确立安全库存再订购点和订购量ibm1219902000万25亿库存降低整合备件库存的全国网络以改进服务支持hydroelectricaespanol121990200万应用统计预测管理水力发电的水库系统施乐公司111975生产率提高50以上缩短反应时间和改进维修人员生产率的维修战略修正经典运筹学应用获奖安防系统指以搭建安全防范管理平台为目的利用综合布线技术通信技术网络互联技术多媒体应用技术安全防范技术网络安全技术等宝洁公司1219972亿重新设计生产和分销系统以降低成本和改进市场进入速度南非国防部12199711亿国防设施和武器系统规模和状态的重新优化设计数字设备公司1219958亿重构供应商工厂分销中心潜在厂址和市
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(Max
problem )
If they are BV, its coefficients =?
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
13
Example 1: Compute the optimal tableau
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
3
Solution:
Solution: x1=number of soldiers produced each week x2=number of trains produced each week
the current basis remain optimal ? <=b1<= ? b1= 100+D 2x1+x2= 100+D x1+x2=
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
15
4.3 Sensitivity Analysis
(
[
)
]
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
11
Tableau
z C BV B 1b B 1 NX NBV C NBV X NBV = 0 z + C BV B 1 N C NBV X NBV = C BV B 1b s.t. BX BV + NX NBV = b X BV + B 1 NX NBV = B 1b X BV , X NBV ≥ 0
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
8
Max Problem New optimal z-value=(old optimal z-value)+(Constraint i's shadown price) △bi Min Problem New optimal z-value=(old optimal z-value)-(Constraint i's shadown price) △bi
max z = x1 + 4 x2 s.t. x1 + 2 x2 ≤ 6 2 x1 + x2 ≤ 8 BV = {x2 , s2 } x1 , x2 ≥ 0
2 0 B= 1 1
Z X BV X NBV RHS 1 0 CBV B1N CNBV CBV B1b 0 Im B1N B1b
14
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
10
4.2 Some Important Formulas
max(min) z = c1 x1 + c2 x2 + s.t. a11 x1 + a12 x2 + a21 x1 + a22 x2 + am1 x1 + an 2 x2 + xi ≥ 0(i = 1,2, + cn xn + a1n xn = b1 + a2 n xn = b2 + amn xn = bm
4
max
z = 3x1 + 2 x2 x1 + x2 + s2 = 80 x1 + s3 = 40 x1 , x2 , s1 , s2 , s3 ≥ 0
s.t. 2 x1 + x2 + s1 = 100
A B C D
s1,x2,s3 x1,x2,s3 x1,x2,s2
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
the current basis remain optimal x2=-C/2 x1+constant/2 ? <=C<= ?
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
NBV
Coefficient of excess variable ei in optimal row 0 = ith element of C BV B 1
(
)
Coefficient of artificial variable ai in optimal row 0 = ith element of C BV B 1 + M
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
9
Importance of Sensitivity Analysis:
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
max z = 3 x1 + 2 x2
subject to( s.t.) 2 x1 + x2 ≤ 100 x1 + x2 ≤ 80 x1 ≤ 40
x1
≥0 x2 ≥ 0
Optimal Solution: z=180, x1=20, x2=60
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
7
Shadow Prices
Shadow Prices for the ith constraint of an LP to be the amount by which the optimal z-value is improved—increased in a max problem and decreased in min problem –if the rhs of the ith constraint is increased by 1
Author:Zhang Zhihai, Dept. of Industrial Engineering, Tsinghua University, 100084, Beijing, China
2
4.1 A Graphical Introduction to Sensitivity Analysis
6
Effect of a Change in a RHS on the LP's Optimal Solution
max z = 3 x1 + 2 x2 x1 + x2 + s2 = 80 x1 + s3 = 40 x1 , x2 , s1 , s2 , s3 ≥ 0 s.t. 2 x1 + x2 + s1 = 100
5
Effect of a Change in an Objective Function Coefficient
max
z = 3 x1 + 2 x2 x1 + x2 + s2 = 80 x1 + s3 = 40 x1 , x2 , s1 , s2 , s3 ≥ 0
s.t. 2 x1 + x2 + s1 = 100
z = C BV X BV + C NBV X NBV s.t. BX BV + NX NBV = b X BV , X NBV ≥ 0
n)
z C BV B 1b B 1 NX NBV C NBV X NBV = 0 z + C BV B 1 N C NBV X NBV = C BV B 1b s.t. BX BV + NX NBV = b X BV + B 1 NX NBV = B 1b X BV , X NBV ≥ 0
Operations Research (1) Research(I)
Dept. of Industrial Engineering
Chapter 4 Sensitivity Analysis and Duality
22:56
1
Context
4.1 A Graphical Introduction to Sensitivity Analysis 4.2 Some Important Formulas 4.3 Sensitivity Analysis 4.4 Sensitivity Analysis When More Than One Parameter is Changed: The 100% Rule 4.5 Finding the Dual of an LP 4.6 Economic Interpretation of the Dual Problem
