线性矩阵不等式1

合集下载

不等式证明与矩阵构造

不等式证明与矩阵构造
线性不等式是一种以等式表达和数学运算操作处理有关限制条件问题的常用的数学方法，它可以用于解决多种应用问题。

本文将结合矩阵构造，介绍线性不等式的证明方法：
一、矩阵构造
1、方程组矩阵构造：矩阵构造是线性不等式证明的基础，即把一组不等式表示为矩阵形式，并根据不等式的不同类别和相互关系，将矩阵构建成符合要求的方式，以便进行证明。

2、矩阵转置：在矩阵构造的基础上，可以对不等式转置（即空间坐标系的变换），当不等式的式子含有负号时，我们可以通过转置将正负号转换，以此来解决等式或不等式的体系。

二、矩阵证明
1、比较矩阵：矩阵证明法是线性不等式最常用的一种证明方法，它具有明确性和方便性。

主要是比较矩阵或变量中任意数字的大小，从而分析两者不等式结果的偏差，以确定不等式判定结果。

2、矩阵替换：另一种常见的矩阵证明法是将不等式中表达式以及相关
数据抽象出来，并将其体现在另一个矩阵模型中，然后对另一个矩阵
模型进行评价，以获得最终的判断结果。

三、矩阵总结
1、方程式解析：通过构建符合线性不等式条件的方程，并分析一组线
性方程是否具有解，如果有解，则证明这组不等式结果正确；
2、证明正确性：当解出每一条不等式的结果后，分别对它们进行证明，通过这组数据进行计算出所有不等式的结果，根据结果分析该组不等
式是不是正确的。

总结：线性不等式的证明主要是结合方程组矩阵构造、矩阵转置、比
较矩阵、矩阵替换方法，从而使线性不等式结果正确。

因此，我们可
以从更宽阔的角度出发，运用数学解决复杂的问题和实际应用。

应用线性矩阵不等式解决时滞系统控制问题

ＳＵＮＨａｏ
（Ｎｏ．９１５５０ＴｒｏｏｐｓｏｆＰＬＡ，Ｄａｌｉａｎ１１６０２３）
ＡｂｓｔｒａｃｔＩｎｔｈｉｓｐａｐｅｒ．ｈｏｗｔｏｓｏｌｖｅＨ。。ｃｏｎｔｒｏｌｐｒｏｂｌｅｍｉｎａｋｉｎｄｏｆｔｉｍｅ－ｄｅｌａｙｓｙｓｔｅｍｂｙｕｓｉｎｇｌｉｎｅａｒｍａｔｒｉｘｉｎｅ — ｑｕａｌｉｔｙ（ＬＭＩ）ｉｓｓｔｕｄｉｅｄ．ＢａｓｅｄｏｎＬｙａｐｕｎｏｖｓｅｃｏｎｄｍｅｔｈｏｄ，ｗｅｐｒｅｓｅｎｔｔｈｅＨｏｏｓｔａｂｉｌｉｔｙｃｏｎｄｉｔｉｏｎ．Ｔｈｒｏｕｇｈｓｏｌｖｉｎｇｔｈｅ
ＴＰ３９１ＤＯＩ：１０．３９６９／ｊ．ｉｓｓｎ１６７２ — ９７２２．２０１４．０３．０２０
中图分类号
ＳｏｌｖｉｎｇＣｏｎｔｒｏｌＰｒｏｂｌｅｍｉｎＴｉｍｅ－ｄｅｌａｙＳｙｓｔｅｍｗｉｔｈＬＭＩ
的重视，已成为系统与控制领域的一大热点问题ｒ１］。本文介绍了一类滞后型离散时滞系统的
小于零。若下式成立
Ｌ（ｚ）一Ｌｏ＋１Ｌ１＋…＋ｘＮＬⅣ ０

《鲁棒控制》-6-线性矩阵不等式

(≤ 0)
为线性矩阵不等式（LMI）。
当存在实向量 x ，使得 F ( x) < 0(≤ 0) ，则称 LMI F ( x) < 0(≤ 0) 可行或存在可
行解。
LMI 的可行解全体构成一凸集。
令 X 是一实对称矩阵，对于任意给定实数矩阵 A 和实对称矩阵 Q ，则矩阵
不等式
AT X + XA + Q < 0
⎢ ⎣
0
⎡I ⎢⎣0
−S12 I
S −1 22
⎤ ⎥ ⎦
⎡ ⎢⎣
S11 S21
S12 S22
⎤ ⎥⎦
⎡I ⎢⎣0
−S12 I
S −1 22
⎤T ⎥ ⎦
0
⎤
S22
−
S21S1−11S12
⎥ ⎦
=
⎡ ⎢
S11
⎣
−
S12
S −1 22
S21
S21
0 ⎤⎡ I
S22
⎥ ⎦
⎢⎣−
S −1 22
S
21
0⎤
I
⎥ ⎦
x (t ) = Ax (t ) + Bu (t ) y (t ) = Cx (t ) + Du (t )
假设 D + DT > 0 。令
H (s) = C (sI − )A −1 B + D
系统无源（passive）: 当 x (0) = 0 时，
∫T 0
uT
(t
)y
(t
)
dt
≥
0
● 系统无源 iff
ALQ
⎤ ⎥
⎥
0 ⎥<0
#
⎥ ⎥

用线性矩阵不等式方法求解控制理论问题_张怡

（ａ）包覆不完全
（ｂ）形成间隙
图１粘结剂对炸药的润湿状况
（２）对于水悬浮法，造粒过程有水存在，此时发生自动铺展的条件为：△Ｇ＝ γＥＢ＋ γＢＷ－ γＥＷ＜０。式中：γＥＢ、γＢＷ、γＥＷ分别为炸药－粘结剂、粘结剂－水、炸药－水界面张力。如果粘结剂满足在空气中能够完全润湿炸药的条件，则上式可整理为：
－１／２－１／２
其中，λｍａｘ（Ｘ，Ｙ）表示矩阵ＹＸＹ的最大特征值。
ＧＥＶＰ是半凸（ｑｕａｓｉｃｏｎｖｅｘ）优化问题。
－１
（４）凸问题（ＣＰ）：ｍｉｎｌｏｄｅｔＡ（Ｘ），ｓ．ｔＡ（Ｘ）＞０，
Ｂ（Ｘ）＞０。
（９）
这里Ａ、Ｂ是仿射依赖于变量Ｘ的对称矩阵，注意当Ａ＞０
－１
等式问题。
在非线性矩阵不等式转化为线性矩阵不等式的许
多问题中，常常用到矩阵的Ｓｃｈｕｒ补性质定理。
# $ 定理（Ｓｃｈｕｒ补）线性矩阵不等式：
Ｑ（Ｘ）Ｓ（ＴＸ）
Ｓ（Ｘ）Ｒ（Ｘ）
（３）
其中Ｑ（Ｘ）＝Ｑ（Ｘ）Ｔ，Ｒ（Ｘ）＝Ｒ（Ｘ）Ｔ，Ｓ（Ｘ）是等价于非线性矩阵
不等式：Ｒ（Ｘ）＞０，Ｑ（Ｘ）－Ｓ（Ｘ）Ｒ（Ｘ）－１Ｓ（Ｘ）Ｔ＞０。（４）
该步骤，直至收敛到问题的最优解。该算法虽简单，但
ห้องสมุดไป่ตู้
效率不高，仅适用于较小规模问题。
１９８８年，Ｎｅｓｔｅｒｏｖ和Ｎｅｍｉｒｏｖｓｋｉｉ提出了内点法，用
来求解具有线性矩阵不等式约束的凸优化问题，取得
了良好的效果。其基本思想是：运用约束集定义一个
凸的障碍函数，将其附加到原问题的目标函数中，以
一个无约束优化问题代替原有的约束优化问题，运用

线性矩阵不等式

则应用引理 2.1.2，可以将矩阵不等式（2.1.6）的可行性问题转化成一个等价的矩阵不等式
AT P PA Q PB
BT P
R0
（2.1.7）
的可行性问题，而后者是一个关于矩阵变量P的线性矩阵不等式。
2.3一些标准的线性矩阵不等式问题
例2.1.1 稳定性问题考虑线性自治系统
x(t) Ax(t)
setlmis([]) X=lmivar(1,[61]) S=lmivar(1,[20;21]) ﹪lst LMI lmiterm([111x],1,A,’s’) lmiterm([111s],c’,c) lmiterm([112x],1,B) lmiterm([122s],-1,1) ﹪2nd LMI lmiterm([-211X],1,1) ﹪3rd LMI lmiterm([-311s],1,1) lmiterm([3110],1) lmisys=getlmis
m 是一组给定的实对称矩阵，（2.1.1）中的不等号“＜”指的是矩阵 F(x)是负定的，即对所有
非零的向量 v Rm , vT F (x)v0 或者 F(x)的最大特征值小于零。
在许多系统与控制问题问题中，问题的变量是以矩阵的形式出现的。例如 Lyapunov 矩阵不等式：
F ( X ) AT X XA Q0
lmivar 函数lmivar用来描述出现在线性矩阵不等式系
统中的矩阵变量，每一次只能描述一个矩阵变量。矩阵变量的描述包括该矩阵变量的结构。该函数的一般表达是：
X=lmivar(type,struct) 这一函数定义了一个新的矩阵变量X。函数中
的第一个输入量type确定了矩阵变量X的类型，第二个输入量struct进一步根据变量X的类型给出该变量的结构。变量的类型分成三类：

鲁棒控制理论与设计第三章矩阵分析和线性矩阵不等式

k<r
则 A 与秩为 k 的任一矩阵 B 之差的 L1 和 L2 范数分别为
min A − B =
rank (B )=k
1
A − Ak
1 = σ k +1
和
(3.1.30)
3－5
第三章矩阵分析和线性矩阵不等式
min A − B 2 =rank (B )=k2A − Ak
2 2
=
σ
2 k +1
+
L
∂A ∂θ
= [ ∂A ∂θ1
,
∂A ∂θ 2
,L ,
∂A ∂θ n
]
(3.1.12)
4）标量对矩阵求导仍为矩阵。设 J 为标量， M 为矩阵，则 ∂J 是以 ∂J 为第 ij 元素的矩阵，
∂M
∂mij
其中 mij 表示 M 矩阵的第 ij 元素。
在上述约定下，有如下一些结果：
1） ∂ (aT x) = aT ； ∂x
−
A21
A -1 11
A12
]
(3.1.5) (3.1.6)
证明：因为
所以有
⎡ A11
⎢ ⎣
A21
A12 ⎤ ⎡ I
A22
⎥ ⎦
⎢⎣−
A−1 22
A21
0⎤
A−1 22
⎥ ⎦
=
⎡ ⎢
A11
⎣
−
A12 0
A−1 22
A21
A12
A−1 22
I
⎤ ⎥ ⎦
det
A ⋅ det
A −1 22
=
det[ A11
3.1.2 矢量与矩阵的微分运算
在鲁棒控制理论和系统建模中，矢量与矩阵的微分运算是非常重要的。本节我们不加证明地给出一些常用到得运算定理和公式。为了叙述方便，采用下列约定。

【江苏省自然科学基金】_线性矩阵不等式(lmi)_期刊发文热词逐年推荐_20140820

2011年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
科研热词网络控制系统马尔可夫跳变量化脉冲耦合神经网络线性矩阵不等式稳定性混合时滞时变时延故障诊断广义系统凸性全局渐近同步 kalman滤波器 h∞滤波器
推荐指数 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词线性矩阵不等式测量数据丢失大系统 h∞控制鲁棒稳定性脉冲耦合神经网络时延导数相关变时滞反应扩散项全局渐 1 1 1 1 1 1 1 1
2013年序号 1 2 3 4 5 6 7 8
推荐指数 1 1 1 1 1 1
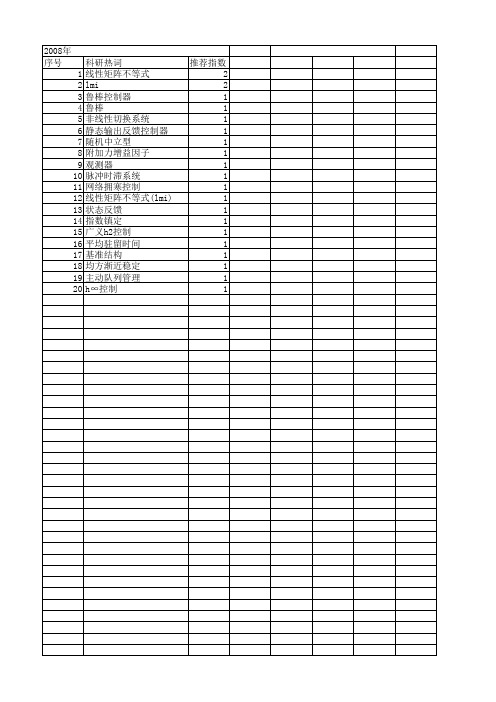
2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
科研热词线性矩阵不等式 lmi 鲁棒控制器鲁棒非线性切换系统静态输出反馈控制器随机中立型附加力增益因子观测器脉冲时滞系统网络拥寒控制线性矩阵不等式(lmi) 状态反馈指数镇定广义h2控制平均驻留时间基准结构均方渐近稳定主动队列管理 h∞控制
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11
科研热词鲁棒随机稳定马尔可夫过程非线性网络控制系统锥补量化耗散控制线性矩阵不等式系统辨识混沌同步
推荐指数 1 1 1 1 1 1 1 1 1 1 1
2013年科研热词间歇过程线性矩阵不等式(lmi) 线性矩阵不等式二次型迭代学习控制主动队列管理 tcp流模型 s-procedure h∞控制推荐指数 1 1 1 1 1 1 1 1

线性矩阵不等式1ppt课件

min s.t.G(x) F (x)
F(x) 0 H (x) 0
9
系统性能分析
10
连续时间系统
3.1.1系统增益指标
考虑 x&(t) Ax(t) Bw(t) z(t) Cx(t)+ Dw(t)
sup size(z) w0 size(w)
11
L2范数
• 对于平方可积的信号 f ，定义
min
s.t. PA AT P CTC 0
BT PB I
P>0
•若有一最优值，则
ie
15
定理2---EP
x&(t) Ax(t) Bw(t) z(t) Cx(t)+ Dw(t)
min
s.t. AQ QAT BBT 0
CQCT I
Q>0
•若有一最优值，则
ep
8
标准的线性矩阵不等式问题
Linear Matrix Inequality (LMI)
➢ 可行性问题(LMIP)—求不等式的可行解
检验是否存在x，使得 F(x) 0成立。
➢ 特征值问题(EVP)－－求不等式的优化解
min s.t.G(x) I
H (x) 0
➢ 广义特征值问题(GEVP)－－仿射矩阵函数的不等式优化问题
• EP(Energy-to-Peak)增益：
ep sup
z
w 2 1
•ห้องสมุดไป่ตู้
EE(Energy-to-Energy)增益：
ee sup
z 2
w 2 1
• PP(Peak-to-Peak)增益：
pp sup
z
w 1
14
定理1---IE

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a)
b) c)
X 0
T 1 X11 X12 0 X11 0 ，且 X 22 X12
1 T X 22 0 ，且 X11 X12 X 22 X12 0
。
Schur补应用
若要证明存在对称矩阵P>0,Q>0,R>0,使得如下不等式成立 AT P PA PBR1BT P Q 0
现有的Riccati方程处理方法中，缺乏寻找参数最佳
值的方法，参数的人为确定给分析和综合结果带来了很大的保守性。
Riccati矩阵方程本身的求解也存在一定的问题，比
如用于迭代求解时，收敛性无法保证。
线性矩阵不等式的引入
基于凸优化内点法，可应用于系统和控制的各个领
域。
1995年，MATLAB推出了求解线性矩阵不等式问
题的LMI工具箱，进一步推动了LMI的飞速发展。
任一可行解均可得到一个控制器，方便实用。
凸（约束）问题
定义（凸集）一个集合 C R k 称为凸的，如果集合中任两点 C 和 C C 及参数 [0,1],
有
C 1 C C
1 2
标准的线性矩阵不等式问题
Linear Matrix Inequality (LMI)
可行性问题(LMIP)—求不等式的可行解特征值问题(EVP)－－求不等式的优化解广义特征值问题(GEVP)－－仿射矩阵函数的不等式优化问题
关于矩阵不等式的一些结论
矩阵变量的替换法存在标量ε>0，对称矩阵X>0,矩阵K,使得
只需证明如下线性矩阵不等式(LMI)成立
AT P PA Q PB 0 T B P R
Schur补：是将非线性矩阵不等式转化为线性矩阵不等式的有效工具
复线性矩阵不等式的处理
复变量实矩阵的映射
a jb
复矩阵实矩阵的映射
M A jB
a b b a
AT P PA+ C TC T B P PB 0 I
C 1 1 C 2称为 C 1 和 C 2 的凸组合。
将矩阵不等式的解约束在矩阵变量定义的空间中
Schur补定理
引理 (Schur Complement) 对于分块对称阵
X11 X T X12 X12 X 22
其中
X 11
为方阵，则以下三个条件是等价的：
S-procedure（S-过程）
存在对称矩阵P>0,使得对满足πTπ ξTCTCξ的所有 ξ 0和π，若要 T AT P PA PB 0 T 0 B P 成立，当且仅当存在标量τ>0和对称矩阵P>0,使得
X A BK T A BK X 2YY T XC T 0 CX I
记 V X ,W KV
存在标量ε>0，对称矩阵V>0,矩阵W,使得
VAT + W T B T + AV + BW 2YY T VC T 0 CV I
A B B A
复矩阵不等式的表示
M 0 A B B A 0
非严格线性矩阵不等式
F 0 F 0
严格线性矩阵不等式
非严格线性矩阵不等式
X F 0 0 0 X 0 X
通常情况下，可将非严格线性矩阵不等式当成严格线性矩阵不等式处理。但一定要视具体情况而定，并不总是正确的。
主要内容
线性矩阵不等式概论鲁棒H∞控制区域极点配置保性能控制时滞系统的分析与综合鲁棒跟踪问题 Matlab的LMI工具箱介绍
线性矩阵不等式概论
Riccati方程存在的问题
需要设计者事先确定一些待定参数。参数的选择不
仅影响到结论的好坏，而且还影响到问题的可解性。