一道高考题的解后反思
对一道光学高考题的错解纠正和反思
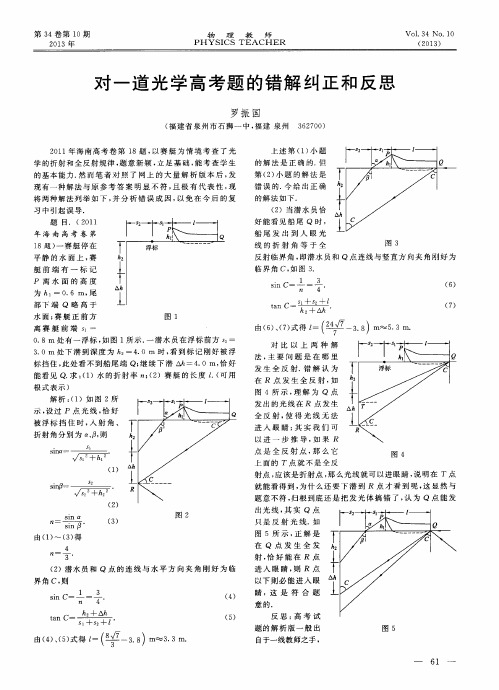
对 比 以 上 两 种 解
法, 主 要 问 题 是 在 哪 里
标挡住 , 此 处 看 不 到 船 尾 端 Q; 继 续下潜 A h 一4 . 0 m, 恰 好 能看见 Q . 求: ( 1 )水 的 折 射 率 n ; ( 2 )赛 艇 的长 度 z . ( 可 用
给 出 正 确 的解 答 .
方法 2 : 变质量二体 系 动量定 理. 对 由空 中绳段 , 和 分离质元 d m 构 成 的二 体 系 , 由质 点 系 动量 定 理 有
进 入 眼睛 , 则 R 点 以下 则 必 能 进 入 眼 睛 ,这 是 符 合 题
意 的. 反 思: 高 考 试
s i n c 一 一 手 .
t a n c 一 丽 . ‘
㈩
( 5 )
/
图5
题的解 析版一 般 出
由 ( 4 ) 、 ( 5 ) 式 得 z 一 ( 学一 3 . 8 ) m ≈ 3 . 3 m .
根式表示 ) 解析: ( 1 )如 图 2所
‘ :
浮标
Q
发 生 全 反 射. 错 解 认 为 在 R 点 发 生 全反 射 , 如 图 4所 示 , 理 解 为 Q 点 发 出 的 光 线 在 R 点 发 生
示, 设过 P点光 线 , 恰 好 被 浮标挡 住 时 , 入射角、 折射 角分别为 a 、 卢 , 则
习 中 引 起误 导 .
题 目. ( 2 0 1 1
错 误 的. 今 给 出 正 确
的解 法 如 下 . ( 2 )当 潜 水 员 恰 好能看见 船尾 Q时 , 船 尾 发 出 到 人 眼 光
会选择恰当方法是一题多解反思后的更高境界——一道高考参数取值范围问题的解题策略比较

g :号 = ) 一 + 1
因此 g x 在 ( , ] 调递增 , ( ) 01单 此时
>, 0
因此
6 一 ≥
.
综 上所 述 , 0>1时 , ≥ 一 ; 0<口 1 当 6 当 ≤
时 ,≥ ~ 6 .
C ] 值 g1= 孚一 = , g )最 =( 一 了 一 ( 大 ) 1
题目 已知函数 ) ÷ + + 3其 = + ,
中口 . ≠0
1 上恒成 立 , ] 即
( ) n 6 足什 么条件 时 ) 得极 值 ? 1 当 ,满 取 () 2 已知 n> , 0 且 ) 区间 ( 1 上 单 调递 在 0, ]
增 , 用 。表示 出 6的取值 范 围. 试 下 面仅 给 出第 ( ) 2 小题 的求 解方法 .
由题 意知 f ( )= t 2x+1 C, b X + i >0在 区 间 ( , 0
或 :一 1 2 ( 去) =一 管 舍云J ・ .
1 上恒成 立 , ] 即
6 一 , (1 ≥ 芋一 o ] 1 ∈ ,. 设 ( = 警 , (1则 g ) 一 一 0] 1 ∈ ,,
① 当 1∈( ,] 即 口 0 1 , ≥l时 ,
√0
①去 () 时 E’, 当 ’ , (Ⅱ √ 0, 、 , 8 1 ∈ 0 得 ^ , g) ;(, , ). g) > ∈1)g <于 ( ( 。 时 o是 ( 在 ( 上调增 ( 单递, 。 单递,去] 调减 此 , 在, 上 因
[ )
即
1
g) 芋 ≤2 一C (一(+)一 x a - ,
等 号成 立 的条 件为 = 1∈( , ] 此 时 01 ,
√0
思解 思源 思教——一道高考试题的探究及反思

() 2 思路 : 二 次 曲线 系 方 程, 过 两 曲线 用 经
( Y 0 . Y ,)= ( )=0的公 共 点 的 曲线 系 方程 是 , ( Y A・ ( Y O 但不 包括 曲线 ( Y ,)+ ,)= ( ,)=
0; ) 反之 , 曲线 系方 程 ( ' . )+A ・ ( y 0并 , . )=
二
上 两点 , Ⅳ( ,) 线段 A 点 12 是 B的 中点. () 1 求直 线 A B的方 程 ; () 2 如果 线 段 A 的垂 直平 分 线 与 双 曲线 相 交 B
于 C D 两 点 , 么 A B, , 四 点 是 否 共 圆? 为 , 那 , CD 什么?
( 0 5年 湖北 卷 ) A, 20 设 B是椭 圆 3 + = Y A上
径 圆 在 的 圆
解法 三 :
+ 一) (÷ = y
() 2 思路 : 根据 圆的几何性质 圆心一定在 弦的
垂直 平 分线 上 , 以根 据 两 条 弦 的 垂直 平 分 线 的 交 所 点 找 出圆心 N, 证 明 Ⅳ到 四个点 A, P, 然后 B, Q的距 离 相等 即可.
12 2 源 于高 考 .. 类 似 的高考 题前 几年就 出现过 :
1
线 P 的方程 :Y Y=0 则 过 A, P, 的二 次 曲 Q 4 x— , B, Q 线 系方程 为 : (Y Y一 ) 4 x— )+ 2 +,一 4 x+ 1 (Y Y A( ) 2)= ( 0A 为参 数 ) 展 开整理 得 : .
( ) 点 P关 于原 点 0的对称 点 为 Q, 明 : 2设 证 A,
P, Q 四点 在 同一 圆上 . B,
√芋 + ÷=f ( 鞠2 ) . _ ( f 3- 丁f .
一道高考题引发的教学思考

一道高考题引发的教学思考2022全国甲卷 14 题:若双曲线C:y2 一= 1(m> 0)的渐近线与圆x2 + (y 一 2)2 = 1相切,则m=.双曲线渐近线方程x一my= 0,由点 (0,2)到直线距离易得= 1 不m=该题属于基础题,但对于该题命题者背后到底想考查一个二次曲线间什么关系?双曲线渐近线 (离心率)刻画双曲线张口大小,换言之与渐近线相切刻画出圆与双曲线恒有 3 个交点. 因此可以考虑将该题作如下变式:变式 1:若双曲线C:y2 一= 1(m> 0)与圆E:x2 + (y一 2)2 = 1有三个不同交点,则m取值范围是 .学生解决问题过程如下:〈y2 一= 1 不(m2 +1)y2 一4y 一m2 +3=0........ *|l x2 +(y一2)2 =1= 16一 4(m2 +1)(3 一m2 ) = 4(m2 一 1)2学生试图用判别式刻画二次曲线间交点个数,却出现了 > 0恒成立的情况. 问题出在哪儿?学生思路是否正确呢?其实仔细观察发现双曲线C与圆E恒有一个公共点 (0,1) ,由两条曲线对称性可知关于y的二次方程*只需要在(1,+w)再产生一个解即可满足条件. 由韦达定理得4 3 一m21+y1 = 2 不y1 = 2 >1不0<m<1这样就可以顺利得到答案.反思:学生为何会m+1 m+1走入这样的解题误区而导致解题出错?原因一:还停留在初中对二次函数(方程) 研究仅限于整个实数集;原因二:受限于直线与二次曲线研究,而对于二次曲线与二次曲线研究不够深入,缺乏深度思考.对该题继续作以下变式:变式 2:已知点P为椭圆C:x2 + y2 = 1上一动点,点 A (0,1),求线段PA最大值.4 32学生在解决变式 2 ,3 时非常迅速,作图很快出答案,大多数都认为当点 P 运动到椭圆下顶点(0,一)时线段PA达到最大 . 可事实真的如此?我们用代数法探究:变式 2:设点P(m,n), A(0,1), f (n) = PA= m+ (n一 1) = 一3n一2n+ 5,n=[一, ]关于 n 的二次函数开口向下,对称轴n=一3 ,:在 [一, ] 单调递减,f (n)max= f (一)= 2+ 4:PA max = +1,答案与学生预期吻合.变式3:设P(m, n), A(0, 1 ), f (n) = PA2 = m2 + (n一1 )2 = 一1n2 一n+ 17, n=[一, ]关于 n 的二次函数开口向下,对称轴n=一,:在[一, 一]单调递增, [一, ]单调递减f (n)max = f (一) = 5:PA max= ,答案与学生预期发生了冲突.那么到底问题出在哪儿?将问题一般化,探究点 A 坐标对于最值影响.变式 4:已知点 P 为椭圆C:+ = 1(a> b> 0)上一动点,点A (0,t) (t> 0) ,求线ab段PA最大值.P(m, n), A(0,t), f (n) = PA= m+ (n一t) = (1 一)n一 2tn+ a+ t , n=[一b, b]关于n2bb2t的二次函数开口向下,对称轴n=一 2 .c当n= 一共一b不t> c2时,f (n)在[一b, b]单调递减f(n)max =f(一b)=(b+t)2当n= 一>一b不t想c2时,f(n)在[一b,一]单调递增,[一,b]单调递减cbccb2ta2t22 a2t221学生的疑问便可以迎刃而解,华罗庚老先生说:数缺形时少直观,形缺数时难入微,该题能够很好的诠释这句话.数学教学中要立足于学生问题产生的原因,针对学生问题去解决问题,做学生学习生活的陪伴者,将课堂还给学生立足于立德树人,服务选材.。
一道高考题的解后反思

(I 是 否 存在平行 于 O 1) A的直 线 , 使 得直 线 , , 与 椭 圆 C有 公共 点 ,且直 线 O A与 , 的距 离等 于 4 7 若 存在 , 出直线 , 求 的方程 ; 不存在 , 若 请说 明理 由. 1试题 评析 本题 巧妙 地 把直 线 与 椭 圆 的位置 关系 的考 查 和
平行 线 间 的距 离公 式 的考 查 融合 在 一 起 ,直 线 只要 满 足题 目所 给 的两个 条件 即可 .
则 : 解 ± 有 4 得: , 挣 , 2
由于 m= 2 1 仨 4 3 4 3 , + _ 4 3 卜 √ ,√ ]
故 这样 的直线 , 不存在 .
法 二 依 题意 ,直线 的方程为 : 3 一2 x y=0,
体 意识 和 参 与度 ,才能 在教 学 活 动 中不 断 发展 学 生
良好的个性 ,如好奇心 ;坚强的信念与意志 ;数学
思维 品质 等 .教 师 要做 到 胜不 骄 败 不馁 ,这样 才 能
意 识 和 能力 ,使 学 生处于 自觉能 动 的 学 习状态 ,感
受 学 习的成 功和乐 趣 .
设椭 圆 C上的任意一点P4oO 23i ) < z , ( s , s 00 c 4 n ( 2)
则 点 P到 直线 , 的距 离
2解法剖析
v
2
1,
2
解
( I)椭 圆 C: + =1.过 程 略 .
1 O lZ
d l s s l8s 詈 =2 i i ) c 。 n l 一
2 6 31 师要转 变教 育观念 .教
福 建 中学数 学
2 1 年 第 9期 02
身 的知识 结 构 ,适 应新 课 程 的要 求 ,不断 提 高 自身 理 论专 业素养 .
在反思中探索 在探索中创新——记一次解高考题的经历

所 以异面直线 c D与 S B所成 的角为 ac0 . rcs () 2 由题 意 , B 为 等腰 三角 形 , B E = AA E A
10, 2 。
‘ . .
所以 S C=
, H= B
,H = C
, 理 同
S D=S n , C=
推关 系中 n =l +—L 也有 “ ”把 两个 ” 1, 1 都改 为 Байду номын сангаас
‘ — l ‘
{” 就成为了全日 制普通高级中学教科书( 必
' 1
常数 “ ” 结果会 怎样 ?把 一个 “ ” 为常数 “ ” 把 n, 1改 n、
1
修) 数学第一 册 ( )人 教 版 ) 10页习 题 3 1 3 上 ( 第 1 , .
。 AC F为正三角形 , D
。
.
.
C = DF , F
又 B C=DE,
‘
.
/ BCD = / CDE= 1 0 . 2 。
.
BF= EF .
() 1求异 面直线 ∞ 与 s B所成 的 角( 用反 三角 函数值表示) ;
() 2 证明 B _ CJ 平面 S B; A
为常数“ ”把 另一个 “ ” 为常数 “ ” n, 1改 一a 结果会 怎
样 ?把一 个“ ” l 改为常数“ ” 把另一个 “ ” 为常数 a, 1改 “” 6 结果又怎样 ?
() 3这个数列 n 的变化趋 势怎样?有没 有极限
存在 ?这 个数列 有没 有通 项公 式 a , 如果有 , 样 怎
() 3 用反三角函数值表示 二面角 B—S C—D 的 大小 ( 本小 问不必写 出解答过 程) . 第 3小问括号 里的 内容 “ 小 问不必 写 出解答 本 过程” 引起笔者的兴趣 , 于是对该 小问的 解法 作了一
一道试题的解法探究与教学反思

一道试题的解法探究与教学反思广西南宁市第三十六中学(530001) 庞 毅[摘 要]通过对一道高三摸底试题进行考情分析、解法探究和问题拓展,揭示试题的本质,并从注重解题经验积累培养数学运算素养、注重信息技术应用培养学生数字素养两个方面提出教学反思。
[关键词]解法探究;教学反思;圆锥曲线;信息技术[中图分类号] G 633.6 [文献标识码] A [文章编号] 1674-6058(2024)05-0025-03解析几何是高考加强“综合性”考查的重要载体。
广西南宁市2024届高中毕业班摸底测试第21题将直线与椭圆的位置关系以及长度计算相结合,问题设计紧扣高考评价体系的“基础性、综合性、应用性、创新性”考查要求,既基础又开放,对高三数学复习备考具有重要的参考意义。
一、试题呈现与考情分析(一)试题呈现已知平面上动点E 到点A (1,0)与到圆B :x 2+y 2+2x -15=0的圆心B 的距离之和等于该圆半径。
记Ε的轨迹为曲线Γ。
(1)说明Γ是什么曲线,并求Γ的方程;(2)设C 、D 是Γ上关于x 轴对称的不同两点,点M 在Γ上,且M 异于C 、D 两点,O 为原点,直线CM 交x 轴于点P ,直线DM 交x 轴于点Q ,试问||OP ·||OQ 是否为定值?若为定值,求出这个定值;若不是定值,请说明理由。
评析:本题主要考查椭圆的定义、标准方程、几何性质和直线方程等主干知识,考查通过代数运算结果判断几何性质的坐标法和函数与方程、转化与化归以及数形结合等数学思想,考查逻辑推理、数学运算等核心素养。
第(2)问是开放性问题,重点考查学生的创新能力和探索精神。
(二)考情分析本题的考试情况如表1所示。
表1 考情分析题目第21题实考人数54110满分12平均分1.15标准差1.77难度0.15区分度0.21满分率0.16零分率29.52从统计的结果来看,本题总体平均分1.15,难度0.15,这个结果出乎命题组的预料。
高三试卷反思数学

时光荏苒,转眼间我们已迈入高三这个紧张而关键的阶段。
数学作为高考的重要科目之一,一直以来都备受重视。
在这段时间里,我认真对待每一次的数学试卷,但成绩总是不尽如人意。
通过对最近一次数学试卷的反思,我总结出以下几点:一、基础知识掌握不牢固在这次数学试卷中,我发现自己在基础知识方面存在不少漏洞。
比如,对于一些基本概念、公式和定理,我虽然能够熟练背诵,但在实际应用中却容易出现错误。
这主要是因为我在学习过程中没有注重知识的理解和运用,只是死记硬背。
因此,在今后的学习中,我要加强对基础知识的理解和掌握,做到灵活运用。
二、解题思路不够清晰在解答数学题时,我发现自己的解题思路不够清晰。
有时候,面对一道题目,我明明知道答案,却无法找到合适的解题方法。
这主要是因为我在解题过程中没有养成良好的思维习惯,没有及时总结归纳解题方法。
为了提高解题能力,我要在平时的学习中多思考、多总结,形成一套适合自己的解题思路。
三、计算能力有待提高在这次数学试卷中,我犯了较多的计算错误。
这主要是因为我在平时的学习中,对计算题不够重视,导致计算能力没有得到很好的锻炼。
为了提高计算能力,我要在今后的学习中多做一些计算题,特别是那些需要细心和耐心完成的题目。
四、时间分配不合理在这次数学试卷中,我因为时间分配不合理,导致有些题目没有足够的时间去思考和解答。
这主要是因为我在做题时,对于难题和易题没有做好区分,导致在难题上浪费了过多的时间。
为了提高时间利用效率,我要在今后的学习中,合理分配时间,确保在规定时间内完成所有题目。
五、心态调整不到位在这次数学试卷中,我因为紧张和焦虑,导致在考试过程中出现了一些失误。
这主要是因为我在考试前没有做好心态调整,没有保持良好的心态。
为了在今后的考试中发挥出更好的水平,我要学会调整心态,保持冷静和自信。
总结:通过对这次数学试卷的反思,我认识到了自己在数学学习上的不足之处。
在今后的学习中,我要努力改进,不断提高自己的数学能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
20 年 1 04 月第 3 .0 .2 版 2121
充分性: 因为l +P : c所以l 葡 一 Fl 2 , 葡
维普资讯
2 0 第 2期 08年
河北理 科教 学研 究
短 文 集锦
+ F 42 I +I F 一 . P + 帝 I E P : c i + P ・ = j — 2 帝 I 2 E P P 1 一 P —
P≥3
Gr t n er s 不等式知 :P ≤4 + R + ee 4 r
3r 2
的新颖的填空题 , 若将其推广为一般, 则得
定 理 E, F是 椭 圆 2 X
2
=
+
1 。>6> (
E l 不等式 :R>2 ur e 1 r
进 而 得 : ∑ t < t t 2 t 2
焦点 , P是椭 圆或双 曲线 上一点 , f 若
+
t 成等差数列 , 比数列 { 的前 n项和为 等 a} s , p , , 成 等 差 数 列 , 有 : 若 r t 则
2 a + p k l a + . 1 r m 1 a + +tn 1( )
J 2, = 半焦距为 , 则△ F的面积 =
3 问题 的引 申
20 07高考全 国卷 ( 第 1 题是 : 比 I) 5 等
数列 { 的前 n项 和为 , a} 已知 l2 , , 2 33 S 成等差数列 , { 的公 比为 则 a} 人教社高 中数学教 材 (0 3 2 0 年版 ) 第一 册( ) 18例 4是 : 上 P2 已知 是等 比数 列 { 的前 n a} 项和 , , , 成等差数列 , 3 6 9 求 证 a , 8a 成等差数列. 2a , 5
≤— — —
≤—
_ 一
曲线上的半焦距为 。则葡 ・ :0的充分 , 膏 必要条件是I +P - c 葡 一 FI 2 . 证明 必要性: 因为葡 . :0 所以 ,
E P上 即 , A F 是 直 角 三 角 形 , 即 EP 且
4R2 2Rr44r 4R2 R24 R2 2 - 4 - 2 - 4 - R2
2 r的一个 有趣 的隔离 :
推论 :2 ≤2 + r r 1 ∑ ( 6一c R≤ )≤ 2 + 1∑ ( 一c r 6 ) 定 ∑ <
≥ z ≥
:
反 思
l遥 _
_ _ _ _
…
2 0 年高考全国卷 Ⅱ有这样一题 :F , 07 l
2
F是 曲 2号= 的 右 点 在P 2 双 线X 一 1左 焦 ,
=
4 c①
在 △ F 中 由 向量 几 何 意 义 得 I E 一 — P
一
_ _ 秽 .的 : !霉
, 。
_ _
P :IP一 I 商 I 2 , FI P 葡 :I : c所以。葡 I I 2
+IF 2 E F 一 . 4 ⑦ 帝 I— 葡 ・ : c P 2 P 一 = ( P 4 ①一 ②得化简整理即 . : . 商 帝 0
一
t t
3
:
0 或双 曲线 一 :1 口>0 b>0 的左 右 ) 一点, 椭圆或双
( 二 =! 垒 )
r P
— 一
( = = 2一
2
p 一2 r f R2 4 -3 一2 - r Z Rr - 2 4 4 4 Rr4 r ) - Rr4 2
‘ .
① , J F P 2 0, l  ̄ - l F :9。故 Z
: c : ,
l :
代入 得l + Fl 2 . ① 丽 一2: P
’
. 一 < √ 号卜
・ . ・
2 问题 的推广
∑ 0 =2 ( Rr ) 3 P P 一6 一3 , r
r.
该 问题将 向量 数 量 积 、 向量 的模 和 圆锥 曲线 焦点 三 角形 融 为一 体 , 一 道难 易 适 中 是
维普资讯
20 0 8年 第 2期 故 : ≤2 +上 ∑ ( r 8 6一c )
r
河 北理科 教 学研 究
短 文集锦
( 安徽 省 舒 城县 杭 埠镇 中心 学校 丁遵 标
2 12 ) 3 3 3
。t 曩
由此 ,我 们便 可得 到欧拉 不 等式 :R≥
—
E :9 ̄故 知 l 0,
.
l :
:。设 0 ,
故 :∑ <
是坐标 原 点, 由向量 中点 公 式 知葡 = 则
幽
,
参考文献
1 匡继 昌 . 常用 不等 式 [ M] . 山东 科 学技 术 出版 社
.
即 + F: 葡 铮l + 葡 一 2 P 南
.
l:2I — l PO :2c
在 双曲 线上, 且两 ・ : , l + 0则 两
P 2= F I
1 问题 的解法
证 明: ‘ . ‘
√ _ 厂 ( 。
= r
( P一0 ( ) P—b ( ) P—c )
2 02
( 以下简 称 问题 ) .
2P
0
‘
解 : 坐 标 原 点 是 0, 三 角 形 F P 2 设 在 l F
‘ ・
≤
0
云 而
2
P
__ 二
一T |一 1旦 : P
中, 由题意及 向量 中点 公 式知 2 : + 所以 l + l l O :2 — P l : P l O 2一 I
,
又. <一 蒂=1 ‘一 1 ‘ 1 + ( ) 一 ,
若引 申到焦点三角形的面积 , 进行思考 ,
则 可得 到 定理 E、 F是 椭 圆 + =1 0>b> (
a‘ 。 0‘ 。
o 或 曲线 一 =1 。>0 6>o 的左 右 ) ( , )
他们都可用如下命题来解答 .
命 题 : P, , , , , ∈ N 且 P, , 设 r t k m n , r
