第十五章欧拉图与哈密顿图
合集下载
离散数学课件15欧拉图与哈密顿图
证明 若G是平凡图,结论显然成立。
下面设G为非平凡图,设G是m条边的n阶无 向图,
并设G的顶点集V={v1,v2,…,vn}。 必要性。因为G为欧拉图,所以G中存在欧 拉回路,
设C为G中任意一条欧拉回路,vi,vj∈V, v2i0,2v0/7j/都23 在C上,
定理15.1的证明
充分性。由于G为非平凡的连通图可知,G中边数 m≥1。
2020/7/23
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ,且G中恰有两个奇度顶点。
证明 充分性。设G的两个奇度顶点分别为u0和v0, 对G加新边(u0,v0),得G =G∪(u0,v0), 则G 是连通且无奇度顶点的图, 由定理15.1可知,G 为欧拉图, 因而存在欧拉回路C ,而C=C -(u0,v0)为G中一 条欧拉通路, 所以G为半欧拉图。
并2行从020/7遍/C23 上G 的i中某的顶欧点拉vr回开路始C行遍i,,i=每1遇,2,到…v,s*j,i,最就后
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ,且G中恰有两个奇度顶点。
证明 必要性。设G是m条边的n阶无向图,因为G为 半欧拉图, 因而G中存在欧拉通路(但不存在欧拉回路), 设Г=vi0ej1vi1…vim-1ejmvim为G中一条欧拉通路, vi0≠vim。 v∈V(G),若v不在Г的端点出现,显然d(v)为偶 数, 若v在端点出现过,则d(v)为奇数,
欧拉对物理力学、天文学、弹道学、航海学、建筑学、音 乐都有研究!有许多公式、定理、解法、函数、方程、常数等 是以欧拉名字命名的。欧拉写的数学教材在当时一直被当作标 准教程。19世纪伟大的数学家高斯曾说过“研究欧拉的著作永 远是了解数学的好方法”。欧拉还是数学符号发明者,他创设 的许多数学符号,例如π,i,e,sin,cos,tg,Σ,f (x)等等, 至今202沿0/7/2用3 。
下面设G为非平凡图,设G是m条边的n阶无 向图,
并设G的顶点集V={v1,v2,…,vn}。 必要性。因为G为欧拉图,所以G中存在欧 拉回路,
设C为G中任意一条欧拉回路,vi,vj∈V, v2i0,2v0/7j/都23 在C上,
定理15.1的证明
充分性。由于G为非平凡的连通图可知,G中边数 m≥1。
2020/7/23
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ,且G中恰有两个奇度顶点。
证明 充分性。设G的两个奇度顶点分别为u0和v0, 对G加新边(u0,v0),得G =G∪(u0,v0), 则G 是连通且无奇度顶点的图, 由定理15.1可知,G 为欧拉图, 因而存在欧拉回路C ,而C=C -(u0,v0)为G中一 条欧拉通路, 所以G为半欧拉图。
并2行从020/7遍/C23 上G 的i中某的顶欧点拉vr回开路始C行遍i,,i=每1遇,2,到…v,s*j,i,最就后
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ,且G中恰有两个奇度顶点。
证明 必要性。设G是m条边的n阶无向图,因为G为 半欧拉图, 因而G中存在欧拉通路(但不存在欧拉回路), 设Г=vi0ej1vi1…vim-1ejmvim为G中一条欧拉通路, vi0≠vim。 v∈V(G),若v不在Г的端点出现,显然d(v)为偶 数, 若v在端点出现过,则d(v)为奇数,
欧拉对物理力学、天文学、弹道学、航海学、建筑学、音 乐都有研究!有许多公式、定理、解法、函数、方程、常数等 是以欧拉名字命名的。欧拉写的数学教材在当时一直被当作标 准教程。19世纪伟大的数学家高斯曾说过“研究欧拉的著作永 远是了解数学的好方法”。欧拉还是数学符号发明者,他创设 的许多数学符号,例如π,i,e,sin,cos,tg,Σ,f (x)等等, 至今202沿0/7/2用3 。
欧拉图与哈密顿图

例15.3 在图15.6中给出的三个图都是 二部图。它们中的那些是哈密顿图?哪些 是半哈密顿图?为什么? 解 在(1)中,易知互补顶点子集 V1={a,f},V2={b,c,d,e}。设此二部图为G1, 则G1=<V1,V2,E>. p(G1-V1)=4>|V1|=2,由 定理15.6及其推论可知,G1不是哈密顿 图,也不是半哈密顿图。
是在G'中存在u到v的路径Г2,显然Г1 与Г2边不重,这说明u,v处于Г1∪Г2 形成的简单回路上。
三、求欧拉图中欧拉回路的算法
设G为欧拉图,一般来说G中存 在若干条欧拉回路,下面介绍两种求 欧拉回路的算法。
1.Fleury算法,能不走桥就不走桥: (1)任取v0∈V(G),令P0=v0. (2)设Pi=v0e1v1e2…eivi已经行遍, 按下面方法来从E(G)-{e1,e2,…,ei}中选 取ei+1: (a)ei+1与vi相关联; (b)除非无别的边可供行遍, 否则ei+1不应该为Gi=G-{e1,e2,…,ei}中的 桥。 (3)当(2)不能再进行时,算法停止。
p(C-V1)达到最大值|V1|,而当V1中顶点在C 上有彼此相邻的情况时,均有p(C-V1)<|V1|, 所以有p(C-V1)≤|V1|.而C是G的生成子图, 所以,有p(G-V1)≤p(C-V1)≤|V1|. 本定理的条件是哈密顿图的必要条件, 但不是充分条件。可以验证彼得松图(图 14.3中(1)所示)满足定理中的条件,但 它不是哈密顿图。当然,若一个图不满足 定理中的条件,它一定不是哈密顿图。
2.逐步插入回路法 设G为n阶无向欧拉图,V(G)={v1,v2,…,vn}, 求G中欧拉回路的逐步插入回路法的算法如下: 开始 i←0,v*=v1,v=v1,P0=v1, G0=G. 1.在Gi中任取一条与V关联的边 e=(v,v'),将e及v’加入到Pi中得到Pi+1. 2.若v '=v*,转3,否则i←i+1,v=v' , 转1.
第十五章欧拉图与哈密顿图

具有哈密顿回路的图称为半哈密顿图。平 凡图是哈密顿图。
图中所示的三个无向图都有哈密顿回路, 所以都是哈密顿图。有向图中,()具有哈 密顿回路,因而它是哈密顿图。()只有哈 密顿通路,但无哈密顿回路,因而它是半哈 密顿图,而()中既无哈密顿回路,也没有 哈密顿通路,因而不是哈密顿图,也不是半 哈密顿图。
∈(),若不在Г的端点出现,显然 ()为偶数,若在端点出现过,则()为 奇数,因为Г只有两个端点且不同,因而 中只有两个奇数顶点。另外,的连通 性是显然的。
充分性: 设的两个奇度顶点分别 为 和,对加新边(),
得' ∪(),则'是连通且无奇度 顶点 的图,由定理可知,‘为欧拉 图,因而存在欧拉回路',而' () 为中一条欧拉通路,所以为半欧拉图。
图
由定理立即可知,图()图 为欧拉图,本图既可以看成圈, ,,之并(为 清晰起见,将个圈画在()中),也 可看成圈与圈 之并(两个圈画在()中)。将() 分解成若干个边不重的圈的并不是() 图特有的性质,任何欧拉图都有这个性 质。
定理 是非平凡的欧拉图当且仅 当是连通的且为若干个边不重的圈的并。
证 读者用定理证明。
下面给出一些哈密顿图和半哈密顿图 的充分条件。
定理 设是阶无向简单图,若对
于中任意不相邻的顶点,均有
()()≥
()
则中存在哈密顿通路。
证: 首先证明是连通图。否则至少 有两个连通分支,设是阶数为 的两个连通分支,设∈(),∈(), 因为是简单图,所以 ()()
()()≤≤
这与()矛盾所以必为连通图。
可以证明,当算法停止时所得简单回路 …()为中一条欧拉回路。
例 图()是给定的欧拉图。某人用算法 求中的欧拉回路时, 走了简单回路 之 后(观看他的错误走法),无法行遍了,试 分析在哪步他犯了错误?
《离散数学》课件-第15章欧拉图与哈密顿图

例如
彼得松图 彼得松图满足定理15.6,但不是哈密顿图。
例15.3 下图中三个图都是二部图,判断它们 哪些是哈密顿图,哪些是半哈密顿图?
G1
G2
G3
二部图与哈密顿图的关系
设二部图G=<V1,V2,E>,
|V2||V1|。若|V2||V1|+2,则
G即不是哈密顿图,又不是半哈
G1
密顿图
(1)G1=<V1,V2,E>, 互补顶点子集为V1={a,f},V2={b,c,d,e}。 则p(G1-V1)=|V2|=4,|V1|=2, p(G1-V1)>|V1|且p(G1-V1)>|V1|+1。 所以G1即不是哈密顿图,又不是半哈密顿图。
亚瑟王和他的骑士们
◼ 亚瑟王一次召见他的p个骑士,已知每一个 骑士在骑士中的仇人不超过p/2-1个。证明:能让 这些骑士围坐在圆桌旁,使每个人都不与他的仇 人相邻。
其它重要的定理
◼ 定理1 如果G是一个n(n3)阶简单图, 且n/2,则G是哈密顿图。
◼ 定理2 如果G是一个n(n3)阶完全图, 且n为奇数,则G是哈密顿图且图中有(n-1)/2个 边不相交的哈密顿回路。
穿过每一道门,通过所有房间?
15.2 哈密顿图
1859年,爱尔兰数学家威廉·哈密尔顿发明 了一个旅游世界的游戏。将一个正十二面体的 20个顶点分别标上世界上大城市的名字,要求 玩游戏的人从某城市出发沿12面体的棱,通过 每个城市恰一次,最后回到出发的那个城市。
哈密尔顿游戏是在左图中如何 找出一个包含全部顶点的圈。
点的回路称为欧拉回路 定义(欧拉图和半欧拉图)
具有欧拉回路的图称为欧拉图 具有欧拉通路无欧拉回路的图称为半欧拉图 规定平凡图是欧拉图
欧拉图于哈密顿图
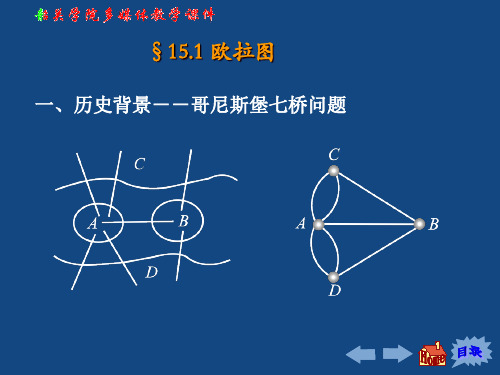
§15.1 欧拉图
一、历史背景--哥尼斯堡七桥问题
}
1
二、定义 欧拉通路 (欧拉迹) ——通过图中每条边一次 且仅一次,并且过每一顶点的通路。 欧拉回路 (欧拉闭迹) ——通过图中每条边一次 且仅一次,并且过每一顶点的回路。 欧拉图 ——存在欧拉回路的图。
}
2
三、无向图是否具有欧拉通路或回路的判定
(3) 具有哈密尔顿回路而没有欧拉回路,
解:
(4) 既没有欧拉回路,也没有哈密尔顿回路。
解:
}
14
作业
习题十五 2、11、14、15、20
}
15
余顶点的入度均等于出度, 这两个特殊的顶点中,一个 顶点的入度比出度大1,另一 个顶点的入度比出度小1。
D 有欧拉回路( D为欧拉图) D 连通, D 中所有
顶点的入度等于出度。
}
6
例3、判断以下有向图是否欧拉图。
}
7
§15.2 哈密尔顿图
一、问题的提出
1859年,英国数学家哈密尔顿,周游世界游戏。
(2)
解:是哈密尔顿图,
存在哈密尔顿回路和通路。
}
11
例1、判断下图是否具有哈密尔顿回路,通路。
(3)
解:不存在哈密尔顿回路,
也不存在哈密尔顿通路。
}
12
例2、画一个无向图,使它
(1) 具有欧拉回路和哈密尔顿回路,
解:
(2) 具有欧拉回路而没有哈密尔顿回路, 解:
}
13
例2、画一个无向图,使它
G 中只有两个奇度 G 有欧拉通路 G 连通,
顶点(它们分别是欧拉通路的
两个端点)。
G有欧拉回路( G为欧拉图) G 连通, G 中均
一、历史背景--哥尼斯堡七桥问题
}
1
二、定义 欧拉通路 (欧拉迹) ——通过图中每条边一次 且仅一次,并且过每一顶点的通路。 欧拉回路 (欧拉闭迹) ——通过图中每条边一次 且仅一次,并且过每一顶点的回路。 欧拉图 ——存在欧拉回路的图。
}
2
三、无向图是否具有欧拉通路或回路的判定
(3) 具有哈密尔顿回路而没有欧拉回路,
解:
(4) 既没有欧拉回路,也没有哈密尔顿回路。
解:
}
14
作业
习题十五 2、11、14、15、20
}
15
余顶点的入度均等于出度, 这两个特殊的顶点中,一个 顶点的入度比出度大1,另一 个顶点的入度比出度小1。
D 有欧拉回路( D为欧拉图) D 连通, D 中所有
顶点的入度等于出度。
}
6
例3、判断以下有向图是否欧拉图。
}
7
§15.2 哈密尔顿图
一、问题的提出
1859年,英国数学家哈密尔顿,周游世界游戏。
(2)
解:是哈密尔顿图,
存在哈密尔顿回路和通路。
}
11
例1、判断下图是否具有哈密尔顿回路,通路。
(3)
解:不存在哈密尔顿回路,
也不存在哈密尔顿通路。
}
12
例2、画一个无向图,使它
(1) 具有欧拉回路和哈密尔顿回路,
解:
(2) 具有欧拉回路而没有哈密尔顿回路, 解:
}
13
例2、画一个无向图,使它
G 中只有两个奇度 G 有欧拉通路 G 连通,
顶点(它们分别是欧拉通路的
两个端点)。
G有欧拉回路( G为欧拉图) G 连通, G 中均
第十五章 欧拉图与哈密顿图

长度大于或等于3的圈,设C为G中一个圈,
删除C上的全部边,得G的生成子图G',
, G2 , 设G'有s个连通分支 G1
公共顶点为,i=1, 2, … , s.
, 每个连通分支 , Gs
至多有k条边,且无奇度顶点,并且设G'i与C的
, G2 , 由归纳假设可知, G1
, 都是欧拉图, , Gs
并设G的顶点集 V={v1, v2, … , vn }.
必要性. 因为G为欧拉图,所以G中存在欧拉回路, 设C为G中任意一条欧拉回路, vi , vj ∈V,
vi, vj都在C上,因而vi , vj 连通,所以G为 连通图.
又vi∈V,vi在C上每出现一次获得2度,
若出现k次就获得2k 度,即d(vi)=2k .
点的入度都等于出度.
Байду номын сангаас
由定理15.3和15.4立即可知,图15.1中所示3个
有向图中只有(4)是欧拉图,没有半欧拉图.
图15.1
由定理15.1立即可知,图15.3(1)图为欧拉图.
图15.3
本图既可以看成圈
v1v2v8v1 , v2v3v4v2 , v4v5v6v4 , v6v7v8v6 之并(为清晰起见,
vim -1e jm vim为G中一条欧拉
vi 0 vim . v V (G ), 若v不在Г的端点出现, 通路,
显然d(v)为偶数,若v在端点出现过,则d(v)为奇数,
因为Г只有两个端点且不同,因而G中只有两个
奇数顶点. 另外,G的连通性是显然的.
充分性. 设G的两个奇度顶点分别为u0和v0,对G加 新边(u0, v0),得G ' =G∪(u0,v0),则G '是 连通且无奇度顶点的图,由定理15.1可知,G ' 为欧拉图,因而存在欧拉回路C ' ,而
欧拉图与哈密顿图

求欧拉图中欧拉回路的算法
Fleury算法;能不走桥就不走桥
1 任取v0∈VG;令P0=v0; 2 设Pi=v0e1v1e2…eivi已经行遍;按下面方法来从
EGe1;e2;…;ei中选取ei+1: a ei+1与vi相关联; b 除非无别的边可供行遍;否则ei+1不应该为
Gi=Ge1;e2;…;ei中的桥; 3当2不能再进行时;算法停止;
例15 1
例15 1 设G是非平凡的且非环的欧拉图;证明: 1λG≥2; 2对于G中任意两个不同顶点u;v;都存在简单回路C含u和v;
证明 1由定理15 5可知;e∈EG;存在圈C;e在C中; 因而pGe=pG;故e不是桥; 由e的任意性λG≥2;即G是2边连通图;
例15 1
例15 1 设G是非平凡的且非环的欧拉图;证明: 1λG≥2; 2对于G中任意两个不同顶点u;v;都存在简单回路C含u和v;
可以验证彼得松图满足定理中的条件;但不是哈密顿图;
若一个图不满足定理中的条件;它一定不是哈密顿图;
推论
推论 设无向图G=<V;E>是半哈密顿图;对于任意的V1V且 V1≠;均有 pGV1≤|V1|+1
证明 设P是G中起于u终于v的哈密顿通路; 令G =G∪u;v在G的顶点u;v之间加新边; 易知G 为哈密顿图; 由定理15 6可知;pG V1≤|V1|; 因此;pGV1 = pG V1u;v ≤ pG V1+1 ≤ |V1|+1
若vi与vj有哈共密同语顿言图;就是在v能i;vj将之间图连中无向所边有vi;v顶j; 由此组成点边都集合能E;安则G排为8在阶无某向个简单初图级; 回路 vi∈V;上dvi为的与图vi有;共同语言的人数;
欧拉图和哈密尔顿图ppt课件

有欧拉通路
全部结点为偶结点, 有欧拉回路
有欧拉通路
。a
a、b、c、e
。a
全部结点为
b。 。c 都为奇结点, 。 。 。 无欧拉通路
b。
。c
d
e
f 与欧拉回路 。 。 。
偶结点, 有欧拉回路
d e f 有欧拉通路
ppt课件
8
例7-8 如图街道,是否存在一条投递线路使 邮递员从邮局a出发通过所有街到一次在回 到邮局a?
可达的:在图G中,结点u和结点v之间存在一
条路,则称结点u到结点v是可达的。
ppt课件
2
无向图的连通性
连通:在无向图G中,结点u和结点v之间存在一 条路,则称结点u与结点v是连通的。约定:任一 结点与自身总是连通的。 连通图:若图G中,任意两个结点均连通,则称G 是连通图,否则称非连通图。对非连通图可分成几
个无公共结点的连通分支。无向图中结点间的连通
关系是等价关系。 图是连通的判定法则:从图中任意一结点出发,
通过某些边一定能到达其它任意一结点,则称
图是连通的。
ppt课件
3
练习1:连通图的判定
指出下列各图是否连通
(1)
(2)
(3)
(4)
(5)
(6)
ppt课件 (7)
(8)
4
欧拉图
设G=<V,E>是连通无向图 欧拉通路:在图G中存在一条通路,经过图G 中每条边一次且仅一次。
第二节 图的连通性
通路和回路 无向图的连通性 有向图的连通性 欧拉图 哈密顿图
ppt课件
1
通路和回路 给定图G V , E
通路: G中前后相互关联的点边交替序列 w=v0e1v1e2…envn称为连接v0到vn的通路。 W中边的数目K称为通路W的长。
全部结点为偶结点, 有欧拉回路
有欧拉通路
。a
a、b、c、e
。a
全部结点为
b。 。c 都为奇结点, 。 。 。 无欧拉通路
b。
。c
d
e
f 与欧拉回路 。 。 。
偶结点, 有欧拉回路
d e f 有欧拉通路
ppt课件
8
例7-8 如图街道,是否存在一条投递线路使 邮递员从邮局a出发通过所有街到一次在回 到邮局a?
可达的:在图G中,结点u和结点v之间存在一
条路,则称结点u到结点v是可达的。
ppt课件
2
无向图的连通性
连通:在无向图G中,结点u和结点v之间存在一 条路,则称结点u与结点v是连通的。约定:任一 结点与自身总是连通的。 连通图:若图G中,任意两个结点均连通,则称G 是连通图,否则称非连通图。对非连通图可分成几
个无公共结点的连通分支。无向图中结点间的连通
关系是等价关系。 图是连通的判定法则:从图中任意一结点出发,
通过某些边一定能到达其它任意一结点,则称
图是连通的。
ppt课件
3
练习1:连通图的判定
指出下列各图是否连通
(1)
(2)
(3)
(4)
(5)
(6)
ppt课件 (7)
(8)
4
欧拉图
设G=<V,E>是连通无向图 欧拉通路:在图G中存在一条通路,经过图G 中每条边一次且仅一次。
第二节 图的连通性
通路和回路 无向图的连通性 有向图的连通性 欧拉图 哈密顿图
ppt课件
1
通路和回路 给定图G V , E
通路: G中前后相互关联的点边交替序列 w=v0e1v1e2…envn称为连接v0到vn的通路。 W中边的数目K称为通路W的长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由定理立刻可知,图中的三 个无向图中,只有()中无奇度顶点, 因而()是欧拉图,而()、()都 有奇度顶点,因而它们都不是欧拉图。
定理 : 无向图是半欧拉图当且仅 当是连通的,且中恰有两个奇度顶点。
证: 必要性 设是条边的阶无向图, 因为为半欧拉图,因而中存在欧拉通路
(但不存在欧拉回路),设 Г… 为中一条欧拉通路, ≠ .
二、判别定理
定理 无向图是欧拉图当且仅当是连 通图,且中没有奇度顶点。
证: 若是平凡图,结论显然成立, 下面设为非平凡图,设是条边的阶 无向图。并设的顶点集{,…}. 必要性: 因为为欧拉图,所以中存
在欧拉回路,设为中任意一条欧拉回路,
∈,都在上,因而连通 所以为连通图。又 ∈,在上每 出现一次获得度,若出现次就获得 度,即(),所以中无奇度顶点。
由定理立即可知,图中() 是半欧拉图,但()不是半欧拉图。
定理 有向图是欧拉图当且仅当 是强连通的且每个顶点的入度都等于出度。 本定理的证明类似于定理 .
定理 有向图是半欧拉图当且仅 当是单向连通的,且中恰有两个奇度 顶点,其中一个的入度比出度大,另一 个的出度比入度大,而其余顶点的入度 都等于出度。
,,…,由归纳假设可知,', ',…'都是欧拉图,因而都存在欧拉 回路‘,,….最后将还原(即将
删除的边重新加上),并从上的某顶点
开始行遍,每遇到 ,就行遍’ 中的 欧拉回路’ ,,…,最后回到,得 回路
… … … … … … …,
此回路经过中每条边一次且仅一次并行 遍中所有顶点,因而它是中的欧拉回 路 ,故为欧拉图。
可以证明,当算法停止时所得简单回路 …()为中一条欧拉回路。
例 图()是给定的欧拉图。某人用算法 求中的欧拉回路时, 走了简单回路 之 后(观看他的错误走法),无法行遍了,试 分析在哪步他犯了错误?
图
解: 此人行遍时犯了能不走桥就不 走桥的错误,因而他没行遍出欧拉回路。 当他走到时,{}为 图()所示。此时为该图中的桥, 而均不是桥,他不应该走,而应 该走或,他没有走,所以犯了错误。 注意,此人在行遍中,在遇到过桥, 处遇到过桥,但当时除桥外他无别的 边可走,所以当时均走了桥,这是不会犯 错误的。
本定理的证明可用归纳法。
例 设是非平凡的且非环的欧拉图, 证明:
λ()≥. ()对于中任意两个不同顶点, 都存在简单回路含和.
证 ()由定理可知, ∈(), 存在圈,在中,因而()(),故 不是桥。由的任意性λ()≥,即是 边连通图。
() ∈(),≠,由的连通 性可知,之间必存在路径Г,设 ' (Г),则在 '中与还必连通,否则, 与必处于 '的不同的连通分支中,这说明 在Г上存在中的桥,这与()矛盾。于
欧拉图与哈密顿图
欧拉图
一.欧拉通路、欧拉回路、欧拉图、半 欧拉图的定义
定义 通过图(无向图或有向图)中所 有边一次且仅一次行遍图中所有顶点 的通路称为欧拉通路,通过图中所有 边一次并且仅一次行遍所有顶点的回 路称为欧拉回路。具有欧拉回路的图 称为欧拉图,具有欧拉通路而无 欧拉回路的图称为半欧拉图。
图
由定理立即可知,图()图 为欧拉图,本图既可以看成圈, ,,之并(为 清晰起见,将个圈画在()中),也 可看成圈与圈 之并(两个圈画在()中)。将() 分解成若干个边不重的圈的并不是() 图特有的性质,任何欧拉图都有这个性 质。
定理 是非平凡的欧拉图当且仅 当是连通的且为若干个边不重的圈的并。
从定义不难看出,欧拉通路是图中经 过所有边的简单的生成通路(经过所有顶 点的通路称为生成通路),类似地,欧拉 回路是经过所有边的简单的生成回路。
在这里做个规定,即平凡图是欧拉图。
图
在图所示各图中,为 ()中的欧拉回路,所以()图为欧拉 图。为()中的一条欧拉通路, 但图中不存在欧拉回路,所以()为半欧 拉图。()中既没有欧拉回路,也没有欧 拉通路,所以()不是欧拉图,也不是半 欧拉图。为()图中的欧拉回路, 所以()图为欧拉图。(),()图中 都既没有欧拉回路,也没有欧拉通路
.逐步插入回路法
设为阶无向欧拉图,(){,…}, 求中欧拉回路的逐步插入回路法的算法如下:
←,*,,, .
.在中任取一条与关联的边 ('),将及’加入到中得到.
.若 '*,转,否则←' , 转.
.若()(),结束,否则,令 (),在中任取一条与 中某顶点关联的边,先将改 写成起点(终点)为的简单回路,再 置*, ←,转.
∈(),若不在Г的端点出现,显然 ()为偶数,若在端点出现过,则()为 奇数,因为Г只有两个端点且不同,因而 中只有两个奇数顶点。另外,的连通 性是显然的。
充分性: 设的两个奇度顶点分别 为 和,对加新边(),
得' ∪(),则'是连通且无奇度 顶点 的图,由定理可知,‘为欧拉 图,因而存在欧拉回路',而' () 为中一条欧拉通路,所以为半欧拉图。
现在再考虑例中图中图 (),用逐步插入回路法可以走出多 条欧拉回路。现在走出一条来:
开始时,置*,,,
,经过步得 ,
是长度为的简单回路,见演示中红边பைடு நூலகம்所示。
在中有条边与上的顶点相关联, 比如取与,先将改写成以为起点 (终点)的简单回路:
', 然后置*,,再经过步得
充分性: 由于为非平凡的连通图可 知,中边数≥.对作归纳法。
()时,由的连通性及无奇度顶 点可知,只能是一个环,因而为欧拉图。
()设≤(≥)时结论成立,要证明 时,结论也成立。由的连通性及
无奇度顶点可知,δ()≥.类似于例 ,用扩大路径法可以证明中存在 长度大于或等于的圈,设为中一个 圈,删除上的全部边,得的生成子 图’ ,设’有个连通分支’’,…, ‘,每个连通分支至多有条边,且无 奇度顶点,并且设‘与的公共顶点为
是在'中存在到的路径Г,显然Г 与Г边不重,这说明处于Г∪Г 形成的简单回路上。
三、求欧拉图中欧拉回路的算法
设为欧拉图,一般来说中存 在若干条欧拉回路,下面介绍两种求 欧拉回路的算法。
.算法,能不走桥就不走桥:
()任取∈(),令. ()设…已经行遍, 按下面方法来从(){,…}中选 取:
否则不应该为{,…}中的 桥。
