习题2.2-2.3
部分习题参考答案(数据结构 李春葆)

int lena=1,j=0; while (p->next!=ha)//求出ha的长度lena { lena++;
p=p->next; }
if (i==0) //将hb的所有数据结点插入到ha的头结点和第1个数据结点之间
{ p=hb->prior;
//p指向hb的最后一个结点/
p->next=ha->next;
//将*p链到ha的第1个数据结点前面
ha->next->prior=p;
ha->next=hb->next;
hb->next->prior=ha;
//将ha头结点与hb的第1个数据结点链起
来
}
else if (i<lena)
q->next->prior=q;
p->next=q;q->prior=p;
q=p->prior;
//q重指向*p的前趋节点
}
return true;
}
}
2.5 设ha=(a1,a2,…,an)和hb=(b1,b2, …,bm) 是两个带头结点的循环单链表,编写将 这两个表合并为带头结点的循环单链表hc的算法。
else
//找到的情况
{ p->freq++;
//频度增1
q=p->prior;
//*q为p前驱节点
while (q!=h && q->freq<p->freq)
计量经济学第二版课后习题答案
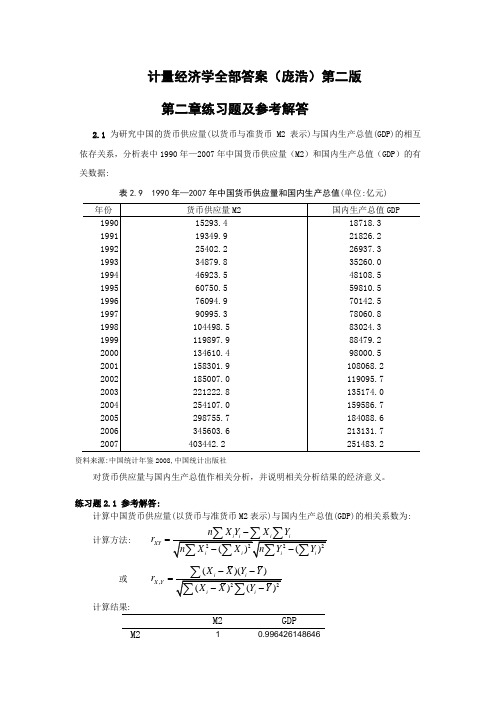
计量经济学全部答案(庞浩)第二版 第二章练习题及参考解答2.1 为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2007年中国货币供应量(M2)和国内生产总值(GDP )的有关数据:表2.9 1990年—2007年中国货币供应量和国内生产总值(单位:亿元)资料来源:中国统计年鉴2008,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明相关分析结果的经济意义。
练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: XY n X Y X Y r -=或 ,()()X Y X X Y Y r --=计算结果:M2GDPM210.996426148646GDP 0.996426148646 1经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。
2.2 为研究美国软饮料公司的广告费用X与销售数量Y的关系,分析七种主要品牌软饮料公司的有关数据表2.10 美国软饮料公司广告费用与销售数量资料来源:(美) Anderson D R等. 商务与经济统计.机械工业出版社.1998. 405绘制美国软饮料公司广告费用与销售数量的相关图, 并计算相关系数,分析其相关程度。
能否在此基础上建立回归模型作回归分析?练习题2.2参考解答美国软饮料公司的广告费用X与销售数量Y的散点图为说明美国软饮料公司的广告费用X与销售数量Y正线性相关。
若以销售数量Y 为被解释变量,以广告费用X 为解释变量,可建立线性回归模型 i i i u X Y ++=21ββ 利用EViews 估计其参数结果为经t 检验表明, 广告费用X 对美国软饮料公司的销售数量Y 确有显著影响。
回归结果表明,广告费用X 每增加1百万美元, 平均说来软饮料公司的销售数量将增加14.40359(百万箱)。
公共营养师技能复习题库

公共营养师技能复习题一、一人一餐的三大产能营养素计算例题:(一)求80岁老人(1800千卡能量/日)午餐蛋白质的需要量解:1、已知80岁老人一日能量需要量为1800千卡,午餐占全天总能量的40%。
1800×40%=720(千卡)2、根据能量需要量计算出午餐蛋白质的需要量。
720×15%=108(千卡)3、将能量转化为蛋白质的质量。
108÷4=27(克)答:80岁老人午餐蛋白质的需要量为27克。
(二)求一名脑力劳动者(一日能量需要量为2400千卡)早餐碳水化合物的需要量解:1、已知脑力劳动者一日能量需要量为2400千卡,早餐占全天总能量的30%。
2400×30%=720(千卡)2、根据能量需要量计算出早餐碳水化合物的需要量。
720×60%=432(千卡)3、将能量转化为蛋白质的质量。
432÷4=108(克)答:脑力劳动者早餐碳水化合物的需要量为108克。
练习题:(三)已知某6岁儿童的一天能量需要量为1300千卡,请你计算出早餐蛋白质需要量。
(保留一位小数)解:1、已知6岁儿童的一天能量需要量为1300千卡,早餐占全天总能量的30%。
1300 × 30% = 390(千卡)2、根据能量需要量计算出早餐中蛋白质所含的能量。
390 × 15% = 58.5(千卡)3、将能量转化为蛋白质的质量。
58.5 千卡÷ 4千卡/克 =14.6克答:6岁儿童的早餐需要蛋白质14.6克。
(四)已知某6岁儿童的一天能量需要量为1300千卡,请你计算出晚餐蛋白质需要量。
(保留一位小数)解:1、已知6岁儿童的一天能量需要量为1300千卡,晚餐占全天总能量的30%。
1300 × 30% = 390(千卡)2、根据能量需要量计算出晚餐中蛋白质所含的能量。
390 × 15% = 58.5(千卡)3、将能量转化为蛋白质的质量。
2023年道路工程练习题和答案(Part23)

2023 年道路工程练习题和答案〔Part23〕共 3 种题型,共 90 题一、单项选择题(共 35 题)1.水泥的安定性是一项表示水泥浆体硬化后是否发生不均匀性〔〕变化的指标。
A:质量B:体积C:高度D:长度【答案】:B【解析】:水泥的安定性是一项表示水泥浆体硬化后是否发生不均匀性体积变化的指标。
2.铺砂法适用于构造深度。
A:测定沥青路面及水泥混凝土路面外表无沟槽路面B:测定沥青路面外表 C:测定水泥混凝土路面外表D:测定基层外表【答案】:A【解析】:用于测定沥青路面及水泥混疑土路面外表构造深度,用以评定路面的宏观粗糙度,路面外表的排水性能及抗滑性能。
3.随沥青含量增加,沥青混合料试件的稳定度将。
A:保持不变B:呈抛物线变化C:递减 D:递增【答案】:B【解析】:沥青混合料马歇尔协作比设计中,沥青混合料试件的稳定度与沥青用量的关系曲线呈抛物线变化变化,稳定度峰值对应的沥青用量a?参与OAC 计算。
4.在一般气候环境中,配制一般水泥混凝土应优先选用。
A:硅酸盐水泥B:一般硅酸盐水泥C:矿渣水泥D:粉煤灰水泥【答案】:B【解析】:一般气候环境中配制一般混凝土优选一般水泥。
一般水泥的性能和应用与同强度等级的硅酸盐水泥极为相近,广泛用于各种混凝土或钢筋混凝土工程,是我国的主要的水泥品种之一。
5.高湿度环境或水下环境的混凝土应优先选择。
A:硅酸盐水泥B:一般硅酸盐水泥C:矿渣水泥D:粉煤灰水泥【答案】:C【解析】:高湿度环境或水下环境的混凝土应优先选择矿渣水泥。
6.应依据工程实际状况、抽检资料以及对合同段工程质量评定结果,对施工单位交工验收申请及其所附资料进展审查并签署意见的单位是〔〕。
A:建设单位B:监理单位 C:设计单位 D:建设主管部门【答案】:B【解析】:监理单位应依据工程实际状况、抽检资料以及对合同段工程质量评定结果,对施工单位交工验收申请及其所附资料进展审查并签署意见。
7.沥青混合料生产协作比阶段确定的最正确沥青用量与目标协作比的结果相差不宜大于〔〕。
汽车理论课后习题答案及MATLAB编程

汽车理论课后习题答案—附MATLAB编程教材:汽车理论(第5版)清华大学余志生主编机械工业出版社出版本文档包含第三章 4.3 5.11 6.2 6.4 6.5所要求的MATLAB编程其它习题答案:第一章:1.1 1.2 1.7 1.8第二章:2.2 2.3 2.4第三章第四章:4.1 4.2 4.3 4.5第五章:5.1 5.8 5.10 5.11 5.12 5.14 5.17第六章:6.1~6.5见本作者另一百度文库文档。
获取方法:点击左上角本作者的昵称,进入本作者的文库,《汽车理论课后习题答案(含MATLAB编程)》第三章:m=3880;%总质量g=9.8;%重力加速度r=0.367;%车轮半径eta_t=0.85;%传动系机械效率f=0.013;%滚动阻力系数CDA=2.77;%空气阻力系数*迎风面积i0=[5.175.435.836.176.33];%主减速器传动比If=0.218;%飞轮转动惯量Iw1=1.798;Iw2=3.598;%两前轮/四后轮转动惯量Iw=Iw1+Iw2;ig4=[6.09 3.091.711];%4挡变速器传动比ig5=[5.56 2.7691.64410.793];%5挡变速器传动比n=600:1:4000;%发动机转速Tq=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4;%4挡发动机for i=1:5Ft1=Tq*ig4(1)*i0(i)/r;%各档对应转速下的驱动力Ft2=Tq*ig4(2)*i0(i)/r;Ft3=Tq*ig4(3)*i0(i)/r;Ft4=Tq*ig4(4)*i0(i)/r;u1=0.377*r*n/(i0(i)*ig4(1));%各档对应转速下的车速u2=0.377*r*n/(i0(i)*ig4(2));u3=0.377*r*n/(i0(i)*ig4(3));u4=0.377*r*n/(i0(i)*ig4(4));F1=m*g*f+CDA*u1.^2/21.15;%各档对应转速下的行驶阻力F2=m*g*f+CDA*u2.^2/21.15;F3=m*g*f+CDA*u3.^2/21.15;F4=m*g*f+CDA*u4.^2/21.15;delta1=1+(Iw+If.*ig4(1).^2.*i0(i).^2.*eta_t)./(m.*r.^2);%汽车旋转质量换算系数delta2=1+(Iw+If.*ig4(2).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta3=1+(Iw+If.*ig4(3).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta4=1+(Iw+If.*ig4(4).^2.*i0(i).^2.*eta_t)./(m.*r.^2);a1=(Ft1-F1)/(delta1*m);%加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);b1=1./a1;%加速度倒数b2=1./a2;b3=1./a3;b4=1./a4;figure(1)subplot(2,3,i)plot(u1,b1,u2,b2,u3,b3,u4,b4);title('加速度倒数-速度曲线');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')gtext(['i0='num2str(i0(i))]);%计算采用2挡起步加速至96.6km/h的原地起步加速时间u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=96.6;x1=[];x2=[];x3=[];x4=[];y=3401;for j=1:3401if u3(j)<=u3minx1=[j];endendq1=max(x1);ua3=u3(q1:y);a3=b3(q1:y);for k=1:3401if u4(k)<=u4minx2=[k];elseif u4(k)<=u4maxx3=[k];endendq2=max(x2);q3=max(x3);ua4=u4(q2:q3);a4=b4(q2:q3);s2=trapz(b2,u2);%二挡运行时间s3=trapz(ua3,a3);%三挡运行时间s4=trapz(ua4,a4);%四挡运行时间s=[s2s3s4];t=sum(s)*1000/3600;%总时间disp('t=');disp(t);gtext(['t='num2str(t)'s']);Pe1=Ft1.*u1./3600;%各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;endPemax=max([max(Pe1)max(Pe2)max(Pe3)max(Pe4)]);%发动机最大功率disp('90%负荷');Pe=0.9*Pemax%90%负荷rou=0.7;Ua=0.377*r*3401./(i0.*ig4(4));B=[1233.9-84.4782.9788-0.0474490.00028230];%负荷特性曲线拟合公式系数,对应n=3403r/min for i=1:5b=B*[1Pe Pe^2Pe^3Pe^4]';%根据拟合公式计算比油耗Qs4(i)=Pe.*b./(1.02.*Ua(i).*rou.*g);%百公里油耗量enddisp('Qs4=');disp(Qs4);tt=[48.423546.351141.555733.379630.5564];figure(2)plot(Qs4,tt,'*')hold onxi=25:0.001:31;pp=interp1(Qs4,tt,xi,'cubic');plot(xi,pp)title('燃油经济性-加速时间曲线');xlabel('燃油经济性--等速百公里油耗(L/100km)');ylabel('动力性--原地起步加速时间(s)');gtext('5.17')gtext('5.43')gtext('5.83')gtext('6.17')gtext('6.33')%5挡发动机for i=1:5Ft1=Tq*ig5(1)*i0(i)/r;%各档对应转速下的驱动力Ft2=Tq*ig5(2)*i0(i)/r;Ft3=Tq*ig5(3)*i0(i)/r;Ft4=Tq*ig5(4)*i0(i)/r;Ft5=Tq*ig5(5)*i0(i)/r;u1=0.377*r*n/(i0(i)*ig5(1));%各档对应转速下的车速u2=0.377*r*n/(i0(i)*ig5(2));u3=0.377*r*n/(i0(i)*ig5(3));u4=0.377*r*n/(i0(i)*ig5(4));u5=0.377*r*n/(i0(i)*ig5(5));F1=m*g*f+CDA*u1.^2/21.15;%各档对应转速下的行驶阻力F2=m*g*f+CDA*u2.^2/21.15;F3=m*g*f+CDA*u3.^2/21.15;F4=m*g*f+CDA*u4.^2/21.15;F5=m*g*f+CDA*u5.^2/21.15;delta1=1+(Iw+If.*ig5(1).^2.*i0(i).^2.*eta_t)./(m.*r.^2);%汽车旋转质量换算系数delta2=1+(Iw+If.*ig5(2).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta3=1+(Iw+If.*ig5(3).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta4=1+(Iw+If.*ig5(4).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta5=1+(Iw+If.*ig5(5).^2.*i0(i).^2.*eta_t)./(m.*r.^2);a1=(Ft1-F1)/(delta1*m);%加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);a5=(Ft5-F5)/(delta5*m);b1=1./a1;%加速度倒数b2=1./a2;b3=1./a3;b4=1./a4;b5=1./a5;figure(3)subplot(2,3,i)plot(u1,b1,u2,b2,u3,b3,u4,b4,u5,b5);title('加速度倒数-速度曲线');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')gtext('1/a5')gtext(['i0='num2str(i0(i))]);%计算采用2挡起步加速至96.6km/h的原地起步加速时间u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=max(u4);u5min=u4max;u5max=96.6;x1=[];x2=[];x3=[];x4=[];x5=[];y=3401;for j=1:3401if u3(j)<=u3minx1=[j];endendq1=max(x1);ua3=u3(q1:y);a3=b3(q1:y);for k=1:3401if u4(k)<=u4minx2=[k];endendq2=max(x2);ua4=u4(q2:y);a4=b4(q2:y);for l=1:3401if u5(l)<=u5minx3=[l];elseif u5(l)<=u5maxx4=[l];endendq2=max(x2);q3=max(x3);q4=max(x4);ua5=u5(q3:q4);a5=b5(q3:q4);s2=trapz(b2,u2);%二挡运行时间s3=trapz(ua3,a3);%三挡运行时间s4=trapz(ua4,a4);%四挡运行时间s5=trapz(ua5,a5);%五挡运行时间s=[s2s3s4s5];t=sum(s)*1000/3600;%总时间disp('t=');disp(t);gtext(['t='num2str(t)'s']);Pe1=Ft1.*u1./3600;%各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;Pe5=Ft5.*u5./3600;endPemax=max([max(Pe1)max(Pe2)max(Pe3)max(Pe4)max(Pe4)]);%发动机最大功率disp('90%负荷');Pe=0.9*Pemax%90%负荷rou=0.7;Ua=0.377*r*3401./(i0.*ig4(4));B=[1233.9-84.4782.9788-0.0474490.00028230];%负荷特性曲线拟合公式系数,对应n=3403r/min for i=1:5b=B*[1Pe Pe^2Pe^3Pe^4]';%根据拟合公式计算比油耗Qs5(i)=Pe.*b./(1.02.*Ua(i).*rou.*g);%百公里油耗量enddisp('Qs5=');disp(Qs5);tt=[93.973058.283444.678445.366744.9793];figure(2)plot(Qs5,tt,'*')hold onxi=30:0.001:100;pp=interp1(Qs5,tt,xi,'cubic');plot(xi,pp)%title('燃油经济性-加速时间曲线');%xlabel('燃油经济性--等速百公里油耗(L/100km)');%ylabel('动力性--原地起步加速时间(s)');gtext('5.17')gtext('5.43')gtext('5.83')gtext('6.17')gtext('6.33')运行结果:t=48.4235t=46.3511t=41.5557t=33.3796t=30.556490%负荷Pe=55.5647Qs4=25.103126.365628.307829.958730.7356图1加速度倒数-速度曲线图2燃油经济性-加速时间曲线4.3%空载(no load)—1;满载(full load)—2m1=4080;m2=9290;hg1=0.845;hg2=1.170;L=3.950;a1=2.100;a2=2.950;b1=L-a1;b2=L-a2;beta=0.38;%利用附着系数与制动强度的关系曲线z=0:0.01:1;phi_f1=L*beta.*z./(b1+z*hg1);%前轮利用附着系数(空载)phi_r1=L*(1-beta).*z./(a1-z*hg1);%空载时后轮利用附着系数(空载)phi_f2=L*beta.*z./(b2+z*hg2);%前轮利用附着系数(满载)phi_r2=L*(1-beta).*z./(a2-z*hg2);%后轮利用附着系数(满载)phi=z;%最理想情况figure(1);plot(z,phi_f1,'g--',z,phi_f2,'g-',z,phi_r1,'b--',z,phi_r2,'b-',z,phi,'k-'); axis([0,1,0,1]);grid on;box off;axis square;title('利用附着系数与制动强度的关系曲线');xlabel('制动强度z/g');ylabel('利用附着系数{\phi}');%ECE法规要求界限hold on;z1=0.2:0.01:0.8;z2=0.15:0.01:0.3;z3=0.3:0.01:1;phi1=(z1+0.07)/0.85;phi2=z2-0.08;phi3=z2+0.08;phi4=(z3-0.02)/0.74;plot(z1,phi1,'r-.',z2,phi2,'r-.',z2,phi3,'r-.',z3,phi4,'r-.'); legend('{\phi}_{f}(空载)','{\phi}_{f}(满载)','{\phi}_{r}(空载)',...'{\phi}_{r}(满载)','{\phi}=z','ECE法规要求界限');legend('Location','northwest');%制动效率曲线Ef1=z./phi_f1*100;Er1=z./phi_r1*100;Ef2=z./phi_f2*100;Er2=z./phi_r2*100;figure(2);plot(phi_f1,Ef1,'k',phi_r1,Er1,'k',phi_f2,Ef2,'b',phi_r2,Er2,'b'); axis([0,1,0,100]);grid on;box off;axis square;title('制动效率曲线');xlabel('附着系数{\phi}');ylabel('制动效率(%)');text(0.25,90,'E_f');text(0.6,88,'满载');text(0.8,90,'E_r');text(0.7,65,'空载');text(0.72,72,'E_r');程序运行结果如下:图1图2 5.11L=3.048;K=0.0024;i=20;ua=0:0.01:120;f=1/L.*(1./(3.6./ua+K.*ua./3.6));syms uF(u)=(1/L.*(1./(1./u+K.*u)))./i;plot(ua,f,'b-');xlabel('u_a(km/h)');ylabel('\omega_r/\delta)_s');F(22.35)运行结果:ans=0.1667386094155036.2f=0.1:0.1:100;Gq1=5.12*10^(-5)./f.^2;Gq2=2.02*10^(-3).*f./f;Gq3=7.98*10^(-2).*f.^2;figure(1);loglog(f,Gq1,'b-');box off;axis square;title('位移功率谱密度'); xlabel('f/Hz');ylabel('G_q(f)/(m^2s)');figure(2);loglog(f,Gq2,'b-');box off;axis square;title('速度功率谱密度'); xlabel('f/Hz');ylabel('G_q_''(f)/(m^2/s)');figure(3);loglog(f,Gq3,'b-');box off;axis square;title('加速度功率谱密度'); xlabel('f/Hz');ylabel('G_q_''_''(f)/(m^2/s^3)');运行结果如下:6.4f1=0.1:0.01:1;f2=1:0.01:10;G1=0.010106.*f1.^2;G2=0.010106.*f2./f2;loglog(f1,G1,'b-');hold onloglog(f2,G2,'b-');title('车身加速度的功率谱密度'); xlabel('f/Hz');ylabel('G_z_''_''(f)/m^-^1'); axis([0.1,10,0.0001,0.1]);运行结果如下:6.51.计算说明1)①幅频特性()122222114z q λζλγ⎡⎤-+⎢=⎢⎥∆⎣⎦,其中0ωλω=,()2222222111141λλγζλγλμμ⎡⎤⎡⎤⎛⎫⎛⎫∆=-+--+-⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦⎣⎦;()12222222211414z z ζλλζλ⎡⎤+⎢=⎢⎥-+⎣⎦;()1222222221414s s s s s p z ζλλζλ⎡⎤+⎢=⎢⎥-+⎣⎦,其中s s ωλω=;②均方根谱()()221~j 2z q H f f ωππ=;()()222~j 2z qH f f ωππ== ;()()2221~1j 2p qz z H f f z qωππ== ;③其他值()0.5360q q G f df σ⎡⎤=⎢⎥⎣⎦⎰ ,()0.536110z z G f df σ⎡⎤=⎢⎥⎣⎦⎰ ,()0.536220z z G f df σ⎡⎤=⎢⎥⎣⎦⎰ ,()0.5360a a G f df σ⎡⎤=⎢⎥⎣⎦⎰()()()()()()13622w 012222412.5362202412.5d 12.5 0.5d d 1d d 4a a a a a a W f G f f f G f f G f f G f f G f f f ⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⎛⎫=+++⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎣⎦⎰⎰⎰⎰⎰其中,()()()()()0.5 0.52 2441 412.512.512.536f f f W f f f f <<⎧⎪⎪<<⎪=⎨<<⎪⎪<<⎪⎩()aw w 020lg L a =2)见1)中计算式3)()()()22004q q q G f G G n n uωπ== ()()()1122363622d ~00d d dd f q q f q f H f G f f G f f q σ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎰⎰ ,其中122d 12f q f γλπ⎡⎤=⎢⎥∆⎣⎦ ()()()1122363622d //~00d d dd F Gq q F G q F H f G f f G f f Gq σ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎰⎰ ,其中122222d 1412F f Gq g λζλμπγ⎡⎤⎛⎫-+⎢⎥⎪+⎢⎥⎝⎭=⎢⎥∆⎢⎥⎢⎥⎣⎦其余见1)中计算式2.程序清单1)f0=1.5;zeta=0.25;gamma=9;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega0=2*pi*f0;omega_s=2*pi*fs;lambda=omega./omega0;lambda_s=omega./omega_s;%计算并绘制幅频特性delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;p_z2=((1+(2*zeta_s.*lambda_s).^2)./((1-lambda_s.^2).^2+(2*zeta_s.*...lambda_s).^2)).^0.5;figure(1)loglog(f,z1_q,'b-',0:0.1:100,(0:0.1:100)./(0:0.1:100),'g-');axis([0.1,100,0.1,10]);grid on ;title('z_1~q 的幅频特性');xlabel('激振频率f/Hz');ylabel('$$|\frac{z_1}{q}|$$','Interpreter','latex');gtext('0:1');figure(2)loglog(f,z2_z1,'b-',0:0.1:1,(0:0.1:1)./(0:0.1:1),'g-',1:0.1:100,1./...(1:0.1:100),'g-');axis([0.1,100,0.01,10]);grid on;title('z_2~z_1的幅频特性');xlabel('激振频率f/Hz');ylabel('$$|\frac{z_2}{z_1}|$$','Interpreter','latex'); gtext('0:1');gtext('-1:1');figure(3)loglog(f,p_z2,'b-');axis([0.1,100,0.01,10]);grid on;title('p~z_2的幅频特性');xlabel('激振频率f/Hz');ylabel('$$|\frac{p}{z_2}|$$','Interpreter','latex');%计算并绘制均方根谱sqrt_Gq=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u);sqrt_Gz1=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z1_q;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sqrt_Ga=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*p_z2.*z2_z1.*z1_q; figure(4)loglog(f,sqrt_Gz1,'b-');grid on;title('车轮位移均方根谱');xlabel('激振频率f/Hz');ylabel('$\sqrt{G_{z''''1}(f)}$','Interpreter','latex'); figure(5)loglog(f,sqrt_Gz2,'b-');grid on;title('车身位移均方根谱');xlabel('激振频率f/Hz');ylabel('$\sqrt{G_{z''''2}(f)}$','Interpreter','latex'); figure(6)loglog(f,sqrt_Ga,'b-');grid on;title('传至人体的位移均方根谱');xlabel('激振频率f/Hz');ylabel('$\sqrt{G_a(f)}$','Interpreter','latex');%计算其它值sigma_q=sqrt(trapz(f,sqrt_Gq.^2));%路面不平度加速度均方根值sigma_z1=sqrt(trapz(f,sqrt_Gz1.^2));%车轮加速度均方根值sigma_z2=sqrt(trapz(f,sqrt_Gz2.^2));%车身加速度均方根值sigma_a=sqrt(trapz(f,sqrt_Ga.^2));%传至人体的加速度均方根值for i=1:Nif f(i)<=2W(i)=0.5;elseif f(i)<=4W(i)=f(i)/4;elseif f(i)<=12.5W(i)=1;elseW(i)=12.5/f(i);endendaw=sqrt(trapz(f,W.^2.*sqrt_Ga.^2));%加权加速度均方根值a0=10^(-6);Law=20*log10(aw/a0);%加权振级format shortdisp('路面不平度加速度均方根值=');disp(sigma_q);disp('车轮加速度均方根值=');disp(sigma_z1);disp('车身加速度均方根值=');disp(sigma_z2);disp('传至人体的加速度均方根值=');disp(sigma_a);disp('加权加速度均方根值=');disp(aw);disp('加权振级=');disp(Law);2)%随fs变化f0=1.5;zeta=0.25;gamma=9;mu=10;fs=1.5:0.01:6;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega0=2*pi*f0;lambda=omega./omega0;for i=1:length(fs)omega_s=2*pi.*fs(i);lambda_s=omega./omega_s;delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;p_z2=((1+(2*zeta_s.*lambda_s).^2)./((1-lambda_s.^2).^2+(2*zeta_s.*...lambda_s).^2)).^0.5;sqrt_Gq=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u);sqrt_Gz1=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z1_q;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sqrt_Ga=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*p_z2.*z2_z1.*z1_q;for j=1:Nif f(j)<=2W(j)=0.5;elseif f(j)<=4W(j)=f(j)/4;elseif f(j)<=12.5W(j)=1;elseW(j)=12.5/f(j);endendaw(i)=sqrt(trapz(f,W.^2.*sqrt_Ga.^2));enda0=10^(-6);Law=20*log10(aw/a0);figure(1)plot(fs,aw);grid ontitle('a_w随f_s的变化曲线');xlabel('f_s/Hz');ylabel('a_w/m·s^-^2');figure(2)plot(fs,Law);grid ontitle('L_aw随f_s的变化曲线');xlabel('f_s/Hz');ylabel('L_a_w/dB');%随zeta_s变化f0=1.5;zeta=0.25;gamma=9;mu=10;fs=3;zeta_ss=0.125:0.001:0.5;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega0=2*pi*f0;omega_s=2*pi.*fs;lambda=omega./omega0;lambda_s=omega./omega_s;for i=1:length(zeta_ss)zeta_s=zeta_ss(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;p_z2=((1+(2*zeta_s.*lambda_s).^2)./((1-lambda_s.^2).^2+(2*zeta_s.*...lambda_s).^2)).^0.5;sqrt_Gq=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u);sqrt_Gz1=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z1_q;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sqrt_Ga=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*p_z2.*z2_z1.*z1_q;for j=1:Nif f(j)<=2W(j)=0.5;elseif f(j)<=4W(j)=f(j)/4;elseif f(j)<=12.5W(j)=1;elseW(j)=12.5/f(j);endendaw(i)=sqrt(trapz(f,W.^2.*sqrt_Ga.^2));enda0=10^(-6);Law=20*log10(aw/a0);figure(1)plot(zeta_ss,aw);grid ontitle('a_w随\zeta_s的变化曲线');xlabel('\zeta_s');ylabel('a_w/m·s^-^2');figure(2)plot(zeta_ss,Law);grid ontitle('L_aw随\zeta_s的变化曲线');xlabel('\zeta_s');ylabel('L_a_w/dB');3)%随f0变化f0=0.25:0.01:3;zeta=0.25;gamma=9;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;lambda_s=omega./omega_s;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(f0)omega0=2*pi*f0(i);lambda=omega./omega0;delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(f0==1.5);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(f0,sm_z2,f0,sm_fd,f0,sm_FdG);axis([0.25,3,-25,10]);grid on;title('各响应量均方根值随f_0变化的曲线');xlabel('f_0/Hz');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB'); legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');legend('Location','southeast');%随zeta变化f0=1.5;zeta0=0.125:0.001:0.5;gamma=9;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;omega0=2*pi*f0;lambda_s=omega./omega_s;lambda=omega./omega0;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(zeta0)zeta=zeta0(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(zeta0==0.25);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(zeta0,sm_z2,zeta0,sm_fd,zeta0,sm_FdG);axis([0.125,0.5,-4,4]);grid on;title('各响应量均方根值随\zeta变化的曲线');xlabel('\zeta');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB'); legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');%随gamma变化f0=1.5;zeta=0.25;gamma0=4.5:0.1:18;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;omega0=2*pi*f0;lambda_s=omega./omega_s;lambda=omega./omega0;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(gamma0)gamma=gamma0(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(gamma0==9);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(gamma0,sm_z2,gamma0,sm_fd,gamma0,sm_FdG);axis([4.5,18,-6,6]);grid on;title('各响应量均方根值随\gamma变化的曲线');xlabel('\gamma');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB'); legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');legend('Location','southeast');%随mu变化f0=1.5;zeta=0.25;gamma=9;mu0=5:0.1:20;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;omega0=2*pi*f0;lambda_s=omega./omega_s;lambda=omega./omega0;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(mu0)mu=mu0(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(mu0==10);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(mu0,sm_z2,mu0,sm_fd,mu0,sm_FdG);axis([5,20,-2,2]);grid on;title('各响应量均方根值随\mu变化的曲线');xlabel('\mu');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB');legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');3.结果分析1)路面不平度加速度均方根值=0.3523车轮加速度均方根值=0.2391车身加速度均方根值=0.0168传至人体的加速度均方根值=0.0161加权加速度均方根值=0.0100加权振级=80.0287分析:根据课本中表6-2,a w=0.0100<0.315,L aw=80.0287<110,故乘客没有不舒适。
人工智能教程习题及答案第2章习题参考解答

第二章知识表示习题参考解答2.3 练习题2.1 什么是知识?它有哪些特性?有哪几种分类方法?2.2 何谓知识表示? 陈述性知识表示法与过程性知识表示法的区别是什么?2.3 在选择知识的表示方法时,应该考虑哪些主要因素?2.4 一阶谓词逻辑表示法适合于表示哪种类型的知识?它有哪些特点?2.5 请写出用一阶谓词逻辑表示法表示知识的步骤。
2.6 设有下列语句,请用相应的谓词公式把它们表示出来:(1)有的人喜欢梅花,有的人喜欢菊花,有的人既喜欢梅花又喜欢菊花。
(2)他每天下午都去玩足球。
(3)太原市的夏天既干燥又炎热。
(4)所有人都有饭吃。
(5)喜欢玩篮球的人必喜欢玩排球。
(6)要想出国留学,必须通过外语考试。
2.7 房内有一只猴子、一个箱子,天花板上挂了一串香蕉,其位置关系如图2. 11所示,猴子为了拿到香蕉,它必须把箱子推到香蕉下面,然后再爬到箱子上。
请定义必要的谓词,写出问题的初始状态(即图2.16所示的状态)、目标状态(猴子拿到了香蕉,站在箱子上,箱子位于位置b)。
图2.11 猴子摘香蕉问题2.8 对习题2.7中的猴子摘香蕉问题,利用一阶谓词逻辑表述一个行动规划,使问题从初始状态变化到目标状态。
2.9 产生式的基本形式是什么?它与谓词逻辑中的蕴含式有什么共同处及不同处?2.10 何谓产生式系统?它由哪几部分组成?2.11 产生式系统中,推理机的推理方式有哪几种?在产生式推理过程中,如果发生策略冲突,如何解决?2.12 设有下列八数码难题:在一个3×3的方框内放有8个编号的小方块,紧邻空位的小方块可以移入到空位上,通过平移小方块可将某一布局变换为另一布局(如图2.12所示)。
请用产生式规则表示移动小方块的操作。
2831231684754765S0S g图2.12 习题2.12的图图2.13 习题2.13的图2.13 推销员旅行问题:设有五个相互可直达且距离已知的城市A、B、C、D、E,如图2.13所示,推销员从城市A出发,去其它四城市各旅行一次,最后再回到城市A,请找出一条最短的旅行路线。
微观经济学-习题第二章消费者行为
第二章 消费者行为-效用理论一. 重点知识回顾 0. 效用(Utility ):指商品满足人的欲望的能力,或指消费者在消费商品时所感受到的满足程度。
追求效用最大化是消费者的行为目标。
1. 基数效用论:效用可以衡量具体数值,可以加总求和以及进行其他的计算,具体的效用量之间的比较是有意义的;1.0.1 总效用(Total Utility ): 指消费者在一定时间内从一定数量的商品的消费中所得到的效用量的总和。
TU=f(Q) .图1 总效用曲线 图2 边际效用曲线1.0.2 边际效用(Marginal Utility ) 指消费者在一定时间内增加一单位的商品的消费所得到的效用量的增量。
1.0.2.1 ()TU Q MU Q∆=∆ 1.0.2.2 0()()limQ TU Q dTU Q MU Q dQ∆→∆==∆,这里看出边际效用是总效用的斜率。
1.0.2.3 边际分析是西方经济学中一种很基本的分析方式。
=因变量的变化量边际量自变量的变化量1.1 基数效用的分析方法:边际效用分析方法。
1.2 基数效用者的基本假设:边际效用递减规律(law of diminishing marginal utility ):在一定时间内,在其它商品的消费数量保持不变的条件下,随着消费者对某种商品消费量的增加,消费者从该商品连续增加的每一消费单位中所得到的效用增量即边际效用是递减的。
p.s. 一般情况下,对于正常商品都是这样;特殊情况:对于收藏者,他们的边际效用是递增的。
比如集邮爱好者收集一套邮票,往往是越到后面的票,其效用越是逐渐递增的。
1.3 该假设的合理性:1.3.1从人的生理和心理的角度:随着相同消费品的连续增加,消费者从每一单位消费品中所感受到的满足程度和对重复刺激的反应程度是递减的。
1.3.2从商品的多用途的角度:消费品的边际效用随消费品的用途重要性的递减而递减。
1.4 基数效用论的消费者均衡(consumer equilibrium ): 1.4.1 货币的边际效用:1.4.1.1 随着货币收入量的增加,对于货币的边际效用是递减的(即货币也满足边际效用递减);1.4.1.2 基数效用论者往往假定货币的边际效用是常数值(记为λ)(这是一种假定,书中的解释比较牵强。
编译原理教程课后习题答案第二章
第二章 词法分析2.1 完成下列选择题:(1) 词法分析器的输出结果是。
a. 单词的种别编码b. 单词在符号表中的位置c. 单词的种别编码和自身值d. 单词自身值(2) 正规式M1和M2等价是指。
a. M1和M2的状态数相等b. M1和M2的有向边条数相等c. M1和M2所识别的语言集相等d. M1和M2状态数和有向边条数相等(3) DFA M(见图2-1)接受的字集为。
a. 以0开头的二进制数组成的集合b. 以0结尾的二进制数组成的集合c. 含奇数个0的二进制数组成的集合d. 含偶数个0的二进制数组成的集合【解答】(1) c (2) c (3) d图2-1 习题2.1的DFA M2.2 什么是扫描器?扫描器的功能是什么?【解答】 扫描器就是词法分析器,它接受输入的源程序,对源程序进行词法分析并识别出一个个单词符号,其输出结果是单词符号,供语法分析器使用。
通常是把词法分析器作为一个子程序,每当词法分析器需要一个单词符号时就调用这个子程序。
每次调用时,词法分析器就从输入串中识别出一个单词符号交给语法分析器。
2.3 设M=({x,y}, {a,b}, f, x, {y})为一非确定的有限自动机,其中f 定义如下:f(x,a)={x,y} f {x,b}={y}f(y,a)=Φ f{y,b}={x,y}试构造相应的确定有限自动机M ′。
【解答】 对照自动机的定义M=(S,Σ,f,So,Z),由f 的定义可知f(x,a)、f(y,b)均为多值函数,因此M 是一非确定有限自动机。
先画出NFA M 相应的状态图,如图2-2所示。
图2-2 习题2.3的NFA M 用子集法构造状态转换矩阵,如表表2-1 状态转换矩阵1b将转换矩阵中的所有子集重新命名,形成表2-2所示的状态转换矩阵,即得到 M ′=({0,1,2},{a,b},f,0,{1,2}),其状态转换图如图2-3所示。
表2-2 状态转换矩阵将图2-3所示的DFA M ′最小化。
internet习题
进行子网划分后, IP地址划分为 “网络-子网-主机”三部分 IP地址={<网络号>,<子网号>, <主机号>}
子网掩码也是一个32位二进制数,用圆点分 隔成四段。
其标识方法是:IP地址中网络和子网部分用 二进制数1表示;主机部分用二进制数0表示。 A,B,C三类IP地址的缺省子网掩码如下: A类:255.0.0.0 B类:255.255.0.0 C类:255.255.255.0
4.获取IP地址
ipconfig命令通常用于显示计算机当前
的 TCP/IP 网络配置值
注意: 应先运行cmd.exe程序,进入DOS窗口
ipconfig命令中使用all参数产生完 整显示,可得到更多配置值 命令格式为:ipconfig /all
2.2
子网与子网掩码
为了更有效地利用IP地址,对IP地址分配 方式进行了改进,将网络进一步划分成子网
2. ADSL的特点:
在一条电话线上可以同时打电话和上网,互不影响 提供高速数据通信能力,为交互式多媒体应用提供 了载体。速率远高于拨号上网 每个用户都有单独的一条线路与ADSL局端相连,能 为每个用户提供固定、独占的保证带宽,而且可以 保证用户发送数据的安全性 无需改造线路,只需要在现有的电话线上安装一个 分离器,即可使用ADSL 安装简单,只需配置好网卡,简单的连线,安装相 应的拨号软件即可完成安装
7.有一个IP地址为209.137.58.211,它属于 ________类IP地址。 A、 A B、B C、C D、D 8. B类IP地址的四组十进制数的范围从 128.0.0.1到________ .255.255.254。 A、128 B、191 C、256 D、192
电工学(下册)电子技术基础-第2章-习题解答
习 题 22.1 电路如图2.1所示,1k ΩR =,测得D 5V U =,试问二极管VD 是否良好(设外电路无虚焊)?解:内部PN 结或电极已开路,D 已损坏。
2.2 电路如图2.2所示,二极管导通电压D(on)U 约为0.7V ,试分别估算开关断开和闭合时输出电压o U 的数值。
图2.1 习题2.1电路图 图2.2 习题2.2电路图解: S 断开:断开VD ,D 5V U =。
所以VD 导通,o 50.7 4.3V U =-=S 闭合:断开VD ,)V (1125D-=⨯+-=RR RU ,所以VD 截止,o 6V U = 2.3 分析判断图2.3所示各电路中二极管是导通还是截止,并计算电压ab U ,设图中的二极管都是理想的。
图2.3 习题2.3电路图解:(a )断开VD ,U D =5+5=10V>0,VD 导通 ,ab 5V U =-;(b)断开VD,D2151V23U=-⨯=-+,VD截止ab252V23U=⨯=+;(c)断开VD1 VD2,D1D212V,5127VU U==-+=,所以VD1优先导通,U D2= −5V,VD2截止,U ab=0V;(d) )断开VD1 VD2,D1D212V,12517VU U==+=所以 VD2优先导通,D15VU=- VD1截止,ab5VU=-2.4 一个无标记的二极管,分别用a和b表示其两只引脚,利用模拟万用表测量其电阻。
当红表笔接a,黑表笔接b时,测得电阻值为500。
当红表笔接b,黑表笔接a时,测得电阻值为100k。
问哪一端是二极管阳极?解:b端是阳极2.5 二极管电路如图 2.4(a)所示,设输入电压i()u t波形如图 2.4(b)所示,在05mst<<的时间间隔内,试绘出输出电压o()u t的波形,设二极管是理想的。
图2.4 习题2.5电路图解:i()2tu t=,断开VD,D6iu u=-,当Du>时,VD导通,即3st>,60.2630.20.2iouu t-=⨯+=++当Du<时,VD截止,即3st<,6Vou=()ou tt/ms2.6 在图2.5所示的电路中,设二极管为理想的,已知i30sin(V)u tω=,试分别画出输出电压ou的波形,并标出幅值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xm ) ) <
*
, 2
= & supp ( ) x ) = & supp ( 'x )
)(S1 '(S1
p ( ' ( xn
x ) ) ! lim p ( ' ( xn
&x 1 = & x 1 x0 + 0, 0 ! p (
1 = lim n p ( x0 ) = 0 n *
(
m *
m
x)) !
, 2
Ax
m
x
x
2
所以 A 是单射.
0 = | ( Ax , x ) | m
故有
( R ( A) )
x= ,
,
所以 R ( A ) 是稠的. 设 { yn } 是 R ( A ) 中的基本列, 并设
9
( R ( A) ) = { } .
R ( A ) 是闭的. R ( A ) = R ( A ) = H , 即 A 是满射 . 所以根据Banach定理, A 1 L( H ). 2.3.4 设 X ,Y 是线性赋范空间,D 是 X 的线性子空间, A : D Y 是线性映射. 求证: (1) 如果 A 连续, D 是闭集,则 A 是闭算子; (2) 如果 A 是连续且是闭算子,则 Y 完备蕴含 D 闭; (3) 如果 A 是一一的闭算子,则 A 1 也是闭算子; (4) 如果 X 完备, A 是一一的闭 算子, R( A) 在 Y 中稠密,并且
x
证明 令
1
x 1 = x + supp ( 'x ) ,
'(S1
def
令
其中 S 是复平面上的单位圆周. 先证明 x 1 是 X 上的范数.
15 16
设 & = & ei ,
'(S1
注意到
'(S1
supp ( '&x ) = & supp 'ei x
) = 'ei
(
)
supp ( ' ( xn
'(S1 m *
18
17
A L( X ,Y ) ,使得 An 强 求证 收敛到 A ,且 A ! lim An . 证明 x X,
A是单射的闭算子 子.
(3)
A 1 也是闭算
2.3.5 用等价范数定理证明 (C [0,1], $ 1 ) 不是Banach空间, 其中 1 f = % 0 | f ( t ) | dt f C [0,1] . 证明 用反证法. 假如 是B空间, C [ 0,1] , $ 1
(
)
13
14
f = max f ( t ) .
5
任取 x [ x ] , 则有 x X, x = [ x] . 证法2 不用开映射定理. 教材p94, 定理 2.3.8 的证明中的 (1)为了证 T 是开映射, 必须且仅 须 > 0, s.t. TB ( ,1) U ( , ) . 取 = 1. 并设 B ( ,1) X 中的开单位球; U ( ,1) X X0 中的开单位球. 下面证明 U ( ,1) = B ( ,1) . x B ( ,1) x <1 [ x] ! x < 1
y =1
L(H) 并且 m > 0 ,使得 | (Ax,x) | m x 2 , x H . 求证 A 1 L(H) . 证明 由条件, x H, A
m x 2 !| (Ax,x) |! x
Ax
Ax
m x
2.3.3 设 H 是Hilbert空间,
7
所以 A 是单射. ? x ( R ( A)) , 0= | (Ax,x) | m x 2 x = , ? 故有 ( R ( A ) ) = { } . 所以 R ( A ) 是稠的. 设 { y n } 是 R ( A ) 中的基本列, 并设 Axn = y n , 则由 Ax m x { xn } 是基 本列.
n k =1 k
( x,z 0 )
||
k
=
( x,
n k =1
n
k =1
( z k ,z 0 )z k
||
)
+x
n k =1
( x,z k ) z k ,z 0 )
M
= (
( x,z k ) zk , z 0 )
无关组就是本身. 用 Gram-Schmidt 过程, 构造出一个正交规范集 n n { z k }k =1 s.t. span { z k }k =1 = span { y k }k =1 . 则有 z k M ( k = 1,2, ,n ) . 令 z 0 = x 0 y 0 , 则 z 0 M. 对 x H,
1
还有一个条件 A 是闭算子, 下面证明 D 闭. 设
11
xn
D ( A) , yn = Axn
xn y
x
12
因为 A 是闭算子, 所以 x D ( A) , y = Ax y R ( A) , x = A 1 y . i.e. A 1 是闭算子. (4) 如果 X 完备,A是单射的闭 R( A) 在 Y 中稠密, 算子, 并且 A 1 连续,那末 R ( A ) = Y.
2.2.1 根据Riesz表示定 y k H, fk ( x ) = ( x,y k )
( k = 1, 2, ,n . n x M = N ( fk ) ( x,y k ) = 0 ( k = 1,2, ,n, x M ( ( x,z ) z k =1 这意味着, y k M ( k = 1,2, ,n ) . n 即得 不妨假定, { y k }k =1 的极大线性
0 ! t !1
" $ 是比 $ 1 强的范数,用等价范数 定理, $ 与 $ 1 等价, 即 M > 0, 使得 f ! M f 1 即
max f ( t ) ! M % 0 f ( t ) dt 0 ! t !1
1
f (t ) , % 0 f ( t ) dt ! max 0! t !1
1
1 Mt f (t) = 0
PM ( PL y ) = PM y 是 L M 上的投影算子 PL M . 即得 PL PM = PL M . 2.3.1 设 X 是Banach空间, X 0 是 X 的闭子空间,映射 : X X / X0 ,定义为 : x [x] x X ,其中 [x] 表 是开映 示含 x 的 商类. 求证 射. 证法1 用开映射定理, 只需证明 满射. 事实上,
1 (0 ! t ! M ) 1 ! t ! 1) (M
(
f
y
C [ 0,1] ) .
1 1 ! M $ 21 M = 2 矛盾. 2.3.6 Gelfand引理设 X 是Banach R1 满足 空间, p : X (1) p( x ) 0 x X ; (2) p(& x ) = & p( x ) & > 0, x X ; (3) p( x1 + x2 ) ! p( x1 ) + p( x2 ), x1 , x2 X (4) 当 xn x 时, p( xn ) p( x ) . 求证: M > 0 ,使得 p( x ) ! M x x X .
2
l( v) = 1 2 v
2
2
2
=1 u 2 v 设 u 0 C,
1
u s.t.
1 2
(
)
(u , v)
1 2
u
2
v C) .
2
u0
u = inf v u ,
v C 2 2
v C, = f ( u0 )
( PM x,y ) = ( PM x,PM y ) = ( x,PM y ) .
(
v C
因此 PL PM = 0 0 = ( PL PM x,y ) = ( PM x,PL y ) , x,y 于是 x L, y M, 有 ( x,y ) = ( PM x,PL y ) = 0 L M. (2) L = M PL + PM = I Ix = x = PM x + PM x PM x = ( I PM ) x, x H PL = PM = ( I PM ) (3) PL PM = PL M PL PM = PM PL ( ) PL PM = PL M = PM PL ( ) 设 PL PM = PM PL 设 P = PL PM , 则有 2 P 2 = ( PL PM ) = PL PM PL PM = PL PL PM PM 2 2 = PL PM = PL PM = P. 即 P 是幂等 算子.从而是投影算子.
' ( S1 , n > N xn xm <
, 2 , 2
)
x))
1 x0 ) ) ! limp ( n n * p ( ) = 0.
xn
下面证明
xn xm
1
( X, x )
1
" xn
完备.
xm 0,
x 1 = xn
x + supp ( ' ( xn
'(S1
x !
(
n > N)
0
xn
完备, " x ( X, 使得 , ( ( 0,1) , N ( N, , xn xm 1 < 2 ( n > N ) ,
( X, x )
x.
xn
, <2 +, ( n > N) . 2 = , 于是 x 1 是 X 上的完备范数,
M > 0, 最后根据等价范数定理, p( x) ! M x . 使得 x 1 ! M x 2.3.7 设 X ,Y 是Banach空间. An L( X ,Y ) ( n = 1,2, $ $ $) . 又对 x X , { An x } 在 Y 中收敛.
