1.2几何图形课件

合集下载

1.2几何图形(2)

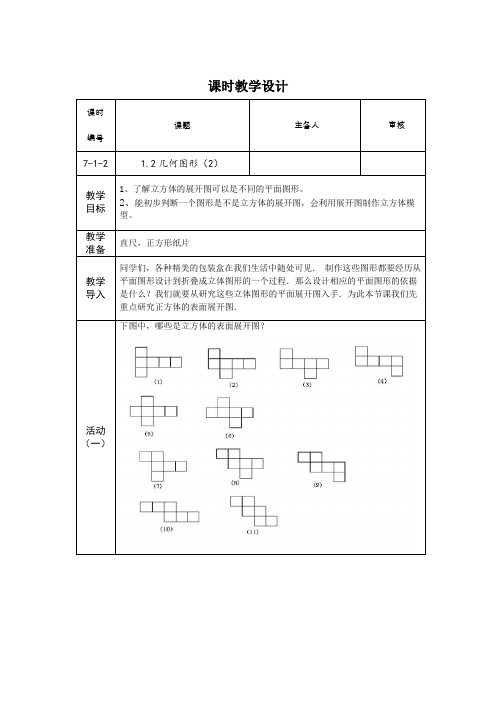
课时教学设计下图中，哪些是立方体的表面展开图？
程
前你祝似锦
活动（二）将包装盒沿它的某些棱剪开，并铺在平面上，得到一个怎样的平面图形？如果展开的方法不同，得到的图形相同吗？动手做一做，然后画一画，你能得到多少种平面图形？画出几种.
活动（三）水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则“祝”、 “你”、 “前”分别表示正方体的______________________.
1.下列图形中，不是立方体表面展开图的是（）
2.在下列图形中（每个小四边形皆为全等的正方形），可以是一个正方体表面展开图的是（）。

九年级上册数学(北师大版)第一章1.2矩形的性质与判定公开课PPT课件

知识小结
两组对边四边形分别平行
平行
一个角
四边形是直角
矩形
四边形集合
平行四边形集合
矩形集合
深入探究
如果四边形ABCD的对角线AC=BD,
这样的四边形是不是矩形?
A
D
B
AC=BD C
都不
A
D
是矩
AC=BD
形
B
C
7
知识探究
如果一个平行四边形的对角线变成相等呢？
A
D
A
D
O
O
B
C
B
C
将AC同时向两边拉长，使AC=BD
∴AD∥BC,AB∥CD.
B
C
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
矩形的判定方法：
有三个角是直角的四边形是矩形。
A
几何语言：
∵ ∠A=∠B=∠C=90° ∴四边形ABCD是矩形
B
D C
16
知识小结
四边形
三个角是直角
四边形集合平行四边形集合
矩形集合
矩形
归纳小结矩形的三种判定方法
有两个角是直角的四边形是矩形吗？
有三个角是直角
C
C
D
C
D
D
A
B
A
B
A
B
(有一个角是直角) (有二个角是直角) (有三个角是直角)
13
情境一：李芳同学用“边—
—直角、边——直角、边—— 直角、边”这样四步，画出了一个四边形，她说这就是一个矩形，她的判断对吗？为什么？
猜想：有三个角是直角的四边形是矩形。
随堂练习

1.2几何图形上课课件

4.一个立方体的每个面上都标了字母，右图是这个立方体的一个展开图。请回答下列问题：（1）如果面A是立方体朝下的面，那么哪个面朝上？（2）如果面F朝前，面B朝左，那么哪个面朝上？（3）如果面C朝右，面D朝后，那么哪个面朝上？
A D C B F E
作业：
1.课本11--12页2 4 5题
2.下边的4个图形中，哪一个是由左边的盒子展开而成的。
1、划过夜空的流星给我们以（
）的形象；
2、打开折扇时，随着扇骨的转动形成一个扇面，给我们以（）的形象； 3、当宾馆的旋转门旋转时，给我们以（形象。）的
点、线、面、体组成的。几何图形是由_______________ 点是构成图形的基本元素直线
点——
动成
点、线、面、体曲线动经过运动变化，就能成组合成各种各样的几平面面——— 何图形，形成多姿多动曲面彩的图形世界。成体———
体
象上面学过的长方体、正方体、圆柱、球、圆锥等这些立体图形，我们称之为几何体，简称为体。
面
平面平面没有（），没有（是向四面八方（）的。
曲面），
１试举例生活中哪些物体的面是平的？哪些物体的面是曲的？
面和面相交的地方是（线和线相交的地方是（
线点
）。）。
面
棱
顶点
交流与发现
挑战自我
（1）用剪刀将一张正方形的纸片剪去一个角，还剩几个角？剪一刀后，能使纸上剩六个角吗？试一试。
五个角
四个角不可能使纸上剩六个角。
三个角
（2）一个立方体共有6个面，如果将这个立方体用刀切成两块，被分成的两个几何体共有几个面？如果切成的，怎样切？用萝卜、马铃薯或橡皮泥做一个立方体，试一试。切断2个面，增加4个面。

高中数学1.2空间几何体的三视图和直观图课件人教版必修二

Z
Z
y
D
O
y
Q
O
x
M
C
N
B
A
x
P
3 画侧棱.过A,B,C,D,各点分别作z轴的平行线,并在这些平行线
上分别截取2cm长的线段AA,BB,CC,DD.
4 成图.顺次连接A ,B ,C,D ,并加以整理(去掉辅助线,将被遮挡住的部分
改为虚线), 就可得到长方体的直观图.
D
Z
B
3cm
4cm
2cm
主视方面
例2.由5个相同的小立方块搭成的几何体如图所示,请画出它的三视图:
主视图
高平齐长对正宽相等
左视图
俯视图
例3.请想象下面三视图所表示的几何图形的实物模型．圆锥
圆台
冰淇淋
练9.画出下面马蹄形磁铁的三视图.
俯
左
练10.从三个方向看下图，试作出其三视图.
从上面
从侧面
O
C
Q
A
M
y
A
D
C
B
C
D
P
C
N
B
x
A
D
A
B
例3．已知几何体的三视图，用斜二测画法画出它的直观图
Z ·
O
y
· O · O
正视图
· O · O
侧视图
y
x
O
x
·
俯视图
三视图从细节上刻画了空间几何体的结构,根据三视图，我们可以得到一个精确的空间几何体,正是因为这个特点，使它在生产活动中得到广泛应用(比如零件图纸、建筑图纸等).直观图是对空间几何体的整体刻画，我们可以根据直观图的结构想象实物的形象．

12几何图形初步认识PPT课件

15
大自然—塑造“形”的艺术家
点的形象
线的形象
面的形象
16
点
线
几何图形
面
体
17
知识小结
点 —— 线与线相交而成
（几何中的点无大小）
几
平面几
何
线 —— 面与面相交而成
（几何中的线无粗细）
何图
图
形
面 —— 包围着体的部分立
形
（几何中的面无厚薄）体
体 —— 物体的图形
图
形
三角形
线段点
圆 •••
You Know, The More Powerful You Will Be
31
结束语
感谢聆听
不足之处请大家批评指导
Please Criticize And Guide The Shortcomings
讲师：XXXXXX
XX年XX月XX日

１
平静的湖面
化妆镜的镜面
（1）面两观个察平面物有面体什或数么情学主景中要,你的的看不平到同面的点是上？无面厚的薄两个面与下面的（2）的试面举曲是例面曲生的活？中哪些物体的面是平的？哪些物体
篮球的球面
井台的侧面 6
下图是一个长方体的模型，面和面相交的地方形成了几条线？
12条线
面和面相交的地方是线。
生活中有很多事物都给我们以线的形象比如 7
8
9
10
线：直线和曲线几何中的线没有粗细
11
下图是一个长方体的模型，线和线相交成几个点？
·· ··
·· ·· 8个点
线和线相交的地方是点。
生活中有很多事物都给我们以点的形象比如 12
临海市

2020青岛版七年级数学上册全册课件【完整版】

第4章数据的收集整理与描述
2020青岛版七年级数学上册全册课件【完整版】
4.1 普查和抽样调查
2020青岛版七年级数学上册全册课件【完整版】
4.2 简单随机抽样
2020青岛版七年级数学上册全册课件【完整版】
2020青岛版七年级数学上册全册课件【完整版】
1.3 线段、射线和直线
2020青岛版七年级数学上册全册课件【完整版】
1.4 线段的比较与作法
2020青岛版七年级数学上册全册课件【完整版】
第2章有理数
2020青岛版七年级数学上册全册课件【完整版】目录
0002页 0126页 0156页 0202页 0237页 0262页 0287页 0328页 0371页 0394页 0426页 0446页 0476页 0500页 0565页 0596页 0643页
第1章基本的几何图形 1.2 几何图形 1.4 线段的比较与作法 2.1 生活中的正数和负数 2.3 相反数与绝对值 3.1 有理数的加法与减法 3.3 有理数的乘方 3.5 利用计算器进行有理数的计算 4.1 普查和抽样调查 4.3 数据的整理第5章代数式与函数的初步认识 5.2 代数式 5.4 生活中的常量与变量第6章整式的加减 6.2 同类项 6.4 整式的加减 7.1 等式的基本性质
2020青岛版七年级数学上册全册课件【完整版】
2.1 生活中的正数和负数
2020青岛版七级数学上册全册课件【完整版】
2.2 数轴
2020青岛版七年级数学上册全册课件【完整版】
2.3 相反数与绝对值
2020青岛版七年级数学上册全册课件【完整版】
第3章有理数的运算
2020青岛版七年级数学上册全册课件【完整版】

北师大版数学必修二课件：1.2直观图

(1)三角形的直观图可能为一条线段. (
)
(2)菱形的直观图可能为长方形. (
)
(3)空间几何体的直观图是唯一的. (
)
(4)如果一个水平放置的△ABC的面积为S,用斜二测画法画出的
直观图的面积为S',那么S与S'的关系是S'= √2 S. (
)
4
答案:(1)× (2)√ (3)× (4)√
探究一
∠x'O'y'=45°.
如图所示,作D'H'⊥x'轴于点H',
√2
则 A'B'=4 cm,A'D'=1 cm,D'H'=
√2
2
cm,
所以 S 四边形 A'B'C'D'=4× =2√2(cm2).
2
探究一
探究二
探究三
易错辨析
探究二画空间几何体的直观图
【例2】画出底面边长为1.2 cm的正方形,侧棱均相等且高为1.5
易错辨析
探究三由直观图还原平面图
【例3】导学号91134004(1)在如图所示的直观图中,A'B'∥y'
轴,B'C'∥A'D'∥x'轴,且B'C'≠A'D',则其对应的平面图形ABCD是(
A.任意梯形
B.直角梯形
C.任意四边形
D.平行四边形
(2)已知等边三角形ABC的直观图△A'B'C'的面积为 ,则等边三
A,B,C,D,即四边形ABCD为底面正方形的直观图.
(3)画高.在z'轴上截取OP,使OP=1.5 cm.

2022年秋高中数学第一章空间向量与立体几何1.2空间向量基本定理课件新人教A版选择性必修第一册

组向量是
()
A．{a，a＋b，a－b}
B．{b，a＋b，a－b}
C．{c，a＋b，a－b}
D．{a＋b，a－b，2a＋b}
【答案】(1)A (2)C
【解析】(1)若向量 a，b 共线，则向量 a，b 所在的直线平行或重合，
故①错；两条异面直线的方向向量可通过平移使得它们在同一平面内，故②错；三个向量两两共面，这三个向量未必共面，如三棱锥 P－ABC 中，P→A，P→B，P→C两两共面，但它们不是共面向量，故③错；根据空间向
三个向量有什么条件？【答案】提示：三个向量不共面．
空间向量的正交分解
1．单位正交基底如果空间的一个基底中的三个基向量__两__两__垂__直__，且长度为1，那
么这个基底叫做__单__位__正__交__基__底__，常用{i，j，k}表示．
2 ．对空间中的任意向量 a ，均可以分解为 xi ， yj ， zk ，使 a ＝ ____x_i＋__y_j_＋__zk___把空间向量分解为三个__两__两__垂__直__的向量，叫做把空间向量进行正交分解．
(2)当三个向量不共面时，才可以表示空间中的任意一个向量． (3)由空间向量基本定理可知只有不共面的三个向量才可以作为基底．
2．以下四个命题中正确的是
()
A．空间的任何一个向量都可用其他三个向量表示
B．若{a，b，c}为空间向量的一组基底，则{a＋b，b＋c，c＋a}构
成空间向量的另一组基＝2，BC＝2，AA1＝6，且记A→B＝a，A→D＝b，A→A1＝ c．
(1)用 a，b，c 表示B→D1，B→1C； (2)求异面直线 BD1 和 B1C 所成角的余弦值．
解：(1)B→D1＝B→A＋A→D＋D→D1＝－a＋b＋c， B→1C＝B→1B＋B→C＝－c＋b． (2)∵a·b＝b·c＝c·a＝0，|a|2＝4，|b|2＝4，|c|2＝36， ∴B→D1·B→1C＝－32，|B→D1|＝2 11，|B→1C|＝2 10， cos〈B→D1，B→1C〉＝－8111010＝－4 51510． ∴异面直线 BD1 和 B1C 所成角的余弦值为4 51510．

1.2空间几何体的三视图和直观图

1 V ( S S S S )h 3
柱体、锥体、台体的体积公式之间有什么关系？
上底扩大
上底缩小
V Sh
S 0
S S V 1 Sh 1 V ( S S S S )h 3 3
S为底面面积， h为锥体高
S , S 分别为上、下
底面面积，h 为台体高
柱体（棱柱、圆柱）的体积公式：
V Sh
（其中S为底面面积，h为柱体的高）
锥体体积
h
椎体（圆锥、棱锥）的体积公式：
1 V Sh 3
（其中S为底面面积，h为高）
由此可知，棱柱与圆柱的体积公式类似，都是底面面积乘高；棱锥与圆锥的体积公式类似，都是 1 底面面积乘高的． 3
台体体积
台体（棱台、圆台）的体积公式

考向二空间几何体的三视图

【例2 】►(2012·湖南) 某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是 ( )．

[审题视点] 根据正视图和侧视图相同逐一判断．
正视图
侧视图
圆台
俯视图
根据三视图想象它们表示的几何体的结构特征
正视图
侧视图
正四棱台俯视图
简单组合体的三视图
水平直观图
正方形的水平直观图
y y
0 0
x
x
1. 水平方向线段长度不变;
变化规则
2. 竖直方向的线段向右倾斜450，长度减半;
3. 平行线段仍然平行.
水平直观图
正三角形的水平直观图

由三视图求几何体的相关量
若一个正三棱柱的三视图如图所示，求这个三棱柱的高和底面边长以及左视图的面积．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（5）将包装盒沿它的某些棱剪开，并铺在平面上。得到一个怎样的平面图形？如果展开的方法不同，得到的图形相同吗？动手做一做，然后画一画。你能得到多少种平面图形？与同学交流。
第一类，中间四连方，两侧各一个，共六种。
第二类，中间三连方，两侧各有一、二个，共三种。
第三类，中间二连方，两侧各有二个，只有一种。
A
B E C D
F
第四类，两排各三个，只有一种。
（6）下列哪个图形是立方体包装盒的展开图？
（1）
（2）
（3）
（6）下列哪个图形是立方体包装盒的展开图？
（1）
（2）
（3）
（7）你能制作一个立方体纸盒吗？与同学交流。
练习
顶点棱面面
1.观察右边的图形，并填空：（1）棱是由____ 面和_____ 面相交而成的；（2）顶点是由_____ 棱和_____ 棱相交而成的。
点动成—— 线线动成—— 面面动成—— 体
体是由面组成面与面相交成线线与线相交成点
• 平面图形
立方体、长方体、圆柱、圆锥、球等都是几何体，下面图中的棱柱（图1—2）、棱锥（图1—3）等也是几何体。几何体简称体。
三棱柱
锥
四棱锥
图1—3
五棱锥
六棱锥
常见立体图形的归类:
· · · · · · · ·
线和线相交的地方是点。
临海市
点
把夜空中的星星看作点.
注意：数学上的点没有大小。
点
线
几何图形
面体
观察下面运动的图片,分别可以看成什么几何图形在运动? 它们的运动又形成了什么几何图形呢?
探究
点动成线
你能用数学语言来描述这一现象吗？
（雨点）
落千到条水线中万看条不线见
柱体
圆柱
棱柱圆锥
立体图形
锥体棱锥圆台台体球体棱台
三棱柱四棱柱五棱柱六棱柱 …… 三棱锥四棱锥五棱锥六棱锥 ……
作业：
填表
面数三棱柱五棱柱十棱柱 5 7 12 4 棱数 9 15 30 6 顶点数 6 10 20 4 图示
三棱锥五棱锥
十棱锥
6
11
10
20
6
11
知识小结
点 —— 线与线相交而成
（几何中的点无大小）
几
何
图形
线 —— 面与面相交而成
（几何中的线无粗细）
平面几何图形立
三角形线段点圆圆柱 •••
面 —— 包围着体的部分
（几何中的面无厚薄）
体
图
体 —— 物体的图形
圆锥棱锥棱柱
•••
形
实验与探究
(1)观察立体形状的包装盒，它是由哪些面组的？这些面的大小和形状都相同吗？ (2)两个面的相接处是什么图形？ (3)棱与棱的相接处是什么图形？ (4)数一数立方体有几条棱?几个顶点？
在圆柱和圆锥中，侧面与底面的交接处都是圆，圆是一条封闭的曲线。
生活中有很多事物都给我们以线的形象比如
线：直线和曲线几何中的线没有粗细
下图是一个长方体的模型，棱和棱的交接处是什么图形？
几个点
8个点
在长方体和正方体中，棱与棱的公共点叫长方体或正方体的顶点
生活中有很多事物都给我们以点的形象比如
2. 圆柱是由几个面组成的？它们分别是什么面？圆柱的侧面和底面相交成什么线？
3.将下列第一行中的各个平面图形分别绕图中的虚线（轴线）旋转一周，就得到第二行的立体图形。你能把各个平面图形与旋转得到的立体图形连接起来吗？
4.一个立方体的每个面上都标了字母，右图是这个立方体的一个展开图。请回答下列问题：（1）如果面A是立方体朝下的面，那么哪个面朝上？（2）如果面F朝前，面B朝左，那么哪个面朝上？（3）如果面C朝右，面D朝后，那么哪个面朝上？
谜语：
点动成线
线动成面
线动成面
观察下面运动的图片,分别可以看成什么几何图形在运动? 它们的运动又形成了什么几何图形呢?
直角三角形绕一条直角边旋转成圆锥体
长方形绕一边旋转成圆柱体
观察下面运动的图片,分别可以看成什么几何图形在运动? 它们的运动又形成了什么几何图形呢?
下图是一个长方体的模型，标有1的面的形状是正方形。
1
1、在围成长方体的各个面中，与1相对应的面有几个？它的形状是什么图形？与它相邻的面是什么形状？
找出相邻两个面的交结处，它的形状是什么图形。
面和面相交的地方是线。在长方体和正方体中，相邻两个面的交接处是一段直的线，我们把它叫做棱。
多少条？
12条线