沪教版 九年级数学 寒假班讲义 第5讲 长方体与三角形(解析版)
沪教版 九年级(上)数学 秋季课程 第2讲 相似三角形(解析版)
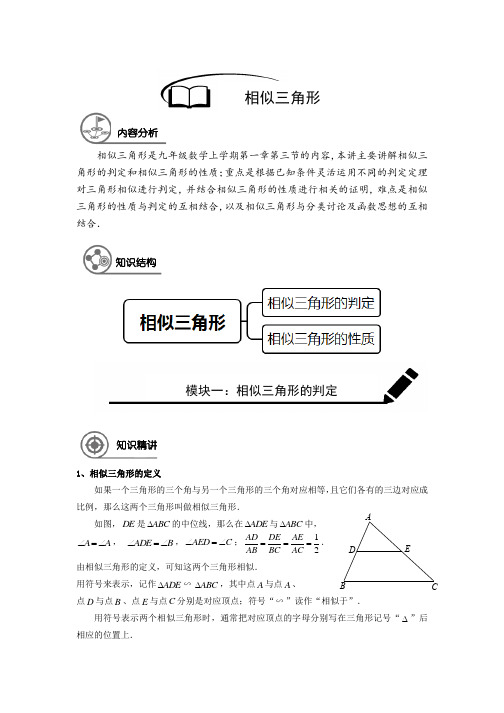
DABCE相似三角形是九年级数学上学期第一章第三节的内容,本讲主要讲解相似三角形的判定和相似三角形的性质;重点是根据已知条件灵活运用不同的判定定理对三角形相似进行判定,并结合相似三角形的性质进行相关的证明,难点是相似三角形的性质与判定的互相结合,以及相似三角形与分类讨论及函数思想的互相结合.1、相似三角形的定义如果一个三角形的三个角与另一个三角形的三个角对应相等,且它们各有的三边对应成比例,那么这两个三角形叫做相似三角形.如图,DE 是ABC ∆的中位线,那么在ADE ∆与ABC ∆中,A A ∠=∠, ADEB ∠=∠,AEDC ∠=∠;12AD DE AE AB BC AC ===. 由相似三角形的定义,可知这两个三角形相似.用符号来表示,记作ADE ∆∽ABC ∆,其中点A 与点A 、点D 与点B 、点E 与点C 分别是对应顶点;符号“∽”读作“相似于”.用符号表示两个相似三角形时,通常把对应顶点的字母分别写在三角形记号“∆”后相应的位置上.相似三角形内容分析知识结构模块一:相似三角形的判定知识精讲2 / 31ABCA 1B 1C 1根据相似三角形的定义,可以得出:(1)相似三角形的对应角相等,对应边成比例;两个相似三角形的对应边的比,叫做这两个三角形的相似比(或相似系数).(2)如果两个三角形分别与同一个三角形相似,那么这两个三角形也相似. 2、相似三角形的预备定理平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似. 如图,已知直线l 与ABC ∆的两边AB 、AC 所在直线分别交于点D 和点E ,则ADE ∆∽ABC ∆.3、相似三角形判定定理1如果一个三角形的两角与另一个三角形的两角对应相等,那么这两个三角形相似. 可简述为:两角对应相等,两个三角形相似.如图,在ABC ∆与111A B C ∆中,如果1A A ∠=∠、1B B ∠=∠,那么ABC ∆∽111A B C ∆.常见模型如下:A BCDEABCDEABCDEABCA 1B 1C 1ABCA 1B 1C 14、相似三角形判定定理2如果一个三角形的两边与另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.可简述为:两边对应成比例且夹角相等,两个三角形相似.如图,在ABC ∆与111A B C ∆中,1A A ∠=∠,1111AB ACA B AC =,那么ABC ∆∽111A B C ∆.5、相似三角形判定定理3如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.可简述为:三边对应成比例,两个三角形相似. 如图,在ABC ∆与111A B C ∆中,如果111111AB BC CAA B B C C A ==,那么ABC ∆∽111A B C ∆.6、直角三角形相似的判定定理如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例,那么这两个直角三角形相似.可简述为:斜边和直角边对应成比例,两个直角三角形相似.如图,在Rt ABC ∆和111Rt A B C ∆中,如果190C C ∠=∠=︒,1111AB BCA B B C =,那么ABC ∆∽111A B C ∆.ABCA 1B 1C 14 / 31【例1】如图,已知点P 是ABC ∆中边AC 上一点,联结BP ,要使ABP ∆∽ACB ∆,那么应 添加的一个条件为____________,或____________,或____________.【答案】C ABP ∠=∠,ABC APB ∠=∠,AB APAC AB=. 【解析】根据相似三角形的判定定理1和判定定理2,题 目中有公共角,只需要加上一个等角或夹这个角的两边对应成比例的条件即可.【总结】考查相似三角形判定定理的应用,注意对定理内容的把握,判定定理2一定是夹等角的两条边对应成比例.【例2】下列命题正确的是( ) A .有一个角是40°的两个等腰三角形相似 B .有一个角是106°的两个等腰三角形相似 C .面积相等的两个直角三角形相似D .两边之比为3 : 5的两个直角三角形相似【答案】B【解析】有一个角是40°的等腰三角形,不能确定这个角是顶角还是底角,即不能确定三 角形形状,A 错误;有一个角是106°的等腰三角形,可以确定这个角一定是等腰三角 形的顶角,则底角大小也必相同,根据相似三角形判定定理1,B 正确;面积相等的直 角三角形,底边长和高长都不能确定,形状不确定,C 错误;两边之比为3:5,不能确 定这两条边是否同为两直角边或者一斜边一直角边,即不能确定直角三角形形状相同,D 错误.【总结】考查相似三角形判定定理的应用,注意一定要对题目提供的条件进行分析的基础上再确定是否能用判定定理证明相似.【例3】下列4⨯4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则例题解析ABCPAB C与ABC ∆相似的三角形所在的网格图形是( )A .B .C .D .【答案】C【解析】根据已知ABC ∆,得对应两直角边之比2ABBC=,三角形与ABC ∆相似,则两条直角边之比也为2,只有C 选项满足.【总结】相似三角形判定定理2可转化为一个三角形中的夹等角的两条边对应成比例.【例4】如图,ABC ∆中,AE 交BC 于点D ,C E ∠=∠,:3:5AD DE =,AE = 8,BD = 4,则DC 的长等于( )A .415B .125C .174D .154【答案】D【解析】由:3:5AD DE =,AE = 8,可得3AD =,5DE =, 由C E ∠=∠,结合一对对顶角BDE ADC ∠=∠,可得BDE ∆∽ADC ∆,由此则有BD DE AD CD =,代入即为453CD =,即得:154CD =,故选D . 【总结】考查相似三角形的判定和性质的综合应用,注意题目中相似图形的对应关系,对应成比例的线段和点一定要准确.【例5】在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似;A BCDE6 / 31乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.对于两人的观点,下列说法正确的是( ) A .两人多对 B .两人都不对C .甲对乙不对D .甲不对,乙对【答案】C【解析】直角三角形扩张以后得到的三角形三边分别与原三角形平行,得到两三角形三个内 角都相等,根据相似三角形判定定理1,可知相似,甲对;乙向外扩张后,矩形两邻边分别变为5和7,3557≠,两矩形的边不对应成比例,可知两矩形不相似,乙不对,故选C .【总结】对于三角形来讲,三角形个内角相等则各对应边比例相等,可以得到两三角形相似,对于其它的多边形来说,角相等不能保证相似,必须再确定两图形的对应边对应成比例才能判定相似,注意相似成立的条件.【例6】如图,ABC ∆中,AB = AC = 5,BC = 6,点M 为BC 中点,MN ⊥AC 于点N ,则 MN =______.【答案】125. 【解析】连结AM .由AB = AC = 5,M 为BC 中点, 可知AM BC ⊥,3BM CM ==,由勾股定理可得:224AM AC CM =-=.由面积法,可得:AM MC MN AC ⋅=⋅,即得431255AM MC MN AC ⋅⨯===. 【总结】考查图形性质的综合应用,本题中也可用“子母三角形”通过相似解题.【例7】如图,在平行四边形ABCD 中,F 是BC 上的一点,直线DF 与AB 的延长线相交于点E ,BP // DF ,且与AD 相交于点P ,则图中有______对相似的三角形.【答案】6.【解析】////AB CD AD BC ,,结合BP // DF ,由相图1图2 11 1 1111 ABCD EFPABCNMABCDEF似三角形预备定理,知CDF ∆、BEF ∆、ABP ∆、AED ∆四三角形两两相似,即共有6对相似三角形.【总结】考查相似三角形的预备定理,由平行可证相似,同时考查相似三角形的传递性.【例8】如图,在直角梯形ABCD 中,AD // BC ,90ABC ∠=︒,AB = 8,AD = 3,BC = 4, 点P 为AB 边上一动点,若PAD ∆与PBC ∆是相似三角形,则满足条件的点P 的个数是( ). A .1个B .2个C .3个D .4个【答案】C【解析】与是相似三角形,根据相似三角形判定定理2,首先易得 90A B ∠=∠=︒,则只需要两三角形夹直角的两边对应成比例即可,分成两种情况讨论,即AD AP BP BC =或AD APBC BP=,可分别得到2AP =或6AP =或247AP =,即满足条件的P 点有3个,故选C . 【总结】考查相似三角形判定定理2的应用,注意进行分类讨论,要经过准确计算,不能直接分两种情况得出两种结果.【例9】如图,在Rt ABC ∆中,90ACB ∠=︒,BC = 3,AC = 4,AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为( )A .32B .76C .256D .2【答案】B【解析】根据勾股定理,可得225AB BC AC =+=,则有 1522BD AB ==,由90BDE ACB ∠=∠=︒,A ∠为公共角, 根据相似三角形判定定理1,可证ABC ∆∽EBD ∆,则有AB BD BE BC =,代入线段可求得256BE =,则76CE BE BC =-=. 【总结】考查相似三角形判定定理和性质的综合应用,先判定再应用性质.【例10】如图,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E ,连接DE ,F 为线 段DE 上一点,且AFE B ∠=∠. (1)求证:ADF ∆∽DEC ∆;(2)若AB = 8,AD =63,AF =43,求AE 的长.【答案】(1)略;(2)6ABCD PABCDE8 / 31AB CDEF【解析】(1)证明:四边形ABCD 是平行四边形,////AB CD AD BC ∴,.180ADF DEC B C ∴∠=∠∠+∠=︒,. 180AFE AFD AFE B ∠+∠=︒∠=∠,, AFD C ∴∠=∠,∴ADF ∆∽DEC ∆.(2)解:由(1)ADF ∆∽DEC ∆,∴AF AD CD DE=, 即43638DE=,解得:12DE =. AE BC ⊥,∴90EAD ∠=︒,根据勾股定理,即得:226AE DE AD =-=.【总结】考查相似三角形判定定理1,和相似三角形的相关性质的结合应用,先判定再应用性质,过程中注意对相关图形及性质的应用.【例11】如图,梯形ABCD 中,AD // BC ,AB = DC ,对角线AC 、BD 相交于点F ,点E 是 边BC 延长线上一点,且CDE ABD ∠=∠. (1)求证:四边形ACED 是平行四边形;(2)联结AE ,交BD 于点G ,求证:DG DFGB DB=. 【答案】略.【解析】证明:(1)AD // BC ,AB = DC ,GBAD CDA∴∠=∠.AB DC AD AD==,,ABD DCA∴∆≅∆.ACD ABD∴∠=∠.CDE ABD∠=∠,ACD CDE∴∠=∠.//AC DE∴.AD // BC,∴四边形ACED是平行四边形.(2)//AD BC,∴AD DFBC FB=.AD DFBC AD DF FB∴=++.四边形ACED是平行四边形,∴AD CE=,∴AD DFBC CE DF FB=++,即AD DFBE DB=.//AD BE,∴DG ADGB BE=,∴DG DFGB DB=.【总结】考查相似中有平行线的情况,即可直接利用图形中的“A”字型和“8”字型等基本图形进行等比例转化.【例12】如图,在ABC∆中,AB = AC,点D、E分别是边AC、AB的中点,DF⊥AC,DF 与CE相交于点F,AF的延长线与BD相交于点G.(1)求证:2AD DG BD=;(2)联结CG,求证:ECB DCG∠=∠.【答案】略【解析】证明:(1)1122AB AC AE AB AD AC===,,,AD AE∴=.AB CDEFG10 / 31BAD CAE ∠=∠, BAD CAE ∴∆≅∆, ABD ACE ∴∠=∠.AD CD DF AC =⊥,, AF CF ∴=. GAC ACE ∴∠=∠.ABD GAD ∴∠=∠. ADB GDA ∠=∠, ADG ∴∆∽BDA ∆.AD DGBD AD∴=,即证2AD DG BD =. (2)AD CD =,2AD DG BD =,2CD DG GB ∴=⋅. 即CD GB DG CD=. GDC BDC ∠=∠, GDC ∴∆∽CDB ∆. DBC DCG ∴∠=∠. AB AC =,同(1)易证ECB DBC ∠=∠,ECB DCG ∴∠=∠.【总结】本题综合性较强,一方面考查了等腰三角形的性质以及线段垂直平分线的性质,另一方面考查了相似三角形的判定及性质,解题时注意对条件认真分析以及灵活运用.【例13】在ABC ∆中,AB = 40,AC = 24,BC = 32,点D 是射线BC 上的一点(不与端点重合),联结AD ,如果ACD ∆与ABC ∆相似,求BD 的值.【答案】14或50或64.【解析】由AB = 40,AC = 24,BC = 32,三角形三边满足222AC BC AB +=,即ABC ∆为直 角三角形,其中90ACB ∠=︒,D 在射线BC 上,相似三角形对应关系不确定,可知存 在以下几种情形:(1)D 在线段BC 上,此时ADC ∆∽BAC ∆,则有AC DCBC AC=,可得18DC =,则321814BD BC DC =-=-=;(2)D 在线段BC 延长线上,ADC ∆∽BAC ∆时,同(1)可得50BD BC DC =+=; (3)D 在线段BC 延长线上,DAC ∆∽BAC ∆时,则有DAC ∆≌BAC ∆,264BD BC ==.【总结】相似三角形的存在性问题,题目未给明对应关系,一定要注意进行分类讨论,本题中的点在射线上则更需要注意在线段延长线上时的情况.【例14】正方形ABCD 的边长为1,M 、N 分别是BC 、CD 上的两个动点,且始终保持AM ⊥MN ,求当BM 为多少时,四边形ABCN 的面积最大,最大面积为多少?【答案】12BM =时四边形ABCN 有最大面积58. 【解析】由90B ∠=︒,则有90BAM AMB ∠+∠=︒,AM ⊥MN ,则90NMC AMB ∠+∠=︒,NMC BAM ∠=∠,由90B C ∠=∠=︒,可证ABM ∆∽MCN ∆.则AB BMMC CN =,设BM x =,则1MC x =-,2CN x x =-, 则有()()2211115122228ABCNS CN AB BC x x x ⎛⎫=+⋅=-++=--+ ⎪⎝⎭. 由此可知当12x =,即12BM =时,四边形ABCN 有面积最大值58.【总结】考查“一线三直角”得到相似的基本模型,综合二次函数的最值问题.【例15】如图,将边长为6 cm 的正方形ABCD 折叠,使点D 落在AB 边的中点E 处,折痕为FH ,点C 落在Q 处,EQ 与BC 交于点G ,则EBG ∆的周长为______cm .【答案】12.【解析】设DF x =,根据翻折的性质,则有EF x =, 6AF x =-,在Rt AEF ∆中,用勾股定理,则有222AE AF EF +=,即()22236x x +-=,解得154x =, 则94AF =,由90A ∠=︒,则有90AFE AEF ∠+∠=︒, 同时90FEG D ∠=∠=︒,则90AEF EBG ∠+∠=︒,ABCDE FGH QA BCDNM12 / 31K MNHG FEDC BA得:AFE BEG ∠=∠,由90A B ∠=∠=︒,可证AEF ∆∽BGE ∆.则AE AF EFBG BE GE==,即9153443BG GE ==,解得4BG =,5EG =,故12EBG C cm ∆=. 【总结】考查“一线三直角”得到相似的基本模型.【例16】如图,Rt ABC ∆中,90ACB ∠=︒,AC = 4 cm ,BC = 2 cm ,D 为BC 的中点,若动 点E 以1 cm /s 的速度从A 点出发,沿着A B A →→的方向运动,设点E 的运动时间为t 秒,联结DE ,当t 为何值时,BDE ∆是直角三角形?【答案】955t =或5t =或35t =或1155t =. 【解析】根据勾股定理,可得2225AB AC BC =+=,点E 沿 A B A →→运动时,B ∠大小固定不变,可能存在90DEB ∠=︒和 90EDB ∠=︒两种情形:(1)当90DEB ∠=︒时,由B B ∠=∠,90DEB C ∠=∠=︒,得DEB ∆∽ACB ∆,则有DB EBAB BC =,即1225EB =,得55EB =,此时存在两种情形,即955t =或1155t =; (2)当90EDB ∠=︒时,由B B ∠=∠,90EDB C ∠=∠=︒,得EDB ∆∽ACB ∆,则有EB DBAB BC =,即1225EB =,得5EB =,此时存在两种情形,即5t =或35t =. 【总结】本题主要考查动点的分类讨论问题,注意运动过程中的不变量.【例17】如图,ABC ∆中,4AB = 5AC ,AD 为ABC ∆的角平分线,点E 在BC 的延长线上, EF ⊥AD 于点F ,点G 在AF 上,FG = FD ,联结EG 交AC 于点H ,若点H 是AC 的中点,求AGFD的值.【答案】43. 【解析】延长AC 到M ,使AM AB =,连结DM ,过点M 作//MN AD 交GE 于点N ,交BE 于K .∵AD 为ABC ∆的角平分线, ∴点D 到AB 、AC 的距离相等. 则54ABD ACD S BD AB CD S AC ∆∆===.ABCDEAB AM BAD MAD AD AD =∠=∠=,,,BAD MAD∴∆≅∆,54DM BD DC∴==.//MN AD,4DC ACCK CM∴==.54DK DC DM∴==,即M DK∆是等腰三角形.EF AD FG FD⊥=,,DEG∴∆是等腰三角形.∵//MN AD,GDE DKM∴∠=∠.∵DK DM DE GE==,,KDM DEG∴∠=∠.//GE DM∴.∴四边形DMNG是平行四边形.2MN GD FD∴==,又H是AC中点,22AG AG AHFD MN HM∴==.∵12211342ACAHHM AC AC==+,∴43AGFD=.【总结】考查角平分线,等腰三角形,全等,相似,平行四边形知识的综合应用,难度大,主要在于添加正确的辅助线.1、相似三角形性质定理1相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.2、相似三角形性质定理2相似三角形周长的比等于相似比.模块二:相似三角形的性质知识精讲14 / 313、相似三角形性质定理3相似三角形的面积的比等于相似比的平方.【例18】如果两个相似三角形的面积之比是9 : 25,其中小三角形一边上的中线长是12 cm ,那么大三角形对应边上的中线长是______cm .【答案】20【解析】根据相似三角形面积比等于相似比平方,可知两三角形相似比3:5k =,两三角形对应中线长之比也等于3:5k =,即得大三角形对应边上中线长为312205cm ÷=.【总结】考查相似三角形的面积比和对应中线比与相似比的关系.【例19】在ABC ∆中,DE // BC ,且D 在AB 边上,E 在AC 边上,若:1:4ADE BCED S S ∆=,则:ADE ABC C C ∆∆=______,:AD DB =______.【答案】5:5,()51:4+【解析】:1:4ADE BCED S S ∆=,得:1:5ADE ABC S S ∆∆=,可得相应相似比1:55:5k ==,则:5:5ADE ABC C C k ∆∆==,:5:5AD AB k ==,()():5:5551:4AD DB =-=+.【总结】考查相似三角形的面积比和对应边长比和周长比与相似比的关系.【例20】如图,梯形ABCD 中,AD // BC ,90B ACD ∠=∠=︒,AB = 2,DC = 3,则ABC ∆ 与DCA ∆的面积比为( )A .2 : 3B .2 : 5C .4 : 9D .2:3【答案】C【解析】由AD // BC ,可得BCA CAD ∠=∠,结合 90B ACD ∠=∠=︒,可证ABC ∆∽DCA ∆,则有23AB k DC ==,则222439ABC DCA S k S ∆∆⎛⎫=== ⎪⎝⎭,故选C .【总结】考查相似三角形的面积比与相似比的关系.例题解析ABCDAB CDE 【例21】如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长 分别是3、4及x ,那么x 的值为( )A .只有1个B .可以有2个C .可以有3个D .有无数个【答案】B 【解析】由6834=,可知这两条边分别为对应边,相似比2k =,第一个直角三角形中第三 边长有两种情况,即226810+=或228627-=,由此得102x=或272x =,解得5x =或7x =,故选B .【总结】考虑相似三角形的相似比,一定要确立好对应关系.【例22】如图,D 、E 分别在ABC ∆的边AB 、AC 上,23AD AE DE AB AC BC ===,且ABC ∆与ADE ∆的周长之差为15 cm ,求ABC ∆与ADE ∆的周长.【答案】45ABC C cm ∆=,30ADE C cm ∆=. 【解析】23AD AE DE AB AC BC ===,可知ADE ∆∽ABC ∆,其相似比23k =,则23ADE ABC C k C ∆∆==,又15ABC ADE C C ∆∆-=,可得:45ABC C cm ∆=,30ADE C cm ∆=.【总结】考查相似三角形的判定和性质的结合应用.【例23】如图,在ABC ∆中,D 、E 分别是AB 、BC 上的点,且DE // AC ,若:1:4BDE CDE S S ∆∆=,则:BDE ACD S S ∆∆=______.【答案】1:20.【解析】由:1:4BDE CDE S S ∆∆=,即得:1:4BE CE =,由DE // AC ,即得:14BD BE AD CE ==,可得:14BCD ACD S BD S AD ∆∆==,则有120BDE ACD S S ∆∆=. 【总结】等高三角形面积比等于底边长之比,结合三角形的相似性质即可.AB CD E16 / 31MNDCBA【例24】如图,在ABC ∆中,90C ∠=︒,将ABC ∆沿直线MN 翻折后,顶点C 恰好落在AB边上的点D 处,已知MN // AB ,MC = 6,23NC =,那么四边形MABN 的面积是______. 【答案】183.【解析】连结CD ,即得MN 垂直平分CD ,由MN // AB , 即得M 是AC 的中点,CMN ∆∽CAB ∆,则221124CMN CAB S CM S AC ∆∆⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,由此可得:133362318322MABN CMN S S MC NC ∆==⨯⋅=⨯⨯=.【总结】考查翻折与相似性质的结合应用.【例25】如图,在平行四边形ABCD 中,AB = 6,AD = 9,BAD ∠的平分线交BC 于E ,交DC 的延长线与F ,BG AE ⊥于G ,42BG =,则EFC ∆的周长为______.【答案】8.【解析】由//AD BC ,得DAE AEB ∠=∠,由AE平分BAD ∠,得BAE DAE AEB ∠=∠=∠, 可得6AB BE ==,由BG AE ⊥,42BG =, 根据勾股定理可得222GE BE BG =-=,则有24AE GE ==,3EC BC BE =-=,由//AB CF ,得EAB ∆∽EFC ∆,由此即得623ABE EFC C BE C EC ∆∆===,由16ABE C AB BE EC ∆=++=,得8EFC C ∆=.【总结】考查相似三角形结合平行四边形特殊图形性质,构造“A ”“8”字型等相关基本图形的应用,本题中注意运用“角平分线与平行线相结合得到等腰”的基本模型.【例26】如图,在ABC ∆中,BE 平分ABC ∠交AC 于点E ,ABC DEFGABCDE过点E 作ED // BC 交AB 于点 D . (1)求证:AE BC BD AC =;(2)如果3ADE S ∆=,2BDE S ∆=,DE = 6,求BC 的长.【答案】(1)略;(2)10. 【解析】(1)证明://ED BCDE AEDEB EBC BC AC∴∠=∠=, DBE EBC ∠=∠ DEB DBE ∴∠=∠ DE BD ∴= BD AEBC AC∴=即证AE BC BD AC = (2)解:由3ADE S ∆=,2BDE S ∆=,即得32ADE BDE S AD BD S ∆∆==,则有35AD AB =,由ED // BC ,可得:35DE AD BC AB ==,代入求得10BC =. 【总结】考查相似三角形面积比与等高三角形面积比的结合应用以及“角平分线与平行线相结合得到等腰”的基本模型的应用.【例27】如图,直角三角形ABC 中,90ACB ∠=︒,AB = 10,BC = 6,在线段AB 上取一点 D ,作DF AB ⊥交AC 于点F ,现将ADF ∆沿DF 折叠,使点A 落在线段DB 上,对应点记为1A ,AD 的中点E 的对应点记为1E ,若11E FA ∆∽1E BF ∆,则AD =______.【答案】165. 【解析】由90ACB ∠=︒,AB = 10,BC = 6,根据勾股定理得 228AC AB BC =-=,由90C EDA ∠=∠=︒,A A ∠=∠,可证ADE ∆∽ACB ∆,则有AF AD DFAB AC BC ==,可设3DE a =,则45AD a AE a ==,,122DE AD a ==,则13EF a =,根据翻折性质,得111213A E AE a E F EF a ====,, 1106BE a =-,11E FA ∆∽1E BF ∆,则有11111E F E AE B EF =,即13210613a a a a=-,解得45a =,由此即得1645AD a ==. 【总结】考查翻折的性质与相似结合,可以把对应边之比转化为同一个三角形的边长之比.【例28】如图,在Rt ABC ∆中,90C ∠=︒,AB = 5,BC = 3,点D 、E 分别在BC 、AC 上,且BD = CE ,设点C 关于DE 的对称点为F ,若DF // AB ,则BD 的长为______.ABCD E F A 1E 118 / 31MFEDCBA【答案】1.【解析】延长DF 交AC 于M , 由勾股定理,可得224AC AB BC =-=,90DFE C DMC A ∠=∠=︒∠=∠,,EFM ∴∆∽DCM ∆∽BCA ∆.3345EF DC BC EF BC EM MC AC EM AB ∴=====,. 设BD x =,则有CE EF x ==,53EM x =,3DC x =-,83MC x =,即有33843x x -=,解得:1x =,即1BD =. 【总结】相似三角形的性质可将两个相似三角形对应边之比转化为一个三角形中对应边长之比,便于计算.【例29】如图,在Rt ABC ∆中,90ACB ∠=︒,AC = 8,BC = 6,CD AB ⊥于点D .点P 从 点D 出发,沿线段CD 向点C 运动,点Q 从点C 出发,沿线段CA 向点A 运动,两点 同时出发,速度都为每秒1个单位长度,当点P 运动到点C 时,两点都停止.设运动 时间为t 秒.(1)求线段CD 的长;(2)设CPQ ∆的面积为S ,求S 与t 之间的关系式,并确定运动过程中是否存在某一时 刻t ,使得:9:100CPQ ABC S S ∆∆=?若存在,求出t 的值;若不存在,请说明理由;(3)当t 为何值时,CPQ ∆为等腰三角形?【答案】(1)245;(2)2248525S t t =-+, 1.8t =或3t =时,:9:100CPQ ABC S S ∆∆=;(3)125t =或14455t =或2411t =. 【解析】(1)根据勾股定理,可得2210AB AC BC =+=, 由直角三角形面积法,则有CD AB AC BC ⋅=⋅,解得:245CD =;(2)过点P 作PH AC ⊥交AC 于H , 90PHC ACB ∠=∠=︒,CPH A ∠=∠, PHC ∴∆∽ACB ∆,PH PCAC AB∴=. ABCDPQH依题意可得CQ PD t ==,则245CP t =-, 代入即为:245810tPH -=, 解得:42449655525PH t t ⎛⎫=-=-+ ⎪⎝⎭.21149624822525525S QC PH t t t t ⎛⎫∴=⋅=-+=-+ ⎪⎝⎭,其中2405t ≤≤; 若存在某一时刻,使得:9:100CPQ ABC S S ∆∆=,则有224891685251002S t t =-+=⨯⨯⨯,整理得:2524270t t -+=,解得:12935t t ==,,均符合题意;(3)分类讨论:①CQ CP =,即245t t =-,解得:125t =; ②PQ CP =,根据等腰三角形的性质可得625QC CH CP ==,即得62455t t =-,解得:14455t =; ③CQ PQ =,同理②,可得52465t t =-, 解得:2411t =. 综上:当CPQ ∆为等腰三角形时,t 的值为125或14455或2411. 【总结】本题综合性较强,考查的知识点比较多,特别是由动点引起的等腰三角形的问题要注意分类讨论,解题方法比较多样,主要是抓住题目中的条件认真分析.20 / 31A B C【习题1】如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中ABC ∆ 相似的是( )A .B .C .D . 【难度】★ 【答案】B【解析】由已知ABC ∆,可得一钝角135ABC ∠=︒,夹这个钝角两边之比22AB BC =,三角形与ABC ∆相似,则必有一角135︒,且夹这个角两边长之比为22,只有B 选项满足. 【总结】相似三角形判定定理2可转化为一个三角形中的夹等角的两条边对应成比例.【习题2】如图,D 是ABC ∆的边AC 上一点,CBD ∠的平分线交AC 于点E ,AE = AB ,则长度为线段AD 、AC 长度比例中项的线段是______.【答案】AE 和AB .【解析】AE = AB ,得ABE AEB ∠=∠,AEB C EBC ∠=∠+∠, 即得ABD DBE C EBC ∠+∠=∠+∠,BE 平分CBD ∠,即为DBE EBC ∠=∠,由此可得ABD C ∠=∠,又A A ∠=∠,即证ABD ∆∽ACB ∆,则有AD ABAB AC=,又AE = AB ,即得. 【总结】考查相似三角形的判定和性质的综合应用,先判定相似再应用性质,注意题目中一个条件的多种用途.【习题3】如图,在ABC ∆中,D 、F 是AB 的三等分点,DE // FG // BC ,分别交AC 于E 、随堂检测ABCDEG .记ADE ∆、四边形DFGE 、四边形FBCG 的面积分别为1S 、2S 、3S ,则123::S S S =______.【答案】1:3:5.【解析】D 、F 是AB 的三等分点,即::1:2:3AD AF AB =, 由DE // FG // BC ,即可得222::1:2:3ADE AFG ABC S S S ∆∆∆=, 即()()112123::1:4:9S S S S S S +++=,得123::1:3:5S S S =. 【总结】考查相似三角形的面积比等于相似比的平方,再进行比例转化即可.【习题4】如图,D 是ABC ∆的边BC 上一点,已知AB = 4,AD = 2,DAC B ∠=∠,若ABD ∆的面积为a ,则ACD ∆的面积为______.【答案】13a .【解析】由DAC B ∠=∠,C C ∠=∠,可得:BAC ∆∽ADC ∆,其相似比422AB k AD ===,由此可得:24BAC ADC S k S ∆∆==,则有3ABD ACD S S ∆∆=,即得:3ACD aS ∆=.【总结】考查相似三角形的面积比等于相似比的平方,再进行比例转化即可.【习题5】如图,矩形ABCD 中,AB = 3,BC = 4,动点P 从A 点出发,按A B C →→的方向在AB 和BC 上移动,记P A = x ,点D 到直线P A 的距离为y ,则y 关于x 的函数图像ABCDA BCD E FG22 / 31xy xy xy xy OOOO3 4 5 3 4 5 3 4 5 3 45 MEDC BA大致是( )A .B .C .D .【答案】B【解析】由运动轨迹可知,动点从A B →的过程中,D 到直线P A 的距离即为AD ,是一条与x 轴平行的直线,D 错误;动点从B C →的过程中,162APD ABCD S S ∆==矩形,即得162xy =,由此可得12y x=,D 直线的距离P A 函数是一段双曲线,可知正确答案是B .【总结】动点问题,进行准确分段分解,化作一段线段上的运动情况即可.【习题6】如图,已知点D 是等腰直角三角形ABC 斜边BC 上的一点,BC = 3BD ,CE ⊥AD , 则AECE=______.【答案】12.【解析】过点D 作DM AC ⊥交AC 于点M , 则有//DM AB ,则CMD ∆为等腰直角三角形, 由CE AC ⊥,可得:ADM ∆∽ACE ∆.12AE AM AM BD CE DM CM CD ∴====. 【总结】考查相似三角形性质的应用,构造平行线即可得到相似.【习题7】在同一时刻,两根木竿在太阳光下的影子如图所示,其中木竿AB = 2 m ,它的影 子BC = 1.6 m ,木竿PQ 的影子有一部分落在了墙上,PM = 1.2 m ,MN = 0.8 m ,则木竿PQ 的长度为______m .【答案】2.3.A B CDPx yAB CPN MQHMNH G FED C BA【解析】如图有 1.2HN PM ==, 0.8PH MN ==,同一时刻影子与木杆长度所成比例相同,则有AB QHBC HN=,得: 1.5QH =,则 2.3PQ QH HP m =+=.【总结】影长问题转化为相似,同一时刻下相似比相同.【习题8】如图,点E 是矩形ABCD 的边BC 上一点,EF ⊥AE ,EF 分别交AC 、CD 于点M 、 F ,BG ⊥AC ,垂足为点G ,BG 交AE 于点H . (1)求证:ABE ∆∽ECF ∆;(2)找出与ABH ∆相似的三角形,并证明;(3)若E 是BC 的中点,BC = 2AB ,AB = 2,求EM 的长.【答案】(1)略;(2)ECM ∆;(3)223. 【解析】(1)证明:EF AE ⊥,90AEB FEC ∴∠+∠=︒.90ABC ∠=︒ 90AEB BAE ∴∠+∠=︒ BAE FEC ∴∠=∠90ABE ECF ∠=∠=︒ ∴ABE ∆∽ECF ∆(2)由(1)BAE FEC ∠=∠,又90ABG GBC GBC BCG ∠+∠=∠+∠=︒ABG ECM ∴∠=∠ ∴ABH ∆∽ECM ∆(3)作MN BC ⊥交BC 于点N , 则有//MN AB ,由BC = 2AB ,得2CN MN =,2BC AB BE CE ==,45AB BE AEB FEC ∴=∠=∠=︒,12EN MN CN ∴==,得1233EN EC ==,则2223EM EN ==. 【总结】考查“子母三角形”中相似的应用.【习题9】如图,在矩形ABCD 中,AB = 2,BC = 3,点E 、F 、G 、H 分别在矩形ABCD 的各边上,EF // AC // HG ,EH // BD // FG ,求四边形EFGH 的周长.【答案】213.【解析】由EF // AC // HG ,EH // BD // FG ,可知四边形EFGH 是平行四边形,且EH AHBD AD=,ABCDEFGH24 / 31HG DH AC AD =,即得:1EH HGBD AC+=,由四边形是矩形,根据勾股定理可得2213AC BD AB BC ==+=,即有113EH HG+=,由此可得:13EH HG +=,故()2213EFGH C EH HG =+=.【总结】考查图形中的“A ”字型等基本图形的叠合应用,可进行比例转化得到一些特定的等量关系即可进行计算.【习题10】如图,在ABC ∆中,AB = AC ,AD ⊥BC 于点D ,BC = 10 cm ,AD = 8 cm .点P 从点B 出发,在线段BC 上以每秒3 cm 的速度向点C 匀速运动,与此同时,垂直于AD 的直线m 从底边BC 出发,以每秒2 cm 的速度沿DA 方向匀速平移,分别交AB 、AC 、 AD 于E 、F 、H ,当点P 到达点C 时,点P 与直线m 同时停止运动,设运动时间为t 秒(t > 0).(1)当t = 2时,连接DE 、DF ,求证:四边形AEDF 为菱形;(2)在整个运动过程中,所形成的PEF ∆的面积存在最大值,当PEF ∆的面积最大时, 求线段BP 的长;(3)是否存在某一时刻t ,使PEF ∆为直角三角形?若存在,请求出此时刻t 的值;若不存在,请说明理由.【答案】(1)略;(2)6;(3)280183t =或4017t =.【解析】(1)证明:当2t =时,24DH t AH ===.AB AC AD BC =⊥,, BD CD ∴=. //EF BC ,EH FH ∴=,∴四边形AEDF 是平行四边形,∵AD EF ⊥,∴四边形AEDF 是菱形. (2)//EF BC ,EF AE AHBC AB AD∴==. 由题意,可得:2DH t =,则有82AH t =-,即得:82108EF t-=. 5102EF t ∴=-+1003t ⎛⎫<≤ ⎪⎝⎭.()22115551021021022222PEF S EF DH t t t t t ∆⎛⎫∴=⋅=-+⋅=-+=--+ ⎪⎝⎭. A BCDEFmH由此可知2t =时,PEF ∆的面积有最大值,此时36BP t ==; (3)①90EPF ∠=︒,分别通过E 、F 向BC 作高,易得两个三角形相似,即有5324521034t tt t t t -=--,解得:280183t =; ②90EFP ∠=︒,过点F 向BC 作高,则有281035t t =-,解得:4017t =; ③90PEF ∠=︒,过点E 向BC 作高, 则有2835t t =,此时不存在;综上所述,280183t =或4017t =时,PEF ∆是直角三角形.【总结】本题是一道考查动点问题的综合题,难度较大,第(2)问中求面积最大值时,要运用配方的思想,第(3)问的直角三角形问题要注意分类讨论,求解时通过作高即可转化为“一线三直角”的基本模型进行求解.26 / 31ABCDE【作业1】如图,在ABC ∆中,DE // BC ,12AD DB =,则下列结论正确的是( ) A .12AE AC =B .12DE BC =C .13ADE ABC ∆=∆的周长的周长D .13ADE ABC ∆=∆的面积的面积【答案】C【解析】12AD DB =,DE // BC ,可得两三角形相似,相似比13AD k AC ==,则其对应边、对应周长之比应为13,对应面积比为21139⎛⎫= ⎪⎝⎭,故选C .【总结】考查相似图形的性质,各个量之比与相似比的关系.【作业2】如图,在ABC ∆中,点D 和点E 分别在边AB 、AC 上,下列条件不能判定ABC ∆ ∽AED ∆的是( ) A .AED B ∠=∠ B .ADE C ∠=∠C .AD AC AE AB=D .AD AE AB AC=【答案】D【解析】根据相似三角形判定定理1和判定定理2,可知ABC 都正确,故选D . 【总结】考查相似三角形判定定理的应用,可将相似比转化为一个图形中对应边之比.【作业3】一副三角尺按如图所示的方式叠放,则AOB ∆与DOC ∆的面积之比课后作业A BCDEABCDO为____________.【答案】13.【解析】由90ABC BCD ∠=∠=︒,可得//AB DC ,则有AOB ∆∽COD ∆,由30D ∠=︒,可得3DC BC =,由AB BC =,可得:1333AB k BC ===,则有213AOB COD S k S ∆∆==. 【总结】考查特殊的直角三角形中的边角关系的转化.【作业4】如图,点D 、E 分别在ABC ∆两边AB 、AC 上,且AD = 31,DB = 29,AE = 30, EC = 32.若50A ∠=︒,则关系式“1ADE B ∠>∠;2AED C ∠=∠;3ADE C ∠>∠;4AED B ∠=∠”中正确的有( )A .1个B .2个C .3个D .4个【答案】A【解析】由AD = 31,DB = 29,可得60AB AD DB =+=,由AE = 30,EC = 32,可得62AC AE EC =+=,则有AE ADAB AC =,又A A ∠=∠, 即得ADE ∆∽ACB ∆,则有ADE C ∠=∠,AED B ∠=∠,可知②③错误,④正确,同时根据“大边对大角”,可知ADE AED ∠<∠,可知①错误,即正确的只有④,故选A .【总结】考查相似三角形的判定定理2和相关相似性质的结合应用,先判定再应用性质,结合“大边对大角”性质即可解决问题.【作业5】在ABC ∆中,P 是AB 上的动点(P 异于A 、B ),过点P 的一条直线截ABC ∆,使截得的三角形与ABC ∆相似,我们不妨称这种直线为过点P 的相似线.ABCDE。
沪教版 九年级数学 暑假同步讲义 第5讲 相似三角形的判定(二)提高讲义 (解析版)

ABCA 1B 1C 1相似三角形的判定是九年级数学上学期第一章第三节的内容,本讲主要讲解相似三角形判定定理3和直角三角形相似的判定定理,并进行了相似三角形判定的相关综合练习.重点是灵活运用相似三角形的各个判定定理,难点是相似三角形与分类讨论及函数思想的互相结合.1、相似三角形判定定理3如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.可简述为:三边对应成比例,两个三角形相似.如图,在ABC ∆与111A B C ∆中,如果111111AB BC CAA B B C C A ==,那么ABC ∆∽111A B C ∆.相似三角形的判定(二)内容分析知识结构模块一:相似三角形判定定理3知识精讲步同级年九2 / 22ABCDEABC D【例1】 ABC ∆的边长分别为a 、b 、c ,111A B C ∆的边长分别为a 、b 、c ,则ABC ∆与111A B C ∆(选填“一定”、“不一定”或“一定不”)相似.【难度】★★ 【答案】不一定.【解析】若a b c ==时,相似;若a 、b 、c 中有两个不等,那么它们就不相似. 【总结】本题考查相似三角形的判定定理3,同时穿插了分类讨论的思想.【例2】 如图,点D 为ABC ∆内一点,点E 为ABC ∆外一点,且满足AB BC ACAD DE AE ==.求证:ABD ∆∽ACE ∆.【答案】略.【解析】AB BC ACAD DE AE == ∴ABC ADE ∆∆∽. ∴BAC DAE ∠=∠, 即BAD DAC CAE DAC ∠+∠=∠+∠.∴BAD CAE ∠=∠.AB ACAD AE= ∴ABD ∆∽ACE ∆. 【总结】本题考查相似三角形的判定定理3和相似三角形的性质知识.【例3】 如图,在ABC ∆中,90ABC ∠=︒,30ACB ∠=︒,2AC =,23CD =,4AD =.求证:ABC ∆∽ACD ∆.【答案】略. 【解析】90ABC ∠=︒,30ACB ∠=︒,2AC =.∴112AB AC ==,∴在Rt ABC ∆中,3BC =.23CD =,4AD =, ∴12AB AC BC AC AD CD ===,∴ABC ∆∽ACD ∆. 【总结】本题考查相似三角形的判定定理3和直角三角形的勾股定理知识.例题解析ABCDEF【例4】 已知:如图,在t R ABC ∆中,90ACB ∠=︒,2AC =,4BC =,点D 在BC 边上,且CAD B ∠=∠. (1)求AD 的长;(2)取AD 、AB 的中点E 、F ,联结CE 、CF 、EF .求证:CEF ∆∽ADB ∆. 【答案】略. 【解析】(1)90ACB ∠=︒,CAD B ∠=∠,CAD CBA ∴∆∆∽ ∴CD AC AD AC CB AB==. ∴2AC CD CB =• ∴1CD =.∴在Rt ADC ∆中,AD(2)点E F 、分别是AD 、AB 的中点,∴12EF BD =. 在Rt ADC ∆、Rt ABC ∆中,12CE AD =,12CF AB =. ∴12CE CF EF AD AB BD ===,∴CEF ∆∽ADB ∆.【总结】本题考查相似三角形的判定定理3、直角三角形的性质和三角形中位线等知识.步同级年九4 / 22【例5】 如图,在梯形ABCD 中,AB // CD ,90A ∠=︒,2AB =,3BC =,1CD =,点E是AD 的中点.(1)求证:CDE ∆∽EAB ∆;(2)CDE ∆与CEB ∆有可能相似吗?若相似,请证明;若不相似,请说明理由. 【答案】略.【解析】(1)证明:过点C 作CF AB ⊥,垂足为F ,如图. 9090A CFB ∠=∠=,,//AD CF ∴.又//AB CD ,∴四边形AFCD 是平行四边形.又90A ∠=,∴平行四边形AFCD 是矩形. 1AF CD AD CF ∴===,,1BF ∴=.在Rt FBC ∆中,2222CF BC BF =-=,22AD ∴=. 点E 是AD 的中点 2ED EA ∴==.∴22DE CD AB AE ==又90D A ∠=∠=,∴CDE ∆∽EAB ∆.(本题还可用其它方法证明)(2)CDE ∆与CEB ∆相似.在Rt DCE ∆中,223CE DC DE =+=, 在Rt CBF ∆中,226BE AE AB =+=,3CE BE CBCD DE CE===, ∴CDE ∆∽CEB ∆. 【总结】本题考查了梯形及相似三角形的判定,着重考查学生对相似三角形的判定方法的理解及运用能力.本题实际上是“一线三直角”模型.模块二:直角三角形相似的判定定理ABCD EFABCDFG1、直角三角形相似的判定定理如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例,那么这两个直角三角形相似.可简述为:斜边和直角边对应成比例,两个直角三角形相似.如图,在Rt ABC ∆和111Rt A B C ∆中,如果190C C ∠=∠=︒,1111AB BCA B B C =,那么ABC ∆∽111A B C ∆.【例6】 如图,在ABC ∆中,CD AB ⊥于D ,DF AC ⊥于F ,DG BC ⊥于G .求证:CF CA CG CB =.【答案】略. 【解析】证明:CD AB ⊥,DF AC ⊥,∴90ADC CFD ∠=∠=.又DCF DCA ∠=∠, ∴DCF ACD ∆∆∽. ∴DC CF AC DC=,即2DC CA CF =•.同理可得:2DC CG CB =•, ∴CF CA CG CB =. 【总结】本题考查了直角三角形相似的判定方法,同时考查了相似三角形的性质等知识.【例7】 已知直角三角形斜边上的高为12,并且斜边上的高把斜边分成3:4两段,则 斜边上的中线长是.【答案】73.知识精讲例题解析ABC A 1B 1C 1A BCDEFA BCDEFM【解析】解:如右图,在Rt ABC ∆中,90ACB ∠=, CD AB ⊥于点D ,AE EB =.设3AD x =,4BD x =,12CD =.易证Rt ADC Rt CDB ∆∆∽,得DC BDAD DC=,得2DC AD DB =•,所以21234x x =•解得x =7AB x ==,而12CE AB =,所以CE = 【总结】本题考查了直角三角形相似的判定方法,同时考查了直角三角形斜边上的中线等相关知识.【例8】 如图,直角梯形ABCD 中,90BCD ∠=︒,AD // BC ,BC CD =,E 为梯形内 一点,且90BEC ∠=︒.将BEC ∆绕点C 旋转90°使BC 与DC 重合,得到DCF ∆,连接 EF 交CD 于点M .已知5BC =,3CF =,求:DM MC 的值.【答案】43.【解析】解:由旋转的性质得:BEC DFC ∆≅∆, 且90BCD ECF ∠=∠=.903BEC ECF EC FC ∴∠=∠===,,5BC CD ==.∴180ECF DFC ∠+∠=, ∴//EC DF .∴DM DFMC EC =.在Rt DCF ∆中,4DF =.∴43DM MC =. 【总结】本题考查了旋转的性质,三角形一边的平行线等相关知识.【例9】 如图,在ABC ∆中,CD AB ⊥于D ,DE AC ⊥于E ,DF BC ⊥于F ,求证:CEF ∆∽CBA ∆.【答案】略. 【解析】证明:CD AB ⊥,DE AC ⊥,∴90ADC CED ∠=∠=.又DCE DCA ∠=∠, ∴DCE ACD ∆∆∽. ∴DC CF AC DC=,即2DC CA CE =•.同理,可得:2DC CF CB =•.A BCD EF∴CA CE CF CB •=•, 即CF CEAC CB=.又FCE BCA ∠=∠, ∴CEF CBA ∆∆∽.【总结】本题考查了三角形相似的判定方法、相似三角形的性质等知识.【例10】 在Rt ABC ∆中,90ACB ∠=︒,CD AB ⊥于点D ,E 是AC 边上的一个动点(不与A 、C 重合),CF BE ⊥于点F ,连接DF . (1)求证:2CB BF BE =; (2)求证:BF AE FD BA =.【答案】略. 【解析】证明:(1)90ACB ∠=,CF BE ⊥,∴90ACB CFB ∠=∠=.又CBF CBE ∠=∠,∴CBF EBC ∆∆∽. ∴CB BEBF CB=,∴2CB BF BE =•.(2)90ACB ∠=,CD BA ⊥,∴90ACB CDB ∠=∠=.又CBD CBA ∠=∠,∴CBD ABC ∆∆∽. ∴CB ABBD CB=,即2CB BD BA =•. ∴BF BE BD BA •=•, ∴FB BD BA BE=又ABE FBD ∠=∠,∴FBD ABE ∆∆∽. ∴FB FDBA AE=.∴BF AE FD BA •=•.【总结】本题考查了三角形相似的判定方法、相似三角形的性质等知识.步同级年九8 / 22【例11】 求证:如果一个三角形的两边和第三边的中线与另一个三角形的对应线段成比例,那么这两个三角形相似.【答案】略.【解析】已知:如图,AD 、11A D 分别是ABC ∆、111A B C ∆边BC 、11B C 上的中线,且111111AC AB ADAC A B A D ==.求证:ABC ∆∽111A B C ∆. 证明:分别延长AD 、11A D 到点1E E 、. 使得1111DE ADD E A D ==,. ∴111122AE AD A E A D ==,.AD 、11A D 分别是ABC ∆、111A BC ∆边BC 、11B C 上的中线,∴1111BD DC B D D C ==,.111111ADB ADC A D B A D C ∠=∠∠=∠, , ∴ADB EDC ∆≅∆,111111A D BE D C ∆≅∆ ∴1111BAD E B A D E ∠=∠∠=∠,.111111AC AB AD AC A B A D ==,∴111111AC AB AEAC A B A E ==. ∴111AEC A E C ∆∆∽,∴1111E E CAD C A D ∠=∠∠=∠,∴111BAD B A D ∠=∠ ,∴111BAC B AC ∠=∠.又1111AB ACA B AC =, ∴111ABC A B C ∆∆∽. 【总结】本题考查了三角形相似的判定方法,并且考查学生通过倍长中线来转化边角的方法.ABCD EF【例12】 如图,在Rt BDC ∆中,点E 在CD 上,DF BC ⊥于F ,DG BE ⊥于G .求证:FG BC CE BG =.【答案】略.【解析】证明:联结GF .90BDC ∠=,DF BC ⊥, ∴90BDC DFB ∠=∠=.又CBD FBD ∠=∠, ∴DBF CBD ∆∆∽. ∴DB BF BC DB=, ∴2DB BF BC =•.90EDB ∠=,GD BE ⊥, ∴90DGB EDB ∠=∠=.又EBD GBD ∠=∠, ∴GBD DBE ∆∆∽. ∴DB EBBG DB=, ∴2DB BG BE =•. ∴BF BC BG BE •=•, 即FB BGBE BC=.又GBF EBC ∠=∠, ∴GBF CBE ∆∆∽.∴GB FG BC CE=, ∴FG BC CE BG •=•. 【总结】本题考查了三角形相似的判定方法、相似三角形的性质等知识,综合性较强,需要通过多次相似证的结论成立.【例13】 如图,90CAB ∠=︒,AD CB ⊥,ACE ∆、ABF ∆是正三角形.求证:DE DF ⊥.【答案】略. 【解析】证明:ACE ∆、ABF ∆是正三角形,∴AC CE AB AF ==,,6060FAB ACE ∠=∠=,.AD BC ⊥, ∴90BDA ADC ∠=∠=. ∴90CAD ACD ∠+∠=.90BAC ∠=, ∴90BAD DAC ∠+∠=. BAD DCA ∴∠=∠.∴DBA DAC ∆∆∽. ∴CD AC AD AB =. ∴CD ECAD AF=.FAB BAD DCA ACE ∠+∠=∠+∠, ∴FAD DCE ∠=∠.∴FAD ECD ∆∆∽. ∴ADF EDC ∠=∠.90ADE EDC ∠+∠=, ∴90ADF EDA ∠+∠=. ∴DE DF ⊥.BCD EFG步同级年九10 / 22AB CD EFGH1 23【总结】本题考查了三角形相似的判定方法、等边三角形的性质等知识.1、相似三角形判定定理1:两角对应相等,两个三角形相似.2、相似三角形判定定理2:两边对应成比例且夹角相等,两个三角形相似.3、相似三角形判定定理3:三边对应成比例,两个三角形相似.4、直角三角形相似的判定定理:斜边和直角边对应成比例,两个直角三角形相似.【例14】 在ABC ∆中,12AB =,15AC =,D 为AB 上一点,3ABBD=,在AC 上取一点E ,得到ADE ∆,若ADE ∆与ABC ∆相似,则AE =.【答案】10或325.【解析】若ADE ∆与ABC ∆相似,则分两种情况:ABC ADE ∆∆∽或ABC AED ∆∆∽,得AD AE AB AC =或AD AEAC AB =,即可得解. 【总结】灵活运用相似三角形的性质定理是解本题的重点,注意分类讨论.【例15】 如图,四边形ABDC 、CDFE 、EFGH 是三个正方形,则123∠+∠+∠的值为多少?【答案】90.【解析】解:设正方形ABDC 、CDFE 、 EFHG 的边长为1.则2AD =,5AF =,1DF =,2HD =,10AH =. ∴2AD DH AHDF AD AF===, ∴ADH FDA ∆∆∽. ∴3DAF ∠=∠. 四边形ABDC 是正方形, ∴AB BD =. ∴145∠=.又21DAF ∠+∠=∠, ∴231∠+∠=∠. ∴12390∠+∠+∠=.【总结】灵活运用相似三角形的判定定理来转化角度是解本题的关键.模块三:相似三角形的判定综合知识精讲例题解析ABCDEAB CDEN M【例16】 如图,正方形ABCD 的边长为2,AE EB =,1MN =,线段MN 的两端在CB 、CD 上滑动,当CM 为何值时,AED ∆与以M 、N 、C 为顶点的三角形相似.【答案】当CM 525时,ADE ∆与以 M 、N 、C 为顶点的三角形相似. 【解析】解:四边形ABDC 是正方形, ∴2AB AD ==. 又AE EB =, ∴1AE =.在Rt CMN ∆中,222MN CM CN =+. ① 当5CM = 时,25CN ,∴5AE AD CM CN = ∴ADE CNM ∆∆∽;② 当25CM =时,5CN =,∴5AE AD CN CM = ∴ADE CMN ∆∆∽. 【总结】本题考查了相似三角形的判定及正方形的性质相关知识点.【例17】如图,AB AC =,2AC AD AE =,求证:BC 平分DBE ∠.【答案】略. 【解析】证明:AB AC =,2AC AD AE =•,∴2AB ADAE =•, 即AB AEAD AB=.又A A ∠=∠, ∴ABD AEB ∆∆∽.∴ABD E ∠=∠. 又AB AC =, ∴ABD DBC ACB ∠+∠=∠.又CBE E ACB ∠+∠=∠, ∴CBD CBE ∠=∠.即BC 平分DBE ∠.【总结】本题考查了相似三角形的判定及三角形外角的性质.【例18】如图,在ABC ∆中,M 在AB 上,且8MB =,12AB =,16AC =,在AC 上步同级年九12 / 22AD求作一点N ,使AMN ∆与原三角形相似,并求AN 的长.【答案】3AN =或163.【解析】解:如右图,要使AMN ∆与原三角形相似,有两种情况:128AB BM ==,,∴4AM =.① 当//MN BC 时,AMN ABC ∆∆∽. ∴AM AN AB AC =,即41216AN =,∴163AN =. ② 当MN 与BC 不平行时,ANM ABC ∆∆∽. ∴AM AN AC AB =,即41612AN=,∴3AN =.∴3AN =或163. 【总结】灵活运用相似三角形的性质定理是解本题的重点.【例19】如图,EM AM ⊥,CE DE =.求证:2ED DM AD CD =.【答案】略.【解析】证明:过点E 作EH CD ⊥于点H ,得90EHD ∠=.EC ED =,EHCD ⊥,∴12DH CD =.EM AM ⊥,∴90M ∠=. ∴EHD M ∠=∠. 又EDH MDA ∠=∠, ∴EHD AMD ∆∆∽. ∴DM AD DH ED=, 即DM ED DA HD •=•.∴12DM ED DA CD •=•,即2ED DM DA CD •=•.【总结】本题考查了相似三角形的判定及等腰三角形的性质等相关知识.【例20】如图,在ABC ∆和DEF ∆中,90A D ∠=∠=︒,3AB DE ==,24AC DF ==.(1)判断这两个三角形是否相似,并说明为什么;(2)能否分别过点A 、D 在这两个三角形中各作一条辅助线,使ABC ∆分割成的两个AB CDEF 三角形与DEF ∆分割成的两个三角形分别对应相似?证明你的结论.【答案】(1)不相似,一组角相等,但夹它的两边不对应成比例,故不相似;(2)能,理由略.【解析】(2)题分割如下:作BAM E ∠=∠交BC 于点M ,作EDN B ∠=∠交EF 于点N ,可证明BAM DEN ∆∆∽,再证明另一对也相似即可.【总结】本题考查了相似三角形的判定知识.【例21】 如图,在ABC ∆中,3AB AC ==,2BC =,点D 、E 、F 分别在AC 、AB 、BC边上,BEF ∆沿着直线EF 翻折后与DEF ∆重合,设CD x =,BF y =.试问DFC ∆是否有可能与ABC ∆相似,如有可能,求出CD 的长;如不可能,说明理由.【答案】DFC ∆有可能与ABC ∆相似,此时65CD =或23.【解析】解:翻折后,BF DF =.当DFC ABC ∆∆∽时,DFC C B ∠=∠=∠. BF DF CD x ∴===,2CF x =-. CD CF CA CB ∴=,即232x x -=. 65x ∴=; 当DFC ACB ∆∆∽时,FDC C B ∠=∠=∠,1BF DF CF ∴===.CD CF CB CA ∴=,即213x =. 23x ∴=. ∴65CD =或23.【总结】本题考查了相似三角形的判定、翻折变换(折叠问题)等的相关知识. 【例22】 如图,ABC ∆是等边三角形,D 是AC 上的一点,BD 的垂直平分线交AB 于E ,交BC 于F .(1)当点D 在边AC 上移动时,DEF ∆中哪一个角的大小始终保持不变?并求出它的度数;(2)当点D 在边AC 上移动时,ADE ∆与哪一个三角形始终相似?并写出证明过程.又AB CDEF 问:当点D移动到什么位置时,这两个三角形的相似比为1?(3)若等边三角形ABC的边长为6,2AD=,试求:BE BF的值.【答案】(1)EDF∠始终不变,且等于60;(2)ADE CFD∆∆∽.证明略;当点D移动到AC中点处时,这两个三角形的相似比为1;(3)45BEBF=.【解析】(1)翻折前后对应角相等;(2)相似比为1,说明ADE CFD∆≅∆,得DE DF=.又DB EF⊥,所以DB垂直平分EF,得BD平分ABC∠,则ABC∆是等边三角形,进而得出结论;(3)45AEDCFDCBE DEBF DF C∆∆===.【总结】本题考查了相似三角形的判定、翻折变换(折叠问题)、相似三角形的性质等的相关知识.ABC DEF ABCDE【习题1】 在ABC ∆中,点G 为重心,若BC 边上的高为6,求点G 到BC 的距离. 【答案】2.【解析】解:如图,联结AG 并延长交BC 于点D ,分别作GE BC ⊥、 AF BC ⊥于点E 、F .由题知,6AF =.点G 为重心, ∴13DG DA =. 又//GE AF , ∴GE DGAF DA=. ∴2GE =. 【总结】本题考查了重心的知识,构造相似形来解答问题.【习题2】 如图,在ABC ∆中,90ACB ∠=︒,CD AB ⊥于D ,E 为AC 上一点,CF BE ⊥ 于F ,联结DF .求证:BD DFBE AE=. 【答案】略. 【解析】证明:90ACB ∠=,CF BE ⊥, ∴90ACB CFB ∠=∠=.又CBF CBE ∠=∠, ∴CBF EBC ∆∆∽. ∴CB BE BF CB=,即2CB BF BE =•. 同理,得:2CB BD BA =•. ∴BF BE BD BA •=•, ∴FB BDBA BE=. 又ABE FBD ∠=∠, ∴FBD ABE ∆∆∽. ∴BD FDBE AE=. 【总结】本题考查了三角形相似的判定方法、相似三角形的性质等知识.【习题3】 已知梯形ABCD 中,AB // CD ,90B ∠=︒,3AB =,6CD =,12BC =,点E在BC 边上自B 点向C 点移动,求使得ABE ∆与ECD ∆相似的BE 的值.【答案】4或632±.【解析】解:由题知:90B C ∠=∠=. ABE ∆与ECD ∆相似,分两种情况:设BE x =.(1)ABE DCE ∆∆∽,得:AB BEDC CE=, 即3612x x=-,解得4x =;(2)ABE ECD ∆∆∽,得:AB BEEC DC=, 随堂检测ABC DEOAB CPQ 即3126xx=-,得212180x x-+=,解得6x=±综上:BE=4或6±【总结】本题考查了相似三角形的性质,着重考查学生分类讨论思想的应用.【习题4】如图,梯形ABCD中,AD//BC,AC与BD相交于点O,过点B作BE//CD交CA的延长线于点E,求证:2OC OA OE=.【答案】略.【解析】//AD CB,∴CO BOOA OD=.//BE CD,∴CO DOOE OB=.∴CO OAOE OC=,∴2OC OA OE=•.【总结】本题考查三角形一边的平行线定理的应用.【习题5】如图,在ABC∆中,90C∠=︒,8BC cm=,6AC cm=,点P从B出发,沿BC方向以2cm/s的速度移动到C点,点Q从C出发,沿CA方向以1cm/s的速度移动到A点.若点P、Q分别同时从B、C出发,经过多少时间CPQ∆与CBA∆相似?【答案】125t=或3211时,CPQ∆与CBA∆相似.【解析】设经过t秒CPQ∆与CBA∆相似,则2BP t=,CQ t=,∴82CP t=-.要使CPQ∆与CBA∆相似,有两种情况:①当CPQ CBA∆∆∽,∴CP CQCB CA=,即8286t t-=,∴125t=;ABCDEO②当CPQ CAB ∆∆∽,∴CP CQCA CB=, 即8268t t -=。
沪教版(上海)数学九年级第一学期2解直角三角形课件

的红地毯问题.(结果保留整数)
解:
l 2 2 cot 36
2米2 2.754. Nhomakorabea536
5.
答:至少要买宽度一定的红地毯长5米. 如果计算结果是5.10米,实际应该买多少米呢?
6米
再见
例题2:在△ABC中,AB= 6 2 ,BC=8,∠B=45°,
求边AC的长度.
一定要有将特殊锐角化归直 角三角形的解题思想.
3、思考:在一般的三角形中,能否由适当的已知元素 求出未知的元素呢?
可以用解直角三角形的知识解决一般三角形中的计 算问题. 就是要把握好转化的技能——通过添加辅助线构建 直角三角形来解决问题.
a、b、c、∠A、∠B这五个元素
间有哪些等量关系呢?
锐角之间的关系:
B
三边之间的关系: c
a
边角之间的关系:
A bC
Rt△ABC中,∠C=900,
B
(1)两锐角互余 : ∠A+∠B=90°
c
a
(2)三边满足勾股定理:
a2+b2=c2
A
b
C
(3)边与角关系:
sinA=cosB= a
c
tanA=cotB= a
假设某一同学现在站在操场上任意一位置C处, 用皮尺测出C点到旗杆底B的距离BC=10米;在C点用 测角仪(测出看旗杆顶A的倾斜角 ∠C=30度 。你能根 据以上数据求出旗杆AB的高度吗?
A
A
画出示意图
30°
C
10米
B
30°
C
30
B
(1)在三角形中共有几个元素?
(2)在Rt△ABC中,∠C=900,
通过本节课的学习,你有哪些收获?我们一起分享吧!
沪教版 九年级数学 暑假同步讲义 第7讲 相似三角形综合 (解析版)

相似三角形综合内容分析相似三角形是初中数学中的重点,也是难点.相当多的知识点可以与相似三角形综合起来考察.本讲将从以下几个方面学习相似三角形的应用,旨在灵活运用相似三角形的判定和性质解决问题.知识结构步同级年九2 / 23G1、平行线与相似三角形利用平行线构造的相似主要有两个基本的模型,即:“A ”字型和“X ”字型.【例1】 过ABC ∆的顶点C 任作一直线,与边AB 及中线AD 分别交于点F 、E .求证:2AE AFED FB = . 【答案】略.【解析】过点D 作//DG AB 交CF 于点G .//DG AB ∴AE AF ED GD =,DG CDBF CB =;AD 是中线, ∴2BC CD =, ∴12DG BF =;∴2AE AF ED BF=. 【总结】题考查三角形一边的平行线知识,要学会构造平行基本模型.【例2】 如图,已知ABC ∆中,AD 、BE 相交于G ,:3:1BD DC =,:1:2AG GD =.模块一:平行线与相似三角形知识精讲例题解析BCDE F求:BG GE的值.【答案】11.【解析】点G作//GM BC交AC于点M.//GM BC∴AG GMAD CD=,EG GMEB CB=;:1:2AG GD=,∴13AG GMAD CD==,:3:1BD DC=,∴14DCBC=,∴112GMBC=,∴112GEEB=,∴:BG GE的值为11.【总结】本题考查了三角形一边的平行线知识,要学会构造平行基本模型.【例3】如图,在ABC∆中,点D在线段BC上,75BAD∠=︒,30CAD∠=︒,AD = 2,BD = 2DC,求AC的长.【答案】3.【解析】过点D作//DM AB交AC于点M.//DM AB,∴75BAD ADM∠=∠=;又180ADM AMD DAM∠+∠+∠=,30CAD∠=∴75AMD∠=,∴AMD ADM∠=∠,∴2AD AM==.//DM AB,∴AM BDAC BC=.又2BD DC=,∴23BD AMBC AC==.∴3AC=.【总结】本题考查了三角形一边的平行线及等腰三角形的相关知识.【例4】已知:P为ABC∆的中位线MN上任意一点,BP、CP的延长线分别交AC、AB于点D和点E.求证:1AD AEDC EB+=.步同级年九4 / 23【答案】略.【解析】过点A 作//GH BC 分别交CE 、BD 的延长线 于点G 、H .MN 是中位线,//.AM MB AN NC MN BC ∴==,,////GH BC MN ∴. ∴AM GP MB PC= GP PC ∴=//GH BC ∴GH GPBC PC=GH BC ∴=;//GH BC ∴AD AH AE AGDC BC EB BC==,∴1AD AEDC EB+= . 【总结】本题考查了平行线分线段成比例定理、三角形一边的平行线、三角形中位线的相关知识.模块二:角平分线与相似三角形知识精讲1、角平分线与相似三角形角平分线类的相似模型如下:分为“内角平分线”和“外角平分线”两种类型,虚线部分为辅助线的作法.【例5】如图,AD 是ABC ∆的内角平分线.求证:AB BDAC DC=. 【答案】略.【解析】过点C 作//CM AB 交AD 的延长线于点M . //CM AB ∴AB BD CM DC=,BAD M ∠=∠ AD 是角平分线∴BAD DAC ∠=∠; ∴M DAC ∠=∠∴AC CM = ∴AB BDAC DC=. 【总结】本题考查了三角形一边的平行线、角平分线及等腰三角形的相关知识.【例6】如图,AD 是ABC ∆的外角平分线.求证:AB BDAC CD=. 【答案】略.【解析】过点B 作//BM AC 交DA 的延长线于点M .//BM AC , ∴AC CDBM DB=,DAC M ∠=∠ 例题解析ACDMAMAABC DEFGAD 是外角平分线, ∴MAD CAD ∠=∠;∴M MAD ∠=∠, 又MAB MAD ∠=∠,∴M MAB ∠=∠.∴AB BM =.∴AB BDAC DC=. 【总结】本题考查了三角形一边的平行线、角平分线及等腰三角形的相关知识.【例7】在ABC ∆中,120BAC ∠=︒,AD 平分BAC ∠交BC 于点D .求证:111AD AB AC=+. 【答案】略.【解析】过点C 作//CM AD 交BA 于点M .//CM AD ,∴AB ADBM CM=,DAC ACM BAD M ∠=∠∠=∠, AD 平分BAC ∠,120BAC ∠=. ∴60BAD CAD ∠=∠=;∴60M ACM ∠=∠= ,ACM ∴∆是等边三角形.∴AC CM AM ==.∴AB AD AB AM MC =+即AB ADAB AC AC=+.∴111AD AB AC=+. 【总结】本题考查了三角形一边的平行线、角平分线及等边三角形的相关知识.【例8】如图,在ABC ∆中,90CAB ∠=︒,CFG B ∠=∠过点C 作CE // AB ,交CAB ∠的平分线AD 于E .(1)不添加字母,找出图中所有的相似三角形,并证明;(2)求证:FC ADCG ED =. 【答案】略.【解析】 (1)①ADB EDC ∆∆∽、②CAB GCF ∆∆∽.DAB CEI证明①: //CE AB ∴ADB EDC ∆∆∽证明②://CE AB 180CAB ACE ∴∠+∠=,90CAB ∠=,90ACE ∴∠=;CAB ACE ∴∠=∠CFG B ∠=∠ ∴CAB GCF ∆∆∽(2)由CABGCF ∆∆∽得FC ABCG AC=ADB EDC ∆∆∽ ∴AB ADEC DE=//CE AB ,EAB CED ∴∠=∠,CAE EAB ∠=∠, ;CAE E ∴∠=∠,CA CE ∴= ∴AB AD AC DE = ∴ FC ADCG DE=. 【总结】本题考查相似三角形的判定和性质等知识.【例9】如图,ABC ∆中,AI 、BI 分别平分BAC ∠、ABC ∠,CE 是ABC ∆的外角ACD ∠的平分线,交BI 延长线于E ,连接CI .(1)ABC ∆变化时,设2BAC α∠=.若用α表示BIC ∠和E ∠,那么BIC ∠=______,E ∠=______;(2)若AB = 1,且ABC ∆与ICE ∆相似,求AC 长. 【答案】(1)90α+,α;(2)略. 【解析】(1)180BAC ABC ACB ∠+∠+∠=,∴1801802ABC ACB BAC α∠+∠=-∠=-.AI 、BI 分别平分BAC ∠、ABC ∠,步同级年九8 / 23BACDABCD 图1图2∴ 12IBC ABC ∠=∠,CI 平分ACB ∠.∴ 12ICB ACB ∠=∠.180IBC ICB BIC ∠+∠+∠=()()1180180902BIC IBC ICB ABC ACB α∴∠=-∠+∠=-∠+∠=+. CE 是ABC ∆的外角ACD ∠的平分线, ∴ 12ACE ACD ∠=∠.()1902ICE ICA ACE ACD ACB ∴∠=∠+∠=∠+∠=. 90BIC ICE E α∠=∠+∠=+,E α∴∠= .(2)ABC ∆与ICE ∆相似,90ICE ∠=, ABC ∴∆是直角三角形时,分三种情况:① 当90ABC ∠=时,E α∠=, 2BAC α∠=, E BAC ∴∠≠∠ .E BCA α∴∠=∠=. 90BAC BCA ∠+∠=, 30α∴=. ∴ 22AC AB ==;② 当90BCA ∠=时,E α∠=, 2BAC α∠=, E BAC ∴∠≠∠ .E ABC α∴∠=∠=,90BAC ABC ∠+∠=, 30α∴=, ∴ 1122AC AB ==; ③ 当90BAC ∠=时, 2BAC α∠=, 45α∴=. ∴ 1AC AB ==;综上所述,1122AC =或或.【总结】本题考查相似三角形的性质及其两三角形相似分类讨论,还考查了三角形角平分线的知识.1、a 2 = b·c 与相似三角形 常见及扩展模型如下:模块三:a 2 = b·c 与相似三角形知识精讲AB CDEH由图1可证:2AB BD BC=;由图2可证:2AB BD BC=,2AD BD DC=,2AC CD CB=.【例10】如图,Rt ABC∆中,90BAC∠=︒,AD BC⊥于点D.求证:2AD BD DC=.【答案】略.【解析】AD BC⊥,∴90ADB ADC∠=∠=.∴90BAD B∠+∠=.90BAC∠=,∴90C B∠+∠=,∴BAD C∠=∠.∴ABD CAD∆∆∽,∴AD BDCD AD=.∴2AD BD CD=•.【总结】本题考查相似三角形的性质及判定等知识.【例11】如图,已知等腰三角形ABC中,AB = AC,高AD,BE相交于点H.求证:24DH DA BC=.【答案】略【解析】AD、BE是高,∴90ADB BEC∠=∠=.∴90HBD C∠+∠=,90CAH C∠+∠=.∴HBD CAH∠=∠,∴HBD CAD∆∆∽.∴HD BDCD AD=即DH AD BD CD=AB AC AD BC=⊥,,∴12BD DC BC==.∴BAD C∠=∠.例题解析AB CDA BCDEF∴214DH AD BC=,∴24DH AD BC=.【总结】本题考查“双高”模型相似的知识.【例12】如图,在直角梯形ABCD中,AB // CD,AB⊥BC,对角线AC⊥BD,垂足为E,AD = BD,过E的直线EF // AB交AD于点F.(1)AF = BE;(2)AF2 = AE·EC.【答案】略.【解析】(1)//EF AB,AF不平行EB,∴四边形FABE是梯形.又AD BD=,∴DAB DBA∠=∠.∴四边形FABE是等腰梯形,∴AF BE=;(2)90AEB CEB∠=∠=,∴90EBA EAB∠+∠=,90ECB EAB∠+∠=.∴EBA ECB∠=∠.∴EBA ECB∆∆∽.∴EB EAEC EB=.∴2EB EA EC=•,∴2AF EA EC=•.【总结】本题考查等腰梯形及相似三角形的判定及性质.【例13】如图,在ABC∆中,AD平分BAC∠,AD的垂直平分线交AB于点E,交AD于点H,交AC于点G,交BC的延长线于点F.求证:2DF CF BF=.【答案】略.【解析】联结AF点F在AD的垂直平分线上,∴AF FD=,FAD ADF∠=∠.FAD FAC DAC∠=∠+∠,ADF BAD B∠=∠+∠∴FAC DAC BAD B∠+∠=∠+∠.又AD平分BAC∠,∴BAD DAC∠=∠,∴FAC B∠=∠.又AFC AFB∠=∠,∴EBA ECB∆∆∽,∴AF FCFB AF=.∴2AF CF BF=•,∴2DF CF BF=•.AB CDEFGHA BCDEFGH TH【总结】本题考查线段垂直平分线、外角定理及相似三角形的判定及性质知识.1、内接矩形与相似三角形 相关模型:常用结论:AT DEAH BC=.【例14】如图,ABC ∆中,3AC =,4BC =,90C ∠=︒,四边形DEFG 为正方形,其中D 、 E 在边AC 、BC 上,F 、G 在AB 上,求正方形DEFG 的边长.【答案】6037. 【解析】设正方形DEFG 的边长为a ,过点C作CH AB ⊥交AB 于点H ,易知:////DG CH DE AB ,DG AD CH AC ∴=,DE CD AB AC = 1DG DECH AB ∴+=在Rt ABC ∆中,34AC CB ==,, 5AB ∴=,125CH =. 模块四:内接矩形与相似三角形知识精讲例题解析ABCD EFGAB CH GFE D11255a a∴+=,6037a∴=,∴正方形DEFG的边长为6037.【总结】本题考查三角形内接正方形的模型,熟练掌握此题涉及的知识点.【例15】ABC∆中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,BC = 15,BC边上的高AD = 10,求正方形EFGH的面积.【答案】36.【解析】设正方形EFGH的边长为a,易知:////HE AD HG BC,.HE BHAD BA∴=,HG AHBC AB=.1HE HGAD BC∴+=,11015a a∴+=,6a∴=,∴正方形EFGH的面积为36.【总结】本题考查三角形内接正方形的模型,熟练掌握此题涉及的知识点.【例16】如图,已知ABC∆中,AC = 3,BC = 4,90C∠=︒,在ABC∆内部求做一正方形,问怎样截取可以使正方形的面积最大,并求出此时正方形的边长.【答案】如图截取,正方形边长为127.【解析】设正方形CDEF的边长为a,易知:////EF CB DE AC,.DE BEAC AB∴=,EF AECB AB=,1DE EFAC CB∴+=.在Rt ABC∆中,34AC CB==,,134a a∴+=.127a∴=.∴正方形DEFC的边长为127.【总结】本题考查三角形内接正方形的模型,还考查了最优化问题,与例16区别.【例17】如图,ABC ∆中,四边形DEFG 为正方形,其中D 、E 在边AC 、BC 上,F 、G 在 AB 上,1ADG CDE S S ∆∆==,3BEF S ∆=,求ABC ∆的面积.【答案】9.【解析】过点D 作//DH CB 交AB 于点H ,可得 DGH EFB ∆≅∆. 4DAH S ∆∴= .易证CDE DAH ∆∆∽,214CDE DAH S CD S DA ∆∆⎛⎫∴== ⎪⎝⎭.12CD DA ∴= , 13CD CA ∴=.CDE CAB ∆∆∽, 219CDE CAB S CD S CA ∆∆⎛⎫∴== ⎪⎝⎭. 9CBA S ∆∴=.【总结】本题要灵活应用相似三角形的面积比等于相似比的平方.步同级年九14 / 23ABCDEFAD1、一线三等角与相似三角形相关模型如下图所示:【例18】已知,在等腰ABC ∆中,AB = AC = 10,以BC 的中点D 为顶点作EDF B ∠=∠,分别交AB 、AC 于点E 、F ,AE = 6,AF = 4,求底边BC 的长.【答案】46. 【解析】EDC B BED ∠=∠+∠,而EDC EDF FDC ∠=∠+∠, ∴B BED EDF FDC ∠+∠=∠+∠.又EDF B ∠=∠,∴BED FDC ∠=∠.AB AC =,∴B C ∠=∠.EDB DCF ∴∆∆∽. BE BDDC CF∴=.106104BDDC -∴=-, 24DC BD ∴=.又12CD DB BC ==, 46BC ∴=. 【总结】本题是对“一线三等角”模型的考查.【例19】如图,直角梯形ABCD 中,AB // CD ,90ABC ∠=︒,点E 在边BC 上,且34AB BE EC CD ==,模块五:一线三等角与相似三角形知识精讲例题解析AD = 10,求AED ∆的面积.【答案】24. 【解析】90ABC ∠=,//AB CD ,∴90DCB ABC ∠=∠=.又34AB BE EC CD ==, ABE ECD ∴∆∆∽.∴AEB EDC ∠=∠. ∴34AE AB ED EC ==.90EDC DEC ∠+∠=,∴90AEB DEC ∠+∠=. ∴90AED ∠=. 在Rt AED ∆中,10AD =,68AE ED ∴==,. 24AED S ∆∴=.【总结】本题考查一线三等角模型的相似问题,还有外角知识、平行的判定等.【例20】矩形ABCD 中,以对角线BD 为一边构造一个矩形BDEF ,使得另一边EF 过原矩形的顶点C .(1)设Rt CBD ∆的面积为1S ,Rt BFC ∆的面积为2S ,Rt DCE ∆的面积为3S ,则1S ______23S S +(用“ > ”、“ = ”、“ < ”填空);(2)写出图中的3对相似三角形,并选择其中一对进行证明. 【答案】(1)=;(2)BFC CED ∆∆∽;BFC DCB ∆∆∽; CED DCB ∆∆∽.【解析】(1)过点C 作CH BD ⊥交BD 于点H ,易得; (2)BCD DCE F FBC ∠+∠=∠+∠,而90BCD F ∠=∠= .∴FBC DCE ∠=∠.BFC CED ∴∆∆∽.【总结】本题主要是考查“一线三等角”模型的相似以及矩形的性质.模块六:旋转与相似三角形例题解析HABCDE FAB CDEM【例21】如图,直角梯形ABCD中,90BCD∠=︒,AD // BC,BC = CD,E为梯形内一点,且90BEC∠=︒,将BEC∆绕点C旋转90°使BC与DC重合,得到DCF∆,联结EF 交CD于M.已知BC = 5,CF = 3,则DM : MC的值为()A.53B.35C.43D.34【答案】C.【解析】旋转后,CEB CFD∆≅∆.5CB CD∴==,3CE CF==,BE DF=,90BEC DFC∠=∠=.在Rt CBE∆中,222BE CE BC+=,4BE∴=.4DF∴=.90ECF∠=,90ECD DCF∴∠+∠=.又90DCF FDC∠+∠=ECD FDC∴∠=∠//CE DF∴43DM DFMC EC∴==.【总结】本题考查旋转的相关知识,平行的判定、三角形一边的平行线的知识.【例22】在ABC∆中,CA = CB,在AED∆中,DA = DE,点D、E分别在CA、AB上.(1)如图1,若90ACB ADE∠=∠=︒,则CD与BE的数量关系是____________;(2)若120ACB ADE∠=∠=︒,将AED∆绕点A旋转至如图2所示的位置,则CD与BE的数量关系是____________.【答案】(1)CD BE=;(2)CD.【解析】(1)90ACB ADE∠=∠=∴//DE BC∴AD DCAE EB=∴2CD BE=;(2)过点C作CH AB⊥交AB于点H120ACB∠=30CAB∴∠=∴CAAH=∴ACAB==由ADE ACB∆∆∽,得:AD ACAE AB=DAE CAB∠=∠,∴ACD ABE∆∆∽∴CD ACBE AB=,∴CD=.【总结】本题考查旋转的相关知识,等腰三角形的相关知识.【例23】把两块全等的直角三角板ABC和DEF叠放在一起,使三角板DEF的锐角顶点D 与三角板ABC的斜边中点O重合,其中90ABC DEF∠=∠=︒,45C F∠=∠=︒,AB = DE= 4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB 相交于点P,射线DF与线段BC相交于点Q.(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证APD∆∽CDQ∆,则A BCDE图1 图2步同级年九18 / 23FAB (Q )CD (O )EPPABCD (O )ABCD (O )QPQ EFEF 图1图2图3此时AP CQ =______;(2)将三角板DEF 由图1所示的位置绕点O 沿逆时间方向旋转,设旋转角为α.其 中090α︒<<︒,问AP CQ 的值是否改变?请说明理由.【答案】(1)8;(2)不改变. 【解析】(1)略;(2)易证APD CDQ ∆∆∽, 得:AP ADCD CQ=AP CQ CD AD ∴•=•. 又42AC =, 22CD AD ∴==, 8AP CQ ∴•=.【总结】本题考查旋转的相关知识,等腰三角形,“一线三等角”得相似等的相关知识.模块七:函数与相似三角形例题解析ABCDEF【例24】如图,已知ABC ∆与ADE ∆都是等边三角形,点D 在BC 边上(点D 不与B 、C重合),DE 与AC 相交于点F .(1)求证:ABD ∆∽DCF ∆;(2)若BC = 1,设BD = x ,CF = y ,求y 关于x 的函数解析式及定义域;(3)当x 为何值时,79AEF ABD S S ∆∆=?【答案】略. 【解析】(1)ABC ∆、ADE ∆是等边三角形 60,60B C E EDA ∴∠=∠=∠=∠=CDF FDA B DAB ∠+∠=∠+∠,CDF DAB ∴∠=∠ ABD DCF ∴∆∆∽;(2)由(1)得ABD DCF ∆∆∽,AB BDDC CF ∴=11x x y ∴=-()201y x x x ∴=-+<<;(2)易证ABD AEF ∆∆∽, AB ADAE AF∴=279AEF ABD S AE S AB ∆∆⎛⎫∴== ⎪⎝⎭ 222279AE AF AB AD ∴== ADE ∆是等边三角形 AD AE ∴= 222279AE AF AB AE ∴== 224981AF AB ∴=1AB = 79AF ∴= 72199y CF ∴==-=, 229x x ∴-+=解得1221,33x x == ∴当2133x x ==或时,79AEF ABD S S ∆∆=.【总结】本题考查旋转的相关知识,“一线三等角”模型,相似的性质等的相关知识.【例25】如图,已知平面直角坐标系中三点A (2,0),B (0,2),P (a ,0)(a < 0),联结BP ,过点P 作PC ⊥PB 交过点A 的直线l 于点C (2,b ).(1)求b 与a 之间的函数关系式;(2)当a 取得最大的整数时,求BC 与x 轴的交点Q 的坐标.【答案】(1)212b a a =-+;(2)8,07Q ⎛⎫⎪⎝⎭.【解析】(1)90BPO OPC BPO PBO ∠+∠=∠+∠= OPC PBO ∴∠=∠90BOP PAC ∠=∠=BPO PCA ∴∆∆∽ OP OBAC AP∴=即22a b a-=--∴212b a a =-+;(2)0a <a ∴取得最大的整数时1a =-32b ∴=-//OB ACOB OQAC QA∴=,即2322OQ OQ =- 87OQ ∴=∴8,07Q ⎛⎫ ⎪⎝⎭.【总结】本题考查相似的判定及性质等知识.【例26】函数k y x =和k y x =-(0k ≠)的图像关于y 轴对称,我们把函数k y x =和k y x=- (0k ≠)叫做互为“镜子”函数,类似地,如果函数y = f (x )和y = h (x )的图像关于y 轴对称,那么我们就把函数y = f (x )和y = h (x )叫做互为“镜子”函数.(1)函数y = 3x – 4的“镜子”函数是________________; (2)函数223y x x =-+的“镜子”函数是________________;xy123–1–2–3123–1–2–3 ABCOAB CDEF (3)如图所示,一条直线与一对“镜子”2y x =(x > 0)和2y x=-(x < 0)的图像分别交 于点A 、B 、C ,如果CB : AB = 1 : 2,点C 在函数2y x =-(x < 0)的“镜子”函数上的对应点的横坐标是12,求点B 的坐标. 【答案】略【解析】(1)34y x =--; (2)223y x x =++; (3)分别过点A 、B 、C 作CC BB AA '''、、 垂直于x 轴,垂足分别为C B A '''、、.设点2,B m m ⎛⎫ ⎪⎝⎭、2,A n n ⎛⎫ ⎪⎝⎭,其中0m >,0n >.由题意,得点1,42C ⎛⎫-⎪⎝⎭. 4CC '∴=,2BB m '=,2AA n '=,A B n m ''=-,12B C m ''=+. 易知////CC BB AA ''', 又:1:2CB AB =所以,可得12().22222(4)3n m m m n n ⎧-=+⎪⎪⎨⎪-=-⎪⎩, 化简得3111433n m m n -=⎧⎪⎨-=⎪⎩,解得 1106m ±=(负值舍去), 1104104,63B ⎛⎫+-∴ ⎪ ⎪⎝⎭. 【总结】本题主要难在第3问,学生不知识怎么下手,要灵活应用相似的相关知识解决问题.【习题1】 如图,AB ⊥BD ,CD ⊥BD ,垂足分别为B 、D ,AC 和BD 相交于点E ,EF ⊥BD , 垂足为F .求证:111AB CD EF+=. 【答案】略.【解析】AB ⊥BD ,CD ⊥BD ,EF ⊥BD ,随堂检测A BCDE FP NMQ∴////AB CD EF∴EF DFAB DB=,EF BFCD DB=∴1EF EFAB DC+=,即111AB CD EF+=.【总结】本题考查了三角形一边的平行线知识的应用.【习题2】如图,在Rt ABC∆中,90B∠=︒,BC = 4cm,AB = 8cm,D、E、F分别为AB、AC、BC边的中点,点P为AB边上一点,过点P作PQ // BC交AC于点Q,以PQ为一边作正方形PQMN,若AP = 3cm,求正方形PQMN与矩形EDBF的公共部分的面积.【答案】34.【解析】DE是中位线,122DE BC cm∴==.D是AB中点,142DA BA cm∴==.//PQ ED,AP PQAD DE∴=.342PQ∴=,32PQ∴=.DN PN PD=-,∴12DN=.∴34S PQ DN=•=公共.【总结】本题考查了三角形一边的平行线等知识的应用.ABCDEF【作业1】 如图,已知AB // EF // CD ,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.【答案】略【解析】BED BCD S BE S BC ∆∆=,BED ABD S EDS AD ∆∆=,又ED ECAD BC=,1BED BED BCD ABD S S S S ∆∆∆∆∴+=,即111BCD ABD BEDS S S ∆∆∆+=. 【总结】本题考查了三角形一边的平行线及同高三角形的面积比可转化为底的比.【作业2】 已知AD 、AE 分别为的内、外角平分线,M 为DE 的中点,求证:22AB BMAC CM=.【答案】略.【解析】联结AM , AD AE 、分别是内、外角的平分线,90DAE ∴∠=.M 是DE 的中点,MA MD ∴=,MA MD ∴=, MAC CAD ADM ∴∠+∠=∠.又ADM BAD B ∠=∠+∠,MAC CAD BAD B ∴∠+∠=∠+∠.BAD DAC ∠=∠,MAC B ∴∠=∠, MAC MBA ∴∆∆∽MC MA ACMA MB AB∴== 22AB MB AC MA ∴=. 【总结】本题考查相似三角形的判定及性质,还有角平分线的相关知识.课后作业ABC D EM。
初三数学寒假讲义 第1讲.三角形 教师版
1中考第一轮复习三角形中考大纲剖析本讲结构12一、等腰三角形二、直角三角形1.直角三角形的边角关系.①.直角三角形的两锐角互余. ②.三边满足勾股定理. ③.边角间满足锐角三角函数.2.特殊直角三角形知识导航3三.尺规构造等腰三角形和直角三角形四.全等三角形全等三角形的性质:全等三角形的对应边相等,对应角相等.全等三角形的判定:⑴SSS;⑵SAS;⑶ASA;⑷AAS;⑸HL.在证明图形的线或角关系时,通常需要将全等与图形变换(旋转、平移、轴对称等)相结合.五.相似三角形相似三角形的性质:⑴相似三角形的对应角相等,对应边成比例,其比值称为相似比.34⑵ 相似三角形对应高的比等于相似比,周长比等于相似比,面积比等于相似比的平方. 相似三角形的判定:⑴ 平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似; ⑵ 两角对应相等,两三角形相似;⑶ 两边对应成比例且夹角相等,两三角形相似; ⑷ 三边对应成比例,两三角形相似. 相似三角形的基本模型:(1)EDC BA(3)ED CBA(4)D CBADCBA(6)EDCBA(2)EDCBA(5)EDCBA(10)(9)(8)A BDEABC DEEDBA【编写思路】由于三角形的知识点非常多,本讲只针对三角形中的重要考点来编写的,侧重于等腰三角形、直角三角形、全等三角形和相似三角形,由于相似三角形在中考中考察的分值较少,而且简单,所以本讲也只是针对相似中的重要模型进行复习,不对学生做太高要求.另外,我们在每一讲中,针对当前考试的热点和难点,设计一种“系列探究”, 使得每一讲有一个复习亮点,为我们第一轮复习锦上添花.本讲的探究是:由“直角三角形斜边中线”引发的“几何最值问题”.【例1】 (1)如图所示的正方形网格中,网格线的交点称为格点,已知A 、B 是两格点,如果C 也是图中的格点,且使得ABC △为等腰三角形,则点C 的个数是( ) A.6 B.7 C.8 D.9(2)在平面直角坐标系中,点A 的坐标为(4),0,点B 的坐标为(410),,点C 在y 轴上,且ABC △是直角三角形,则满足条件的C 点的坐标为 .(2010顺义一模)(3)已知:如图,在ABC △中,B ACB ∠=∠,点D 在AB 边上,点 E 在AC 边的延长线上,且BD CE =, 连接DE 交BC 于F .求证:DF EF =. (2012海淀期中)模块一 特殊三角形夯实基础ACFEDB5(4)如图所示,在△ABC 中,BC =6,E ,F 分别是AB ,AC 的中点,点P 在射线EF 上,BP 交CE 于D ,点Q 在CE 上且BQ 平分∠CBP ,设BP =y ,PE =x .当CQ =21CE 时,y 与x 之间的函数关系式是 .【解析】(1)C ,“两圆一垂”;(2)(0,0),(0,10),(0,2),(0,8).“两垂一圆”确定四个点之后,用勾股求得; (3)证明:过D 点作AC 的平行线交BC 于点G , 则∠B =∠ACB =∠BGD ;∴BD =DG =CE ; 易证△DFG ≌△EFC ;∴DF =EF .注:本题方法很多,还可以过D 作BC 平行线,或过E 作AB 的平行线,由“平行线截等腰三角形”得新等腰三角形.(4)y = –x +6; 提示:延长BQ 与射线EF 相交,由“平行线加角平分线”得到等腰三角形.【例2】 (1)如图,正方形ABCD 的边长为2, 将长为2的线段QF 的两端放在正方形相邻的两边上同时滑动.如果点Q 从点A 出发,沿 图中所示方向按A D C B A →→→→滑动到点A 为止,同时点 F 从点B 出发,沿图中所示方向按B A D C B →→→→滑动到 点B 为止,那么在这个过程中,线段QF 的中点M 所经过的路线围 成的图形的面积为( ) (2010宣武一模) A. 2 B. 4-π C.π D.1π-(2)如图,在△ABC 中,∠C =90°,AC =4,BC =2,点A 、C 分别在x 轴、y 轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动, 在运动过程中,点B 到原点的最大距离是( )A . 222+B .52C .62D . 6(2010西城二模)以下探究主题为:几何最值问题 【探究1】如图,ABC △为等边三角形,边长AB =4,点A 、C 分别在x 轴、y轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动,在运动过程中,点B 到原点的最大距离是________.【探究2】如图,在ABC △中,∠C =90°,AC =4,BC =3,点A 、C 分别在x 轴、 y 轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动, 在运动过程中,点B 到原点的最小距离是__________.能力提升6【探究3】 如图,在Rt ABC △中,∠ACB =90°,∠B =30°,CB =33, 点D 是平面上一点且CD =2,点P 为线段AB 上一动点,当△ABC 绕点C 任意旋转时,在旋转过程中线段DP 长度的最大值为_______,最小值为_______.【解析】(1)C ,由“直角三角形斜边中线等于斜边的一半”可知BM 、CM 、CM 、AM 均等于FQ 的一半,于是M 的轨迹围成一个半径为1的圆;(2)A ,如右图1,取AC 中点D ,连结OD 、BD ,当OD 、B 三点共线时,OB 的值最大;探究1:AC 中点D ,连结OD 、BD ,当O 、D 、B 三点共线时,OB 的值最大;探究2:如右图2,取AC 中点D ,连结OD 、BD ,当O D 、B 三点共线时,OB 2;探究3:“△ABC 绕点C 旋转”等价于“CD 绕点C 旋转”,如下图1,连结CP ,当PD=PC+CD 时, PD 最大,当PD =︱PC-CD ︱时,PD 最小. 如图2,当P 与B 重合,PD 取最大值为2,如 图3,当CP ⊥AB 时,PD 2. 图1图2图3PD CBAPDCBAP ()ABCD【点评】动线段最值的求法一般可总结为两种方法(仅供参考):(1)将动线段作为一个三角形的一边,且另两边为定值,但是形状可变化,如下左图,“外共线”值最大,“内共线”值最小(已知AB 、BP 为定值,求动线段AP 的最大或最小值);(2)如下右图,垂线段最短,端点处最大(已知点P 是线段BC 上的动点,求线段AP 的最大或最小值).P 2(P 1)CB AP模块二 全等三角形PDC B A图1图27【例3】 △ABC 与△CDE 均为等边三角形,点C 为公共顶点,连结AD 、BE 相交于点P ,BE 交AC于点M ,AD 交CE 于点N ,(1)如图1,当点B 、C 、D 在同一直线上,请证明以下结论:① AD =BE ;② 连结PC ,则PC 平分∠BPD ; ③ 60APB ∠=︒;④ 连结MN ,则△MCN 为等边三角形; ⑤ PB=P A+PC ,PD=PE+PC(⑥ 连结AE ,点P 为△ACE 的费马点. 学生版上没有) (2)如图2,当△CDE 绕点C 旋转任意角度时,(1)中的5个结论仍成立吗?图1图2ABCDNPMENMPEDCBA【解析】(1)由ACD BCE △≌△可得①;过点C 分别作AD 、BE 边上的高,由“全等三角形面积相等”或者通过证明“全等三角形对应边上的高相等”可得两高相等,证得②;由“八”字模型倒角证得③;由BMC ACN △≌△或者CND CME △≌△得CN=CM ,证得④;由120APC EPC ∠=∠=︒,在四边形ABCP 和EDCP 中利用旋转可证得⑤;由⑤中的结论可知PA+PC+PE=BE ,120APC EPC APE ∠=∠=∠=︒,点P 到△ACE 的三个顶点的距离和最小,即可证得⑥. (2)结论①②③⑤⑥均成立.【例4】 在△ABC 中,AB =AC ,∠BAC =α(︒<<︒600α),将线段BC 绕点B 逆时针旋转60°得到线段BD .图1图2A BCDEDCBA(1)如图1,直接写出∠ABD 的大小(用含α的式子表示);(2)如图2,∠BCE =150°,∠ABE =60°,判断△ABE 的形状并加以证明;能力提升夯实基础8图3图2图12n-1B 2C 2A CB 1C 1C 1B 1C B A(3)在(2)的条件下,连结DE ,若∠DEC =45°,求α的值. (2013北京中考)【解析】(1)1302α︒-;(2)ABE △为等边三角形,连接AD 、CD 、EB∵线段BC 绕点B 逆时针旋转60︒得到线段BD 则BC BD =,60DBC ∠=︒ 又∵60ABE ∠=︒∴160302ABD DBE EBC α∠=︒-∠=∠=︒-且BCD △为等边三角形.在ABD △与ACD △中AB ACAD AD BD CD=⎧⎪=⎨⎪=⎩∴ABD △≌ACD △(SSS ) ∴1122BAD CAD BAC α∠=∠=∠=∵150BCE ∠=︒ ∴11180(30)15022BEC αα∠=︒-︒--︒=在ABD △与EBC △中BEC BAD EBC ABD BC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ABD △≌EBC △(AAS )∴AB BE = ∴ABE △为等边三角形 (3)∵60BCD ∠=︒,150BCE ∠=︒∴1506090DCE ∠=︒-︒=︒又∵45DEC ∠=︒ ∴DCE △为等腰直角三角形 ∴DC CE BC == ∵150BCE ∠=︒∴(180150)152EBC ︒-︒∠==︒ 而130152EBC α∠=︒-=︒ ∴30α=︒【点评】第(2)问考察的是一类由旋转形成的全等模型,如图,若BAC DAE ∠=∠ ①ABC △为等腰三角形(AB=AC ); ②ADE △为等腰三角形(AD=AE );③ABD ACE △≌△以上三个命题有二推一,通常两个三角形为等边三角形. 此题欲证ABE △为等边三角形,已知DBC △为等边三角形,则需证ABD △≌EBC △即可.【例5】 (1)已知在△ABC 中,BC=a .如图1,点B 1 、C 1分别是AB 、AC 的中点,则线段B 1C 1的长是_______;如图2,点B 1 、B 2 ,C 1 、C 2分别是AB 、AC 的三等分点,则线段B 1C 1 + B 2C 2的值是__________;如图3, 点12......、、、nB B B ,夯实基础模块三 相似三角形BABCDE912......、、、n C C C 分别是AB 、AC 的(n +1)等分点,则线段B 1C 1 + B 2C 2+……+ B n C n 的值是 ______.(2)如图,在矩形ABCD 中, AB =4,BC =6,当直角三角板MPN 的直角顶点P 在BC 边上移动时,直角边MP 始终经过点A ,设直角 三角板的另一直角边PN 与CD 相交于点Q .BP =x ,CQ=y ,那么y 与x 之间的函数图象大致是( )【解析】(1)1,2a a ,12na 提示:由“A”字相似模型来求B n C n 的长; (2)D 提示:“三垂”相似模型;【例6】 如图1,在等腰直角△ABC 中,∠BAC =90°,AB =AC =2,点E 是BC 边上一点,∠DEF =45°且角的两边分别与边AB ,射线CA 交于点P ,Q .(1)如图2,若点E 为BC 中点,将∠DEF 绕着点E 逆时针旋转,DE 与边AB 交于点P ,EF 与CA的延长线交于点Q .设BP 为x ,CQ 为y ,试求y 与x 的函数关系式,并写出自变量x 的取值范围; (2)如图3,点E 在边BC 上沿B 到C 的方向运动(不与B ,C 重合),且DE 始终经过点A ,EF 与边AC 交于Q 点.探究:在∠DEF 运动过程中,△AEQ 能否构成等腰三角形,若能,求出BE 的长;若不能,请说明理由.(2012东城期末)能力提升10【解析】(1)∵ ∠BAC =90°,AB =AC =2, ∴ ∠B =∠C,BC =又∵FEB FED DEB EQC C ∠=∠+∠=∠+∠,DEF C ∠=∠, ∴ ∠DEB =∠EQC . ∴ △BPE ∽△CEQ . ∴BP CEBE CQ=. 设BP 为x ,CQ 为y , ∴y =. ∴ 2y x =自变量x 的取值范围是0<x <1. (2)解:∵ ∠AEF =∠B =∠C ,且∠AQE >∠C ,∴ ∠AQE >∠AEF . ∴ AE ≠AQ .当AE =EQ 时,可证△ABE ≌ECQ . ∴ CE =AB =2 . ∴ BE =BC -EC=2. 当AQ =EQ 时,可知∠QAE =∠QEA =45°.∴ AE ⊥BC . ∴ 点E 是BC 的中点. ∴ BE. 综上,在∠DEF 运动过程中,△AEQ 能成等腰三角形,此时BE长为2.【思维拓展训练】提高班训练1. 如图,直角三角形纸片ABC 中,∠ACB =90°,AC=8,BC =6.折叠该纸片使点B 与点C 重合,折痕与AB 、BC 的交点分别为D 、E . (1)DE 的长为 ;(2)将折叠后的图形沿直线AE 剪开,原纸片被剪成三块, 其中最小一块的面积等于 . 【解析】4,4训练2. ⑴如图1,已知矩形ABCD 中,点E 是BC 上的一动点,过点E 作EF ⊥BD 于点F ,EG ⊥AC 于 点G ,CH ⊥BD 于点H ,试证明CH =EF +EG ;图3GEFL ABC DABCD EFGH图2图1H GFE DCBA⑵ 若点E 在BC 的延长线上,如图2,过点E 作EF ⊥BD 于点F ,EG ⊥AC 的延长线于点G ,CH ⊥BD 于点H , 则EF 、EG 、CH 三者之间具有怎样的数量关系,直接写出你的猜想;⑶ 如图3,BD 是正方形ABCD 的对角线,L 在BD 上,且BL =BC , 连接CL ,点E 是CL 上任一点, EF ⊥BD 于点F ,EG ⊥BC 于点G ,猜想EF 、EG 、BD 之间具有怎样的数量关系,直接写出你的猜想;⑷ 观察图1、图2、图3的特性,请你根据这一特性构造一个图形,使它仍然具有EF 、EG 、CH 这样的线段,并满足⑴或⑵的结论,写出相关题设的条件和结论. (2010房山二模) 【解析】(1)设对角线交点为O ,连结OE ,用面积法证明;(2)CH=EF-EG ;(3)连结AC 交BD 于点O ,由(1)的结论可知CO=EF+EG ,于是12BD EF EG =+;(4)只要有等腰三角形就行,例如可以在等腰梯形中构造. 训练3. 如图1,四边形ABCD 是正方形,点G 是BC 上任意一点,DE AG ⊥于点E ,BF AG ⊥于点F .⑴ 求证:DE BF EF -=.⑵ 当点G 为BC 边中点时,试探究线段EF 与GF 之间的数量关系,并说明理由. ⑶ 若点G 为CB 延长线上一点,其余条件不变.请你在图2中画出图形,写出此时DE 、BF 、EF 之间的数量关系(不需要证明).图2图1ABCDG G FEDCB A【解析】(1)由AED BFA △≌△可得;(2)EF =2GF ,易证AFB BFG ABG △∽△∽△,于是2AB AF BFBG BF FG===,所以AF =2BF , BF =2FG ,所以EF =2FG ; (3)DE+BF=EF .模块一 特殊三角形 课后演练【演练1】 ⑴如图,等腰ABC △中,AB AC =,20A =︒∠,线段AB 的垂直平分线交AB 于D ,交AC 于E ,连接BE ,则CBE ∠等于( ) A .80° B . 70° C .60° D .50°⑵ 在等腰ABC △中,AB AC =,中线BD 将这个三角形的周长分别为15和 12两个部分,则这个等腰三角形的底边长为______________.⑶ 如图,等边三角形ABC 中,D 、E 分别为AB 、BC 边上的点,AD BE =,AE 与CD 交于点F ,AG CD ⊥于点G ,则AGAF = . 【解析】(1)C ; (2)7或11;(3【演练2】 如图,P 为边长为2的正三角形中任意一点,连接P A 、PB 、P C ,过P 点分别做三边的垂线,垂足分别为D 、E 、F ,则PD+PE+PF= ;阴影部分的面积为__________.实战演练图1EDCB AG FEDCBA模块二 全等三角形 课后演练【演练3】 在ABC △中,AB AC =,CG BA ⊥交BA 的延长线于点G .一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直 角顶点为F ,一条直角边与AC 边在一条直线上,另一条直角边 恰好经过点B .⑴ 在图1中请你通过观察、测量BF 与CG 的长度,猜想并写 出BF 与CG 满足的数量关系,然后证明你的猜想;⑵ 当三角尺沿AC 方向平移到图2所示的位置时,一条直角边仍 与AC 边在同一直线上,另一条直角边交BC 边于点D ,过点D 作DE BA ⊥于点E .此时请你通过观察、测量DE 、DF 与CG 的 长度,猜想并写出DE DF +与CG 之间满足的数量关系,然后 证明你的猜想;⑶当三角尺在⑵的基础上沿AC 方向继续平移到图3所示位置 (点F 在线段AC 上,且点F 与点C 不重合)时,⑵中的猜想是 否仍然成立?(不用说明理由) 【解析】⑴ BF CG =;在ABF ∆和ACG ∆中,∵90F G FAB GAC AB AC ∠=∠=︒∠=∠=,,, ∴(AAS)ABF ACG ∆∆≌, ∴BF CG =. ⑵ DE DF CG +=;过点D 作DH CG ⊥于点H (如图4). ∵DE BA ⊥于点E ,90G DH CG ∠=︒⊥,,∴四边形EDHG 为矩形,∴DE HG DH BG =,∥,∴GBC HDC ∠=∠, ∵AB AC =,∴FCD GBC HDC ∠=∠=∠,又∵90F DHC CD DC ∠=∠=︒=,, ∴(AAS)FDC HCD ∆∆≌,∴DF CH =.∴GH CH DE DF CG +=+=,即DE DF CG +=. ⑶ 仍然成立.(注:本题还可以利用面积或三角函数来证明,比如⑵中连结AD )【演练4】 图中是一副三角板,45︒的三角板Rt DEF △的直角顶点D 恰好在30︒的三角板Rt ABC △斜边AB 的中点处,304590A E EDF ACB ∠=︒∠=︒∠=∠=︒,,,DE 交AC 于点G ,GM AB ⊥ 于M .⑴ 如图1,当DF 经过点C 时,作CN AB ⊥于N ,求证:AM DN =.⑵ 如图2,当DF AC ∥时,DF 交BC 于H ,作HN AB ⊥于N ,⑴的结论仍然成立,请 你说明理由.图2图1EHABCFGMN NMGF ECBAE 3E 2E 1D 4D 3D 2D 1CBA 【解析】⑴ ∵3090A ACB ∠=︒∠=︒,,D 是AB 的中点,∴BC BD =,60B ∠=︒∴△BCD 是等边三角形.又∵CN DB ⊥,∴12DN DB =,∵90EDF ∠=︒,BCD ∆是等边三角形.∴30ADG ∠=︒,而30A ∠=︒,∴GA GD =.∵GM AB ⊥,∴12AM AD =又∵AD DB =,∴AM DN =.⑵ ∵DF AC ∥,∴30BDF A ∠=∠=︒,90AGD GDH ∠=∠=︒,∴60ADG ∠=︒.∵60B ∠=︒,AD DB =,∴ADG DBH ∆∆≌,∴AG DH =,又∵BDF A ∠=∠,GM AB ⊥,HN AB ⊥, ∴AMG DNH ∆∆≌.∴AM DN =.模块三 相似三角形 课后演练【演练5】 如图,已知Rt ABC △,1D 是斜边AB 的中点,过1D 作11D E AC ⊥于1E ,连接1BE 交1CD 于2D ;过2D 作22D E AC ⊥ 于2E ,连接2BE 交1CD 于3D ;过3D 作33D E AC ⊥于3E ,…, 如此继续,可以依次得到点45n D D D ,,…,,分别记11BD E △, 22BD E △,33BD E △,…,n n BD E △的面积为123S S S ,,,…n S . 则n S =_________ABC S △(用含n 的代数式表示).【解析】()211n +第十八种品格:坚持品格教育—坚持有些人,做事是怕别人说失败,为不失败而坚持。
沪教版 九年级数学 暑假同步讲义 第6讲 相似三角形的性质提高讲义 (解析版)

相似三角形的性质内容分析相似三角形的性质是九年级数学上学期第一章第三节的内容,本讲主要讲解相似三角形的3个性质定理.重点是灵活应用相似三角形的性质,难点是相似三角形的性质与判定的互相结合.知识结构模块一:相似三角形性质定理1知识精讲1、相似三角形性质定理1相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.步同级年九2 / 23【例1】 求证:相似三角形对应高的比等于相似比. 【答案】略【解析】已知:如图,111ABC A B C ∆∆∽,且相似比为k ,AD 、11A D 分别是BC 、11B C 的高.求证:11ADk A D =. 证明:111ABC A B C ∆∆∽,1B B ∴∠=∠,11ABk A B =; 又AD 、11A D 分别是BC 、11B C 的高,11190BDA B D A ∴∠=∠=,111ABD A B D ∴∆∆∽,1111AB ADk A B A D ∴==. 【总结】本题考查相似三角形的判定和性质. 【例2】 求证:相似三角形对应中线的比等于相似比. 【答案】略【解析】已知:如图,111ABC A B C ∆∆∽,且相似比为k ,AD 、11A D 分别是边BC 、11B C 的中线. 求证:11ADk A D =. 证明:111ABC A B C ∆∆∽, 1B B ∴∠=∠,1111AB CBk A B C B ==; 又AD 、11A D 分别是边BC 、11B C 的中线,12BD BC ∴=,111112B D BC =,∴11DB k D B =,1111AB BD A B B D ∴=,111ABD A B D ∴∆∆∽,1111AB AD k A B A D ∴==. 【总结】本题考查相似三角形的判定和性质的运用.【例3】 求证:相似三角形对应角平分线的比等于相似比. 【答案】略【解析】已知:如图,111ABC A B C ∆∆∽,且相似比为k ,AD 、11A D 分别是BAC ∠、111B AC ∠例题解析AB C D EA 1E 1D 1 C 1B 1 ABCD EF的角平分线.求证:11ADk A D =.证明:111ABC A B C ∆∆∽, 1B B ∴∠=∠,111BAC B AC ∠=∠,11ABk A B =;又AD 、11A D 分别是BAC ∠、111B AC ∠的角平分线,11111111,22BAD BAC B A D B AC ∴∠=∠∠=∠,111BAD B A D ∴∠=∠,111ABD A B D ∴∆∆∽,1111AB ADk A B A D ∴==.【总结】本题考查相似三角形的判定和性质.【例4】 如图,ABC ∆和111A B C ∆中,AD 和BE 是ABC ∆的高,11A D 和11B E 是111A B C ∆的高,且1C C ∠=∠,1111AD ABA D AB =. 求证:1111AD BEA DB E =【答案】略 【解析】 证明:1111AB ADA B A D =,又111ADB A D B ∠=∠,111ABD A B D ∴∆∆∽, 111ABD A B D ∴∠=∠,又1C C ∠=∠,111ABC A B C∴∆∆∽,又BE 、11B E 分别是ABC ∆、111A B C ∆的高,1111BE AB E B A B ∴=,1111BE ADE B A D ∴=. 【总结】本题考查相似三角形的判定和性质的综合运用.【例5】 如图,D 是ABC ∆的边BC 上的点,BAD C ∠=∠,BE 是ABC ∆的角平分线,交 AD 于点F ,1BD =,3CD =,求BF :BE .【答案】12.【解析】解:BE 是ABC∆的角平分线,∴ABF EBC ∠=∠,又BAD C ∠=∠,AB CD EFGHKAB CE FGDHP ABF CBE∴∆∆∽,AB BFCB BE∴=,又BAD C∠=∠,ABD ABC∠=∠BAD BCA∴∆∆∽,AB BDBC BA∴=,14ABAB∴=,2AB∴=,12ABBC∴=,1:2BF BE∴=.【总结】本题考查相似三角形的判定和性质的综合运用.【例6】如图,在ABC∆中,矩形DEFG的一边DE在BC边上,顶点G、F分别在AB、AC边上,AH是BC边上的高,AH与GF交于点K.若32AH cm=,48BC cm=,矩形DEFG的周长为76cm,求矩形DEFG的面积.【答案】2360cm.【解析】解:设DG xcm=,()38FG x cm=-矩形DEFG,//90GF BC GDB∴∠=,,GF AGBC AB∴=,又AH是高,90AHB∴∠=,GDB AHB∴∠=∠//DG AH∴,DG BGAH AB∴=,1DG GFAH BC∴+=,3813248x x-∴+=,20x∴=,∴20DG cm=,18FG cm=,2360DEFGS cm∴=矩形.【总结】本题考查三角形一边的平行线定理,矩形的周长面积等知识.【例7】如图,矩形DEFG的边EF在ABC∆的边BC上,顶点D、G分别在边AB、AC上,AH为BC边上的高,AH交DG于点P,已知3AH=,5BC=,设DG的长为x,矩形DEFG的面积为y,求y关于x的函数解析式及其定义域.【答案】()233055y x x x=-+<<.【解析】解:矩形DEFG,//,90GD BC DEC∴∠=,GD ADBC AB∴=,又AH是高,90AHC∴∠=,DEC AHC ∴∠=∠,//DE AH ∴, DE BD AH AB ∴=,1DG DEBC AH∴+=,153x DE ∴+=,又DEFG S y x DE ==•矩形,20x ∴=,∴yDE x=,153x y x ∴+=,∴()233055y x x x =-+<<. 【总结】本题考查三角形一边的平行线定理,矩形的面积等知识.【例8】 一块直角三角形木板的一条直角边AB 长为1.5m ,面积为1.5m 2,现需把它加工成一个面积最大的正方形桌面,请甲、乙两位同学设计加工方案,甲设计方案如图(1),乙设计方案如图(2).你认为哪位同学设计的方案较好?请说明理由(加工损耗忽略不计,计算结果中可保留分数).【答案】甲同学方案好,理由略.【解析】解:211.52ABC S AB BC m ∆=•=,又 1.5AB m =,2CB m ∴=∴在Rt ABC ∆中, 2.5AC m =.① 按甲的设计:设DE x =,正方形DEFB ,//,//ED BF EF CB ∴, DE CE AB CA ∴=,EF AE CB AC =,1DE EF BA CB ∴+=,11.52x x∴+=,67x m ∴=,23649DEFB S m ∴=正;②按乙的设计:过点B 作BH AC ⊥交AC 于点H ,得//DG BH ,DG ADBH AB∴=, 设DE x =,则DG x =,正方形DGFE ,//ED AC DE DG ∴=,,DE BD AC BA ∴=,1DE DGCA HB ∴+=,1122ABC S AB BC AC BH ∆=•=•,65BH m ∴=,162.55x x ∴+=, ABCDEF步同级年九6 / 23ABCDEF3037x m ∴=,29001369DGFE S m ∴=正; 综上,甲设计方案好.【总结】本题考查了三角形一边的平行线,正方形的面积等知识,本题考查了最优化问题.1、相似三角形性质定理2相似三角形周长的比等于相似比.【例9】 如果两个相似三角形的最长边分别为35厘米和14厘米,它们的周长相差60厘米,那么大三角形的周长是.【答案】100cm .【解析】两三角形的相似比为5:2,则周长比为5:2,设大三角形周长为5acm ,小三角形周长为2acm ,则5260a a -=,所以20a =,所以大三角形的周长为100cm . 【总结】相似三角形的周长比等于相似比.【例10】如图,在ABC ∆中,12AB =,10AC =,9BC =,AD 是BC 边上的高.将ABC∆沿EF 折叠,使点A 与点D 重合,则DEF ∆的周长为. 【答案】312. 模块二:相似三角形性质定理2知识精讲例题解析A BCD PABCPQ 【解析】由折叠得EF 垂直平分AD ,AD 是BC 上的高, //EF BC ∴,AEF ABC ∴∆∆∽,12AEF ABC C C ∆∆∴=,9101231ABC C ∆=++=,312AEF C ∆∴=. 【总结】本题考查相似三角形的性质和判定.【例11】如图,梯形ABCD 的周长为16厘米,上底3CD =厘米,下底7AB =厘米,分别延长AD 和BC 交于点P ,求PCD ∆的周长. 【答案】152cm .【解析】解:梯形ABCD ,//CD AB ∴,AEF ABC ∴∆∆∽,37PDC PAB C CD C AB ∆∆∴==,即327PDC PDC ABCD C C C CD ∆∆=+-梯形,31667PDC PDC C C ∆∆∴=+-,152PDC C cm ∆∴=.【总结】本题考查相似三角形的性质和判定.【例12】如图,在ABC ∆中,=90C ∠︒,5AB =,3BC =,点P 在AC 上(与点A 、C不重合),点Q 在BC 上,PQ //AB .当PQC ∆的周长与四边形P ABQ 的周长相等时,求CP 的长. 【答案】247.【解析】解:CPQ PABQ C C ∆=四边形,CP CQ PQ BQ PQ AP AB ∴++=+++, CP CQ BC CQ AC CP AB ∴+=-+-+,5AB =,3BC =,90C ∠=,4AC ∴=,345CP CQ CQ CP ∴+=-+-+,6CP CQ ∴+=,//PQ AB ,CP CQCA CB∴=, ∴643CP CP -=,247CP =. 【总结】本题考查了三角形一边的平行线性质,主要考查了学生的推理能力.AB CDEF【例13】如图,等边三角形ABC边长是7厘米,点D、E分别在AB和AC上,且43ADAE=,将ADE∆沿DE翻折,使点A落在BC上的点F上.(1)求证:BDF∆∽CFE∆;(2)求BF的长.【答案】(1)略;(2)5.【解析】(1)证明:ADE∆翻折成FDE∆.ADE FDE∴∆≅∆,A EFD∴∠=∠,ABC∆是等边三角形,60A B C∴∠=∠=∠=,60EFD B C∴∠=∠=∠=,DFC DFE EFC∠=∠+∠,DFC B BDF∠=∠+∠,EFC BDF∴∠=∠,BDF CFE∴∆∆∽.(2)由(1)知BDF CFE∆∆∽,BDFCFEC DFC EF∆∆∴=,又ADE FDE∆≅∆,AD DF AE EF∴==,,43BDFCFEC ADC AE∆∆∴==,43BF BD DF BF ABCE FC EF CF AC+++∴==+++,74773BFBF+∴=-+,5BF∴=.【总结】本题考查相似三角形的性质及判定,轴对称的性质,应用相似三角形周长比等于相似比是解决本题的关键.ABCD EA B CDEF1、相似三角形性质定理3:相似三角形的面积的比等于相似比的平方. 【例14】如图,在ABC ∆中,点D 、E 在AB 、AC 上,DE //BC ,ADE ∆和四边形BCED的面积相等,求AD :BD 的值. 【答案】21+.【解析】解://DE BC ,ADE ABC ∴∆∆∽,2ADE ABC S AD S AB ∆∆⎛⎫∴= ⎪⎝⎭,ADE BCED S S ∆=四边形,12ADE ABC S S ∆∆∴=,12AD AB ∴=,12121AD DB ∴==+-. 【总结】本题考查相似三角形的判定及性质.【例15】如图,在正三角形ABC 中,D 、E 、F 分别是BC 、AC 、AB 上的点,DE AC ⊥,EF AB ⊥,FD BC ⊥,则DEF ∆的面积与ABC ∆的面积之比等于() (A )1:3 (B )2:3(C )3:2(D )3:3【答案】A 【解析】解:ABC ∆是等边三角形,60A B C ∴∠=∠=∠=,又DE AC ⊥,EF AB ⊥,FD BC ⊥,90AFE FDB DEC ∴∠=∠=∠=, 30AEF BFD EDC ∴∠=∠=∠=, 60EFD FDE FED ∴∠=∠=∠=,1123BD BD BF DF ==,, ∴FDE ∆是等边三角形,AFE BDF ∴∆≅∆,模块三:相似三角形性质定理3知识精讲例题解析ABCDEFAF BD∴=,FDE ABC∴∆∆∽,2DEFABCS DFS AB∆∆⎛⎫∴= ⎪⎝⎭,设AF x=,则BD x=,2BF x=,DF=,DFAB∴=13DEFABCSS∆∆∴=.【总结】本题考查相似三角形的性质及判定,直角三角形的性质,等边三角形的性质等知识.【例16】如图,在ABC∆中,AD BC⊥,BE AC⊥,D、E分别为垂足.若60C∠=︒,1CDES∆=,求四边形DEAB的面积.【答案】3.【解析】解:AD BC BE AC⊥⊥,,90CDA BEC∴∠=∠=.90CDA BEC∴∠=∠=,CBE CAD∴∆∆∽,CD CACE CB∴=.90CDA BEC∴∠=∠=,CBE CAD∴∆∆∽,CD CACE CB∴=,DCE ACB∴∆∆∽,2DCEACBS CDS CA∆∆⎛⎫∴= ⎪⎝⎭,又60C∠=,30CBE CAD∴∠=∠=,12CDCA=,14DCEACBSS∆∆∴=,13DCEBDEASS∆∴=四边形,A B C DE FO1CDE S ∆=,3DEAB S ∴=四边形.【总结】本题考查相似三角形的性质及判定,直角三角形的性质等知识.【例17】 如图,BE 、CD 是ABC ∆的边AC 、AB 上的中线,且相交于点F ,联结DE .求ADE BFC SS ∆∆的值.【答案】43. 【解析】分别过点A 、F 作AH BC ⊥、FG BC ⊥,交BC 分别于点H 、G ,得//FG AH ,FG KFAH AK=. 联结AF 并延长交BC 于点K .CD 、BE 是ABC ∆的中线,//DE BC ∴,12DE BC =,F 是重心,13KF AK ∴=,13GF AH ∴=. 11113322444ADE S DE AH DE AH DE FG DE FG ∆====,11222BFC S BC FG DE FG DE FG ∆===,34ADE BFC S S ∆∆∴=.【总结】本题考查三角形一边的平行线,重心的意义,三角形中位线及三角形的面积等. 【例18】如图,在矩形ABCD 中,AB = 2cm ,BC = 4cm ,对角线AC 与BD 交于点O ,点E 在BC 边上,DE 于AC 交于点F ,EDC ADB ∠=∠.求:(1)BE 的长; (2)CEF ∆的面积.【答案】(1)3cm ;(2)215cm .【解析】解:(1) 矩形ABCD ,2AB DC cm ∴==,且//AD BC ,ADB DBC ∴∠=∠, EDC ADB ∠=∠,EDC DBC ∴∠=∠,CDE CBD ∴∆∆∽,CD CE CB CD∴=,242CE∴=,1CE cm ∴=,3BE cm ∴=; (2)//AD BC ,∴4AD DFEC EF ==,5DCE CFES DE S EF ∆∆∴==, 又11212CDE S ∆=⨯⨯=,215CFE S cm ∆∴=.【总结】本题考查相似三角形的判定及性质,矩形的性质,同高三角形的面积比等于底边的比等知识.AB CDEOAAB C DE FG【例19】如图,Rt ABC∆中,点D是BC延长线上一点,直线EF//BD交AB于点E,交AC于点G,交AD于点F,若13AEG EBCGS S∆=四边形,求CFAD的值.【答案】21.【解析】解://EF BD,AEG AEC∴∆∆∽,AE AFAB AD∴=,2AEGABCS AES AB∆∆⎛⎫∴= ⎪⎝⎭,13AEG EBCGS S∆=四边形,14AEGABCSS∆∆∴=,12AE AFAB AD∴==,Rt ABC∆,90ACD ACB∴∠=∠=,CF∴是中线,12CF AD∴=,12CFAD∴=.【总结】本题考查相似三角形的性质,直角三角形的性质,三角形一边的平行线等知识.【例20】如图,在ABC∆中,BD AC⊥于点D,CE AB⊥于点E,EC和BD相交于点O,联结DE.若16EODS∆=,36BOCS∆=,求AEAC的值.【答案】23.【解析】解:BD AC CE AB⊥⊥,,90BEO CDO∴∠=∠=,A A∠=∠,AEC ADB∴∆∆∽,AE ADAC AB∴=,ADE ABC∴∆∆∽,AE DEAC BC∴=.EOB DOC∠=∠,EOB DOC∴∆∆∽,EO BOOD OC∴=,EOD BOC∠=∠,EOD BOC∴∆∆∽,2164369EODBOCS EDS CB∆∆⎛⎫∴===⎪⎝⎭,23EDBC∴=,23AEAC∴=.【总结】本题考查相似三角形的性质及判定知识.【例21】如图,90ACB∠=︒,DF AB⊥于点F,45EFBE=,14DCE BFES S∆∆=,且CE = 5,求:(1)BC 的长;(2)CEF S ∆.【答案】(1)352;(2)15. 【解析】解:(1)FD AB ⊥,90EFB ∴∠=,90ACB ∠=,90BCD ∴∠=,EFB BCD ∴∠=∠,FEB CED ∠=∠,BFE DCE ∴∆∆∽,2BFE DCE S EF S CE ∆∆⎛⎫∴= ⎪⎝⎭,又14DCE BFE S S ∆∆=,2FE CE ∴=,45FE BE =,25CE BE ∴=.5CE =,252BE ∴=,352BC ∴=; (2)45FE BE =,10EF ∴=,152BF =,17522BEF S BF EF ∆∴==, 又52BFE FEC S EB S CE ∆∆==,15FEC S ∆∴=.【总结】本题考查相似三角形的性质及判定,直角三角形的性质等知识.步同级年九14 / 23【习题1】 已知:D 、E 、F 分别是ABC ∆的边BC 、CA 、AB 的中点.求证:=4ABC DEF S S ∆∆. 【答案】略. 【解析】解:D 、E 、F 分别是ABC ∆的边BC 、CA 、AB 的中点,12DF EF DE AC BC AB ∴===,DEF ABC ∴∆∆∽,214DEF ABC S DF S AC ∆∆⎛⎫∴== ⎪⎝⎭, 4ABC DEF S S ∆∆∴=.【总结】本题考查三角形中位线,相似三角形的性质及判定知识.【习题2】 如图,DE 是ABC ∆的中位线,N 是DE 的中点,CN 的延长线交AB 于点M ,若ABC S ∆= 24,求AMNE S 四边形.【答案】略.【解析】解:联结AN .DE 是ABC ∆的中位线, //DE BC ∴,12DE BC =,ADE ABC ∴∆∆∽, 164ADE ABC S S ∆∆∴== ,N 是DE 的中点,132ADN ADE S S ∆∆∴==,//DE BC ,14DN BC =,14DM BM ∴=,1133DM BD AD ∴==,113DMN ADN S S ∆∆∴==,615ADE DMN AMNE S S S ∆∆∴=-=-=四边形.【总结】本题考查相似三角形面积比等于相似比的平方,还考查了等高三角形面积比等于底边的比.随堂检测ACDE NMAB CD EFABC DE F GH P【习题3】 如图,正方形DEFG 的边EF 在ABC ∆的边BC 上,顶点D 、G 分别在边AB 、AC 上,AH 是ABC ∆的高,BC = 60厘米,AH = 40厘米,求正方形DEFG 的边长.【答案】24.【解析】设正方形EFGD 的边长为x , //DG BC ,DG AD APBC AB AH∴==. 406040x x-∴=,24x ∴=, ∴正方形EFGD 的边长为24.【总结】本题考查三角形内接正方形的相关知识,主要还是通过比例相等来列式建立关系.【习题4】 如图,在ABC ∆中,点D 在边BC 上,DE //AB ,DE 交AC 于点E ,点F 在边AB 上,且AF CEFB AE=. (1)求证:DF //AC ;(2)如果BD :DC = 1:2,ABC ∆的面积为18cm 2,求四边形AEDF 的面积. 【答案】略. 【解析】(1)证明://DE AB ,CE CDAE BD∴=,AF CE FB AE =,AF CDFB BD∴=,//DF AC ∴; (2)解://DF AC ,//DE AB ,BDF BCA ∴∆∆∽,CDE CBA ∆∆∽.2BDF ABC S BD S BC ∆∆⎛⎫∴= ⎪⎝⎭,2CDE ABC S CD S BC ∆∆⎛⎫∴= ⎪⎝⎭,:1:2BD DC =,1233BD CD BC BC ∴==,,19BDF ABC S S ∆∆∴=,49CDE ABC S S ∆∆=,49ABC AEDF S S ∆∴=四边形,218ABC S cm ∆=,28AEDF S cm ∴=四边形.【总结】本题考查三角形内接平行四边形的相关知识,还考查了相似三角形的性质等.步同级年九16 / 23【习题5】 梯形ABCD 的面积为S ,AB //CD ,AB = b ,CD = a (a < b ),对角线AC 、BD相交于点O ,BOC ∆的面积为29S ,求a :b 的值.【答案】略.【解析】解:如图,设COD S ∆的面积为1S , AOB S ∆的面积为2S ,ABCD S S =梯形, //AB CD ,∴ABD ABC S S ∆∆=,∴ABD AOB ABC AOBS S S S ∆∆∆∆-=-,∴29AOD BOC S S S ∆∆==, 得1225299S S S S S +=-=......①12AOD BOCS S OD S OB S ∆∆==,∴212481BOC AOD S S S S S ∆∆==......② 联立①②,1221259481S S S S S S ⎧+=⎪⎪⎨⎪=⎪⎩,解得:119S S =,249S S =, COD AOB ∆∆∽,2COD AOB S CD S AB ∆∆⎛⎫∴= ⎪⎝⎭,2122S a S b ∴=, b a < ,12S S ∴< ,12a b ∴=. 【总结】本题考查了梯形的对角线分割成的四个三角形的面积关系.【习题6】 在锐角∆ABC 中,矩形DEFG 的顶点D 在AB 边上,顶点E 、F 在BC 边上, 顶点G 在AC 边上,如果矩形DEFG 的长为6,宽为4,设底边BC 上的高为x ,∆ABC的面积为y ,求y 与x 的函数关系式.【答案】23(4)4x y x x =>-.【解析】解:如图, 矩形DEFG ,//90GD BC DEC ∴∠=,,GD ADBC AB∴=. 又 AH 是高,90AHC ∴∠=.DEC AHC ∴∠=∠,//DE AH ∴, DE BDAH AB ∴=, 1DG DE BC AH ∴+=, 641BC x∴+=, 64xBC x ∴=-, 又 12ABC S y BC AH ∆==,∴()2344x y x x =>-.【总结】本题考查三角形一边的平行线定理,矩形的面积等知识.【习题7】 如图,在ABC ∆中,90A ∠=︒,BC = 10,ABC ∆的面积为25,点D 为AB 边A步同级年九18 / 23H上任意一点(点D 不与点A 、B 重合),过点D 作DE //BC ,交AC 于点E .设DE = x , 以DE 为折线将ADE ∆翻折(使ADE ∆落在四边形DBCE 所在的平面内),所得的'A DE ∆ 与梯形DBCE 重叠部分的面积记为y .(1)用x 表示ADE ∆的面积;(2)求出010x <<时,y 与x 的函数关系式. 【答案】略. 【解析】解:(1)//DE BC ,ADE ABC ∴∆∆∽,2ADE ABC S DE S BC ∆∆⎛⎫∴= ⎪⎝⎭.DE x =,10BC =,25ABC S ∆=,∴22125104ADEx S x ∆⎛⎫== ⎪⎝⎭.(2)1252ABC S BC AG ∆==,10BC =, 5AG ∴=. 若点'A 在边BC 上,则ADE ∆的高AH 为25,12AH AG ∴=,ADE ABC ∆∆∽,12DE BC ∴=,5x ∴=.①当05x <≤时,'214ADE A DE y S S x ∆∆===;②当510x <<时,MNED y S =梯形,如图2,ADE ABC ∆∆∽,DE AHBC AG∴=.12AH x ∴=,152GH x ∴=-.A MN A DE ∆∆’’∽,''MN AGDE A H∴=.∵'115522AG x x x ⎛⎫=--=- ⎪⎝⎭, ()25MN x ∴=-,∴()()1112105222MNED y S MN DE GH x x x ⎛⎫==+=-+-⎪⎝⎭梯形,即2310254y x x =-+-;综上,()()221054310255104x x y x x x ⎧<≤⎪⎪=⎨⎪-+-<<⎪⎩,,.【总结】本题考查了相似三角形的性质和判定,以及建立函数关系式,审题很关键,而且要分清楚运动过程中重叠部分面积到底怎么求. .图2ABCD EA BCDO【作业1】 如图,在梯形ABCD 中,AD //BC ,AOD S ∆= 4平方米,BOC S ∆= 9平方米,则=ABCD S 梯形平方米.【答案】25. 【解析】解://AD BC ,AOD COB ∴∆∆∽,2249AOD COB S DO AO S OB OC ∆∆⎛⎫⎛⎫∴=== ⎪ ⎪⎝⎭⎝⎭,23DO AO OB OC ∴==.23AOD AOB S DO AO S OB OC ∆∆===, 2266AOB DOC S cm S cm ∆∆∴==,,225ABCD S cm ∴=梯形.【总结】本题考查相似三角形的面积比等于相似比的平方,同高三角形的面积比等于底边的比.【作业2】 如图,在ABC ∆中,点D 、E 分别在AB 、AC 上,DE //BC ,ACD B ∠=∠.(1)写出图中所有与ADE ∆相似的三角形(不必证明);(2)如果CD = 20cm ,BC = 30cm ,BCD ∆的面积为18cm 2,求ABC ∆的面积.【答案】略.【解析】(1)ADE ABC ∆∆∽,ADE ACD ∆∆∽,ACD ABC ∆∆∽,EDC DCB ∆∆∽;(2)由(1)知:EDC DCB ∆∆∽,∴ ED DCDC CB =, 2EDC DCBS DC S CB ∆∆⎛⎫= ⎪⎝⎭, 20CD cm =,30CB cm =,218DCB S cm ∆=,403DE cm ∴=,28EDC S cm ∆=.∵18BCDS=,∴18826DBCE S =+=梯形.//DE BC ,∴ADE ABC ∆∆∽,∴21681EDA ABC S DE S CB ∆∆⎛⎫== ⎪⎝⎭,∴6581DBCE ABC S S =梯形, ∴21635ABCS cm ∆= 【总结】本题考查相似三角形的判定和性质知识.课后作业AB CDE F【作业3】如图,梯形ABCD中,AD//BC,E是腰AB上的一点,过点E作BC的平行线交CD于点F,已知AD = 2,BC = 6.(1)如果2=3AEEB,试求EF的长;(2)如果2=3AEFDEBCFSS梯形梯形,试求EF的长.【答案】(1)185EF=;(2)EF=【解析】解:(1)过点A作//AN DC交BC于点N,交EF于点M.////AD NC FE,∴四边形ANCD是平行四边形,四边形AMFD是平行四边形,2AD MF NC∴===,6BC=,4BN∴=.//EF BC,AE EMAB BN∴=,23AEEB=,25AEAB∴=,25MENB∴=,85EM∴=,185EF∴=.(2)分别延长BA、CD交于点G.//AD BC,∴219ADGGBCS ADS CB∆∆⎛⎫==⎪⎝⎭,设2AEFDS a=梯形,3EBCFS a=梯形,则5ABCDS a=梯形,∴159GDA GDAADG ADGABCDS SS S S a∆∆∆∆==++梯形,∴58ADGS a∆=,∴55852128GDAGEFaSS a a∆∆==+,//EF AD,∴222521ADGGEFS ADS EF EF∆∆⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭,∴EF=【总结】本题考查梯形的相关知识,包括梯形的辅助线的添法,还有相似三角形的性质及判定等知识.ABCDE O【作业4】 ABC ∆中,AB = 5,BC = 6,AC = 7,点D 、E 分别在边AB 、AC 上,且DE //BC . (1)如果ADE ∆的面积与梯形BCED 的面积相同,求DE 的长; (2)如果ADE ∆的周长与梯形BCED 的周长相同,求DE 的长. 【答案】(1)2)72. 【解析】解:(1)ADE BCED S S ∆=梯形,12ADE ABC S S ∆∆∴=.//DE BC ,ADE ABC ∴∆∆∽,212ADE ABC S DE S BC ∆∆⎛⎫∴== ⎪⎝⎭,2DE BC ∴=,6BC =,DE ∴=;(2)ADE BCED C C ∆=梯形,AD AE DE DE BD CE BC ∴++=+++,576AD AE DA AE ∴+=-+-+,9AD AE ∴+=. //DE BC ,AD AE DE AB AC BC ∴==,9576AD AD DE-∴==,154DA ∴=,92DE ∴=.【总结】本题考查了相似三角形的判定及性质.【作业5】 如图,在ABC ∆中,BE AC ⊥,CD AB ⊥.若1ADE S ∆=,4ABC S ∆=,求A ∠的度数.【答案】30.【解析】解:CD AB BE AC ⊥⊥,,90ODB BEC ∴∠=∠=, 9090DOB DBO EOC ECO ∴∠+∠=∠+∠=,DOB EOC ∠=∠,DBO ECO ∴∠=∠,A A ∠=∠,ABE ACD ∴∆∆∽,AC ADAB AE∴=,又A A ∠=∠,ADE ACB ∴∆∆∽,214ADE ABC S AE S AB ∆∆⎛⎫∴== ⎪⎝⎭12AE AB ∴=,90AEB ∠=,30A ∴∠=. 【总结】本题考查相似三角形的性质及判定以及直角三角形的性质等知识.【作业6】 如图,在等边ABC ∆中,点D 、E 分别在BC 、AC 上,BD = CE ,AD 与BE 交于点F .如果AB = 12,BD = 4,求:BDF ADB S S ∆∆.A【答案】17.【解析】解:过点A作AG BC⊥交BC于点G.ABC∆是等边三角形,606AB BC ABC C BG CG∴=∠=∠===,,,∵BD = 4,2DG∴=.BD CE=,ABD BCE∴∆≅∆,BAD EBC∴∠=∠.60ABE EBC∠+∠=,60ABE BAD∴∠+∠=.BFD ABF BAF∠=∠+∠,60BFD∴∠=,60BFD ABD∴∠=∠=,BDF ADB∴∆∆∽,2BDFADBS BDS AD∆∆⎛⎫∴= ⎪⎝⎭.在Rt ABG∆中,222AG AB BG=-,AG∴=,在Rt ADG∆中,222AD AG DG=+,AD∴=217BDFADBS BDS AD∆∆⎛⎫∴==⎪⎝⎭.【总结】本题考查相似三角形的性质及判定以及等边三角形的性质等知识.【作业7】如图,梯形ABCD中,AD//BC,BC = 3AD,E是腰AB上的一点,连接CE.(1)如果CE AB⊥,AB = CD,BE = 3AE,求B∠的度数;(2)设BCE∆和四边形AECD的面积分别为S1和S2,且2S1 = 3S2,试求BEAE的值.【答案】(1)60°;(2)4.【解析】解:(1)分别延长BA 、CD 交于点M ,如图所示. //AD BC ,MAD MBC ∴∆∆∽,13AD MA BC MB ∴==,即3MB MA =. 设2MA x =,则6MB x =,4AB x ∴=.3EB AE =,3BE x AE x ∴==,.3BE ME x ∴==,又CE AB ⊥,CB MC ∴=,又MB MC =,MBC ∴∆为等边三角形,60B ∴∠=.(2)//AD BC ,MAD MBC ∴∆∆∽,219MAD MBC S AD S CB ∆∆⎛⎫∴== ⎪⎝⎭. 设3MAD S S a ∆==,则9MBC S a ∆=,128S S a +=. 又1223S S =,1245S a ∴=,2165S a =,3S a =,∴32178MEC ECB S S S ME S EB S ∆∆+===, 设7ME k =,则815EB k MB k ==,,153AM MB k ∴==,752AE k k k ∴=-=,∴4BE AE=. 【总结】本题考查梯形的相关知识,包括梯形的辅助线的添法,还有同高三角形的面积比可以转化为底边的比等知识.。
沪教版 九年级(上)数学 秋季课程 第4讲 解直角三角形(解析版)

解直角三角形是九年级上学期第二章第二节的内容,通过本节的学习,需要掌握直角三角形中,除直角外其余五个元素之间的关系,并熟练运用锐角三角比的意义解直角三角形,以及解直角三角形的相关应用.重点在于理解仰角、俯角、方向角、坡度、坡角等概念,并能利用其解决实际问题;难点在于,若一个三角形不是直角三角形,要有意识把它化归为解直角三角形的问题.1、解直角三角形在直角三角形中,由已知元素求出所有未知元素的过程,叫做解直角三角形.在t R ABC∆中,如果=90C∠︒,那么它的三条边和两个锐角之间有以下的关系:(1)三边之间的关系:222a b c+=(2)锐角之间的关系:90A B∠+∠=︒(3)边角之间的关系:sin cosaA Bc==,cos sinbA Bc==tan cotaA Bb==,cot tanbA Ba==解直角三角形内容分析知识结构模块一:解直角三角形知识精讲2 / 26【例1】ABC ∆中,90C ∠=︒,已知AB = 6.4,40B ∠=︒,则A ∠=______,AC =______,BC =______.(sin400.64︒≈,sin500.77︒≈,边长精确到0.1)【答案】50︒,4.1,4.9.【解析】9050A B ∠=︒-∠=︒,根据锐角三角形比的定义,sin ACB AB=,即得sin40 6.40.64 4.096 4.1AC AB =⋅︒≈⨯=≈,同理sin50 4.9BC AB =⋅︒≈.【总结】考查直角三角形中锐角三角比的定义和应用.【例2】若菱形的周长为8,相邻两内角之比为3 : 1,则菱形的高是______. 【答案】2.【解析】菱形周长为8,则其边长为2,相邻两内角之比为3 : 1,则较小内角为1180454︒⨯=︒,则菱形高为2sin 452︒=.【总结】考查菱形性质和相关锐角三角比的应用.【例3】如图,OAB ∆中,OA = OB ,125AOB ∠=︒.已知点A 的坐标是(4,0),则点B的坐标是____________.(用锐角三角比表示)【答案】()4cos554sin55-︒︒,. 【解析】过点B 作BM x ⊥轴交x 轴于点M , 则有18055BOM AOB ∠=︒-∠=︒, 由4BO AO ==,可得cos55MO BO =⋅︒,sin55BM BO =⋅︒,点B 在第二象限,可知其坐标即为()4cos554sin55-︒︒,. 【总结】考查平面直角坐标系中点坐标与线段长度的转换,结合锐角三角比相关知识解题.【例4】如图,在ABC ∆中,90BAC ∠=︒,AB = AC ,D 为边AC 的中点,DE BC ⊥于点E ,连接BD ,则tan DBC ∠的值为( )例题解析A BOxyMAB CDEOA .13B .21-C .23-D .14【答案】A【解析】设AB AC a ==,90BAC ∠=︒,可得2BC a =,45C ∠=︒,D 为AC 中点,则有1122CD AC a ==,DE BC ⊥,可得2sin 4DE CE CD C a ==⋅=, 则324BE BC CE a =-=,214tan 3324aDE DBC BE a ∠===. 【总结】考查等腰直角三角形中的锐角三角比的应用.【例5】如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,E 是边AD 的中点,若AC =10,DC =25,则BO =______,EBD ∠的度数约为____°____'(参考数据:1tan 2634'2︒≈). 【答案】5,18,26.【解析】根据矩形性质,10BD AC ==,152BO BD ==, 根据勾股定理,2245AB BD AB =-=,E 是AD 中点,则25AE AB ==,251tan 245AB ADB AD ∠===,则有2634'ADB ∠=︒,45AEB ∠=︒,即得:452634'1826'EBD AEB ADB ∠=∠-∠=︒-︒=︒.【总结】本题一方面考查矩形性质,另一方面考查锐角三角比的应用.【例6】在锐角ABC ∆中,AB = 14,BC = 14,84ABC S ∆=,求cot C 的值. 【答案】7136-. 【解析】作AD BC ⊥交BC 于D ,则有12ABC S AD BC ∆=⋅,得:22841214ABC S AD BC ∆⨯===,根据勾股定理可得22213BD AB AD =-=,则14213713cot 126CD C AD --===. 【总结】解三角形,通过作高把线段放到直角三角形中即可.【例7】如图,ABC ∆中,23AB =,AC = 2,边BC 上的高3AD =,求ABC S ∆和BAC ∠的大小.【答案】23ABC S ∆=,90BAC ∠=︒.【解析】AD BC ⊥,根据锐角三角比的定义,则有AB CDEABCD4 / 2631sin 223AD B AB ===,3sin 2AD C AC ==,可得:30B ∠=︒,60C ∠=︒,可知90BAC ∠=︒,所以1232ABC S AB AC ∆=⋅=. 【总结】解直角三角形的应用,直接采用特殊角锐角三角比,也可直接用勾股定理解题.【例8】如图,在锐角ABC ∆,4sin 5B =,tan 2C =,且40ABC S ∆=,求BC 的长. 【答案】10【解析】作AD BC ⊥交BC 于点D ,由4sin 5B =,可设4AD a =,则有5AB a =,根据勾股定理得:223BD AB AD a =-=,因为tan 2C =,则2CD a =,5BC BD CD a =+=,11454022ABC S AD BC a a ∆=⋅=⋅⋅=,即24a =,解得:2a =,即得:510BC a ==.【总结】考查锐角三角比的应用,通过作高把线段放到直角三角形中即可.【例9】如图,ABC ∆中,30B ∠=︒,45C ∠=︒,22AB AC -=-,求BC 的长. 【答案】31+.【解析】过点A 作AD BC ⊥交BC 于D ,设AD a =,由30B ∠=︒,45C ∠=︒,可得:2AB a =,3BD a =,CD a =,2AC a =.∵22AB AC -=-,∴2222a a -=-, 解得:1a =,由此可得331BC BD CD a a =+=+=+.【总结】考查锐角三角比的应用,通过作高把线段放到直角三角形中,把题目中的线段用一条线段表示出来即可.【例10】如图,先将斜边AB 长6 cm ,30A ∠=︒的直角三角板ABC 绕点C 顺时针方向旋转 90°至''A B C ∆位置,再沿CB 向左平移,使点B 落在原三角板ABC 位置的斜边AB 上,则平移的距离为______.【答案】()33cm -. ''B 【解析】30A ∠=︒,得'sin303BC AB cm B C =⋅︒==,cos3033AC AB cm =⋅︒=,则有'333AB =-,得()()'''3tan 333333B B AB A cm =⋅=-⨯=-.ABCAB CDABCD【总结】考查锐角三角比的应用,通过作高把线段放到直角三角形中,把题目中的已知线段用一条线段表示出来即可.【例11】如图,正方形ABCD 中,E 为边BC 上一点,将正方形折叠,使A 点与E 点重合,折痕为MN ,若1tan 3AEN ∠=,DC + CE =10.(1)求ANE ∆的面积;(2)求sin ENB ∠的值.【答案】(1)103;(2)35.【解析】(1)设正方形边长为a ,由1tan 3AEN ∠=,可得:13BE a =,则有23CE a =,CD a =,DC + CE =10,即2103a a +=,解得:6a =,则123BE a ==,设AN m =,根据翻折的性质,则有EN AN m ==,6BN m =-,在Rt BNE ∆中用勾股定理,则有222BN BE NE +=,即()22262m m -+=,解得:103m =,11102223ANE S BE AN m ∆=⋅=⨯=;(2)由(1)可得2BE =,103NE =,则23sin 1053BE ENB NE ∠===. 【总结】解直角三角形的应用,注意充分利用翻折的性质和其中的相关等量关系.【例12】如图,四边形ABCD 中,90A C ∠=∠=︒,120B ∠=︒,AB = 4,BC = 2,求四边形的面积.【答案】2633.【解析】延长AB 、DC 交于点E ,90A C ∠=∠=︒,120B ∠=︒,60D CBE ∴∠=∠=︒. 由BC = 2,得tan 602324CE BC BE BC =︒⋅===,. 由AB = 4,即得8AE AB BE =+=,则有83cot 603AD AE =⋅︒=. A BC D EN MABCD E6 / 26即得:1118312638223222323ABCD ADE BCE S S S AD AE BC CE ∆∆=-=⋅-⋅=⨯⨯-⨯⨯=. 【总结】利用割补法求面积,关键在于对特殊角的利用,不能把特殊角分开,延长即可.【例13】如图,在四边形ABCD 中,已知AD = AB = BC ,连接AC ,且30ACD ∠=︒,23tan 3BAC ∠=,CD = 3,求AC 的长. 【答案】635或63.【解析】过点B 作BE AC ⊥交AC 于E ,过点D 作DF AC ⊥交AC 于F , 则有12AE CE AC ==,设AE a =,由23tan 3BAC ∠=,可得:233BE a =,根据勾股定理即可得22213AB BE AE a BC AD =+===,由30ACD ∠=︒,CD = 3,可得3sin302DF CD =⋅︒=,33cos302CF CD =⋅︒=,在Rt ADF ∆中用勾股定理,则有222AF DF AD +=,即222333212223a a ⎛⎫⎛⎫⎛⎫-+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 整理,得:25183270a a -+=,解得:1335a =,233a =,均符合题意,即得6325AC a ==或63AC =.【总结】考查锐角三角比的应用,通过作高把线段放到直角三角形中,把题目中的线段用一条线段表示出来即可.【例14】小智在学习特殊角的三角比时发现,将如图所示的矩形纸片ABCD 沿过B 点的直 线折叠,使点A 落在BC 上的点E 处,折痕BM .还原后,再沿过点E 的直线折叠,使 点A 落在BC 上的点F 处,折痕EN .利用这种方法,可以求出tan67.5︒的值是21+,试证明之.【答案】略.【解析】证明:第一次折叠,由翻折的性质,得:AB BE =,有45AEB ∠=︒,第二次折叠,由翻折的性质,得:AE EF =,有2AEB AFB ∠=∠, 则有22.5AFB ∠=︒,67.5FAB ∠=︒,设AB a =,则有BE a =,2AE a EF ==,则有()21BF a =+,A BCDEFNM AB CD E F仰角 视线水平线俯角铅垂线()21tan 67.5tan 21a BFFAB ABa+︒=∠===+.【总结】考查翻折性质与特殊角锐角三角比的结合运用,注意线段长度的合理转换.【例15】在平面直角坐标系内,放置了5个如图所示的正方形(用阴影表示).点1B 在y 轴 上,点1C 、1E 、2E 、2C 、3E 、4E 、3C 在x 轴上.已知正方形1111A B C D 的边长为1, 1160B C O ∠=︒,11B C //22B C //33B C ,则点3A 到x 轴的距离是( )A .3318+ B .3118+ C .336+ D .316+ 【答案】D【解析】由1160B C O ∠=︒,11B C //22B C //33B C ,可得: 22233460B C E B C E ∠=∠=︒,由11122290B C D B C D ∠=∠=︒,得:11122360C D E C D E ∠=∠=︒, 1111221cos602D E C D B E =⋅︒==则2222223sin 603B E BC CD ===︒,2322343cos606D E C D B E =⋅︒==,由此可得3A 到x 轴的距离即为()3433311cot 601366B E ⎛⎫+⋅+︒=+⨯= ⎪ ⎪⎝⎭,故选D . 【总结】考查特殊角锐角三角比的应用,注意进行边角转化.1、仰角与俯角在测量过程中,常常会遇到仰角和俯角.如图,当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,视线在水平线下方的角叫做俯角.模块二:解直角三角形的应用知识精讲x yO8 / 26北北偏东30°南偏西45°北偏西70°南偏东50°30° 70° 45° 50°hl2、方向角指北或指南方向线与目标方向线所成的小于90°的角叫做方向角. 如图:北偏东30°,北偏西70°,南偏东50°,南偏西45°.3、坡度(坡比)、坡角在修路、挖河、开渠等设计图纸上,都需要注明斜坡的倾斜程度.如图,坡面的铅垂高度h 和水平宽度l 的比叫做坡面的坡度(或坡比),记作i ,即h i l=. 坡度通常写成1 : m 的形式,如1:1.5i =. 坡面与水平面的夹角叫做坡角,记作α.坡度i 与坡角α之间的关系:tan hi l α==.【例16】如图,为测量一棵与地面垂直的树OA 的高度,在距离树的底端30米的B 处,测 得树顶A 的仰角ABO ∠为α,则树OA 的高度为( )A .30tan αB .30sin αC .30tan αD .30cos α【答案】C【解析】转化为直角三角形中求长度的问题,根据锐角三角比定义可得tan OAOB α=,即得30tan OA α=,故选C .【总结】考查锐角三角比在实际问题中的应用.例题解析A BO【例17】如图,一艘海轮位于灯塔P 的北偏东55°方向,距离灯塔2海里的点A 处.如果海轮沿着正南方向航行到灯塔的正东方向,那么海轮航行的距离AB 的长是( )海 里A .2B .2sin 55°C .2cos 55°D .2tan 55°【答案】C【解析】转化为直角三角形中求长度的问题,根据锐角三角比定义可得cos ABPAB PA ∠=,即得2cos55OA =︒,故选C .【总结】考查锐角三角比在实际问题中的应用.【例18】如图所示,某公园入口处原有三级台阶,每级台阶高为18厘米,深为30厘米, 为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A ,斜坡的起始点为C ,现设计斜坡BC 的坡度i = 1 : 5,那么AC 的长度是______厘米.【答案】210【解析】依题意可得31854BD =⨯=, 23060AD =⨯=,根据坡度的含义, 可得:270BDCD i==,由此可得210AC CD AD cm =-=.【总结】考查坡度的实际应用和理解.【例19】如图,斜面AC 的坡度为1 : 2,AC =35米,坡顶有一旗杆BC ,旗杆顶端B 点与 A 点有一条彩带相连,若AB = 10米,则旗杆BC 的高度为( )米A .5B .6C .8D .3+5【答案】A【解析】斜坡坡度为1 : 2,即12CD AD =,设CD a =,则有2AD a =, 根据勾股定理可得535AC a ==,解得3a =,即得:3CD =,6AD =,根据勾股定理可得228BD AB AD =-=,则5BC BD CD m =-=.【总结】考查坡度的实际应用和理解,结合勾股定理进行实际计算.C ABDABP 北ABC D10 / 26【例20】如图,要在宽为22米的大道AB 两边安装路灯,路灯的灯臂CD 长2米,且与灯 柱BC 成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO 与灯臂CD 垂直.当灯罩的 轴线DO 通过公路路面中心线时照明效果最佳.此时,路灯的灯柱BC 的高度应该设计 为( )米 A .1122- B .1123-C .11322-D .1134-【答案】D【解析】延长OD 、DC 交于点E .90B ODC ∠=∠=︒,120BCD ∠=︒, 60DOB DCE ∴∠=∠=︒,由BC = 2,tan 602324DE DC CE DC ∴=︒⋅===,.依题意可知:O B =11,即得:tan 60113BE OB =⋅︒=, 则()1134BC BE CE m =-=-.【总结】考查利用锐角三角比求线段长度,关键在于对特殊角的利用,不能把特殊角分开,延长即可.【例21】如图,为测得一栋大厦CD 的高度,一人先在附近一楼房的底端A 点观测大厦顶 端C 处的仰角是60°,然后爬到该楼房顶端B 处观测大厦底部D 处的俯角是30°,已知楼房高AB 约是45 m ,根据以上观测数据可求大厦的高CD 是______m .【答案】135.【解析】90BAD ADC ∠=∠=︒,30ADB ∠=︒,60CAD ∠=︒,则有tan 60453AD AB =⋅︒=,tan60135CD AD m =⋅︒=.【总结】考查俯角仰角与特殊角锐角三角比的结合应用.【例22】如图,小智在大楼30米高(即PH = 30米)的A BCDABCH PQABC DO E窗口P 处进行观测,测得山坡上A 处的俯角为15°,山脚B 处的俯角为60°.已知山坡的坡度为1:3,点P 、H 、B 、C 、 A 在同一平面上,点H 、B 、C 在同一直线上,且PH HC ⊥.则山坡上A 、B 两点间的距离为______.【答案】203m .【解析】依题意有60PBH ∠=︒,15QPA ∠=︒, 山坡坡度为1:3,则有30ABC ∠=︒,由此可得:9030BPH PBH ∠=︒-∠=︒,90ABP ∠=︒, 9045APB BPH QPA ∠=︒-∠-∠=︒,则有203sin 60PHBP ==︒,203AB PB m ==.【总结】考查俯角仰角与特殊角锐角三角比的结合应用.【例23】某单位拟建造地下停车库,设计师提供了车库入口设计示意图(如图),按规定, 地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限 高,请你计算图中CE 的长.(参考数据:sin180.309︒≈,cos180.951︒≈,tan180.325︒≈,cot18 3.078︒≈,结果精确到0.1 m )【答案】2.3m .【解析】依题意得18BAD ∠=︒,tan 9tan18BD AB BAD =⋅∠=︒, 9tan180.5CD BD BD =-=︒-, 9072BDA BAD ∠=︒-∠=︒,则有9018DCE BDA ∠=︒-∠=︒, 由此可得()cos 9tan180.5cos189sin180.5cos18CE CD DCE =⋅∠=︒-⨯︒=︒-︒由上述数据,即可得90.3090.50.951 2.3055 2.3CE m ≈⨯-⨯=≈.【总结】考查锐角三角比在解决实际问题中的具体应用,注意题目要求,考虑需要涉及到哪些相关的锐角三角比.ABC D E9 m0.5 m12 / 26【例24】小方在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车 吊臂的支点O 距离地面高'2OO =米.当吊臂顶端由点A 抬升至点'A (吊臂长度不变) 时,地面B 处的重物(高度不计)被吊至'B 处,紧绷着的吊缆''A B AB =.AB 垂直地面'O B 于点B ,直线''A B 垂直地面'O B 于点C ,吊臂长度'10OA OA ==米,且3cos 5A =,1sin '2A =. (1)求重物在水平方向移动的距离BC ;(2)求重物在竖直方向提升的高度'B C .【答案】(1)3m ;(2)()536m -. 【解析】(1)如图,则有4sin 1085OD OA A m =⋅=⨯=, ''1sin 1052OF OA A m =⋅=⨯=,则3BC FD OD OF m ==-=;(2)由(1)可得:cos 6AD OA A m =⋅=,则'''8AB AD DB AD OO m A B =+=+==, ''2253A F OA OF m =-=,则()''''5328536B C A F FC A B m =+-=+-=-. 【总结】考查锐角三角比在解决实际问题中的具体应用,注意题目要求,考虑需要涉及到哪些相关的锐角三角比,注意看清楚题目提供的条件.【例25】如图,是一座人行天桥的示意图,天桥的高度是10米,CB DB ⊥,坡面AC 的坡 角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC 的坡度 为3:3i =.若新坡角下需留3米宽的人行道,问离原坡角(A 点处)10米的建筑物是否需要拆除?(参考数据:2 1.414≈,3 1.732≈)【答案】需要拆除.【解析】依题意有45CAB ∠=︒, 则10AB BC ==,DC 的坡度为3:3i =,即得:103CDBD i==,由此可得:10310AD BD AB =-=-,则点A 距人行道外侧距离至少为103103103710.3210-+=-≈>,由此可知建筑物需要拆除.【总结】考查锐角三角比在解决实际问题中的具体应用.【例26】数学兴趣小组准备利用所学的知识测量公路旁某广告牌的高度.如图所示,先在水平面上点A 处测得对广告牌上沿点C 的仰角为30°,然后沿AH 方向前进10米至点A BCD FDA BA 'B ' O 'OCC DG 广告牌B 处,测得对广告牌下沿点D 的仰角为60°.已知矩形广告牌垂直于地面的一边CD高2米.求广告牌的高度GH (结果保留根号).【答案】()531m -.【解析】作DE BH ⊥交BH 于E , 设BE a =,则有tan 3DE BE DBE a =⋅∠=, 32CE CD DE a =+=+,由30CAE ∠=︒,得332310AE CE a AB BE a ==+=+=+,解得:53a =-,由此可得()()323532531GH CE a m ==+=⨯-+=-.【总结】考查锐角三角比在解决实际问题中的具体应用,注意线段长度的转化和等量关系.【例27】如图,轮船甲位于码头O 的正西方向A 处,轮船乙位于码头O 的正北方向C 处, 测得45CAO ∠=︒.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们 的速度分别为45 km /h 和36 km /h .经过0.1 h ,轮船甲行驶至B 处,轮船乙行驶至D 处, 测得58DBO ∠=︒.此时B 处距离码头O 有多远?(参考数据:sin580.85︒≈,cos580.53︒≈,tan58 1.60︒≈)【答案】13.5km .【解析】依题意可得:450.1 4.5AB km =⨯=, 360.1 3.6CD km =⨯=,由45CAO ∠=︒,可知 4.5AO CO BO ==+,8.1DO CO CD BO =+=+,58DBO ∠=︒,得tan tan58DODBO BO∠==︒,即8.1 1.60BO BO+≈,解得:13.5BO km =.【总结】考查锐角三角比在解决实际问题中的具体应用,注意线段长度的转化和等量关系.【例28】如图,MN 表示一段笔直的高架道路,线段AB 表示高架道路旁的一排居民楼.已 知点A 到MN 的距离为15米,BA 的延长线与MN 相交于点D ,且30BDN ∠=︒,假设汽车在高架道路上行驶时,周围39米以内会受到噪音的影响.A BCD O北东14 / 26(1)过点A 作MN 的垂线,垂足为H .如果汽车沿着从M 到N 的方向在MN 上行驶, 当汽车到达点P 处时,噪音开始影响这一排居民楼,那么此时汽车与点H 的距离为多少米?(2)降低噪音的一种方法是在高架道路旁安装隔音板.当汽车行驶到点Q 时,它与这一排 居民楼的距离QC 为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(结果精确到1米,参考数据:3 1.7≈)【答案】(1)36;(2)89.【解析】(1)39AP =,根据勾股定理可得:2222391536PH AP AH m =-=-=;(2)30BDN ∠=︒,得278DQ QC m ==, cot 30153DH AH m =⋅︒=,由此可得隔音板长度:361537811415389PQ PH DH DQ m =-+=-+=-≈.【总结】考查锐角三角比在解决实际问题中的具体应用,注意将题目中的语言转化为数学符号语言.【例29】台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风 暴,有极强的破坏力.据气象部门观测,某沿海城市A 正南方向相距220 km 的B 处有 一台风中心,中心最大风力为12级,每远离台风中心20 km ,风力就会减弱一级.现 台风中心正以15 km /h 的速度沿北偏东30°方向移动,如图所示.若城市所受风力达到或超过4级,则称为受台风影响.(1)设台风中心风力不变,该城市是否会受到这次台风的影响?请说明理由. (2)如该城市受台风影响,那么台风影响该城市的持续时间有多长? (3)该城市受到台风影响时的最大风力为几级? 【答案】(1)会受影响;(2)415h ;(3)6.5级. 【解析】(1)作AD BC ⊥交BC 于D , 则有sin 110AD AB B km =⋅=,不受台风影响的最小距离为()12420160km -⨯=,因为110160<,故该城市会受到台风影响;(2)设在E 点处该城市开始受到台风影响,则有160AE km =,根据勾股定理可得:223015DE AE AD =-=,则受影响时间为2301515415h ⨯÷=;(3)台风中心到达D 点处距该城市最近,受到最大风力影响, 受到的最大风力即为1211020 6.5-÷=级.【总结】考查锐角三角比在解决实际问题中的具体应用,关键是找准题目要求的临界位置结AB CDP NMQH AB CD E合题意进行求解.【例30】某水库大坝的横截面积是如图所示的四边形ABCD ,其中AB // CD .瞭望台PC 正 前方水面上有两艘渔船M 、N ,观察员在瞭望台顶端P 处观测渔船M 的俯角31α=︒, 观测渔船N 的俯角45β=︒.已知MN 所在直线与PC 所在直线垂直,垂足为E ,PE 长为30米.(1)求两渔船M 、N 之间的距离(结果精确到1米)(2)已知坝高24米,坝长100米,背水坡AD 的坡度i = 1 : 0.25.为了提高大坝的防洪能 力,某施工队在大坝的背水坡填筑土石方加固,加固后坝顶加宽3米,背水坡FH 的坡 度为i = 1 : 1.5.施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效 率提高到原来的1.5倍,结果比原计划提前20天完成加固任务.施工队原计划平均每天填筑土石方多少立方米?(参考数据:tan310.60︒≈,sin310.52︒≈)【答案】(1)20m ;(2)600. 【解析】(1)3050tan 0.60PE ME m α=≈=,30tan PENE m β==,由此可得:20MN ME NE m =-=;(2)作DG AB ⊥交AB 于G ,作 FQ BH ⊥交BH 于Q .依题意有:24DG FQ ==,AD 坡度i = 1 : 0.25,即得:16DGAG i ==,FH 坡度i = 1 : 1.5,即得:236FQHQ i ==,AB C D E F NM P JHG Q16 / 26由此可得336633AH GQ HQ AG =+-=+-=,则填筑土石方总量为()()11005024333432002DG DF AH ⋅+⨯=⨯⨯+=方,设原计划每天填筑x 方,可列方程4320012 1.5122043200x x x ⎛⎫+--= ⎪⎝⎭,解得:600x =,经检验,600x =是原方程的根,即原计划每天填筑土石方600立方米.【总结】考查实际问题的应用,主要是对题目要求进行准确分析.【习题1】如图,菱形ABCD 的边长为15,3sin 5BAC ∠=,则对角线AC 的长为______. 【答案】24.【解析】连结BD 交AC 于点O ,则有AC BD ⊥,2AC AO =,由3sin 5BAC ∠=,即35BO AB =,得9BO =, 勾股定理得2212AO AO BO =-=,则224AC AO ==. 【总结】考查菱形的性质结合锐角三角比基础知识的应用.【习题2】有一个相框的侧面抽象为如图所示的几何图形,已知BC = BD = 15 cm , 40CBD ∠=︒,则点B 到CD 的距离为______cm .(参考数据:sin200.342︒≈,cos200.940︒≈,sin400.642︒≈,cos400.766︒≈,结果精确到0.1 cm )【答案】14.1.【解析】作BE CD ⊥,则有1202CBE CBD ∠=∠=︒,故B 到CD 的距离cos 150.94014.1BE BC CBE cm =⋅∠≈⨯=. 【总结】考查锐角三角比和等腰三角形性质的结合应用.随堂检测AB CDOABC DEABCDE F G 【习题3】如图,为了测得电视塔的高度AB ,在D 处用高为1米的测角仪CD 测得电视塔 顶端A 的仰角为30°,再向电视塔方向前进100米到达F 处,又测得电视塔顶端A 的 仰角为60°,则这个电视塔的高度AB 为( )A .503米B .51米C .()503+1米D .101米【答案】C【解析】60AEG ∠=︒,得:tan 603AG EG EG =⋅︒=,30ACG ∠=︒,则有cot 3033CG AG AG EG =⋅︒==,则有2100CE CG EG EG =-==,得:50EG =,3503AG EG ==,()5031AB AG BG m =+=+.故选C . 【总结】考查特殊角锐角三角比的实际应用,相应线段长度转化.【习题4】如图,ABC ∆中,90C ∠=︒,3sin 5B =.D 是BC 上一点,已知45ADC ∠=︒,DC = 6,求tan BAD ∠的值.【答案】17.【解析】过点D 作DE AB ⊥交AB 于点E .由90C ∠=︒,3sin 5B =,可设3AC a =,则5AB a =, 根据勾股定理可得224BC AB AC a =-=,由45ADC ∠=︒,可得3CD AC a ==, 则BD BC CD a =-=,由90C DEB B B ∠=∠=︒∠=∠,,即得ACB ∆∽DEB ∆,则有55AC BC AB a DE BE BD a ====,由此可得35DE a =,45BE a =,则215AE AB BE a =-=, 即得315tan 2175aDE BAD AE a ∠===.【总结】解直角三角形,通过作高把线段放到直角三角形中再通过相应的线段比例关系把三角形中的相关线段表示出来即可.【习题5】如图,ABC ∆和ADE ∆都是等边三角形,AB = 2AD ,已知45BAD ∠=︒,AC 与DE 相交于点F ,ABC ∆的面积为3,求阴影部分的面积.【答案】334-【解析】作CG AB ⊥交AB 于点G ,作FH AE ⊥交AE 于点H , 则有6045E B EAF BAD ∠=∠=︒∠=∠=︒,.设ABC ∆边长为a ,则有1322BG a CG a ==,,ABCD EA BCDE FG H18 / 261133222ABC S CG AB a a ∆=⋅=⋅⋅=,即得24a =,解得:2a =,即22AB AD ==,得ADE ∆边长为1,则有1AE =,设FH h =,则有3cot 603EH EF h =⋅︒=,AH FH h ==,即得3113AE AH FH h ⎛⎫=+=+= ⎪ ⎪⎝⎭,解得332h -=,13324S AE FH -=⋅=阴. 【总结】考查特殊角的锐角三角比与特殊图形的结合应用.【习题6】如图,在四边形ABCD 中,45A C ∠=∠=︒,105ADB ABC ∠=∠=︒. (1)若AD = 2,求AB ;(2)若232AB CD +=+,求AB .【答案】(1)62+;(2)31+. 【解析】(1)作DE AB ⊥交AB 于点E , 由45A ∠=︒,可得:cos452AE AD DE =⋅︒==,由105ADB ∠=︒,可得:30ABD ∠=︒,即得cot 306BE DE =⋅︒=,则62AB =+;(2)作BF CD ⊥交CD 于点F ,由(1)可得()31AB DE =+,设DE a =,则有2BD a =,由45A C ∠=∠=︒,105ADB ABC ∠=∠=︒,可得60BDC ∠=︒,则有cos60DF BD a =⋅︒=,3BF a CF ==,即得()31CD a AB =+=,由232AB CD +=+,即可得31AB =+. 【总结】考查特殊角锐角三角比的应用,通过作高解直角三角形即可.【习题7】2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度为20千米.中 国救援队火速赶往灾区救援,探测出某建筑物废墟下方C 处有生命迹象.在废墟一侧 某面上选两探测点A 、B ,点A 、B 相距2米,探测线与该面的夹角分别是30°和45°(如图),试确定生命所在的点C 与探测面的距离(参考数据:2 1.414≈,3 1.732≈)【答案】2.732m .【解析】作CD AB ⊥交直线AB 于点D . 由题意可得:30CAD ∠=︒,45CBD ∠=︒, 则有cot 303AD CD CD =⋅︒=,BD CD =,即()312AB AD BD CD =-=-=,AB CDEFABC30°45° DEDCB A解得:31 2.732CD m =+≈【总结】考查特殊角锐角三角比的应用,通过作高解直角三角形即可.【习题8】利用几何图形,求sin 18°的值.【答案】514-.【解析】如图,ABC ∆为“黄金三角形”,AD 、BE 分别为其顶角和一底角角平分线,则有18BAD ∠=︒,12BD BC =,根据相似可证得“黄金三角形中”512BC AC -=, 则有51sin184BD AC -︒==. 【总结】考查“黄金三角形”的性质的应用.【习题9】如图,港口B 位于港口O 正西方向120 km 处,小岛C 位于港口O 北偏西60° 方向上.一艘游船从港口O 出发,沿OA 方向(北偏西30°)以v km /h 的速度驶离港 口O ,同时一艘快艇从港口B 出发,沿北偏东30°的方向以60 km /h 的速度驶向小岛C ,在小岛C 用1 h 加装补给物资后,立即按原来的速度给游船送去.(1)快艇从港口B 到小岛C 需要多长时间?(2)若快艇从小岛C 到与游船相遇恰好用时1 h ,求v 的值及相遇处与港口O 的距离. 【答案】(1)1h ;(2)40v =,相遇处与港口O 的距离120km . 【解析】(1)依题意可得60CBO ∠=︒,30BOC ∠=︒, 则有90ACB ∠=︒,此时sin 60BC OB BOC km =⋅∠=,则快艇到小岛的时间为60601h ÷=;(2)延长BC 交AO 于点D . 由题意可知60CD BC ==,则有AB BO =, 由30AOC ∠=︒,可得60BOD ∠=︒, 即BOD ∆为等边三角形,相遇点D 与港口距离120OD OB km ==,船速()12011140/v km h =÷++=. A B CO北北东D20 / 26【总结】考查方位角的应用,计算速度时注意不要遗漏时间.【习题10】如图所示,已知边长为2的正三角形ABC 沿直线l 顺时针滚动.(1)当ABC ∆滚动一周到111A B C ∆的位置时,A 点所运动的路程约为______;(精确到0.1) (2)设ABC ∆滚动240°,C 点的位置为'C ,当ABC ∆滚动480°时,A 点的位置再'A ,请你利用正切的两角和公式()tan tan tan 1tan tan αβαβαβ++=-,求出''CAC CAA ∠+∠的度数.【答案】(1)8.4;(2)30︒. 【解析】(1)A 点转过的圆心角度数 为1202240︒⨯=︒,由此可得运动路程为:240288 3.148.418033ππ⨯⨯=≈≈; (2)作'C D AC ⊥交直线AC 于点D ,作'A E AC ⊥交直线AC 于点E . 则有''2sin 603C D A E ==︒=,2215AD =⨯+=,4219AE =⨯+=,则有''3tan 5C D CAC AD ∠==,''3tan 9A E CAA AE ∠==,根据上述公式,代值计算,则有()''''''33tan tan 359tan 1tan tan 333159CAC CAA CAC CAA CAC CAA +∠+∠∠+∠===-∠⋅∠-⨯,即得''30CAC CAA ∠+∠=︒.【总结】阅读题,抓住题目中的运动过程,准确分析即可进行解题应用.ABCA 1B 1C 1DE【作业1】如图,将正方形ABCD 的边BC 延长到点E ,使得CE = AC ,AE 与CD 相交于点F ,求E ∠的余切值.【答案】21+.【解析】设正方形边长为a ,则有2AC a CE ==, ()21BE BC CE a =+=+,()21cot 21aBEE ABa+===+.【总结】考查根据一些特殊角锐角三角比计算一些相关锐角三角比的思想方法.【作业2】如图,在矩形ABCD 中,AB = 8,BC = 12,E 是BC 的中点,连接AE ,将ABE ∆沿AE 折叠,点B 落在点F 处,连接FC ,则sin EFC ∠的值为______.【答案】45.【解析】连结BF , 根据翻折的性质,可得BE EF FC ==,可证得BFC ∆为直角三角形,AE BF ⊥,即得//AE CF ,所以EFC AEF AEB ∠=∠=∠. 由8AB =,6BE =, 勾股定理得:2210AE AB BE =+=,则84sin sin 105AB EFC AEB AE ∠=∠===.【总结】考查翻折性质的应用,通过等角转化求角的锐角三角比.课后作业AB C D EFA B CDEF22 / 26【作业3】如图,AD 是ABC ∆的中线,1tan 3B =,2cos 2C =,2AC =.求:(1)BC 的长;(2)sin ADC ∠的值.【答案】(1)4;(2)22.【解析】(1)作AE BC ⊥交BC 于点E , 则cos 1CE AC C AE =⋅==,由1tan 3AE B BE ==,即得:3BE =,则4BC CE CE =+=;(2)因为AD 是ABC ∆中线,则有2BD CD ==,即得:1DE CD CE =-=,由勾股定理,得:222AD AE DE =+=,则有12sin 22AE ADC AD ∠===. 【总结】解三角形,通过作高把边转化到直角三角形中即可.【作业4】如图,轮船从B 处以每小时60海里的速度沿南偏东20°的方向匀速航行,在B 处观测灯塔A 位于南偏东50°方向上.轮船航行40分钟到达C 处,在C 处观测灯塔A 位于北偏东10°方向上,则C 处与灯塔A 的距离是( )A .20海里B .40海里C .2033海里D .4033海里【答案】D .【解析】依题意可得:30ABC ACB ∠=∠=︒,则有AB AC =,作AD BC ⊥交BC 于D ,轮船行程即260403BC =⨯=,则有1202BD CD BC ===,403cos 3CD AC ACB ==∠. 【总结】考查方位角知识的应用,本题重点在于准确分析相关角度的大小再利用特殊角的锐角三角比解决问题.ABCD EABC 北东D【作业5】如图,在ABC ∆中,45B ∠=︒,562AB =,D 是BC 上一点,AD = 5,CD = 3,求ADC ∠的度数及AC 的长.【答案】60ADC ∠=︒,19AC =.【解析】作AE BC ⊥交BC 于点E ,则有56253sin 222AE AB B =⋅=⨯=, 3sin 2AE ADE AD ∠==,即得sin 60ADE ∠=︒, 则1522DE AD ==,则12CE CD DE =-=,勾股定理得2219AC AE CE =+=.【总结】考查特殊角锐角三角比的应用,作高把线段放到直角三角形中即可.【作业6】如图,点D 在ABC ∆的边BC 上,C BAD DAC ∠+∠=∠,4tan 7BAD ∠=,65AD =,CD = 13,求线段AC 的长.【答案】265.【解析】作DE AB ⊥交AB 于点E ,作AF BC ⊥交BC 于点F , 作DAG BAD ∠=∠交CD 于点G ,作DH AG ⊥交AG 于点H . ∵4tan 7DE BAD AE ∠==,勾股定理得22265AE DE AD +==,∴4DE =,7AE =.∵AD 为角平分线,根据角平分线性质有4DH DE ==,7AH AE ==,C BAD DAC ∠+∠=∠,即C BAD DAH GAC ∠+∠=∠+∠,即得:C GAC ∠=∠.∴AG CG =,设AG a =,则有7GH a =-,13DG a =-,在Rt DGH ∆中,∵222DH HG DG +=,∴()()2224713a a +-=-,解得:263a =, 即263AG GC ==,此时13133DG a =-=. 在ADG ∆中用面积法,则有DH AG AF DG ⋅=⋅,即2613433AF ⨯=⋅, 即得8AF =,Rt ADF ∆勾股定理,得()22226581DF AD AF =-=-=,则12CF CD DF =-=,由此可得2222812413AC AF CF =+=+=.【总结】本题综合性较强,综合应用了锐角三角比、角平分线的性质、面积法等解三角形常用的方法,主要是根据题目条件进行变化得出最终结果.【作业7】如图,一栋楼房AB 背后有一台阶CD ,台阶每层高0.2米,且AC = 17.2米.设太阳光线与水平地面的夹角为α,当60α=︒时,测得楼房在地面上的影长AE = 10米.现D AB CE HF EGABCD24 / 26有一只小猫睡在台阶的MN 这层上晒太阳.(参考数据:3 1.73≈)(1)楼房的高度约为多少米?(2)过了一会儿,当45α=︒时,问小猫能否还晒到太阳?请说明理由. 【答案】(1)17.3m ;(2)能.【解析】(1)根据锐角三角比的含义,tan AB AE α=,则有tan 10317.3AB AE m α=⋅=≈;(2)45α=︒时,影长即为tan 17.3AB m α⋅=, 17.317.20.10.2m m -=<,即影子的落点正在在台阶侧面CM 上,此时小猫还是可以晒到太阳的.【总结】考查利用锐角三角比解决实际问题,化为实际三角形模型即可.【作业8】如图,CD 是ABC ∆的中线,已知90ACD ∠=︒,3cos 5A =,求tan BCD ∠的值. 【答案】38.【解析】由90ACD ∠=︒,3cos 5AC A AD ==,可设3AC a =,则5AD a =,根据勾股定理,可得:224CD AD AC a =-=. 延长CD 到E ,使DE CD =,连结AE .由AD BD =,CDB ADE ∠=∠,可证CDB EDA ∆≅∆,则有BCD E ∠=∠,由此可得:33tan tan 248AC a BCD E CE a ∠=∠===⨯.【总结】考查“倍长中线法”在解三角形中的应用,可进行等角转化,将不便计算的角放到直角三角形中即可.【作业9】如图,在梯形ABCD 中,AD // BC ,AB = 4,BC = 6,DAC B AEF ∠=∠=∠,点E 、F 分别在BC 、AC 上(点E 与B 、C 不重合),设BE = x ,AF = y .(1)求cos B ;ABCDENM ABCDE(2)求证:ABE ∆∽ECF ∆; (3)求y 关于x 的代数式;(4)当点E 在BC 上移动时,AEF ∆是否有可能是直角三角形?若有可能,请求出BE 的长;若不能,请说明理由.【答案】(1)34;(2)略;(3)26164x x y -+=;(4)23BE =或3BE =.【解析】(1)作AG BC ⊥交BC 于点G , //AD BC , DAC ACB ∴∠=∠. DAC B ∠=∠, B ACB ∴∠=∠.AB AC ∴=, 132BG CG BC ∴===.3cos 4BG B AB ∴==.(2)证明:AEC B BAE AEF FEC ∠=∠+∠=∠+∠,又B AEF ∠=∠, BAE FEC ∴∠=∠,B ACB ∠=∠,∴ABE ∆∽ECF ∆.(3)由ABE ∆∽ECF ∆,则有AB BEEC CF=,即464x x y =--,整理得:26164x x y -+=; (4)①90AEF B ∠=∠<︒,即AEF ∠不可能为直角;②90EAF ∠=︒,则有3cos cos 4AC ACE B EC ∠===,4AC AB ==,则有163EC =,则162633BE BC EC =-=-=;③90AFE ∠=︒,此时则有90AEB EFC ∠=∠=︒,此时点E 与点G 重合,即为BC 中点,此时3BE =;综上所述,23BE =或3BE =.【总结】考查“一线三等角”证相似的基本模型,同时对直角三角形的存在性问题可转化为固定角的锐角三角比不变的问题.【作业10】如图(a )所示,已知正方形ABCD 在直线MN 的上方,BC 在直线MN 上,E是BC 上一点,以AE 为边在直线MN 的上方作正方形AEFG .(1)连接GD ,求证:ADG ∆≌ABE ∆;(2)连接FC ,观察并猜测FCN ∠的度数,并说明理由;ABCDE FG。
沪教版(五四学制)九年级数学上册2相似三角形的性质课件

则:SABC ? S DEF
M
N
类似三角形性质定理3:
类似三角形的面积的比等于类似比的平方。
∵ △ABC∽ △DEF,且
类似比为k
S ABC S DEF
k2
或
∵ △ABC∽ △DEF
SABC
AB 2
SDEF DE
已知两个三角形类似,根据下列数据填表
求 SABC 的值。
1.(1)如果把一个三角形的三边的长扩大为
本来的100倍,那么这个三角形的面积扩大为本来
的
倍。
1.(2)如果一个三角形保持形状不变但面积
扩大为本来的100倍,那么这个三角形的边长扩大
为本来的
倍。
S1
100S1
2.已知:D、E、F分别是△ABC的边BC、 CA、AB的中点.
求证:S A B C 4S D E F
两个三角形类似可得出的结论:
1.根据定义:类似三角形对应角相等,对应边成比 例。 2.根据类似三角形性质定理1:
类似三角形对应高、对应中线和对应角平分线的 比等于类似比。
类似三角形周长的比与类似比的关系
已知△ABC∽ △DEF,点A、B、C对应点 D、E、F,△ABC与△DEF的类似比为k,把
这两个三角形的周长分别记作
类似比
k
对应中线的比
1
2 对应角平分线的比
对应高的比 对应周长的比 对应面积的比
5 9 4 100
1.已知△ABC∽ △DEF,点A、B、C对 应点D、E、F,它们的周长分别为48和60,
且AB=12,EF=25 ,求BC、DE的长。
D
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 长方体的元素及特征1、元素:长方体有六个面,八个顶点,十二条棱.2、特征:(1)长方体的每个面都是长方形.(2)长方体的十二条棱可以分为三组,每组中的四条棱的长度相等. (3)长方体的六个面可以分为三组,每组中的两个面的形状和大小相同. 二、 长方体的直观图画法:斜二侧画法水平放置的长方体直观图通常画法的基本步骤:第一步:画平行四边形ABCD ,使AB 等于长方体的长,AD 等于长方体宽的二分之一,45DAB ∠=︒.(如图1所示)第二步:过AB 分别画AB 的垂线AE 、BF ,过C 、D 分别画CD 的垂线CG 、DH ,使它们的长度都等于长方体的高.(如图2所示)第三步:顺次联结E 、F 、G 、H .(如图3所示)第四步:将被遮住的线段改用虚线(隐藏线)表示.(如图4所示)长方体与三角形知识结构模块一:长方体的再认识知识精讲2 / 27图4表示的长方体通常表示为ABCD -EFGH .它的六个面通常表示为:平面ABCD 、平面ABFE 、平面BCGF 等.它的十二条棱通常分别表示为:棱AB 、棱AE 、棱EF 等. 三、 长方体中棱与棱的位置关系如图4所示的长方体ABCD -EFGH 中:棱EH 与棱EF 所在的直线在同一平面内,它们有唯一的公共点,我们称这两条棱相交.棱EF 与棱AB 所在的直线在同一平面内,但它们没有公共点,我们称这两条棱平行.棱EH 与棱AB 所在的直线既不平行,也不相交,我们称这两条棱异面. 四、 长方体中棱与平面的位置关系如图5,直线PQ 垂直于平面ABCD ,记作:直线PQ 平面ABCD ,读作:直线PQ 垂直于平面ABCD .如图6,直线PQ 平行于平面ABCD ,记作:直线PQ // 平面ABCD ,读作:直线PQ 平行于平面ABCD .如图4所示的长方体ABCD -EFGH 中:棱EF 与面BCGF ,棱FG 与面ABFE ,棱BF 与面ABCD 都给我们以直线与平面垂直的形象.棱EF 与面ABCD ,棱BF 与面ADHE ,都给我们以直线与平面平行的形象.ABCDABC D EFGHABCD E FGHABCD E FGH图1 图2 图3图4ABC D PQ ABCD PQ图5图6五、 长方体中平面与平面的位置关系如图7,平面α垂直于平面β,记作平面α⊥平面β,读作平面α垂直于平面β.如图8,平面α平行于平面β,记作平面α//平面β,读作平面α平行于平面β. 如图4所示的长方体ABCD -EFGH 中:面EFGH ,面ABFE 与面BCGF 三个面中,任意两个都给我们以平面与平面垂直的形象.面ABCD 与面EFGH ,面BCGF 与面ADHE ,面ABFE 与面DCGH ,都给我们以平面与平面平行的形象.【例1】 如图,已知长方体ABCD -EFGH .(1)哪些棱与AB 平行? (2)哪些棱与AB 垂直? (3)哪些棱与AB 异面?【答案】(1)棱EF 、HG 、DC 与AB 平行; (2)棱EA 、FB 、DA 、CB 与AB 相交; (3)棱EH 、GF 、DH 、CG 与AB 异面.【解析】长方体中与一个棱平行的有3条,垂直的有4条,异面的有4条. 【总结】考查长方体中相关基本概念.【例2】 如图,已知长方体ABCD -EFGH ,与平面ADHE 平行的平面是____________,与例题解析ABC D EFGH4 / 27平面ADHE 垂直的平面是____________.【答案】平面BCGF ;平面ABFE 、平面ABCD 、平面DCGH 、平面EFGH .【解析】长方体中与任何一个面平行的面有1个,与任何一个面垂直的 有4个面.【总结】考查长方体中平面间的关系.【例3】 下列关于长方体的说法中正确的是( )A .长方体中互相平行的棱不一定相等B .长方体中12条棱的位置关系只有平行和相交C .长方体中相对的两个面一定平行D .长方体中6个面的面积都相等 【答案】C【解析】A 、互相平行的棱一定相等;B 、还有异面;D 、6个面不一定相等,当棱长都相等 时,六个面的面积都相等. 【总结】考查长方体的基本元素的认知.【例4】 关于长方体有下列三个结论:○1长方体中每个面都是长方形; ○2长方体中每两个面都互相垂直; ○3长方体中相对的两个面是全等的长方形. 其中结论错误的个数是( ) A .0个 B .1个 C .2个 D .3个【答案】B【解析】①正确;②对面互相平行,错误;③正确. 【总结】考查长方体中每个面的特征及面与面之间的关系.【例5】 如图,已知长方体ABCD -EFGH .这个长方体中与棱HE 平行的平面是____________,与棱HE 垂直的平面是____________.【答案】平面ABCD 、BCGF ;平面ABFE 、平面DCGH .ABCD EFGHABCD EFGH【解析】长方体中与任何一条棱平行的面有两个,与任何一条棱垂直的面也有两个.【总结】考查长方体中棱与面的位置关系.【例6】已知一个长方体的长、宽、高的比是3 : 2 : 1,它的所有棱长的和是72 cm,那么这个长方体的体积是______3cm.【答案】3162cm.【解析】设长、宽、高分别为3x、2x、x,则()++=,x x x42372解得:3x=,∴长、宽、高分别为9、6、3,∴体积为3⨯⨯=.963162cm【总结】考查长方体的体积的计算.6 / 2734ABCD O一、 邻补角1、邻补角的概念:两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角叫做互为邻补角.如图,1∠与2∠有一条公共边OD ,它们的另一条边OA 、OB 互为反向延长线,则1∠与2∠互为邻补角.2、若1∠与2∠互为邻补角,则12180∠+∠=︒.3、互为邻补角的两个角一定互补,但互补的两个角不一定互为邻补角. 二、 对顶角1、对顶角的概念:两个角有公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种关系的两个角叫做互为对顶角.如图,3∠与4∠有一个公共顶点O ,并且3∠的两边OB 、OC 分别与4∠的两边OA 、OD 互为反向延长线,则1∠与2∠互为对顶角.2、对顶角相等. 三、 垂线1、垂线的概念:如果两条直线的夹角为直角,那么就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.模块二:相交线与平行线ADOB12 知识精讲abl 1 2 3 456 7 82、垂直的符号:记作:“⊥”,读作:“垂直于”,如:CD AB ⊥,读作“AB 垂直于CD ”. 注:垂直是特殊的相交.3、在平面内,过直线上或直的一点作已知直线的垂线可以作一条,并且只能作一条.简单地说:过一点,有且仅有一条直线与已知直线垂直. 4、联结直线外一点与直线上各点的所有线段中,垂线段最短. 5、点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离. 如果一个点在直线l 上,那么就说这个点到直线l 的距离为零.四、 同位角、内错角、同旁内角若直线a ,b 被直线l 所截:(1)同位角:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.如:1∠和5∠.(2)内错角:两个角分别在截线的两侧,且在两条直线之间,具有这样位置关系的一对角叫做内错角.如:3∠和5∠.(3)同旁内角:两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角.如3∠和6∠.注意:三线八角是位置关系,数量上没有确定的关系. 五、 平行线1、平行线的定义:同一平面内不想交的两条直线叫做平行线.“平行”用符号“//”表示.2、经过直线外一点,有且只有一条直线与已知直线平行.3、平行线的判定:(1)两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 简单地说,同位角相等,两直线平行.8 / 27ABCD EF (2)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 简单地说,内错角相等,两直线平行.(3)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行. 简单地说,同旁内角互补,两直线平行. 4、平行线的性质:(1)两条平行线被第三条直线所截,同位角相等; 简单地说:两直线平行,同位角相等.(2)两条平行线被第三条直线所截,内错角相等; 简单地说:两直线平行,内错角相等.(3)两条平行线被第三条直线所截,同旁内角互补; 简单地说:两直线平行,同旁内角互补相等.(4)如果两条直线都与第三条直线平行,那么这两条直线也互相平行.(5)两条平行线中,任意一条直线上的所有点到另一条直线的距离都是一个定值,这个定值叫做这两条平行线间的距离.【例7】 如图,CEB ∠的邻补角为______,CEB ∠的对顶角为______;在图中,找出一对同位角,可以是______和______,找出一对同旁内角,可以是______和______.【答案】∠CEA 、∠BED ;∠AED ;∠CBE 和∠FEA ;∠CBE 和∠FEB 等. 【解析】同位角像字母F ,同旁内角像字母U . 【总结】考查三线八角的基本概念.【例8】 在同一平面中,如果直线a b ⊥,b c ⊥,那么直线a 与c 的位置关系是______;如例题解析ABCDEF果直线a // b ,c a ⊥,那么直线b 与c 的位置关系是______.【答案】平行;垂直.【解析】同一平面内,垂直于同一条直线的两条直线互相平行. 【总结】考查同一平面内直线间的位置关系.【例9】 如图,已知AB // CD ,BF 与CD 相交于点E ,如果46DEF ∠=︒,那么B ∠=______. 【答案】134°.【解析】∵∠BEC =∠DEF =46°(对顶角相等) 又∵AB ∥CD ,∴∠B =180°-∠BEC =180°-46°=134°. 【总结】考查平行线的性质及对顶角性质的综合运用.【例10】 下列说法正确的是( )A .直线外一点到这条直线的距离是这点到这条直线的垂线段B .同位角相等C .如果两个角互补,那么这两个角是邻补角D .过一点有且只有一条直线垂直于已知直线 【答案】D【解析】A 、直线外一点到这条直线的距离这点到这条直线的垂线段的长度,故错误; B 、两直线平行,同位角相等,错误; C 、邻补角不仅互补而且有公共边,错误; 故选D .【总结】考查基本概念及直线间的位置关系.【例11】 已知直线1l //2l ,直线3l 分别与直线1l 、直线2l 相交;点A 在直线1l 上,点B 在直线2l 上,点A 、B 在直线3l 的同侧;点C 在直线3l 上,且点C 不在1l 与2l 上.设直线AC 与1l 所夹的锐角为α,直线BC 与2l 所夹的锐角为β.试问α、β、ACB ∠之10 / 27间有怎样的数量关系?证明你的结论.【解析】(1)当点C 在直线1l 与2l 之间时,如图1, 过点C 作CE ∥1l ,则ACE α∠=, BCE β∠=, 又ACB ACE BCE ∠=∠+∠, ∴ACB αβ∠=+;(2)当点C 不在直线1l 与2l 之间时. ①当点C 接近2l 时,如图2,过点C 作CE ∥1l ,则ACE α∠=,BCE β∠=, 又ACB ACE BCE ∠=∠-∠, ∴ACB αβ∠=-; ②当点C 接近1l 时, 同理可得:ACB βα∠=-.【总结】本题综合性较强,注意考查平行线的性质及角的和差的综合性运用,注意要分类讨 论.E βαCBAl 3l 2l 1图1EβαCBAl 3l 2l 1图2一、三角形的边与角1、三角形的三边关系:三角形任意两边的和大于第三边,任意两边之差小于第三边.2、三角形的高、中线、角平分线:①在三角形中,从一个顶点向它的对边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的高;②联结三角形一个顶点及其对边中点的线段叫做三角形的中线;③三角形一个内角的平分线与这个角的对边相交,这个角顶点与交点之间的线段叫做三角形的角平分线.3、三角形的内角和:三角形的内角和等于180°.※一个三角形的三个内角中最多有一个钝角或直角.4、三角形的外角:(1)三角形的一个外角等于与它不相邻的两个内角的和;(2)三角形的外角和定义:对于三角形的每个内角,从与它相邻的两个外角中取一个,这样取得的三个外角相加所得的和,叫做三角形的外角和;三角形的外角和等于360°.5、三角形的分类三角形(按角分)⎧⎪⎧⎨⎨⎪⎩⎩直角三角形(有一个内角为直角)锐角三角形斜三角形(无一内角为直角)钝角三角形;三角形(按边分)⎧⎪⎧⎨⎨⎪⎩⎩不等边三角形底边和腰不等的等腰三角形等腰三角形等边三角形.模块三:三角形知识精讲12 / 27二、 全等三角形1、全等形的概念:能够重合的两个图形叫做全等形.一般三角形 直角三角形判定边角边(S .A .S .)角边角(A .S .A .) 角角边(A .A .S .) 边边边(S .S .S .)具备一般三角形的判定方法 斜边和一条直角边对应相等(H .L .)性质对应边相等,对应角相等对应中线相等,对应高相等,对应角平分线相等注:①判定两个三角形全等必须有一组边对应相等; ②全等三角形面积相等. 3、证明题的思路:SAS HL SSS AAS SAS AAS ASA ASA AAS ⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎪⎪⎪⎧⎪⎨⎨⎪⎨⎪⎪⎪⎪⎪⎩⎩⎪⎪⎪⎧⎪⎨⎪⎩⎩找夹角()已知两边找直角()找第三边()若边为角的对边,则找任意角()找已知角的另一边()已知一边一角边为角的邻边找已知边的对角()找夹已知边的另一角()找两角的夹边()已知两角找任意一边() 三、 等腰三角形1、等腰三角形的两个底角相等,简称:等边对等角.2、等腰三角形的顶角平分线、底边上的中线、底边的高互相重合,简称:等腰三角形三线合一.3、等腰三角形是轴对称图形,它的对称轴是顶角的角平分线所在的直线.4、等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等,这个三角形是等腰三角形.简称:等角对等边.四、 直角三角形1、直角三角形全等的判定:斜边与一直角边对应相等的两个直角三角形全等(H .L .). 2、直角三角形的性质:(1)两个定理定理1:直角三角形的两个锐角互余;定理2:直角三角形斜边上的中线等于斜边的一半.(2)两个推论推论1:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;推论2:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.3、勾股定理(1)如果直角三角形两直角边分别为a、b,斜边为c,那么一定有222a b c+=,即直角三角形两直角边的平方和等于斜边的平方.(2)勾股定理逆定理:如果三角形的三边满足222a b c+=,那么三角形是直角三角形.例题解析【例12】(2014学年·杨浦区二模·第4题)下列命题中,真命题是()A.周长相等的锐角三角形都全等B.周长相等的直角三角形都全等C.周长相等的钝角三角形都全等D.周长相等的等腰直角三角形都全等【答案】D【解析】A、B、C不一定全等,D、周长相等的等腰直角三角形可以由“SSS”判断出全等.【总结】考查全等三角形的概念及判定方法的运用.【例13】(2015学年·闸北区二模·第5题)如图,已知BDA CDA∠=∠,则不一定能使14 / 27ABCDE ABD ∆≌ACD ∆的条件是( )A .BD CD =B .AB AC =C .B C ∠=∠D .BAD CAD ∠=∠【答案】B【解析】A 、可以通过“SAS ”判断出全等;C 、可以通过“AAS ”判断出; D 、可以通过“ASA ”判断出. 【总结】考查全等三角形的判定.【例14】 (2015学年·徐汇区二模·第6题)下列命题中假命题是( )A .两边及第三边上的高对应相等的两个三角形全等B .两边及第三边上的中线对应相等的两个三角形全等C .两边及它们的夹角对应相等的两个三角形全等D .两边及其中一边上的中线对应相等的两个三角形全等 【答案】A【解析】可通过画图举出反例.【总结】考查全等三角形的判定,注意当出现三角形边上的高时,通常都要分两种情况讨论.【例15】 (2014学年·静安区、青浦区二模·第6题)三角形的内心是( )A .三边垂直平分线的交点B .三条角平分线的交点C .三条高所在直线的交点D .三条中线的交点【答案】B【解析】A 是外心;C 是垂心;D 是重心. 【总结】考查三角形中四心的基本概念.【例16】 (2015学年·静安区二模·第15题)在Rt ABC ∆中,90C ∠=︒,A ∠、B ∠的平分线相交于点E ,那么AEB ∠的度数是______.【答案】135°.【解析】∠AEB =180°-∠BAE -∠ABE =180°-()12A B ∠+∠=180°-45°=135°. 【总结】考查三角形内角和及其外角性质的综合应用.【例17】 (2014学年·静安区、青浦区二模·第13题)如图,在Rt ABC ∆中,90ACB ∠=︒,AB = 2 AC ,点E 在中线CD 上,BE 平分ABC ∠,那么DEB ∠的度数是______.【答案】45°.【解析】∵AB =2AC ,90ACB ∠=︒,CDABABCM HABC∴∠ABC =30°.又∵CD 为中线 ,∴BD = CD ∴∠BDC =120°.又∵BE 平分∠ABC , ∴∠DBE =15°, ∴∠DEB =180°-∠BDC -∠DBE =45°.【总结】本题主要考查直角三角形的性质定理的推论及三角形内角和的综合运用.【例18】 (2014学年·徐汇区二模·第4题)如图,已知ABC ∆中,90ACB ∠=︒,CH 、CM分别是斜边AB 上的高和中线,则下列结论不正确的是( ) A .222AB AC BC =+B .2CH AH HB =C .12CM AB =D .12CB AB =【答案】D【解析】A 、勾股定理,正确;B 、射影定理,正确;C 、直角三角形斜边中线等于斜边一半,正确;D 、只有当∠A=30°时才成立,错误. 【总结】考查三角形的基本性质及其推论的运用.【例19】 (2014学年·徐汇区二模·第16题)如图,DE 为ABC ∆的中位线,点F 在DE 上,且AFB ∠为直角,若AB = 8,BC = 10,则EF 的长为______.【答案】1【解析】∵DE 为中位线,∴152DE BC ==. ∵DF 为直角三角形ABF 斜边AB 上的中线,∴DF =142AB =,∴EF =DE -DF =1.【总结】考查直角三角形的性质及中位线定理的综合运用.【例20】 如图,网格中小正方形的边长均为1,ABC ∆的三个顶点在格点上.求证:ABC ∆是等腰直角三角形. 【答案】略.【解析】由图易知:5AC BC ==,10AB =, ∴222AC BC AB +=,∴△ABC 为等腰直角三角形. 【总结】考查勾股定理及其逆定理的综合运用.BAEFCD16 / 27AB CDEP【例21】 如图,已知Rt ABC ∆中,90C ∠=︒,AD 平分A ∠,交边BC 于点D ,AB = 10,AC = 6,求点D 到边AB 的距离.【答案】3.【解析】过D 作DE ⊥AB 于点E ,则DC =DE (角平分线上的点到角两边的距离相等) 所以AE =AC =6,设DC =DE =x ,则DB = 8-x ,BE =4, 在Rt BDE 中,由勾股定理得: ()22248x x +=-, 解得:x =3, ∴点D 到边AB 的距离为3.【总结】考查角平分线性质定理及勾股定理的综合运用.【例22】 如图,等边三角形ABC 的两条角平分线BD 、CE 相交于点P ,BP = 10 cm ,求PD的长.【答案】5cm .【解析】∵△ABC 为等边三角形,CE 平分∠ACB∴∠ACE =30°, 又∵BP =10cm , ∴CP =10cm∴PD =152PC cm =(直角三角形中30°角所对的边等于斜边的一半)【总结】考查等边三角形及直角三角形的性质的综合运用.【例23】 (2014学年·崇明县区二模·第15题)如图,已知ABC ∆和ADE ∆均为等边三角形,点D 在BC 边上,DE 与AC 相交于点F ,如果AB = 9,BD = 3,那么CF 的长度为______.【答案】2【解析】∵60B ADE C ∠=∠=∠=, ∴△ABD ∽△DCF , ∴AB BD DC CF =, 即936CF =,∴CF =2. 【总结】考查利用一线三等角证明相似.【例24】 (2014学年·虹口区二模·第14题)在Rt ABC ∆中,90C ∠=︒,点G 是Rt ABC ∆的ABCEFDABCDE重心,如果CG = 6,那么斜边AB 的长等于______.【答案】18.【解析】延长CG 交AB 于点D ,则CD =392CG =,所以AB =2CD =18.【总结】考查重心的性质及直角三角形的性质的综合运用.【例25】 如果等腰三角形腰上的高等于腰长的一半,那么这个三角形的顶角的度数为______.【答案】30°或150°.【解析】直角三角形中30°对应的边等于斜边的一半. 【总结】考查直角三角形的性质,注意要分类讨论.【例26】 (2015学年·宝山区、嘉定区二模·第21题)如图,在ABC ∆中,按以下步骤作图:①分别以A ,B 为圆心,大于12AB 的长为半径画弧,相交于两点M ,N ;②联结MN ,直线MN 交ABC ∆的边AC 于点D ,联结BD .如果此时测得34A ∠=︒,BC = CD . 求ABC ∠与C ∠的度数.【答案】∠ABC =102°,∠C =44°.【解析】由题意知MN 为AB 的垂直平分线,∴∠DBA =∠A=34°, ∵BC =DC ∴∠CBD =∠CDB =∠DBA +∠A=68°, ∴∠ABC =34°+68°=102°,∠C =44°【总结】考查垂直平分线的性质定理及三角形内角和的综合运用.【例27】 已知Rt ABC ∆中,90C ∠=︒,AC = 4,BC = 3.以ABC ∆的边AC 为一边的等腰三角形,它的第三个顶点D 在ABC ∆的斜边AB 上,求这个等腰三角形的周长.【答案】98+. 【解析】(1)当AC 为底边时, 由勾股定理,得:AB =5,∵点D 在边AB 上且△ACD 为等腰三角形, ∴D 为AB 中点, ∴ACDC=AD +CD +AC =AB +AC =5+4=9;(2)当AC为腰时,利用勾股定理的等面积,可得CD =∴448ACDC+=+. 【总结】考查等腰三角形性质及勾股定理的运用,注意分类讨论.NM ABD C18 / 27ABCDEMH【例28】 已知ABC ∆中,90A ∠=︒,AB = AC ,D 为BC 的中点.(1)如图,E 、F 分别是AB 、AC 上的点,且BE = AF ,求证:DEF ∆是等腰直角三角形. (2)如果E 、F 分别是AB 和CA 的延长线上的点,且BE = AF ,那么DEF ∆是否仍为等腰直角三角形?证明你的结论.【答案】略.【解析】(1)连接AD ,∵ABC 为等腰直角三角形且D 为BC 中点, ∴AD =BD ,∠B =∠CAD =45° 在△ADF 与△BDE 中, ∵AF =EB ,∠B =∠CAD ,AD =BD ∴△ADF ≌△BDE (SAS ) ∴DE =DF ,∠BDE =∠ADF又∵∠ADE +∠BDE =90°,∴∠ADF +∠ADE =90°, ∴△DEF 为等腰直角三角形(2)仍是等腰直角三角形,证明方法同(1). 【总结】考查等腰三角形的性质及三角形全等的证明.【例29】 如图,在ABC ∆形外作等腰Rt ABD ∆和等腰Rt ACE ∆,使90BAD ∠=︒,90CAE ∠=︒,作AH BC ⊥于H ,延长HA ,交DE 于M ,求证:DM = ME .【答案】略.【解析】∵AB =AD ,90BAC DAE ∠=∠=,AC =AE ∴△BAC ≌△DAE ,∴∠ADE =∠ABC ,∠AED =∠ACB .又∵∠ABC =∠CAH =∠MAD ,∠ACB =∠BAH =∠MAE ∴∠ADE =∠MAD ,∠AED =∠MAE ∴AM =DM ,AM =EM ∴DM =ME【总结】本题综合性较强,考查的知识点比较多,包含等腰直角三角形的性质、同角的余角 相等、等角对等边等,说理时要认真分析,找到其中的联系.ABCDEF【例30】如图,在菱形ABCD中,120BAD∠=︒,M、N分别为BC、CD上的点,求证:若AMN∆有一个内角等于60°,则AMN∆是正三角形.【答案】略.【解析】连接AC,∵四边形ABCD为菱形且∠BAD=120°,∴△ABC、△ADC是等边三角形∴AC=AD,∠ACM=∠D=60°又∵∠MAC+∠CAN=60°=∠CAN+∠NAD,∴∠MAC=∠NAD在△ACM与△ADN中,∵AC=AD,∠ACM=∠D=60°,∠MAC=∠NAD∴△ACM≌△ADN,∴AM=AN,又∵△AMN有一个内角等于60°,∴△AMN是等边三角形.【总结】本题主要考查了等边三角形的性质及菱形性质的综合运用.ABCD NM20 / 27ABCDEP【习题1】 (2015学年·奉贤区二模·第5题)下列说法中,正确的是( )A .关于某条直线对称的两个三角形一定全等B .两个全等三角形一定关于某条直线对称C .面积相等的两个三角形一定关于某条直线之间对称D .周长相等的两个三角形一定关于某条直线之间对称 【答案】A【解析】B 、C 、D 都不一定.【习题2】 (2014学年·长宁区、金山区二模·第7题)如图,已知AD 是ABC ∆的边BC 上的高,下列能使ABD ∆≌ACD ∆的条件是( ) A .45B ∠=︒ B .90BAC ∠=︒ C .BD AC = D .AB AC =【答案】D【解析】若AB =AC ,在直角三角形ABD 和直角三角形ACD 中, ∵AB =AC ,AD =AD ,∴△ABD ≌△ACD (HL ) 【总结】考查直角全等三角形的判定.【习题3】 画一个长、宽、高分别为3 cm 、2 cm 、2.5 cm 的长方体的直观图. 【答案】图略【解析】先画出一个平行四边形是关键,注意正面看不到的边要用虚线联结. 【总结】考查基本作图能力,利用斜二测法画长方体.【习题4】 如图,已知等边三角形ABC 中,点D 在边AB 上,点E 在边BC 上,AD = BE ,那么CPE ∠=______.【答案】60°.随堂检测D CB AA B CI【解析】在△ABE 与△CAD 中, ∵AD =BE ,∠B =∠BAC ,AB =AC ,∴△ABE ≌△CAD (SAS ) ,∴∠ACD =∠BAE ∴∠CPE =∠CAE +∠ACD =∠CAE +∠BAE =∠BAC =60° 【总结】考查全等三角形的性质及三角形外角性质的综合运用.【习题5】 (2015学年·崇明县二模·第14题)如图,在已知的ABC ∆中,按以下步骤作图:① 分别以B ,C 为圆心,以大于12BC 的长为半径作弧,两弧相交于两点M ,N ;②作直线MN 交AB 于点D ,连接CD .若CD AC =,50A ∠=︒,则ACB ∠的度数为______. 【答案】105°.【解析】由题意知MN 为线段BC 的垂直平分线, ∴∠B =∠BCD ,∵CD =AC ,∠A =50°,∴∠CDA =50°,∠ACD =180°-50°-50°=80°, 又∵∠B +∠BCD =∠CDA , ∴∠BCD =25°, ∴∠ACB =∠ACD +∠BCD =105°.【总结】考查线段垂直平分线的性质及三角形内角和的综合运用.【习题6】 已知ABC ∆中,B ∠和C ∠两角的平分线相交于点I ,60ABC ∠=︒,45ACB ∠=︒,求AIB ∠的度数. 【答案】112.5°.【解析】由题意知AI 为∠BAC 的角平分线,∴∠BAI =()11802ABC ACB ︒-∠-∠=()1180604537.52︒-︒-︒=︒,∴∠AIB =180°-30°-37.5°=112.5°【总结】考查角平分线性质及三角形内角和的运用,注意三角形的三条角平分线交于同一点. 【习题7】 已知:如图,在四边形ABCD 中,BC > BA ,AD = DC ,BD 平分ABC ∠.求证:180A C ∠+∠=︒. 【答案】略【解析】在BC 上取点E ,使得BE =AB ,连接DE则△ADB ≌△EDB . ∴AD =DE ,∠A =∠BED ,D NABCMABCD E∵AD = DC ,∴DE = DC ,∴∠DEC=∠C.∵∠BED+∠DEC=180°,∴∠A+∠C=180°.【总结】考查截长补短法辅助线的添加.【习题8】已知:如图,在四边形ABCD中,90A∠=︒,BD = DC,BC = 2AB.求证:点D在ABC∠的角平分线上.【答案】略【解析】过点D作DH⊥BC于点H,∵BD=CD,∴H为BC中点,又∵BC=2AB,∴BA=BH在△ABD与△HBD中,∵∠A=∠BHD=90°,BA=BH,BD=BD,∴△ABD≌△HBD∴点D在∠ABC的角平分线上【总结】考查等腰三角形的性质及全等三角形的证明.【习题9】已知,在ABC∆中,AB = AC,点P在直线BC上,PD⊥AB于点D,PE⊥AC 于点E,BH是ABC∆的高.(1)当点P在边BC上时(如图),求证:PD PE BH+=;(2)当点P在边BC的延长线上时,试探索PD、PE、BH之间的数量关系.【答案】略【解析】(1)连接AP,∵12ABCS AC BH=⨯⨯△,ABCDHAB CDEPH22/ 27ABCDEF G又1122ABC ABP ACP S S S AB PD AC PE =+=⨯⨯+⨯⨯△△△=1()2AB PD PE ⨯⨯+∴PD +PE =BH ; (2)证法同(1).【总结】考查利用三角形面积相等证明线段间的等量关系.【习题10】 (2014学年·徐汇区二模·第23题)如图,已知在正方形ABCD 中,点E 在CD 边上,过C 点作AE 的垂线交于点F ,联结DF ,过点D 作DF 的垂线交AF 于点G ,联结BG .(1)求证:ADG ∆≌CDF ∆;(2)如果E 为CD 的中点,求证:BG AF ⊥. 【答案】略.【解析】(1)∵∠ADG =∠CDF = 90°-∠GDC ,∠DAG = 90°-∠DEA ,∠DCF = 90°-∠CEF , 又∵∠DEA =∠CEF , ∴∠DAG =∠DCF . 在△ADG 与△CDF 中,∵∠ADG =∠CDF ,AD =CD ,∠DAG =∠DCF , ∴△ADG ≌△CDF (ASA )(2)设正方形边长为a ,由△ADE ∽△CFE 得,AG =CF =55a , 由AG ABDE AE=,∠BAG =∠AED ,得:△ABG ∽△EAD , 即∠AGB =90°,∴BG ⊥AF .【总结】考查全等三角形的证明及相似证明的综合运用.【作业1】 (2015学年·徐汇区二模·第3题)如图,在ABC ∆中,BC 的垂直平分线EF 交ABC ∠的平分线BD 于E ,如果60BAC ∠=︒,24ACE ∠=︒,那么BCE ∠的大小是( ) A .24°B .30°C .32°D .36°【答案】C【解析】由题意,知:∠ABE =∠EBF =∠BCE ,课后作业BAD CE F24 / 27A BCDE∴∠BCE =()()180318060243A ACE ︒-∠-∠÷=︒-︒-︒÷=32°.【总结】考查线段垂直平分线及角平分线的性质及三角形内角和的综合运用.【作业2】 (2014学年·金山区二模·第5题)如图,AB // CD ,13D ∠=︒,28B ∠=︒,那么E ∠等于( ) A .13° B .14° C .15° D .16°【答案】C【解析】∵AB ∥CD∴∠BCD =∠B =28°(两直线平行内错角相等)又∵∠BCD =∠D +∠E , ∴∠E =∠BCD -∠D =28°-13°=15°. 【总结】考查平行线的性质及三角形内外角的关系.【作业3】 (2014学年·虹口区二模·第6题)下列命题中,真命题是( )A .有两边和一角对应相等的两个三角形全等B .有两边和第三边上的高对应相等的两个三角形全等C .有两边和其中一边上的高对应相等的两个三角形全等D .有两边和第三边上的中线对应相等的两个三角形全等 【答案】D【解析】A 、“SSA ”不能判断全等,错误;B 、见例14,错误; C 、有形内高和形外高两种,错误;D 、正确. 【总结】考查三角形全等的判定.【作业4】 已知长方体ABCD -EFGH 的直观图如图所示,图中AD = 2 cm ,那么长方体中棱AD 的实际长度是______cm .【答案】22cm .【解析】立体图形中比例斜着是21:, ∴AD 的实际长度是22cm .【总结】考查长方体立体图形实际长度与直观图的长度比.【作业5】 已知:如图,DE // FG ,BAE ∠和ABG ∠的平分线交于点C ,过点C 的直线交射线AE 于点P ,交射线BG 于点Q .ABCD EFGH A CDEF GP HA B CDEFABCDE F求证:AP BQ AB +=. 【答案】略【解析】过点C 作CH ∥DE 交AB 于点H ,∵CH ∥DE , ∴∠EAC =∠ACH . 又∵AC 平分∠EAB ,∴∠EAC =∠CAB , ∴∠ACH =∠CAB ,∴AH =CH .同理BH =CH ,∴AH =HB ,∴H 是AB 中点 又∵HC ∥DE ∥FG , ∴AP +BQ =2CH , 又∵AB=AH +BH =2CH , ∴AP +BQ =AB .【总结】考查角平分线性质及平行线性质的综合运用.【作业6】 已知,ABC ∆中,=B C ∠∠,D 是边BC 上一点,DE AB ⊥,垂足是点E ,DF BC ⊥,DF 交边AC 于点F ,160AFD ∠=︒,求EDF ∠的度数.【答案】70°【解析】∵∠CFD =180°-∠AFD =20°,又∵∠B =∠C ,∠BED =∠CDF , ∴∠BDE =∠CFD =20°, ∴∠EDF =90°-∠BDE =70°. 【总结】考查三角形外角性质的综合运用.【作业7】 已知:如图,在ABC ∆中,AB = AC ,AD ⊥BC ,垂足为点D ,BE = CF .求证:DE = DF . 【答案】略【解析】∵AB =AC ,AD ⊥BC ,∴∠B =∠C ,BD =CD在△BDE 与△CDF 中, ∵BE =CF ,∠B =∠C ,BD =CD , ∴△BDE ≌△CDF (SAS ) ∴DE =DF【总结】考查等腰三角形的性质及全等三角形的证明.【作业8】 如图,已知AD // BC ,点E 是DC 的中点,AE 平分BAD ∠,求AEB ∠的度数. 【答案】90°.【解析】过E 作EF ∥AD ,则F 为AB 中点,∠AEF =∠DAE .AB CDEF。
