概率论与数理统计教案(48课时)
概率论与数理统计、概率论03-第48讲 相合性_49

4.相合性准则
定义:设ˆX1,, Xn 为参数的估计量,
若对于任意 ,当n 时,
ˆn P
即 0,有limP n
ˆn
0 成立.
则称ˆn为的相合估计量或一致估计量.
2Hale Waihona Puke 例1:设总体X的k阶矩E( X k ) k (k 2)存在,
X1,, Xn是一样本,证明:
(1)
证明:Pˆ 1.6 2(1(1.6)) 0.11,
0, lim P ˆ 0 不成立. n
所以,ˆ不是的相合估计.
6
例3:设总体X U 0,, X1,, Xn是一样本,
证明ˆ1
2 X 和ˆ2
n
1 n
X n都是的相合估计.
证明:ˆ1 2X P 2E(X) , ˆ1是的相合估计.
7
E ˆ , Dˆ 2
A2是 2 E ( X 2 )相 合 估 计 .
4
(2)因为D( X ) 2 2 12
B2
1 n
n i1
(Xi
X)2
A2
X
2,
根据依概率收敛性质,
B2 A2 X2是2的相合估计.
而S
2
n n 1
B2也是
2的相合估计.
(3) S S2是的相合估计.
5
例2:设总体X ~ N (,1), X1,, Xn是一样本, ˆ Xn ,证明:ˆ不是的相合估计.
Al
1 n
n i1
X il是l的相合估计,l
1,...,k;
(2)B2, S 2是D( X ) 2的相合估计; (3) S是的相合估计.
3
证明:(1)由辛钦大数定律知,对l 1,...,k,
概率论与数理统计教案
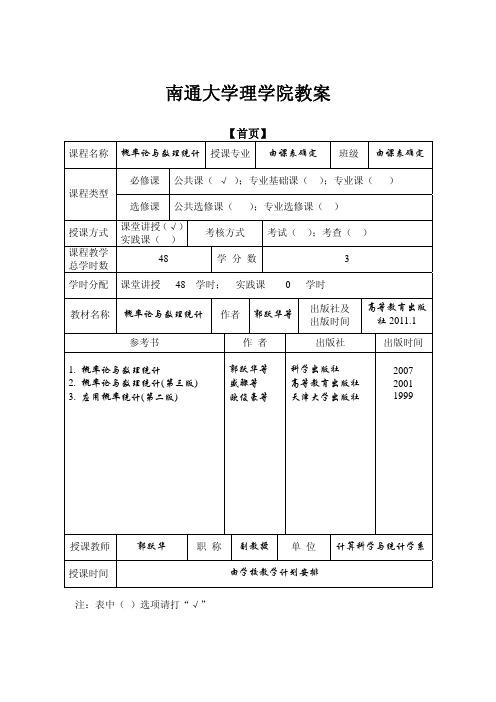
重点: 随机变量独立性的概念及应用,用图形定限法和分布函数法求两个独立随 机变量和的分布. 难点: 随机变量独立性的理解及应用,两个独立随机变量和的概率分布的确定.
概率统计练习题第 3 章习题
南通大学理学院教案
周 次 第 周, 第 9 次课 4.2 方差 板书结合多媒体 年 月 日
章节名称 授课方式 课堂讲授
教学目的及要求 主要教学内容 重点与难点 练习与作业 参考资料
1. 切比雪夫(Chebyshev)不等式, 切比雪夫(Chebyshev)大数定律和伯努利(Bernoulli) 大数定律; 2.独立同分布的中心极限定理和棣莫佛—拉普拉斯(De Moivre-Laplace)中心极限 定理; 3.棣莫佛—拉普拉斯中心极限定理在实际问题中的应用.
章节名称 授课方式 课堂讲授
1.4 条件概率 教学时数 3
教学目的及要求 主要教学内容 重点与难点 练习与作业 参考资料
1. 了解条件概率的概念, 掌握概率的乘法公式、 全概率公式, 会应用贝叶斯(Bayes) 公式解决比较简单的问题; 2.理解事件的独立性概念,熟练掌握独立事件的乘法公式.
1.条件概率; 2.计算概率的五大公式之: 乘法公式,全概率公式,Bayes 公式; 3.事件独立性的概念.
重点: 事件的表示;概率的性质. 难点: 复杂事件的表示与分解.
概率统计练习题第 1 章习题
南通大学理学院教案
周 次 第 周, 第 2 次课 1.3 古典概型与几何概型 课堂讲授 教学时数 3 教学手段 板书结合多媒体 年 月 日
章节名称 授课方式
教学目的及要求 主要教学内容 重点与难点 练习与作业 参考资料
章节名称 授课方式
教学手段
教学目的及要求 主要教学内容 重点与难点 练习与作业 参考资料
概率统计1.1-1.3(48学时)(浙大盛骤)

第七章
第八章
参数估计
假设检验
第一章 概率论的基本概念
概率论序言 第一节 随机试验 第二节 样本空间、随机事件 第三节 频率与概率 第四节 等可能概型(古典概型) 第五节 条件概率 第六节 独立性
序言
1.确定性现象 2.统计规律性 3.随机现象
在自然界和人的实践活动中经常遇到各种 各样的现象,这些现象大体可分为两类:一 类是确定的,例如“在一个标准大气压下, 纯水加热到100摄氏度时必然沸腾。”“向上 抛一块石头必然下落。”,“同性电荷相斥, 异性电荷相吸。”等等,这种在一定条件下 有确定结果的现象称为必然现象(确定性现 象);
2. 和事件 : 事件 A、B 至少有一个发生所构成 的
事件叫做事件 A 与事件 B 的和 .记作 A B .
A
B
类似地 , 称事件 A1、A2、 、An 中至少有一个发
、An 的和事件 . 生的事件为事件 A1、A2、 n 记之为 A1 A2 An , 简记为 Ai . i 1 中至少有一个发生的事 件为 称事件 A1、A2、
例如:S2 中事件 A={HHH,HHT,HTH,HTT} 表示 “第一次出现的是正面” S6 中事件 B1={t|t1000} 表示 “灯泡是次品” 事件 B2={t|t 1000}
表示 “灯泡是合格品”
事件 B3={t|t1500}
表示“灯泡是一级品”
• 例:对于试验E2:将一枚硬币抛掷三次, 观察正面H、反面T出现的情况. (1)事件A1:“第一次出现的是正面H”,则 A1={HHH,HHT,HTH,HTT} (2)事件A2:“三次出现同一面”,则 A2={HHH,TTT} (3)事件A3:“出现二次正面”,则 A2={HHT,HTH,THH}
概率论与数理统计教案(48课时)

《概率论与数理统计》课程教案第一章 随机事件及其概率一.本章的教学目标及基本要求(1) 理解随机试验、样本空间、随机事件的概念;(2) 掌握随机事件之间的关系与运算,;(3) 掌握概率的基本性质以及简单的古典概率计算; 学会几何概率的计算;(4) 理解事件频率的概念,了解随机现象的统计规律性以及概率的统计定义。
了解概率的公理化定义。
(5) 理解条件概率、全概率公式、Bayes 公式及其意义。
理解事件的独立性。
二.本章的教学内容及学时分配第一节 随机事件及事件之间的关系第二节 频率与概率 2学时第三节 等可能概型(古典概型) 2 学时第四节 条件概率第五节 事件的独立性 2 学时三.本章教学内容的重点和难点1) 随机事件及随机事件之间的关系;2) 古典概型及概率计算;3)概率的性质;4)条件概率,全概率公式和Bayes 公式5)独立性、n 重伯努利试验和伯努利定理四.教学过程中应注意的问题1) 使学生能正确地描述随机试验的样本空间和各种随机事件;2) 注意让学生理解事件,,,,,A B A B A B A B AB A ⊂⋃⋂-=Φ…的具体含义,理解事件的互斥关系;3) 让学生掌握事件之间的运算法则和德莫根定律;4) 古典概率计算中,为了计算样本点总数和事件的有利场合数,经常要用到排列和组合,复习排列、组合原理;5) 讲清楚抽样的两种方式——有放回和无放回;五.思考题和习题思考题:1. 集合的并运算⋃和差运算-是否存在消去律?2. 怎样理解互斥事件和逆事件?3. 古典概率的计算与几何概率的计算有哪些不同点?哪些相同点?习题:第二章 随机变量及其分布一.本章的教学目标及基本要求(1) 理解随机变量的概念,理解随机变量分布函数的概念及性质, 理解离散型和连续型随机变量的概率分布及其性质,会运用概率分布计算各种随机事件的概率;(2) 熟记两点分布、二项分布、泊松分布、正态分布、均匀分布和指数分布的分布律或密度函数及性质;二.本章的教学内容及学时分配第一节 随机变量第二节 第二节 离散型随机变量及其分布离散随机变量及分布律、分布律的特征第三节 常用的离散型随机变量常见分布(0-1分布、二项分布、泊松分布) 2学时第四节 随机变量的分布函数分布函数的定义和基本性质,公式第五节 连续型随机变量及其分布连续随机变量及密度函数、密度函数的性质 2学时第六节 常用的连续型随机变量常见分布(均匀分布、指数分布、正态分布)及概率计算 2学时三.本章教学内容的重点和难点a) 随机变量的定义、分布函数及性质;b) 离散型、连续型随机变量及其分布律或密度函数,如何用分布律或密度函数求任何事件的概率;c) 六个常见分布(二项分布、泊松分布、几何分布、均匀分布、指数分布、正态分布);四.教学过程中应注意的问题a) 注意分布函数(){}F x P X x =<的特殊值及左连续性概念的理解;b) 构成离散随机变量X 的分布律的条件,它与分布函数()F x 之间的关系;c) 构成连续随机变量X 的密度函数的条件,它与分布函数()F x 之间的关系;d) 连续型随机变量的分布函数()F x 关于x 处处连续,且()0P X x ==,其中x 为任意实数,同时说明了()0P A =不能推导A =Φ。
概率论与数理统计教案(48课时)

概率论与数理统计教案(48课时)Chapter 1: XXX1.Learning Objectives and Basic Requirements:1) Understand the concepts of random experiments。
sample space。
and random events;2) Master the nships and ns een random events;3) Master the basic XXX。
learn how to XXX;4) Understand the concept of event frequency。
know the XXX random phenomena。
and the XXX.5) XXX。
the law of total probability。
Bayes' theorem。
and their XXX.2.Teaching Content and Time n:n 1: XXXn 2: XXX (2 hours)n 3: XXX (Classical Probability) (2 hours)n 4: XXXn 5: Independence of Events (2 hours)3.XXX:1) Random events and nships een random events;2) XXX;3) Properties of probability;4) nal probability。
the law of total probability。
and Bayes' theorem;5) XXX。
XXX。
XXX.4.XXX:1) Enable students to correctly describe the sample space of random experiments and us random events;2) Pay n to helping students understand the specific meanings of events such as A∪B。
国家精品课 概率论与数理统计教案

国家精品课概率论与数理统计教案国家精品课“概率论与数理统计”教案一、课程概述课程名称:概率论与数理统计授课人:XXX授课对象:本科生课程时长:48学时二、教学目标1. 知识目标:掌握概率论与数理统计的基本概念、原理和方法,理解其在实际问题中的应用。
2. 能力目标:培养学生运用概率论与数理统计知识解决实际问题的能力,提高其逻辑思维和创新能力。
3. 情感态度价值观:培养学生对概率论与数理统计的兴趣,增强其科学素养,为其今后学习、工作打下坚实基础。
三、教学内容与要求1. 概率论基础:介绍概率的基本概念、条件概率、独立性等,要求学生掌握概率的计算和实际应用。
2. 随机变量及其分布:介绍随机变量及其分布函数,常见的随机变量分布类型,以及随机变量的数字特征等。
3. 数理统计基础:介绍数理统计的基本概念、参数估计和假设检验等,要求学生掌握参数估计和假设检验的方法。
4. 回归分析与方差分析:介绍一元线性回归分析、多元线性回归分析和方差分析等,要求学生掌握相关分析和回归分析的方法。
5. 课程实践:组织学生进行实际问题的概率论与数理统计应用,提高其解决实际问题的能力。
四、教学方法与手段1. 理论教学:采用讲授法、讨论法等教学方法,帮助学生理解概率论与数理统计的基本概念和原理。
2. 实验教学:通过实验课程和课程实践,让学生亲自动手操作,加深对理论知识的理解。
3. 教学手段:采用多媒体教学、在线学习等手段,丰富课程内容的表现形式,提高学生的学习兴趣。
五、教学评价与反馈1. 作业评价:布置适量的作业,及时批改和反馈,了解学生对课程内容的掌握情况。
2. 测验与考试:定期进行测验和考试,检查学生的学习成果,促使其巩固所学知识。
概率论与数理统计教案

概率论与数理统计教案教案标题:探索概率论与数理统计教学目标:1. 理解概率论与数理统计的基本概念和原理。
2. 掌握概率论与数理统计的常用方法和技巧。
3. 培养学生的数理思维和问题解决能力。
教学内容:1. 概率论的基本概念和概率计算方法。
a. 概率的定义和性质。
b. 事件与样本空间。
c. 条件概率与乘法定理。
d. 独立事件与加法定理。
e. 随机变量与概率分布。
2. 数理统计的基本概念和统计分析方法。
a. 总体与样本。
b. 抽样与抽样分布。
c. 参数估计与假设检验。
d. 常见的概率分布(如正态分布、二项分布等)。
教学步骤:第一课时:概率论的基本概念和概率计算方法1. 导入:通过一个生活中的例子引入概率的概念,激发学生对概率的兴趣。
2. 讲解概率的定义和性质,引导学生理解概率的基本概念。
3. 通过实例演示事件与样本空间的关系,并引导学生进行概率计算。
4. 引入条件概率与乘法定理,通过实例演示条件概率的计算方法。
5. 引入独立事件与加法定理,通过实例演示独立事件的计算方法。
6. 引入随机变量的概念和概率分布,通过实例演示随机变量的计算方法。
7. 总结本节课的内容,布置课后作业。
第二课时:数理统计的基本概念和统计分析方法1. 复习上节课的内容,解答学生的疑问。
2. 导入总体与样本的概念,通过实例演示总体与样本的关系。
3. 引入抽样与抽样分布的概念,通过实例演示抽样分布的计算方法。
4. 讲解参数估计的基本原理和方法,通过实例演示参数估计的计算方法。
5. 引入假设检验的概念和步骤,通过实例演示假设检验的计算方法。
6. 介绍常见的概率分布,如正态分布、二项分布等,讲解其特点和应用。
7. 总结本节课的内容,布置课后作业。
教学方法:1. 案例分析法:通过实际生活中的案例,引导学生理解概率论与数理统计的概念和方法。
2. 问题导向法:提出问题,引导学生思考和探索解决问题的方法。
3. 合作学习:组织学生进行小组合作,共同解决问题和讨论案例。
概率论与数理统计教案(48课时)(最新整理)

( x, y )G
,注意二重积分运算知识点的复习。
d) 二维均匀分布的密度函数的具体表达形式。
五.思考题和习题
思考题:1. 由随机变量 X ,Y 的边缘分布能否决定它们的联合分布?
2. 条件分布是否可以由条件概率公式推导? 3. 事件的独立性与随机变量的独立性是否一致? 4.如何利用随机变量之间的独立性去简化概率计算,试举例说明。 习题:
第四章 随机变量的数字特征 一.教学目标及基本要求
(1)理解数学期望和方差的定义并且掌握它们的计算公式;
(2)掌握数学期望和方差的性质与计算,会求随机变量函数的数学期望,特别是利用
期望或方差的性质计算某些随机变量函数的期望和方差。
(3)熟记 0-1 分布、二项分布、泊松分布、正态分布、均匀分布和指数分布的数学期
第四节 二维随机变量的函数的分布
已知(X,Y)的分布率 pij 或密度函数 (x, y) ,求 Z f ( X ,Y ) 的分布律或密度
函数Z (z) 。特别如函数形式: Z X Y , Z max( X ,Y ), Z min( X ,Y ) 。
2 学时
三.本章教学内容的重点和难点
a) 二维随机变量的分布函数及性质,与一维情形比较有哪些不同之处;
5.列举正态分布的应用。
习题:
第三章 多维随机变量及其分布
一.教学目标及基本要求
(1)了解二维随机变量概念及其联合分布函数概念和性质,了解二维离散型和连续 型随机变量定义及其概率分布和性质,了解二维均匀分布和正态分布。
(2)会用联合概率分布计算有关事件的概率,会求边缘分布。 (3)掌握随机变量独立性的概念,掌握运用随机变量的独立性进行概率计算。 (4)会求两个独立随机变量的简单函数(如函数 X+Y, max(X, Y), min(X, Y))的分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*《概率论与数理统计》课程教案第一章随机事件及其概率一.本章的教学目标及基本要求(1)理解随机试验、样本空间、随机事件的概念;(2)掌握随机事件之间的关系与运算,;(3)掌握概率的基本性质以及简单的古典概率计算; 学会几何概率的计算;(4)理解事件频率的概念,了解随机现象的统计规律性以及概率的统计定义。
了解概率的公理化定义。
(5)理解条件概率、全概率公式、Bayes 公式及其意义。
理解事件的独立性。
二.本章的教学内容及学时分配第一节随机事件及事件之间的关系第二节频率与概率2学时第三节等可能概型(古典概型) 2 学时第四节条件概率第五节事件的独立性 2 学时三.本章教学内容的重点和难点1)随机事件及随机事件之间的关系;2)古典概型及概率计算;3)概率的性质;4)条件概率,全概率公式和Bayes公式5)独立性、n 重伯努利试验和伯努利定理四.教学过程中应注意的问题1)使学生能正确地描述随机试验的样本空间和各种随机事件;2) 注意让学生理解事件,,,,,A B A B A B A B AB A ⊂⋃⋂-=Φ…的具体含义,理解事件的互斥关系;3) 让学生掌握事件之间的运算法则和德莫根定律;4) 古典概率计算中,为了计算样本点总数和事件的有利场合数,经常要用到排列和组合,复习排列、组合原理;5) 讲清楚抽样的两种方式——有放回和无放回;五.思考题和习题思考题:1. 集合的并运算⋃和差运算-是否存在消去律? 2. 怎样理解互斥事件和逆事件?3. 古典概率的计算与几何概率的计算有哪些不同点?哪些相同点? 习题:第二章 随机变量及其分布一.本章的教学目标及基本要求(1) 理解随机变量的概念,理解随机变量分布函数的概念及性质, 理解离散型和连续 型随机变量的概率分布及其性质,会运用概率分布计算各种随机事件的概率;(2) 熟记两点分布、二项分布、泊松分布、正态分布、均匀分布和指数分布的分布律或密度函数及性质;二.本章的教学内容及学时分配第一节 随机变量 第二节 第二节 离散型随机变量及其分布离散随机变量及分布律、分布律的特征第三节 常用的离散型随机变量常见分布(0-1分布、二项分布、泊松分布) 2学时第四节 随机变量的分布函数分布函数的定义和基本性质,公式第五节 连续型随机变量及其分布连续随机变量及密度函数、密度函数的性质 2学时第六节 常用的连续型随机变量常见分布(均匀分布、指数分布、正态分布)及概率计算 2学时三.本章教学内容的重点和难点a) 随机变量的定义、分布函数及性质;b) 离散型、连续型随机变量及其分布律或密度函数,如何用分布律或密度函数求任何事件的概率;c) 六个常见分布(二项分布、泊松分布、几何分布、均匀分布、指数分布、正态分布);四.教学过程中应注意的问题a) 注意分布函数(){}F x P X x =<的特殊值及左连续性概念的理解; b)创作编号:GB8878185555334563BT9125XW创作者: 凤呜大王*c) 构成离散随机变量X 的分布律的条件,它与分布函数()F x 之间的关系; d) 构成连续随机变量X 的密度函数的条件,它与分布函数()F x 之间的关系; e) 连续型随机变量的分布函数()F x 关于x 处处连续,且()0P X x ==,其中x为任意实数,同时说明了()0P A =不能推导A =Φ。
f)注意正态分布的标准化以及计算查表问题;五.思考题和习题思考题:1. 函数,0()1,0xxe x F x e x -⎧<⎪=⎨-≥⎪⎩是否是某个随机变量的分布函数? 2. 分布函数()F x 有两种定义——{}{}P X x or P X x <≤,主要的区别是什么?3. 均匀分布与几何概率有何联系?4. 讨论指数分布与泊松分布之间的关系。
5.列举正态分布的应用。
习题:第三章 多维随机变量及其分布一.教学目标及基本要求(1) 了解二维随机变量概念及其联合分布函数概念和性质,了解二维离散型和连续型随机变量定义及其概率分布和性质,了解二维均匀分布和正态分布。
(2) 会用联合概率分布计算有关事件的概率,会求边缘分布。
(3) 掌握随机变量独立性的概念,掌握运用随机变量的独立性进行概率计算。
(4) 会求两个独立随机变量的简单函数(如函数X+Y , max(X, Y), min(X, Y))的分布。
二.教学内容及学时分配第一节 二维随机变量二维随机变量及其分布,离散型随机变量及其分布律、连续型随机变量及其密度函数、它们的性质、n 维随机变量 2学时第二节 边缘分布边缘分布律、边缘密度函数 2学时第三节 条件分布 1学时第四节 相互独立的随机变量两个变量的独立性,n 个变量的独立性 1学时 第四节 二维随机变量的函数的分布已知(X,Y)的分布率p ij 或密度函数(,)x y ϕ,求(,)Z f X Y =的分布律或密度函数()Z z ϕ。
特别如函数形式:,max(,),min(,)Z X Y Z X Y Z X Y =±==。
2学时三.本章教学内容的重点和难点a) 二维随机变量的分布函数及性质,与一维情形比较有哪些不同之处;b) 边缘密度函数的计算公式:()(,)X x x y dyϕϕ+∞-∞=⎰的运用,特别是积分限的确定和变量x 的取值范围的讨论;c) 随机变量独立性的判定条件以及应用独立性简化计算,如由边缘分布律或密度函数可以确定联合分布律或联合密度函数;d) 推导Z X Y =+的密度函数的卷积公式:()(,)X Y t x t x dxϕϕ+∞+-∞=-⎰,正确使用卷积公式;e) 在X ,Y 独立性的条件下,推导max(,),min(,)Z X Y Z X Y ==的密度函数,注意它们在可靠性方面的应用。
四.教学过程中应注意的问题a) 注意联合分布函数能决定任意随机变量X 或Y 的分布(边缘分布),反之则不能确定(X ,Y)的联合分布,由正态分布可以说明;b) 在判断两个随机变量是否独立过程中,如果存在某点00(,)x y ,使得:0000(,)()()P X x Y y P X x P Y y ==≠==或0000(,)()()X Y x y x y ϕϕϕ≠,则称变量X 与Y 不独立; c) 一般计算概率使用如下公式:(,)((,))(,)x y GP X Y G x y dxdyϕ∈∈=⎰⎰,注意二重积分运算知识点的复习。
d) 二维均匀分布的密度函数的具体表达形式。
五.思考题和习题思考题:1. 由随机变量,X Y 的边缘分布能否决定它们的联合分布? 2. 条件分布是否可以由条件概率公式推导? 3. 事件的独立性与随机变量的独立性是否一致?4.如何利用随机变量之间的独立性去简化概率计算,试举例说明。
习题:第四章 随机变量的数字特征一.教学目标及基本要求(1) 理解数学期望和方差的定义并且掌握它们的计算公式;(2) 掌握数学期望和方差的性质与计算,会求随机变量函数的数学期望,特别是利用期望或方差的性质计算某些随机变量函数的期望和方差。
(3) 熟记0-1分布、二项分布、泊松分布、正态分布、均匀分布和指数分布的数学期 望和方差;(4) 了解矩、协方差和相关系数的概念和性质,并会计算。
二.教学内容及学时分配第一节数学期望离散型、连续型随机变量的数学期望、随机变量函数的数学期望、数学期望的应用、数学期望的性质3学时第二节方差方差的概念及计算、方差的性质、常见分布的数学期望及方差简单归纳2学时第三节协方差与相关系数2学时第四节矩和协方差矩阵1学时三.本章教学内容的重点和难点a)数学期望、方差的具体含义;b)创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*c)数学期望、方差的性质,使用性质简化计算的技巧;特别是级数的求和运算。
d)期望、方差的应用;四.本章教学内容的深化和拓宽将数学期望拓展到数学期望向量和数学期望矩阵;协方差及相关系数概念和公式拓宽到n维随机变量的协方差矩阵和相关系数矩阵。
五.教学过程中应注意的问题a)一个随机变量并不一定存在数学期望和方差,也有可能数学期望存在,而方差不存在,如柯西分布是最著名的例子;b)数学期望的一个具体的数字,不是函数;c)由方差的定义知,方差是非负的;d) 独立性和不相关性之间的关系,一般地,X 与Y 独立,则X 与Y 不相关,反之则不然,但对于正态分布,两者却是等价的;六.思考题和习题思考题:1. 假定一个系统由5个电子元件组装而成,假定它们独立同服从于指数分布,将它们串接起来,求系统的平均寿命,若将它们并行连接,其系统的平均寿命是多少?并比较其优劣。
2. 方差的定义为什么不是||E X EX -?3. 工程上经常遇到计算误差,它是否与方差是同一个概念? 4.协方差与相关系数有什么本质上的区别?5.随机变量X 与Y 独立可以推导cov(,)0X Y =,反之呢?对正态分布又如何呢?习题:第五章 大数定律和中心极限定理一.教学目标及基本要求了解切比雪夫不等式、大数定律和中心极限定理。
二.教学内容及学时分配第一节 大数定律第二节 中心极限定理 2学时三.本章教学内容的重点和难点大数定律和中心极限定理的含义;四.本章教学内容的深化和拓宽中心极限定理的条件拓宽。
五.教学过程中应注意的问题1)大数定律的变形,大数定律的证明关键是使用了切比契夫不等式; 2)注意中心极限定理的条件和结论,如何使用这一结论解决应用题; 习题:第六章 样本及抽样分布一.教学目标及基本要求(1) 理解总体、样本和统计量的概念;了解经验分布函数 (2) 掌握样本均值、样本方差及样本矩的计算。
(3) 了解卡方分布、t-分布和F 分布的定义及性质,了解分位数的概念并会查表计算概率。
(4) 掌握在正态总体下样本均值、样本方差、t 统计量的分布及性质。
二.教学内容及学时分配(1)第一节 总体与样本第二节 统计量(包括经验分布函数) 2学时第三节 几个常用的分布正态分布,2χ-分布,t-分布,F-分布)、抽样分布定理、分位数 2学时三.本章教学内容的重点和难点a) 数理统计与概率论在研究问题和方法上的根本区别; b) 总体、样本的概念;c) 统计量的定义和常用的统计量;d) 正态分布以及由正态分布导出的三大统计分布,抽样分布定理,分位数的概念。
e) 2χ-分布、t -分布和F -分布的定义四.教学过程中应注意的问题a) 正态分布的标准化:若2~(,)X N a σ,则~(0,1)X aN σ-;b) “独立正态变量之和仍为正态变量”和中心极限定理的应用; c) 对三大统计分布定义深入分析,补充例子加以说明,如14,,X X 取自正态总体2(0,2)N ,的一个样本,令221234(2)(34)Y a X X b X X =-+-,求系数,a b ,使Y 服从2χ-分布,并求自由度;d) 查常用分布数值表是实际计算中不可缺少的一步,务必掌握;e) 掌握统计学的思想应该从正态总体出发,因为数理统计学的许多基本理论是在正态总体的假定下建立起来的;六.思考题和习题思考题:1. 样本平均值、中位数、众数的定义和区别。
