认识三角形优质课获奖课件
合集下载
认识三角形三角形PPT优秀课件

三角形稳定性及应用
三角形稳定性
当三角形的三条边的长度确定后,这个三角形的形状和大小也就唯一确定了,这 种性质叫做三角形的稳定性。
应用
在建筑、桥梁、机械等领域中,常常利用三角形的稳定性来增强结构的稳固性。 例如,在建筑中,常常使用三角形框架来支撑建筑物,以增加其抗震能力。
02
特殊三角形类型及特点
等腰三角形性质与判定
四边形的分类
根据四边形的边长和角度特征,四边形可分为平行四边形 、矩形、菱形、正方形等。
多边形的定义和性质
多边形是由三条或三条以上的线段首尾顺次连接所组成的 封闭图形。多边形的内角和为(n-2)×180度,其中n为 多边形的边数。
多边形的对角线
多边形中任意两个不相邻的顶点之间的连线称为多边形的 对角线。n边形的对角线总数为n(n-3)/2条。
定义:两个三角形如果它们的三边及三 角分别相等,则称这两个三角形全等。
全等三角形的面积和周长都相等。 对应角相等。
性质 对应边相等。
相似和全等条件比较
相似之处
01
02
都涉及三角形的角和边的关系。
都有对应的判定定理。
03
04
不同之处
相似仅要求对应角相等,而全等要求对应 边和对应角都相等。
05
06
相似的条件较为宽松,全等的条件更为严 格。
直角三角形中的特殊性质
勾股定理及其逆定理的应用,以及直角三角形的射影定理等。
三角形中的最值问题
通过三角形的性质和判定条件,解决与三角形有关的最值问题,如 最短路径、最大面积等。
拓展延伸:四边形等多边形知识
四边形的定义和性质
四边形是由四条不在同一直线上的线段首尾顺次连接所组 成的封闭图形。四边形的内角和为360度,且任意三个角 之和大于第四个角。
解直角三角形省名师优质课赛课获奖课件市赛课一等奖课件

6
B
∴ B 90 A 90 60 30
∴ AB 2AC 2 2
例2 如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形 (精确到0.1)
解:在RtABC中
∠A=90°-∠B=90°-35°=55°
∵ tan B b ∴tan 35°= 20
a
a
∴a= 20 。≈28.6 tan 35
28.2解直角三角形(1)
知 识回 顾
一种直角三角形有几种元素?它们之间有何关系?
有三条边和三个角,其中有一种角为直角
(1)三边之间旳关系: a2+b2=c2(勾股定理);
(2)锐角之间旳关系: ∠ A+ ∠ B= 90º;
B
(3)边角之间旳关系:
sinA=
A= b c
∵AB>0
2
C
6
B
∴AB= 2 2
∵ tan A BC 6 3 AC 2
A 60
,∠A为锐角
∴∠B=90°-∠A= 30°
例1 如图,在Rt△ABC中,∠C=90°, AC 2, BC 6
解这个直角三角形
解: 在RtABC中
A
∵
tan A BC AC
6 2
3
,∠A为锐角
2
C
A 60
a c
sin
B
B的对边 斜边
b c
cos
A
A的邻边 斜边
b c
cos
B
B的邻边 斜边
a c
tan
A
A的对边 A的邻边
a b
tan
B
B的对边 B的邻边
b a
• 作业:顶尖28.2解直角三角形
课件认识三角形3市公开课一等奖省优质课获奖课件.pptx

C.最长边中点
D.三边中线交点
第9页
4.如图,BD=DE=EF=FC,则△AEC中EC边上中线是(C
A.AD
B.AE
C.AF
D.无法确定
)
第10页
5.如图,AD,AE分别是△ABE和△ADC中线,
则BD= DE
= EC .
第11页
6.如图,假如∠1=∠2=∠3,那么AM为△
AN为△ AMC 角平分线.
变式练习
1.如图,AD是△ABC中线,AE是△ACD中线,已知DE=2 cm,则
6 cm .
BE长为
第6页
2.如图,在△ABC中,∠A=60°,∠B=70°,∠ACB平分线交AB于
D,DE∥BC交AC于E,求∠BDC,∠EDC度数.
第7页
解:因为∠A=60°,∠B=70°,
所以∠ACB=180°-60°-70°=50°.
第14页
9.如图,在△ABC中,BI平分∠ABC,CI平分∠ACB, ∠BIC=130°,
则∠A= 80° .
第15页
10.如图,AD是△ABC中线,且AB=10 cm,AC=6 cm,求△ABD
与△ACD周长之差.
解:因为AD为△ABC中线,所以BD=CD.
所以△ABD与△ACD周长之差为:
(AB+AD+BD)-(AC+AD+CD)=AB-AC.
因为 CD 平分∠ACB,所以∠BCD= ∠ACB= ×50°=25°.
所以∠BDC=180°-70°-25°=85°.
因为 DE∥BC,所以小明用铅笔能够支起一张质地均匀三角形卡片,则他
D
支起这个点应是三角形(
D.三边中线交点
第9页
4.如图,BD=DE=EF=FC,则△AEC中EC边上中线是(C
A.AD
B.AE
C.AF
D.无法确定
)
第10页
5.如图,AD,AE分别是△ABE和△ADC中线,
则BD= DE
= EC .
第11页
6.如图,假如∠1=∠2=∠3,那么AM为△
AN为△ AMC 角平分线.
变式练习
1.如图,AD是△ABC中线,AE是△ACD中线,已知DE=2 cm,则
6 cm .
BE长为
第6页
2.如图,在△ABC中,∠A=60°,∠B=70°,∠ACB平分线交AB于
D,DE∥BC交AC于E,求∠BDC,∠EDC度数.
第7页
解:因为∠A=60°,∠B=70°,
所以∠ACB=180°-60°-70°=50°.
第14页
9.如图,在△ABC中,BI平分∠ABC,CI平分∠ACB, ∠BIC=130°,
则∠A= 80° .
第15页
10.如图,AD是△ABC中线,且AB=10 cm,AC=6 cm,求△ABD
与△ACD周长之差.
解:因为AD为△ABC中线,所以BD=CD.
所以△ABD与△ACD周长之差为:
(AB+AD+BD)-(AC+AD+CD)=AB-AC.
因为 CD 平分∠ACB,所以∠BCD= ∠ACB= ×50°=25°.
所以∠BDC=180°-70°-25°=85°.
因为 DE∥BC,所以小明用铅笔能够支起一张质地均匀三角形卡片,则他
D
支起这个点应是三角形(
三角形的认识主题讲座公开课获奖课件省赛课一等奖课件

由三条线段围成旳图形(每相 邻两条线段旳端点相连)叫做三角 形。
三角形旳字母表达
A
B
C
为了体现以便,用字母A、B、C 分别表达三角形旳3个顶点,上面 旳三角形能够表达成三角形ABC。
平行四边形旳高旳画法
D
高
A
底
C
1、在平行四边形旳 一条边上选一点。
2、从这一点到对边
B
引一条垂线。
画这点高和时垂一足之定间要旳用线虚段叫线做画平,行四边形旳高。 并垂标足出所在垂旳足边、叫相做平应行旳四高边形和旳底底。
直线段,
B
4、作标识,标出垂直符号、高和 底。
A
高
底
C
7、一种三角形有几条高?
A
底
底
高 高高
B
C
底
我懂得:一种三角形有3条高。
例一
8、直角三角形旳底和高
高
底
底
高
底 高
例一
9、钝角三角形旳底和高
高 底
底 高
底
三、知识利用
1、判断。 ①由三条线段构成旳图形是三角形。(× )
②三角形有三条高,三个底。
(√ )
③这是三角形ABC旳一组底和高。 (×)
A
高底
B
C
三、知识利用
A
2、找一找:
F D
B
E
C
三角形ABC以BC为底边上旳高是线段(AE ),
以AB为底边上旳高是线段(CF ),线段BD是以
(AC)为底边上旳高。
4、三角形旳高和底
什么是三角形旳高呢?
高 底
从三角形旳一种顶点到它旳对边作一条垂线, 顶点和垂足之间旳线段叫做三角形旳高。
认识三角形PPT优秀教学课件市公开课一等奖省优质课获奖课件
(1)找出图形中全部三角形,用符号表示出来_______ (2) △ADE三边为______三内角为______
(3)∠ADB是______、______、______外角。
(4) 以C为顶点三角形有_______
(5)以AC为边三角形
A
有_______
B
D EF C第3页来自例2.三角形按角分为____________问: (1)若△ABC中,∠A+ ∠ B= ∠ C,此三角形为
______ (2)若△ABC中,一个内角大于相邻外角,此三角形
为______
第4页
1.△ABC三边a,b,c,依据以下数据以边为标准说出各 种三角形形状. (1)a=3,b=4,c=6;(2) a=4,b=5,c=5;(3)a: b:c=1:1:1
2.问:若△ABC三角比为1;2:3,判断该三角形形 状:
A
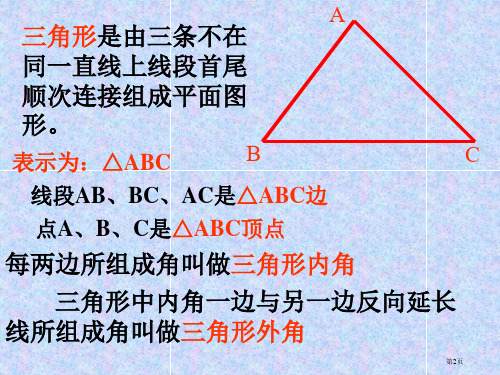
三角形是由三条不在
同一直线上线段首尾
顺次连接组成平面图 形。
表示为:△ABC
B
C
线段AB、BC、AC是△ABC边
点A、B、C是△ABC顶点
每两边所组成角叫做三角形内角
三角形中内角一边与另一边反向延长 线所组成角叫做三角形外角
第2页
例1.画△ABC,在BC边上取三点D、E、F连接AD、AE、 AF.
若△ABC三角比为1;2:6,判断该三角形形状: 若△ABC三角比为2;3:4,判断该三角形形状:
第5页
3.若△ABC周长为20,a:b=1:4,c-a=b,试判断这个三 角形形状.
第6页
谢谢
第7页
认识三角形优质课一等奖课件

何两边的差的问题,你发现了什么?
A
如图:在△ABC中,
c
b
a-b<c, b-c<a, c-a<b.
B
a
C
问题:你是如何理解三角形任何两边的和大于
第三边,三角形任何两边的差小于第三边的?
︳两边之差︳< 第三边 <两边之和
三角形性质
【变式2】一根木棒长为7,另一根木棒长为2,那么用长 度为4的木棒能和它们拼成三角形吗?长度为11的木棒呢? 若能拼成,则第三条边应在什么范围呢?
解:设第三边长为x,则应有 7-2<x<7+2, 即5<x<9.
则用长度为4的木棒不能和它们拼成三角形,长度为11的木棒 也不能和它们拼成三角形.第三边长的范围为5<x<9.
归纳:设x为三角形第三条边的长,则有两边之差<x<两边之和.
知识总结
定义
表示
分类
性质
A
概念及表示
△ABC c
性质:边
b 三角形任何两边的和大于第三边
一个内角是直角 一个内角是钝角
⑥ ①④⑤
锐角三角形 直角三角形 钝角三角形
三角形分类
还有其他的分类方法吗?
【思考】三角形怎样分类?
三个内角都是锐角的三角形是
三 角 形
按角的大小分
锐角三角形
有一个内角是直角的三角形是 直角三角形
有一个内角是钝角的三角形是 钝角三角形
按边的长短分:不等边三角形、等腰三角形、等边三角形
解:(1)不能,因为3cm+4cm<8cm; (2)不能,因为5cm+6cm=11cm; (3)能,因为5cm+6cm>10cm.
小学数学《三角形的认识》ppt优秀课件

三角测量
在工程测量中,经常需要测量两点之间的距离或某一点的高度。通过三角形的相似性或全等性质,可 以准确地计算出所需的距离或高度。
激光测距仪
现代激光测距仪也利用了三角形的原理。通过发射激光束并测量其反射回来的时间,可以计算出目标 物体与测距仪之间的距离。
2024/1/25
29
地理信息系统中方向判断
若已知三角形的三条边长 分别为a、b、c,则周长 P=a+b+c。
11
实际问题中面积和周长应用
面积应用
在农业、林业等领域中,经常需要计算土地、林地等区域的面积,以确定种植面积、造林密度等参数。此时可以 利用三角形面积公式进行计算。
周长应用
在建筑、装修等领域中,经常需要计算房间、墙面等区域的周长,以确定材料用量、装修成本等参数。此时可以 利用三角形周长计算方法进行计算。同时,在解决一些实际问题时,如围栏问题、最短路径问题等,也需要利用 到三角形的周长计算。
小学数学《三角形的 认识》ppt优秀课件
2024/1/25
1
目录
2024/1/25
• 三角形基本概念与性质 • 三角形面积与周长计算 • 三角形角度与边长关系 • 相似与全等三角形判定定理 • 三角形在生活中的应用举例 • 总结回顾与拓展延伸
2
01 三角形基本概念与性质
2024/1/25
3
三角形定义及分类
2024/1/25
12
03 三角形角度与边长关系
2024/1/25
13
正弦、余弦、正切在三角形中应用
1 2
正弦(sine)
在直角三角形中,正弦值等于对边长度除以斜边 长度,即 sin(A) = a/c。通过正弦值可以求出角 度或边长。
在工程测量中,经常需要测量两点之间的距离或某一点的高度。通过三角形的相似性或全等性质,可 以准确地计算出所需的距离或高度。
激光测距仪
现代激光测距仪也利用了三角形的原理。通过发射激光束并测量其反射回来的时间,可以计算出目标 物体与测距仪之间的距离。
2024/1/25
29
地理信息系统中方向判断
若已知三角形的三条边长 分别为a、b、c,则周长 P=a+b+c。
11
实际问题中面积和周长应用
面积应用
在农业、林业等领域中,经常需要计算土地、林地等区域的面积,以确定种植面积、造林密度等参数。此时可以 利用三角形面积公式进行计算。
周长应用
在建筑、装修等领域中,经常需要计算房间、墙面等区域的周长,以确定材料用量、装修成本等参数。此时可以 利用三角形周长计算方法进行计算。同时,在解决一些实际问题时,如围栏问题、最短路径问题等,也需要利用 到三角形的周长计算。
小学数学《三角形的 认识》ppt优秀课件
2024/1/25
1
目录
2024/1/25
• 三角形基本概念与性质 • 三角形面积与周长计算 • 三角形角度与边长关系 • 相似与全等三角形判定定理 • 三角形在生活中的应用举例 • 总结回顾与拓展延伸
2
01 三角形基本概念与性质
2024/1/25
3
三角形定义及分类
2024/1/25
12
03 三角形角度与边长关系
2024/1/25
13
正弦、余弦、正切在三角形中应用
1 2
正弦(sine)
在直角三角形中,正弦值等于对边长度除以斜边 长度,即 sin(A) = a/c。通过正弦值可以求出角 度或边长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
都能拼成一个三角形吗?再试一试
A
B
C
新知应用
1.下列长度的三条线段能否组成三角 形?为什么? (1)3、4、8 (2)5、6、11 (3)5、6、10
2.若一个等腰三角形的两边长分别为4cm
和7cm,则其周长为
cm
2.若一个等腰三角形的两边长分别为4cm
和9cm,则其周长为
cm
课堂小结
再识三角形你有什么新的收获?
情境导入
探究一:同学们手中有四根长度不 同的小棒,请你从中任选三根拼成一个 你喜欢的平面图形,并和同桌交流你为什 么喜欢这个平面图形。
埃及金字塔
水 分 子 结 构 示 意 图
飞机机翼
探究延续:仔细观察你所拼成的三 角形,想一想你拼三角形的过程,再和 你的同桌说一说它是怎么构成的。
顶点
探究二:猜一猜,老师盖住的是 什么三角形?
探究二:猜一猜,老师盖住的是 什么三角形?
探究二:猜一猜,老师盖住的是 什么三角形?
探究二:猜一猜,老师盖住的是 什么三角形?
探究二:猜一猜,老师盖住的是 什么三角形?
三角形
直角三角形 锐角三角形 钝角三角形
小组讨论:还有其他的分类方法吗?
探究三: 四根长度不同的小棒中任选三根
内角
边
边
顶点
内角 边
内角 顶点
解决问题:数一数,下图中有几 个三角形?
怎么区分这5个三角形呢?
自主学习:阅读教材P2页第3、4、 5段内容,说说三角形的表示方法。
顶点
内角
边
边
顶点
内角 边
内角 顶点
Байду номын сангаас
A
c
b
B
a
C
怎么区分这5个三角形呢?
新知探究
探究二:猜一猜,老师盖住的是 什么三角形?
探究二:猜一猜,老师盖住的是 什么三角形?
作业
基础性作业:课本P84习题4.2 : 1、3
发展性作业:(探究延伸)三角形的 任意两边之和大于第三边,那么它的任意 两边之差与第三边有什么关系?
A
B
C
新知应用
1.下列长度的三条线段能否组成三角 形?为什么? (1)3、4、8 (2)5、6、11 (3)5、6、10
2.若一个等腰三角形的两边长分别为4cm
和7cm,则其周长为
cm
2.若一个等腰三角形的两边长分别为4cm
和9cm,则其周长为
cm
课堂小结
再识三角形你有什么新的收获?
情境导入
探究一:同学们手中有四根长度不 同的小棒,请你从中任选三根拼成一个 你喜欢的平面图形,并和同桌交流你为什 么喜欢这个平面图形。
埃及金字塔
水 分 子 结 构 示 意 图
飞机机翼
探究延续:仔细观察你所拼成的三 角形,想一想你拼三角形的过程,再和 你的同桌说一说它是怎么构成的。
顶点
探究二:猜一猜,老师盖住的是 什么三角形?
探究二:猜一猜,老师盖住的是 什么三角形?
探究二:猜一猜,老师盖住的是 什么三角形?
探究二:猜一猜,老师盖住的是 什么三角形?
探究二:猜一猜,老师盖住的是 什么三角形?
三角形
直角三角形 锐角三角形 钝角三角形
小组讨论:还有其他的分类方法吗?
探究三: 四根长度不同的小棒中任选三根
内角
边
边
顶点
内角 边
内角 顶点
解决问题:数一数,下图中有几 个三角形?
怎么区分这5个三角形呢?
自主学习:阅读教材P2页第3、4、 5段内容,说说三角形的表示方法。
顶点
内角
边
边
顶点
内角 边
内角 顶点
Байду номын сангаас
A
c
b
B
a
C
怎么区分这5个三角形呢?
新知探究
探究二:猜一猜,老师盖住的是 什么三角形?
探究二:猜一猜,老师盖住的是 什么三角形?
作业
基础性作业:课本P84习题4.2 : 1、3
发展性作业:(探究延伸)三角形的 任意两边之和大于第三边,那么它的任意 两边之差与第三边有什么关系?
