广东省广州市高考数学一轮复习专项检测试题13三视图
高考一轮复习专题训练理科数学三视图和参数方程(含详细答案)

高考一轮复习专题训练理科数学三视图和参数方程(含详细答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高考一轮复习专题训练理科数学三视图和参数方程(含详细答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高考一轮复习专题训练理科数学三视图和参数方程(含详细答案)的全部内容。
三视图及参数方程(含答案)一.选择题(共9小题)1.中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器﹣﹣商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12。
6(立方寸),则图中的x为()A.1.2 B.1。
6 C.1.8 D.2.42.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是()A.8 B.C.12 D.163.如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积()A.B.C.D.4.若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是()A.2cm2B.cm3C.3cm3D.3cm35.某三棱锥的三视图如图所示,该三棱锥的体积为()A.80 B.40 C.D.6.某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为()A.B.C.D.37.某几何体的三视图如图所示,则该几何体的体积为()A.16+8πB.8+8πC.16+16πD.8+16π8.高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的()A.B.C.D.9.一个几何体的三视图如图所示,则这个几何体的体积是()A.B.1 C.D.2二.选择题(共21小题)10.已知椭圆C中心在原点、焦点在x轴上,椭圆C上的点到焦点的最大值为3,最小值为1.(Ⅰ)求椭圆C的标准方程;(Ⅱ)若直线l:y=kx+m(k≠0)与椭圆交于不同的两点M、N(M、N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线l过定点,并求出定点的坐标.11.在极坐标系中,已知圆C的圆心,半径r=3.(1)求圆C的极坐标方程;(2)若点Q在圆C上运动,P在OQ的延长线上,且|OQ|:|QP|=3:2,求动点P的轨迹方程.12.以平面直角坐标系的原点为极点,以x轴的正半轴为极轴建立极坐标系.设曲线C的参数方程为(α是参数),直线l的极坐标方程为ρcos(θ+)=2.(1)求直线l的直角坐标方程和曲线C的普通方程;(2)设点P为曲线C上任意一点,求点P到直线l的距离的最大值.13.在平面直角坐标系中,直线l过点P(2,)且倾斜角为α,以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=4cos(θ﹣),直线l与曲线C相交于A,B两点;(1)求曲线C的直角坐标方程;(2)若,求直线l的倾斜角α的值.14.在平面直角坐标系xOy中,曲线C1的参数方程为(θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.(Ⅰ)求C1和C2在直角坐标系下的普通方程;(Ⅱ)已知直线l:y=x和曲线C1交于M,N两点,求弦MN中点的极坐标.15.在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C1的参数方程为为参数),曲线C2的极坐标方程为.(1)求曲线C1的普通方程和曲线C2的直角坐标方程;(2)设P为曲线C1上一点,Q曲线C2上一点,求|PQ|的最小值.16.在直角坐标系xOy中,曲线C1的参数方程为(α为参数),以原点O为极点,x轴的正半轴为级轴,建立极坐标系,曲线C2的极坐标方程ρsin(π+)=4(I)求曲线C1的普通方程和曲线C2的直角坐标方程;(Ⅱ)设P为曲线C1上的动点,求点P到曲线C2上的距离的最小值的值.17.在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立坐标系,直线l的参数方程为,(t为参数),曲线C1的方程为ρ(ρ﹣4sinθ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.(1)求点Q的轨迹C2的直角坐标方程;(2)直线l与直线C2交于M,N两点,若|MN|≥2,求实数a的取值范围.18.已知圆C的极坐标方程为ρ=4cosθ﹣6sinθ,直线l的参数方程为(t为参数).若直线l与圆C相交于不同的两点P,Q.(1)写出圆C的直角坐标方程,并求圆心的坐标与半径;(2)若弦长|PQ|=4,求直线l的斜率.19.已知曲线C1的极坐标方程为ρcosθ﹣ρsinθ+2=0,曲线C2的参数方程为(α为参数),将曲线C2上的所有点的横坐标变为原来的3倍,纵坐标变为原来的倍,得到曲线C3.(1)写出曲线C1的参数方程和曲线C3的普通方程;(2)已知点P(0,2),曲线C1与曲线C3相交于A,B,求|PA|+|PB|.20.在极坐标系中,射线l:θ=与圆C:ρ=2交于点A,椭圆Γ的方程为ρ2=,以极点为原点,极轴为x轴正半轴建立平面直角坐标系xOy(Ⅰ)求点A的直角坐标和椭圆Γ的参数方程;(Ⅱ)若E为椭圆Γ的下顶点,F为椭圆Γ上任意一点,求•的取值范围.21.已知曲线C的参数方程是(α为参数)(1)将C的参数方程化为普通方程;(2)在直角坐标系xOy中,P(0,2),以原点O为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程为ρcosθ+ρsinθ+2=0,Q为C上的动点,求线段PQ的中点M到直线l的距离的最小值.22.已知在直角坐标系中,曲线的C参数方程为(φ为参数),现以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=.(1)求曲线C的普通方程和直线l的直角坐标方程;(2)在曲线C上是否存在一点P,使点P到直线l的距离最小?若存在,求出距离的最小值及点P的直角坐标;若不存在,请说明理由.23.已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,若直线l的极坐标方程为psin(θ﹣)=2.(1)把直线l的极坐标方程化为直角坐标系方程;(2)已知P为椭圆C:上一点,求P到直线l的距离的最小值.24.在平面直角坐标系xOy中,已知直线为参数).现以坐标原点O为极点,以x轴非负半轴为极轴建立极坐标系,设圆C的极坐标方程为ρ=2cosθ,直线l与圆C交于A,B两点,求弦AB的长.25.在直角坐标系xOy中,曲线C1的参数方程为(α为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线.(Ⅰ)写出曲线C1,C2的普通方程;(Ⅱ)过曲线C1的左焦点且倾斜角为的直线l交曲线C2于A,B两点,求|AB|.26.在极坐标系中,曲线C1:ρ=2cosθ,曲线.以极点为坐标原点,极轴为x轴正半轴建立直角坐标系xOy,曲线C的参数方程为(t 为参数).(Ⅰ)求C1,C2的直角坐标方程;(Ⅱ)C与C1,C2交于不同四点,这四点在C上的排列顺次为P,Q,R,S,求||PQ|﹣|RS||的值.27.极坐标系的极点为直角坐标系的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线C的极坐标方程为ρ=2(cosθ+sinθ).(1)求C的直角坐标方程;(2)直线l:为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.28.在直角坐标系中,以原点O为极点,x轴为正半轴为极轴,建立极坐标系.设曲线C:(α为参数);直线l:ρ(cosθ+sinθ)=4.(Ⅰ)写出曲线C的普通方程和直线l的直角坐标方程;(Ⅱ)求曲线C上的点到直线l的最大距离.29.在直角坐标系xoy 中,直线l的参数方程为,(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点o为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ.(Ⅰ)求圆C在直角坐标系中的方程;(Ⅱ)若圆C与直线l相切,求实数a的值.30.已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标是ρ=2asinθ,直线l的参数方程是(t为参数).(1)若a=2,M为直线l与x轴的交点,N是圆C上一动点,求|MN|的最大值;(2)若直线l被圆C截得的弦长为,求a的值.2017年02月14日茕翾熙的高中数学组卷参考答案与试题解析一.选择题(共9小题)1.(2017•武昌区模拟)中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器﹣﹣商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12。
广东省高考数学一轮复习 立体几何备考试题 理

广东省2015年高考数学理一轮复习备考试题:立体几何一、选择题1.(珠海2015届高三9月摸底)如图是一个几何体的三视图,则该几何体的体积为( )A .163πB .16πC .83πD .8π2、(2013广东高考)某四棱台的三视图如图所示,则该四棱台的体积是 ( )A . 4B .143C .163D .63、(2013广东高考)设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( )A . 若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥4、(2012广东高考)某几何体的三视图如图1所示,它的体积为( )A.12πB.45πC.57πD.81π5、(2011广东高考)如图1 ~ 3,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为侧视图俯视图第1题图A .. C ..6、(广州海珠区2015届高三8月摸底)已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是A .若//,//,m n αα则//m nB .若m α⊥,n α⊂,则m n ⊥C .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥二、解答题7、(2014广东高考)如图4,四边形ABCD 为正方形,PD ⊥平面ABCD ,030DPC ∠=,AF PC ⊥于点F ,//FE CD ,交PD 于点E . (1)证明:CF ADF ⊥平面 (2)求二面角D AF E --的余弦值8、(2013广东高考)如图1,在等腰直角三角形ABC 中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE =O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CD B '--的平面角的余弦值.图5CDP BAEF9、(2012广东高考)如图5所示,在四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,点E 在线段PC 上,PC ⊥平面BDE .(Ⅰ)证明:BD ⊥平面PAC ;(Ⅱ)若1PA =,2AD =,学科网求二面角B PC A --的正切值.是边长为1的10、(2011广东高考)如图5,在锥体P ABCD -中,ABCD 菱形,且60DAB ∠=,PA PD ==2PB =,,E F 分别是BC ,PC 的中点.(1)证明:AD ⊥平面DEF ;(2)求二面角P AD B --的余弦值.11、(2014广州一模)如图5,在棱长为a 的正方体1111ABCD A B C D -中,点E 是棱1D D 的中点,点F 在棱1B B 上,且满足12B F FB =. (1)求证:11EF AC ⊥;(2)在棱1C C 上确定一点G , 使A ,E ,G ,F 四点共面,并求此时1C G 的长;(3)求平面AEF 与平面ABCD 所成二面角的余弦值..CO BDECDOBE'A图1图2C1C1D ABDEF1A1B图512、(珠海2015届高三9月摸底)如图,长方体1111ABCD A B C D -中,E F G 、、分别为11AB C D DC 、、中点,123AB AD AC ==,(1)求证:1C E AFC 平面.(2)求二面角F AC G --的正切值.13、(广州海珠区2015届高三8月)如图,四棱锥ABCD P -中,底面ABCD 为正方形,PD PA =,⊥PA 平面PDC ,E 为棱PD 的中点.(1)求证:PB // 平面EAC ; (2)求证:平面PAD ⊥平面ABCD ; (3)求二面角B AC E --的余弦值.14、(2014届肇庆二模)如图5,在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,且∠DAB =60︒. 侧面PAD 为正三角形,其所在的平 面垂直于底面ABCD ,G 为AD 边的中点.(1)求证:BG ⊥平面PAD ;(2)求平面PBG 与平面PCD 所成二面角的平面角的 余弦值;(3)若E 为BC 边的中点,能否在棱PC 上找到一点F , 使平面DEF ⊥平面ABCD ,并证明你的结论.15.(2014届深圳二模)如图5,已知△ABC 为直角三角形,∠ACB 为直角.以AC 为直径作半圆O,使半圆O 所在平面⊥平面ABC,P 为半圆周异于A,C 的任意一点. (1) 证明:AP ⊥平面PBC(2) 若PA=1,AC=BC=2,半圆O 的弦PQ ∥AC,求平面PAB 与平面QCB 所成锐二面角的余弦值.G FEA 1D 1C 1B 1D CBA第18题图答案:1、A2、B3、D4、C5、B6、B 7(1)证明: PD ⊥平面ABCD , AD ⊂平面ABCD ∴PD AD ⊥ ①四边形ABCD 为正方形 ∴AD CD ⊥ ② AD CD D ⋂= AD ∴⊥平面PCD CF ⊂平面PCD AD CF ⊥ ③AF PC ⊥即AF CF ⊥ ④ 且AF AD A ⋂= CF ∴⊥平面ADF (2)方法1(传统法)过E 作EG DF ⊥交DF 于GGH AF ⊥交AF 于H ,连接EH EDG ∠就是所求二面角的平面角 (过程略)方法2(向量法)由(1)可得,,,AD PD AD DC PD DC ⊥⊥⊥,在Rt PDC ∆中,,30DPC CD a ∠==,则由(1)知PF DF ⊥,所以3cos302PF PD a ==, 因为//FE CD ,所以EF PF PEDC PC PD==,所以34EF a =,4PE =,所以4ED =,所以3(0,0,),(,0,0),(,,0),(0,,0)444aA a E F C a , 则333(,0,),(,),4a a a AE a AF a =-=- 设平面AEF 的法向量为(,,)n x y z =,则00nAE n AF ⎧⋅=⎪⎨⋅=⎪⎩,得03044az a x yaz ⎧-=⎪⎪⎪+-=⎪⎩, 取1x =,则0z y ==,所以3(1,0,n =由(1)可知,平面ADF的法向量为3(,0)4aCF =-,所以004cos ,||||nCF n CF n CF a +⋅<>====⋅设二面角D AF E--为θ,则cos θ=8、(Ⅰ) 在图1中,易得3,OC AC AD ===连结,OD OE ,在OCD∆中,由余弦定理可得OD 由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥,C D OBE'AH理可证A O OE '⊥, 又ODOE O =,所以A O '⊥平面BCDE .(Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角.结合图1可知,H 为AC 中点,故2OH =,从而AH '==所以cos OH A HO A H '∠=='所以二面角A CD B '--向量法:以O 点为原点,建立空间直角坐标系O xyz -则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧=⎪⎨-+=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,n =- 由(Ⅰ) 知,(OA '=为平面CDB 的一个法向量,所以cos ,53n OA n OA n OA '⋅'===',即二面角A CD B '--.9、解析:(Ⅰ)因为PC ⊥平面BDE ,BD ⊂平面BDE ,所以PC BD ⊥.又因为PA ⊥平面ABCD ,BD ⊂平面ABCD ,所以PA BD ⊥.而PC PA P =,PC ⊂平面PAC ,PA ⊂平面PAC ,所以BD ⊥平面PAC .(Ⅱ)由(Ⅰ)可知BD ⊥平面PAC ,而AC ⊂平面PAC ,所以BD AC ⊥,而ABCD 为矩形,所以ABCD 为正方形,于是2AB AD ==.CDPBAE FH 法1:以A 点为原点,AB 、AD 、AP 为x 轴、y 轴、z 轴,建立空间直角坐标系A BDP -.则()0,0,1P 、()2,2,0C 、()2,0,0B 、()0,2,0D ,于是()0,2,0BC =,()2,0,1PB =-.设平面PBC 的一个法向量为=1n (),,x y z ,则00BC PB ⎧⋅=⎪⎨⋅=⎪⎩11n n ,从而2020y x z =⎧⎨-=⎩,令1x =,得()1,0,2=1n .而平面PAC 的一个法向量为=2n ()2,2,0BD =-.所以二面角B P CA --的余弦值为c o s ,⋅<>=121212=n n n n n n ,于是二面角B PC A --的正切值为3.法2:设AC 与BD 交于点O ,连接OE .因为PC ⊥平面BDE ,OE ⊂平面BDE ,BE ⊂平面BDE ,所以PC OE ⊥,PC BE ⊥,于是OEB ∠就是二面角B PC A --的平面角.又因为BD ⊥平面PAC ,OE ⊂平面PAC ,所以OEB ∆是直角三角形.由OEC ∆∽PAC ∆可得OEPAOC PC=,而2A B A D ==,所以AC =OC =1PA =,所以3PC =,于是13PA OE OC PC =⨯=OB =B PC A --的正切值为3OBOE=.10、(1)证明:取AD 的中点H ,连接,,PH BH BD∵PA PD =,∴AD PH ⊥∵在边长为1的菱形ABCD 中,60DAB ∠= ∴△ABD 是等边三角形∴AD HB ⊥,PH HB H = ∴AD ⊥平面PHB ∴AD PB ⊥∵,E F 分别是BC ,PC 的中点 ∴EF ∥PB ,HB ∥DE ∴AD DE ⊥,AD EF ⊥,DEEF E =∴AD ⊥平面DEF(2)解:由(1)知PH AD ⊥,HB AD ⊥ ∴PHB ∠是二面角P AD B--的平面角 易求得PH BH ==∴2227334cos2PH HB PBPHBPH HB+--+-∠==⋅∴二面角P AD B--的余弦值为7-11、推理论证法:111DD D=1D D.因为H,连结BH AE.中,过点F作FG BH,则FG AE.四点共面.1113BF C C a==,EF DB M=与平面ABCD的交线.,垂足为N,连结FB BN B=,所以,所以AM与平面ABCDMB在△ABM中,AB a=,135ABM∠=,所以2222cos135AM AB MB AB MB=+-⨯⨯⨯sin135,sin135a⨯=1故平面AEF 与平面ABCD 所成二面角的余弦值为 空间向量法:(1)证明:以点D 为坐标原点,DA ,DC ,1DD 所在的直线分别为x 轴,y 轴,z 轴,建立如图的空间直角坐标系, 则(),0,0A a ,()1,0,A a a ,()10,,C a a ,所以()11,,0AC a a =-,,EF a a ⎛= 因为221100AC EF a a =-++=,所以11AC EF ⊥.所以11EF AC ⊥. (2)解:设()0,,G a h ,因为平面11ADD A 平面11BCC B ,平面11ADD A 平面AEGF AE =,平面11BCC B 平面AEGF FG =,所以FGAE .所以存在实数λ,使得FG AE λ=. 因为AE a ⎛=- ,FG a⎛=- 1λ=,h .所以1C G CC = ,E ,G ,F 四点共面. (3)解:由(1)知AE a ⎛=- ,0,AF a ⎛= 设(),,x y z =n 是平面AEF 的法向量,则0,0.AE AF ⎧=⎪⎨=⎪⎩n n 即取6z =,则3x =,2y =-.所以()3,2,6=-n 是平面AEF 的一个法向量. 而()10,0,DD a =是平面ABCD 的一个法向量, 设平面AEF 与平面ABCD 所成的二面角为θ,则11DD DD n n=故平面AEF 与平面ABCD 所成二面角的余弦值为12、解:(1).证明:在长方体1111ABCD A B C D -中,E F 、分别为11AB C D 、中点,∴1AE C F 且1AE C F =∴四边形1AEC F 是平行四边形∴1C E AF …………………………………………………………3分 AF AFC ⊂平面,1C E AFC ⊄平面 ∴1C E AFC 平面 ……………………………5分(2).长方体1111ABCD A B C D -中,F G 、分别为11C D DC 、中点,123AB AD AC ==, ∴FG ABCD ⊥平面 ……………………………7分过F 做FH AC ⊥于H ,又AC FG ⊥∴AC FGH ⊥平面 ∴GH AC ⊥∴FHG ∠就是二面角F AC G --的平面角 ……………………………9分FG =,在ACG ∆中,GH AC AD CG ⋅=⋅∴AD CG GH AC ⋅==……………………11分 ∴直角三角形FGH中tan 3FG FHG GH ∠=== ………………………………13分∴二面角F AC G --的正切值为3……………………………14分13. H G F E A 1D 1C 1B 1DC B A14、(1)证明:连结BD.因为ABCD为棱形,且∠DAB=60°,所以 ABD为正三角形. (1分)又G为AD的中点,所以BG⊥AD. (2分)又平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD , (3分) ∴BG ⊥平面PAD . (4分) 解:(2)∵△PAD 为正三角形,G 为AD 的中点,∴PG ⊥AD .∵PG ⊂平面PAD ,由(1)可得:PG ⊥GB . 又由(1)知BG ⊥AD .∴PG 、BG 、AD 两两垂直. (5分)故以G 为原点,建立如图所示空间直角坐标系G xyz -,330cos =︒=PD PG ,360sin =︒=AB GB , (6分)所以(0,0,0)G ,(0,1,0)D,(P,)2,0C ,(0,1,,PD =(3,2,PC = (7分) 设平面PCD 的法向量为0()0n PD n x y z n PC ⎧=⎪=⎨=⎪⎩·,,,∴·,即020y y ⎧=⎪+= 令1z =,则1(131)x y n =-==-,,, (8分) 又平面PBG 的法向量可为()020AD =,,, (9分) 设平面PBG 与平面PCD 所成二面角的平面角为θ,则∴2cos ||||2n AD n AD θ===·· 即平面PBG 与平面PCD . (10分) (3)当F 为PC 的中点时,平面DEF ⊥平面ABCD . (11分) 取PC 的中点F ,连结DE ,EF ,DF ,CG ,且DE 与CG 相交于H .因为E 、G 分别为BC 、AD 的中点,所以四边形CDGE 为平行四边形,故H 为CG 的中点. 又F 为CP 的中点,所以FH //PG . (12分) 由(2),得PG ⊥平面ABCD ,所以FH ⊥平面ABCD . (13分) 又FH ⊂平面DEF ,所以平面DEF ⊥平面ABCD . (14分)15、。
2024_2025学年高考数学一轮复习解题技巧方法第六章第1节三视图:排点法新高考不考教师版

三视图:排点法学问与方法当三视图由直角三角形、矩形或正方形构成时,一般考虑用长方体、正方体切割,此时借助排点法,可以通过推理来协助空间想象,降低难度,请观看视频学习排点法的用法.典型例题【例1】(2024·新课标III 卷)下图为某几何体的三视图,则该几何体的表面积是( )A.6+B.4+C.6+D.4+【解析】该几何体的直观图如图中的三棱锥A BCD -,由所给三视图可知正方体的棱长为2,所以几何体的表面积11322622S =⨯⨯⨯+⨯=+【答案】C【例2】(2017·北京)某四棱锥的三视图如下图所示,则该四棱锥的最长棱的长度为( )A. B. C. D.2【解析】如图,四棱锥S ABCD -即为题干三视图对应的几何体,由所给三视图可知正方体的棱长为2,明显SC 为正方体的体对角线,是四棱锥最长的棱,SC =【答案】B强化训练1.(2017·北京·★★★)某三棱锥的三视图如下图所示,则该三棱锥的体积为()A.60B.30C.20D.10【解析】这里用长方体切割来进行协助空间想象,如图,三棱锥A BCD-即为题干三视图对应的几何体,结合三视图数据可求得其体积115341032V=⨯⨯⨯⨯=.【答案】D2.(2010·辽宁·★★★)如下图所示,网格纸的小正方形边长是l,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱长为______【解析】如图所示的三棱锥A BCD-即为题干多面体,最长的棱是AD=【答案】3.(★★★)已知某几何体的三视图如下图所示,三视图是边长为1的等腰直角三角形和边长为1的正方形,则该几何体的体积为()A.16B.13C.12D.23【解析】几何体如图中的三棱锥A BCD-,其中正方体棱长为1,则111111326V=⨯⨯⨯⨯=.【答案】A4.(★★★)如下图所示,网格纸上小正方形边长为l,粗线画出的是某几何体的三视图,则该几何体的体积为()A.16B.13C.1D.43【解析】几何体如图中的三棱锥A BCD-,其中正方体棱长为2,则几何体的体积114222323V =⨯⨯⨯⨯=.【答案】D5.(2014·新课标I 卷·★★★★)如下图所示,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )A. B.6 C. D.4【解析】如图,三棱锥A BCD -即为题干的多面体,正方体的棱长是4,可求得4AD AB ==,AC BC ==BD =,6CD =,所以最长的棱的长度为6.【答案】B。
一轮复习50道三视图练习题
23.若一个几何体的三视图如图所示,则此几何体的体积为( )
A. B. C. D.
24.某几何体的三视图如图所示,则该几何体的外接球的球面面积为( )
A.5πB.12πC.20πD.8π
25.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为( )
A. B. C. D.
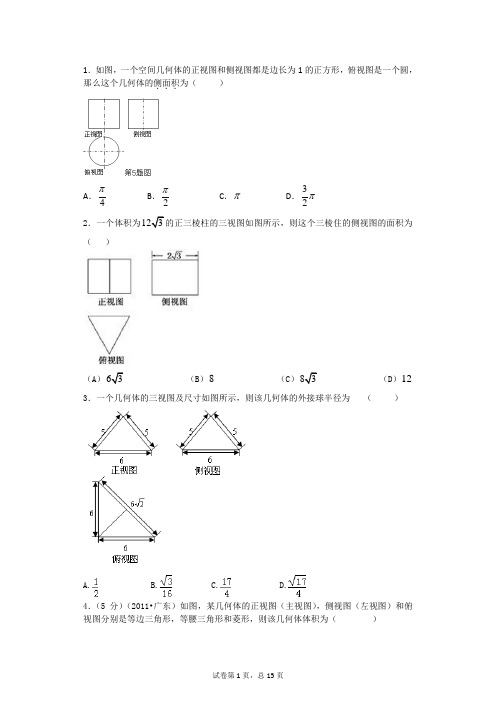
1.如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为()
A. B. C. D.
2.一个体积为 的正三棱柱的三视图如图所示,则这个三棱住的侧视图的面积为( )
(A) (B) (C) (D)
3.一个几何体的三视图及尺寸如图所示,则该几何体的外接球半径为()
26.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )
A.9B.10C.11D.
27.某几何体的三视图如图所示,则它的表面积为( )
A. B.
C. D.
28.如图是一个空间几何体的三视图,则该几何体的外接球的表面积为
A. B. C. D.
29.一个几何体的三视图如图所示,则这个几何体的体积等于
A. B. C. D.
30.已知一空间几何体的三视图如图所示,则该几何体的体积为( )
A. πcm3B.3πcm3C. πcm3D. πcm3
31.某几何体的三视图如题(6)所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为( )
(A)1 (B) (C) (D)
A. B. C. D.
7.已知一个三棱锥的三视图如图所示,其中俯视图是等腰三角形,则该三棱锥的体积为( )
A. B. C. D.
高考数学大一轮复习配套课时训练:第七篇 立体几何 第1节 空间几何体的结构及三视图和直观图(含答案)

第七篇立体几何(必修2)第1节空间几何体的结构及三视图和直观图课时训练练题感提知能【选题明细表】A组一、选择题1.(2013山东烟台模拟)如图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧(左)视图的面积为( C )(A)8π(B)6π(C)4+(D)2+解析:该组合体的侧(左)视图为其中正方形的边长为2,三角形为边长为2的三角形,所以侧(左)视图的面积为22+×22×=4+,故选C.2.(2013山东莱州模拟)一个简单几何体的正(主)视图,侧(左)视图如图所示,则其俯视图不可能为①长方形;②直角三角形;③圆;④椭圆.其中正确的是( C )(A)①(B)② (C)③ (D)④解析:当该几何体的俯视图为圆时,由三视图知,该几何体为圆柱,此时,正(主)视图和侧(左)视图应相同,所以该几何体的俯视图不可能是圆,其余都有可能.故选C.3.(2013韶关市高三调研)某几何体的三视图如图所示,根据图中标出的数据,可得这个几何体的表面积为( B )(A)4+4 (B)4+4(C) (D)12解析:由三视图知该几何体为正四棱锥P ABCD,底面边长为2,高PO=2,如图所示,取CD的中点E,连接OE、PE,则PE==,因此几何体的表面积为2×2+×2×4×=4+4,故选B.4.如果一个水平放置的图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( A )(A)2+(B)(C)(D)1+解析:由题意画出斜二测直观图及还原后原图,由直观图中底角均为45°,腰和上底长度均为1,得下底长为1+,所以原图上、下底分别为1,1+,高为2的直角梯形.所以面积S=(1++1)×2=2+.故选A.5.(2013北京东城区模拟)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( D )(A)1 (B)2 (C)3 (D)4解析:由题意可知,几何体是三棱锥,其放置在长方体中形状如图所示,利用长方体模型可知,此三棱锥A BCD的四个面中,全部是直角三角形.故选D.6.(2013广州市毕业班测试(二))一个圆锥的正(主)视图及其尺寸如图所示,若一个平行于圆锥底面的平面将此圆锥截成体积之比为1∶7的上、下两部分,则截面的面积为( C )(A)π(B)π (C)π(D)4π解析:由题意知,该几何体是底面半径为3,高为4的圆锥.由截面性质知截面圆半径为×3=,故截面的面积为π·()2=,故选C.7.下面是关于四棱柱的四个命题:①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;②若过两个相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;③若四个侧面两两全等,则该四棱柱为直四棱柱;④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱.其中真命题为( D )(A)①②(B)①③(C)②③(D)②④解析:对于①,平行六面体的两个相对侧面与底面垂直且互相平行,而另两个相对侧面可能与底面不垂直,则不是直棱柱,故①假;对于②,两截面的交线平行于侧棱,且垂直于底面,故②真;对于③,作正四棱柱的两个平行菱形截面,可得满足条件的斜四棱柱(如图(1)所示),故③假;对于④,四棱柱一个对角面的两条对角线,恰为四棱柱的对角线,故对角面为矩形,于是侧棱垂直于底面的一条对角线,同样侧棱也垂直于底面的另一条对角线,故侧棱垂直于底面,故④真.故选D.二、填空题8.如图所示的Rt△ABC绕着它的斜边AB旋转一周得到的图形是.解析:过Rt△ABC的顶点C作线段CD⊥AB,垂足为D,所以Rt△ABC绕着它的斜边AB旋转一周后应得到的是以CD作为底面圆的半径的两个圆锥的组合体.答案:两个圆锥的组合体9.一个几何体的正(主)视图为一个三角形,则这个几何体可能是下列几何体中的(填入所有可能的几何体前的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.解析:显然①②⑤均有可能;当三棱柱放倒时,其正(主)视图可能是三角形,所以③有可能,④不可能.答案:①②③⑤10.如图,点O为正方体ABCD A′B′C′D′的中心,点E为平面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影可能是(填出所有可能的序号).解析:空间四边形D′OEF在正方体的平面DCC′D′上的投影是①;在平面BCC′B′上的投影是②;在平面ABCD上的投影是③,而不可能出现投影为④的情况.答案:①②③11.(2013山东烟台模拟)如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正(主)视图是边长为2的正方形,俯视图为正三角形,则侧(左)视图的面积为.解析:因为俯视图为正三角形,所以俯视图的高为,侧视图为两直角边分别为2、的矩形,所以侧(左)视图的面积为2.答案:2三、解答题12.(2013西工大附中模拟)已知四棱锥P ABCD的三视图如图所示,求此四棱锥的四个侧面的面积中最大值.解:由三视图可知该几何体是如图所示的四棱锥,顶点P在底面的射影是底面矩形的顶点D.底面矩形边长分别为3,2,△PDC是直角三角形,直角边为3与2,所以S△PDC=×2×3=3.△PBC是直角三角形,直角边长为2,,三角形的面积为×2×=.△PAB是直角三角形,直角边长为3,2;其面积为×3×2=3.△PAD也是直角三角形,直角边长为2,2,三角形的面积为×2×2=2. 所以四棱锥P ABCD的四个侧面中面积最大的是前面三角形的面积为3.13.圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392 cm2,母线与轴的夹角为45°,求这个圆台的高、母线长和底面半径.解:圆台的轴截面如图.设圆台的上、下底面半径分别为x cm和3x cm,延长AA1交OO1的延长线于点S.在Rt△SOA中,∠ASO=45°,则∠SAO=45°.所以SO=AO=3x,OO1=2x.又×(6x+2x)×2x=392,解得x=7.所以圆台高OO母线长l=OO1=14 cm,底面半径分别为7 cm和21 cm.B组14.(2013广州高三调研)已知四棱锥P ABCD的三视图如图所示,则四棱锥P ABCD的四个侧面中面积最大的是( C )(A)3 (B)2(C)6 (D)8解析:四棱锥如图所示,PM=3,×4×=2,S△PDC=S△PAB=×4×3=6,S△PBC=S△PAD=×2×3=3,故四个侧面中面积最大的是6.15.(2013北京西城检测)三棱锥D ABC及其三视图中的正视图和侧视图如图所示,则棱BD的长为.解析:取AC的中点E,连结BE,DE,由正(主)视图可知BE⊥AC,BE⊥DE.DC⊥平面ABC且DC=4,BE=2,AE=EC=2.所以BC====4,即BD====4.答案:416.三棱锥V ABC的底面是正三角形,顶点在底面ABC上的射影为正△ABC的中心,其三视图如图所示:(1)画出该三棱锥的直观图;(2)求出侧(左)视图的面积.解:(1)直观图如图所示.(2)根据三视图间的关系可得BC=2,作AM⊥BC于M,连结VM,过V作VO⊥AM于O,过O作EF∥BC交AB,AC于F、E,则△VEF即侧(左)视图.由=,得EF=.又VA=4,AM==3.则AO=2,VO===2.××2=4.所以S即侧(左)视图的面积为4.。
广东省高三数学一轮复习 试题选编9 三视图及空间几何体的表面积与体积 理

广东省2014届高三理科数学一轮复习试题选编9:三视图及空间几何体的表面积与体积一、选择题1 .(广东省汕头市2013年普通高中高三教学质量测试试题(二)理科数学试卷)某三棱锥的三视图如图所示,该三棱锥的体积是 ( )A .403B C .503D .6【答案】A2 .(广东省东莞市2013届高三第二次模拟数学理试题)如图是一个几何体的三视图,若它的体积是则a =( )AB CD 【答案】C 3 .(广东省广州市2013届高三调研测试数学(理)试题)已知四棱锥P ABCD -的三视图如图1所示,则四棱锥P ABCD -的四个侧面中面积最大的是俯视图侧视图正视图图1( )A .3 B.C .6D .8【答案】C分析:三棱锥如图所示,3PM =,142PDC S ∆=⨯=12332PBC PAD S S ∆∆==⨯⨯=,14362PAB S ∆=⨯⨯=222N4 .(广东省江门市2013年高考模拟考试(即一模)数学(理)试题 )右图是某个四面体的三视图,该四面体的体积为( )A .72B .36C .24 D.12【答案】D 5 .(广东省梅州市2013届高三3月总复习质检数学(理)试题)如图是一个几何体的三视图,若它的体积是,则a=( )AB CD 【答案】C 6 .(广东省汕头市2013届高三上学期期末统一质量检测数学(理)试题)如图正四棱锥(底面是正方形,顶点在底面的射影是底 面的中心)P-ABCD 的底面边长为6cm,侧棱长为 5cm,则它的侧视图的周长等于 ( )A .17cmB .cm 5119C .16cmD .14cm【答案】D 7 .(广东省茂名市2013届高三第一次模拟考试数学(理)试题)若某一几何体的正视图与侧视图均为边长是1的正方形,且其体积为12,则该几何体的俯视图可以是【答案】C8 .(广东省揭阳市2013届高三3月第一次高考模拟数学(理)试题(含解析))一简单组合体的三视图及尺寸如图(1)示(单位: cm )则该组合体的体积为.( )A .720003cmB .640003cmC .560003cmD .440003cm 图(1)【答案】B由三视图知,该组合体由两个直棱柱组合而成,故其体积360401020405064000()V cm =⨯⨯+⨯⨯=,故选B .9 .(广东省湛江市2013届高三4月高考测试(二)数学理试题(WORD 版)的线段,在该几何体的侧视图与俯视图中,这条棱的( )52【答案】C10.(广东省“六校教研协作体”2013届高三第二次(11月)联考数学(理)试题)已知一个空间几何体的三视图如右图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 ( )A .4 cm 3B .5 cm 3C .6 cm 3D .7 cm 3【答案】 ( )A . 11.(广东省揭阳市2013年高中毕业班第二次高考模拟考试理科数学试题)一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图 如图(1)示,则该几何体的体积为 ()俯视图侧视图A .7B .223C .476D .233图(1)【答案】依题意可知该几何体的直观图如右上图,其体积为.3112322111323-⨯⨯⨯⨯⨯=,故选 D .12.(2013广东高考数学(理))某四棱台的三视图如图所示,则该四棱台的体积是( )A .4B .143 C .163D .6【答案】B;由三视图可知,该四棱台的上下底面边长分别为1和2的正方形,高为2,故()2211412233V =⨯=,,故选B .13.(广东省广州市2013届高三4月综合测试(二)数学理试题(WORD 版))一个圆锥的正(主)视图及其尺寸如图2所示.若一个平行于 圆锥底面的平面将此圆锥截成体积之比为1﹕7的上、下两部分,则截面的面积为 ( )正视图俯视图侧视图第5题图侧视图正视图A .14π B .πC .94π D .4π【答案】C14.(广东省珠海市2013届高三9月摸底(一模)考试数学(理)试题)如图是某几何体的三视图,则此几何体的体积是___( )A .36B .108C .72D .180【答案】B15.(广东省珠海一中等六校2013届高三5月高考模拟考试数学(理)试题)已知某四棱锥的三视图,如右图.则此四棱锥的体积为 ( )A .3B .4C .5D .6【答案】【解析】如图,四棱锥A BCDE -.图216243V=⨯⨯=.故选B.16.(广东省湛江一中等“十校”2013届高三下学期联考数学(理)试题)某几何体的三视图如图所示,当a b+取最大值时,这个几何体的体积为()A.16B.13C.23D.12【答案】D17.(广东省云浮市2012-2013新兴县第一中学高三阶段检测试题数学(三)(理) )已知某几何体的三视图如图所示,则该几何体的体积为()A.8π3B.3πC.10π3D.6π俯视图侧视图正视图第7题图4【答案】B 18.(广东省潮州市2013届高三第二次模拟考试数学(理)试题)已知一个几何体的三视图及其大小如图1,这个几何体的体积=V ( )A .π12B .π16C .π18D .π64【答案】B 19.(广东省肇庆市2013届高三上学期期末统一检测数学(理)试题)已知某个几何体的三视图如图2所示,根据图中标出的尺寸(单位:cm),则这个几何体的体积是 ( )A .38cmB .312cmC .324cmD .372cm【答案】B 解析:三视图的直观图是有一个侧面垂直于底面三棱锥,底面是底边长为6高为4的等腰三角形,三棱锥的高为3,所以,这个几何体的体积116431232V =⨯⨯⨯⨯=20.(2010年高考(广东理))如图1,△ABC 为正三角形,AA ′∥BB ′∥CC ′,CC ′⊥平面ABC 且3AA ′=23BB ′= CC ′=AB ,则多面体ABC —A ′B ′C ′的正视图(也称主视图)是【答案】 D .21.(广东省汕头市东山中学2013届高三第二次模拟考试数学(理)试题(详解))若某空间几何体的三视图如图所示,则该几何体的体积是【答案】B22.(2013年广东省佛山市普通高中高三教学质量检测(一)数学(理)试题)一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )A .9B .10C .11D .232【答案】C1 1 正视图 侧视图俯视图第4题图图侧视图 图2俯视图图3 23.(2011年高考(广东理))如图1 ~ 3,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯则该几何体的体积为A .C.案】B 【答则33V Sh === 24.(广东省韶关市2013届高三4月第二次调研测试数学理试题)一空间几视图如右图所示,该几何体的体积为12π+853,则正视图与侧何体的三视图中x的值为A .5B .4 C .3D .2【答案】C25.(广东省惠州市2013届高三4月模拟考试数学理试题(WORD 版))如图是某简单组合体的三视图,则该组合体的体积为( )A .πB .2)π+C .D .2)+【答案】【解析】由三视图可知几何体是由截面相同的半个圆锥与半个三棱锥组合而成的.圆椎底面半径为6,椎体底面边长为12,高为.1111361262)3232V ππ=⨯⨯⨯⨯+⨯⨯⨯⨯=+故选B .26.(广东省广州市2013届高三3月毕业班综合测试试题(一)数学(理)试题)某空间几何体的三视图及尺寸如图1,则该几何体的体积是图1俯视图正视图( ) A .2 B .1 C .23 D .13【答案】A二、填空题27.(广东省汕头市第四中学2013届高三阶段性联合考试数学(理)试题)已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形则此三棱锥的体积等于_____________ .【答案】328.(广东省潮州市2013届高三上学期期末教学质量检测数学(理)试题)若一个正三棱柱的三视图如下图所示,则这个正三棱柱的体积为__________.主视图俯视图左视图【答案】由左视图知正三棱柱的高2h =,设正三棱柱的底面边长a ,=故4a =,底面积142S =⨯⨯=故2V Sh ===. 29.(广东省深圳市2013届高三第二次调研考试数学理试题(2013深圳二模))某简单组合体的三视图如图2,其中正视图与侧视图相同(尺寸如图,单位:cm),则该组合体的体积是________3cm (结果保留π)【答案】13π+30.(广东省汕头市东山中学2013届高三下学期入学摸底考试数学(理)试题)一个几何体的三视图如图所示,正视图是正方形,俯视图为半圆,侧视图为矩形,则其表面保积为________【答案】π34+;31.(广东省茂名市实验中学2013届高三下学期模拟(二)测试数学(理)试题(详解))某几何体的三视图如图所示,且该几何体的体积为3,则正视图中的x=____【答案】332.(广东省中山市2013届高三上学期期末统一考试数学(理)试题)若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积...等于_______【答案】6+33.(广东省肇庆市2013届高三4月第二次模拟数学(理)试题)图2是一个组合体的三视图,根据图中数据,可得该几何体的表面积等于(几何体的接触面积可忽略不计)___________【答案】40π解析:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面及为 22422222648.S ππππ=⨯+⨯⨯+⨯⨯=34.(2013届广东省高考压轴卷数学理试题)已知某棱锥的三视图如右图所示,则该棱锥的体积为__________ .【答案】2 四棱锥底面是直角梯形,面积为()122132⨯⨯+=,高为2,则体积为235.(广东省海珠区2013届高三上学期综合测试(一)数学(理)试题)一个几何体的三视图如图2所示,则该几何体的体积为__________.【答案】12π+36.(广东省茂名市2013届高三4月第二次高考模拟数学理试题(WORD版))一个几何体的三视图如图所示,则这个几何体的体积为___【答案】10 3正视图俯视图侧视图图2。
广东新高考数学理科一轮总复习课时练习13.1空间几何体的三视图和直观图(含答案详析)
第十三章 立体几何第1讲 空间几何体的三视图和直观图1.以下命题:①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;③圆柱、圆锥、圆台的底面都是圆;④一个平面截圆锥,得到一个圆锥和一个圆台.其中正确命题的个数为( )A .0个B .1个C .2个D .3个2.如图K13-1-1,正方形O ′A ′B ′C ′的边长为1 cm ,它是水平放置的一个平面图形的直观图,则原图形的周长为( )A .6 cmB .8 cmC .(2+4 2) cmD .(2+2 3) cm图K13-1-1 图K13-1-23.(2013年广东肇庆一模)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图K13-1-2所示,则其侧视图的面积为( )A.64B.62C.22D. 2 4.(2014年广东广州一模)一个四棱锥的底面为菱形,其三视图如图K13-1-3所示,则这个四棱锥的体积是________.图K13-1-35.若一个底面是正三角形的三棱柱的正视图如图K13-1-4,则其侧面积等于( )A. 3 B .2 C .2 3 D .6图K13-1-4 图K13-1-56.如图K13-1-5,直三棱柱的正视图面积为2a2,则侧视图的面积为________.7.在图K13-1-6的三个图中,上面是一个长方体截去一个角所得多面体的直观图,它的主视图和左视图在下面画出.K13-1-6(1)在主视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积.8.图K13-1-7(1)为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.(1)如图K13-1-7(2)所示的方框内已给出了该几何体的俯视图,请在方框内画出该几何体的正(主)视图和侧(左)视图;(2)求四棱锥B-CEPD的体积;(3)求证:BE∥平面PDA.(1) (2)图K13-1-7第十三章 立体几何第1讲 空间几何体的三视图和直观图1.B 2.B 3.A 4.45.D 解析:由正视图知:三棱柱是以底面边长为2,高为1的正三棱柱,所以侧面积为3×2×1=6. 6.3a 2 解析:由主视图面积可求出直三棱柱的高为2a ,底面的正三角形的高为32a ,故左视图的面积为2a ·32a =3a 2. 7.解:(1)如图D89.图D89 (2)所求多面体体积V =V 长方体-V 正三棱锥=4×4×6-13×⎝⎛⎭⎫12×2×2)×2=2843. 8.(1)解:该组合体的正视图和侧视图如图D90.图D90(2)解:∵PD ⊥平面ABCD ,PD ⊂平面PDCE ,∴平面PDCE ⊥平面ABCD .∵BC ⊥CD ,∴BC ⊥平面PDCE .∵S 梯形PDCE =12(PD +EC )·DC =12×3×2=3, ∴四棱锥B -CEPD 的体积为V B -CEPD =13S 梯形PDCE ·BC =13×3×2=2. (3)证明:∵EC ∥PD ,PD ⊂平面PDA ,EC ⊄平面PDA ,∴EC ∥平面PDA .同理,BC ∥平面PDA .∵EC ⊂平面EBC ,BC ⊂平面EBC ,且EC ∩BC =C ,∴平面EBC∥平面PDA.又∵BE⊂平面EBC,∴BE∥平面PDA.。
【步步高】(广东专用)2015高考数学一轮复习 第1讲 空间几何体的结构、三视图和直观图同步检测 文
第八章立体几何第1讲空间几何体的结构、三视图和直观图一、选择题1. 下列四个几何体中,几何体只有主视图和左视图相同的是( )A.①② B.①③C.①④ D.②④解析由几何体分析知②④中主视图和左视图相同.答案 D2.以下关于几何体的三视图的论述中,正确的是( ).A.球的三视图总是三个全等的圆B.正方体的三视图总是三个全等的正方形C.水平放置的正四面体的三视图都是正三角形D.水平放置的圆台的俯视图是一个圆解析画几何体的三视图要考虑视角,但对于球无论选择怎样的视角,其三视图总是三个全等的圆.答案 A3.将正方体(如图(a)所示)截去两个三棱锥,得到图(b)所示的几何体,则该几何体的侧视图为( ).解析还原正方体后,将D1,D,A三点分别向正方体右侧面作垂线,D1A的射影为C1B,且为实线,B1C被遮挡应为虚线.答案 B4.若某几何体的三视图如图所示,则这个几何体的直观图可以是( ).解析A,B的正视图不符合要求,C的俯视图显然不符合要求,答案选D.答案 D5.一个平面四边形的斜二测画法的直观图是一个边长为a的正方形,则原平面四边形的面积等于( ).A.24a2 B.22a2 C.22a2 D.223a2解析根据斜二测画法画平面图形的直观图的规则,可以得出一个平面图形的面积S与它的直观图的面积S′之间的关系是S′=24S,本题中直观图的面积为a2,所以原平面四边形的面积等于a224=22a2.故选B.答案 B6.一个锥体的正视图和侧视图如图所示,下面选项中,不可能是该锥体的俯视图的是( ).解析选项C不符合三视图中“宽相等”的要求.答案 C二、填空题7.如图所示,E、F分别为正方体ABCD-A1B1C1D1的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面DCC1D1上的投影是________(填序号).解析B在面DCC1D1上的投影为C,F、E在面DCC1D1上的投影应分别在边CC1和DD1上,而不在四边形的内部,故①③④错误.答案②8.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为________.解析(构造法)由主视图和俯视图可知几何体是正方体切割后的一部分(四棱锥C1- ABCD),还原在正方体中,如图所示.多面体最长的一条棱即为正方体的体对角线,如图即AC1.由正方体棱长AB=2知最长棱AC1的长为2 3.答案2 39.利用斜二测画法得到的:①三角形的直观图一定是三角形;②正方形的直观图一定是菱形;③等腰梯形的直观图可以是平行四边形;④菱形的直观图一定是菱形.以上正确结论的序号是________.解析由斜二测画法的规则可知①正确;②错误,是一般的平行四边形;③错误,等腰梯形的直观图不可能是平行四边形;而菱形的直观图也不一定是菱形,④也错误.答案①10.图(a)为长方体积木块堆成的几何体的三视图,此几何体共由________块木块堆成;图(b)中的三视图表示的实物为________.图(a) 图(b)解析(1)由三视图可知从正面看到三块,从侧面看到三块,结合俯视图可判断几何体共由4块长方体组成.(2)由三视图可知几何体为圆锥.答案 4 圆锥三、解答题11.如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的主视图和左视图在下面画出(单位:cm).(1)在主视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积;解 (1)如图.(2)所求多面体的体积V =V 长方体-V 正三棱锥=4×4×6-13×⎝ ⎛⎭⎪⎫12×2×2×2=2843(cm 3).12.已知圆锥的底面半径为r ,高为h ,且正方体ABCD -A 1B 1C 1D 1内接于圆锥,求这个正方体的棱长.解 如图所示,过内接正方体的一组对棱作圆锥的轴截面,设圆锥内接正方体的棱长为x ,则在轴截面中,正方体的对角面A 1ACC 1的一组邻边的长分别为x 和2x .∵△VA 1C 1∽△VMN , ∴2x 2r =h -x h ,∴x =2rh2r +2h. 即圆锥内接正方体的棱长为2rh2r +2h.13.正四棱锥的高为3,侧棱长为7,求侧面上斜高(棱锥侧面三角形的高)为多少? 解 如图所示,在正四棱锥S -ABCD 中,高OS =3,侧棱SA =SB =SC =SD =7, 在Rt △SOA 中,OA =SA 2-OS 2=2,∴AC =4.∴AB =BC =CD =DA =2 2. 作OE ⊥AB 于E ,则E 为AB 中点.连接SE ,则SE 即为斜高,在Rt △SOE 中,∵OE =12BC =2,SO =3,∴SE =5,即侧面上的斜高为 5.14. (1)如图1所示的三棱锥的三条侧棱OA 、OB 、OC 两两垂直,那么该三棱锥的侧视图是图2还是图3?(2)某几何体的三视图如图4,问该几何体的面中有几个直角三角形? (3)某几何体的三视图如图5,问该几何体的面中有几个直角三角形?解 (1)该三棱锥在侧(右)投影面上的投影是一直角三角形,该三棱锥的侧视图应是图2.(2)该几何体是三棱锥,其直观图如图所示,其中OA 、OB 、OC 两两垂直,∴△OAB 、△OAC 、△OBC 都是直角三角形,但△ABC 是锐角三角形.设AO =a ,OC =c ,OB =b ,则AC =a 2+c 2,BC =c 2+b 2,AB =a 2+b 2,∴cos ∠BAC =a 2a 2+b 2·c 2+a 2>0,∴∠BAC 为锐角.同理,∠ABC 、∠ACB 也是锐角.综上所述,该几何体的面中共有三个直角三角形.(3)该几何体是三棱锥,其直观图如图所示,其中,AB ⊥BC ,AB ⊥BD ,BD ⊥CD ,∴DC ⊥面ABD ,∴DC ⊥AD ,∴△ACD也是直角三角形.∴该几何体的面中共有四个直角三角形.。
2020届高考数学理一轮复习空间几何体及其三视图、直观图文科
文数
课标版
第一节 空间几何体及其三视图、直观图
教材研读
栏目索引
1.空间几何体的结构特征
多 (1)棱柱:侧棱都① 平行且相等 ,上、下底面平行且是② 全等 的多边形. 面 (2)棱锥:底面是多边形,侧面是有一个公共顶点的三角形. 体 (3)棱台:可以由平行于棱锥底面的平面截棱锥得到,其上、下底面是③ 相似 多边形
旋 (1)圆柱:可以由④ 矩形 绕其任一边所在直线旋转得到. 转 (2)圆锥:可以由直角三角形绕其⑤ 直角边 所在直线旋转得到. 体 (3)圆台:可以由直角梯形绕其⑥ 垂直于底边的腰 所在直线或等腰梯形绕其上、下
底边中点的连线所在直线旋转得到,也可由平行于圆锥底面的平面截圆锥得到. (4)球:可以由半圆或圆绕其⑦ 直径 所在直线旋转得到
栏目索引
2.三视图与直观图
三视图 画三视图的规则:长对正,高平齐,宽相等 空间几何体的直观图常用⑧ 斜二测 画法来画,规则如下: (1)原图形中x轴、y轴、z轴两两垂直(原点为O),直观图中相应x'轴,y'轴满足∠x'O'y'=
直观图 ⑨ 45°(或135°) (O'为原点),z'轴与x'轴和y'轴所在平面垂直. (2)原图形中平行于坐标轴的线段在直观图中仍 平行于相应坐标轴 ,平行于x轴 和z轴的线段长度在直观图中保持原长度 不变 ,平行于y轴的线段长度在直观 图中长度为 原来的一半
栏目索引
2-1 (2014课标Ⅰ,8,5分)如图,网格纸的各小格都是正方形,粗实线画出 的是一个几何体的三视图,则这个几何体是 ( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱 答案 B 由题中三视图可知该几何体的直观图如图所示,则这个几何 体是三棱柱,故选B.
(新课标)高考数学一轮复习名校尖子生培优大专题三视图新人教A版【含答案】
(新课标)高考数学一轮复习名校尖子生培优大专题三视图新人教A版【考纲解读】1.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二侧法画出它们的直观图.2.会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.3.会画出某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求).【考点预测】高考对此部分内容考查的热点与命题趋势为:1.立体几何是历年来高考重点内容之一,在选择题、填空题与解答题中均有可能出现,难度不大,主要考查空间中线线、线面、面面的位置关系的判定与证明,考查表面积与体积的求解,考查三视图等知识,在考查立体几何基础知识的同时,又考查数形结合思想、转化与化归等数学思想,以及分析问题、解决问题的能力.2高考将会继续保持稳定,坚持考查立体几何的基础知识,命题形式相对会较稳定.【要点梳理】1.空间几何体的三视图三视图是观测者从不同位置观察同一个几何体,画出的空间几何体的图形。
他具体包括:(1)正视图:物体前后方向投影所得到的投影图;它能反映物体的高度和长度;(2)侧视图:物体左右方向投影所得到的投影图;它能反映物体的高度和宽度;(3)俯视图:物体上下方向投影所得到的投影图;它能反映物体的长度和宽度;2.空间几何体的直观图(1)斜二测画法①建立直角坐标系,在已知水平放置的平面图形中取互相垂直的OX,OY,建立直角坐标系;②画出斜坐标系,在画直观图的纸上(平面上)画出对应的O’X’,O’Y’,使=450(或1350),它们确定的平面表示水平平面;③画对应图形,在已知图形平行于X轴的线段,在直观图中画成平行于X‘轴,且长度保持不变;在已知图形平行于Y轴的线段,在直观图中画成平行于Y‘轴,且长度变为原来的一半;④擦去辅助线,图画好后,要擦去X轴、Y轴及为画图添加的辅助线(虚线)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三视图
考查内容:空间图形的三视图,柱体、锥体、球体的体积公式和表面积公式。
1、下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( D )
A、 B、 C、 D、
1、 2、
2、已知四棱锥的三视图如图,则四棱锥的全面积为( A )
A、B、C、5D、4
3、正视图为一个三角形的几何体可以是。
(写出三种)
三棱锥、三棱柱、圆锥
4、一个几何体的三视图如图所示,则这个几何体的体积为。
4、5、6、
5、若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于。
答案:
6、如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多
面体最长的一条棱的长为。
7、8、9、
解析:由三视图可知,此多面体是一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥,所以最长棱长为。
7、若某几何体的三视图(单位:)如图所示,则此几何体的体积是____。
答案:144
8、如图是一个几何体的三视图,若它的体积是,则。
答案:。
9、一个几何体的三视图如图所示,则这个几何体的体积为。
设几何体的体积为,则。
10、11、
10、设某几何体的三视图如下(单位为),则该几何体的体积为。
