辽宁省辽河油田第二高级中学2020届高三数学10月月考试题文
辽宁省辽河油田第二高级中学2020届高三数学上学期期末考试试题 文

辽宁省辽河油田第二高级中学2020届高三数学上学期期末考试试题文时间:120分钟 分值:150分一、选择题(每题一个选项,每题5分共60分)1.复数z 满足()1i i z +=,则在复平面内复数z 所对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限2.已知{}lg 0A x x =>,{}12B x x =-<,则A B =U ( ) A .{}11x x x <-≥或 B .{}1x x >-C .{}3x x >D .{}13x x <<3.一个体积可忽略不计的小球在边长为2的正方形区域内随机滚动,则它在离4个顶点距离都大于1的区域内的概率为( ) A .π4B .2πC .π12- D . 14π-4.设0534a ⎛⎫= ⎪⎝⎭.,0443b ⎛⎫= ⎪⎝⎭.,()334log log 4c =,则( )A .a c b <<B .c a b <<C .c b a <<D .a b c <<5.若x ,y 满足1010330x y x y x y +-≥--≤-+≥⎧⎪⎨⎪⎩,则2z x y =-的最小值为( )A .1-B .2-C .2D .16.正项等差数列{}n a 的前n 和为n S ,已知2375150a a a +-+=,则9S =( ) A .35 B .36 C .45 D .547.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,则“2cos a b C =”是“ABC △是等腰三角形”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件8.设向量(),4x =-a ,()1,x =-b ,向量a 与b 的夹角为锐角,则x 的范围为( ) A .()2,2-B .()0,+∞C .[]2,2-D .()()0,22,+∞U9.一个几何体的三视图如图所示,则这个几何体的体积等于( )A .90B .72C .68D .6010.执行如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( )A .12s >B .35s >C .45s >D .710s >11.过双曲线()22221,0x y a b a b-=>的左焦点F 作圆222x y a +=的切线,切点为T ,延长FT交双曲线右支于点P .若线段PF 的中点为M ,O 为坐标原点,则OM MT -与b a -的大小关系是( ) A .OM MT b a -=- B .OM MT b a -<- C .OM MT b a ->-D .无法确定12.设函数()244,143,1x x f x x x x -≤⎧⎪=⎨-+>⎪⎩,()2log g x x =,则函数()()()h x f x g x =-的零点个数是( ) A .1B .2C .3D .4二、填空题(每小题5分,每题5分共20分) 13.若ABC △的内A ,B 满足()sin 2cos sin BA B A=+,则tan B 的最大值为 .14.已知椭圆()2211221110x y a b a b +=>>与双曲线()2222222210,0x y a b a b -=>>有公共的左、右焦点1F ,2F ,它们在第一象限交于点P ,其离心率分别为1e ,2e ,以1F ,2F 为直径的圆恰好过点P ,则221211e e +=________. 15.若241x y +=,则2x y +的取值范围为_____.16.已知函数()32f x x ax =-在()1,1-上没有最小值,则a 的取值范围是__________. 三.解答题:(共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(12分)已知正项等比数列{}n a 满足126a a +=,324a a -=. (1)求数列{}n a 的通项公式; (2)记2211log log n n n b a a +=,求数列{}n b 的前n 项和n T .18.(12分)随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在A 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为A 市使用共享单车情况与年龄有关?(2)现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率. 参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.参考数据:19.(12分)如图1所示,平面多边形CDEF 中,四边形ABCD 为正方形, EF AB ∥,22AB EF ==,沿着AB 将图形折成图2,其中90AED ∠=︒,AE ED =,H 为AD 的中点.(1)求证:EH BD ⊥;(2)求四棱锥D ABFE -的体积.20. (12分)已知抛物线2:2C y px =过点()1,1A . (1)求抛物线C 的方程;(2)过点()3,1P -的直线与抛物线C 交于M ,N 两个不同的点(均与点A 不重合).设直线AM ,AN 的斜率分别为1k ,2k ,求证:1k ,2k 为定值.21. 已知函数()()ln 1f x x a x =+-. (1)讨论()f x 的单调性;(2)当()f x 有最大值,且最大值大于22a -时,求a 的取值范围.选做题:共10分。
辽宁省辽河油田第二高级中学2020届高三数学12月月考试题文[含答案]
![辽宁省辽河油田第二高级中学2020届高三数学12月月考试题文[含答案]](https://img.taocdn.com/s3/m/9ae9f141bb68a98271fefa64.png)
,
,
,
,
,
,
共 种可能,
其中至少有 个轻度拥堵的有:
,
,
,
,
,
,
,
,
共 种可能.
…………10 分
所以所选 个路段中至少 个路段轻度拥堵的概率为
. …………12 分
19.(本小题满分 12 分)
解:(1)由题可知
,,
,
,.
椭圆 的方程为
.
…………4 分
(2)易知当直线 的斜率为 或直线 的斜率不存在时,不合题意.
(本小题满分 10 分)已知直线 :
( 为参数, 为 的倾斜角),以坐标原点
为极点, 轴的正半轴为极轴建立极坐标系,曲线 为:
.
(Ⅰ)若直线 与曲线 相切,求 的值;
(Ⅱ)设曲线 上任意一点的直角坐标为 ,求 的取值范围.
23. [选修 4-5:不等式选讲]
(本小题满分 10 分已知 a 0 , b 0 , c 0 ,函数 f x x a x b c . (1)当 a b c 1时,求不等式 f x 5的解集; (2)若 f x 的最小值为 3 ,求 a b c 的值,并求 1 1 1 的最小值.
,化为: ,解得
;
当
时,化为:
综上可得:不等式
的解集为:
(2)由绝对值三角不等式得
,解得
由柯西不等式得
. ;.............5 分
,
,当且仅当
时,等号成立,
因此,
的最小值为
.............................................................1
的直线 与椭圆 相交于不同的两点 , .若点
2019-2020学年辽宁省辽河油田第二高级中学高二10月月考数学试题

辽河油田第二高中2019-2020学年高二年级第一学期月考数学试卷★祝考试顺利★注意事项:1、答题前,请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:每个小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
3、主观题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。
答案用0.5毫米黑色签字笔写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非选修题答题区域的答案一律无效。
5、保持卡面清洁,不折叠,不破损,不得使用涂改液、胶带纸、修正带等。
6、考试结束后,请将本试题卷、答题卡、草稿纸一并依序排列上交。
一、选择题(每道小题5分,满分60分)1.若双曲线x2-ky2=1的一个焦点是(3,0),则实数k=()A. B. C. D.2.已知两个向量,且,则的值为()A. 1B. 2C. 4D. 83.设抛物线y2=2px的焦点在直线2x+3y-8=0上,则该抛物线的准线方程为()A. B. C. D.4.已知双曲线的一条渐近线方程是,它与椭圆有相同的焦点,则双曲线的方程为()A. B. C.D.5.双曲线15y2-x2=15与椭圆=1的()A.焦点相同B. 焦距相同C. 离心率相等D. 形状相同6.已知双曲线的一条渐近线过点,且双曲线的一个焦点在抛物线y2=2px(p>0)的准线上,则p等于()A. B. C. 2 D. 17.已知△ABC中,A、B的坐标分别为(0,2)和(0,-2),若三角形的周长为10,则顶点C的轨迹方程是()A. B.C. D.8.已知,,若,则点的坐标为()A. B. C. D.9.已知空间向量=(1,y,2),=(-2,1,2),若2-与垂直,则||等于()A. B. C. D.10.已知抛物线的焦点为双曲线的右焦点,且其准线被该双曲线截得的弦长是,则该双曲线的离心率为()A. B. C. D.11.设F1,F2是椭圆(0<b<2)的左、右焦点,过F1的直线L交椭圆于A,B两点,若|AF2|+|BF2|最大值为5,则椭圆的离心率为()A. B. C. D.12.过双曲线(a>0,b>0)的右焦点F且平行于其一条渐近线的直线L与另一条渐近线交于点A,直线L与双曲线交于点B,且|BF|=2|AB|,则双曲线的离心率为()A. B. C. D. 2二、填空题(每道小题5分,满分20)13.已知抛物线上一点M到焦点的距离为3,则点M到x轴的距离为______.14.若,,则=______.15.已知椭圆C的焦点为和,长轴长为6,设直线交椭圆C于A、B两点求弦AB的中点坐标______.16.已知点P是抛物线x=y2上的一个动点,则点P到点A(0,2)的距离与点P到y轴的距离之和的最小值为______.三、简答题(满分70分,17题10分,其余每题12分)17.分别求出满合下列条件的圆锥曲线的标准方程:(1)过点,且与椭圆有相同焦点的双曲线;(2)过点(-2,-1)的抛物线.18.已知空间三点A(-1,2,1),B(0,1,-2),C(-3,0,2)(1)求向量的夹角的余弦值,(2)若向量垂直,求实数k的值.19.已知椭圆C:1(a>b>0),四点中恰有两个点为椭圆C的顶点,一个点为椭圆C的焦点.(1)求椭圆C的方程;(2)若斜率为1的直线L与椭圆C交于不同的两点A,B,且,求直线L方程.20.已知F1、F2是椭圆C:+=1(a>b>0)的左、右焦点,点Q(-,1)在椭圆上,线段QF2与y轴的交点M,且点M为QF2中点(1)求椭圆C的方程;(2)设P为椭圆C上一点,且∠F1PF2=,求△F1PF2的面积.21.已知抛物线的焦点为F,若过点F且斜率为1的直线与抛物线交于A,B两点,且.(1)求抛物线C的方程;(2)若平行于AB的直线与抛物线C相切于点P,求的面积.22.已知抛物线C:x2=2py(0<p<2)的焦点为F,M(2,y0)是C上的一点,且.(1)求C的方程;(2)直线L交C于A、B两点,k OA•k OB=-2且△OAB的面积为16,求L的方程.答案和解析一、选择题 CCAAB BBDBD AC二、填空题 2 3(,)三、解答题17.解:(1)∵双曲线与椭圆有相同焦点,∴焦点坐标为,又∵双曲线过点,∴,即,∴,∴双曲线的标准方程为;(2)∵抛物线过点,∴抛物线的焦点在轴负半轴或轴负半轴,∴设抛物线的标准方程为或,代入,解得,,∴抛物线的标准方程为或.18..解:(1)=(1,-1,-3),=(-2,-2,1),||==,=3.=-2+2-3=-3.∴===-.(2)∵向量垂直,∴•=3+(3k-1)-k=0,3×11+(3k-1)×(-3)-9k=0,解得k=2.19.解:(1)椭圆表示焦点在x轴上的椭圆,故P2(1,0)为椭圆的焦点,所以P1(,0)为椭圆长轴的端点,P4(0,1)为椭圆短轴的端点,故a=,b=c=1,所以椭圆C的方程为+y2=1;(2)设直线l的方程为y=x+m,代入椭圆方程x2+2y2=2 化简得3x2+4mx+2m2-2=0,因为直线l与椭圆C交于A,B两点,所以△=16m2-12(2m2-2)=24-8m2>0,解得-<m<,设A(x1,y1),B(x2,y2),x1+x2=-,x1x2=,∴|AB|=|x1-x2|=•=•=•=,解得m=±,∴直线l的方程为y=x或y=x-.20.解:(1)设M(0,y),∵M是线段QF2的中点,∴F2(),∴,解得a2=4,b2=2.∴椭圆的标准方程为:;(2)由∠F1PF2=,可知,∴,解得PF1=PF2=2.∴.21.解:(1)由题可知F(,0),则该直线AB的方程为:y=x-,代入y2=2px,化简可得x2-3px+=0.设A(x1,y1),B(x2,y2),则有x1=x2=3p.∵|AB|=8,∴有x1+x2+p=8,解得p=2,∴抛物线的方程为:y2=4x.(2)设l方程为y=x+b,代入y2=4x,可得x2+(2b-4)x+b2=0,因为l为抛物线C的切线,∴△=0,解得b=1,∴l的方程为:y=x+1.切点P的坐标为(1,2)又直线AB的方程为,点P到直线AB的距离,的面积.22.解:(1)将M(2,y0)代入x2=2py得y0=,又|MF|=y0-(-)=+=,∴p=1,∴抛物线的方程为x2=2y,(2)直l的斜率显然存在,设直线l:y=kx+b,A(x1,y1)、B(x2,)由得:x2-2kx-2b=0∴x1+x2=2k,x1x2=-2b由,k OA k OB=•==-=-2,∴b=4∴直线方程为:y=kx+4,所以直线恒过定点(0,4),原点O到直线l的距离d=,∴S OAB=×d|AB|=ו==2=16,∴4k2+32=64,解得k=±2所以直线方程为:y=±2x+4.。
辽宁省辽河油田第二高级中学2020学年高一数学下学期第一次月考试题(无答案)
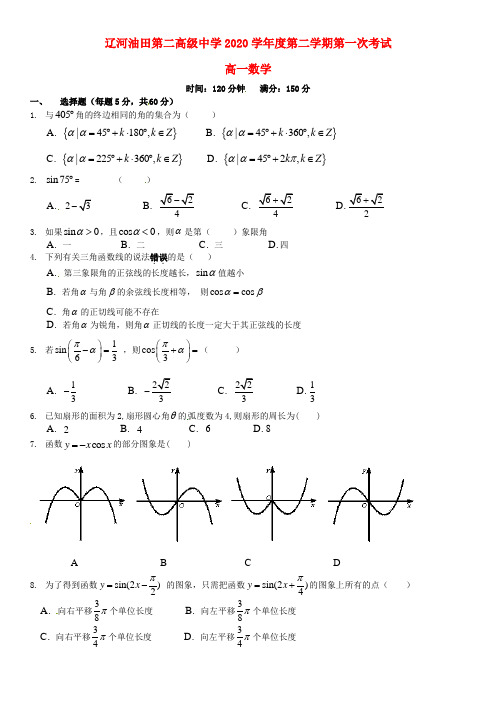
辽河油田第二高级中学2020学年度第二学期第一次考试高一数学时间:120分钟 满分:150分一、 选择题(每题5分,共60分)1. 与405︒角的终边相同的角的集合为( )A. {}|45180,k k Z αα=︒+⋅︒∈B. {}|45360,k k Z αα=︒+⋅︒∈C. {}|225360,k k Z αα=︒+⋅︒∈D. {}|452,k k Z ααπ=︒+∈2. sin 75︒= ( )A. 23-B.624- C. 624+ D.622+ 3. 如果sin 0α>,且cos 0α<,则α是第( )象限角A. 一B. 二C. 三D.四 4. 下列有关三角函数线的说法错误..的是( ) A. 第三象限角的正弦线的长度越长,sin α值越小B. 若角α与角β的余弦线长度相等, 则cos cos αβ=C. 角α的正切线可能不存在D. 若角α为锐角,则角α正切线的长度一定大于其正弦线的长度5. 若1sin 63πα⎛⎫-=⎪⎝⎭ ,则cos 3πα⎛⎫+= ⎪⎝⎭( ) A. 13- B. 223- C. 223 D.136. 已知扇形的面积为2,扇形圆心角θ的弧度数为4,则扇形的周长为( )A. 2B. 4C. 6D.8 7. 函数cos y x x =-的部分图象是( )A B C D8. 为了得到函数sin(2)2y x π=-的图象,只需把函数sin(2)4y x π=+的图象上所有的点( ) A. 向右平移38π个单位长度 B. 向左平移38π个单位长度C. 向右平移34π个单位长度D. 向左平移34π个单位长度9. 函数()f x 的最小正周期为2,且13x =是()f x 的一条对称轴,则()f x 的解析式可以是( ) A.()sin()6f x x ππ=+ B. ()sin(2)6f x x ππ=-C.5()cos()6f x x ππ=-D. ()sin(2)6f x x π=-10. 若1cos 7α=,11cos()14αβ+=-,,0,2παβ⎛⎫∈ ⎪⎝⎭,则β= ( ) A.6π B. 4π C. 3π D.6π-11. 设0,,0,22ππαβ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭,1sin tan cos βαβ+=,则( ) A. 32παβ-=B. 22παβ-=C. 32παβ+=D.22παβ+=12.函数()ln cos f x x =是( )A. 奇函数B. 偶函数C. 既不是奇函数,也不是偶函数D. 既是奇函数,又是偶函数二、 填空题(每题5分,共20分) 13. 若α是第二象限角,则3α不是..第 象限角. 14. 已知函数)20,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的部分图象如图所示,则)(x f 的解析式是第14题图 15. 若13cos 6sin 6,cos18cos 6sin18sin 622a b =-=-o o o o o o ,则a b (选填“>”“<”“=”) 16. 函数()3sin ,(0)f x x ωω=>,在0,πω⎡⎤⎢⎥⎣⎦上的图象如图所示,R 为图象的最高点,若存在直线0y y = 与函数图象交于PQ 两点,使得三角形PQR 为等边三角形,则ω的取值范围是第16题图三、解答题(共70分)17. (10分)已知sin 2cos αα=. (Ⅰ) 求sin cos 2sin cos αααα-+的值.(Ⅱ)22sin sin cos cos αααα+-的值.18.(12分)已知角α的终边与单位圆的交点为5(,)5m . (Ⅰ) 求m 的值和tan α的值.(Ⅱ) 若角α为第一象限角,求2cos()cos()2tan()3cos()cos()2παπαπαπαα-+-+++--的值.19.(12分)已知函数()tan(2)4f x x π=+.(Ⅰ) 求()f x 的定义域.(Ⅱ) 求使得()1f x =成立的所有x 的取值集合.20.(12分)已知()sin 3cos f x a x x =+,且12f π⎛⎫=⎪⎝⎭. (Ⅰ) 求()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域.(Ⅱ) 将函数()f x 的图象上的所有点纵坐标不变,横坐标缩短到原来的12,得到函数()g x 的图象,求函数()g x 的单调递增区间.21.(12分)已知,0,2παβ⎛⎫∈ ⎪⎝⎭,且7sin(2)sin 5αβα+=. (Ⅰ)证明:tan()6tan αββ+=. (Ⅱ)若tan 3tan αβ=,求α的值.22. (12分)已知函数)20,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的图象与x 轴的交点中,相邻两个交点之间的距离为3π,且图象上一个最低点为7(,2)2M π-. (Ⅰ)求函数()f x 的解析式.(Ⅱ)将函数()f x 的图象纵坐标不变,横坐标缩短到原来的16,再将图象向右平移3π个单位,得到函数()g x 的图象,若方程()0g x k +=在区间0,2π⎡⎤⎢⎥⎣⎦上只有一个实数解,求k 的取值范围。
辽宁省辽河油田第二高级中学2020-2021学年高二10月月考数学试题

辽宁省辽河油田第二高级中学2020-2021学年高二10月月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知向量()()1,1,0,1,0,2,a b ==-且ka b +与2a b -互相垂直,则k =( ) A .75 B .1 C .35 D .152.已知直线()1:2140l x m y +++=与2:360l mx y +-=平行.则实数m 的值( ) A .2 B .-3 C .2± D .-3或2 3.若直线l 的方向向量为a =(1,0,2),平面α的法向量为(2,1,1)n =-,则( ) A .//l αB .l α⊥C .l α⊂或//l αD .l 与α斜交 4.设(2,1),(4,1)A B -,则以线段AB 为直径的圆的方程是( )A .22(3)2x y -+=B .22(3)8x y -+=C .22(3)2x y ++=D .22(3)8x y ++= 5.已知向量(0,3,3)a =和(1,1,0)b =-分别是直线l 和m 的方向向量,则直线l 与m 所成的角为( )A .6πB .4πC .3πD .2π6.已知直线l 10y -+=,则下列结论正确的是( )A .直线l 的倾斜角是6πB .若直线m :10x -+=,则l m ⊥C .点)到直线l 的距离是1D .过()2与直线l 40y --=7.设直线l 的一个方向向量()6,2,3d =,平面α的一个法向量()1,3,0n =-,则直线l 与平面α的位置关系是( ).A .垂直B .平行C .直线l 在平面α内D .直线l 在平面α内或平行8.已知直线10kx y k ---=和以()3,1M -,()3,2N 为端点的线段相交,则实数k 的取值范围为( )A .32k ≤B .12k ≥-C .1322k -≤≤D .12k ≤-或32k ≥ 9.已知圆22220x y x y a +-++=截直线20x y +-=所得弦的长度为4,则实数a 的值是( )A .8-B .6-C .5-D .4-10.已知以()4,3C -为圆心的圆与圆221x y +=相内切,则圆C 的方程为( ) A .()()224336x y -++=B .()()224316x y ++-= C .()()224336x y ++-= D .()()224316x y -++= 11.平行于直线4x y +=且与圆221x y +=相切的直线的方程是( )A .0x y ++=或0x y +=B .0x y -+=或0x y -=C .10x y ++=或10x y +-=D .40x y +-=或40x y ++=12.在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑A BCD -中,AB ⊥平面BCD ,BC CD ⊥,且AB BC CD ==,M 为AD 的中点,则异面直线BM 与CD 夹角的余弦值为( )A .3BCD .4二、填空题13.已知直线l 与平面α垂直,直线l 的一个方向向量为()1,3,u z →=,向量()3,2,1v →=-与平面α平行,则z =______.14.若向量()()122212a b ==-,,,,,,且,a b 夹角的余弦值为________.15.已知直线1l :420mx y +-=与2l :250x y n -+=互相垂直,其垂足为()1,p ,则m n p +-的值为________.16.已知:如图,在60︒的二面角的棱上有A B 、两点,直线AC BD 、分别在这个二面用的两个半平面内,且都垂直AB ,已知4,6,8AB AC BD ===,则CD =__________.三、解答题17.已知圆22:2440C x y x y +-+-=和直线:3490l x y -+=,点P 是圆C 上的动点.(1)求圆C 的圆心坐标及半径;(2)求点P 到直线l 的距离的最小值.18.已知圆C 经过点()31A ,和点()20B -,,且圆心C 在直线24y x =-上. (1)求圆C 的方程;(2)过点()14D -,的直线l 被圆C 截得的弦长为6,求直线l 的方程. 19.如图,长方体1111ABCD A B C D -中,11,2AB AD AA ===,点P 为1DD 的中点.(1)求证:直线1//BD 平面PAC ;(2)求异面直线1BD 与AP 所成角的正弦值.20.已知圆C 经过()1,5A -,()5,5B ,()6,2D -三点.(1)求圆C 的标准方程;(2)求经过点()3,2E -且和圆C 相切的直线l 的方程.21.如图,四棱锥P ABCD -中,PC 垂直平面ABCD ,AB AD ⊥,AB CD ∥,222PD AB AD CD ====,E 为PB 的中点.(Ⅰ)证明:平面EAC⊥平面PBC;(Ⅱ)求直线PD与平面AEC所成角的正弦值.-中,底面ABCD为平行四边形,PA⊥底面ABCD,22.如图,在四棱锥P ABCDAP=.∠=,AB=AD=360ABC(1)求证:平面PCA⊥平面PCD;(2)设E为侧棱PC上的一点,若直线BE与底面ABCD所成的角为45°,求二面角--的余弦值.E AB D参考答案1.A【分析】首先表示出ka b +与2a b -的坐标,再根据ka b +与2a b -互相垂直,得到()()20ka b a b +-=计算可得;【详解】解:因为()1,1,0a =,()1,0,2b =-()1,,2ka b k k ∴+=-,()23,2,2a b -=-又因为ka b +与2a b -互相垂直,所以()()20ka b a b +-=,33240k k ∴-+-=,解得75k =故选:A .【点睛】 本题考查空间向量的坐标运算,属于基础题.2.A【分析】由两直线平行的条件直接列方程求解即可【详解】解:因为直线()1:2140l x m y +++=与2:360l mx y +-=平行,所以(1)23m m +=⨯,且462m ≠-⨯,解得2m =故选:A【点睛】此题考查已知两直线平行求参数,考查运算能力,属于基础题.3.C【分析】由l 的方向向量(1,0,2)a = ,平面α的法向量(2,1,1)n =- 可得0a n ⋅=,从而得解.【详解】∵(1,0,2)a = ,(2,1,1)n =-,∴()1201210a n ⋅=⨯-+⨯+⨯= ,即l α⊂或//l α.故选:C.【点睛】本题考查利用直线l 的方向向量与平面α的法向量关系判断线面位置关系.属于基础题. 4.A【分析】根据中点公式计算出圆心坐标,根据两点间的距离公式计算出圆的半径,从而可得圆的标准方程.【详解】AB 的中点坐标为(3,0),圆的半径为||2AB r === 所以圆的方程为22(3)2x y -+=.故选:A.【点睛】本题考查了圆的标准方程,意在考查学生的计算能力.属于基础题.5.C【分析】根据数量积公式,即可求得答案.【详解】 (0,3,3)a =,(1,1,0)b =-根据数量积公式:cos a ba b a b ⋅⋅=可得:1cos 2a b ⋅=== 直线l 与m 所成的角为:3π. 故选: C.【点睛】本题主要考查了向量法求线线角,解题关键是掌握向量法求线线角的方法和线线角的定义,考查了分析能力和计算能力,属于基础题.6.D【分析】根据直线的倾斜角、斜率、点到直线的距离公式、两直线平行的条件逐一判断各个选项即可.【详解】∵l10y -+=,即1y =+,∴直线的斜率k =∴3πα=,则A 错;()(1+10-⨯=≠,则B 错;点)到直线l2=,则C 错;过()2与直线l平行的直线方程是2y x =-+,40y --=,则D 对; 故选:D .【点睛】本题主要考查直线的方程,属于基础题.7.D【解析】∵直线l 的一个方向向量()6,2,3d =,平面α的一个法向量()1,3,0n =-∴6(1)23300d n ⋅=⨯-+⨯+⨯=∴直线l 在平面α内或平行故选D.8.D【分析】直线10kx y k ---=过定点()1,1P -,分别求出PM k 和PN k ,结合图形,可求出答案.【详解】由题意,直线10kx y k ---=可化为()110k x y ---=,令1x =,得1y =-,即该直线过定点()1,1P -,111312PM k +==---,213312PN k +==-,所以当12k ≤-或32k ≥时,直线10kx y k ---=和以()3,1M -,()3,2N 为端点的线段相交.故选:D.【点睛】 本题考查了直线系方程的应用,以及过两点的直线的斜率的求法,考查了数形结合的解题思想方法,是中档题.9.D【分析】根据题意,将圆的方程变形为标准方程,分析其圆心与半径,求出圆心到直线的距离,结合直线与圆的位置关系可得22242r d ⎛⎫=+ ⎪⎝⎭,计算可得答案.【详解】根据题意,圆22220x y x y a +-++=,即22(1)(1)2x y a -++=-,其圆心为()1,1-,半径r =圆心到直线20x y +-=的距离d == 又由圆截直线20x y +-=所得弦的长度为4, 则有22242422r d a ⎛⎫=+=+=- ⎪⎝⎭,解可得4a =-.故选:D .【点睛】本题考查直线和圆相交弦长的计算,属于基础题.10.C【分析】先判断点()4,3C -在圆221x y +=的外部,然后设所求圆的半径为r ,再由15r -==求解. 【详解】 因为()2243251-+=>,所以点()4,3C -在圆221x y +=的外部, 设以()4,3C -为圆心的圆的半径为:r ,则15r -==,解得6r =,所以所求圆的方程为:()()224336x y ++-=.故选:C【点睛】本题主要考查圆与圆的位置关系的应用,还考查了运算求解的能力,属于基础题. 11.A【分析】根据两直线平行,设出切线方程,再根据圆心到切线的距离等于圆的半径列等式可解得结果.【详解】依题意设圆的切线方程为0x y m ++=,1=,解得m =所以所求圆的切线方程为0x y ++=或0x y +=.故选:A【点睛】本题考查了两直线平行的位置关系,考查了求圆的切线方程,考查了点到直线的距离公式,属于基础题.12.C【分析】画出四面体A BCD -,建立坐标系,利用向量法求异面直线所成角的余弦值即可.【详解】四面体A BCD -是由正方体的四个顶点构成的,如下图所示建立如下图所示的空间直角坐标系,设正方体的棱长为2(0,0,0),(2,0,0),(2,2,0),(1,1,1)B C D M(1,1,1),(0,2,0)BM CD ==cos ,33||BM CDBM CD BM CD⋅〈〉===⋅因为异面直线夹角的范围为0,2π⎛⎤⎥⎝⎦,所以异面直线BM 与CD 故选:C【点睛】 本题主要考查了利用向量法求异面直线夹角的余弦值,属于中档题.13.3【分析】根据向量的垂直关系计算即可.【详解】因为直线l 与平面α垂直,()1,3,u z →=为直线l 的一个方向向量,向量()3,2,1v →=-与平面α平行,所以0u v →→⋅=,即()()1,3,3,2,13630z z z ⋅-=-+=-=,解得3z =故答案为:3【点睛】本题主要考查了向量垂直的坐标运算,考查了直线的方向向量,属于容易题.14.49【分析】 根据cos ,||||a b a b a b ⋅〈〉=⋅求解即可. 【详解】 2244a b ⋅=-+=,||143,||413a b =++==++= 4cos ,9||||a b a b a b ⋅∴〈〉==⋅ 故答案为:49【点睛】 本题主要考查了求空间中两个向量的夹角,属于基础题.15.0【分析】利用两直线垂直斜率的关系求出m ,再将点()1,p 分别代入直线1l ,2l 的方程中求出,n p ,即可得出m n p +-的值.【详解】 将直线1l ,2l 化为12,4255m n y x y x =-+=+ 直线1l ,2l 相互垂直,2145m ∴-⨯=-,解得10m =将1,x y p ==代入10420x y +-=,解得2p =-将x 1,y 2==-代入250x y n -+=,解得12n =-101220m n p ∴+-=-+=故答案为:0【点睛】本题主要考查了根据两直线垂直求参数的值,属于中档题.16.【解析】CD CA AB BD =++,所以()()222222CD CA AB BD CA AB BD CA AB CA BD AB BD =++=+++⋅+⋅+⋅ 21636642068cos 011648683π⎛⎫=++++⨯⨯+=-= ⎪⎝⎭,所以217CD =【点睛】本题考查了利用平面向量解决立体几何的问题,也是比较容易忽视的方法,所求的向量用已知向量表示以后,转化为数量积的计算,本题的关键是利用三角形法则的推论,用,,CA AB BD 表示CD .17.(1)圆心坐标()1,2-,半径为3;(2)1【分析】(1)将圆化为标准方程:()()22129x y -++=,即可求解.(2)求出圆心到直线的距离,减去半径即可.【详解】(1)由圆22:2440C x y x y +-+-=, 化为()()22129x y -++=,所以圆C 的圆心坐标()1,2-,半径为3.(2)由直线:3490l x y -+=,所以圆心到直线的距离4d ==,所以点P 到直线l 的距离的最小值为431-=.【点睛】本题考查了圆的标准方程、写出圆的圆心与半径、点到直线的距离公式,属于基础题.18.(1)22(1)(2)13x y -++=;(2)4380x y +-=.【分析】(1)利用圆心在直线24y x =-上,设出圆心的坐标,再由圆心分别到,A B 的距离相等,建立方程求出圆C 的方程;(2)由弦长公式得出圆心到直线l 的距离,设出直线l 的方程,由点到直线的距离公式求出斜率,从而得出直线l 的方程.【详解】解:(1)由于圆心C 在直线24y x =-上,可设圆心()2,24C a -圆C 经过点()31A ,和点()20B -,故有CA CB =,2222(3)(25)(2)(24)a a a a ∴-+-=++- 求得1a =,故圆心()12C -,,半径为CB = 故要求的圆的方程为22(1)(2)13x y -++=. (2)过点()14D -,的直线1被圆C 截得的弦长为6 故圆心C 2=显然直线l 的斜率存在,设为k ,则直线l 即;()41y k x -=+,即40kx y k -++=. 2=,求得43k =- 故直线l 的方程为48033x y --+=,即4380x y +-=. 【点睛】本题主要考查了求圆的方程以及根据弦长求参数的值,涉及了点到直线的距离公式的应用,属于中档题.19.(1)证明见解析;(2)12. 【分析】 (1)设AC 和BD 交于点O ,则O 为BD 的中点,证得1//PO BD ,结合线面平行的判定定理,即可求解;(2)由(1)知,1//PO BD ,得到异面直线1BD 与AP 所成的角就等于PO 与AP 所成的角,在直角APO ∆中,即可求解.【详解】(1)设AC 和BD 交于点O ,则O 为BD 的中点,连结PO ,又因为P 是1DD 的中点,故1//PO BD又因为PO ⊂平面PAC ,1BD ⊄平面PAC所以直线1//BD 平面PAC .(2)由(1)知,1//PO BD ,所以异面直线1BD 与AP 所成的角就等于PO 与AP 所成的角,故APO ∠即为所求;因为12PA PC AO AC ====且PO AO ⊥,在直角APO 中,可得1sin2AO APO AP ∠===.【点睛】本题主要考查了线面平行的判定与证明,以及异面所成角的求解,其中解答中熟记线面位置关系的判定定理和性质定理,以及异面直线所成角的解法是解答的关键,着重考查推理与运算能力.20.(1)22(2)(1)25x y -+-=,(2)3x =-或125460x y -+=【分析】(1)根据题意,设所求圆的一般方程为220x y Dx Ey F ++++=,将三点坐标代入计算可得,,D E F 的值,即可得圆C 的一般方程,变形可得答案;(2)根据题意,分析圆C 的圆心与半径,进而分别讨论直线l 的斜率存在与不存在时直线l 的方程,综合即可得答案【详解】解:(1)设所求圆的一般方程为220x y Dx Ey F ++++=,则125502525550364620D E F D E F D E F +-++=⎧⎪++++=⎨⎪++-+=⎩,解得4,2,20D E F =-=-=-,所以所求圆的一般方程为2242200x y x y +---=,即22(2)(1)25x y -+-=, 所以圆C 的标准方程为22(2)(1)25x y -+-=,(2)由(1)可知圆C :22(2)(1)25x y -+-=的圆心(2,1)C ,半径为5, 若直线l 的斜率不存在时,直线l 的方程为3x =-,圆心(2,1)C 到直线l 的距离5d =,与圆相切,符合题意,若直线l 的斜率存在时,设直线l 的斜率为k ,则直线l 的方程为2(3)y k x -=+,即320kx y k -++=,则有5d ==,解得125k =, 所以直线l 的方程为125460x y -+=,综上,直线l 的方程为3x =-或125460x y -+=【点睛】此题考查直线与圆的位置关系,涉及圆的标准方程,考查直线方程的求法,属于基础题21.(Ⅰ)见证明【分析】 (Ⅰ)可证AC ⊥ 平面PBC ,从而得到平面ACE ⊥平面PBC .(Ⅱ)在平面PBC 内过P 作CE 的垂线,垂足为F ,由(1)可知PF ⊥平面AEC ,从而PDF ∠就是所求的线面角,利用解直角三角形可得其正弦值.【详解】(Ⅰ)证明: PC ⊥平面ABCD ,AC ⊂平面ABCD , 故PC AC ⊥.又2,1,AB CD AD AB ==⊥,所以AC BC == 故222AC BC AB +=,即AC BC ⊥ ,而BC PC C ⋂=,所以AC ⊥平面PBC ,因为AC ⊂平面ACE ,所以平面ACE ⊥平面PBC .(Ⅱ)PC ⊥平面ABCD ,CD ⊂平面ABCD , 故PC CD ⊥.又2PD =,所以PC =在平面AEC 内,过点P 作PF CE ⊥,垂足为F .由(Ⅰ)知平面ACE ⊥平面PBC , PF ⊂平面PBC ,平面ACE平面PBC EC = 所以PF ⊥平面ACE . 由面积法得:即12CE PF PC BC ⋅=⋅. 又点E 为AB的中点,12CE PB ==.所以PF =. 又点E 为AB 的中点,所以点P 到平面ACE 的距离与点B 到平面ACE 的距离相等. 连结BD 交AC 于点G ,则2GB DG =.所以点D 到平面AEC 的距离是点B 到平面ACE 的距离的一半,即12PF . 所以直线PD 与平面AEC所成角的正弦值为12PF PD .另解:如图,取AB 的中点F ,如图建立坐标系.因为2PD =,所以CP =(0,0,0)C ,(0,1,0)D,P ,(1,1,0)A ,(1,1,0)B -,11(,22E -.(0,1,PD =.(1,1,0)CA =,11(,22CE =-. 设平面AEC 的一个法量为(,,)n x y z =,则0,0,222x y x y z +=⎧⎪⎨-+=⎪⎩取,得1x =1y =-,z =(1,1,n =-. 设直线PD 与平面AEC 所成角为θ,则sin cos ,n PD θ=20==.【点睛】面面垂直的判定可由线面垂直得到,而线面垂直可通过线线垂直得到,注意面中两条直线是相交的.由面面垂直也可得到线面垂直,注意线在面内且线垂直于两个平面的交线.空间中的角的计算,可以建立空间直角坐标系把角的计算归结为向量的夹角的计算,也可以构建空间角,把角的计算归结平面图形中的角的计算.22. 【分析】(Ⅰ)推导出CD⊥AC,PA⊥CD,从而CD⊥平面PCA ,由此能证明平面PCA⊥平面PCD . (Ⅱ)以A 为坐标原点,AB ,AC ,AP 分别为x ,y ,z 轴,建立空间直角坐标系,利用向量法能求出二面角E ﹣AB ﹣D 的余弦值.【详解】解:(Ⅰ)在平行四边形ABCD 中,∠ADC=60°,CD =AD =,由余弦定理得2220AC AD CD 2AD?CDcos ADC 1232cos609∠=+-=+-⨯=, ∴222AC CD AD +=,∴∠ACD=90°,即CD⊥AC,又PA⊥底面ABCD ,CD ⊂底面ABCD ,∴PA⊥CD,又AC CD C ⋂=,∴CD⊥平面PCA.又CD ⊂平面PCD ,∴平面PCA⊥平面PCD.(Ⅱ)如图,以A 为坐标原点,AB ,AC ,AP 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系.则()A 0,0,0,)B ,()C 0,3,0,()D ,()P 0,0,3.设()E x,y,z ,()PE λPC 0λ1=≤≤,则()()x,y,z 3λ0,3,3-=-∴x=0,y 3λ=,z 33λ=-,即点E 的坐标为()0,3λ,33λ-∴()BE λ,33λ=--又平面ABCD 的一个法向量为()n 0,0,1=∴sin45°cosBE,n ==解得1λ3= ∴点E 的坐标为()0,1,2,∴()AE 0,1,2=,()AB 3,0,0=, 设平面EAB 的法向量为()m x,y,z = 由m?AB 0m?AE 0⎧=⎨=⎩得020x y z =⎧⎨+=⎩ 令z=1,得平面EAB 的一个法向量为()m 0,2,1=-∴m?n cosm,n m n 5===. 又二面角E-AB-D 的平面角为锐角,所以,二面角E-AB-D 的余弦值为【点睛】本题考查面面垂直的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.。
辽宁省2020届高三数学10月月考试题文

高三数学月考试题 文一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1、设{}U -1012=,,,,集合{}21,A x x x U =<∈,则U C A =( ) A .{}012,, B .{}-1,12, C .{}-1,02, D .{}-1,01,2、若复数z 满足(1)3z i i +=-,则z 的共轭复数z =( ) A .23i -- B .23i -C .23i +D .23i -+3、设,a b R ∈, 则 “2()0a b a -<”是“a b <”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件4、《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“盖”的术:置如其周,令相承也.又以高乘之,三十六成一.该术相当于给出了用圆锥的底面周长L 与高h ,计算其体积V 的近似公式21.36v L h ≈它实际上是将圆锥体积公式中的圆周率π近似取为3.那么近似公式2275v L h ≈相当于将圆锥体积公式中的π近似取为( ) A.227 B.258C.15750D.3551135、在区间[-1,1]上随机取一个数x ,则sin πx 4的值介于-12与22之间的概率为 ( )A. 14B. 13C. 23D. 566、已知(0,)2πα∈,(0,)2πβ∈,且2sin 2cos 2cos (1sin )αβαβ=+,则下列结论正确的是( )A .22παβ-=B .22παβ+=C .2παβ+=D .2παβ-=7、ABC ∆中,2AB =,AC =45BAC ∠=︒,P 为线段AC 上任意一点,则PB PC ⋅的取值范围是( ) A .1,14⎡⎤-⎢⎥⎣⎦ B .1,04⎡⎤-⎢⎥⎣⎦ C .1,42⎡⎤-⎢⎥⎣⎦ D .1,22⎡⎤-⎢⎥⎣⎦8、已知幂函数()y f x =过点(4,2),令(1)(),n a f n f n n N +=++∈,记数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,则10n S =时,n 的值是( ) A .10B .120C .130D .1409、四个函数:①sin y x x =⋅;②cos y x x =⋅;③cos y x x =⋅;④2xy x =⋅的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )A .④①②③B .①④②③C .③④②①D .①④③② 10、已知0,0x y >>,182x y x y-=-,则2+x y 的最小值为( )A B . C . D .4 11、一个圆锥的母线长为2,圆锥的母线与底面的夹角为4π,则圆锥的内切球的表面积为( )A .8πB .24(2π- C .24(2π+ D .232(249π 12、已知,(0,)2παβ∈,sin sin 0βααβ->,则下列不等式一定成立的是( )A .2παβ+<B .2παβ+=C .αβ<D .αβ>二.填空题:本大题共4小题,每小题5分 13、求值:100lg 20log 25+=________14、已知函数()4cos()f x x ωϕ=+(0,0ωϕπ><<)为奇函数,(,0),(,0)A a B b 是其图像上两点,若a b -的最小值是1,则1()6f =_________15、数列{}n a 中,12a =,22a =,*21(1),n n n a a n N +-=+-∈,n S 是数列{}n a 的前n 项和,则60S =_______16、下列命题中,正确命题的序号为 (写出所有正确命题的序号).①函数()(0)af x x x x=+>的最小值为 ②已知定义在R 上周期为4的函数()f x 满足(2)(2)f x f x -=+,则()f x 一定为偶函数; ③定义在R 上的函数()f x 既是奇函数又是以2为周期的周期函数,则(1)(4)(7)0f f f ++=;④已知函数32()(0)f x ax bx cx d a =+++≠,则0a b c ++=是()f x 有极值的必要不充分条件;⑤已知函数()sin f x x x =-,若0a b +>,则()()0f a f b +>. 三.解答题:解答应写出文字说明,证明过程或演算步骤. 17、(本小题满分12分)如图,OPQ 是半径为2,圆心角为3π的扇形,C 是扇形弧上的一动点, 记COP θ∠=,四边形OPCQ 的面积为S .(1)找出S 与θ的函数关系;(2)试探求当θ取何值时,S 最大,并求出这个最大值. 18、(本小题满分12分) 已知数列{}n a 中,12811-=a ,0≠n a ,且641311+=+++n n n a S S , (1)求n a (2)若n n a log b 4=,n n b b b T +++= 21,当n 为何值时,n T 取最小值?并求出最小值。
辽宁省辽河油田第二高级中学2019_2020学年高二数学10月月考试题

辽宁省辽河油田第二高级中学2019-2020学年高二数学10月月考试题时间:120分钟满分:150分一、选择题(每道小题5分,满分60分)1.若双曲线x2-ky2=1的一个焦点是(3,0),则实数k=()A. B. C. D.2.已知两个向量,且,则的值为()A. 1B. 2C. 4D. 83.设抛物线y2=2px的焦点在直线2x+3y-8=0上,则该抛物线的准线方程为()A. B. C. D.4.已知双曲线的一条渐近线方程是,它与椭圆有相同的焦点,则双曲线的方程为()A. B. C.D.5.双曲线15y2-x2=15与椭圆=1的()A.焦点相同B. 焦距相同C. 离心率相等D. 形状相同6.已知双曲线的一条渐近线过点,且双曲线的一个焦点在抛物线y2=2px(p>0)的准线上,则p等于()A. B. C. 2 D. 17.已知△ABC中,A、B的坐标分别为(0,2)和(0,-2),若三角形的周长为10,则顶点C的轨迹方程是()A. B.C. D.8.已知,,若,则点的坐标为()A. B. C. D.9.已知空间向量=(1,y,2),=(-2,1,2),若2-与垂直,则||等于()A. B. C. D.10.已知抛物线的焦点为双曲线的右焦点,且其准线被该双曲线截得的弦长是,则该双曲线的离心率为()A. B. C. D.11.设F1,F2是椭圆(0<b<2)的左、右焦点,过F1的直线L交椭圆于A,B两点,若|AF2|+|BF2|最大值为5,则椭圆的离心率为()A. B. C. D.12.过双曲线(a>0,b>0)的右焦点F且平行于其一条渐近线的直线L与另一条渐近线交于点A,直线L与双曲线交于点B,且|BF|=2|AB|,则双曲线的离心率为()A. B. C. D. 2二、填空题(每道小题5分,满分20)13.已知抛物线上一点M到焦点的距离为3,则点M到x轴的距离为______.14.若,,则=______.15.已知椭圆C的焦点为和,长轴长为6,设直线交椭圆C于A、B两点求弦AB的中点坐标______.16.已知点P是抛物线x=y2上的一个动点,则点P到点A(0,2)的距离与点P到y轴的距离之和的最小值为______.三、简答题(满分70分,17题10分,其余每题12分)17.分别求出满合下列条件的圆锥曲线的标准方程:(1)过点,且与椭圆有相同焦点的双曲线;(2)过点(-2,-1)的抛物线.18.已知空间三点A(-1,2,1),B(0,1,-2),C(-3,0,2)(1)求向量的夹角的余弦值,(2)若向量垂直,求实数k的值.19.已知椭圆C:1(a>b>0),四点中恰有两个点为椭圆C的顶点,一个点为椭圆C的焦点.(1)求椭圆C的方程;(2)若斜率为1的直线L与椭圆C交于不同的两点A,B,且,求直线L方程.20.已知F1、F2是椭圆C:+=1(a>b>0)的左、右焦点,点Q(-,1)在椭圆上,线段QF2与y轴的交点M,且点M为QF2中点(1)求椭圆C的方程;(2)设P为椭圆C上一点,且∠F1PF2=,求△F1PF2的面积.21.已知抛物线的焦点为F,若过点F且斜率为1的直线与抛物线交于A,B两点,且.(1)求抛物线C的方程;(2)若平行于AB的直线与抛物线C相切于点P,求的面积.22.已知抛物线C:x2=2py(0<p<2)的焦点为F,M(2,y0)是C上的一点,且.(1)求C的方程;(2)直线L交C于A、B两点,k OA•k OB=-2且△OAB的面积为16,求L的方程.答案和解析一、选择题 CCAAB BBDBD AC二、填空题 2 3 (,)三、解答题17.解:(1)∵双曲线与椭圆有相同焦点,∴焦点坐标为,又∵双曲线过点,∴,即,∴,∴双曲线的标准方程为;(2)∵抛物线过点,∴抛物线的焦点在轴负半轴或轴负半轴,∴设抛物线的标准方程为或,代入,解得,,∴抛物线的标准方程为或.18..解:(1)=(1,-1,-3),=(-2,-2,1),||==,=3.=-2+2-3=-3.∴===-.(2)∵向量垂直,∴•=3+(3k-1)-k=0,3×11+(3k-1)×(-3)-9k=0,解得k=2.19.解:(1)椭圆表示焦点在x轴上的椭圆,故P2(1,0)为椭圆的焦点,所以P1(,0)为椭圆长轴的端点,P4(0,1)为椭圆短轴的端点,故a=,b=c=1,所以椭圆C的方程为+y2=1;(2)设直线l的方程为y=x+m,代入椭圆方程x2+2y2=2 化简得3x2+4mx+2m2-2=0,因为直线l与椭圆C交于A,B两点,所以△=16m2-12(2m2-2)=24-8m2>0,解得-<m<,设A(x1,y1),B(x2,y2),x1+x2=-,x1x2=,∴|AB|=|x1-x2|=•=•=•=,解得m=±,∴直线l的方程为y=x或y=x-.20.解:(1)设M(0,y),∵M是线段QF2的中点,∴F2(),∴,解得a2=4,b2=2.∴椭圆的标准方程为:;(2)由∠F1PF2=,可知,∴,解得PF1=PF2=2.∴.21.解:(1)由题可知F(,0),则该直线AB的方程为:y=x-,代入y2=2px,化简可得x2-3px+=0.设A(x1,y1),B(x2,y2),则有x1=x2=3p.∵|AB|=8,∴有x1+x2+p=8,解得p=2,∴抛物线的方程为:y2=4x.(2)设l方程为y=x+b,代入y2=4x,可得x2+(2b-4)x+b2=0,因为l为抛物线C的切线,∴△=0,解得b=1,∴l的方程为:y=x+1.切点P的坐标为(1,2)又直线AB的方程为,点P到直线AB的距离,的面积.22.解:(1)将M(2,y0)代入x2=2py得y0=,又|MF|=y0-(-)=+=,∴p=1,∴抛物线的方程为x2=2y,(2)直l的斜率显然存在,设直线l:y=kx+b,A(x1,y1)、B(x2,)由得:x2-2kx-2b=0∴x1+x2=2k,x1x2=-2b由,k OA k OB=•==-=-2,∴b=4∴直线方程为:y=kx+4,所以直线恒过定点(0,4),原点O到直线l的距离d=,∴S OAB=×d|AB|=ו==2 =16,∴4k2+32=64,解得k=±2所以直线方程为:y=±2x+4.。
辽宁省辽河油田第二高级中学2020_2021学年高二数学10月月考试题2

辽宁省辽河油田第二高级中学2020-2021学年高二数学10月月考试题(考试时间120分钟)一、单项选择题(本大题共12小题,每题5分,共60.0分)1.已知向量,且,则k的值为A. B. 1 C. D.2.已知直线:与:平行.则实数m的值A.2B.C.D. 或23.若直线l的方向向量为0,,平面的法向量为1,,则A. B. C. 或 D. l与斜交4.设,,则以线段AB为直径的圆的方程是A. B. C.D.5.已知向量3,和1,分别是直线l和m的方向向量,则直线l与m所成的角为A. B. C. D.6.已知直线l:,则下列结论正确的是A.直线l的倾斜角是B. 若直线m:,则C. 点到直线l的距离是1D. 过与直线l平行的直线方程是7.设直线l的一个方向向量2,,平面的一个法向量3,,则直线l与平面的位置关系是A. 垂直B. 平行C. 直线在平面内D. 直线在平面内或平行8.已知直线和以,为端点的线段相交,则实数k的取值范围为A. B. C. D. 或9.已知圆截直线所得弦的长度为4,则实数a的值是A. B. C. D.10.已知以为圆心的圆与圆相内切,则圆C的方程为A. B.C. D.11.平行于直线且与圆相切的直线的方程是A. 或B. 或C. 或D. 或12.在九章算术中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑中,平面BCD,,且,M为AD的中点,则异面直线BM与CD夹角的余弦值为A. B. C. D.二、填空题(本大题共4小题,每题5.0分,共20分)13.已知直线l与平面垂直,直线l的一个方向向量为,向量与平面平行,则______.14.若向量,且夹角的余弦值为________.15.已知直线:与:互相垂直,其垂足为,则的值为________.16.如图,夹角为的二面角的棱上有A、B两点,线段AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知,,,则CD的长为_______.三、解答题(本大题共6小题,共70.0分)17.(10分)已知圆和直线,点P是圆C上的动点.求圆C的圆心坐标及半径求点P到直线l的距离的最小值.18.(12分)已知圆C经过点和点,且圆心C在直线上.求圆C的方程;过点的直线1被圆C截得的弦长为6,求直线1的方程.19.(12分)如图,长方体中,,,点P为的中点.求证:直线平面PAC;求异面直线与AP所成角的正弦值.20.(12分)已知圆C经过,,三点.Ⅰ求圆C的标准方程;Ⅱ求经过点且和圆C相切的直线l的方程.21.(12分)如图,四棱锥中,平面ABCD,,,,E为PB的中点.证明:平面平面PBC;求直线PD与平面ACE所成角的正弦值.22.(12分)如图所示,在四棱锥中,底面ABCD为平行四边形,底面ABCD,,,,.求证:平面平面PCD;设E为侧棱PC上的一点,若直线BE与底面ABCD所成的角为,求二面角的余弦值.高二数学考试教师用卷一、选择题23.已知向量,且,则k的值为A. B. 1 C. D.【答案】A24.已知直线:与:平行.则实数m的值A. 2B.C.D. 或2 【答案】A25.若直线l的方向向量为0,,平面的法向量为1,,则A. B. C. 或 D. l与斜交【答案】C26.设,,则以线段AB为直径的圆的方程是A. B. C.D.【答案】A27.已知向量3,和1,分别是直线l和m的方向向量,则直线l与m所成的角为A. B. C. D.28.已知直线l:,则下列结论正确的是A. 直线l的倾斜角是B. 若直线m:,则C. 点到直线l的距离是1D. 过与直线l平行的直线方程是【答案】D29.设直线l的一个方向向量2,,平面的一个法向量3,,则直线l与平面的位置关系是A. 垂直B. 平行C. 直线在平面内D. 直线在平面内或平行【答案】D30.已知直线和以,为端点的线段相交,则实数k的取值范围为A. B. C. D. 或【答案】D31.已知圆截直线所得弦的长度为4,则实数a的值是A. B. C. D.32.已知以为圆心的圆与圆相内切,则圆C的方程为A. B.C. D.【答案】C33.平行于直线且与圆相切的直线的方程是A. 或B. 或C. 或D. 或【答案】A34.在九章算术中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑中,平面BCD,,且,M为AD的中点,则异面直线BM与CD夹角的余弦值为A. B. C. D.【答案】C二、填空题35.已知直线l与平面垂直,直线l的一个方向向量为,向量与平面平行,则______.【答案】336.若向量,且夹角的余弦值为________.【答案】37.已知直线:与:互相垂直,其垂足为,则的值为【答案】038.如图,夹角为的二面角的棱上有A、B两点,线段AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知,,,则CD的长为_______.【答案】三、解答题39.已知圆和直线,点P是圆C上的动点.求圆C的圆心坐标及半径求点P到直线l的距离的最小值.【答案】解:圆的标准方程为,圆心坐标为,半径为.圆心C到直线l的距离点P到直线l的距离的最小值为1.40.已知圆C经过点和点,且圆心C在直线上.求圆C的方程;过点的直线1被圆C截得的弦长为6,求直线1的方程.【答案】解:由于圆心C在直线上,可设圆心,圆C经过点和点,故有,,求得,故圆心,半径为,故要求的圆的方程为.过点的直线1被圆C截得的弦长为6,故圆心C到直线的距离为,显然直线l的斜率存在,设为k,则直线l即;,即.由,求得,故直线l的方程为,即.41.如图,长方体中,,,点P为的中点.求证:直线平面PAC;求异面直线与AP所成角的正弦值.【答案】证明:设AC和BD交于点O,连接PO,,O分别是,BD的中点,,又面PAC,面PAC,面PAC.解:由知,,异面直线与AP所成的角就等于PO与AP所成的角,即为异面直线与AP所成角,,,且,异面直线与AP所成角的正弦值为:.42.已知圆C经过,,三点.Ⅰ求圆C的标准方程;Ⅱ求经过点且和圆C相切的直线l的方程.【答案】解:Ⅰ根据题意,设过,,三点的圆的一般方程为,则有,解可得,,,故所求圆的一般方程为,变形可得,故圆C的标准方程为,Ⅱ由Ⅰ的结论,圆C的方程为,其圆心,半径,若直线l的斜率不存在,直线l的方程为,圆心到直线l的距离,与圆相切,符合题意,若直线l的斜率存在,设直线l的斜率为k,则直线l的方程为,即,则有,解可得,故直线l的方程为;综合可得:直线l的方程为或.43.如图,四棱锥中,平面ABCD,,,,E为PB的中点.证明:平面平面PBC;求直线PD与平面ACE所成角的正弦值.【答案】解:证明:因为平面ABCD,平面ABCD,所以.又,,,,所以.所以,故AC,又,平面PBC,平面PBC,所以平面PBC,又平面ACE,所以平面平面PBC.解法一:因为平面ABCD,平面ABCD,所以.又,所以过点P作,垂足为M.由知平面平面PBC,所以平面ACE.在中,由等面积法得.又点E为AB的中点,所以,所以.连接BD交AC于点G,则所以点D到平面ACE的距离是点B到平面ACE的距离的一半,又点P到平面ACE的距离与点B到平面ACE的距离相等,所以点D到平面ACE的距离为.设直线PD与平面ACE所成的角为,所以直线PD与平面ACE所成角的正弦值.解法二:如图,取AB的中点F,以C为原点,CF,CD,CP所在的直线为x轴,y轴,z轴,建立空间直角坐标系.因为,所以.所以0,,1,,0,,1,,,.则.设平面ACE的法向量为,则取,得,,所以.设直线PD与平面ACE所成的角为,则直线PD与平面ACE所成角的正弦值.44.如图所示,在四棱锥中,底面ABCD为平行四边形,底面ABCD,,,,.求证:平面平面PCD;设E为侧棱PC上的一点,若直线BE与底面ABCD所成的角为,求二面角的余弦值.【答案】证明:在平行四边形ABCD中,,,,由余弦定理得,所以,所以,所以.因为底面ABCD,底面ABCD,所以.又,所以平面PCA.又平面PCD,所以平面平面PCD.解:E为侧棱PC上的一点,若直线BE与底面ABCD所成的角为,如图所示,以A为坐标原点,AB,AC,AP分别为x,y,z轴,建立空间直角坐标系,则0,,0,,3,,3,,0,,设y,,,则y,,3,,所以,.因为平面ABCD的一个法向量0,,所以,,解得,所以点E的坐标为1,,所以1,,0,,设平面EAB的法向量y,,则取,得,设二面角的平面角为,由题意知为锐角,则,所以二面角的余弦值为.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辽宁省辽河油田第二高级中学2020届高三数学10月月考试题文
时间:120分钟满分:150分
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
3???????x|1B2x?x|?2A????,则,( 1.已知集合)?BA?x??{x|?2?x|x?2}x?0}{0}?|x{x D.
A. C.
B.
{x|?3?x?2}
3?bi??z?Rz??b(的实部和虚部相等,则2.已知复数)i
32. CA.. B. D2322
条件,则p是条件,q的3. ,己知向量( )
B. 必要不充分条件 A.充分不必要条件D.
C.既不充分也不必要条件充要条件
的一个对称中心是4. ( ) 函数
D.A. B. C.5.《周髀算经》中一个问题:从冬至之日起,小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气的日影子长依次成等差数列,若冬至、立春、春分的37.54.5尺,则冬至的日影子长为:(日影子长的和是)尺,芒种的日影子长为
15.512.510.59.5尺D. C. A. 尺尺 B. 尺
??nm是两个不同的平面,则下列命题正确的是( ,)是两条不同的直线, ,6.已知????m//m//nn//n?mm?//n B.若,,若A.则则,,??????////m??m??//mm? ,,则则,C.若D.,若yxyxx的图象( cos3)7.要得到函数=一sin3的图象,只需将函数sin3=+2??3个单位长度 B.向右平移个单位长度向右平移A. 42- 1 -
??个单位长度个单位长度 D.向左平移C.向左平移24x?x q:f(x):p,?Rx2?22?的
图像必过原点,则成立;命题奇函数对于8..已知命题恒有下列结论正确的是()
?p?q p?(?q)qp??q为假 D.为真 B. CA..为真为真
OOABC?tD B则已知,为若,内一点,,且三点共线,,9.)的值为(1211D.
B. A.
C.
2433)(xf x的取值范围为则满足10. 函数的与其导函数的图象如图, ) (
(0,4)(??,0)(1,4) A. B.
4)(0,(0,1)(4,??)
D. C.3 ??????,11,???f(x?1))(xy?f x?1时,为奇函数,当11.已知函数的定义域为,且1?)f(x2x???x2f(x)的所有根之和等于(),则2A.4 B.5 C.6 D.12
11???f?)xf(R?x R满足,对任意的.的定义域为已知函数12.,当??
22???????20)?cosf(sin]?[0,2的解集为( )
时,不等式????????1175524????????,,,, D. A. C. B. ????????
66663333????????二、填空题(本题共4小题,每小题5分,共20分). 11????x2)?f(x xff(0)?,则.已知函数13,若满足条件对于任意实数
f(x)2f(2018)?______.
- 2 -
anSaSaq= 21=}的前项和为,则公比,若+=114.已知所有项均为正数的等比数列{,nn414ABC?P2?3BCAC?713?AB,15.已知三棱锥且,,的三条
侧棱两两互相垂直,.则此三棱锥外接球的表面积为___________B?C(2a?b)tan2bsinc,,ba
ABC?C,A,B3c=2,的内角,16. 的对边分别为,已知ABC?面积的最大值为则
_____________.题为必考题,每分.解答应写出文字说明,证明过程或演算步骤.第17-21三、解答题:共70.
23题为选考题,考生根据要求作答第22,个试题考生都必须作答.}{aa,a,aa?1,.
成等比数列中,(本题满分12分)在公差不为零的等差数列17. n8124a}a{;(1)求数列的通项公式nn1?bT?b?b?????b}{b T.
,求(2)若数列满足,nnn12n n a?a n?n1
分)已知函数(本题满分12.
18.
)求函数最小正周期和单调递增区间;1(的
满足A,其中的三个内角(2的对边分别为)已知,若锐角
.
,求且的面积19. (本题满分12分)随着手机的发展,“微信”逐渐成为人们支付购物的一种形式.某机构对“使用微信支付”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信支付”赞成人数如下表.
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面列联表,并判断是否有99%2?2的把握认为“使用微信支付”的态度与人的年龄有关;
- 3 -
),65[55人不人中至少有1行追踪调查,求2的被调查人中随机选取2(Ⅱ)若从年龄在人进. 赞成使用微信交流的概率参考数据:
)…(KkP0.15 0.10 0.05 0.025 0.010 0.005 0.001 22d??cn?a?b.
,其中)db?a?c)(?(ab)(c?d)(CDEFABCD所在平面互相垂直,12分)如图,菱形直角梯形和(本题满分20.
??BAD4,CF?2,AB?DE?DECD?/CF,60,DE/AF?BD;求证:.(1)
CDEF?A的体求四棱锥
(2) 积.
2x xlnae??x)f(x?xafe)函数本小题满分21.(12分)为常数,曲线((为自然对数的底数),yxx。
=处的切线方程为(e+1)0-在=1a的值;求实数(Ⅰ)5xf )的最小值大于(Ⅱ)证明:(。
2ln? 4. 两题中任选一题作答,如果多做,则按所做的第一题记分22、23请考生在:坐标系与参数方程选修4-4- 4 -
中,以坐标原点为极点,10轴正半轴为极轴建立极坐分)在直角坐标系22. (本题满分
的直线标系.已知曲线的参,过点
分别相交于两点.数方程,直线与曲线
的直角坐标方程和直线的普通方程;(1)写出曲线,使得成等比数列,并对你的结论说明理由.(2 )是否存在实数:不等式选讲选修4-5
10分)已知函数(本题满分23.
(1,解不等式)若
的不等式的解集为(,且,求 2)若关于
证:
月考试生物答案高三101-5 DBDAB
CDCC
6-10 B- 5 -
11-15 DAACC
16-20 CDDDD
21-25 ABADD
26-30 CCCBD
31-35 DDCAA
36-40 CCACB
41-45 DCDCC
46-50 ACCDA
51【答案】(1)线粒体核仁 RNA聚合酶
(2)AGU 是 a→b
(3)用少量的mRNA迅速合成大量的蛋白质(提高蛋白质合成的效率)
2 ,配子;减数分裂形成配子时联会紊乱;1)D(52【答案】)缺失;基因突变;基因突变产生了新基因(2 )前者发生在同源染色体之间,后者发生在非同源染色体之间(
3 61 一种氨基酸可对应多个密码子(密码子具有简并性))(
4 1)酵母菌;酵母菌是兼性厌氧型,醋酸菌是需氧型53【答案】()细胞质基质或线粒体;酸性;重铬酸钾;灰绿色(2 )乙醛;缺少糖源(3 4)()蛋白;脂肪(
5 )比色法;亚硝胺(6-
6 -
- 7 -。
