最新北京市朝阳区2012届高三上学期期末考试试题
2011-2012北京市朝阳区高三上学期期末英语试题

北京市朝阳区2011—2012学年度高三年级第一学期期末统一考试英语试题(考试时间120分钟满分150分)注意事项:1. 试卷分为四个部分,答试卷第一至第三部分时(第16至第20题,第71至第75题除外),每小题选出答案后,用2B铅笔把答题卡上对应题目的答案选中涂满涂黑,黑度以盖住框内字母为准。
如需改动,用橡皮擦除干净后再选涂其它答案项。
在试卷上答题无效。
2. 答试卷第四部分时,必须用黑色字迹的签字笔按题号顺序答在答题卡答题区域相应位置内,未在对应的答题区域作答或超出答题区域作答均不得分。
第一部分:听力理解(共三节,30分)第一节(共5小题;每小题1. 5分,共7. 5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后。
你将有10秒钟的时间回答有关小题和阅读下一小题。
每段对话你将听一遍。
1. Which language does Mr. White speak well?A. German.B. French.C. Japanese.2. What has caused the man’s headache?A. Too little sleep.B. Some medicine.C. The sun.3. Where does the conversation probably take place?A. In a post office.B. In a shop.C. In a hotel.4. Why did the man fail to attend the party?A. He didn't take a note of the party.B. He didn’t know about the party.C. He wasn't invited to the party.5. What are the two speakers talking about?A. The man' s sister.B. An actor.C. A film.第二节(共10小题;每小题1. 5分,满分15分)请听下面4段对话或独白。
北京市朝阳区2012届上学期高三期末考试试题政治(附答案)

北京市朝阳区2012届高三上学期期末考试试题政治(考试时间90分钟满分100分)考生须知:1.考生要认真填写密封线内的内容。
2.本试卷共分为两个部分。
第一部分为选择题,共24题,48分;第二部分为非选择题,共4道大题,52分。
3.试卷所有答案必须填涂或书写在答题纸上,在试卷上作答无效。
第一部分必须用2B铅笔作答;第二部分必须用黑色字迹的签字笔作答。
4.考试结束后,考生应将试卷和答题纸放在桌面上,待监考员收回。
第一部分选择题(共48分)一、选择题在每小题列出的四个选项中,只有一项是最符合题目要求的。
本大题共24小题,每小题2分,共计48分。
中国共产党第十七届中央委员会第六次全体会议审议通过《中共中央关于深化文化体制改革、推动社会主义文化大发展大繁荣若干重大问题的决定》。
完成1、2题。
1.《决定》指出“要广泛开展民族精神教育,大力弘扬爱国主义、集体主义、社会主义思想,增强民族自尊心、自信心、自豪感”。
我们之所以“要广泛开展民族精神教育”,是因为它()①能不断增强我国的国际竞争力②体现了中华民族的整体风貌③可以提高中华民族的综合素质④凝聚着中华民族文他的结晶A.①②B.①③C.②④D.③④2.随着我国经济实力的增强和经济体制改革进入到新的发展阶段,文化体制改革势在必行。
这蕴含的历史唯物主义哲理是()A.用发展的观点看问题B.实践是认识发展的动力C.生产力决定生产关系D.经济基础决定上层建筑3.2000年以《女生日记》拉开“杨红樱校园小说系列”序幕,与其后的《男生日记》、《淘气包马小跳系列》一起,在学生、老师和家长中引起巨大反响。
杨红樱因此被称为中国的J·K·罗琳。
大家说:“杨红樱的作品引领儿童心灵的健康成长,教会了孩子感动。
”这表明()①文化影响人们的交往行为②优秀文化可以丰富人的精神世界③文化决定人的成长与发展④文化能潜移默化、深远持久地影响人A.①②B.①③C.②④D.③④4.多读一些向你传递真善美、高尚道德和科学素养的书,你的生命一定会浸透了书香,一定会成为熠熠生辉的发光体,成为一个品德高尚的人,引导、照耀、温暖别人和后人。
#北京市朝阳区2012届高三上学期期末考试试题(数学理)word版

北京市朝阳区2012届高三上学期期末考试试题数学(理) 2012.1(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)注意事项:考生务必将答案答在答题卡上,在试卷上答无效。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知平面向量(3,1)=a ,(,3)x =b ,且a ⊥b ,则实数x 的值为 ( ) A .9 B .1 C .1- D . 9-2.设集合{}U =1,2,3,4,{}25M =x U x x+p =0∈-,若{}2,3U C M =,则实数p 的值 为 ( ) A .4- B . 4 C .6- D .63. 设数列{}n a 是公差不为0的等差数列,11a =且136,,a a a 成等比数列,则{}n a 的前n 项和n S 等于 ( )A . 2788n n +B .2744n n+ C .2324n n + D .2n n +4.执行如图所示的程序框图,输出的S 值为( ) A .1 B .1- C . 2- D .05.已知函数()sin f x x x =+,设()7a f π=,()6b f π=,()3c f π=,则,,a b c 的大小关系是 ( )A. a b c <<B.c a b <<C.b a c <<D.b c a << 6.函数2()2xf x a x=--的一个零点在区间(1,2)内,则实数a 的取值范围是( ) A .(1,3) B .(1,2) C .(0,3) D . (0,2)7. 已知正方形ABCD的边长为,将ABC ∆沿对角线AC 折起,使平面ABC ⊥平面ACD ,得到如图所示的三棱锥B ACD -.若O 为AC 边的中点,M ,N 分别为线段DC ,BO 上的动点(不包括端点),且BN CM =.设BN x =,则三棱锥N AMC -的体积()y f x =的函数图象大致是( )A .B .C .D .8.已知集合{(,)|,,}A x y x n y na b n ===+∈Z ,{(,)|,B x y x m ==2312,y m =+m ∈Z }.若存在实数,a b 使得A B ≠∅成立,称点(,)a b 为“£”点,则“£”点在平面区域22{(,)|108}C x y x y =+≤内的个数是 ( ) A. 0 B. 1 C. 2 D. 无数个第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在答题卡上.9.已知有若干辆汽车通过某一段公路,从中抽取200辆汽车进行测速分析,其时速的频率分布直方图如图所示,则时速在区间[60,70)上的汽车大约有 辆.ADB NMOC时速(km/h )01002 003 00440 50 60 70 8010.某几何体的三视图如图所示,则这个几何体的体积是 .11. 在平面直角坐标系中,不等式组0,40,x y x y x a +≥⎧⎪-+≥⎨⎪≤⎩所表示的平面区域的面积是9,则实数a 的值为 .12. 设直线10x my --=与圆22(1)(2)4x y -+-=相交于A ,B 两点,且弦AB的长为m 的值是 .13. 某公司购买一批机器投入生产,据市场分析每台机器生产的产品可获得的总利润y (万元)与机器运转时间x (年数,x *∈N )的关系为21825y x x =-+-.则当每台机器运转年时,年平均利润最大,最大值是 万元.14. 已知两个正数,a b ,可按规则c ab a b =++扩充为一个新数c ,在,,a b c 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.(1)若1,3a b ==,按上述规则操作三次,扩充所得的数是__________;(2)若0p q >>,经过6次操作后扩充所得的数为(1)(1)1mnq p ++-(,m n 为正整数),则,m n 的值分别为______________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本题满分13分)在锐角ABC ∆中,a ,b ,c 分别为内角A ,B ,C 所对的边,且满足2sin 0b A -=.(Ⅰ)求角B 的大小;(Ⅱ)若5a c +=,且a c >,b =AB AC 的值.16. (本题满分13分)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A 所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A 指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(,)a b (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动). (Ⅰ)求某个家庭得分为(5,3)的概率?(Ⅱ)若游戏规定:一个家庭的得分为参与游戏的两人得分之和,且得分大于等于8的家庭可以获得一份奖品.请问某个家庭获奖的概率为多少?(Ⅲ)若共有5个家庭参加家庭抽奖活动.在(Ⅱ)的条件下,记获奖的家庭数为X ,求X的分布列及数学期望.17. (本题满分13分)如图,在四棱锥S ABCD -中,平面S AD ⊥平面ABCD .底面ABCD 为矩形,,AD AB ==,SA SD a ==.(Ⅰ)求证:CD SA ⊥; (Ⅱ)求二面角C SA D --的大小.18. (本题满分13分)已知函数1()ln(1)1xf x ax x-=+++(0x ≥,a 为正实数). (Ⅰ)若1a =,求曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)求函数()f x 的单调区间;(Ⅲ)若函数()f x 的最小值为1,求a 的取值范围.19. (本题满分14分)已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12,直线l 过点(4,0)A ,(0,2)B ,且与椭圆C 相切于点P .(Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在过点(4,0)A 的直线m 与椭圆C 相交于不同的两点M 、N ,使得23635AP AM AN =⋅?若存在,试求出直线m 的方程;若不存在,请说明理由.20. (本题满分14分) 数列{}n a ,{}n b (1,2,3,n =)由下列条件确定:①110,0a b <>;②当2k ≥时,k a 与k b 满足:当011≥+--k k b a 时,1-=k k a a ,211--+=k k k b a b ;当011<+--k k b a 时,211--+=k k k b a a ,1-=k k b b . (Ⅰ)若11a =-,11b =,写出234,,a a a ,并求数列}{n a 的通项公式;(Ⅱ)在数列}{n b 中,若s b b b >>> 21(3s ≥,且*s ∈N ),试用11,b a 表示k b },,2,1{s k ∈;(Ⅲ)在(Ⅰ)的条件下,设数列}{n c (*)n ∈N 满足211=c ,0n c ≠, 2212m n n n mc c c ma -+=-+(其中m 为给定的不小于2的整数),求证:当m n ≤时,恒有1<n c .参考答案 2012.1一、选择题:二、填空题:三、解答题:(15)(本小题满分13分)解:2sin 0b A -=,2sin sin 0A B A -=, ……………………………………………… 2分因为sin 0A ≠,所以23sin =B . …………………………………………………3分 又B 为锐角, 则3B π=. …………………………………………… 5分(Ⅱ)由(Ⅰ)可知,3B π=.因为b =根据余弦定理,得 2272cos3a c ac π=+-,………………………………………7分整理,得2()37a c ac +-=.由已知 5a c +=,则6ac =.又a c >,可得 3a =,2c =. ……………………………………… 9分于是222cos214b c a A bc +-===, ………………………… 11分所以cos cos 2114AB AC AB AC A cb A ====. …………… 13分 (16)(本小题满分13分)解:(Ⅰ)记事件A :某个家庭得分情况为(5,3).111()339P A =⨯=.所以某个家庭得分情况为(5,3)的概率为19.……………………………… 4分(Ⅱ)记事件B :某个家庭在游戏中获奖,则符合获奖条件的得分包括(5,3),(5,5),(3,5)共3类情况.所以1111111()3333333P B =⨯+⨯+⨯=.所以某个家庭获奖的概率为13. ………………………………………… 8分(Ⅲ)由(Ⅱ)可知,每个家庭获奖的概率都是13,所以1~(5,)3X B .00551232(0)()()33243P X C ==⋅=,11451280(1)()()33243P X C ==⋅=,22351280(2)()()33243P X C ==⋅=,33251240(3)()()33243P X C ==⋅=,44151210(4)()()33243P X C ==⋅=,5505121(5)()()33243P X C ==⋅=. ………………………………… 11分 所以X 分布列为:所以533EX np ==⨯=. 所以X 的数学期望为53. ……………………………………………… 13分(17)(本小题满分13分)证明:(Ⅰ)因为平面SAD ⊥平面ABCD ,CD AD ⊥,且面SAD 面ABCD AD =, 所以CD ⊥平面SAD . 又因为SA ⊂平面SAD所以CD SA ⊥. …………………………………………… 6分 (Ⅱ)由(Ⅰ)可知,CD SA ⊥.在SAD ∆中,SA SD a ==,AD ,所以SA SD ⊥, 所以SA ⊥平面SDC .即SA SD ⊥,SA SC ⊥,所以CSD ∠为二面角C SA D --的平面角. 在Rt CDS ∆中,tan CD CSD SD ∠===所以二面角C SA D --的大小3π. …………………………………… 13分 法二:取BC 的中点E , AD 的中点P .在SAD ∆中,SA SD a ==,P 为AD 的中点,所以,SP AD ⊥. 又因为平面SAD ⊥平面ABCD ,且平面SAD 平面ABCD AD =所以,SP ⊥平面ABCD .显然,有PE AD ⊥. ……………………………… 1分 如图,以P 为坐标原点,PA 为x 轴,PE 为y 轴,PS为z 轴建立空间直角坐标系,则)S,,0,0)A ,,0)B,(,0)C ,(,0,0)D . ………………………………………………………………3分(Ⅰ)易知2(0,3,0),(,0,)CD a SA a =-= 因为0CD SA ⋅=,所以CD SA ⊥. …………………………………………………………… 6分 (Ⅱ)设(,,)x y z =n 为平面CSA 的一个法向量,则有00SA CA ⎧⋅=⎪⎨⋅=⎪⎩n n ,即0=⎪-=⎩,所以=n . ……………………………… 7分显然,EP ⊥平面SAD ,所以PE 为平面SAD 的一个法向量,所以(0,1,0)=m 为平面SAD 的一个法向量.……………………………………… 9分所以 1cos ,2<>==n m ,所以二面角C SA D --的大小为3π. ………………………………………… 13分(18)(本小题满分13分)解:(Ⅰ)当1a =时,1()ln(1)1xf x x x-=+++, 则212()1(1)f x x x -'=+++. ………………………………………………… 2分 所以(1)0f '=.又(1)ln 2f =,因此所求的切线方程为ln 2y =. ………… 4分(Ⅱ)22222()1(1)(1)(1)a ax a f x ax x ax x -+-'=+=++++. ………………………… 5分 (1)当20a -≥,即2a ≥时,因为0x ≥,所以()0f x '>,所以函数()f x 在[)0,+∞上单调递增. ………………………………………………………………… 6分 (2)当20a -<,即02a <<时,令()0f x '=,则220ax a +-=(0x ≥),所以x =.因此,当x ∈时,()0f x '<,当)x ∈+∞时,()0f x '>.所以函数()f x 的单调递增区间为)+∞,函数()f x 的单调递减区间为. ………………………………………………………………… 10分 (Ⅲ)当2a ≥时,函数()f x 在[)0,+∞上单调递增,则()f x 的最小值为(0)1f =,满足题意. ………………………………………………………………… 11分当02a <<时,由(Ⅱ)知函数()f x的单调递增区间为)+∞,函数()f x的单调递减区间为,则()f x的最小值为f ,而(0)1f =,不合题意.所以a 的取值范围是[)2,+∞. ………………………………………………… 13分(19)(本小题满分14分)解: (Ⅰ)由题得过两点(4,0)A ,(0,2)B 直线l 的方程为240x y +-=.………… 1分 因为12c a =,所以2a c =,b =. 设椭圆方程为2222143x y c c+=,由2222240,1,43x y x y c c+-=⎧⎪⎨+=⎪⎩消去x 得,224121230y y c -+-=. 又因为直线l 与椭圆C 相切,所以221244(123)0c ∆=-⨯-=,解得21c =.所以椭圆方程为22143x y +=. ……………………………………………… 5分 (Ⅱ)易知直线m 的斜率存在,设直线m 的方程为(4)y k x =-,…………………… 6分由22(4),1,43y k x x y =-⎧⎪⎨+=⎪⎩消去y ,整理得2222(34)3264120k x k x k +-+-=. ………… 7分由题意知2222(32)4(34)(6412)0k k k ∆=-+->,解得1122k -<<. ……………………………………………………………… 8分 设11(,)M x y ,22(,)N x y ,则21223234k x x k+=+,2122641234k x x k -=+. …… 9分又直线:240l x y +-=与椭圆22:143x y C +=相切, 由22240,1,43x y x y +-=⎧⎪⎨+=⎪⎩解得31,2x y ==,所以3(1,)2P . ……………………………10分则2454AP =. 所以3645813547AM AN ⋅=⨯=.又AM AN ⋅==212(1)(4)(4)k x x =+--21212(1)(4()16)k x x x x =+-++22222641232(1)(416)3434k k k k k -=+-⨯+++ 2236(1).34k k=++ 所以223681(1)347k k +=+,解得4k =±.经检验成立. …………………… 13分 所以直线m的方程为4)y x =-. …………………………………… 14分 (20)(本小题满分14分)(Ⅰ)解:因为011=+b a ,所以112-==a a ,02112=+=b a b . 因为0122<-=+b a ,所以212223-=+=b a a ,023==b b . 因为33102a b +=-<,所以334124a b a +==-,430b b ==.所以1234111,1,,24a a a a =-=-=-=-. …………………………………… 2分由此猜想,当2≥k 时,011<+--k k b a ,则22111---=+=k k k k a b a a ,10k k b b -==.… 3分 下面用数学归纳法证明:①当2k =时,已证成立. ②假设当k l =(l *∈N ,且2l ≥)猜想成立, 即110l l a b --+<,10l l b b -==,102l l a a -=<. 当1k l =+时,由102l l a a -=<, 10l l b b -==得0l l a b +<,则10l l b b +==,1022l l ll a b a a ++==<. 综上所述,猜想成立.所以22221111(2)222n n n n a a n ---⎛⎫⎛⎫=⨯=-⋅=-≥ ⎪⎪⎝⎭⎝⎭.故211,12.2n n n a n --=⎧⎪=⎨-≥⎪⎩. ……………………………………………… 6分(Ⅱ)解:当s k ≤≤2时,假设110k k a b --+<,根据已知条件则有1-=k k b b ,与s b b b >>> 21矛盾,因此110k k a b --+<不成立, …………… 7分 所以有110k k a b --+≥,从而有1k k a a -=,所以1a a k =. 当011≥+--k k b a 时,1-=k k a a ,211--+=k k k b a b , 所以111111()22k k k k k k k a b b a a b a -----+-=-=-; …………………… 8分 当s k ≤≤2时,总有111()2k k k k b a b a ---=-成立.又110b a -≠,所以数列}{k k a b -(s k ,,2,1 =)是首项为11b a -,公比为12的等比数列,11121)(-⎪⎭⎫⎝⎛-=-k k k a b a b ,1,2,,k s =,又因为1a a k =,所以111121)(a a b b k k +⎪⎭⎫⎝⎛-=-. …………………………… 10分(Ⅲ)证明:由题意得2212m n n n mc c c ma -+=-+n n c c m+=21. 因为211n n n c c c m +=+,所以2110n n n c c c m+-=>. 所以数列{}n c 是单调递增数列. …………………………………… 11分 因此要证)(1m n c n ≤<,只须证1<m c . 由2≥m ,则n n n c c m c +=+211<n n n c c c m++11,即1111n n c c m +->-.…… 12分 因此1122111)11()11()11(1c c c c c c c c m m m m m +-++-+-=--- m m m m 121+=+-->. 所以11m mc m <<+.故当m n ≤,恒有1<n c . …………………………………………………14分。
2012年北京市朝阳区高三第一学期期末统一考试
北京市朝阳区2010~2011学年度高三年级第一学期期末统一考试生物试卷2011.1 (卷面总分100分考试时间90分钟)一、选择题(共30小题,每小题只有一个正确选项,每小题1分,共30分)1.下列关于细胞内元素和化合物的叙述,正确的是A.细胞内主要储能物质是糖类B.精瘦肉细胞中含量最多的化合物是蛋白质C.淀粉、纤维素、乳糖的最终水解产物都是葡萄糖D.构成DNA的单体的种类、数目、排列顺序决定了蛋白质的多样性2.下列有关生物的共同特征的叙述,正确的是A.酵母菌、乳酸菌都是细菌,且都能进行有丝分裂,遗传都遵循遗传的基本定律B.酵母菌、乳酸菌、硝化细菌都不含叶绿素,且都是分解者,都能进行有氧呼吸C.乳酸菌、硝化细菌、蓝藻都是原核生物,且都有细胞壁,体内含有DNA和RNA两类核酸分子D.乳酸菌、硝化细菌都是异养生物,在电镜下可观察到核糖体附着在内质网上3.矿工中有一种常见的职业病——硅肺,其发病原因是肺部吸入硅尘后,吞噬细胞会吞噬硅尘,却不能产生分解硅尘的酶。
硅尘进入体内可破坏细胞的生物膜系统,导致细胞通透性改变,使肺部细胞死亡,进而肺功能受损。
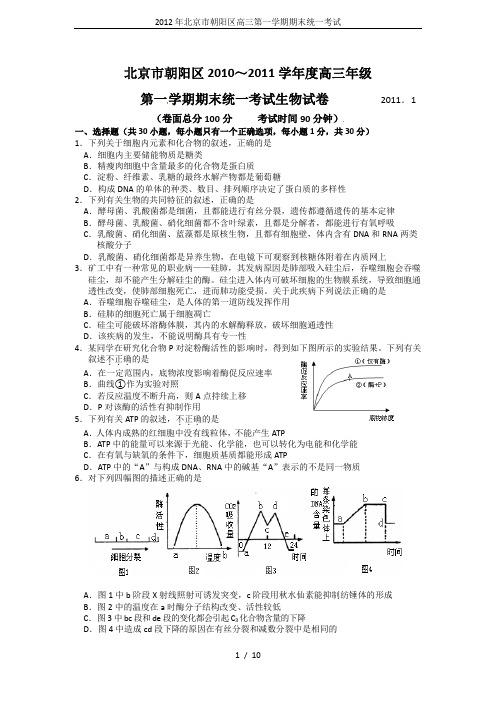
关于此疾病下列说法正确的是A.吞噬细胞吞噬硅尘,是人体的第一道防线发挥作用B.硅肺的细胞死亡属于细胞凋亡C.硅尘可能破坏溶酶体膜,其内的水解酶释放,破坏细胞通透性D.该疾病的发生,不能说明酶具有专一性4.某同学在研究化合物P对淀粉酶活性的影响时,得到如下图所示的实验结果。
下列有关叙述不..的是.正确A.在一定范围内,底物浓度影响着酶促反应速率B.曲线①作为实验对照C.若反应温度不断升高,则A点持续上移D.P对该酶的活性有抑制作用5.下列有关ATP的叙述,不正确...的是A.人体内成熟的红细胞中没有线粒体,不能产生ATPB.ATP中的能量可以来源于光能、化学能,也可以转化为电能和化学能C.在有氧与缺氧的条件下,细胞质基质都能形成ATPD.ATP中的“A”与构成DNA、RNA中的碱基“A”表示的不是同一物质6.对下列四幅图的描述正确的是A.图1中b阶段X射线照射可诱发突变,c阶段用秋水仙素能抑制纺锤体的形成B.图2中的温度在a时酶分子结构改变、活性较低C.图3中bc段和de段的变化都会引起C3化合物含量的下降D.图4中造成cd段下降的原因在有丝分裂和减数分裂中是相同的7.右图为某雄性哺乳动物细胞分裂某时期的示意图。
北京市朝阳区2012届高三上学期期末考试试题(物理)word版

北京市朝阳区2012届高三上学期期末考试试题物理(考试时间90分钟满分100分)一、本题共13小题,每小题3分。
共39分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.很好地解释了α粒子散射实验并提出原子核式结构模型的科学家是()A.汤姆生B.爱因斯坦C.德布罗意D.卢瑟福2.用绿光照射一个光电管,能产生光电效应,欲使光电子从阴极逸出时最大初动能增大,可以()A.改用红光照射B.改用紫光照射C.增加绿光照射时间D.增加绿光照射强度3.图中P为放在匀强磁场中的天然放射源,其放出的射线在磁场的作用下分成a、b、c三束,以下判断正确的是()A.a为α射线、b为β射线、c为γ射线B.a为β射线、b为γ射线、c为α射线C.a为α射线、b为γ射线、c为β射线D.a为γ射线、b为α射线、c为β射线4.绝缘细线的一端与一带正电的小球M相连接,另一端固定在天花板上,在小球M下面的一绝缘水平面上固定了另一个带电小球N,在下列情况下,小球M能处于静止状态的是()5.2011年12月美国宇航局发布声明宣布,通过开普勒太空望远镜项目证实了太阳系外第一颗类似地球的、可适合居住的行星。
该行星被命名为开普勒一22b(Kepler一22b),距离地球约600光年之遥,体积是地球的2.4倍。
这是目前被证实的从大小和运行轨道来说最接近地球形态的行星,它每290天环绕着一颗类似于太阳的恒星运转一圈。
若行星开普勒一22b绕恒星做圆运动的轨道半径可测量,万有引力常量G已知。
根据以上数据可以估算的物理量有()A.行星的质量B.行星的密度C.恒星的质量D.恒星的密度6.质量为m 的汽车在平直公路上行驶,发动机的功率P 和汽车受到的阻力f 均恒定不变。
在时间t 内,汽车的速度由0v 增加到最大速度m v ,汽车前进的距离为s ,则在这段时间内可以表示发动机所做功W 的计算式为( )A .W Pt =B .W fs =C .2201122m W mv mv =- D .212m W mv fs =+ 7.正方形区域ABCD 中有垂直于纸面向里的匀强磁场,一个α粒子(不计重力)以一定速度从AB 边的中点M 沿既垂直于AB 边又垂直于磁场的方向射入磁场,正好从AD 边的中点N 射出。
朝阳期末

北京市朝阳区2011—2012学年度高三年级第一学期期末统一考试历史试题(考试时间90分钟,满分100分)一、选择题共32小题,每小题1.5分,共48分。
在下列各题的四个选项中,选出最符合题目要求的一项。
1.五四运动被称为创造一种新的现代的文明以挽救中国。
“新”的主要表现是()A.知识分子发挥着移风易俗的重要作用B.激发人们强烈的民族意识和爱国热情C.弘扬科学和民主成为五四的精神核心D.爱国主义与宣传马克思主义逐步结合2.“中国最初的共产主义支部是于1920年5月在上海和北京组织起来的”有的“党纲就是‘劳工专政,生产组合’八个字。
”上述材料表明()A.中国共产党的诞生B.建立无产阶级政权C.筹备工人阶级政党D.工农运动蓬勃开展3.孙中山在三民主义中提出“平均地权”“节制资本”其目的是()A.推动农工运动的开展,“辅助其经济组织”B.实现“土地国有后,必能耕者而后授其田”C.达成“盖民国之民权,唯民国之国民乃能享之”D.反对“少数人占经济之势力,垄断社会之财源”4.20世纪20 ~40年代,中国革命中心从珠江流域向黄河流域转移。
完成转移的直接因素有()A.北伐战争和红军长征B.北伐战争和抗日故争C.红军长征和抗日战争D.抗日战争和解放战争5.在土地革命历史时期,探索中国民主革命策略转变的文献是()A.《湖南农民运动考察报告》B.《中国的红色政权为什么能够存在?》C.《中国革命和中国共产党》D.《关于正确处理人民内部矛盾的问题》6.与中国共产党诞生初期相比,国共十年对峙时期共产党日渐成熟体现在A.认识到发动工人运动重要性B.建立以国共合作为基础的统一战线.C.提出共产党的民主革命纲领D.独立自主地探索中国革命发展道路7.对右面两则材料理解准确的是()①七七抗战揭开了全面抵抗的序幕②此战发生于相持阶段的正面战场③民族统一战线领导积极抗战的典范④反映国人对抗日英烈的敬重与纪念A.①②B.①③④C.①④D.②③④8.1939年1月在讨论建立陕甘宁边区参议会的问题上,毛泽东发表讲话指出“……而这民主又是苏维埃在现阶段的发展物,现在各阶级,工农商学兵各界都可参加参议会。
北京市朝阳区2012届高三上学期期末考试化学试题.pdf
* 愿同学们:每天学到一点新知识,每天拥有一份好心情! * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * 仔细观察下列各组图形,你发现了什么? 每组图形的形状和大小完全相同。
(1) (2) (3)(4) 两个能够重合的图形叫做全等图形. 全等图形的形状和大小完全相同. 形状相同,但大小不同, 因此它们不是全等图形. 大小相同,但形状不相同,它们也不是全等图形. 40平方米 40平方米 大小相同,形状也相同,它们是全等图形. 下列各图形是不是全等图形? F E D C B A 能够重合的两个三角形叫做全等三角形。
它们会全等吗? 小试身手 下列说法是否正确,并简要说明理由: (1) 边长相等的正方形都是全等图形. (2) 同一面中华人民共和国国旗上,4个小五角星都是全等图形. (3) 面积相等的两个三角形是全等三角形. (4) 两个全等三角形的面积相等 对 对 错 对 A B C D E F 如果△ ABC 与△DEF会互相重合,顶点A与顶点( )重合,顶点B与顶点( )重合,顶点C与顶点( )重合。
AB边与( )边重合, BC边与( )边重合,AC边与( )边重合。
∠ A与( )重合,∠B与( )重合,∠C与 ( )重合。
D E F DE EF DF ∠D ∠E ∠F 两个全等三角形重合时,互相重合的顶点叫对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角。
“全等”用符号“≌ ”表示 记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。
比如△ABC≌△DFE A B C D E F △ABC≌△DEF 试一试,摆一摆 用符号来表示两个全等三角形: C A B D O O A C D B △AOC ≌ △DOB △AOC ≌ △BOD 1、若△AOC≌△BOD,对应 边是___________________,对应角是________________; A B O C D 2、若△ABD≌△ACD,对应边是_________________________,对应角是_________________; A B C D 3、若△ABC≌△CDA,对应 边是________________,对应角是_______________; A B C D AC与BD,AO与BO,CO与DO ∠A与∠B, ∠ C与∠ D, ∠ AOC与∠ BOD AB与AC,BD与CD,AD与AD ∠BAD 与∠CAD, ∠B与 ∠C, ∠ADB与∠ADC AB与CD,BC与DA,AC与CA 1 2 3 4 ∠1与 ∠2, ∠3 与∠4, ∠ B与 ∠ D 两个全等三角形的位置变化了,对应边、对应角的大小有变化吗?由此你能得到什么结论? 全等三角形的对应边相等,对应角相等。
【VIP专享】2012-2013年朝阳区高三年级第一学期期末数学(文)试题及答案
10.在 ABC 中,角 A , B , C 所对的边分别为 a , b , c ,且 b2 c2 a2 bc ,则 A =
1. 设集合 A {x 0 x 2} ,集合 B {x log2 x 0} ,则 A B 等于
A.x | x 2 B.x | x 0
2.已知 i 是虚数单位,若复数 (1 ai)(2 i) 是纯虚数,则实数 a 等于
A. 2
B. 1 2
3.“ k 1 ”是“直线 x y k 0 与圆 x2 y2 1 相交”的
雅思博教育
北京市朝阳区 2012-2013 学年度高三年级第一学期期末统一考试
数学测试题(文史类)
(考试时间 120 分钟 满分 150 分) 本试卷分为选择题(共 40 分)和非选择题(共 110 分)两部分
第一部分(选择题 共 40 分)
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,选出 符合题目要求的一项.
3
1
正视图
正 视 图
俯视图
D. 2
保目标火热招生中
开始
输入 x k 0
x x5
2013.1
k k 1
x 23?
否 是
输出 k
结束
保目标火热招生中
雅思博教育
7.
已知函数
值范围是
A. , 1
f
(x)
ex a, x
2x
1,
x
0, ( a R 0
B. , 0
),若函数
8. 在棱长为1的正方体 ABCD A1B1C1D1 中, P1 , P2 分别为线段 AB , BD1 (不包括端
A.充分不必要条件 C.充分必要条件
2012年北京市朝阳区高三年级第一学期期末统一考试(数学理)
北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷(理工类) 2012.1(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)注意事项:考生务必将答案答在答题卡上,在试卷上答无效。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知平面向量(3,1)=a ,(,3)x =b ,且a ⊥b ,则实数x 的值为 ( ) A .9 B .1 C .1- D . 9-2.设集合{}U =1,2,3,4,{}25M =x U x x+p =0∈-,若{}2,3U C M =,则实数p 的值 为 ( ) A .4- B . 4 C .6- D .63. 设数列{}n a 是公差不为0的等差数列,11a =且136,,a a a 成等比数列,则{}n a 的前n 项和n S 等于 ( )A . 2788n n +B .2744n n + C .2324n n+D .2n n +4.执行如图所示的程序框图,输出的S 值为( )A .1B .1-C . 2-D .05.已知函数()sin f x x x =,设()7a f π=,()6b f π=,()3c f π=,则,,a b c 的大小关系是 ( )A. a b c <<B.c a b <<C.b a c <<D.b c a <<6.函数2()2xf x a x=--的一个零点在区间(1,2)内,则实数a 的取值范围是( ) A .(1,3) B .(1,2) C .(0,3) D . (0,2)7. 已知正方形ABCD的边长为将ABC ∆沿对角线AC 折起,使平面ABC ⊥平面ACD ,得到如图所示的三棱锥B ACD -.若O 为AC 边的中点,M ,N 分别为线段DC ,BO 上的动点(不包括端点),且BN CM =.设BN x =,则三棱锥N AMC -的体积()y f x =的函数图象大致是( )A .B .C .D .8.已知集合{(,)|,,A x y x n yn a b n ===+∈Z ,{(,)|,B x y x m ==2312,y m =+m ∈Z }.若存在实数,a b 使得AB ≠∅成立,称点(,)a b 为“£”点,则“£”点在平面区域22{(,)|108}C x y x y =+≤内的个数是 ( ) A. 0 B. 1 C. 2 D. 无数个第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在答题卡上.9.已知有若干辆汽车通过某一段公路,从中抽取200辆汽车进行测速分析,其时速的频率分布直方图如图所示,则时速在区间[60,70)上的汽车大约有 辆.ADB N MOC时速(km/h )010003 004 40 50 60 70 8010.某几何体的三视图如图所示,则这个几何体的体积是 .11. 在平面直角坐标系中,不等式组0,40,x y x y x a +≥⎧⎪-+≥⎨⎪≤⎩所表示的平面区域的面积是9,则实数a 的值为 .12. 设直线10x my --=与圆22(1)(2)4x y -+-=相交于A ,B 两点,且弦AB的长为m 的值是 .13. 某公司购买一批机器投入生产,据市场分析每台机器生产的产品可获得的总利润y (万元)与机器运转时间x (年数,x *∈N )的关系为21825y x x =-+-.则当每台机器运转 年时,年平均利润最大,最大值是 万元.14. 已知两个正数,a b ,可按规则c ab a b =++扩充为一个新数c ,在,,a b c 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.(1)若1,3a b ==,按上述规则操作三次,扩充所得的数是__________;(2)若0p q >>,经过6次操作后扩充所得的数为(1)(1)1m nq p ++-(,m n 为正整数),则,m n 的值分别为______________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本题满分13分)在锐角ABC ∆中,a ,b ,c 分别为内角A ,B ,C 所对的边,且满足2sin 0b A -=.(Ⅰ)求角B 的大小;(Ⅱ)若5a c +=,且a c >,b =AB AC 的值.16. (本题满分13分)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A 所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A 指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(,)a b (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动). (Ⅰ)求某个家庭得分为(5,3)的概率?(Ⅱ)若游戏规定:一个家庭的得分为参与游戏的两人得分之和,且得分大于等于8的家庭可以获得一份奖品.请问某个家庭获奖的概率为多少?(Ⅲ)若共有5个家庭参加家庭抽奖活动.在(Ⅱ)的条件下,记获奖的家庭数为X ,求X的分布列及数学期望.17. (本题满分13分)如图,在四棱锥S ABCD -中,平面SAD ⊥平面ABCD .底面ABCD 为矩形,,AD AB =,SA SD a ==.(Ⅰ)求证:CD SA ⊥;(Ⅱ)求二面角C SA D --的大小.18. (本题满分13分)已知函数1()ln(1)1xf x ax x-=+++(0x ≥,a 为正实数). (Ⅰ)若1a =,求曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)求函数()f x 的单调区间;(Ⅲ)若函数()f x 的最小值为1,求a 的取值范围.19. (本题满分14分)已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12,直线l 过点(4,0)A ,(0,2)B ,且与椭圆C 相切于点P .(Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在过点(4,0)A 的直线m 与椭圆C 相交于不同的两点M 、N ,使得23635AP AM AN =⋅?若存在,试求出直线m 的方程;若不存在,请说明理由.20. (本题满分14分) 数列{}n a ,{}n b (1,2,3,n =)由下列条件确定:①110,0a b <>;②当2k ≥时,k a 与k b 满足:当011≥+--k k b a 时,1-=k k a a ,211--+=k k k b a b ;当011<+--k k b a 时,211--+=k k k b a a ,1-=k k b b . (Ⅰ)若11a =-,11b =,写出234,,a a a ,并求数列}{n a 的通项公式;(Ⅱ)在数列}{n b 中,若s b b b >>> 21(3s ≥,且*s ∈N ),试用11,b a 表示k b },,2,1{s k ∈;(Ⅲ)在(Ⅰ)的条件下,设数列}{n c (*)n ∈N 满足211=c ,0n c ≠, 2212m n n n mc c c ma -+=-+(其中m 为给定的不小于2的整数),求证:当m n ≤时,恒有1<n c .北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷答案(理工类) 2012.1二、填空题:三、解答题:(15)(本小题满分13分)解:2sin 0b A -=,2sin sin 0A B A -=, ……………………………………………… 2分因为sin 0A ≠,所以23sin =B . …………………………………………………3分 又B 为锐角, 则3B π=. …………………………………………… 5分(Ⅱ)由(Ⅰ)可知,3B π=.因为b =根据余弦定理,得 2272cos3a c ac π=+-,………………………………………7分整理,得2()37a c ac +-=.由已知 5a c +=,则6ac =.又a c >,可得 3a =,2c =. ……………………………………… 9分于是222cos2b c a A bc +-===, ………………………… 11分所以cos cos 21AB AC AB AC A cb A ====. …………… 13分 (16)(本小题满分13分)解:(Ⅰ)记事件A :某个家庭得分情况为(5,3).111()339P A =⨯=.所以某个家庭得分情况为(5,3)的概率为19.……………………………… 4分(Ⅱ)记事件B :某个家庭在游戏中获奖,则符合获奖条件的得分包括(5,3),(5,5),(3,5)共3类情况.所以1111111()3333333P B =⨯+⨯+⨯=.所以某个家庭获奖的概率为13. ………………………………………… 8分(Ⅲ)由(Ⅱ)可知,每个家庭获奖的概率都是13,所以1~(5,)3X B .00551232(0)()()33243P X C ==⋅=,11451280(1)()()33243P X C ==⋅=,22351280(2)()()33243P X C ==⋅=,33251240(3)()()33243P X C ==⋅=,44151210(4)()()33243P X C ==⋅=,5505121(5)()()33243P X C ==⋅=. ………………………………… 11分所以533EX np ==⨯=. 所以X 的数学期望为53. ……………………………………………… 13分(17)(本小题满分13分) 证明:(Ⅰ)因为平面SAD ⊥平面ABCD , CD AD ⊥,且面SAD 面ABCD AD =, 所以CD ⊥平面SAD . 又因为SA ⊂平面SAD所以CD SA ⊥. …………………………………………… 6分 (Ⅱ)由(Ⅰ)可知,CD SA ⊥.在SAD ∆中,SA SD a ==,AD =, 所以SA SD ⊥,所以SA ⊥平面SDC . 即SA SD ⊥,SA SC ⊥,所以CSD ∠为二面角C SA D --的平面角.在Rt CDS ∆中,tan CDCSD SD ∠=== 所以二面角C SA D --的大小3π. …………………………………… 13分 法二:取BC 的中点E , AD 的中点P .在SAD ∆中,SA SD a ==,P 为AD 的中点,所以,SP AD ⊥. 又因为平面SAD ⊥平面ABCD ,且平面SAD 平面ABCD AD =所以,SP ⊥平面ABCD .显然,有PE AD ⊥. ……………………………… 1分 如图,以P 为坐标原点,P A 为x 轴,PE 为y 轴,PS为z 轴建立空间直角坐标系,则)S,,0,0)A ,,0)B,(,0)C ,(,0,0)D . ………………………………………………………………3分(Ⅰ)易知2(0,3,0),(,0,)CD a SA a =-= 因为0CD SA ⋅=,所以CD SA ⊥. …………………………………………………………… 6分 (Ⅱ)设(,,)x y z =n 为平面CSA 的一个法向量,则有0SA CA ⎧⋅=⎪⎨⋅=⎪⎩n n ,即0=⎪-=⎩,所以=n . ……………………………… 7分显然,EP ⊥平面SAD ,所以PE 为平面SAD 的一个法向量,所以(0,1,0)=m 为平面SAD 的一个法向量.……………………………………… 9分所以 1cos ,2<>==n m , 所以二面角C SA D --的大小为3π. ………………………………………… 13分(18)(本小题满分13分)解:(Ⅰ)当1a =时,1()ln(1)1xf x x x-=+++, 则212()1(1)f x x x -'=+++. ………………………………………………… 2分 所以(1)0f '=.又(1)ln 2f =,因此所求的切线方程为ln 2y =. ………… 4分(Ⅱ)22222()1(1)(1)(1)a ax a f x ax x ax x -+-'=+=++++. ………………………… 5分 (1)当20a -≥,即2a ≥时,因为0x ≥,所以()0f x '>,所以函数()f x 在[)0,+∞上单调递增. ………………………………………………………………… 6分(2)当20a -<,即02a <<时,令()0f x '=,则220ax a +-=(0x ≥),所以x =.因此,当x ∈时,()0f x '<,当)x ∈+∞时,()0f x '>.所以函数()f x 的单调递增区间为)+∞,函数()f x 的单调递减区间为. ………………………………………………………………… 10分 (Ⅲ)当2a ≥时,函数()f x 在[)0,+∞上单调递增,则()f x 的最小值为(0)1f =,满足题意. ………………………………………………………………… 11分当02a <<时,由(Ⅱ)知函数()f x 的单调递增区间为)+∞,函数()f x的单调递减区间为,则()f x 的最小值为f ,而(0)1f =,不合题意.所以a 的取值范围是[)2,+∞. ………………………………………………… 13分(19)(本小题满分14分)解: (Ⅰ)由题得过两点(4,0)A ,(0,2)B 直线l 的方程为240x y +-=.………… 1分因为12c a =,所以2a c =,b =. 设椭圆方程为2222143x y c c+=, 由2222240,1,43x y x y c c+-=⎧⎪⎨+=⎪⎩消去x 得,224121230y y c -+-=. 又因为直线l 与椭圆C 相切,所以221244(123)0c ∆=-⨯-=,解得21c =. 所以椭圆方程为22143x y +=. ……………………………………………… 5分 (Ⅱ)易知直线m 的斜率存在,设直线m 的方程为(4)y k x =-,…………………… 6分由22(4),1,43y k x x y =-⎧⎪⎨+=⎪⎩消去y ,整理得2222(34)3264120k x k x k +-+-=. ………… 7分 由题意知2222(32)4(34)(6412)0k k k ∆=-+->,解得1122k -<<. ……………………………………………………………… 8分 设11(,)M x y ,22(,)N x y ,则21223234k x x k+=+,2122641234k x x k -=+. …… 9分 又直线:240l x y +-=与椭圆22:143x y C +=相切, 由22240,1,43x y x y +-=⎧⎪⎨+=⎪⎩解得31,2x y ==,所以3(1,)2P . ……………………………10分 则2454AP =. 所以3645813547AM AN ⋅=⨯=.又AM AN ⋅==212(1)(4)(4)k x x =+--21212(1)(4()16)k x x x x =+-++22222641232(1)(416)3434k k k k k -=+-⨯+++2236(1).34k k =++ 所以223681(1)347k k +=+,解得4k =±.经检验成立. …………………… 13分 所以直线m的方程为4)4y x =±-. …………………………………… 14分 (20)(本小题满分14分) (Ⅰ)解:因为011=+b a ,所以112-==a a ,02112=+=b a b . 因为0122<-=+b a ,所以212223-=+=b a a ,023==b b . 因为33102a b +=-<,所以334124a b a +==-,430b b ==. 所以1234111,1,,24a a a a =-=-=-=-. …………………………………… 2分 由此猜想,当2≥k 时,011<+--k kb a ,则22111---=+=k k k k a b a a ,10k k b b -==.… 3分 下面用数学归纳法证明:①当2k =时,已证成立.②假设当k l =(l *∈N ,且2l ≥)猜想成立,即110l l a b --+<,10l l b b -==,102l l a a -=<. 当1k l =+时,由102l l a a -=<, 10l l b b -==得0l l a b +<,则10l l b b +==,1022l l l l a b a a ++==<. 综上所述,猜想成立. 所以22221111(2)222n n n n a a n ---⎛⎫⎛⎫=⨯=-⋅=-≥ ⎪ ⎪⎝⎭⎝⎭. 故211,1 2.2n n n a n --=⎧⎪=⎨-≥⎪⎩. ……………………………………………… 6分(Ⅱ)解:当s k ≤≤2时,假设110k k a b --+<,根据已知条件则有1-=k k b b ,与s b b b >>> 21矛盾,因此110k k a b --+<不成立, …………… 7分 所以有110k k a b --+≥,从而有1k k a a -=,所以1a a k =. 当011≥+--k k b a 时,1-=k k a a ,211--+=k k k b a b , 所以111111()22k k k k k k k a b b a a b a -----+-=-=-; …………………… 8分 当s k ≤≤2时,总有111()2k k k k b a b a ---=-成立. 又110b a -≠,所以数列}{k k a b -(s k ,,2,1 =)是首项为11b a -,公比为12的等比数列, 11121)(-⎪⎭⎫ ⎝⎛-=-k k k a b a b ,1,2,,k s =,又因为1a a k =,所以111121)(a a b b k k +⎪⎭⎫ ⎝⎛-=-. …………………………… 10分 (Ⅲ)证明:由题意得2212mn n n mc c c ma -+=-+ n n c c m +=21. 因为211n n n c c c m +=+,所以2110n n n c c c m+-=>. 所以数列{}n c 是单调递增数列. …………………………………… 11分 因此要证)(1m n c n ≤<,只须证1<m c .由2≥m ,则n n n c c m c +=+211<n n n c c c m ++11,即1111n n c c m +->-.…… 12分 因此1122111)11()11()11(1c c c c c c c c m m m m m +-++-+-=--- mm m m 121+=+-->. 所以11m m c m <<+. 故当m n ≤,恒有1<n c . …………………………………………………14分。
北京市朝阳区2012届高三上学期期末历史试题.doc
北京市朝阳区2012届高三上学期期末考试试题历史试题(考试时间90分钟,满分100分)一、选择题共32小题,每小题1.5分,共48分。
在下列各题的四个选项中,选出最符合题目要求的一项。
1.五四运动被称为创造一种新的现代的文明以挽救中国。
“新”的主要表现是()A.知识分子发挥着移风易俗的重要作用 B.激发人们强烈的民族意识和爱国热情C.弘扬科学和民主成为五四的精神核心 D.爱国主义与宣传马克思主义逐步结合2.“中国最初的共产主义支部是于1920年5月在上海和北京组织起来的”有的“党纲就是‘劳工专政,生产组合’八个字。
”上述材料表明()A.中国共产党的诞生B.建立无产阶级政权C.筹备工人阶级政党D.工农运动蓬勃开展3.孙中山在三民主义中提出“平均地权”“节制资本”其目的是()A.推动农工运动的开展,“辅助其经济组织”B.实现“土地国有后,必能耕者而后授其田”C.达成“盖民国之民权,唯民国之国民乃能享之”D.反对“少数人占经济之势力,垄断社会之财源”4.20世纪20 ~40年代,中国革命中心从珠江流域向黄河流域转移。
完成转移的直接因素有()A.北伐战争和红军长征B.北伐战争和抗日故争C.红军长征和抗日战争D.抗日战争和解放战争5.在土地革命历史时期,探索中国民主革命策略转变的文献是()A.《湖南农民运动考察报告》B.《中国的红色政权为什么能够存在?》C.《中国革命和中国共产党》D.《关于正确处理人民内部矛盾的问题》6.与中国共产党诞生初期相比,国共十年对峙时期共产党日渐成熟体现在A.认识到发动工人运动重要性B.建立以国共合作为基础的统一战线.C.提出共产党的民主革命纲领D.独立自主地探索中国革命发展道路7.对右面两则材料理解准确的是()①七七抗战揭开了全面抵抗的序幕②此战发生于相持阶段的正面战场③民族统一战线领导积极抗战的典范④反映国人对抗日英烈的敬重与纪念A.①②B.①③④C.①④D.②③④8.1939年1月在讨论建立陕甘宁边区参议会的问题上,毛泽东发表讲话指出“……而这民主又是苏维埃在现阶段的发展物,现在各阶级,工农商学兵各界都可参加参议会。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市朝阳区2012届高三上学期期末考试试题物理(考试时间90分钟满分100分)一、本题共13小题,每小题3分。
共39分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.很好地解释了α粒子散射实验并提出原子核式结构模型的科学家是()A.汤姆生B.爱因斯坦C.德布罗意D.卢瑟福2.用绿光照射一个光电管,能产生光电效应,欲使光电子从阴极逸出时最大初动能增大,可以()A.改用红光照射B.改用紫光照射C.增加绿光照射时间D.增加绿光照射强度3.图中P为放在匀强磁场中的天然放射源,其放出的射线在磁场的作用下分成a、b、c三束,以下判断正确的是()A.a为α射线、b为β射线、c为γ射线B.a为β射线、b为γ射线、c为α射线C.a为α射线、b为γ射线、c为β射线D.a为γ射线、b为α射线、c为β射线4.绝缘细线的一端与一带正电的小球M相连接,另一端固定在天花板上,在小球M下面的一绝缘水平面上固定了另一个带电小球N,在下列情况下,小球M能处于静止状态的是()5.2011年12月美国宇航局发布声明宣布,通过开普勒太空望远镜项目证实了太阳系外第一颗类似地球的、可适合居住的行星。
该行星被命名为开普勒一22b(Kepler一22b),距离地球约600光年之遥,体积是地球的2.4倍。
这是目前被证实的从大小和运行轨道来说最接近地球形态的行星,它每290天环绕着一颗类似于太阳的恒星运转一圈。
若行星开普勒一22b绕恒星做圆运动的轨道半径可测量,万有引力常量G已知。
根据以上数据可以估算的物理量有()A.行星的质量B.行星的密度C.恒星的质量D.恒星的密度6.质量为m 的汽车在平直公路上行驶,发动机的功率P 和汽车受到的阻力f 均恒定不变。
在时间t 内,汽车的速度由0v 增加到最大速度m v ,汽车前进的距离为s ,则在这段时间内可以表示发动机所做功W 的计算式为( )A .W Pt =B .W fs =C .2201122m W mv mv =-D .212m W mv fs =+7.正方形区域ABCD 中有垂直于纸面向里的匀强磁场,一个α粒子(不计重力)以一定速度从AB 边的中点M 沿既垂直于AB 边又垂直于磁场的方向射入磁场,正好从AD 边的中点N 射出。
若将磁感应强度B 变为原来的2倍,其他条件不变,则这个α粒子射出磁场的位置是( )A .A 点B .ND 之间的某一点C .CD 之间的某一点 D .BC 之间的某一点8.如图所示,电源内阻不可忽略。
开关S 闭合后,在变阻器R 0的滑动端向上滑动的过程中 ( )A .电压表与电流表的示数都增大B .电压表与电流表的示数都减小C .电压表的示数增大,电流表的示数减小D .电压表的示数减小,电流表的示数增大9.下表是一辆电动自行车的部分技术指标,参考表中数据判断以下说法正确的是( )A .自行车每秒钟消耗的电能为180JB .电动机每秒钟消耗的电能为180JC .电动机的内电阻为6ΩD .电动机的内电阻为1Ω10.如图所示,在水平方向的匀强电场中,一初速度为0v 的带电微粒沿着竖直平面内的直线由A 点运动到B 点的过程中,微粒的( )A .电势能一定减少,动能一定减少B .电势能一定增加,动能一定增加C .电势能一定减少,动能一定增加D .电势能一定增加,动能一定减少11.带电粒子(不计重力),以速度v 射入某一空间,下列说法正确的是( )A .如果空间只存在匀强电场,则带电粒子穿过该空间时,动能、动量一定发生变化B .如果空间只存在匀强磁场,则带电粒子穿过该空间时,动能、动量一定发生变化C .如果空间只存在匀强电场,则带电粒子穿过该空间时,动能可能不变、动量一定发生变化D .如果空间同时存在匀强电场和匀强磁场,则带电粒子穿过该空间时,动能和动量一定发生变化12.一个初动能为E 的小物块从斜面底端冲上足够长的斜面,返回斜面底端时速度大小为v ,该过程物体克服摩擦力做功为2E 。
若小物块冲上斜面的初动能变为2E ,则( )A .返回斜面底端时动能为34EB .返回斜面底端时动能为32EC .返回斜面底端时速度大小为2vD13.如图所示,若x 轴表示时间,y 轴表示速度,则该图像反映了质点做匀减速直线运动时,速度与时间的关系。
若x 轴和y 轴分别表示不同的物理量,则该图像可以反映某种情况下,相应的物理量之间的关系。
下列说法正确的是( )A .若x 轴表示时间,),轴表示重力势能,则该图像可表示自由落体运动物体的重力势能随时间变化的规律B .若x 轴表示时间,y 轴表示动量,则该图像可表示不计空气阻力情况下,竖直上抛物体在向上运动过程中,动量随时间变化的规律C .若x 轴表示时间,y 轴表示感应电动势,则该图像可表示闭合回路中磁感应强度随时间均匀减少时,闭合回路中感应电动势随时间变化的规律D .若x 轴表示时间,y 轴表示感应电流,则该图像可表示闭合回路中磁感应强度随时间均匀减少时,闭合回路中感应电流随时间变化的规律二、本题共3小题,共20分。
把答案填在答题纸相应的横线上。
14.(6分)在“探究共点力合成规律”的实验中,某同学经历了以下实验步骤:A .在白纸上按比例做出两个力F 1和F 2的图示,根据平行四边形定则作图求出合力F ;B .只用一个测力计,通过细绳把橡皮筋拉同样长度;C .记下两个测力计F 1和F 2的读数,并且记录它们的方向;D .在水平放置的木板上,垫一张白纸,把橡皮筋的一端固定在板上P 点,用两条细绳连接在橡皮筋的另一端,通过细绳同时用两个测力计互成角度地拉橡皮筋,使橡皮筋与细绳的连接点到达某一位置O ,并记下此位置,如图所示;E .记下测力计的读数F '和细绳方向,按同一比例做出这个力的图示,比较这个实测合力F '和按平行四边形定则求出的合力F ,看它们的大小和方向是否相近;F .改变两测力计拉力的大小和方向,多次重复实验,从实验得出结论。
(1)上述实验步骤中有一步骤有明显的错误,这个步骤是 (填选项前的字母); 正确的操作应为 。
(2)将以上实验步骤按正确顺序排列,应为 (填选项前的字母)。
15.(6分)如图所示,若多用电表的选择开关处于下表中所指的挡位,请在答题纸的表格中填出相应的读数。
16.(8分)某兴趣小组利用拉力传感器和速度传感器“验证动能定理”。
如图。
他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连接,用拉力传感器记录小车受到拉力的大小。
在水平桌面上相距50.0cm 的A 、B 两点各安装一个速度传感器,记录小车通过A 、B 两点的速度大小。
小车中可以放置砝码。
下表是他们测得的数据,其中M 是小车、砝码和拉力传感器的总质量,2221||v v 是两个速度传感器记录的速度的平方差,可以据此计算出M 的动能变化量△E 。
F 是拉力传感器受到的拉力,W 是F 在A 、B 间所做的功。
(1)根据测量数据计算,表格中3E ∆= ;W 3= 。
(2)根据表中的数据,在坐标纸上标出3E ∆和W 3对应的数据点,并作出E W ∆-图线。
(3)E W ∆-图线没有通过原点的原因可能是 。
三、本题共5小题。
共41分。
解答应写出必要的文字说明、方程式和重要的演算步骤。
只写出最后答案的不能得分,有数值计算的题。
答案中必须明确写出数值和单位,g 取10m /s 2。
把答案填在答题纸相应的空白处。
17.(6分)如图所示,质量m=2.0kg 的物体在恒力F=20N 作用下,由静止开始沿水平面运动 1.0x m =,力F 与水方向的夹角37α=︒’,物体与水平面间的动摩擦因数μ=0.5,求该过程中:(sin 370.6,cos370.8︒=︒=)(1)拉力F 对物体所做的功W ;(2)地面对物体的摩擦力f 的大小;(3)物体获得的动能k E 。
18.(6分)如图所示,质量为m的小球B,用长为l的细绳吊起处于静止状态,质量为m 的A球沿半径为l的光滑1/4圆弧轨道,在与O点等高位置由静止释放,A球下滑到最低点与B球相碰,若A球与B球碰撞后立刻粘合在一起,求:(1)A球下滑到最低点与B球相碰之前瞬间速度v的大小;(2)A球与B球撞后粘合在一起瞬间速度v共共的大小;(3)A球与B球撞后的瞬间受到细绳拉力F的大小。
19.(7分)如图所示为质谱仪的原理图,电荷量为q、质量为m的带正电的粒子从静止开始经过电势差为U的加速电场后,进入粒子速度选择器,选择器中存在相互垂直的匀强电场和匀强磁场,匀强电场的场强为E,方向水平向右。
带电粒子能够沿直线穿过速度选择器,从G点既垂直直线MN又垂直于磁场的方向射人偏转磁场。
偏转磁场是一个以直线MN为边界、方向垂直纸面向外的匀强磁场。
带电粒子经偏转磁场后,最终达到照相底片的H点。
已知偏转磁场的磁感应强度为B2,带电粒子的重力可忽略不计。
求:(1)粒子从加速电场射出时速度v的大小;(2)粒子速度选择器中匀强磁场的磁感应强度B1的大小和方向;(3)带电粒子进入偏转磁场的G点到照相底片H点的距离L。
20.(10分)质量M=3.0kg的长木板置于光滑水平面上,木板左侧放置一质量m=1.0kg 的木块,右侧固定一轻弹簧,处于原长状态,弹簧正下方部分的木板上表面光滑,其它部分的木板上表面粗糙,如图所示。
现给木块04.0/v m s的初速度,使之向右运动,在木板与木块向右运动过程中,当木板和木块达到共速时,木板恰与墙壁相碰,碰撞过程时间极短,木板速度的方向改变,大小不变,最后木块恰好在木板的左端与木板相对静止。
求:v;(1)木板与墙壁相碰时的速度1E;(2)整个过程中弹簧所具有的弹性势能的最大值pm2l。
(12分)两根相距L=0.5m的足够长的金属导轨如图甲所示放置,他们各有一边在同一水平面上,另一边垂直于水平面。
金属细杆ab、cd的质量均为m=50g,电阻均为R=1.0Ω,它们与导轨垂直接触形成闭合回路,杆与导轨之间的动摩擦因数μ=0.5,导轨电阻不计。
整个装置处于磁感应强度大小B=1.0T、方向竖直向上的匀强磁场中。
当ab 杆在平行于水平导轨的拉力F作用下沿导轨向右运动时,从某一时刻开始释放cd杆,v随时间变化的图像如图乙所示(在0~1.0s和2.0~3.0s 并且开始计时,cd杆运动速度cd内,cd做匀变速直线运动)。
(1)求在0~1.0s时间内,回路中感应电流的大小;(2)求在0~3.0s时间内,ab杆在水平导轨上运动的最大速度;(3)已知1.0~2.0s内,ab杆做匀加速直线运动,在图丙中画出在0~3.0s内,拉力F随时间变化的图像。
(不需要写出计算过程,只需画出图线)。
