七年级数学下册第四章三角形4.1认识三角形4.1.2认识三角形课件
合集下载
北师大版七年级数学下册第四章《认识三角形》公开课课件(共14张PPT)
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/7/222021/7/222021/7/222021/7/227/22/2021
14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年7月22日星期四2021/7/222021/7/222021/7/22
(1)当∠A=50°时,求∠BIC; (2)当∠BIC=130°时,求∠A.
A
DI E
C
B
12
概要
通过折纸、画图等活动，体验并获得了三角形的“角平 分线”、“中线”的概念与性质。
在三角形中，一个内角的平分 线与它的对边相交，
A 12
这个角的顶点与交点之间的
线段 叫三角形的角平分线。
B
∠1=∠D2
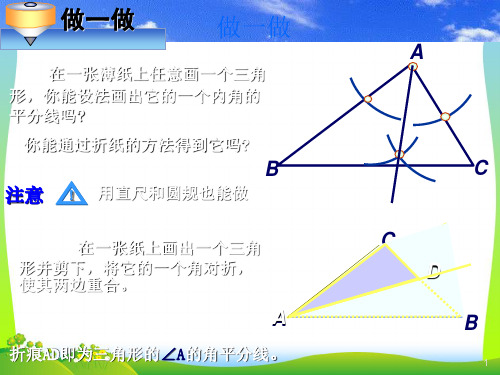
做一做
做一做
在一张薄纸上任意画一个三角 形，你能设法画出它的一个内角的 平分线吗?
你能通过折纸的方法得到它吗?
B 注意 ! 用直尺和圆规也能做
在一张纸上画出一个三角 形并剪下，将它的一个角对折， 使其两边重合。
A
折痕AD即为三角形的∠A的角平分线。
A
C C
D B
1
三角形的角平分线的定义
以前所学的“角平分线”是一条射线，
7
分别指出图5—13中△ABC 的三条高。 A A
D
F
B
C
D
B
C
图5—13
E
直角边BC边上的
高是 AB
;
直角边AB边上的
高是 CB
;
AB边上的高是: CE BC边上的高是: AD CA边上的高是：BF
七年级数学下册 第四章 三角形 4.1 认识三角形(第2课时)课件下册数学课件
为 世纪金榜导学号( ) C
A.12
B.16
C.20
D.16或20
第二十页，共二十九页。
【火眼金睛】
等腰三角形的一边(yībiān)长为4,另一边长为5,求周长.
第二十一页，共二十九页。
【正解】当腰长为4时,三角形三边分别(fēnbié)为4,4,5, 因为4+4=8>5,所以能构成三角形,此时周长为13, 当腰长为5时,三角形三边分别为4,5,5, 因为4+5=9>5,所以能构成三角形,此时周长为14. 综上可知,周长为13或14.
C.45°
D.60°
第十八页，共二十九页。
★2.若等腰三角形的周长为10 cm,其中一边(yībiān)长为2 cm,
则该等腰三角形的底边长为 ( )
A
A.2 cm B.4 cm C.6 cm D.8 cm
第十九页，共二十九页。
★3.一个等腰三角形的两边长分别(fēnbié)为4,8,则它的周长
第二十六页，共二十九页。
【变式二】若a=4,b=6.三角形的周长(zhōu chánɡ)是小于16的偶数. (1)求第三边c的长. (2)求△ABC的周长.
第二十七页，共二十九页。
解:(1)因为a,b,c是△ABC的三边,a=4,b=6,
所以(suǒyǐ)2<c<10,
因为三角形的周长是小于16的偶数, 所以2<c<6, 所以c=4. (2)当c=4时,△ABC的周长为4+6+4=14.
第十一页，共二十九页。
【题组训练】
1.(2019·滨海县期中)已知三根木棒中有两根长分别
是20厘米和30厘米,用这三根木棒恰好(qiàhǎo)能钉成一个三
认识三角形课件数学北师大版七年级下册
解：因为∠A＝∠B＋20°，∠C＝ ∠A＋50°，
所以∠C＝∠B＋20°＋50° ＝ ∠B＋70°.
因为∠A＋ ∠B＋ ∠C ＝180°，
所以∠B ＋20°＋∠B＋70°＋∠B＝180°.
所以∠B＝30°. 所以∠A＝50°，∠C ＝100°.
知识点 3 直角三角形的性质
1. 三角形按内角的大小分类
锐角三角形
三角形
直角三角形
钝角三角形
分类示意图如图4-1-4.
知3－讲
知3－讲
2. 直角三角形的表示 直角三角形可以用符号“Rt △”表
示，直角三角形ABC 可以写成Rt △ ABC.
注意：“Rt △”后必须紧跟表示直角三角形的三个
顶点的大写字母，不能单独使用．如“直角三角形的边”
不能写成“Rt △的边”.
在△ ABE 中，
6
∠B
AE 所对的角是_____，
∠ BAE 所对的边是_____
BE .AD
∠AED
在△ ADE 中是________所对的边，
在△ ADC 中是
_______所对的边.
∠C
知识点 2 三角形内角和定理
知2－讲
1. 定理 三角形三个内角的和等于180° .
几何语言：在△ ABC 中，∠ A+ ∠ B+ ∠ C=180° .
时，一般根据三角形内角和
所以n+2n+3n=180，解得n=30.
为180°列方程求解.
所以∠ A=30°，∠ B=60°，∠ C=90°.
知2－练
2-1. 在△ ABC 中， 若∠A=60°，∠ B ∶∠C=2∶1，则
∠ B等于( D )
A. 10°
七年级数学认识三角形ppt课件
三角形在数学建模中的应用举例
利用三角形解决实际问题
01
如测量高度、距离等，通过构建三角形模型进行求解。
三角形在几何变换中的应用
02
通过三角形的性质研究平移、旋转、对称等几何变换。
三角形在函数图像中的应用
03
利用三角形的性质研究一次函数、二次函数等图像的性质。
提高解题能力，培养创新思维
01
掌握三角形的基本性质和定理
七年级数学认识三角形ppt课 件
目录
• 三角形基本概念与性质 • 三角形边长与角度关系 • 三角形全等与相似 • 解直角三角形及其应用 • 三角形面积计算与拓展 • 三角形综合应用与拓展延伸
01
三角形基本概念与性质
三角形的定义及分类
三角形的定义
由三条线段首尾顺次连接而成的图 形。
三角形的分类
按边可分为等边三角形、等腰三角 形和一般三角形；按角可分为锐角 三角形、直角三角形和钝角三角形。
如果三角形的三边长a，b，c满足a² + b² = c²，那么这个三角 形是直角三角形。
03
三角形全等与相似
全等三角形定义及判定方法
01
02
03
04
05
定义
SSS（三边全等） SAS（两边和夹角 ASA（两角和夹 AAS（两角和一
全等）
边全等）
边全等）
能够完全重合的两个三角形 叫做全等三角形。
三边对应相等的两个三角形 全等。
面积法在几何问题中的应用
面积法求线段长
通过构造相似三角形，利 用面积比求出线段长。
面积法证线段相等
通过证明两个三角形面积 相等，从而证明两条线段 相等。
面积法证线段平行
北师大版数学七年级下册 4.1认识三角形 课件ppt 共4份打包)
三条中线， 交于一点
(2)钝角三角形和直角三角形的中线又是怎样的？ 折一折，画一画，并与同伴交流.
归纳：三角形的三条中线交于一点，这个交点就 是三角形的重心.
例1 在△ABC中，AC＝5cm，AD是△ABC的中 线，若△ABD的周长比△ADC的周长大2cm， 则BA＝__7_c_m____.
提示：将△ABD与△ADC的周长之差转化为 边长的差.
的正误.
A
（1）AD是△ABE的角平分线( × )
（2）BE是△ABD边AD上的中线( ×)
12 E
（3）BE是△ABC边AC上的中线( √ ) F
G
H
B
D
C
4.在ΔABC中,CD是中线,已知BC－AC=5cm,ΔDBC
的周长为25cm,求ΔADC的周长.
A
解：因为CD是△ABC的中线，
D
所以BD＝AD，
第3课时 三角形的中线、角平分线
1 三角形的中线
三角形的“中线”
在三角形中，连接一个顶
点与它对边中点的线段，叫作
这个三角形的中线(median).
AE是BC边上的中线.
B
A
C E BE=EC
议一议 (1)在纸上画出一个锐角三角形，确定它的中线.
你有什么方法？它有多少条中线？它们有怎样的 位置关系?
小结
中线：连接三角形的顶 点与对边中点的线段.
三角形中几条 重要线段
角平分线：平分内角且与 三角形对边相交的线段.
2 三角形的角平分线
思考 在一张薄纸上任意画一个三角形，你能设
法画出它的一个内角的平分线吗?你能通过折 纸的方法得到它吗?
A 用量角器画最简便，用圆规也能.
在一张纸上画出一个 B 一个三角形并剪下，将它 的一个角对折，使其两边 重合.
(2)钝角三角形和直角三角形的中线又是怎样的？ 折一折，画一画，并与同伴交流.
归纳：三角形的三条中线交于一点，这个交点就 是三角形的重心.
例1 在△ABC中，AC＝5cm，AD是△ABC的中 线，若△ABD的周长比△ADC的周长大2cm， 则BA＝__7_c_m____.
提示：将△ABD与△ADC的周长之差转化为 边长的差.
的正误.
A
（1）AD是△ABE的角平分线( × )
（2）BE是△ABD边AD上的中线( ×)
12 E
（3）BE是△ABC边AC上的中线( √ ) F
G
H
B
D
C
4.在ΔABC中,CD是中线,已知BC－AC=5cm,ΔDBC
的周长为25cm,求ΔADC的周长.
A
解：因为CD是△ABC的中线，
D
所以BD＝AD，
第3课时 三角形的中线、角平分线
1 三角形的中线
三角形的“中线”
在三角形中，连接一个顶
点与它对边中点的线段，叫作
这个三角形的中线(median).
AE是BC边上的中线.
B
A
C E BE=EC
议一议 (1)在纸上画出一个锐角三角形，确定它的中线.
你有什么方法？它有多少条中线？它们有怎样的 位置关系?
小结
中线：连接三角形的顶 点与对边中点的线段.
三角形中几条 重要线段
角平分线：平分内角且与 三角形对边相交的线段.
2 三角形的角平分线
思考 在一张薄纸上任意画一个三角形，你能设
法画出它的一个内角的平分线吗?你能通过折 纸的方法得到它吗?
A 用量角器画最简便，用圆规也能.
在一张纸上画出一个 B 一个三角形并剪下，将它 的一个角对折，使其两边 重合.
4.1认识三角形 第二课时-七年级数学下册课件(北师大版)
数，所以x 的值只能是4或6，所以三角形的第三边Байду номын сангаас长
是4或6.
总结
通过多个条件确定三角形第三边的方法：
已知两边
第三边的范围
第三边小于已知两边的 和而大于已知两边的差
附加条件
确定第 三边
1 三角形两边长分别为3和5，第三边的长可以是8吗？ 可以是2吗？说说你的理由.
解：不可以是8，也不可以是2.理由：三角形任意两 边之和大于第三边，任意两边之差小于第三边．
④三角形按角分类应分为锐角三角形、直角三角形和
钝角三角形．其中正确的有( C )
A．1个
B．2个
C．3个
D．4个
知识点 3 三角形的三边关系
议一议 (1)元宵节的晚上，房梁
上亮起了彩灯(如图)， 装有黄色彩灯的电线 与装有红色彩灯的电线哪根长呢？说明你的理由. (2)在一个三角形中，任意两边之和与第三边的长度有 怎样的关系？为什么？
则该等腰三角形的底边长为( A )
A．2 cm
B．4 cm
C．6 cm
D．8 cm
2 如图，在△ABC 中，BC＝BA，点D 在AB上，且 AC＝CD＝DB，则图中的等腰三角形有( C )
A．1个 B．2个 C．3个 D．4个
3 △ABC 的三边长a，b，c 满足关系式(a－b )(b－c )(c－a )
归纳
三角形任意两边之和大于第三边.
做一做 分别量出(图4-14)三个三角形的三边长度，并填入空格内.
(1)a＝________， (2)a＝________， (3)a＝________， b＝________， b＝________， b＝________， c＝________， c＝________， c＝________，
初中初一数学认识三角形PPT课件pptx
01三角形定义02三角形分类由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形。
按边可分为不等边三角形、等腰三角形；按角可分为锐角三角形、直角三角形、钝角三角形。
三角形定义及分类三角形内角和定理三角形内角和定理三角形的三个内角之和等于180°。
推论直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角之和；三角形的一个外角大于任何一个和它不相邻的内角。
三角形外角性质三角形外角性质三角形的一个外角等于与它不相邻的两个内角的和；三角形的一个外角大于与它不相邻的任一内角。
应用利用外角性质求角度；利用外角性质证明两直线平行。
等腰、等边三角形特性等腰三角形特性两腰相等，两底角相等；顶角的平分线、底边上的中线、底边上的高互相重合（三线合一）。
等边三角形特性三边相等，三个内角都相等且均为60°；任意两边之和大于第三边；任意一边都大于另外两边之差。
SAS全等条件及应用举例SAS全等条件两边和它们之间的夹角对应相等的两个三角形全等。
应用举例在证明两个三角形全等时，如果已知两边及夹角相等，可以直接应用SAS条件进行证明。
03两角和它们的夹边对应相等的两个三角形全等。
ASA 全等条件两角和其中一个角的对边对应相等的两个三角形全等。
AAS 全等条件在证明两个三角形全等时，如果已知两角及夹边或两角及一边相等，可以分别应用ASA 或AAS 条件进行证明。
应用举例ASA 与AAS 全等条件SSS全等条件及证明过程SSS全等条件三边对应相等的两个三角形全等。
证明过程通过构造辅助线或利用已知条件，证明两个三角形的三边分别对应相等，从而得出两个三角形全等的结论。
HL直角三角形全等条件HL全等条件一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应相等，则这两个直角三角形全等。
应用举例在证明两个直角三角形全等时，如果已知斜边和一条直角边相等，可以直接应用HL条件进行证明。
判定方法两角对应相等，则两三角形相似。
北师大版数学七年级下册 4.1认识三角形 ppt 共4份打包)
解：因为AD是△ABC的角平分线，∠BAC＝60°， 所以∠DAC＝∠BAD＝30°. 因为CE是△ABC的高，∠BCE＝40°， 所以∠B＝50°， 所以∠ADB＝180°－∠B－∠BAD
＝180°－30°－50° ＝100°.
1.下列各组图形中，哪一组图形中AD是△ABC 的高( D )
C AD
=50°. 所以AE是△ABC的角平分线，且∠BAC=82°， 所以∠CAE=41°， 所以∠DAE=∠DAC－∠CAE=50°－41°= 9°.
小结
高的定义
三角形的高
高的性质
锐角三角形的三条高 都在三角形的内部.
直角三角形的三条高 交于直角顶点.
钝角三角形的三条高 所在直线交于一点.
它们有怎样的位置关系？
(2) AC边上的高是 BD ;
直角边BC边上的高是 AB ; B
C
直角边AB边上的高是 BC ;
直角三角形的三条高交于直角顶点.
钝角三角形的三条高
A
(1) 你能画出钝角三角形的三条
高吗？
F
D
B
Байду номын сангаас
C
E
(2) AC边上的高呢？AB边上呢？ BC边上呢？
BF
CE
AD
A
(3)钝角三角形的三条高
一个三角形有三个顶点， 应该有三条高.
锐角三角形的三条高
(1) 你能画出这个三角形的三条高吗? 如图所示；
(2) 这三条高之间有怎样的位置关系？
O
锐角三角形的三条高交于同一点；
(3) 锐角三角形的三条高是在三角 形的内部还是外部?
锐角三角形的三条高都在三角形的内部.
直角三角形的三条高
A
＝180°－30°－50° ＝100°.
1.下列各组图形中，哪一组图形中AD是△ABC 的高( D )
C AD
=50°. 所以AE是△ABC的角平分线，且∠BAC=82°， 所以∠CAE=41°， 所以∠DAE=∠DAC－∠CAE=50°－41°= 9°.
小结
高的定义
三角形的高
高的性质
锐角三角形的三条高 都在三角形的内部.
直角三角形的三条高 交于直角顶点.
钝角三角形的三条高 所在直线交于一点.
它们有怎样的位置关系？
(2) AC边上的高是 BD ;
直角边BC边上的高是 AB ; B
C
直角边AB边上的高是 BC ;
直角三角形的三条高交于直角顶点.
钝角三角形的三条高
A
(1) 你能画出钝角三角形的三条
高吗？
F
D
B
Байду номын сангаас
C
E
(2) AC边上的高呢？AB边上呢？ BC边上呢？
BF
CE
AD
A
(3)钝角三角形的三条高
一个三角形有三个顶点， 应该有三条高.
锐角三角形的三条高
(1) 你能画出这个三角形的三条高吗? 如图所示；
(2) 这三条高之间有怎样的位置关系？
O
锐角三角形的三条高交于同一点；
(3) 锐角三角形的三条高是在三角 形的内部还是外部?
锐角三角形的三条高都在三角形的内部.
直角三角形的三条高
A
《认识三角形》优秀课件pptx
应用：判断三条线段能否构成三角形、求三角形周长取值范围等
三角形内心、外心、重心概念
内心
三角形内切圆的圆心， 到三角形三边距离相等
外心
三角形外接圆的圆心， 到三角形三个顶点距离 相等
重心
三角形三条中线的交点 ，具有将三角形面积平 分等性质
塞瓦定理和梅内劳斯定理简介
塞瓦定理
在一个三角形中，如果有三条过顶点且与对边有交点的线， 那么这三个交点是共线的当且仅当三条线的交点与对应顶点 的连线满足一定的比例关系
适用范围
适用于所有已知三边长的三角形面 积计算。
三角形面积与边长关系
等底等高原则
若两个三角形底边相等且高相等 ，则它们的面积相等。
边长比例关系
对于相似三角形，其面积之比等 于对应边长之比的平方。
三角形不等式
任意两边之和大于第三边，任意 两边之差小于第三边，与面积大
小有一定关联。
实际应用问题举例
土地测量
《认识三角形》优秀 课件pptx
目录
• 三角形基本概念与性质 • 三角形边角关系探究 • 三角形面积计算方法 • 三角形在生活中的应用 • 三角形相关数学问题解析 • 创新思维与拓展训练
01
三角形基本概念与性质
三角形定义及分类
三角形定义
由不在同一直线上的三条线段首 尾顺次相接所组成的图形。
三角形分类
01
在三角形中，当角度发生变化时，与之对应的边长也会发生变
化。
边长变化对角度的影响
02
在三角形中，当边长发生变化时，与之对应的角度也会发生变
化。
角度与边长的相互制约关系
03
在三角形中，角度与边长之间存在着相互制约的关系，即当一
个量发生变化时，另一个量也会随之变化。
三角形内心、外心、重心概念
内心
三角形内切圆的圆心， 到三角形三边距离相等
外心
三角形外接圆的圆心， 到三角形三个顶点距离 相等
重心
三角形三条中线的交点 ，具有将三角形面积平 分等性质
塞瓦定理和梅内劳斯定理简介
塞瓦定理
在一个三角形中，如果有三条过顶点且与对边有交点的线， 那么这三个交点是共线的当且仅当三条线的交点与对应顶点 的连线满足一定的比例关系
适用范围
适用于所有已知三边长的三角形面 积计算。
三角形面积与边长关系
等底等高原则
若两个三角形底边相等且高相等 ，则它们的面积相等。
边长比例关系
对于相似三角形，其面积之比等 于对应边长之比的平方。
三角形不等式
任意两边之和大于第三边，任意 两边之差小于第三边，与面积大
小有一定关联。
实际应用问题举例
土地测量
《认识三角形》优秀 课件pptx
目录
• 三角形基本概念与性质 • 三角形边角关系探究 • 三角形面积计算方法 • 三角形在生活中的应用 • 三角形相关数学问题解析 • 创新思维与拓展训练
01
三角形基本概念与性质
三角形定义及分类
三角形定义
由不在同一直线上的三条线段首 尾顺次相接所组成的图形。
三角形分类
01
在三角形中，当角度发生变化时，与之对应的边长也会发生变
化。
边长变化对角度的影响
02
在三角形中，当边长发生变化时，与之对应的角度也会发生变
化。
角度与边长的相互制约关系
03
在三角形中，角度与边长之间存在着相互制约的关系，即当一
个量发生变化时，另一个量也会随之变化。
北师大版七年级数学下册认识三角形课件
如图，已知△ABC，点D为BC延长线上一点，试探究∠A+∠B与 ∠ACD有怎样的数量关系，并说明理由.
A
B CD
5.三角形外角和定理：三角形外角等于和它不相邻的两内角和.
1.如图所示：∠1+∠2+∠3+∠4+∠5+∠6等于 360 度.
1 6
2
3
5
2.在△ABC中，
4
（1）C 70,A 50, 则 B 60 ；
（ ✔） （ ✔） （ ✔） （ ✔）
（ ❌）
变式2：在△ABC中，∠A:∠B：∠C=2：3：4，求三角形各内角度数.
例2
1.什么叫三角形？
A
2.如何表示三角形？
3.三角形的顶点、角、边可以怎么表示？
B
C
4.三角形内角和定理：三角形三个内角的和等于180° 符号语言：三在△ABC中，∠A+∠B+∠C=180°
1、如右图，
（1）图中共有 5 个三角形， 分别是 ADE, AEB, BCE，ACB, ADB ；
D
E
C
（2）其中，以AEB, ADB, ABC ；
(3)以C为一个内角的三角形有 2 个，分别
是 CEB, CAB ，D对边有 AE, AB .
A
B
C
4.三角形内角和定理：三角形三个内角的和等于180° 符号语言：在△ABC中，∠A+∠B+∠C=180°
5.三角形外角和定理：三角形外角等于和它不相邻的两内角和.
6.三角形的分类：①按角分类；②按边分类.
已知：如图，∠A=65°，∠B=25°，∠C=40°，求∠D的度数.
A
B
D
C
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
C
BC AC AB
AB+BC AC+BC
B
c
(2)在一个三角形中,任意两边之和与第三边的 长度有怎样的关系?为什么?由此你能得到什么结论?
议一议
A
C B
在A点的小狗，为了尽快吃到B点的香肠，它选 择A—B路线，而不选择A—C—B路线，难道小狗也懂 数学？ 验证
三角形任意两边之和大于第三边
分别量出下面三个三角形的三边长度，并填入空 格内。
a
a= b= c=
b c
， ， 。
a
a= b= c=
b
a
b
， ， 。，并与第三边 比较，你能得到什么结论？ 任意三角形的两边之差，小于第三边 验证
a= b= c=
c
有两根长度分别为5cm和8cm的木棒，用长度为 2cm的木棒与它们能摆成三角形吗？为什么？长度为 13cm的木棒呢？动手摆一摆。
解题技巧三角形第三边的取值范围是:
两边之差<第三边<两边之和
1．用两根长度分别为4㎝和7㎝的两根木棒, （1）用长度为2 ㎝的木棒能与它们组成三角形 吗?为什么? （2）用长度为11㎝的木棒呢? （3）如果第三边是正整数,那么第三边可能是 哪几个数? 2、三条线段的长度分别为： （1）3、8、10 （ 2） 5、 2 、 7 （3）5、5、11 （4）13、12、20 能组成三角形的有（ ）组
三角形三边之间的关系
很高兴，和同学们度 过了愉快的一节课
再见
初中数学;七年级(下册)
4.1.2 ; 认识三角形;
知识回顾
由不在同一直线上的三条线段首尾顺次相接所组
成的图形叫做三角形（triangle）。 三角形可以用符号“”表示，如上图是顶点为 A,B,C的三角形，记作“ABC”.它的三边有时也 用a,b,c来表示。 A
c
b
B
a
C
若将方屋顶的框架图抽象成一个几何图形，标 出字母，请聪明的你尽可能多的表示这些三角形。
A
F B D E G
C
看一看 想一想
观察下面的三角形，你能发现它们各自的边长之 间有什么关系吗？
有两边相等的三角形叫做等腰三角形，如图 三边都相等的的三角形叫做等边三角形，也 叫正三角形
顶角
腰
腰
底角
底边
底角
A B A B A
(1) 元宵节的晚上，房梁上亮起 了彩灯，装有黄色彩灯的电线与装有 红色彩灯的电线哪根长呢？说明你的 理由。 C 利用你发现的规律填空 AB+AC
BC AC AB
AB+BC AC+BC
B
c
(2)在一个三角形中,任意两边之和与第三边的 长度有怎样的关系?为什么?由此你能得到什么结论?
议一议
A
C B
在A点的小狗，为了尽快吃到B点的香肠，它选 择A—B路线，而不选择A—C—B路线，难道小狗也懂 数学？ 验证
三角形任意两边之和大于第三边
分别量出下面三个三角形的三边长度，并填入空 格内。
a
a= b= c=
b c
， ， 。
a
a= b= c=
b
a
b
， ， 。，并与第三边 比较，你能得到什么结论？ 任意三角形的两边之差，小于第三边 验证
a= b= c=
c
有两根长度分别为5cm和8cm的木棒，用长度为 2cm的木棒与它们能摆成三角形吗？为什么？长度为 13cm的木棒呢？动手摆一摆。
解题技巧三角形第三边的取值范围是:
两边之差<第三边<两边之和
1．用两根长度分别为4㎝和7㎝的两根木棒, （1）用长度为2 ㎝的木棒能与它们组成三角形 吗?为什么? （2）用长度为11㎝的木棒呢? （3）如果第三边是正整数,那么第三边可能是 哪几个数? 2、三条线段的长度分别为： （1）3、8、10 （ 2） 5、 2 、 7 （3）5、5、11 （4）13、12、20 能组成三角形的有（ ）组
三角形三边之间的关系
很高兴，和同学们度 过了愉快的一节课
再见
初中数学;七年级(下册)
4.1.2 ; 认识三角形;
知识回顾
由不在同一直线上的三条线段首尾顺次相接所组
成的图形叫做三角形（triangle）。 三角形可以用符号“”表示，如上图是顶点为 A,B,C的三角形，记作“ABC”.它的三边有时也 用a,b,c来表示。 A
c
b
B
a
C
若将方屋顶的框架图抽象成一个几何图形，标 出字母，请聪明的你尽可能多的表示这些三角形。
A
F B D E G
C
看一看 想一想
观察下面的三角形，你能发现它们各自的边长之 间有什么关系吗？
有两边相等的三角形叫做等腰三角形，如图 三边都相等的的三角形叫做等边三角形，也 叫正三角形
顶角
腰
腰
底角
底边
底角
A B A B A
(1) 元宵节的晚上，房梁上亮起 了彩灯，装有黄色彩灯的电线与装有 红色彩灯的电线哪根长呢？说明你的 理由。 C 利用你发现的规律填空 AB+AC