全等三角形经典模型总结-5.2
八上全等三角形模型总结

八上全等三角形模型总结在初中数学学习中,我们经常会遇到各种几何形状的问题。
其中,三角形是最基本且重要的一种几何形状。
我们可以通过研究三角形的性质和特点来解决与之相关的问题。
而全等三角形模型是解决三角形问题的重要工具之一。
本文将以八上全等三角形模型为主题,总结全等三角形的定义、判定方法和一些相关的性质和定理。
一、全等三角形的定义全等三角形是指具有相同形状和大小的三角形。
也就是说,如果两个三角形的对应边长和对应角度都相等,那么这两个三角形就是全等三角形。
二、全等三角形的判定方法1. SSS判定法:如果两个三角形的三边分别对应相等,那么这两个三角形就是全等的。
2. SAS判定法:如果两个三角形的两边长和夹角对应相等,那么这两个三角形就是全等的。
3. ASA判定法:如果两个三角形的两个角度和夹边对应相等,那么这两个三角形就是全等的。
4. RHS判定法:如果两个直角三角形的斜边和一个锐角对应相等,那么这两个直角三角形就是全等的。
三、全等三角形的性质和定理1. 全等三角形的对应边和对应角相等。
2. 如果两个三角形的两边和夹角对应相等,那么这两个三角形是全等的。
3. 如果两个三角形的两个角度和夹边对应相等,那么这两个三角形是全等的。
4. 如果两个三角形的三边对应相等,那么这两个三角形是全等的。
5. 全等三角形的任意两边之间的夹角相等。
6. 全等三角形的任意两角之间的边长比相等。
7. 全等三角形的高线、中线、角平分线和垂直平分线都相等。
8. 全等三角形的面积相等。
四、全等三角形的应用全等三角形在几何问题中有着广泛的应用。
我们可以通过全等三角形来解决各种求角度、求边长以及证明等问题。
下面举例说明:例1:已知两个三角形的两边和夹角分别相等,证明这两个三角形是全等的。
解:根据全等三角形的性质,我们知道如果两个三角形的两边和夹角对应相等,那么这两个三角形是全等的。
所以,根据已知条件,我们可以得出这两个三角形是全等的。
例2:已知一个三角形的两边和夹角分别等于另一个三角形的两边和夹角,证明这两个三角形是全等的。
中考数学总复习全等三角形的五种模型

全等三角形的五种模型一、手拉手模型已知:△ABE和△ACD为两个的等腰三角形,∠BAE=∠CAD=∠α,连接EC,BD交于点O结论:①△ABD ≌△AEC;②∠α+∠BOC=180°;③OA平分∠BOC已知:△ABD和△ACE均为等腰直角三角形,连接CD,BE交于点O结论:①△ACD ≌△ABE;②∠BOC=90°;③OA平分∠BOC已知:直线AB的同一侧作△ABD和△BCE都为等边三角形,连接AE,CD,二者交点为H结论:①△ABE≌△DBC;②AE=DC;③∠DHA=60°;④△AGB≌△DFB;⑤△EGB≌△CFB;⑥连接GF,GF∥AC;⑦连接HB,HB平分∠AHC模型应用1. (2010·深圳改编)如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D 在AB上.(1)求证:△AOC≌△BOD;(2)判断△CAD是什么形状的三角形,说明理由.2.如图,△ABC与△ADE都是等腰直角三角形,连接CD,BE,CD,BE相交于点O,判断CD 与BE的位置关系,并说明理由半角模型已知:正方形ABCD中,E,F分别是BC,CD边上的点,且∠EAF=45°结论:将△ADF绕点A旋转90°到△ABG,则:①EF=DF+BE;②△CEF的周长为正方形ABCD周长的一半已知:正方形ABCD中,E,F分别是BC,CD边上的点,且∠EAF=45°结论:将△AEB绕点A为旋转90°到△ADE′,则:EF=DF-BE已知:在正方形ABCD中,AB=1,E,F分别是边BC,CD上的点,连接EF,AE,AF,过A 作AH⊥EF于点H,BE=EH结论:①△ABE≌△AHE;②△AHF≌△ADF;③∠EAF=45°;④EF=BE+DF模型应用3. (2015·深圳改编)如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE 折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③∠GDE=45°;④DG=DE.在以上4个结论中,正确的共有()A. 1个B. 2 个C. 3 个D. 4个4. 如图,在正方形ABCD中,AB=1,E,F分别是边BC,CD上的点,连接EF,AE,AF,过A作AH⊥EF于点H.若EF=BE+DF,那么下列结论:①AE平分∠BEF;②FH=FD;③∠EAF =45°;④S△EAF=S△ABE+S△ADF;⑤△CEF的周长为2.其中正确结论的个数是() A. 2 B. 3C. 4D. 5第三题第四题倍长中线模型已知:在△ABC 中,AD 是BC 边中线结论:延长AD 到E ,使DE =AD ,连接BE ,则:①△ADC ≌△EDB ;②AD< 21(AB +AC)已知:在△ABC 中,AD 是BC 边中线结论:作CF ⊥AD 于F ,作BE ⊥AD 的延长线于E ,连接BE ,则:①△BDE ≌△CDF ;②BE ∥FC模型应用6. 已知:在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE =AC ,延长BE 交AC 于F ,求证:AF =EF.一直线三垂直模型已知:AE=DE,AE⊥DE,∠B=∠C=90结论:①△ABE≌△ECD;②BC=AB+CD已知:在正方形ABCD中,∠ABF=∠C=90°,AF⊥BE,交于点H结论:①△ABF≌△BCE;②EC=AB-FC模型应用7. (2016·深圳改编)如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF 为正方形,过点F作FG∠CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S∠FAB∠S四边形CBFG=1∠2;③∠ABC=∠ABF.其中正确的结论的个数是()A.1B. 2C. 3D. 08. 如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③MD=2AM=4EM.其中正确的结论有()A. 0个B. 1个C. 2个D. 3个9. 如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE∠AG于点E,BF∠DE,交AG 于点F.给出以下结论:①∠AED∠∠BFA;②DE-BF=EF;③∠BGF∠∠DAE;④DE-BG=FG.其中正确的有()A. 1个B. 2个C. 3个D. 4个10. (2018·深圳)如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角且点E,A,B三点共线,AB=4,则阴影部分的面积是________.对角互补模型已知:已知∠AOB=∠DCE=90°,OC平分∠AOB结论模型应用11.(2012·深圳)如图,Rt∠ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形6,则另一直角边BC的长为________.对角线交于点O,连接OC,已知AC=5,OC=212. (2017·深圳)如图,在Rt∠ABC中,∠ABC=90°,AB=3,BC=4,Rt∠MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.。
全等三角形的10个模型(一)2024

全等三角形的10个模型(一)引言概述:全等三角形是指两个或多个三角形的对应边和对应角完全相等的情况。
全等三角形在几何学中有广泛的应用,不仅在证明和推导定理时起到重要的作用,还在实际问题的解决中提供了有力的工具。
本文将介绍十个关于全等三角形的模型。
这些模型旨在帮助读者更好地理解和运用全等三角形的性质和应用。
正文:1. 模型一:完全相等的三边- 全等三角形的基本条件就是三边相等。
- 通过边的对应关系确定两个三角形是否全等。
- 证明时可利用边长相等的性质进行推导。
2. 模型二:完全相等的两边和夹角- 如果已知两个三角形的两边和夹角都相等,则这两个三角形全等。
- 通过边角边(SAS)或角边角(ASA)的条件可以判定两个三角形相等。
3. 模型三:完全相等的两角和夹边- 如果已知两个三角形的两角和夹边都相等,则这两个三角形全等。
- 边角边(SAS)或角边角(ASA)的条件可以判定两个三角形相等。
4. 模型四:等腰三角形和全等条件- 等腰三角形是指两边相等或两角相等的三角形。
- 如果两个三角形中有一个是等腰三角形,且两个等腰三角形的两边或两角都相等,则这两个三角形全等。
5. 模型五:直角三角形和全等条件- 直角三角形是指其中一个角为90度的三角形。
- 如果两个三角形中有一个是直角三角形,且两个直角三角形的两边或两个锐角均相等,则这两个三角形全等。
总结:通过十个模型的介绍,我们可以看到全等三角形是几何学中一个重要而广泛应用的概念。
理解全等三角形的性质和应用对于解决几何问题具有重要意义。
在实际问题中,我们常常可以利用全等三角形的模型来推导和证明定理,从而得出更深入的结论。
全等三角形的相关模型总结概要

全等三角形的相关模型总结概要1、角平分线模型应用1、角平分性质模型:辅助线:过点G作GE射线AC(1)、例题应用:①如图1,在,那么点D到直线AB的距离是 cm、②如图2,已知,,、、图1 图2①2 (提示:作DEAB交AB于点E)②,,,,、(2)、模型巩固:练习一:如图3,在四边形ABCD中,BC>AB,AD=CD,BD平分、、求证:图3练习二:已知如图4,四边形ABCD中,图4练习三:如图5,交CD于点E,交CB于点F、(1)求证:CE=CF、(2)将图5中的△ADE沿AB向右平移到的位置,使点落在BC边上,其他条件不变,如图6所示,是猜想:于CF又怎样的数量关系?请证明你的结论、图5 图6练习四:如图7,,P是AB的中点,PD平分∠ADC、求证:CP平分∠DCB、ADECBP2143 图7练习五:如图8,AB>AC,∠A的平分线与BC的垂直平分线相交于D,自D作DE⊥AB,DF⊥AC,垂足分别为E,F、求证:BE=CF、图8练习六:如图9所示,在△ABC 中,BC边的垂直平分线DF交△BAC的外角平分线AD于点D,F为垂足,DE⊥AB于E,并且AB>AC。
求证:BE-AC=AE。
图9练习七:如图10,D、E、F分别是△ABC的三边上的点,CE=BF,且△DCE的面积与△DBF的面积相等,求证:AD平分∠BAC。
2、角平分线+垂线,等腰三角形比呈现辅助线:延长ED交射线OB于F 辅助线:过点E作EF∥射线OB(1)、例题应用:①、如图1所示,在△ABC中,∠ABC=3∠C,AD是∠BAC的平分线,BE⊥AD于F。
求证:证明:延长BE交AC于点F。
②、已知:如图2,在,分析:此题很多同学可能想到延长线段CM,但很快发现与要证明的结论毫无关系。
而此题突破口就在于AB=AD,由此我们可以猜想过C点作平行线来构造等腰三角形、证明:过点C作CE∥AB交AM的延长线于点E、例题变形:如图,,,求证:① ② (3)、模型巩固:练习一、如图3,ΔABC是等腰直角三角形,∠BAC=90,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E。
完整全等三角形的相关模型总结推荐文档
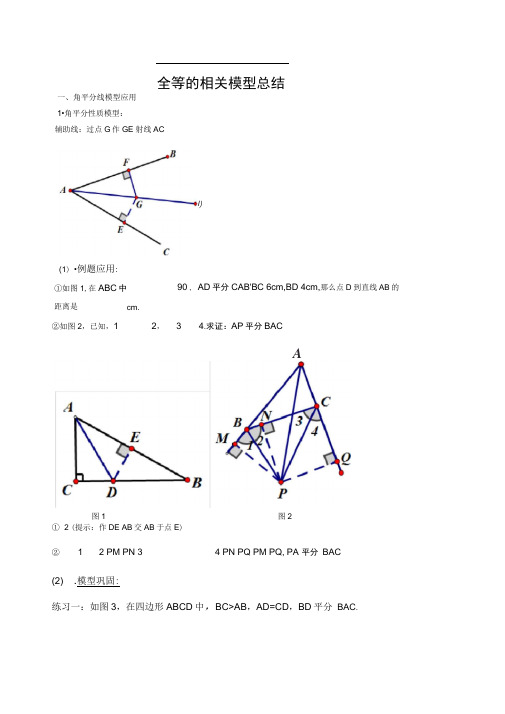
全等的相关模型总结一、角平分线模型应用 1•角平分性质模型:②如图2,已知,1 2, 3 4.求证:AP 平分BACA① 2 (提示:作DE AB 交AB 于点E )②1 2 PM PN 3 4 PN PQ PM PQ, PA 平分 BAC(2) .模型巩固:练习一:如图3,在四边形ABCD 中,BC>AB ,AD=CD ,BD 平分 BAC .①如图1,在ABC 中 距离是90°, AD 平分CAB'BC 6cm,BD 4cm,那么点D 到直线AB 的cm.I)(1) •例题应用: 辅助线:过点G 作GE 射线AC图1图2•求证: A C 180练习二:已知如图4,四边形ABCD中,B D 1800,BC CD•求证:AC平分BAD.练习三:如图5 Rt ABC中,ACB 90 , CD AB,垂足为D , AF平分CAB,交CD于点E 交CB于点F.(1)求证:CE=CF.(2)将图5中的△ ADE沿AB向右平移到ADE的位置,使点E落在BC边上,其他条件不变,如图6所示,是猜想:BE于CF又怎样的数量关系?请证明你的结论图5 图6练习四:如图7,/ A 90,AD // BC,P是AB的中点,PD平分/ ADC求证:CP 平分/ DCB图7练习五:如图 8, AB> AC / A 的平分线与 BC 的垂直平分线相交于 D,自D 作DE L AB, DF 丄AC,垂足 分别为E , F .求证:BE=CF图8练习六:如图9所示,在△ ABC 中,BC 边的垂直平分线 DF 交厶BAC 的外角平分线 AD 于点D , F 为垂足,DE 丄AB 于E ,并且 AB>AC 。
求证:BE — AC=AE 。
练习七: 如图10, D 、E 、F 分别是△ ABC 的三边上的点, CE=BF ,且△ DCE 的面积与厶 DBF 的面 积相等,求证:AD 平分/ BAC 。
全等三角形常见模型整理

全等三角形几何模型归纳总结《全等三角形几何模型归纳总结——那些年我们一起追的“全等”》嘿,各位小伙伴们!今天咱来唠唠全等三角形几何模型这档子事。
这可是咱在几何世界里摸爬滚打的一大法宝呀!全等三角形就像是一对双胞胎,长得一模一样,各种特征都完全相符。
咱和它们打交道的过程,那真是有苦有乐啊!就比如说那“手拉手”模型吧,就像是两个好兄弟手牵手一起走。
看到这种模型,咱就得赶紧瞪大眼睛,找到那关键的对应边和对应角,一旦弄清楚了,那解决问题就跟玩似的。
有时候我都感觉自己像是个小侦探,在各种图形里寻找线索呢!还有那个“一线三等角”模型,嘿,这可神奇了!一条线上面整出来三个等角,就像变魔术一样。
刚开始遇到的时候,还真有点摸不着头脑,心里直犯嘀咕:“这是啥玩意呀?”不过随着咱经验的积累,慢慢地也能看穿它的小把戏啦。
有时候碰到那些复杂的图形,感觉就像是掉进了一个大迷宫,找不着北。
但咱可不能气馁,得静下心来仔细分析分析,说不定就能找到那隐藏的全等三角形。
一旦找到了,就像是找到了迷宫的出口,那叫一个痛快!不过,也有犯迷糊的时候。
明明感觉能找到全等三角形,可就是差那么一点点,死活对不上。
这时候就恨不得给自己脑袋上敲两下,让自己清醒清醒。
但咱不能怕失败呀,失败是成功的妈妈嘛,多总结总结经验,下次咱就能一眼看穿啦。
在这个过程中,咱也得学会和小伙伴们一起探讨。
有时候自己一个人苦思冥想半天,还不如小伙伴的一句话点拨呢。
这样大家一起研究,一起进步,多有意思呀!全等三角形几何模型就是咱几何世界里的宝藏,等着咱去挖掘。
虽然有时候会遇到困难,但每次突破难关的时候,那种成就感真是无与伦比。
所以呀,大家可别小瞧了这些模型,好好研究它们,咱就能在几何的海洋里畅游啦!让我们一起加油,把全等三角形几何模型玩得团团转!哈哈!。
全等三角形模型最全面汇总

全等三角形几何模型时间:2020.03.12编辑:陆海霞知识回顾PART ONE全等三角形知识回顾一般三角形直角三角形判定边角边(SAS)角边角(ASA)角角边(AAS)边边边(SSS)两直角边对应相等一边一锐角对应相等斜边、直角边定理(HL)性质对应边相等,对应角相等(其他对应元素也相等,如对应边上的高相等)备注判定三角形全等必须有一组对应边相等全等三角形知识点基础模型PART TWO全等三角形基础模型模型细分PART THREE123456(1)BP、CP分别是∠ABC、∠ACE的角平分线,则∠P=90+12∠ (1)BP、CP分别是∠ABC、∠ACE的角平分线,则∠P=12∠ (1)BP、CP分别是∠CBD、∠BCE的角平分线,则∠P=90−12∠[模型特征] :过等腰直角A的直角顶点或者正方形的一条直线。
[解题思路]:过等腰直角A的另外两个顶点作该直线的垂线段,会有两个全等三角形( AAS)△ABE≌△BCDED=AE-CD△ABE≌△BCDEC=AB-CD△ABE≌△BCDBC=BE+ED=A B+CD同侧:点P在线段AB上异侧:点P在线段AB延长线上变式:将A的中线延长一倍构造全等三角形,利用的思维模式是全等变换中的“旋转”。
此法多用于构造全等△(通常用“SAS"证明)和证明边之间的关系(将不在同一个三角形里的边转移到同一个三角形,从而利用三边关系证明)模型常用于:证明三条线段长度的“和”或“差”及其比例关系。
[模型特征] :两个等腰A或者两个等边三角形有一个公共的点。
[解题思路] :首先证明两个三角形全等( SAS,A为公共点所在的角)。
如果要求角的度数的话,通过求该角所在的A中另外两个角之和。
1)遇60'旋60",造等边三角形 2)遇90°旋90,造等腰直角3)遇等腰旋顶角,造旋转全等 4)遇中点旋180',造中心对称1、△ABE和△ACF均为等边三角形结论:(1)△ABF≌△AEC .(2)∠BOE=∠BAE=60° .(3)OA平分∠EOF .(四点共圆证)拓展:△ABC和△CDE均为等边三角形结论:(1)AD=BE;(2)∠ACB=∠AOB;(3)△PCQ为等边三角形;(4)PQ∥AE;(5)AP=BQ;(6)CO平分∠AOE;(四点共圆证) (7)OA=OB+OC;(8)OE=OC+OD .((7),(8)需构造等边三角形证明)[模型特点] :过等腰三角形的顶点引两条射线,使两条射线的夹角为顶角的一半。
(完整)全等三角形的相关模型总结,推荐文档.docx

全等的相关模型总结一、角平分线模型应用1.角平分性质模型:辅助线:过点G 作 GE射线AC(1) .例题应用:①如图 1,在ABC中,C900, AD 平分 CAB , BC 6cm, BD 4cm,那么点 D 到直线 AB 的距离是cm.②如图 2,已知,1 2 ,34 .求证: AP平分 BAC .图 1图2① 2(提示:作 DE AB 交 AB 于点 E )②12 , PM PN ,3 4 , PN PQ , PM PQ, PA平分 BAC .(2).模型巩固:练习一:如图3,在四边形 ABCD 中, BC>AB , AD=CD ,BD 平分BAC ..求证:A C180图3练习二:已知如图4,四边形 ABCD 中,B D 1800 , BC CD.求证: AC 平分BAD .图 4练习三:如图5,Rt ABC 中, ACB900, CD AB, 垂足为 D , AF 平分CAB ,交 CD 于点 E ,交 CB 于点 F.(1)求证: CE=CF.(2)将图 5 中的△ ADE 沿 AB 向右平移到A' D ' E '的位置,使点 E'落在BC边上,其他条件不变,如图 6 所示,是猜想:BE'于 CF 又怎样的数量关系?请证明你的结论.图 5图6练习四:如图7,∠ A90 , AD ∥ BC , P 是 AB的中点, PD平分∠ ADC.求证: CP平分∠ DCB.A D214E3PB C图 7练习五:如图8,AB> AC,∠ A 的平分线与 BC的垂直平分线相交于D,自 D 作 DE⊥ AB,DF⊥ AC,垂足分别为 E, F.求证: BE=CF.图 8练习六:如图9 所示,在△ ABC 中, BC 边的垂直平分线DF 交△ BAC 的外角平分线AD 于点 D, F 为垂足, DE ⊥AB 于 E,并且 AB>AC 。
求证: BE- AC=AE 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形相关模型总结一、角平分线模型(1)角平分线+两边垂线→全等三角形:角平分线的性质定理:角平分线上的点到角的两边距离相等;已知:AD平分∠BAC,CD⊥AC,垂足为C,过点D作DB⊥AB,垂足为B;辅助线:过点D作DB⊥AB,垂足为B;结论:①△ACD≌△ABD;② CD= DB(角分线垂两边,对称全等必呈现)(2)角平分线+垂线模型等腰三角形必呈现:遇到垂直于角平分线的线段,则延长该线段与角的另一边相交,构成等腰三角形;已知:OP平分∠AOB,MP⊥OP,垂足为P,延长MP交OB于点N;结论:①△OPM≌△OPN ;②△OMN为等腰三角形;③P是MN的中点(三线合一);(3)在角的两边上截取相等的线段,构造全等三角形:已知:OC是∠AOB的角平分线,D为OC上一点;辅助线:在OA上取一点E,在OB取一点F,使得OE=OF,并连接DE,结论:△OED≌△OFD ;(4)作平行线① 以角分线上一点作角的另一边的平行线,则△OAB 等腰三角形;② 过一边上的点作角平分线的平行线与另一边的反向延长线相交,则△ODH 等腰三角形; 已知:OP 平分∠MON ,AB ∥ON , 已知:OC 平分∠AOD ,DH ∥OC , 结论: △OAB 等腰三角形 结论: △ODH 等腰三角形角平分线+两边垂线→全等三角形 辅助线:过点G 作GE 射线AC已知:AD 是∠BAC 的角平分线,CD ⊥AC ,DB ⊥AB , 求证:CD=DB证明:∵AD 是∠BAC 的角平分线,∴∠1=∠2,∵CD ⊥AC ,DB ⊥AB , ∴∠ACD=∠ABD=90°, 在△ACD 和△ABD 中,∴△ACD ≌△ABD (AAS ) ∴CD=BD⊥⎪⎩⎪⎨⎧AD =AD 90=ABD ∠=ACD ∠2∠=1∠例1:已知:∠1=∠2,∠3=∠4,求证:AP平分∠BAC.例2:如图,AB>AC,∠A的平分线与BC的垂直平分线相交于D,过D作DE⊥AB、DF⊥AC,垂足分别为E、F.求证:BE=CF.例4:如图,在△ABC中,M为BC的中点,DM⊥BC,DM与∠BAC的角平分线交于点D,DE⊥AB,DF⊥AC,E、F为垂足,求证:BE=CF.角平分线+垂线模型等腰三角形必呈现例1:如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BE交BA的延长于F.求证:BD=2CE例2、如图,在△ABC中,∠BAC的角平分线AD交BC于点D,且AB=AD,作CM⊥AD 交AD的延长线于M. 求证:2AM=(AB+AC)例3:如图,已知△ABC中,CF平分∠ACB,且AF⊥CF,∠AFE+∠CAF=180°,求证:EF∥BC.截取构造全等:例1:如图,AB>AC ,∠1=∠2,求证:AB -AC>BD -CD 。
例2:如图,AB//CD ,BE 平分∠ABC ,CE 平分∠BCD ,点E 在AD 上,求证:BC=AB+CD.例3:在ABC ∆中,AB AC >,AD 是BAC ∠的平分线.P 是AD 上任意一点.求证:AB AC PB PC ->-.例4:已知△ABC 中,AB =AC ,∠A =100°,∠B的平分线交AC 于D ,求证:AD +BD =BCE C D B PAAC B D角平分线+平行线模型例、△ABC的两条角平分线OB、OC相交于点O,MN经过点O,且MN∥BC交AB、A C分别于点M、N;求证:△AMN的周长是AB+ A C;二、等腰直角三角形模型(一)旋转中心为直角顶点,在斜边上任取一点的旋转全等:操作过程:(1)将△ABD逆时针旋转90°,得△ACM ≌△ABD,从而推出△ADM为等腰直角三角形. (2)辅助线作法:过点C作MC⊥BC,使CM=BD,连结AM.(二)旋转中心为斜边中点,动点在两直角边上滚动的旋转全等:操作过程:连结AD.(1)使BF=AE(或AF=CE),导出△BDF ≌△ADE.(2)使∠EDF+∠BAC=180°,导出△BDF ≌△ADE.(三)构造等腰直角三角形(1)利用以上(一)和(二)都可以构造等腰直角三角形(略);(2)利用平移、对称和弦图也可以构造等腰直角三角形.(四)将等腰直角三角形补全为正方形,如下图:【题型1】证角等如图,Rt △ABC 中,∠BAC =90°,AB =AC ,M 为AC 中点,连结BM ,作AD ⊥BM 交BC 于点D ,连结DM ,求证:∠AMB =∠CMD .解析:作等腰Rt △ABC 关于BC 对称的等腰Rt △BFC ,延长AD 交CF 于点N ,∵AN ⊥BM ,由正方形的性质,可得AN =BM ,易证Rt △ABM ≌Rt △CAN ,∴∠AMB =∠CND ,CN =AM , ∵M 为AC 中点,∴CM =CN ,∵∠1=∠2,可证得△CMD ≌△CND , ∴∠CND =∠CMD , ∴∠AMB =∠CMD .【题型2】判定三角形形状如图,Rt △ABC 中,∠BAC = 90°,AB =AC ,AD =CE ,AN ⊥BD 于点M ,延长BD 交NE 的延长线于点F ,试判定△DEF 的形状.解析:作等腰Rt △ABC 关于BC 对称的等腰Rt △BHC ,可知四边形ABHC 为正方形,延长AN 交HC 于点K , ∵AK ⊥BD ,可知AK =BD ,易证:Rt △ABD ≌Rt △CAK , ∴∠ADB =∠CKN ,CK =AD , ∵AD =EC ,∴CK =CE ,易证△CKN ≌△CEN ,∴∠CKN =∠CEN ,易证∠EDF =∠DEF ,∴△DEF 为等腰三角形.21NFA BCDM E EMDCBA ABCD E FNMKHM NFE D C BA【题型3】利用等积变形求面积如图,Rt △ABC 中,∠A =90°,AB =AC ,D 为BC 上一点,DE ∥AC ,DF ∥AB ,且BE =4,CF =3,求S 矩形DFAE .解析:作等腰Rt △ABC 关于BC 的对称的等腰Rt △GCB ,可知四边形ABGC 为正方形,分别延长FD 、ED 交BG 、CG 于点N 、M , 可知DN =EB =4,DM =FC =3,由正方形对称性质,可知S 矩形DFAE =S 矩形DMGN =DM ·DN =3⨯4=12.【题型4】求线段长如图,△ABC 中,AD ⊥BC 于点D ,∠BAC =45°,BD =3,CD =2,求AD 的长.解析:以AB 为轴作Rt △ADB 的对称的Rt △AEB ,再以AC 为轴作Rt △ADC 的对称的Rt △AFC .可知BE =BD =3,FC =CD =2,延长EB 、FC 交点G ,∵∠BAC =45°, 由对称性,得∠EAF =90°,且AE =AD =AF ,易证四边形AFGE 为正方形,且边长等于AD ,设AD =x ,则BG =x -3,CG =x -2,在Rt △BCG 中,由勾股定理,得()()222235x x -+-=, 解得x =6,即AD =6.【题型5】求最小值如图,Rt △ABC 中,∠ACB =90°,AC =BC =4,M 为AC 的中点,P 为斜边AB 上的动点,求PM +PC 的最小值.解析:将原图形通过引辅助线化归为正方形,即作Rt △ACB 关于AB 对称的Rt △ADB ,可知四边形ACBD 为正方形,连接CD ,可知点C 关于AB 的对称点D ,连接MD 交AB 于点P ,连接CP ,则PM +PC 的值为最小,最小值为:PM +PC =DM=GMNFED C BAF EDCBA GFED CBADCBAM PDBC AMPB C AC 1ABC ED D E(C )B AC 1C 1AB C ED 1AB CEDED CB A21三、三垂直模型(弦图模型)例题:已知AB ⊥BD ,ED ⊥BD ,AB =CD ,BC =DE ,⑴求证:AC ⊥CE ;⑵若将△CDE 沿CB 方向平移得到①②③④等不同情形,1AB C D =,其余条件不变,试判断AC ⊥C 1E 这一结论是否成立?若成立,给予证 明;若不成立,请说明理由.① ② ③ ④解析:⑴∵AB ⊥BD ,ED ⊥BD∴90∠=∠=︒B D在ABC △与CDE △中=⎧⎪∠=∠⎨⎪=⎩AB CD B D BC DE ,∴ABC CDE △≌△(SAS )∴1∠=∠E∵290∠+∠=︒E ,∴90∠=︒ACE ,即AC ⊥CE⑵ 图①②③④四种情形中,结论永远成立,证明方法与⑴完全类似,只要证明1ABC C DE △≌△∴1∠=∠ACB C ED∵1190∠+∠=︒C ED DC E ∴190∠+∠=︒DC E ACB ,∴AC ⊥C 1E四、手拉手模型【探究一】“手拉手”模型基本构图;如图1,若A B C ∆与ADE ∆旋转全等,则必有ABD ∆与ACE ∆为两个顶角相等的等腰三角形(即相似的等腰三角形);反之,如图2,若有两个顶角相等的等腰三角形ABD ∆与ACE ∆共顶角顶点,则必有ABC ∆与ADE ∆旋转全等;而图2正是“手拉手”模型的基本构图;【探究二】将探究一中的普通等腰三角形换成特殊的图形,例如等边三角形、等腰直角三角形、正方形,然后再探究结论如何变化;如图3、图4、图5,当两个等边三角形、等腰直角三角形、正方形共顶点时,ABC ∆与ADE ∆仍然旋转全等,并且有两个共同的结论; 结论1:ABC ∆≌ADE ∆;DE BC =;结论2:BC 与DE 所夹锐角等于两个等腰三角形的顶角;(倒角方法如下图6、图7、图8的八字模型)图1EDC BA图2EDBA图3EDCBA 图4E D CB A FG 图5ED CBA 图6图7图8【探究三】将探究二中的特殊图形旋转后结论是否仍然成立; 如下图9、图10、图11易得探究二中的两个结论仍然成立;【探究四】深化探究二中图3的结论; 如图12,可得结论1:ABC ∆≌ADE ∆;DE BC =;结论2:︒=∠=∠=∠=∠60CAE BAD COE BOD ;结论3:如图12、图13、图14,可得三对三角形全等(ABC ∆≌ADE ∆;AHD ∆≌AGB ∆;AGC ∆≌AHE ∆)结论4:如图15,连接GH ,可得AGH ∆为等边三角形;(由结论3可得AH AG =)结论5:BE GH ∥;(由结论4可得︒=∠=∠60BAD AGH )结论6:连接AO ,可得AO 平分BOE ∠;(如图16,分别作BC AM ⊥、DE AN ⊥,AM 与AN 分别是全等三角形ABC ∆与ADE ∆对应边BC 和DE 上的高,故相等)图9E图10图11图12图13图14图15NM O 图16EDC BASFEDCBAMPNMHGFEDCB A例题1:如图,DA ⊥AB ,EA ⊥AC ,AD=AB ,AE=AC ,则下列正确的是( ) A. ABD ACE △≌△ B. ADF AES △≌△C. BMF CMS △≌△D. ADC ABE △≌△解析:D例题2:如图,正五边形ABDEF 与正五边形ACMHG 共点于A ,连接BG 、CF ,则线段BG 、CF 具有什么样的数量关系并求出∠GNC 的度数. 解析:先证ABG AFC △≌△可得BG =CF ,∠=∠ACF AGB∵∠=∠NPG APC ∴108∠=∠=︒GNC GAC五、半角模型 条件:1,+=1802αββθβ=︒且,两边相等 . 思路:1、旋转辅助线:①延长CD 到E ,使ED=BM ,连AE 或延长CB 到F ,使FB=DN ,连AF②将△ADN 绕点A 顺时针旋转90°得△ABF ,注意:旋转需证F 、B 、M 三点共线结论:(1)MN =BM +DN ; (2)=2CMNCAB ;(3)AM 、AN 分别平分∠BMN 、∠MND .2、翻折(对称)辅助线:①作AP ⊥MN 交MN 于点P② 将△ADN 、△ABM 分别沿AN 、AM 翻折,但一定要证明M 、P 、N 三点共线 .FDEGCB ANM CBA 例题1:如图,△ABC 是边长为3的等边三角形,△BDC 是等腰三角形,且∠BDC =120°.以 D 为顶点作一个60°角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,则△AMN 的周长为 .【解析】 6例题2:如图,在四边形ABCD 中,180∠+∠=︒B ADC ,AB AD =,E 、F 分别是边BC 、CD 延长线上的点,且12EAF BAD =∠∠,求证:EF BE FD =-解析:证明:在BE 上截取BG ,使BG DF =,连接AG .∵180B ADC +=︒∠∠,180ADF ADC +=︒∠∠, ∴B ADF =∠∠. ∵AB AD =, ∴ABG ADF △≌△.∴BAG DAF =∠∠,AG AF =.∴12BAG EAD DAF EAD EAF BAD +=+==∠∠∠∠∠∠.∴GAE EAF =∠∠. ∵AE AE =, ∴AEG AEF △≌△. ∴EG EF =∵EG BE BG =-,∴EF BE FD =-.FEDCBA附:正方形半角模型正方形ABCD ,E 、F 分别在边BC 、CD 上,且︒=∠45EAF ,AE 、AF 分别交BD 于H 、G ,连EF .一、全等关系(1)求证:①EF BE DF =+;②22HG BH DG =+;③AE 平分BEF ∠,AF 平分DFE ∠.二、相似关系(2)求证:①DG CE 2=;②BH CF 2=;③HG EF 2=. (3)求证:④DH BG AB ⋅=2;⑤HG BG AG ⋅=2;⑥21=⋅CF DF CE BE . 三、垂直关系(4)求证:①EG AG ⊥;②FH AH ⊥;③BEABHCF =∠tan . (5)、和差关系求证:①BE DG BG 2=-;②DH DF AD 2=+; ③||2||DG BH DF BE -=-.。
