(完整版)重庆巴蜀中学2018-2019学度初一上年末数学试题及解析
2018-2019学年重庆市渝中区巴蜀中学七年级(上)期末数学试卷(含解析)

2018-2019学年重庆市渝中区巴蜀中学七年级(上)期末数学试卷(考试时间:120分钟满分:150分)一、选择题(每小题4分,共计48分)1.﹣4的相反数是()A.B.4 C.D.﹣42.如图,是由4个大小相同的正方体搭成的几何体,其主视图是()A.B.C.D.3.下列方程中是一元一次方程的是()A.2x+3=B.7x=9 C.x2+6x=0 D.x+y=84.单项式﹣x2y的系数和次数分别为()A.﹣,3 B.﹣,2 C.,3 D.,25.下列调查适合普查的是()A.调查2013年6月市场上某品牌饮料的质量B.了解中央电视台直播“嫦娥三号”登月的全国收视率情况C.环保部门调查长江某段水域的水质情况D.了解某班同学在巴蜀中学八十周年校庆时参加志愿者活动的时间6.在方程组中,代入消元可得()A.3y﹣1﹣y=7 B.y﹣1﹣y=7 C.3y﹣3=7 D.3y﹣3﹣y=77.为了解参加运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄.就这个问题来说,下面说法中正确的是()A.抽取的100名运动员的年龄是样本B.2000名运动员是总体C.100名运动员是抽取的一个样本容量D.每个运动员是个体8.若a5n+2b3与﹣5a3n+6b3是同类项,则n等于()A.2 B.0 C.D.39.将一副三角板如图放置,若∠BOC=∠AOD,则∠BOC=()A.36°B.25°C.30°D.45°10.如图,M是线段AB的中点,NB为MB的三分之一,MN=a,则AB表示为()A. a B. a C.2a D.3a11.2019年足球亚洲杯正在阿联酋进行,这项起源于我国“蹴鞠”的运动项目近年来在我国中小学校园得到大力推广,某次校园足球比赛规定:胜一场得3分,平一场得1分,负一场得0分,某足球队共进行了8场比赛,得了12分,该队获胜的场数有几种可能()A.3 B.4 C.5 D.612.如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1,A2,A3,…,若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,…,依此类推,则第11圈的长为()A.72 B.79 C.87 D.94二、填空题(每小题3分,共30分)13.请将34510000用科学记数法表示为.14.若5x m﹣1+5y n﹣3=﹣1是关于x、y的二元一次方程,则m+n=.15.若2x+3y=﹣1,则6x+9y+5=.16.若是关于x、y的方程x+ay=3的解,则a值为;17.一种商品零售价为800元,为适应竞争,商店按零售价的九折降价后再让利60元销售,仍可获得10%的利润率,则该商品进价为元.18.若|x+3y﹣5|与(3x﹣y﹣3)2互为相反数,则2x+y=.19.父子二人今年的年龄和为44岁,已知两年前父亲的年龄是儿子的4倍,那么今年儿子的年龄是.20.若关于x、y的二元一次方程组的解满足x+y=11,则k的值是.21.已知线段AB=12,在直线AB上取一点P,恰好使AP=2PB,点Q为PB的中点,则线段AQ的长为;22.甲乙两车以不同的速度匀速从A地向B地前进,甲以80km/h先出发1小时,随后乙出发追甲,在还有40km追上甲车时,甲车突然以原速一半的速度返回,并在途中与乙相遇,乙以原速继续向B地前进,乙到达B地时与甲相距156km并立即以原速返回A地,在甲乙再次相遇时,乙随即以原速一半的速度继续返回A 地,在相遇后1.6小时,乙返回A地,此时甲距A地还有16km,则A、B两地间的距离是km.三、解答题(共72分)23.(8分)有理数的计算:(1)﹣1+(2+1)+(3﹣1)(2)﹣2+(﹣1)2019÷×[12﹣()2+]24.(8分)整式的化简:(1)a﹣(2a﹣3b)+2(3b﹣2a)(2)3a2b﹣[4ab2﹣3(ab2+a2b)﹣ab2]﹣6a2b25.(12分)解方程(组)(1)4﹣3(8﹣x)=5(x﹣2);(2)﹣=1;(3);26.(6分)冬至吃饺子是我国的传统习俗.君子阑餐饮公司为了解市民对去年销量较好的猪肉饺子、海鲜饺子、鱼肉饺子、山珍饺孑(以下分别用A、B、C、D表示)这四种不同口味饺子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查惰况绘制成如图的两幅统计图(尚不完整).请根据以上信息回答:(1)本次参加抽样调查的居民有人;(2)补全统计图;(3)若该居民区有6000人,请估算该居民区爱吃山珍饺子的人数.27.(6分)化简求值:2m2﹣[4(m2+n2﹣2mn)﹣2(n2﹣5mn)]﹣n2,其中|m+4|+(m+n+9)2=0.28.(7分)如图,∠AOB=180°,∠BOC=80°,OD平分∠AOC,∠DOE=3∠COE,求∠BOE.29.(7分)若甲、乙两种商品的单价之和为500元,因为季节变化,甲商品降价10%,乙商品提价5%,调价后,甲、乙两商品的单价之和比原单价之和提高2%,求甲、乙两种商品的原来单价?30.(8分)如图,在数轴上有两个长方形ABCD和EFGH,这两个长方形的宽都是2个单位长度,长方形ABCD 的长AD是4个单位长度,长方形EFGH的长EH是8个单位长度,点E在数轴上表示的数是5,且E、D两点之间的距离为12.(1)填空:点H在数轴上表示的数是,点A在数轴上表示的数是.(2)若线段AD的中点为M,线段EH上一点N,EN=EH,M以每秒4个单位的速度向右匀速运动,N以每秒3个单位的速度向左运动,设运动时间为x秒;当x=秒时,原点O恰为线段MN的三等分点.(3)若长方形ABCD以每秒2个单位的速度向右匀速运动,长方形EFGH固定不动,设长方形ABCD运动的时间为t(t>0)秒,两个长方形重叠部分的面积为S,求S与t的关系式.31.(10分)一个多位自然数分解为末三位与末三位以前的数,让末三位数减去末三位以前的数,所得的差能被7整除,则原多位数一定能被7整除.(1)判断864192 (能/不能)被7整除,证明任意一个三位以上的自然数都满足上述规律;(2)一个自然数t可以表示为t=p2﹣q2的形式,(其中p>q且为正整数),这样的数叫做“平方差数”,在t的所有表示结果中,当|p﹣q|最小时,称p2﹣q2是t的“平方差分解”,并规定F(t)=,例如,32=62﹣22=92﹣72,|9﹣7|<|6﹣2|,则F(32)==.已知一个五位自然数,末三位数m=500+10y+52,末三位以前的数为n=10(x+1)+y(其中1≤x≤8,1≤y≤9且为整数),n为“平方差数”,交换这个五位自然数的十位和百位上的数字后所得的新数能被7整除,求F(n)的最大值.参考答案与试题解析1.【解答】解:﹣4的相反数是:4.故选:B.2.【解答】解:从正面看易得第一层有3个正方形,第二层最左边有一个正方形.故选:D.3.【解答】解:A.属于分式方程,不符合一元一次方程的定义,即A项错误,B.符合一元一次方程的定义,是一元一次方程,即B项正确,C.属于一元二次方程,不符合一元一次方程的定义,即C项错误,D.属于二元一次方程,不符合一元一次方程的定义,即D项错误,故选:B.4.【解答】解:单项式﹣x2y的系数和次数分别为:﹣,3.故选:A.5.【解答】解:A、调查2013年6月市场上某品牌饮料的质量如果普查,所有饮料都报废,这样就失去了实际意义,故本选项错误;B、了解中央电视台直播“嫦娥三号”登月的全国收视率情况因为普查工作量大,适合抽样调查,故本选项错误;C、环保部门调查长江某段水域的水质情况不必全面调查,大概知道水质情况就可以了,适合抽样调查,故本选项错误;D、了解某班同学在巴蜀中学八十周年校庆时参加志愿者活动的时间是准确度要求高的调查,适于全面调查,故本选项正确,故选:D.6.【解答】解:将x=y﹣1代入3x﹣y=7,得:3(y﹣1)﹣y=7,去括号,得:3y﹣3﹣y=7,故选:D.7.【解答】解:A.抽取的100名运动员的年龄是样本,此选项正确;B.2000名运动员的年龄情况是总体,此选项错误;C.100是抽取的一个样本容量,此选项错误;D.每个运动员的年龄情况是个体,此选项错误;故选:A.8.【解答】解:∵a5n+2b3与﹣5a3n+6b3是同类项,∴5n+2=3n+6,n=2.故选:A.9.【解答】解:由图形可知,∠BOC=∠AOB+∠COD﹣∠AOD,∴∠BOC=90°+90°﹣5∠BOC,解得,∠BOC=30°,故选:C.10.【解答】解:∵M是线段AB的中点,∴AM=BM=AB,∵NB为MB的三分之一,∴MN=BM=AB∵MN=a,∴AB=3a故选:D.11.【解答】解:设该队获胜x场,平y场,则负(8﹣x﹣y)场,依题意,得:3x+y=12,∴y=12﹣3x,∴,,,,.又∵x+y≤8,∴该队可能获胜2场、3场或4场.故选:A.12.【解答】解:设第n圈的长为a n(n为正整数).观察图形,可知:a1=7=2×4﹣1,a2=15=4×4﹣1,a3=23=6×4﹣1,…,∴a n=2n×4﹣1=8n﹣1(n为正整数),∴a11=8×11﹣1=87.故选:C.13.【解答】解:34510000=3.451×107,故答案为:3.451×107.14.【解答】解:∵5x m﹣1+5y n﹣3=﹣1是关于x、y的二元一次方程,∴m﹣1=1,n﹣3=1,解得:m=2,n=4,∴m+n=6.故答案为:615.【解答】解:当2x+3y=﹣1时,原式=3(2x+3y)+5=3×(﹣1)+5=﹣3+5=2,故答案为:2.16.【解答】解:∵是关于x、y的方程x+ay=3的解,∴代入得:2+a=3,解得:a=1,故答案为:117.【解答】解:设该商品的进价为x元,依题意,得:800×0.9﹣60﹣x=10%x,解得:x=600.故答案为:600.18.【解答】解:由题意知|x+3y﹣5|+(3x﹣y﹣3)2=0,则,①+②,得:4x+2y=8,所以2x+y=4,故答案为:4.19.【解答】解:设今年儿子x岁,则今年父亲(44﹣x)岁,依题意,得:44﹣x﹣2=4(x﹣2),解得:x=10.故答案为:10.20.【解答】解:解方程组,得:①﹣②,得3y=k+7,,①+2×②,得3x=13k﹣8,∴,∵x+y=11,∴,即14k=34,∴.故答案为:.21.【解答】解:当点P在点A左侧时,AP<PB,则不合题意,当点P在AB之间时,∵AP=2PB,AB=12∴PB=4∵点Q为PB的中点,∴PQ=2=BQ∴AQ=AB﹣QB=10当点P在点B右侧时,∵AP=2PB,AB=12∴PB=12∵点Q为PB的中点,∴PQ=6=BQ∴AQ=AB+BQ=18综上所述:AQ=10或18故答案为:10或1822.【解答】解:设乙车速度为x千米/小时,在甲乙再次相遇时,乙随即以原速一半的速度继续返回A地,在相遇后1.6小时,乙返回A地,此时甲距A地还有16km,可得:,解得:x=100,设甲车返回前,乙车行驶了m小时,然后行驶了n小时到达B地,依题意得:,解得,∴A、B两地间的距离=100×(2+1.4)=340km.故答案为:34023.【解答】解:(1)原式=﹣1+2+1+3﹣1=﹣1+6=5;(2)原式=﹣2﹣1××(12﹣+)=﹣2﹣×12=﹣2﹣9=﹣11.24.【解答】解:(1)a﹣(2a﹣3b)+2(3b﹣2a)=a﹣2a+3b+6b﹣4a=﹣5a+9b;(2)3a2b﹣[4ab2﹣3(ab2+a2b)﹣ab2]﹣6a2b=3a2b﹣4ab2+3(ab2+a2b)+ab2﹣6a2b=3a2b﹣4ab2+3ab2+a2b+ab2﹣6a2b=﹣2a2b.25.【解答】解:(1)去括号得:4﹣24+3x=5x﹣10,移项得:3x﹣5x=﹣10﹣4+24,合并同类项得:﹣2x=10,系数化为1得:x=﹣5,(2)方程两边同时乘以10得:2(4x+2)﹣(5x﹣9)=10,去括号得:8x+4﹣5x+9=10,移项得:8x﹣5x=10﹣9﹣4,合并同类项得:3x=﹣3,系数化为1得:x=﹣1,(3)原方程组可整理得:②﹣①×2得:y=8,把y=8代入①得:x﹣24=﹣7,解得:x=17,方程组得解为:.26.【解答】解:(1)本次参加抽样调查的居民有(人);(2)A的百分比为,C的百分比为:100%﹣30%﹣40%﹣10%=20%,C的人数为:600×20%=120(人),如图所示:(3)该居民区爱吃山珍饺子的人数6000×40%=2400(人);故答案为:600.27.【解答】解:原式=2m2﹣(2m2+4n2﹣8mn﹣3n2+10mn)﹣n2=2m2﹣(2m2+n2+2mn)﹣n2=﹣n2﹣2mn,∵|m+4|+(m+n+9)2=0,∴m+4=0,m+n+9=0,解得:m=﹣4,n=﹣5,故原式=﹣×(﹣5)2﹣2×(﹣4)×(﹣5)=﹣﹣40=﹣.28.【解答】解:∵∠AOB=180°,∠BOC=80°,∴∠AOC=100°,∵OD平分∠AOC,∴∠COD=∠AOC=50°,又∵∠DOE=3∠COE,∴∠COE=∠COD=25°,∴∠BOE=∠BOC﹣∠COE=55°.29.【解答】解:设甲商品的原单价为x元,则乙商品的原单价为(500﹣x)元,依题意,得:(1﹣10%)x+(1+5%)(500﹣x)=500×(1+2%),解得:x=100,∴500﹣x=400.答:甲商品的原单价为100元,乙商品的原单价为400元.30.【解答】解:(1)∵长方形EFGH的长EH是8个单位长度,且点E在数轴上表示∴点H在数轴上表示的数是5+8=13∵E、D两点之间的距离为12点D表示的数为5﹣12=﹣7∵长方形ABCD的长AD是4个单位长∴点A在数轴上表示的数是﹣7﹣4=﹣11故答案为:13,﹣11(2)由题意知,线段AD的中点为M,则M表示的数为﹣9,线段EH上一点N且EN=EH,则N表示的数为7;由M以每秒4个单位的速度向右匀速运动,N以每秒3个单位的速度向左运动,则经过x秒后,M点表示的数为4x﹣9,N点表示的数为7﹣3x;①当OM=2ON时,则有|4x﹣9|=2|7﹣3x|,解得:x=2.3(经验证,不符合题意,舍去)或x=2.5②当ON=2OM时,则有|7﹣3x|=2|4x﹣9|,解得:x=2.2或x=5(经验证,不符合题意,舍去)综上所述,当x=2.2或x=2.5时,原点O恰为线段MN的三等分点.故答案为:x=2.2或x=2.5.(3)由题意知,当0<t<6时,长方形ABCD和EFGH无重叠,些时S=0当6≤t≤12时,两个长方形重叠部分的面积为S=,即S=.当t>12时,长方形ABCD和EFGH无重叠,S=0.31.【解答】解:(1)864192的末三位数为192,末三位以前的数为864∴192﹣864=﹣672∵﹣672÷7=﹣96∴864192能被7整除故答案为:能证明:设这个多位数的末三位数为a,末三位以前的数为b则这个多位数可表示为1000b+a根据题意得,a﹣b=7n(n为整数)∴a=7n+b则1000b+a=1000b+7n+b=1001b+7n∵1001b+7n可以被7整除∴1000b+a可以被7整除∴任意一个三位以上的自然数都满足这个规律.(2)∵m=500+10y+52,1≤y≤9①当1≤y≤4时,m的百位数字为5,十位数字为(y+5),个位数字为2∴调换百位数字和十位数字后所得的新数为100(y+5)+52根据题意100(y+5)+52﹣10x﹣10﹣y可以被7整除整理得98y﹣7x+539+y﹣3x+3能被7整除∵98y﹣7x+539能被7整除∴只需y﹣3x+3能被7整除即可解得或或或∵n=10(x+1)+y∴n=71或52或33或84根据题意71=362﹣352,此时F(71)=10652=142﹣122,此时F(52)=1933=172﹣162=72﹣42,|17﹣16|<|7﹣4|,此时F(33)=4984=222﹣202=102﹣42,|22﹣20|<|10﹣6|,此时F(84)=31∴当1≤y≤4时,F(n)最大为106②当5≤y≤9时,m的百位数字为6,十位数字为(y﹣5),个位数字为2 调换百位数字和十位数字后所得的新数为100(y﹣5)+62根据题意100(y﹣5)+62﹣10x﹣10﹣y可以被7整除整理得98y﹣7x﹣448+y﹣3x可以被7整除∵98y﹣7x﹣448可以被7整除∴只需y﹣3x能被7整除即可解得或或或∵n=10(x+1)+y∴n=55或36或87或68根据题意55=282﹣272=82﹣32,|28﹣27|<|8﹣3|,此时F(55)=82 36=102﹣82,此时F(36)=1387=442﹣432=162﹣132,|44﹣43|<|16﹣13|,此时F(87)=13068=182﹣162,此时F(68)=25∴当5≤y≤9时,F(n)的最大值为130综上,F(n)的最大值为130。
巴蜀中学初一(上)期末试题——数学

D· · · · a c o b重庆市巴蜀中学第一学期期末考试初2019级(一上)数学试题卷一、选择题(每题4分,共48分) 1. 8的相反数是( ) A. 18B.18-C. 8D. 8-2.关于单项式3223a b π-,下列说法正确的是( ) A.系数为23-B.次数为 5C.次数为 6D.系数为233. 以下问题不适合全面调查的是( ) A.调查某班学生每周课前预习的时间 B.调查某中学在职教师的身体健康状况 C.调查全国中小学生课外阅读情况D.调查某校篮球队的身高情况4. 单项式13m x y -与4n xy 是同类项,则mn 的值为( )A.9B.8C.6D.35. 如图,将一副三角板的直角顶点重合,摆放 在桌面上,125AOD ∠=︒,则BOC ∠=( ) A.25︒ B.65︒C.55︒D.35︒ (第5题图)6. 为了了解参加运动会的2000名运动员的年龄情况,从中抽查了200名运动员的年龄,就这个问题来说:下面说法中正确的是( ) A.2000名运动员是总体 B.每个运动员是个体C.抽取的200名运动员的年龄是样本D.200名运动员是抽取的一个样本容量7.若()1220a a x ---=是关于x 的一元一次方程,则a =( )A.2±B.2C.0D.2- 8.二元一次方程3215x y +=的正整数解有( )组A.1B.2C.3D.无数组9.有理数a 、b 、c 在数轴上的对应点的位置如图所示,那么化简:c a b c a b --++-=( ) A.22b a -B.22c a -C.222b a c -+D.0 (第9题图) 10.已知70AOB ∠=︒,30BOC ∠=︒,OD 平分AOC ∠,则AOD ∠的度数( )A.50︒B.40︒C.10︒或40︒D.50︒或20︒图形① 图形② 图形③ 图形④AN B CMD我 蜀 学 中 我 我 蜀爱学11.在正方体的六个面上,分别标上“我、爱、巴、蜀、中、学”六个字,如图是正方体的三种不同摆法,则三种摆法的左侧面上三个字分别是( ) A.爱、中、巴 B.中、爱、巴C.巴、中、学D.爱、中、学12.观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,……,按此规律,图形⑦中星星的颗数是( )A.43B.45C.41D.53二、填空题(每题4分,共32分)13.2016年天猫“双11”狂欢夜成交额为1207亿元,则数据1207亿元用科学记数法记为 元 14.若32x y =⎧⎨=⎩是关于x ,y 的二元一次方程21ax y -=的解,则a 的值为15.已知代数式23y x -的值为7-,则代数式698y x -+的值为16.如图2:3:4AOB COB COD ∠=∠=∠=, 射线ON ,OM 分别平分AOB ∠和COD ∠, 又90MON ∠=︒,则AOB ∠=(第16题图) 17.钟表11∶55,时针与分针的夹角的度数是18.一种商品零售价为600元,为适应竞争,商店按零售价的八折降价并让利40元销售,仍可 获利10%,则进价 元。
重庆市巴蜀中学初一上学期期末考试数学试卷(附答案)

.
16. 若 −5xny2 与 12x3y2m 是同类项,则 m + n =
.
17. 当 x = 1 时,代数式 ax2 − 2bx + 1 的值等于 5,则当 x = −1 时,代数式 2ax2 + 4bx − 1 的值为
.
18. 如图,已知 ∠AOB = 90◦,OM 平分 ∠BOC,ON 平分 ∠AOC,那么 ∠M ON =
(2) 当 P Q = 5 时,求所有符合条件的 t 的值,并求出此时点 Q 所对应的数;
(3) 若点 P 一直沿数轴的正方向运动,点 Q 运动到点 B 时,立即改变运动方向,沿数轴 的负方向运动,到达点 A 时,随即停止运动,在点 Q 的整个运动过程中,是否存在合 适的 t 值,使得 P Q = 8?若存在,求出所有符合条件的 t 值,若不存在,请说明理由.
当 C 在线段 AB 上时:AC = AB − BC = 5 − 3 = 2; 如图 2,
当 C 在 AB 的延长线上时,AC = AB + BC = 5 + 3 = 8.
9. 观察图形可知,“董”字的对面的字是“动”.
10. 设商品的原价为 x 元,则可知第一次打折后价钱为:(x × 0.9) 元,
初一第一学期期末考试
数学参考答案
1 2 3 4 5 6 7 8 9 10 A D BCAAACC D 11 12 CC 1. 2. a 的 3 倍为 3a,小 1 即为 3a − 1. 3. ∵ 一个角是 40◦, ∴ 这个角的余角是 90◦ − 40◦ = 50◦. 4.A、应为 a − (b + c) = a − b − c,故本选项错误; B、应为 a + (b + c) = a + b + c,故本选项错误; C、a + b − c = a + (b − c),正确; D、应为 a − b + c = a − (b − c),故本选项错误. 原式 =89◦59′60′′ − 18◦50′45′′ 5. =71◦9′15′′. 6.把 x = 1 代入方程得:2 + m = 3, 解得:m = 1. 7.∵ 两点之间线段最短, ∴ 把弯曲的河道改直,就能缩短路程. 8.如图 1,
七年级上册重庆巴蜀中学数学期末试卷测试卷(含答案解析)
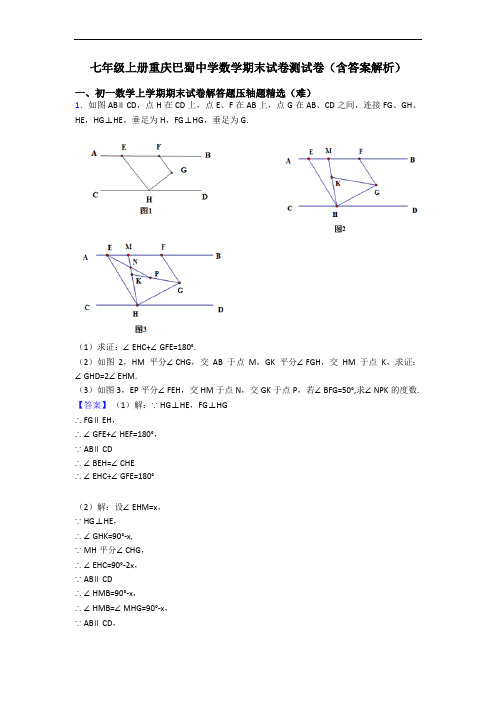
七年级上册重庆巴蜀中学数学期末试卷测试卷(含答案解析)一、初一数学上学期期末试卷解答题压轴题精选(难)1.如图AB∥CD,点H在CD上,点E、F在AB上,点G在AB、CD之间,连接FG、GH、HE,HG⊥HE,垂足为H,FG⊥HG,垂足为G.(1)求证:∠EHC+∠GFE=180°.(2)如图2,HM平分∠CHG,交AB于点M,GK平分∠FGH,交HM于点K,求证:∠GHD=2∠EHM.(3)如图3,EP平分∠FEH,交HM于点N,交GK于点P,若∠BFG=50°,求∠NPK的度数. 【答案】(1)解:∵HG⊥HE,FG⊥HG∴FG∥EH,∴∠GFE+∠HEF=180°,∵AB∥CD∴∠BEH=∠CHE∴∠EHC+∠GFE=180°(2)解:设∠EHM=x,∵HG⊥HE,∴∠GHK=90°-x,∵MH平分∠CHG,∴∠EHC=90°-2x,∵AB∥CD∴∠HMB=90°-x,∴∠HMB=∠MHG=90°-x,∵AB∥CD,∴∠BMH+∠DHM=180°,即∠BMH+∠GHM+∠GHD =180°,∴90°-x+90°-x+∠GHD =180°,解得,∠GHD =2x,∴∠GHD=2∠EHM;(3)解:延长FG,GK,交CD于R,交HE于S,如图,∵AB∥CD,∠BFG=50°∴∠HRG=50°∵FG⊥HG,∴∠GHR=40°,∵HG⊥HE,∴∠EHG=90°,∴∠CHE=180°-90°-40°=50°,∵AB∥CD,∴∠FEH=∠CHE=50°,∵EP是∠HEF的平分线,∴∠SEP= ∠FEH=25°,∵GH平分∠HGF,∴∠HGS= ∠HGF=45°,∴∠HSG=45°,∵∠SEP+∠SPE=∠HSP=45°,∴∠EPS=20°,即∠NPK=20°.【解析】【分析】(1)根据HG⊥HE,FG⊥HG可证明FG∥EH,从而得∠GFE+∠HEF=180°,再根据AB∥CD可得∠BEH=∠CHE,进而可得结论;(2)设∠EHM=x,根据MH是∠CHG的平分线可得∠MHG=90°-x,∠EHC=90°-2x,根据平行线的性质得∠HMB=90°-x,从而得∠HMB=∠MHG,再由平行线的性质得∠BMH+∠DHM=180°,从而可得结论;(3)分别延长FG,GK,交CD于R,交HE于S,由AB∥CD得∠HRG=50°,由FG⊥HG得∠GHR=40°,由MH平分∠CHG得∠CHE=50°,由AB∥CD得∠MEH=∠CHE=50°,可得∠SEP=25°,最后由三角形的外角可得结论.2.已知:如图(1)∠AOB和∠COD共顶点O,OB和OD重合,OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β.(1)如图(2),若α=90°,β=30°,求∠MON;(2)若将∠COD绕O逆时针旋转至图(3)的位置,求∠MON(用α、β表示);(3)如图(4),若α=2β,∠COD绕O逆时针旋转,转速为3°/秒,∠AOB绕O同时逆时针旋转,转速为1°/秒,(转到OC与OA共线时停止运动),且OE平分∠BOD,请判断∠COE与∠AOD的数量关系并说明理由.【答案】(1)解:∵OM为∠AOD的平分线,ON为∠BOC的平分线,α=90°,β=30°∴∠MOB=∠AOB=45°∠NOD=∠BOC=15°∴∠MON=∠MOB+∠NOD=45°+15°=60°.(2)解:设∠BOD=γ,∵∠MOD= = ,∠NOB= =∴∠MON=∠MOD+∠NOB-∠DOB= + -γ=(3)解:① 为定值,设运动时间为t秒,则∠DOB=3t-t=2t,∠DOE= ∠DOB=t,∴∠COE=β+t,∠AOD=α+2t,又∵α=2β,∴∠AOD=2β+2t=2(β+t).∴【解析】【分析】(1)根据角平分线的定义,分别求出∠MOB和∠NOD,再根据∠MON=∠MOB+∠NOD,可求出∠MON的度数。
重庆市巴蜀中学七年级上期末数学试题含解析

重庆市巴蜀中学七年级(上)期末数学试卷一、选择题(每题4分,共48分)1.在﹣2,﹣1,0,2这四个数中,最小的数是()A.﹣2B.﹣1C.0D.22,以下说法正确的选项是()2.对于单项式5πRA.系数为5B.系数为5πC.次数为3D.次数为43.如图,有一个正方体纸巾盒,它的平面睁开图是()A.B.C.D.4.以下说法正确的选项是()A.一对乡村育龄夫妻第一胎生女孩,四年后还同意生一胎,有人说第二胎必为男孩B.事件发生的频次就是它的概率C.质检部门在某商场的化妆品柜台随意抽取100件化妆品进行质量检测,发现有2件为不合格产品,我们就说这个柜台的产品合格率为98%D.成语“十拿九稳”,从数学上看,就是指“失败”是一种不行能事件5.如图,AB=12cm,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度是()A.4cmB.6cmC.8cmD.10cm6.如图,点B,O,D在同向来线上,若∠1=15°,∠2=105°,则∠AOC的度数是()A.75°B.90°C.105°D.125°7.若代数式4x﹣5与的值相等,则x的值是()A.1B.C.D.28.计算﹣3(x﹣2y)+4(x﹣2y)的结果是()A.x﹣2yB.x+2yC.﹣x﹣2yD.﹣x+2y9.某工程队共有27人,每日每人可挖土4方,或运土5方,为使挖出的土实时运走,应分派挖土和运土的人分别是()A.12人,15人B.14人,13人C.15人,12人D.13人,14人10.若单项式2x n y m﹣n与单项式3x3y2n的和是5x n y2n,则m与n的值分别是()A.m=3,n=9B.m=9,n=9C.m=9,n=3D.m=3,n=311.已知方程组的解也是方程3x﹣2y=0的解,则k的值是()A.k=﹣5B.k=5C.k=﹣10D.k=1012.如图①是一块瓷砖的图案,用这类瓷砖来铺设地面,假如铺成一个2×2的正方形图案(如图②),此中完好的圆共有5个,假如铺成一个3×3的正方形图案(如图③),此中完好的圆共有13个,假如铺成一个4×4的正方形图案(如图④),此中完好的圆共有25个,若这样铺成一个10×10的正方形图案,则此中完好的圆共有()个.A.145B.146C.180D.181二、填空题(每空3分,共30分)13.5的相反数是.14.计算2a﹣(﹣1+2a)=.15.假如收入50元记作+50元,那么支出20元记作.16.每年的5月31日为世界无烟日,睁开无烟日活动旨在提示世人抽烟有害健康,号召全世界抽烟者主动放弃抽烟,全球每年因抽烟而引起疾病死亡的人数大概为5400000人,数据5400000人用科学记数法表示为人.17.如图,数轴上点A、B所表示的两个数的和的绝对值是.18.如图是六个棱长为1的立方块构成的一个几何体,其俯视图的面积是.19.以下图,两块三角板的直角极点O重叠在一同,且OB恰巧均分∠COD,则∠AOD的度数是度.20.一块腕表上午10:45时针和分针所夹锐角的度数是.21.圣诞节到了,商铺进行打折促销活动.妈妈以八折的优惠购置了一件运动服,节俭28元,那么妈妈购置这件衣服实质花销了元.22.某网店老板经营销售甲、乙两种款式的浮潜装备,每件甲种款式的收益率为30%,每件乙种款式的收益率为50%,当售出的乙种款式的件数比甲种款式的件数少40%时,这个老板获得的总收益率是40%;当售出的乙种款式的件数比甲各种款式的件数多80%时,这个老板获得的总收益率是.三、解答题(共27题)23.计算:(1)18﹣6÷(﹣2)×(﹣);(2)(﹣﹣)×24+(1﹣0.5)+3×.24.解方程(组):(1)7﹣3(x+1)=2(4﹣x)(2).2225.先化简,再求值:3(x﹣2xy)﹣4[xy﹣1+(﹣xy+x)],此中x=﹣4,y=.26.巴蜀中学对本校初2017届500名学生中中考参加体育加试测试状况进行检查,依据男生1000米及女生800米测试成绩整理,绘制成不完好的统计图,(图①,图②),请依据统计图供给的信息,回答以下问题:(1)该校毕业生中男生有人;扇形统计图中a=;(2)补全条形统计图;(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?27.以下图.(1)已知∠AOB=9°0,∠BOC=3°0,OM均分∠AOC,ON均分∠BOC,求∠MON的度数;(2)∠AOB=α,∠BOCβ=,OM均分∠AOC,ON均分∠BOC,求∠MON的大小.28.某汽车专卖店销售A、B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额96万元,本周已售出2辆A型车和1辆B型车,销售额为62万元.(1)求每辆A型车和B型车的售价各是多少?(2)跟着汽车限购限号政策的实行,估计下周起A,B两种型号的汽车价钱在原有的基础上均有上升,若A型汽车价钱上升m%,B型汽车价钱上升3m%,则同时购置一台A型车和一台B型车的花费比涨价前多12%,求m的值.29.张老师周末到某家居建材市场购置沙发、橱窗和地板三样物件,刚巧该市场推出“迎圣诞元旦双节”优惠活动,详细优惠状况以下:购物总金额(原价)优惠率不超出5000元的部分10%超出5000元且不超出10000元的部分20%超出10000元且不超出20000元的部分30%⋯⋯(1)若购置三样物件原价8000元,恳求出张老师实质的付款金额?(2)若购置三样物件实质花销了6820元.①恳求出三件物件的原价总合是多少钱?②几日后,张老师发现地板的款式不适合需要退货,该市场规定:花费者需支付优惠差额(即退货商品在购置时所享受的优惠),而且还要支付商品原价5%的手续费,最后该市场退还了张老师2345元,请问地板原价是多少钱?重庆市巴蜀中学七年级(上)期末数学试卷参照答案与试题分析一、选择题(每题4分,共48分)1.在﹣2,﹣1,0,2这四个数中,最小的数是()A.﹣2B.﹣1C.0D.2【考点】有理数大小比较.【剖析】由于正数大于全部负数,0大于负数,所以负数最小,﹣2<﹣1,所以﹣2最小.【解答】解:﹣2<﹣1<0<2,应选A.2.对于单项式5πR2,以下说法正确的选项是()A.系数为5B.系数为5πC.次数为3D.次数为4【考点】单项式.【剖析】依据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,全部字母的指数和叫做这个单项式的次数.【解答】解:单项式5πR2的系数是5π,次数是2,应选:B.3.如图,有一个正方体纸巾盒,它的平面睁开图是()A.B.C.D.【考点】几何体的睁开图.【剖析】由平面图形的折叠及正方体的睁开图解题.【解答】解:察看图形可知,一个正方体纸巾盒,它的平面睁开图是.应选:B.4.以下说法正确的选项是()A.一对乡村育龄夫妻第一胎生女孩,四年后还同意生一胎,有人说第二胎必为男孩B.事件发生的频次就是它的概率C.质检部门在某商场的化妆品柜台随意抽取100件化妆品进行质量检测,发现有2件为不合格产品,我们就说这个柜台的产品合格率为98%D.成语“十拿九稳”,从数学上看,就是指“失败”是一种不行能事件【考点】用样本估计整体;随机事件;概率的意义.【剖析】正确理解频次和概率的观点,掌握随机事件的观点,剖析即可.【解答】解:A、第二胎可能是男孩,也可能是女孩,是随机事件,错误;B、事件发生的频次就是它的概率,概率其实不等同于频次,观点混杂,错误;C、切适用样本估计整体的统计思想,正确;D、混杂了频次与概率的观点,错误.应选C.5.如图,AB=12cm,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度是()A.4cmB.6cmC.8cmD.10cm【考点】两点间的距离.【剖析】依据中点的定义求出AC、BC的长,依据题意求出AD,联合图形计算即可.【解答】解:∵AB=12cm,C为AB的中点,∴AC=BC=AB=6cm,∵AD:CB=1:3,∴AD=2cm,∴DC=AC﹣AD=4cm,∴DB=DC+BC=10cm,应选:D.6.如图,点B,O,D在同向来线上,若∠1=15°,∠2=105°,则∠AOC的度数是()A.75°B.90°C.105°D.125°【考点】角的计算.【剖析】由图示可得,∠2与∠BOC互补,联合已知可求∠BOC,又由于∠AOC=∠COB+∠1,即可解答.【解答】解:∵∠2=105°,∴∠BOC=18°0﹣∠2=75°,∴∠AOC=∠1+∠BOC=1°5+75°=90°.应选:B.7.若代数式4x﹣5与的值相等,则x的值是()A.1B.C.D.2【考点】解一元一次方程.【剖析】依据题意列出方程,求出方程的解即可获得x的值.【解答】解:依据题意得:4x﹣5=,去分母得:8x﹣10=2x﹣1,解得:x=,应选B.8.计算﹣3(x﹣2y)+4(x﹣2y)的结果是()A.x﹣2yB.x+2yC.﹣x﹣2yD.﹣x+2y【考点】整式的加减.【剖析】原式去括号归并即可获得结果.【解答】解:原式=﹣3x+6y+4x﹣8y=x﹣2y,应选:A.9.某工程队共有27人,每日每人可挖土4方,或运土5方,为使挖出的土实时运走,应分派挖土和运土的人分别是()A.12人,15人B.14人,13人C.15人,12人D.13人,14人【考点】二元一次方程组的应用.【剖析】用二元一次方程组解决问题的重点是找到2个适合的等量关系.此题中有2个定量:工程队的人数,沙的吨数,可依据定量找到两个等量关系:挖沙人数+运沙人数=27,4×挖沙人数=5×运沙人数.依据这两个等量关系可列出方程组.【解答】解:设分派挖沙x人,运沙y人,则,解得,∴应分派挖沙15人,运沙12人.应选C.10.若单项式2x n y m﹣n与单项式3x3y2n的和是5x n y2n,则m与n的值分别是()A.m=3,n=9B.m=9,n=9C.m=9,n=3D.m=3,n=3【考点】归并同类项.【剖析】依据同类项的观点,列出方程求解.【解答】解:由题意得,,解得:.应选C.11.已知方程组的解也是方程3x﹣2y=0的解,则k的值是()A.k=﹣5B.k=5C.k=﹣10D.k=10【考点】解三元一次方程组.【剖析】依据三元一次方程组的观点,先解方程组,获得x,y的值后,代入4x﹣3y+k=0求得k的值.【解答】解:解方程组,得:,把x,y代入4x﹣3y+k=0得:﹣40+45+k=0解得:k=﹣5.应选A.12.如图①是一块瓷砖的图案,用这类瓷砖来铺设地面,假如铺成一个2×2的正方形图案(如图②),此中完好的圆共有5个,假如铺成一个3×3的正方形图案(如图③),此中完好的圆共有13个,假如铺成一个4×4的正方形图案(如图④),此中完好的圆共有25个,若这样铺成一个10×10的正方形图案,则此中完好的圆共有()个.A.145B.146C.180D.181【考点】规律型:图形的变化类.【剖析】依据给出的四个图形的规律能够知道,构成大正方形的每个小正方形上有一个完好的圆,所以圆的数量是大正方形边长的平方,每四个小正方形构成一个完好的圆,从而可得这样的圆是大正方形边长减1的平方,从而可得若这样铺成一个10×10的正方形图案,则此中完整的圆共有102+(10﹣1)2=181个.【解答】解:剖析可得完好的圆是大正方形的边长减1的平方,从而可知铺成一个10×10的正方形图案中,完好的圆共有102+(10﹣1)2=181个.应选D.二、填空题(每空3分,共30分)13.5的相反数是﹣5.【考点】相反数.【剖析】依据相反数的观点解答即可.【解答】解:依据相反数的定义有:5的相反数是﹣5.故答案为﹣5.14.计算2a﹣(﹣1+2a)=1.【考点】整式的加减.【剖析】此题考察了整式的加减、去括号法例两个考点.先依据去括号法例去掉整式中的小括号,再归并整式中的同类项即可.【解答】解:原式=2a+1﹣2a=1.故答案为:1.15.假如收入50元记作+50元,那么支出20元记作﹣20元.【考点】正数和负数.【剖析】依据正数和负数表示相反意义的量,收入记为正,可得支出的表示方法.【解答】解:假如收入50元记作+50元,那么支出20元记作﹣20元,故答案为:﹣20元.16.每年的5月31日为世界无烟日,睁开无烟日活动旨在提示世人抽烟有害健康,号召全世界抽烟者主动放弃抽烟,全球每年因抽烟而引起疾病死亡的人数大概为5400000人,数据6人.5400000人用科学记数法表示为5.4×10【考点】科学记数法—表示较大的数.【剖析】科学记数法的表示形式为a×10n的形式,此中1≤|a|<10,n为整数.确立n的值时,要看把原数变为a时,小数点挪动了多少位,n的绝对值与小数点挪动的位数同样.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将5400000用科学记数法表示为:5.4×106.故答案为:5.4×106.17.如图,数轴上点A、B所表示的两个数的和的绝对值是1.【考点】数轴;绝对值;有理数的加法.【剖析】第一依据数轴获得表示点A、B的实数,而后求其和绝对值即可.【解答】解:解:从数轴上可知:表示点A的数为﹣3,表示点B的数是2,则﹣3+2=﹣1,|﹣1|=1,故答案为:1.18.如图是六个棱长为1的立方块构成的一个几何体,其俯视图的面积是5.【考点】简单组合体的三视图.【剖析】先得出从上边看所获得的图形,再求出俯视图的面积即可.【解答】解:从上边看易得第一行有3个正方形,第二行有2个正方形,共5个正方形,面积为5.故答案为5.19.以下图,两块三角板的直角极点O重叠在一同,且OB恰巧均分∠COD,则∠AOD的度数是135度.【考点】角均分线的定义.【剖析】此题是有公共定点的两个直角三角形问题,经过图形可知∠AOC+∠BOC=9°0,∠BOD+∠BOC=9°0,同时∠AOC+∠BOC+∠BOD+∠BOC=18°0,能够经过角均分线性质求解.【解答】解:∵OB均分∠COD,∴∠COB=∠BOD=4°5,∵∠AOB=9°0,∴∠AOC=4°5,∴∠AOD=13°5.故答案为:135.20.一块腕表上午10:45时针和分针所夹锐角的度数是52.5°.【考点】钟面角.【剖析】第一依据题意画出草图,再依据钟表表盘的特点:表面上每一格30°,进行解答.【解答】解:10:45,时针和分针中间相差1个大格.∵钟表12个数字,每相邻两个数字之间的夹角为30°,∴上午10:45时针和分针所夹锐角的度数是1×30°=52.5°.故答案为:52.5°.21.圣诞节到了,商铺进行打折促销活动.妈妈以八折的优惠购置了一件运动服,节俭28元,那么妈妈购置这件衣服实质花销了112元.【考点】一元一次方程的应用.【剖析】设这件运动服的标价为x元,则妈妈购置这件衣服实质花销了0.8x元,由题意可得出对于x的一元一次方程,解之即可求出x的值,故妈妈购置这件衣服实质花销的钱数即可得出.【解答】解:设这件运动服的标价为x元,则妈妈购置这件衣服实质花销了0.8x元,依据题意得,x﹣0.8x=28,解得:x=140,0.8x=112,故妈妈购置这件衣服实质花销了112元.故答案为112.22.某网店老板经营销售甲、乙两种款式的浮潜装备,每件甲种款式的收益率为30%,每件乙种款式的收益率为50%,当售出的乙种款式的件数比甲种款式的件数少40%时,这个老板获得的总收益率是40%;当售出的乙种款式的件数比甲各种款式的件数多80%时,这个老板获得的总收益率是45%.【考点】分式方程的应用.【剖析】可设甲、乙的进价,甲种款式售出的件数为未知数,依据售出的乙种款式比售出的甲种款式的件数少40%时,这个老板获得的总收益率为40%获得甲、乙进价之间的关系,从而求适当售出的乙种款式的件数比甲种款式的件数多80%时,这个老板的总收益率即可.【解答】解:设甲种款式进价为a元,则售出价为1.3a元;乙种款式的进价为b元,则售出价为1.5b元;若售出甲种款式x件,则售出乙种款式0.6x件,依题意有=40%,解得:a=0.6b,当售出的乙种款式的件数比甲种款式的件数多80%时,设甲种款式的件数为y件,则乙种款式的件数1.8y件,则==45%.答:这个老板获得的总收益率是45%.故答案为:45%.三、解答题(共27题)23.计算:(1)18﹣6÷(﹣2)×(﹣);(2)(﹣﹣)×24+(1﹣0.5)+3×.【考点】有理数的混杂运算.【剖析】(1)原式先计算乘除运算,再计算加减运算即可获得结果;(2)原式利用乘法分派律及乘法法例计算即可获得结果.【解答】解:(1)原式=18﹣1=17;(2)原式=21﹣4﹣18++2=1.24.解方程(组):(1)7﹣3(x+1)=2(4﹣x)(2).【考点】解二元一次方程组;解一元一次方程.【剖析】(1)依据一元一次方程的解法即可解答;(2)利用加减消元法即可解答.【解答】解:(1)7﹣3(x+1)=2(4﹣x)7﹣3x﹣3=8﹣2x﹣3x+2x=8﹣7﹣x=1x=﹣1.(2)整理方程组得:①×2得:12x﹣4y=10③③﹣②得:9x=4,解得:x=,把x=代入①得:﹣2y=5,解得:y=﹣.所以方程组的解为:.2225.先化简,再求值:3(x﹣2xy)﹣4[xy﹣1+(﹣xy+x)],此中x=﹣4,y=.【考点】整式的加减—化简求值.【剖析】原式去括号归并获得最简结果,把x与y的值代入计算即可求出值.【解答】解:原式=3x2﹣6xy﹣xy+4+6xy﹣6x2=﹣3x2﹣xy+4,当x=﹣4,y=时,原式=﹣48+2+4=﹣42.26.巴蜀中学对本校初2017届500名学生中中考参加体育加试测试状况进行检查,依据男生1000米及女生800米测试成绩整理,绘制成不完好的统计图,(图①,图②),请依据统计图供给的信息,回答以下问题:(1)该校毕业生中男生有300人;扇形统计图中a=12;(2)补全条形统计图;(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?【考点】概率公式;扇形统计图;条形统计图.【剖析】(1)男生人数为20+40+60+180=300;8分对应百分数用8分的总人数÷500;(2)8分以下总人数=500×10%=50,此中女生=50﹣20,10分总人数=500×62%=310,此中女生人数=310﹣180=130,从而补全直方图;(3)可利用样本的百分数去估计整体的概率,即可求出答案.【解答】解(1)如图,男生人数为20+40+60+180=300,8分对应百分数为(40+20)÷500=12%,故答案为:300,12;(2)补图以下图:(3)500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是=.27.以下图.(1)已知∠AOB=9°0,∠BOC=3°0,OM均分∠AOC,ON均分∠BOC,求∠MON的度数;(2)∠AOB=α,∠BOCβ=,OM均分∠AOC,ON均分∠BOC,求∠MON的大小.【考点】角均分线的定义.【剖析】(1)依据题意可知,∠AOC=12°0,由OM均分∠AOC,ON均分∠BOC;推出∠MOC=∠AOC=6°0,∠CON=∠BOC=1°5,由图形可知,∠MON=∠MOC﹣∠CON,即∠MON=4°5;(2)同理可得,∠MOC=(α+β),∠CON=β,依据图形即可推出∠MON=∠MOC﹣∠CON=(α+β)﹣β=α.【解答】解:(1)∵∠AOB=9°0,∠BOC=3°0,∴∠AOC=∠AOB+∠BOC=9°0+30°=120°,∵OM均分∠AOC,ON均分∠BOC,∴∠MOC=∠AOC=6°0,∠CON=∠BOC=1°5,∴∠MON=∠MOC﹣∠CON=6°0﹣15°=45°;故答案为:45°;(2)同理可得,∠MOC=(α+β),∠CON=β,则∠MON=∠MOC﹣∠CON=(α+β)﹣β=α.28.某汽车专卖店销售A、B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额96万元,本周已售出2辆A型车和1辆B型车,销售额为62万元.(1)求每辆A型车和B型车的售价各是多少?(2)跟着汽车限购限号政策的实行,估计下周起A,B两种型号的汽车价钱在原有的基础上均有上升,若A型汽车价钱上升m%,B型汽车价钱上升3m%,则同时购置一台A型车和一台B型车的花费比涨价前多12%,求m的值.【考点】二元一次方程的应用.【剖析】(1)每辆A型车和B型车的售价分别是x万元、y万元.则等量关系为:1辆A型车和3辆B型车,销售额为96万元,2辆A型车和1辆B型车,销售额为62万元;(2)依据:“A型汽车价钱上升的部分+B型汽车价钱上升的部分=同时购置A、B型汽车比原价高的部分”列方程求解可得.【解答】解:(1)设每辆A型车和B型车的售价分别是x万元、y万元.则,解得.答:每辆A型车的售价为18万元,每辆B型车的售价为26万元;(2)依据题意,得:18×m%+26×3m%=(18+26)×12%,解得:m=5.5,答:m的值为5.5.29.张老师周末到某家居建材市场购置沙发、橱窗和地板三样物件,刚巧该市场推出“迎圣诞元旦双节”优惠活动,详细优惠状况以下:购物总金额(原价)优惠率不超出5000元的部分10%超出5000元且不超出10000元的部分20%超出10000元且不超出20000元的部分30%⋯⋯(1)若购置三样物件原价8000元,恳求出张老师实质的付款金额?(2)若购置三样物件实质花销了6820元.①恳求出三件物件的原价总合是多少钱?②几日后,张老师发现地板的款式不适合需要退货,该市场规定:花费者需支付优惠差额(即退货商品在购置时所享受的优惠),而且还要支付商品原价5%的手续费,最后该市场退还了张老师2345元,请问地板原价是多少钱?【考点】一元一次方程的应用.【剖析】(1)设三件物件的原价总合是x元,由花销的钱数可知,商品的原价应在5000元﹣10000元之间,依据原价﹣优惠的钱数=花销的钱数列出方程解答即可;(2)设地板的原价为a元,由退回的钱数可知,商品的原价应在5000元以内,依据原价﹣优惠的钱数﹣支付原价的手续费=2345,列出方程解答即可.【解答】解:(1)购置三样物件原价8000元,张老师实质的付款金额为8000×80%=6400元;(2)设三件家电的原价总合是x元,由题意得,x﹣5000×10%﹣(x﹣5000)×20%=6820,解得:x=7900.答:三件家电的原价总合是7900元.(2)设地板的原价为a元,由题意得a﹣10%a﹣20%a=2345,解得:a=3350.答:地板的原价为3350元.。
重庆巴蜀中学人教版七年级上册数学期末试卷及答案-百度文库

12.某商店有两个进价不同的计算器都卖了135元,其中一个盈利25%,另一个亏本25%,在这次买卖中,这家商店( )
A.不赔不赚B.赚了9元C.赚了18元D.赔了18元
二、填空题
13.如果实数a,b满足(a-3)2+|b+1|=0,那么 =__________.
26.(1)化简:3x2﹣ ;
(2)先化简,再求值:2(a2﹣ab﹣3.5)﹣(a2﹣4ab﹣9),其中a=﹣5,b= .
27.计算:﹣6÷2+ ×12+(﹣3) .
28.已知:如图,平面上有A、B、C、D、F五个点,根据下列语句画出图形:
(Ⅰ)直线BC与射线AD相交于点M;
(Ⅱ)连接AB,并反向延长线段AB至点E,使AE= BE;
16.已知a,b是正整数,且 ,则 的最大值是______.
17.请先阅读,再计算:
因为: , , ,…, ,
所以:
则 _________.
18.按照下面的程序计算:
如果输入 的值是正整数,输出结果是166,那么满足条件的 的值为___________.
19.小何买了5本笔记本,10支圆珠笔,设笔记本的单价为a元,圆珠笔的单价为b元,则小何共花费_____元(用含a,b的代数式表示).
(Ⅲ)①在直线BC上求作一点P,使点P到A、F两点的距离之和最小;
②作图的依据是.
29.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为 和 ,现将一个半径为 的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为 (如图甲),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高 (如图乙).
【七年级数学】2018年重庆市巴蜀中学七年级数学上期末试卷(带答案和解释)

2018年重庆市巴蜀中学七年级数学上期末试卷(带答案和
解释)
2018学年重庆市巴蜀中学七年级(上)期末数学试卷
参考答案与试题解析
一、选择题(每题4分,共48分)
1.在﹣2,﹣1,0,2这四个数中,最小的数是()
A.﹣2B.﹣1c.0D.2
【考点】有理数大小比较.
【分析】因为正数大于一切负数,0大于负数,所以负数最小,﹣2<﹣1,所以﹣2最小.
【解答】解﹣2<﹣1<0<2,
故选A.
2.对于单项式5πR2,下列说法正确的是()
A.系数为5B.系数为5πc.次数为3D.次数为4
【考点】单项式.
【分析】根据单项式系数、次数的定义求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.【解答】解单项式5πR2的系数是5π,次数是2,
故选B.
3.如图,有一个正方体纸巾盒,它的平面展开图是()
A. B. c. D.
【考点】几何体的展开图.
【分析】由平面图形的折叠及正方体的展开图解题.
【解答】解观察图形可知,一个正方体纸巾盒,它的平面展开图是.。
2018-2019学年七年级(上)期末数学试题(解析版)

2018-2019学年七年级(上)期末数学试卷一、选择题(本大题共8小题,共24.0分)1. 如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是()A. B. C. D.【答案】B【解析】【分析】检测质量时,与标准质量偏差越小,合格的程度就越高.比较与标准质量的差的绝对值即可.【详解】|+0.6|=0.6,|-0.2|=0.2,|-0.5|=0.5,|+0.3|=0.3 ,而0.2<0.3<0.5<0.6 ,∴B球与标准质量偏差最小,故选B.【点睛】本题考查的是绝对值的应用,理解绝对值表示的意义是解决本题的关键.2. 用式子表示“a的2倍与b的差的平方”,正确的是()A. 2(a﹣b)2B. 2a﹣b2C. (a﹣2b)2D. (2a﹣b)2【答案】D【解析】【分析】根据代数式的表示方法,先求倍数,然后求差,再求平方.【详解】解:a的2倍为2a,与b的差的平方为(2a﹣b)2故选:D.【点睛】本题考查了列代数式的知识,列代数式的关键是正确理解题目中的关键词,比如本题中的倍、差、平方等,从而明确其中的运算关系,正确的列出代数式.3. 在下面四个几何体中,左视图、俯视图分别是长方形和圆的几何体是()A. B. C. D.【答案】A【解析】【分析】逐一判断出各几何体的左视图、俯视图即可求得答案.【详解】A 、圆柱的左视图是长方形,俯视图是圆,符合题意;B 、圆锥的的左视图是等腰三角形,俯视图是带有圆心的圆,不符合题意;C 、长方体的左视图是长方形,俯视图是长方形,不符合题意;D 、三棱柱的左视图是长方形,俯视图是三角形,不符合题意,故选A .【点睛】本题考查了简单几何体的三视图,熟练掌握常见几何体的三视图是解题的关键.4. 下列各式中运算正确的是( )A. 224a a a +=B. 4a 3a 1-=C. 2223a b 4ba a b -=-D. 2353a 2a 5a +=【答案】C【解析】【分析】根据合并同类项的法则逐一进行计算即可.【详解】A. 222a a 2a +=,故A 选项错误;B. 4a 3a a -=,故B 选项错误;C. 2223a b 4ba a b -=-,正确;D. 23a 与32a 不是同类项,不能合并,故D 选项错误,故选C .【点睛】本题考查了合并同类项法则的应用,注意:合并同类项时,把同类项的系数相加作为结果的系数,字母和字母的指数不变.5. 如图,能用∠1、∠ABC、∠B 三种方法表示同一个角的是( ) A. B. C.D.【答案】A【解析】【分析】根据角的表示法可以得到正确解答.【详解】解:B、C、D选项中,以B为顶点的角不只一个,所以不能用∠B表示某个角,所以三个选项都是错误的;A选项中,以B为顶点的只有一个角,并且∠B=∠ABC=∠1,所以A正确.故选A .【点睛】本题考查角的表示法,明确“过某个顶点的角不只一个时,不能单独用这个顶点表示角”是解题关键.6. 如图,经过刨平的木板上的A,B两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是()A. 两点之间,线段最短B. 两点确定一条直线C. 垂线段最短D. 在同一平面内,过一点有且只有一条直线与已知直线垂直【答案】B【解析】【分析】根据“经过两点有且只有一条直线”即可得出结论.【详解】解:∵经过两点有且只有一条直线,∴经过木板上的A、B两个点,只能弹出一条笔直的墨线.故选B.【点睛】本题考查了直线性质,牢记“经过两点有且只有一条直线”是解题的关键.7. 在下列式子中变形正确的是( )A. 如果a b =,那么a c b c +=-B. 如果a b =,那么a b 33=C. 如果a 63=,那么a 2=D. 如果a b c 0-+=,那么a b c =+【答案】B【解析】【分析】根据等式的性质逐个判断即可.【详解】A 、∵a=b ,∴a+c=b+c ,不是b-c ,故本选项不符合题意;B 、∵a=b ,∴两边都除以3得:a b 33=,故本选项符合题意; C 、∵a 63=,∴两边都乘以3得:a=18,故本选项不符合题意; D 、∵a-b+c=0,∴两边都加b-c 得:a=b-c ,故本选项不符合题意,故选B .【点睛】本题考查了等式的性质,能熟记等式的性质的内容是解此题的关键.8. 直线l 外一点P 与直线l 上两点的连线段长分别为3cm ,5cm ,则点P 到直线l 的距离是( )A. 不超过3cmB. 3cmC. 5cmD. 不少于5cm【答案】A【解析】【分析】根据直线外的点与直线上各点的连线垂线段最短,可得答案.【详解】解:直线外的点与直线上各点的连线垂线段最短,得点P 到直线l 的距离是小于或等于3,故选A .【点睛】本题考查了点到直线的距离,直线外的点与直线上各点的连线垂线段最短. 二、填空题(本大题共10小题,共30.0分)9. 元月份某天某市的最高气温是4℃,最低气温是-5℃,那么这天的温差(最高气温减最低气温)是______℃.【答案】9【解析】【分析】利用最高气温减最低气温,再根据减去一个数等于加上这个数的相反数计算即可.【详解】这天的温差为4-(-5)=4+5=9(℃),故答案为9【点睛】本题考查有理数的减法的应用,正确列出算式,熟练掌握有理数减法的运算法则是解题的关键. 10. 我国倡导的“一带一路”建设将促进我国与世界各国的互利合作,“一带一路”地区覆盖总人口约为4400000000人,将数据4400000000用科学记数法表示为______.【答案】4.4×109【解析】【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>10时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】4400000000的小数点向左移动9位得到4.4,所以4400000000用科学记数法可表示为:4.4×109, 故答案为4.4×109. 【点睛】本题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.11. 若3x =-是关于x 的一元一次方程250x m ++=的解,则m 的值为___________.【答案】1【解析】把x =−3代入方程得:−6+m +5=0,解得:m =1,故答案为1.12. 若|x -12|+(y +2)2=0,则(xy )2019的值为______. 【答案】-1【解析】【分析】根据非负数的性质列出算式,求出x 、y 的值,计算即可.【详解】∵|x-12|+(y+2)2=0, ∴x-12=0,y+2=0, ∴x=12,y=-2,∴(xy)2019=(-1)2019=-1,故答案为-1.【点睛】本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.13. 若a+b=2019,c+d=-5,则代数式(a-2c)-(2d-b)=______.【答案】2029【解析】【分析】根据去括号、添括号法则把原式变形,代入计算,得到答案.【详解】(a-2c)-(2d-b)=a-2c-2d+b=(a+b)-2(c+d)=2019+10=2029,故答案为2029.【点睛】本题考查的是整式的加减混合运算,掌握去括号、添括号法则是解题的关键.注意整体思想的应用.14. 一个正方体的平面展开图如图所示,将它折成正方体后“扬”字对面是______字.【答案】美【解析】【分析】注意正方体的空间图形,从相对面入手,分析及解答问题.【详解】对于正方体的平面展开图中相对的面一定相隔一个小正方形,由图形可知,“扬”字对面是“美”字,故答案为美.【点睛】本题考查了正方体的平面展开图,对于正方体的平面展开图中相对的面一定相隔一个小正方形,据此作答.15. 若∠A=45°30′,则∠A的补角等于_______________.【答案】134°30′【解析】试题分析:根据补角定义:如果两个角的和等于180°(平角),就说这两个角互为补角可得答案.解:∵∠A=45°30′,∴∠A的补角=180°﹣45°30′=179°60′﹣45°30′=134°30′,故答案为134°30′.考点:余角和补角;度分秒的换算.16. 如图,将一副直角三角板叠放在一起,使其直角顶点重合于点O,若∠DOC=26°,则∠AOB=______°.【答案】154【解析】【分析】先根据∠COB=∠DOB-∠DOC求出∠COB,再代入∠AOB=∠AOC+∠COB,即可求解.【详解】∵∠COB=∠DOB-∠DOC=90°-26°=64°,∴∠AOB=∠AOC+∠COB=90°+64°=154°,故答案是:154.【点睛】本题考查了角度的计算,弄清角的和差关系是解题的关键.17. 已知线段AB=6cm,C是线段AB的中点,E是直线AB上的一点,且CE=13AB,则线段AE=______cm.【答案】1或5【解析】【分析】由已知C是线段AB中点,AB=6,求得AC=3,进一步分类探讨:E在线段AC内;E在线段CB内;由此画图得出答案即可.【详解】∵C是线段AB的中点,AB=6cm,∴AC=12AB=3cm,CE=13AB=2cm,①如图,当E在线段AC上时,AE=AC-CE=3-2=1cm;②如图,E在线段CB上,AE=AC+CE=3+2=5cm,所以AE=1cm或5cm,故答案为1或5.【点睛】本题考查线段中点的意义,线段的和与差,分类探究是解决问题的关键.18. 某中学初三(6)班十几名同学毕业前和数学老师合影留念,一张彩色底片要0.6元,扩印一张相片0.5元,每人分一张,免费赠送老师一张(由学生出钱),每个学生交0.6元刚好,则相片上共有______人.【答案】12【解析】【分析】扩印费+0.5×照片上人数=0.6×学生数,把相关数值代入计算即可.【详解】设相片上共有x人,0.6+0.5x=0.6×(x-1),解得x=12,故答案为12.【点睛】本题考查一元一次方程的应用,弄清题意,得到所需总费用的等量关系是解决本题的关键.三、计算题(本大题共4小题,共32.0分)19. 计算:(1)14-(-12)+(-25)-17.(2)(12-13)÷(-16)-22×(-4).【答案】(1)-16;(2)15【解析】【分析】(1)根据有理数的加减法法则进行计算即可;(2)按顺序先计算括号内的减法、乘方,然后再按运算顺序进行计算即可. 【详解】(1)14-(-12)+(-25)-17=14+12+(-25)+(-17)=-16;(2)(12-13)÷(-16)-22×(-4)=16×(-6)-4×(-4)=(-1)+16=15.【点睛】本题考查了有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.20. 化简:(1)(5a-3b)-3(a-2b);(2)3x2-[7x-(4x-3)-2x2].【答案】(1)2a+3b;(2)5x2-3x-3【解析】【分析】(1)先按照去括号法则去掉整式中的小括号,再合并整式中的同类项即可;(2)先按照去括号法则去掉整式中的小括号,然后去中括号,最后合并整式中的同类项即可.【详解】(1)原式=5a-3b-3a+6b=2a+3b;(2)原式=3x2-[7x-4x+3-2x2]=3x2-7x+4x-3+2x2=5x2-3x-3.【点睛】本题考查整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则.21. 解方程:(1)2x+3=11-6x.(2)x24+-2x16-=1【答案】(1)x=1;(2)x=-4.【解析】【分析】(1)按移项、合并同类项、系数化为1的步骤进行求解即可得;(2)按去分母、去括号、移项、合并同类项、系数化为1的步骤进行求解即可得.【详解】(1)2x+6x=11-3,8x=8,x=1;(2)3(x+2)-2(2x-1)=12,3x+6-4x+2=12,3x-4x=12-6-2,-x=4,x=-4.【点睛】本题主要考查解一元一次方程,去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a形式转化.22. 先化简,再求值,2(3ab2-a3b)-3(2ab2-a3b),其中a=-12,b=4.【答案】a3b,1 2 -.【解析】【分析】根据乘法分配律,先去括号,再合并同类项进行化简,再代入求值. 【详解】解:原式=6ab2﹣2a3b﹣6ab2+3a3b=a3b,当a=12-,b=4时,原式=3142⎛⎫-⨯⎪⎝⎭=12-.故答案为1 2 -【点睛】本题考核知识点:整式化简求值.解题关键点:根据乘法分配律去括号,再合并同类项.四、解答题(本大题共6小题,共64.0分)23. 如图,点P是∠AOB的边OB上的一点.(1)过点P画OB的垂线,交OA于点C;(2)过点P画OA的垂线,垂足为H;(3)线段PH的长度是点P到______的距离,______是点C到直线OB的距离,线段PC、PH、OC这三条线段大小关系是______(用“<”号连接).【答案】(1)见解析;(2)见解析;(3)OA,PC的长度,PH<PC<OC.【解析】【分析】(1)利用三角板过点P画∠OPC=90°即可;(2)利用网格特点,过点P画∠PHO=90°即可;(3)利用点到直线的距离可以判断线段PH的长度是点P到OA的距离,PC是点C到直线OB的距离,根据垂线段最短即可确定线段PC、PH、OC的大小关系.【详解】(1)如图所示;(2)如图所示;(3) 线段PH的长度是点P到OA的距离,PC是点C到直线OB的距离,根据垂线段最短可知PH<PC<OC,故答案为OA,PC,PH<PC<OC.【点睛】本题主要考查了基本作图----作已知直线的垂线,另外还需利用点到直线的距离才可解决问题.24. 某小组计划做一批“中华结”,如果每人做6个,那么比计划多做了8个;如果每人做4个,那么比计划少做了42个.请你根据以上信息,提出一个用一元一次方程解决的问题,并写出解答过程.【答案】计划做多少个“中华结”?答案见解析.【解析】【分析】首先提出问题:这批“中华结”的个数是多少?设该批“中华结”的个数为x个,根据加工总个数=单人加工个数×人数,结合该小组人数不变找出关于x的一元一次方程,解之即可得出结论.【详解】这批“中华结”的个数是多少?设计划做“中华结”的个数为x个.根据题意,得:842 64x x+-=.解得:x=142.答:计划做“中华结”的个数为142个.【点睛】本题考查了一元一次方程应用.25. 阅读下面一段文字:问题:0.8⋅能用分数表示吗?探求:步骤①设x=0.8⋅,步骤②10x=10×0.8⋅,步骤③10x=8.8⋅,步骤④10x =8+0.8⋅,步骤⑤10x =8+x ,步骤⑥9x =8,步骤⑦x =89. 根据你对这段文字的理解,回答下列问题:(1)步骤①到步骤②的依据是______;(2)仿照上述探求过程,请你尝试把0.36⋅⋅表示成分数的形式.【答案】(1)等式的基本性质2:等式两边都乘以或除以同一个数(除数不能为0),所得的等式仍然成立;(2)见解析,114x =. 【解析】【分析】(1)利用等式的基本性质得出答案;(2)利用已知设x=0.36⋅⋅,进而得出100x=36+x ,求出即可.【详解】(1)步骤①到步骤②,等式的两边同时乘10,依据的是等式的基本性质2:等式两边都乘以或除以同一个数(除数不能为0),所得的等式仍然成立,故答案为等式的基本性质2:等式两边都乘以或除以同一个数(除数不能为0),所得的等式仍然成立;(2)设x=0.36⋅⋅,100x=100×0.36⋅⋅,100x=36.36⋅⋅,100x=36+ 0.36⋅⋅,100x=36+x ,99x=36,解得:x=411. 【点睛】本题主要考查了等式的基本性质以及一元一次方程的应用,根据题意得出正确等量关系是解题关键.26. 如图,直线AB 、CD 、EF 相交于点O ,OG ⊥CD ,∠BOD =32°.(1)求∠AOG 的度数;(2)如果OC 是∠AOE 的平分线,那么OG 是∠AOF 的平分线吗?请说明理由.【答案】(1)∠AOG=58°;(2)OG是∠AOF的平分线,见解析.【解析】【分析】(1)根据对顶角的性质,可得∠AOC的度数,根据角的和差,可得答案;(2)根据角平分线的性质,可得∠AOC与∠COE的关系,根据对顶角的性质,可得∠DOF与∠COE的关系,根据等量代换,可得∠AOC与∠DOF的关系,根据余角的性质,可得答案.【详解】(1)由对顶角相等,得∠AOC=∠BOD=32°,由角的和差,得∠AOG=∠COG-∠AOC=90°-32°=58°;(2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线,理由如下:由OC是∠AOE的平分线,得∠COE=∠AOC=32°,由对顶角相等,得∠DOF=∠COE,等量代换,得∠DOF=∠AOC,∠AOC+∠AOG=∠COG=90°,∠DOF+∠FOG=∠DOG=90°,由等角的余角相等,得∠AOG=∠FOG,OG是∠AOF的平分线.【点睛】本题考查了对顶角、邻补角,(1)利用了对顶角相等的性质,角的和差;(2)利用了对顶角相等的性质,角的和差,还利用了余角的性质:等角的余角相等.27. 为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.若某户居民1月份用水38m ,则应收水费:264(86)20⨯+⨯-=元.(1)若该户居民2月份用水312.5m ,则应收水费______元;(2)若该户居民3、4月份共用水315m (4月份用水量超过3月份),共交水费44元,则该户居民3,4月份各用水多少立方米?【答案】(1)48;(2)三月份用水34m .四月份用水113m .【解析】【分析】(1)根据表中收费规则即可得到结果;(2)分两种情况:用水不超过36m 时与用水超过36m ,但不超过310m 时,再这两种情况下设三月份用水3m x ,根据表中收费规则分别列出方程即可得到结果.【详解】(1)应收水费()()264106812.51048⨯+⨯-+⨯-=元.(2)当三月份用水不超过36m 时,设三月份用水3m x ,则()226448151044x x +⨯+⨯+--= 解之得411x =<,符合题意.当三月份用水超过36m 时,但不超过310m 时,设三月份用水3m x ,则()()264626448151044x x ⨯+-+⨯+⨯+⨯--=解之得36x =<(舍去)所以三月份用水34m .四月份用水113m .28. 如图,点O 在直线AB 上,OC ⊥AB ,△ODE 中,∠ODE =90°,∠EOD =60°,先将△ODE 一边OE 与OC 重合,然后绕点O 顺时针方向旋转,当OE 与OB 重合时停止旋转.(1)当OD 在OA 与OC 之间,且∠COD =20°时,则∠AOE =______;(2)试探索:在△ODE 旋转过程中,∠AOD 与∠COE 大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.【答案】(1)130°;(2)∠AOD与∠COE的差不发生变化,为30°;(3)∠AOE=131.25°或175°.【解析】【分析】(1)求出∠COE的度数,即可求出答案;(2)分为两种情况,根据∠AOC=90°和∠DOE=60°求出即可;(3)根据∠AOE=7∠COD、∠DOE=60°、∠AOC=90°求出即可.【详解】(1)∵OC⊥AB,∴∠AOC=90°,∵OD在OA和OC之间,∠COD=20°,∠EOD=60°,∴∠COE=60°-20°=40°,∴∠AOE=90°+40°=130°,故答案为130°;(2)在△ODE旋转过程中,∠AOD与∠COE的差不发生变化,有两种情况:①如图1、∵∠AOD+∠COD=90°,∠COD+∠COE=60°,∴∠AOD-∠COE=90°-60°=30°,②如图2、∵∠AOD=∠AOC+∠COD=90°+∠COD,∠COE=∠DOE+∠DOC=60°+∠DOC,∴∠AOD-∠COE=(90°+∠COD)-(60°+∠COD)=30°,即△ODE在旋转过程中,∠AOD与∠COE的差不发生变化,为30°;(3)如图1、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,∴90°+60°-∠COD=7∠COD,解得:∠COD=18.75°,∴∠AOE=7×18.75°=131.25°;如图2、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,∴90°+60°+∠COD=7∠COD,∴∠COD=25°,∴∠AOE=7×25°=175°,即∠AOE=131.25°或175°.【点睛】本题考查了角的有关计算的应用,能根据题意求出各个角的度数是解此题的关键.注意分类思想的运用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆巴蜀中学2018-2019学度初一上年末数学试题及解析
初2017级(一上)数学测试题
(满分:150分考试时间:120分钟)
一、选择(每小题4分,共48分) 1、下列各数中,最小的数是()
A.-2
B.-0.5
C.0
D.|-2|
2、如图,在下列几何体中,主视图与其他几何体主视图形状不一样的是()
3、下列各式计算正确的是()
A.8
442x x x =+ B.y x y x 6
3
2
)(= C.5
3
2)(x x = D.8
5
3
)(x x x =-⋅-
4、下列调查中,适合采用全面调查(普查)的是() A.浙江卫视《奔跑吧,兄弟》节目收视率的调查
B.要保证嫦娥三号卫星的成功发射,对它的零件采用的检查方式
C.调查重庆市全市中小学生节约用水的意识
D.要了解一批签字笔笔芯的使用寿命
5、如图,AB 是直线,O 是直线上一点,OC 、OD 是两条射线,则图中小于平角的角有() A.3个B.4个C.5个D.6个
6、已知1-=x 是方程24=+x ax 的解,则a 的值是() A.-6B.6C.2D.-2
7、如图,是正方体包装盒的表面积展开图,如在其中的三个正方形A 、B 、C 、D 内分别填上适当的数,使得将这个表面积展开图沿虚线折成正方形后,相对面上的两数字互为相反数,
则填在A 、B 、C 内的三个数字依次为() A.0,1,-2B.0,-2,1C.1,0,-2D.-2,0,1
8、如图,已知线段AB 长为10cm ,C 是线段AB 上任意一点,则AC 的中点与BC 的中点距离是()
A.3cm
B.4cm
C.5cm
D.不能确定
9、下列各多项式的乘法中,能用平方差公式计算的有()
①)2)(2(xy xy +-;②))((n m n m +--;③))((b a b a ---;④)1)(1(-++-b a b a
A.1个
B.2个
C.3个
D.4个 10、若n 为正整数,则计算n n 21
2)2(2)2(-⨯+-+的结果是()
A.0B.1C.1
22
+n D.1
22
+-n
11、观察下列图形及图形所对的算式,根据你发现的规律计算1+8+16+24+......+8n (n 为正整数)的结果()
1+8=?1+8+16=?1+8+16+24=? A.2n B.2)12(-n C.2)2(+n D.2
)12(+n
12、))(2(b a b a M -+=,)(32
b ab N -=(其中b a ≠),则M ,N 的大小关系是() A.N M > B.N M < C.N M = D.无法确定 二、填空(每题3分,共30分)
13、单项式5
32y
x π-的系数是。
14、2015年1月18日,重庆遭遇雾霾天,整个城市被“深埋”,空气中的PM2.5的浓度持续增高。
其中PM2.5是指直径小于或等于0.0000025m 的颗粒物,将0.0000025m 用科学计数法表示是m 。
15、若63)1(|
|-=+-a x a 是关于x 的一元一次方程,则a 的值为。
16、已知93,23==n m
,则m n +23=。
17、如图,正方形ABCD 的边长为a,以直线AB 为轴将正方形旋转一周,所得圆柱的主视图的周长为。
18、若两块直角三角板的直角顶点重合为如图所示的位置,若AOD ∠=1100,则BOC ∠的度数为。
19、如图是小正方体组成的几何体的三视图,则该几何体共有个小正方体组成。
20、已知3,72
2
=+=+b a b a ,则代数式)2)(2(--b a 的值为。
21、如图,已知AOC BOC ∠=∠2,OD 平分AOB ∠,且,20=∠COD 则AOB ∠=度。
22、老张在装修新房时想在客厅的地面按照图1所示的正方形图案铺贴仿古地板砖,图1是由四块尺寸完全相同的长方形砖拼成的一个正方形,中间还可另外嵌一个面积为m m 1.01.0⨯的小正方形花砖(花砖老张已另买)。
但老张买砖时只看中了如图2所示的一款较大的正方形地砖,于是只能将其按照图3的方式切割出图1所需的长方形砖在进行铺贴,
经过计算这样切割会让每块地砖产生0.12m 2废料,已知老张家客厅的面积为30m 2,请你帮老张算一下他需购买图2这款地砖块。
三、解答(共72分)
23、计算(每小题5分,共10分) (1)2
3
4
)
3
1
()2()3(1-+---+-π(2)3
23)5.01(24)436187(⨯÷-+⨯--
24、整式的化简(每小题5分,共10分)
(1)2
)2())(4(b a b a b a --+-(2)xy xy xy y x 2
1
)23(2
2÷+- 25、解方程(每小题6分,共12分) (1)x x 45)32(2-=-(2)15
1
312=--+x x 26、(8分)先化简,再求值
b b a b a b b a a b ÷-++-+24)2()2)(2(;其中a,b 满足0)12(|4|2=-++b a
27、(10分)学校为了了解我校七年级学生课外阅读的喜好,随机抽取我校七年级的部分学生进行问卷调查(每人只选一种书籍)。
下图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息回答问题:
(1)这次活动一共调查了名学生;
(2)补全条形统计图
(3)在扇形统计图中,喜欢漫画的部分所占圆心角是度;
(4)若七年级共有学生2800人,请你估计喜欢“科普常识”的学生人数共有多少名? 28、(10分)某开发商进行商铺促销,广告上写着如下条款:投资者购买商铺后,必须由开发商代租赁5年,5年期满后由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:
方案一:按照商铺标价一次性付清铺款,每年可获得的租金为商铺标价的10%;
方案二:按商铺标价的八折一次性付清铺款,前3年商铺的租金收益归开发商所有,3年后每年可获得的租金为商铺标价的9%
(1)问投资者选择哪种购铺方案,5年后所获得的投资收益率更高?为什么? (注:%100⨯=
实际投资额
投资收益
投资收益率)
(2)对同一标价的商铺,甲选择了购铺方案一,乙选择了购铺方案二,那么5年后两人获得的收益相差7.2万元。
问甲乙两人各投资了多少万元?
29、(12分)老张装修完新房,元旦期间又到苏宁电器购买冰箱、电视机和洗衣机三件家电,刚好该商场推出新年优惠活动,具体优惠情况如下表:
已知老张购买者三件物品一共花费了7150元。
(1)求出三件家电的原价总共是多少钱?
(2)提货后,老张发现洗衣机的尺寸不合适需要退货,该商场规定:消费者要支付优惠率差额(即退货商品在购物时所享受的优惠),并且还要支付商品原价12%的手续费,最终该商场退还了老张1180元钱,请问该洗衣机原价是多少钱?。
