GOOGLE MAPS地图投影全解析
墨卡托投影

地图投影为什么地图数学要素:地图投影、比例尺、控制点、坐标网、高程系、地图分幅等。
在我的印象中,比例尺从打小开始接触地图就强调其重要性,关联着距离量测。
当时还有指北针等要注意的事项,主要关注于地图的使用。
后来一不小心入了GIS的门,还得学会更深入的使用地图数据甚至是编制地图。
这时候,大学GIS第一门课程《地图投影》就来了。
当时的注意点完全被繁琐的公式迷惑,不过看着用C语言在那小黑块的屏幕画出一幅幅漂亮的投影地图,还是相当的快乐。
时至今日,又多了解些相关知识,重新回顾复习整理下。
在个人的认知地图中,限于区域范围,可认为是平面图形,加上自我中心位置和日常距离的估测,基本上就构成了认知坐标系,无需要什么投影知识。
事实上,地球表面是曲面,而地图是二维的平面,两者之间必然有个映射关系,(数学上的射影几何?)才可对应出大地坐标系。
分三个步骤来完成投影:1)确定地球椭球体(Spheroid/Ellipsoid),需要长半轴、短半轴、曲率三个参数。
(模拟地球的形状)2)若要逼近某特定地区,则需要大地基准(Geodetic Datum)。
(椭球体的原点the position of the origin、方向 the orientation、缩放比例 the scale等)我国现在采取西安1980坐标系基准点,同时也有国家1985高程基准。
3)如何投影,这就涉及高斯-克吕格投影等诸多投影方式的存在,等角等积等距离,方位圆柱圆锥等分类。
因此,就地图投影坐标系参数来看,分为两个部分:Ellipsoid 、 Datum ;Projection。
Ellipsoid与Datum是相关联的,一般提到某个Datum,则其Ellipsoid也包含在内;两者的对应关系是一对多,即一个Ellipsoid可以为多个Datum所用,不同的Datum的Ellipsoid可以是相同的。
由于世界各地区投影类型的不同,因此在叠加、复合不同来源空间数据时,必需首先进行投影转换、配准等设置。
3.2地图投影及其分类,3.3常用的地图投影解析PPT参考幻灯片
轴投影
5
§3 常用的地图投影
❖ 1.墨卡托投影(等角正圆柱投影) 投影原理:设想地球为一透明球体,球心置一点光
源,将圆柱投影面沿赤道与地球相切,地球上的经纬网格投 影到圆柱面上
6
墨卡托投影绘制的世界地图
§3 常用的地图投影
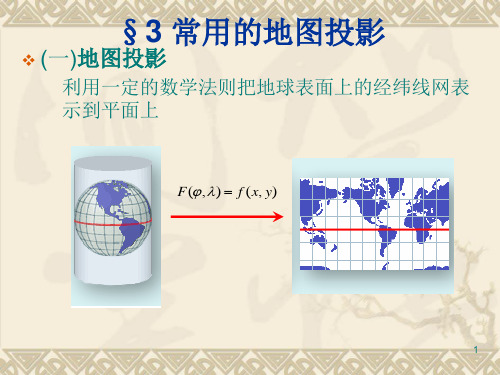
❖ (一)地图投影
利用一定的数学法则把地球表面上的经纬线网表 示到平面上
F(, ) f (x, y)
1
❖ 1. 地图投影的失真
由于地球椭球体表面是曲面,而地图通常是要绘制在平 面图纸上,因此制图时首先要把曲面展为平面,然而球 面是个不可展的曲面,即把它直接展为平面时,不可能 不发生破裂或褶皱。
为了保证地图的精度,采用分带投影方法,即将投 影范围的东西界加以限制,使其失真不超过一定的 限度,这样把许多带结合起来,可成为整个区域的 投影。
我国规定1:1 万、1:2.5 万、1:5 万、1:10万、 1:25 万、1:50 万比例尺地形图,均采用高斯克 -吕格投影。1:2.5 至1:50 万比例尺地形图采用 经差6 °分带,1:1 万比例尺地形图采用经差3° 分带。
绘制机场专用航图和涉及仪表飞行程序的基础用图; 国家大地测量和五十万分之一及更大比例尺的国家基本地形
图
13
❖ 高斯投影坐标网
经纬网(地理坐标网)
114°00 14
16
30° 202
40´
α
3396
94 -δ TH/TC
92
18 20 A( 20218 , 3394 )
90
TH/TC= α+(± δ)
第九章-地图投影及地形图的应用解析PPT课件

H5 0B0 0 1 0 0 2
1:100 1:100
比
图
图
例
幅
幅
万 图 幅 行
万 图 幅 列
尺 代 码
行 号 字
列 号 字
号号
符
符
字字 符符
码
-
码
14
码码
已知武汉某地的大地坐标为北纬3031,东经11428, H50
1:5000~1:500000地形图的行列号可按下式计算:
行号= int(BN B) 1 B
列号= int(L LW ) 1 L
式中LW、BN为1:100万地形图图廓西北角的经纬度
-
15
比例尺 代码
1:50万 B
1:25万 C
1:10万 D
1:5万 E
1:2.5万 F
1:1万 G
1:5000 H
x y
f1(L,B) f2(L,B)
f1(,) f2(,)
当给定不同的具体条件时,就可得到不同种类的投影公式。根据 公式将一系列的经纬线交点(L,B)或(,)计算成平面直角 坐标(x, y),并展绘于平面上,即可建立经纬线平面表象,构成
地图的数学基础。
-
3
二、高斯投影
按投影变形分类:地图投影可分为等角投影(正形投 影) 、等积投影和任意投影。 高斯投影是一种等角横切椭圆柱投影
-
12
1:100万地形图的分幅与编号
60 V01 02
H01
B01 0 A01 -180
1:100万
31
Google 地图切片URL地址解析

[置顶][置顶]Google 地图切片URL地址解析分类:GIS 2012-05-19 11:56 8564人阅读评论(4) 收藏举报googleurlchromeserviceweb目录(?)[+]一、Google地图切片的投影方式及瓦片索引机制1.Google地图采用的是Web墨卡托投影(如下图),为了方便忽略了两极变形较大的地区,把世界地图做成了一个边长等于赤道周长的正方形(赤道长度为6378137米),原点在正方形中心,即经纬度为(0,0)处。
Web墨卡托投影的X,Y坐标取值范围为:[-20037508.3427892,20037508.3427892],对应的经度取值范围为[-180,180],对应的纬度范围则为[-85.05112877980659,85.05112877980659]。
具体投影解释请参考墨卡托投影:2.Google 地图的索引机制是TMS(Tile Map Service) 规范的一个变种,其地图瓦片如下图进行索引:Google 瓦片坐标系:把地球投影后形成的正方形划分为2 的level(缩放级别) 次幂个地图瓦片,原点在左上角,类似于像素坐标系;详细解释参见Google MapsAPI 文档。
TMS瓦片坐标系:TMS与Google的地图瓦片切割方法相同,不同的是TMS的原点在左下角。
转换关系:TMS 与Google 坐标系的X 、Z是相等的,Y 的转换关系为:Y(TMS) + Y(Google) = Math.pow(2,zoom) - 1注:关于投影和瓦片索引机制强烈推荐阅读:Tiles à la Google Maps: Coordinates, Tile Bounds and Projection,文中详细分析了地图瓦片涉及各类坐标的转换关系及具体算法,包括瓦片坐标(Google、TMS、Bing QuadTree)、像素坐标、WGS84 经纬度、Mercator 投影平面坐标等。
web 墨卡托投影

Web墨卡托投影坐标系:
以整个世界范围,赤道作为标准纬线,本初子午线作为中央经线,两者交点为坐标原点,向东向北为正,向西向南为负。
X轴:由于赤道半径为6378137米,则赤道周长为2*PI*r = 2*20037508.3427892,因此X轴的取值范围:[-20037508.3427892,20037508.3427892]。
Y轴:由墨卡托投影的公式可知,同时上图也有示意,当纬度φ接近两极,即90°时,y值趋向于无穷。这是那些“懒惰的工程师”就把Y轴的取值范围也限定在[-20037508.3427892,20037508.3427892]之间,搞个正方形。
懒人的好处,众所周知,事先切好静态图片,提高访问效率云云。俺只是告诉你为什么会是这样子。因此在投影坐标系(米)下的范围是:最小(-20037508.3427892, -20037508.3427892 )到最大 (20037508.3427892, 20037508.3427892)。
但是,“等角”不可避免的带来的面积的巨大变形,特别是两极地区,明显的如格陵兰岛比实际面积扩大了N倍。不过要是去两极地区探险或科考的同志们,一般有更详细的资料,不会来查看网络地图的,这个不要紧。
为什么是圆形球体,而非椭球体?
这说来简单,仅仅是由于实现的方便,和计算上的简单,精度理论上差别0.33%之内,特别是比例尺越大,地物更详细的时候,差别基本可以忽略。
PROJECTION["Mercator_1SP"],
PARAMETER["central_meridian",0],
PARAMETER["scale_factor",1],
PARAMETER["false_easting",0],
Google Maps地图投影全解析

Google Maps地图投影全解析Google Maps、Virtual Earth等网络地理所使用的地图投影,常被称作Web Mercator或Spherical Mercator,它与常规墨卡托投影的主要区别就是把地球模拟为球体而非椭球体。
什么是墨卡托投影?墨卡托(Mercator)投影,又名“等角正轴圆柱投影”,荷兰地图学家墨卡托(Mercator)在1569年拟定,假设地球被围在一个中空的圆柱里,其赤道与圆柱相接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅标准纬线为零度(即赤道)的“墨卡托投影”绘制出的世界地图。
从球到平面,肯定有个转换公式,这里就不再罗列。
Google为什么选择墨卡托投影?墨卡托投影的“等角”特性,保证了对象的形状的不变行,正方形的物体投影后不会变为长方形。
“等角”也保证了方向和相互位置的正确性,因此在航海和航空中常常应用,而在计算人们查询地物的方向时不会出错。
墨卡托投影的“圆柱”特性,保证了南北(纬线)和东西(经线)都是平行直线,并且相互垂直。
而且经线间隔是相同的,纬线间隔从标准纬线(此处是赤道,也可能是其他纬线)向两级逐渐增大。
但是,“等角”不可避免的带来的面积的巨大变形,特别是两极地区,明显的如格陵兰岛比实际面积扩大了N倍。
不过要是去两极地区探险或可靠的同志们,一般有更详细的资料,不会来查看网络地图的,这个不要紧。
为什么是圆形球体,而非椭球体?这说来简单,仅仅是由于实现的方便,和计算上的简单,精度理论上差别0.33%之内,特别是比例尺越大,地物更详细的时候,差别基本可以忽略。
Web墨卡托投影坐标系:以整个世界范围,赤道作为标准纬线,本初子午线作为中央经线,两者交点为坐标原点,向东向北为正,向西向南为负。
X轴:由于赤道半径为6378137米,则赤道周长为2*PI*r = 20037508.3427892,因此X轴的取值范围:[-20037508.3427892,20037508.3427892]。
《Google Map中的瓦片》
《Google Map中的瓦片》分类:地图2013-07-03 11:56631人阅读评论(0)收藏举报一、墨卡托投影google map使用的是EPSG:900913标准墨卡托投影(等角圆术地图投影)y = R*ln(tan(pi/4 + a/2))x = R*b当y等于piR时,投影图正好为一个正方形,可行到纬度为85.05113度,把以Google map 的最大纬度为[-85.05113,85.05113],最大经度为[-180,180]。
赤道长度为6378137米,那么根据公式可求科最大边界[-20037508.342789244,20037508.342789244]米。
二、瓦片金字塔google map是由256*256的图片拼接而成的,称为瓦片。
在初始等级(0)时,整个地球只投影在一张瓦片上,也就是256像素代表了40075016.685578488米。
即40075016.685578488/256=156543.033928041(米/像素)。
缩入由四叉树实现,即放大一个级别后,原来一张图片分裂成4张。
见下图三、瓦片url形如:/vt/lyrs=m@180000000&hl=zh-CN&gl=cn&src=app&x=3&y=1&z=2&s =Gamt0:服务器名(Google Map有四个服务器)hl:语言x:瓦片X轴的信息编号y:瓦片Y轴的信息编号z:瓦片的缩放级别s:""和"Galileo"共8个字符(无实际意义)计算关系:mt = (x + y) % 4s = (3 * x + y) % 8空白瓦片url/intl/zh-CN_cn/mapfiles/transparent.png 注意:瓦片信息编号是从左上角(0,0)开始的。
Google map中的墨卡托投影
墨卡托投影,又称等角正切圆柱投影,其原理是假设有一个与在赤道与地球相切的圆柱面,先把球面映射到这个圆柱面,再把这个圆柱面展开成为一个平面。
在墨卡托投影中,强调角度不变——假定地球表面有两点A和B,在地球球面上,B相对于A的角度是北偏东,那么经过墨卡托投影之后,在平面地图上,B相对于A的角度仍然是北偏东。
这一点在航海中非常重要,因为在茫茫大海中,没有什么参照物,只能根据罗盘或者星象来判断方位,如果地图上终点相对于出发点的方位角和实际的方位角不同,那么这样的地图在航海中没有实际意义。
正因为如此,海图一般都是采用墨卡托投影规则制作的(极地海图除外)。
例:设地球的半径为R,已知地球上一点P的坐标是,其中表示经度,范围是-<<,负数表示西经,正数表示东经;B表示维度,范围是-<<,负数表示南纬,正数表示北纬。
将地球球面通过墨卡托投影映射到平面直角坐标系中,以0度经线与赤道的交点的映射点为原点,X轴与纬线平行,并取东方为正方向;Y轴与经线平行,并取北方为正方向。
求P点在平面直角坐标系中的映射点P'的坐标(Xp',Yp')。
解:根据墨卡托投影的原理可知,墨卡托投影是由一个和地球赤道相切的圆柱面展开而成的,所以展开之后的图形的宽度就是地球赤道的长度,P'点的X坐标就是通过P'点的经线与赤道的交点到0度经线和赤道的交点之间的距离,也就是赤道线的一部分,其值为:求P’点的Y坐标稍微麻烦一点,我们看下图:因为墨卡托投影要遵循的一个原则是方向角不变,所以映射过程中X方向和Y方向的缩放比例要相同。
从图中我们可以知道,纬度为的纬线圈,投影过后变成和赤道一样长的一条直线,所以纬度为的点附近一个非常小的区域,投影过后,水平方向的放大比率是:而根据墨卡托投影的规则,该块小区域垂直方向上上的放大比率也应该是,在投影之前的地球表面上,小块区域竖直方向的边长就是经线的一部分,我们可以用地球的半径乘以一个小角度来表示:那么投影之后的小区域竖直方向上的边长应该是:在上式中,对纬度进行积分,我们便可以计算出纬度是的点,投影之后的Y坐标是:所以,最终的结果就是:也许你会怀疑,这个积分是怎样计算出来的,说实话我也没有搞清楚,据说是骨灰级的数学家算出来的,如果你想验证,我建议你从微分入手,证明下式成立,可能会容易一些:至此,我们已经了解了墨卡托投影的原理和坐标转换的算法,但是还只能是比较粗浅的了解,为了能够深入掌握这种投影技术,这里有几个思考题供大家练习:1)很多人错误地认为,用一个柱面把地球罩起来,柱面与地球的赤道相切,在地球球心处点一盏灯,假设地球表面是半透明的,那么在柱面上能够得到地球表面的影子,把柱面上地球表面的影子固定下来,把柱面沿着0度经线裁开,展开成为平面图,就完成了墨卡托投影。
测绘技术中的地图投影方法解析
测绘技术中的地图投影方法解析地图投影是测绘技术中的一个重要领域,在地理信息系统和地图制作中起着至关重要的作用。
地图投影方法是将地球上的三维地球表面投射到二维地图上的过程,通过这一过程可以解决地球表面的曲面变换问题。
一、地图投影的基本概念地球是一个不规则的椭球体,而地图是一个平面。
由于地球的形状和地图的平面形状不一样,所以需要进行地图投影。
地图投影就是将地球上的经纬度坐标投影到平面坐标上的过程。
在地图投影中,有很多种投影方法可供选择,每种投影方法都有其独特的优势和特点。
下面将介绍几种常见的地图投影方法。
二、等角地图投影等角地图投影是指投影后的地图上,任意两条曲线的夹角等于地球上对应两条经线的夹角。
这种地图投影方法可以保持角度的真实性,因此在地图上的形状和方位保持得相对准确。
最著名的等角地图投影是墨卡托投影。
墨卡托投影在航海和航空中得到广泛应用,其特点是经纬线呈直线排列,但在高纬度地区会出现严重变形。
墨卡托投影在航海导航和地图制作中得到广泛应用。
三、等面积地图投影等面积地图投影是指投影后的地图上,任意两个区域的面积比在地球上保持不变。
这种地图投影方法可以保持地图上相对大小的真实性,因此在面积统计和地理分析中具有重要的意义。
兰勃特投影是一种常见的等面积地图投影,其特点是保持区域形状和面积的真实性,但在投影后的地图上,经纬线呈不规则曲线排列。
兰勃特投影在地理统计和地质勘探中得到广泛应用。
四、等距地图投影等距地图投影是指投影后的地图上,任意两个点之间的距离在地球上保持不变。
这种地图投影方法可以保持地图上的距离和比例的真实性,因此在测量和导航中非常重要。
鲁宾投影是一种常见的等距地图投影,其特点是保持地图上任意两个点之间的直线距离不变。
鲁宾投影在航空地图和地理勘探中得到广泛应用。
五、斯特雷格投影斯特雷格投影是一种将球面投影到平面上的方法,其特点是保持图形在大面积上的形和相对距离。
这种地图投影方法在气候学、地质学和地理信息系统中得到广泛应用。
常用地图投影
地图投影概述一、高斯-克吕格投影和UTM投影1.1 高斯-克吕格投影与UTM投影异同高斯-克吕格(Gauss-Kruger)投影与UTM投影(Universal Transverse Mercator,通用横轴墨卡托投影)都是横轴墨卡托投影的变种。
从投影几何方式看,高斯-克吕格投影是“等角横切圆柱投影”,投影后中央经线保持长度不变,即比例系数为1;UTM投影是“等角横轴割圆柱投影”,圆柱割地球于南纬80°和北纬84°两条纬线圈,投影后两条割线上没有变形,中央经线上长度比0.9996。
从计算结果看,两者主要差别在比例因子上,高斯-克吕格投影中央经线上的比例系数为1,UTM投影为0.9996。
从分带方式看,两者的分带起点不同,高斯-克吕格投影自0度子午线起每隔经差6度自西向东分带,第1带的中央经度为3°;UTM投影自西经180°起每隔经差6度自西向东分带,第1带的中央经度为-177°,因此高斯-克吕格投影的第1带是UTM的第31带。
从坐标伪偏移看,两投影的东伪偏移量都是500公里;高斯-克吕格投影的北伪偏移为零,UTM北半球投影北伪偏移为零,南半球则为10000公里。
1.2 高斯-克吕格投影简介高斯-克吕格(Gauss-Kruger)投影,是一种“等角横切椭圆柱投影”。
德国数学家、物理学家、天文学家高斯(CarlFriedrich Gauss,1777一 1855)于十九世纪二十年代拟定,后经德国大地测量学家克吕格(JohannesKruger,1857~1928)于1912年对投影公式加以补充,故名。
设想用一个椭圆柱横切于地球椭球体上投影带的中央经线,按照投影带中央经线投影为直线且长度不变和赤道投影为直线的条件,将中央经线两侧一定经差范围内的椭球面正形投影于椭圆柱面。
然后将圆柱面沿过南北极的母线剪开展平,即获高斯一克吕格投影平面。
高斯一克吕格投影后,除中央经线和赤道为直线外,其他经线均为对称于中央经线的曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Google Maps地图投影全解析Google Maps、Virtual Earth等网络地理所使用的地图投影,常被称作Web Mercator或Spherical Mercator,它与常规墨卡托投影的主要区别就是把地球模拟为球体而非椭球体。
建议先对地图投影知识做一个基本的了解,《地图投影为什么》。
什么是墨卡托投影?墨卡托(Mercator)投影,又名"等角正轴圆柱投影",荷兰地图学家墨卡托(Mercator)在1569年拟定,假设地球被围在一个中空的圆柱里,其赤道与圆柱相接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅标准纬线为零度(即赤道)的"墨卡托投影"绘制出的世界地图。
从球到平面,肯定有个转换公式,这里就不再罗列。
Google们为什么选择墨卡托投影?墨卡托投影的"等角"特性,保证了对象的形状的不变行,正方形的物体投影后不会变为长方形。
"等角"也保证了方向和相互位置的正确性,因此在航海和航空中常常应用,而Google 们在计算人们查询地物的方向时不会出错。
墨卡托投影的"圆柱"特性,保证了南北(纬线)和东西(经线)都是平行直线,并且相互垂直。
而且经线间隔是相同的,纬线间隔从标准纬线(此处是赤道,也可能是其他纬线)向两级逐渐增大。
但是,"等角"不可避免的带来的面积的巨大变形,特别是两极地区,明显的如格陵兰岛比实际面积扩大了N倍。
不过要是去两极地区探险或可靠的同志们,一般有更详细的资料,不会来查看网络地图的,这个不要紧。
(图片来源:IDVUX博客)为什么是圆形球体,而非椭球体?这说来简单,仅仅是由于实现的方便,和计算上的简单,精度理论上差别0.33%之内,特别是比例尺越大,地物更详细的时候,差别基本可以忽略。
Web墨卡托投影坐标系:以整个世界范围,赤道作为标准纬线,本初子午线作为中央经线,两者交点为坐标原点,向东向北为正,向西向南为负。
X轴:由于赤道半径为6378137米,则赤道周长为2*PI*r=20037508.3427892,因此X 轴的取值范围:[-20037508.3427892,20037508.3427892]。
Y轴:由墨卡托投影的公式可知,同时上图也有示意,当纬度φ接近两极,即90°时,y值趋向于无穷。
这是那些"懒惰的工程师"就把Y轴的取值范围也限定在[-20037508.3427892,20037508.3427892]之间,搞个正方形。
懒人的好处,众所周知,事先切好静态图片,提高访问效率云云。
俺只是告诉你为什么会是这样子。
因此在投影坐标系(米)下的范围是:最小(-20037508.3427892,-20037508.3427892)到最大(20037508.3427892,20037508.3427892)。
对应的地理坐标系:按道理,先讲地理坐标系才是,比如球体还是椭球体是地理坐标系的事情,和墨卡托投影本关联不大。
简单来说,投影坐标系(PROJCS)是平面坐标系,以米为单位;而地理坐标系(GEOGCS)是椭球面坐标系,以经纬度为单位。
具体可参考《坐标系、坐标参照系、坐标变换、投影变换》。
经度:这边没问题,可取全球范围:[-180,180]。
纬度:上面已知,纬度不可能到达90°,懒人们为了正方形而取的-20037508.3427892,经过反计算,可得到纬度85.05112877980659。
因此纬度取值范围是[-85.05112877980659,85.05112877980659]。
其余的地区怎么办?没事,企鹅们不在乎。
因此,地理坐标系(经纬度)对应的范围是:最小(-180,-85.05112877980659),最大(180, 85.05112877980659)。
至于其中的Datum、坐标转换等就不再多言。
相关坐标计算:关于Google Maps等的组织方式——地图瓦片金字塔,估计我在这里重复一遍这玩意,怕也是没人看了。
尽管原理都一样,但具体到写不同厂商不同数据源的代码时,你会发现,可缩放级别数不一样,最小级别不一样,编码方式不一样,比如Google的QRST,微软的四叉树,OSGeo的TMS等。
然而,你或许也不必这么麻烦,因为这些算法在网络上早已遍布朝野,你尽可从他人博客中获取,或是从开源软件里学习。
这本身都不是秘密,微软自己也是公布的。
《Tilesàla Google Maps》用交互性地方式可得到任一Tile的边界范围,各种流行编码方式等。
该页面的链接都非常有价值,部分也是本文写作的重要参考。
作者用python完成了下列坐标之间转换算法:经纬度(出现在KML中的坐标,WMS的BBOX参数等),平面坐标XY(米,Web Mercator投影坐标系),金字塔的XYZ(即X轴的位置,Y轴的位置,和缩放级别ZoomLevel),每个Tile的编码Key值(QRST或0123等)。
转换时,还需要注意两个概念,Ground Resolution和Map Scale。
(图片来源:)Ground Resolution,地面分辨率,类似Spatial Resolution(空间分辨率),我们这里主要关注用象元(pixel size)表示的形式:一个像素(pixel)代表的地面尺寸(米)。
以Virtual Earth 为例,Level为1时,图片大小为512*512(4个Tile),那么赤道空间分辨率为:赤道周长/512。
其他纬度的空间分辨率则为纬度圈长度/512,极端的北极则为0。
Level为2时,赤道的空间分辨率为赤道周长/1024,其他纬度为纬度圈长度1024。
很明显,Ground Resolution取决于两个参数,缩放级别Level和纬度latitude,Level决定像素的多少,latitude决定地面距离的长短。
地面分辨率的公式为,单位:米/像素:ground resolution=(cos(latitude*pi/180)*2*pi*6378137meters)/ (256*2level pixels)Map Scale,即地图比例尺,小学知识,图上距离比实地距离,两者单位一般都是米。
在Ground Resolution的计算中,由Level可得到图片的像素大小,那么需要把其转换为以米为单位的距离,涉及到DPI(dot per inch),暂时可理解为类似的PPI(pixelper inch),即每英寸代表多少个像素。
256*2level/DPI即得到相应的英寸inch,再把英寸inch 除以0.0254转换为米。
实地距离仍旧是:cos(latitude*pi/180)*2*pi*6378137 meters;因此比例尺的公式为,一般都化为1:XXX,无单位:map scale=256*2level/screen dpi/0.0254/(cos(latitude*pi/180)* 2*pi*6378137)=1:(cos(latitude*pi/180)*2*pi*6378137*screen dpi)/(256*2level *0.0254)其实,Map Scale和Ground Resolution存在对应关系,毕竟都和实地距离相关联,两者关系:map scale=1:ground resolution*screen dpi/0.0254meters/inch 《Virtual Earth Tile System》列举了Virtual Earth在赤道上,Level、像素数、地面分辨率、地图比例尺的对应关系,同时本文也简单介绍了Mercator投影和上述两个概念,推荐。
此外,《Addressing Google Maps image tiles》应用程序,输入经纬度和缩放级别,即可缩放到相应的Google Maps位置,而且可以显示出查找过程的QRST。
JavaScript实现的算法,也可以抓下来和《Tilesàla Google Maps》对比下,从经纬度到到Tile编码的转换。
WKT形式表示Google Maps和Virtual Earth等的流行程度不用多讲,然而他们所使用的Web Mercator或Spherical Mercator在很长一段时间内并没有被EPSG的投影数据库所接纳。
EPSG认为它不能算作科学意义上的投影,所以只是给了一个EPSG:900913的标号(SRID),这个标号游离在EPSG常规标号范围之外。
(EPSG、SRID是什么?参见《EPSG、SRID》。
)到了2008年5月(据SharpGIS同学),EPSG恍然明白,不管椭球体还是球体,其实都是对地球的模拟,只是精确程度上的差别,没有本质上的不同。
或者是不得不接受广泛的事实标准,接纳了这个投影,定义投影坐标系PROJCS的名字为"Popular Visualisation CRS /Mercator",SRID为EPSG:3785;地理坐标系GEOGCS的名字为"Popular Visualisation CRS",SRID为"EPSG:4055"。
这些标号已经进入"正常范围"。
(PS:这个Visualisation是英式英语写法?)PROJCS的WKT《Well Known Text》写法如下,GEOGCS、Datum等的WKT表示参见《Spherical/Web Mercator:EPSG code3785》。
附带说一句,Web Mercator在ESRI公司的编号(ESRI叫它Well Known ID?)暂时是102113,或许偶尔用得到。
PROJCS["Popular Visualisation CRS/Mercator",GEOGCS["Popular Visualisation CRS",DATUM["Popular_Visualisation_Datum",SPHEROID["Popular Visualisation Sphere",6378137,0,AUTHORITY["EPSG","7059"]],TOWGS84[0,0,0,0,0,0,0],AUTHORITY["EPSG","6055"]],PRIMEM["Greenwich",0,AUTHORITY["EPSG","8901"]],UNIT["degree",0.01745329251994328,AUTHORITY["EPSG","9122"]],AUTHORITY["EPSG","4055"]],UNIT["metre",1,AUTHORITY["EPSG","9001"]],PROJECTION["Mercator_1SP"],PARAMETER["central_meridian",0],PARAMETER["scale_factor",1],PARAMETER["false_easting",0],PARAMETER["false_northing",0],AUTHORITY["EPSG","3785"],AXIS["X",EAST],AXIS["Y",NORTH]]附记:这个问题算是老问题,费这么多时间,主要就是分享,毕竟自己还算是相当明白。
