鄂温克中学八年级数学上册 14.1.4 (4)同底数幂的除法教学案(无答案)(新版)新人教版
八年级数学上册 14.1.4 整式的乘法 同底数幂的除法学案(新版)新人教版

同底数幂的除法学习目标:1.理解同底数幂的除法运算法则,能灵活运用法则进行计算,并能解决实际问题.2.探索推导“同底数幂的除法运算法则”的过程中,让学生体会从特殊到一般的数学归纳思想,继续培养学生的推理能力和语言、符号的表达能力.学习重点:能灵活运用同底数幂的除法运算法则进行计算 .学习难点:应用同底数幂的除法运算法则解决数学问题.学习过程:一、自主学习,导入新课问题一: (用2分钟时间快速解答下面6个问题,看谁反映的快!)1.我们已经知道同底数幂的乘法法则:a m ·a n =a m+n ,那么同底数幂怎么相除呢?2. (1)用你学过的知识完成下面计算.①23·22=2( ) ②103·104=10( ) ③a 4·a 3=a ( )(2)根据上面的计算,由除法和乘法是互为逆运算,你能直接写出下面各题的结果吗? ①25÷22= ;②107÷103= ;③a 7÷a3= (a≠0).3.仿例计算:(用幂的形式填空)①=⨯⨯⨯=÷2222222525 个 ; ②=÷371010 = ; ③=÷37a a = .4.类比探究:①一般地,当m 、n 为正整数,且m >n 时 ()()()a a a a a a a a a nm =∙∙∙∙∙∙=÷ 个个, ②你还能利用除法的意义来说明这个运算结果吗?③观察上面式子左右两端,你发现它们各自有什么样的特点?它们之间有怎样的运算规律?请你概括出来:5.总结法则:同底数幂的除法性质: a m ÷a n = (m 、n 为正整数,m>n ,a≠0)文字语言:同底数幂相除, .6.(1)32÷32 =9÷9= (2)32÷32 =3( )-( )=3( )= (3)a n ÷a n =a ( )-( )=a ( )=1,也就是说,任何不为0的数的 次幂等于1;字母作底数,如果没有特别说明一般不为0.二、合作学习,获取新知问题二: 1、计算(1)38a a ÷ (2)()()310a a -÷- (3)()()4722a a ÷(4)x 6÷x = ;(6)(-x)4÷(-x) = ;三、深入探究 ,活学活用问题三: 1.你会计算 (a+b)4÷(a+b)2吗?2.在幂的运算中,如果底数是多项式,法则还适用吗?3.做一做 (1)(x – y )7 ÷(x – y ) (2)(– x – y )3÷(x+y )24.由a m ÷a n =a m-n 可知:a m-n =a m ÷a n ,你会逆用这个公式吗?试一试:⑴已知3m =5,3n =4,求32m-n 的值. ⑵已知的值。
人教版八年级上册14.1.4同底数幂相除课程教学设计

14.1.4同底数幂相除【学习目标】:1.理解同底数幂的除法法则,会进行同底数幂的除法的运算。
2.懂得零指数幂的意义,并会进行相关运算。
【学习重点】:同底数幂的除法的运算性质和零指数幂的意义。
【学习难点】:同底数幂的除法的运算中指数的运算。
【学习过程】:(一)、知识回顾 同底数幂的乘法的计算法则是什么?用字母怎样表示?复习巩固(1)107 ×104 ; (2)x 2 · x 5; (3)(103)3; (4) (-x 3)2; (5)( 2a )3 (6)(-5b)3 ;(二)新课讲解:1、探索并推导同底数幂的除法的性质1.计算:(1)( )·28=216 (2)( )·53=55(3)( )·105=107 (4)( )·a 3=a 6 2.计算:(1)216÷28=( ) (2)55÷53=( )(3)107÷105=( )(4)a 6÷a 3=( )上述运算能否发现商与除数、被除数有什么关系?(教师出示问题)问1 你在解决问题2时,用到了什么知识?你能 叙述这一知识吗?537373221010a a ÷÷÷, , 问2 这三个算式属于 哪种运算?你能概括一下它们是怎样计算出来的吗?问4 你能用语言概括这一性质吗?同底数幂除法的性质:同底数幂相除,底数不变,指数相减. 思考与讨论 为什么a ≠0?下面的计算结果对不对?(1) x 6÷x 2=x 4; 对(2) 68÷62=64;不对,66 (3) a 5÷b 2=a 3; 不对 (4) (-c)4÷(-c)2=-c 2.不对,(-c)2=c 2(三)例题讲解例 计算: (1)x 8÷x 2 . (2) (ab) 5÷(ab)2..(3 a 4 ÷a (4)(-a )7÷(-a )5.(5)(-b) 5÷(-b)2.随堂练习(1) x 7÷x 5; (2) m 8÷m 8;(3) (-a)10÷(-a)7; (4)(xy)5÷(xy)3;问3 你能用上述方法计算 吗? m n a a ÷(四)探究 问题3 当被除式的指数等于除式的指数时: (1)如果根据这条性质计算 结果是多少? (2)如果根据除法意义计算 结果是多少?m n a a ÷m n a a ÷分别根据除法的意义填空,你能得什么结论?(1)32÷32= = ;(2)103÷103= = ;(3)a m ÷a m = = (a ≠0).规定: a 0=1 (a ≠ 0 )即任何不等于0的数的0次幂都等于1.例如:20030=1 (-896)0=1 (xy )0=1 (xy 9)0=1 (-m 7)0=1 (x+y )0=1 (五 )反馈练习(1) x 7÷x 5; (2) m 8÷m 8;(3) (-a)10÷(-a)7; (4)(xy)5÷(xy)3;(六)练习:提升训练.已知:x a =4,x b =9求(1) x a-b (2) x 3a-2b随堂练习一、选择题1、(2016.德州中考)下列运算错误的是( )A .a+2a=3a B.(a 2)3=6 C.a 2 .a 3 =a 5D.a 6÷a 3=a 22、(2016.泰安中考)下列计算正确的是( )A.(a 3)2=a 6B.(-2a)2=-4a 2C.m 3 .m 2=m 6D.a 6÷a 2=a 4 3、下列说法正确的是( )A.(π-3.14)0没有意义B.任何数的 0 次幂都等于1C.(8×106)÷(2×109)=4×103D.若(x+4)0=1,则x≠-44、已知(x-5)x=1,则整数X的值可能为—————5、如果x m=4,xn=8(m,n为自然数)那么x3m-n=-------------(五)课堂小结:(1)本节课学习了哪些主要内容?(2)同底数幂的除法法则a m÷a n=a m-n(a≠0,m,n都是正整数,并且m>n). (3)0指数幂a0=1 (a≠0)(4)同底数幂的除法法则的逆用a m-n=a m÷a n (a≠0,m,n都是正整数,并且m>n). (六)布置作业:(1)a9÷a3(2)212÷27(3)(-x)4÷(-x)(4)(-3)11÷(-3)。
人教版八年级上册数学教案:14.1.4整式的除法:同底数幂的除法
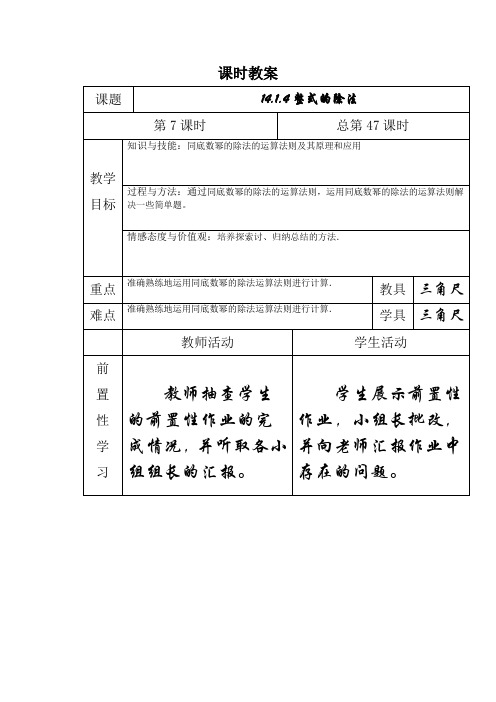
2.计算:(1)()·28=216(2)()·53=55
(3)()·105=107(4)()·a3=a6
3.再计算:(1)216÷28=( ) (2)55÷53=( )
(3)107÷105=( ) (4)a6÷a3=( )
4.提问:上述运算能否发现商与除数、被除数有什么关系?
难点
准确熟练地运用同底数幂的除法运算法则进行计算.
学具
三角尺
教师活动
学生活动
前
置
性
学
习
教师抽查学生的前置性作业的完成情况,并听取各小组组长的汇报。
学生展示前置性作业,小组长批改,并向老师汇报作业中存在的问题。
小
组
合
作
学
习
1.问题:一种数码照片的文件大小是28 K,一个存储量为26M(1M=210K)
小组内个人展示先学成果,相互交流,明确答案。
对疑难问题,小组内共同讨论完成。
提出质疑,组长解答。
汇
报
交
流
教师指导学生归纳总结,并适时点拨、评价。
1.同底数幂相除, 底数不变,指数相减.
即:am÷an=am-n.( )
1.指数m,n都是正整数,并且m>n
2.规定:a0=1(a≠0) 即:任何不等于0的数的0次幂都等于1课时教案ຫໍສະໝຸດ 课题14.1.4整式的除法
第7课时
总第47课时
教学目标
知识与技能:同底数幂的除法的运算法则及其原理和应用
过程与方法:通过同底数幂的除法的运算法则,运用同底数幂的除法的运算法则解决一些简单题。
情感态度与价值观:培养探索讨、归纳总结的方法.
重点
准确熟练地运用同底数幂的除法运算法则进行计算.
《同底数幂的除法》教案

14.1.4整式乘法第4课时教学任务分析教学过程设计一、创设问题情境,激发学生兴趣,引出本节内容活动1 复习同底数幂的乘法:a m·a n=a m+n(m、n都是正整数).幂的乘方:(a m)n=a mn(m、n都是正整数).积的乘方:(ab)n= a n b n(n为正整数).计算:(1)(-a)3(-a)2;(2)(ab)5;(3)(y m)3.活动2一种细胞每分裂一次,1个细胞变成2个细胞,细胞分裂的一个周期大约是12时,现有210个细胞经过分裂变成220个细胞,所需的时间大约是多少? 你是怎样计算的?列式:12×(220÷210)=?教师活动设计这是和数学有密切联系的现实世界中的一个问题,让同学们根据幂的意义和除法的意义,得出这个问题的结果,初步感受同底数幂的除法运算.根据除法的意义填空,看看计算结果有什么规律?(1)55÷53=________;(2)a3÷a2=________.学生活动设计学生独立思考,利用除法的意义填空,根据自己所填结果,探索、归纳同底数幂的除法法则.教师活动设计引导自主探索,发现规律,归纳同底数幂的除法法则.a m÷a n=a m-n(a≠0,m、n都是正整数,并且m>n).即:同底数幂相除,底数不变,指数相减.例(1)a9÷a3;(2)212÷27;(3)(-x)4÷(-x).练习活动3 根据除法意义填空,你有什么发现?(1)55÷52=________;(2)107÷107=________;(3)a6÷a6=______(a≠0).师生活动设计学生独立完成填空,根据所填结果,教师引导学生根据幂的除法法则得出结论:a0=1(a≠0).即:任何不等于0的数的0次幂都是1.在这个过程中要学生理解a不能等于0的原因.二、问题引申,巩固同底数幂的除法法则活动4 计算:(1)a7÷a4;(2)(-x)6÷(-x)3;(3)(xy)4÷(xy);(4)b2m+2÷b2;(5)(m-n)8÷(n-m)3;(6)(-m)4÷(-m)2.学生活动设计让适当数量的学生板演,其余的学生自行分析过程和结果.(1)a7÷a4 = a7-4 = a3;(a≠0);(2)(-x)6÷(-x)3=(-x)6-3=(-x)3=-x3 (x≠0);(3)(xy)4÷(xy)=(xy)4-1=(xy)3=x3y3 (xy≠0);(4)b2m+2÷b2=b(2m+2)-2=b2m (b≠0);(5)(m-n)8÷(n-m)3=(n-m)8÷(n-m)3=(n-m)8-3=(n-m)5(m≠n);(6)(-m)4÷(-m)2=(-m)4-2=(-m)2= m2(m≠0).教师活动设计鼓励学生独立完成计算,之后引导学生探索.1.a m÷a n=a m-n(a≠0,m、n是正整数,且m>n)中的a可以代表数,也可以代表单项式、多项式等.2.第(5)题,(m-n)8÷(n-m)3不是同底的,而应把它们化成同底,或将(m-n)8化成(n-m)8,或把(n-m)3化成-(m-n)3.3.第(6)题,易错为(-m)4÷(-m)2=-m2.-m2的底数是m,而(-m)2的底数是-m,所以(-m)4÷(-m)2=(-m)2=m2.三、归纳小结、布置作业小结:同底数幂的除法法则,0指数幂的意义.作业:。
2024~2025学年度八年级数学上册第4课时 同底数幂的除法教学设计

识.
活动二:实践探究, 获取新知 设计意图 通过提出问题,
让学生积极参与到课 堂中来,并且引导学 生自主探索,发现规 律,从而掌握同底数 幂的除法的运算性 质.探究过程由特殊 到一般,符合学生的 认知规律,同时培养 学生分析问题以及归 纳概括的能力.
探究点 1 同底数幂的除法的性质 我们知道 106×105=1011,根据乘法与除法互为逆运算,所以 1011÷105=106. 经观察,我们发现 1011÷105=1011-5=106. 问题 1 接下来请大家思考,指数换成字母,10m÷10n=? 仿照上面的计算,我们可以得到 10m÷10n=10m-n. 问题 2 如果把 10 换成字母,即 am÷an,大家猜想一下结论是否成立呢? 我们来计算 am÷an(a≠0,m,n 都是正整数,并且 m>n). 根据除法是乘法的逆运算,计算被除数除以除数所得的商,就是求一个
(3)原式=x2-x6-x8+x8=x2-x6;
(4)原式=a4·a5+a10÷a+8a9=a9+a9+8a9=10a9.
培优点一 利用方程思想和同底数幂的除法求值 例 1 如果 x2m-1÷x2=xm+1,求 m 的值. 分析:将等式左边化为底数为 x 的幂的形式,底数相同,指数就相等了,依此列出方程,解方程即可. 解:x2m-1÷x2=x2m-3=xm+1,所以 2m-3=m+1,解得 m=4. 培优点二 逆用同底数幂的除法的性质求值或证明 例 2 已知 xa=4,xb=6,xc=9. (1)求 x2a+b 的值;(2)求 xb-2c 的值;(3)求证:2b=a+c. 分析:若指数为和的形式,则考虑逆用同底数幂的乘法的性质;若指数为差的形式,则考虑逆用同底 数幂的除法的性质;若指数为乘积的形式,则考虑逆用幂的乘方的性质. (1)解:x2a+b=x2a·xb=(xa)2·xb=42×6=96. (2)解:xb-2c=xb÷(xc)2=6÷92= 2 .
《同底数幂的除法》数学教案

《同底数幂的除法》数学教案
一、教学目标:
1. 理解并掌握同底数幂的除法法则。
2. 能够运用同底数幂的除法法则解决实际问题。
3. 培养学生的逻辑思维能力和计算能力。
二、教学重点与难点:
1. 重点:理解和掌握同底数幂的除法法则。
2. 难点:运用同底数幂的除法法则解决实际问题。
三、教学过程:
(一)导入新课
通过回顾旧知识,引入新课题。
例如,复习幂的概念和性质,引导学生思考“如果两个幂的底数相同,指数不同,那么这两个幂之间有什么关系呢?”
(二)新课讲解
1. 引导学生观察、分析、归纳,得出同底数幂的除法法则:a^m / a^n =
a^(m-n) (a≠0,m,n都是正整数,m>n)。
2. 解释法则的意义,并举例说明。
(三)课堂练习
设计一些基础题和提高题,让学生独立完成,然后集体讨论答案,教师进行点评。
(四)拓展应用
设计一些实际问题,让学生运用所学的知识去解决,以培养他们的实际应用能力。
(五)小结与作业
总结本节课的主要内容,布置适当的课后作业。
四、教学策略:
1. 创设情境,激发学生的学习兴趣。
2. 注重学生的主体地位,引导他们自主学习和探究。
3. 运用多媒体教学手段,增强教学效果。
人教版八年级上册数学14.1.4同底数幂的除法(教案)
最后,我认为在总结回顾环节,我还可以做得更细致一些。我可以让学生们自己来总结今天学习的要点,我来补充和纠正。这样不仅能够检验学生对知识点的掌握情况,还能提高他们的归纳总结能力。
五、教学反思
在今天的同底数幂的除法教学中,我注意到了几个值得反思的方面。首先,我发现学生们对于指数相减的概念普遍感到困惑。在讲解这个部分时,我应该更加形象、具体地解释指数相减的含义,或许可以通过更多的实际例子来帮助学生理解这一概念。
例如,我可以用简单的面积问题来解释:如果一块地面积是4平方米,我们要将它分成边长为2米的正方形小块,那么每块面积就是2平方米。这里的除法实际上就是同底数幂的除法,即4平方米(2的平方)除以2平方米(2的平方),结果是2的零次方,也就是1块。这样的例子可以帮助学生更好地理解指数相减的实质。
其次,我发现在实践活动环节,学生们在分组讨论时,有些小组的讨论并没有深入到问题的核心。我应该在分组时更加明确每个小组的讨论方向,提供更具体的讨论问题,以便引导学生进行更有深度的探讨。
此外,我也注意到在小组讨论的过程中,一些学生不够积极。为了鼓励他们参与进来,我应该在讨论中加入更多的互动环节,比如轮流发言、小组竞赛等,以提高他们的参与度和积极性。
(2)难点举例:
a.在复合运算中,如(2^5 ÷ 2^2) ÷ 2^3,解释先进行括号内的除法运算,得到2^3,再与2^3相除,得到2^(3-3) = 2^0 = 1;
b.在实际问题中,如“一块土地面积为4平方米,如果将其分成边长为2米的正方形小地块,问可以分成多少块?”引导学生识别4平方米为2的平方(2^2),而正方形小地块的面积为2的平方(2^2),通过同底数幂的除法(4 ÷ 2^2 = 2^2 ÷ 2^2 = 2^(2-2) = 2^0 = 1),得出可以分成1块,从而加深对法则应用的理解。
14.1.4(4)同底数幂的除法 说课稿 2022—2023学年人教版数学八年级上册
14.1.4(4) 同底数幂的除法一、教学内容本节课主要讲解同底数幂的除法,即指数相同,底数相同的两个数幂的除法运算。
通过本节课的学习,学生将掌握同底数幂的除法的运算规律和解题方法。
二、教学目标1.理解同底数幂的除法的概念和运算规律;2.掌握同底数幂的除法的运算方法;3.能够运用所学知识解决相关问题。
三、教学重点和难点1.教学重点:同底数幂的除法的运算规律和解题方法;2.教学难点:能够灵活运用所学知识解决实际问题。
四、教学过程步骤一:引入对同学们进行启发性的问题引入,如:小明在做数学题时遇到了一个问题,他不知道如何计算 8^5 / 8^2,你们能给他一些建议吗?引导同学们思考同底数幂的除法应该遵循哪些运算规律。
步骤二:概念讲解引导同学们回顾指数幂的概念和运算规律,再引入同底数幂的除法。
同底数幂的除法可以通过先化简为同底数幂的乘法来解决。
即对于 a^n / a^m,我们可以化简为 a^(n-m)。
通过示例计算,帮助同学们理解运算规律,并引导同学们总结同底数幂的除法的运算规律。
步骤三:运算方法讲解给同学们提供一些具体的运算方法实例,引导他们通过化简为同底数幂的乘法来计算同底数幂的除法。
通过示例运算,帮助同学们掌握运算方法,并培养他们灵活运用的能力。
步骤四:解题示例讲解选取一些典型的题目进行解题示范,引导同学们运用所学知识解决实际问题。
通过解题示例,帮助同学们巩固所学知识,并提高解题能力。
步骤五:练习提供一定数量的练习题,让同学们独立进行解答。
布置练习题的同时,对同学们的解题过程进行监控和指导,及时纠正错误和提供帮助。
步骤六:小结对本节课所学内容进行小结,强调同底数幂的除法的运算规律和解题方法。
鼓励同学们积极参与讨论,梳理知识框架,加深对所学内容的理解。
五、课堂总结通过对同底数幂的除法的讲解和练习,同学们掌握了同底数幂的除法的运算规律和解题方法。
在今后的学习中,同学们要多做练习,掌握灵活运用的技巧,提高解题能力。
人教版数学八年级上册14.1.4 同底数幂的除法(第一课时)教案
同底数幂的除法(第一课时)一、教学目标:1.探索同底数幂的除法运算性质.2.理解0次幂的规定.3.运用法则计算单项式除以单项式.二、重点难点1.重点准确、熟练地运用法则进行计算.2.难点根据乘、除互逆的运算关系得出法则.三、教学过程1.创设情境,复习导入前面我们学习了同底数幂的乘法,请同学们回答如下问题,看哪位同学回答得快而且准确.叙述同底数幂的乘法性质.【教法说明】通过复习引起学生回忆,巩固同底数幂的乘法性质,同时为本节的学习打下基础.2.提出问题,引出新知思考问题:(a5÷a3=?)这个问题就是让我们去求一个式子,使它与相乘的积为a5,这个过程能列出一个算式吗?由一个学生回答,教师板书.这就是我们这节课要学习的同底数幂的除法运算.3.导向深入,揭示规律(1)自学课本102页后小组合作,讨论下列问题,(学生完成探究一,时间5分钟)我们通过同底数幂相乘的运算法则可知:同底数幂相除,底数不变,指数相减.学生活动:同桌研究讨论,并试着推导得出结论.提出问题:在运算过程当中,除数能否为0?学生回答:不能.(并说明理由)由此得出:同底数幂相除,底数.教师指出在我们所学知识范围内,公式中的m、n 为正整数,且m>n,最后综合得出:一般地,这就是说,a m÷a n= a m-n (a≠0, m、n都是正整数,且m>n)尝试反馈,理解新知例1 计算:(1)a12÷a7(2)x7÷x4(3) 10m÷10n (4) x5÷x4例2 计算:(1)(2)(3) (x-y)5÷(x-y)(4) a9÷(a4 a2) (2)当同底数幂的除法变成小组合作指数也相等时又得到什么结果呢?学生在学案上完成探究任务二(时间5分钟)将探究结论由学生板演完成之后,由学生总结出结论:任何不等于0的数的0次幂都等于1.教师活动:统计做题正确的人数,同时给予肯定或鼓励.反馈练习,巩固知识例3 计算:(1)a0= (2)x0 = (3) 10m÷10m = (4) x5÷x5=(3)小组合作完成探究三(时间5分钟)将探究的过程在白板上展示出来,并总结出单项式除以单项式的规律。
八年级数学上册《同底数幂的除法》教案、教学设计
为了巩固学生对同底数幂的除法的理解和应用,以及提高他们的数学思维能力,我设计了以下作业:
1.基础巩固题:请学生完成教材第chapter页的习题1-5,重点在于运用同底数幂的除法法则进行计算,并解释每一步的运算过程。
-通过这些题目,学生可以加强对同底数幂除法法则的记忆,提高运算速度和准确度。
(二)过程与方法
在本章节的教学过程中,教师应注重以下过程与方法的指导:
1.通过导入实际问题,引导学生发现同底数幂的除法运算规律,培养学生观察、分析、归纳的能力。
2.采用讲解、示范、讨论等多种教学手段,帮助学生理解同底数幂的除法法则,并能够灵活运用。
3.设计不同难度的练习题,让学生在练习中掌握同底数幂的除法运算,提高学生的实际操作能力。
4.互动问答:在讲解过程中,不断提问学生,检查他们对法则的理解程度,并鼓励他们提出疑问。
(三)学生小组讨论
在小组讨论环节,我将鼓励学生积极参与,通过合作解决问题,加深对同底数幂的除法的理解。
1.分组活动:将学生分成小组,每个小组讨论一个或多个问题,如“如何用同底数幂的除法法则解决实际问题?”
2.问题引导:提供一些具有挑战性的问题,引导学生深入探讨同底数幂的除法法则。
-这类题目旨在培养学生的逻辑思维能力和创新精神,鼓励他们在数学学习中提出自己的见解。
4.小组合作研究:布置一个小组研究课题,要求学生合作探讨同底数幂的除法在科学、工程或经济领域的应用,并以小组报告的形式展示研究成果。
-通过合作研究,学生可以学习如何协同工作,提高沟通和表达能力,同时拓展对数学知识应用范围的认识。
4.引导学生通过合作、探究的学习方式,发现并解决同底数幂运算中的问题,培养学生的团队协作能力和创新精神。
(三)情感态度与价值观
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14.1.4同底数幂的除法(学历案) 授课时间:2016.11.16
教学目标:1. 理解并掌握同底数幂的除法法则.
2. 经历 )0(10≠=a a 的得出过程,能够运用其进行运算.
3. 理解同底数幂的除法法则逆用. 教学重点:理解同底数幂的除法法则.
教学难点:熟练运用同底数幂的除法法则进行计算.
学习过程:
一、自主学习 要求:(课前自学课本102页—103页内容,对有疑惑内容做标记)
1.叙述同底数幂的乘法运算法则( )
由同底数幂相乘可得:16
88
222
=⨯,
所以根据除法的意义:2
16
÷28 =2
8
2.填空: (1)( )·28
=216
(2)( )·53
=55
(3)( )·105=107 (4)( )·a 3=a 6
3.再计算: (1)2
16
÷28=( ) (2)55÷53
=( )
(3)107
÷105
=( ) (4)a 6
÷a 3
=( )
◆提问:上述3题运算能否发现商与除数、被除数中的底数,指数有什么关系? 通过自主学习得到
归纳:同底数幂相除, , 。
1.(看103页例1,仿照例1完成下列各题)、
(1)57x x ÷ (2)710)()(a a -÷- (3)a a ÷5 (4)35)()(xy xy ÷
2.下面各式的计算是否正确?如果不对,应当怎样改正?
(1)326x x x =÷ (2)33a a a =÷
(3)224)()(c c c -=-÷- (4)()325)()(x y x y y x --=-÷-
二、问题探究
1、根据除法的意义填空:
(1)99÷=___ (2)2233÷=______ (3)m
m a a ÷=______(a ____)
2、根据同底数幂除法填空:
(1)
)
(999=÷(2)
)
(
22333=÷ (3))
(
a
a a m m =÷(a _____)
3、对比1、2题的结果,填空:
(1)1___90 (2)1___30
(3)a 0=___(a___0)
任何___________的数的0次幂
4.练习:(1)68
÷68
=______ (2)
=-0)3(π_____ (3) 若(2x+1)0=1,则x 的取值范___________
三.问题探究
1.同底数幂除法法则的逆用公式:
2.练习:若5
=a
x
,30
=a
y
则=
-a
x
y
四、归纳总结巩固新知 1、知识点的归纳总结:
(1)公式:同底数幂相除,•底数_____ ,指数______. 即:a
m
÷a n
=______.(0___a ,m ,n 都是正整数,并且m__n)
(2)a 0
=___(a___0)
即:任何不等于____的数的____次幂都等于_____.
(3)
五.作业:卷子一张
=÷a
a n
m (a___ 0,m,n 都是正整数,并且m___n ) a 0
=___(a___0)
=-a
n
m ______________ (a___0,m,n
都是正整数,并且m___n )
=-a
n m __________(a____0,m,n 都是正整数,并且m____n )
六.课堂达标 1、计算:(100分) (1) 2
4
x
x ÷ (2)a a ÷4
(3) 3
5)()(ax ax ÷
(4)2
252)()(x x ÷ (5)35
)()
(b a b a -÷- (6)23)()(ab ab -÷
(7)2
423)(x x x ⋅÷ (8) ()()22212)(++-÷--n n n a b a b b a
(9) 若b a y
x ==5,5求的y
x -25
值?
(10)当a _______时,代数式0
)34(+a 的值为1
2.选作题(20分) (11) 若13=-a
a 求的a 值?。
