理论力学综合教程——动力学
合集下载
理论力学动力学第一章PPT课件
.
29
（7）矢量的投影
el
a
l
e
l l l
为l 方向的单位矢量
alaelacos
a在自身方向上的投影
当 a 指向已知时a > 0
aaaeaa当
a
指向未知时
a > 0 假设方向对
（8）若
假设 a 的指向为
ea
a < 0 与假设方向 相反
ai bi ail bil
.
30
（9）注意区别：矢量的投影与矢量分解的分量
dt . 指向运动方向
34
加速度 加速度大小
a
dv
r
a vdt r
（1.3）
加速度方向：速度矢端图的切线方向 注意： r(t)v,(t)a,(t) 都与参考空间有关
第一篇 运动学
运动学----从几何角度研究物体的运动规律，如点 的运动方程（轨迹）、速度、加速度，刚体的转 动方程，角速度、角加速度等
一、几个重要概念 1.参考空间（参照系）
参考空间常与某物体（参照物）固连，
但 参考空间参照物
参照物——有限大，参考空间——无限大
描述物体的运动必须指明相对于哪个参考空间
自由度 S —— 广义坐标的个数
.
18
不同研究对象、运动形式与自由度
研究对象
运动形式
空间运动 平面运动
自由
S=3
S=2
质点
非自由
S<3
S<2
质点系
n个质点
刚体
无穷多质点
自由 非自由
自由 非自由
S=3n S<3n S=6 S<6
.
S=2n S<2n S=3 S<3
注册工程师基础《理论力学》-动力学
x
a
P1 M
W
ma = P1 − W
P1
=W
+W g
a
答案：B
一、质点动力学
[例 题]
G F
已知：以上抛的小球质量为m，受空气阻力
G = −k v
，则对图示坐标轴Ox，小球的运动微
分方程为：
（A） mx = mg− kx
（B） mx = −mg− kx （C） mx = −mg+ kx （D） mx = mg+ kx
J OO
=
J CC
+
m( l )22 2
=
1 3
ml 22
O
zC
z1
C
d
C
m
l
二、动力学普遍定理
1、物理量
（5）力的功 ● 常力的功
M1
F M2
θv
W = F cosθ S
S
● 变力的功
G MM22
G MM22
∫ ∫ W1122 = F ⋅ dr = F cosθ ds
MM11
MM11
● 重力的功
二、动力学普遍定理
（7）动能定理
T2－T1＝W12
（8）机械能守恒
T +V = E = 常数
2．定理
二、动力学普遍定理
2．定理
质量相同的两均质圆盘，放在光滑水平面 上，在圆盘的不同位置上，各作用一水平力F 和F′，使圆盘由静止开始运动，设F = F′， 试判断那个圆盘动能大？
A F′ B F
三、达朗贝尔原理
x B
maCx = Fx = 0
答案：C
二、动力学普遍定理
2．定理
（4）动量矩定理
Chapter2理论力学动力学部分
第二章 动力学部分 本章包含三部分内容： 第一部分介绍力学系统的基本动力学量； 第二部分介绍系统动力学的基本定 律；第三部分讨论刚体平面运动的动力学问题。 1. 力学系统的基本动力学量 考虑质点系 Pi i 1, 2,..., N 。 设坐标系 OaXYZ 为固定坐标系， 坐标系 Oxyz 相对固定坐标系 OaXYZ 为动坐标系。 (1) 质心 质点系在固定坐标系中的质心记为 G，其相对坐标系原点 Oa 的向径定义为 N m R i i i 1 RG M N 式中 R i 是质点 Pi 相对坐标系原点 Oa 的向径 Oa Pi ， M mi 为系统的总质量；
i 1
(5) 系统动能 在定系 OaXYZ 中，系统的动能定义为
1 N 2 (2.1.9) mV i i 2 i 1 ①柯尼希定理：系统的动能等于位于系统随质心的平动动能加上系统相对质心运动的动能。 证明：设 OaXYZ 为固定坐标系，Gxyz 为以质心为坐标原点的平动坐标系，质点 Pi 相对定系的速度 为 V i ，相对动系的速度为 v ir 。由式(2.1.9)得到 1 N T mi V i V i 2 i 1 1 N mi V G v ir V G v ir 2 i 1 N 1 N 1 N mi V G V G mi V G v ir mi v ir v ir 2 i 1 2 i 1 i 1 T
(3) 动能定理 对式(2.1.9)求导得到
d V i dT 1 N d V i 1 N mi V i mi V i dt 2 i 1 dt 2 i 1 dt N mi ai V i
i 1 N
e i d R i Fi Fi dt i 1 N N N e i e i dT F i F i d R i F i d R i F i d R i dW e dW i
i 1
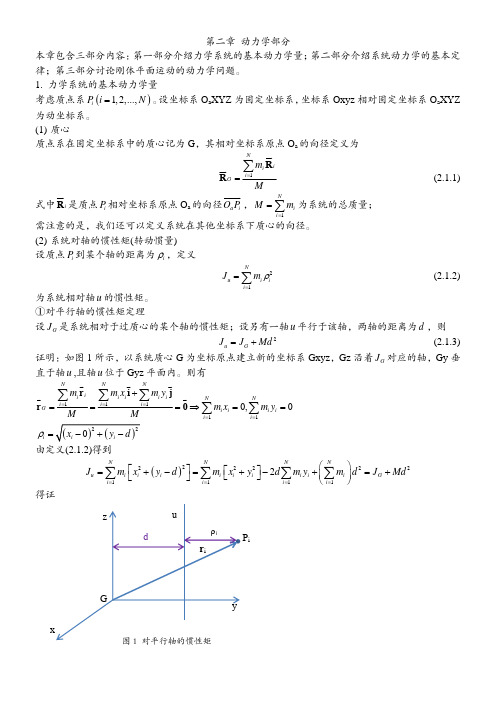
(5) 系统动能 在定系 OaXYZ 中，系统的动能定义为
1 N 2 (2.1.9) mV i i 2 i 1 ①柯尼希定理：系统的动能等于位于系统随质心的平动动能加上系统相对质心运动的动能。 证明：设 OaXYZ 为固定坐标系，Gxyz 为以质心为坐标原点的平动坐标系，质点 Pi 相对定系的速度 为 V i ，相对动系的速度为 v ir 。由式(2.1.9)得到 1 N T mi V i V i 2 i 1 1 N mi V G v ir V G v ir 2 i 1 N 1 N 1 N mi V G V G mi V G v ir mi v ir v ir 2 i 1 2 i 1 i 1 T
(3) 动能定理 对式(2.1.9)求导得到
d V i dT 1 N d V i 1 N mi V i mi V i dt 2 i 1 dt 2 i 1 dt N mi ai V i
i 1 N
e i d R i Fi Fi dt i 1 N N N e i e i dT F i F i d R i F i d R i F i d R i dW e dW i
E374-理论力学-动力学 (23)
37
yy y(x,t) 2 F(x x)
F(x)
质量： x
作用力： F(x x) F(x)
x
x x
x
加速度：
a
d
2
y(x, dt2
t)
若弦只沿 y 轴振动，即: dx 0 dt
dy(x,t) y(x,t) ;
dt
t
d
2
y( x, t ) dt 2
2
y( x, t ) t 2
x : 0 F(x x)cos( ) F(x)cos
k1
m
k2
3
控 制 振 动
主 动 减 震
4
控 10 制8 振6
4
动2
工作频率
共振频率
0
0
0.5
1
1.5
2
2
t
1.75
工作频率
1.5
1.25
1
0.75
共振频率
0.5
0.25
0.6 0.8 1 1.2 1.4 1.6 1.8 2
t
ASME J. of Engineering for Gas Turbines and Power,
解的特性讨论 B
h
(02 2 )2 4 2 2
（1）当 0
B
h
02
H /m k/m
H k
（2）当 0
B
h
2
0
（3）当 0
（4）当
2 0
4
2
B h
2
B 取得极大值
22
例：已知：m0, m, e,，k,求滑块的动力学方程。
o
解：应用质心运动定理
m
x
yy y(x,t) 2 F(x x)
F(x)
质量： x
作用力： F(x x) F(x)
x
x x
x
加速度：
a
d
2
y(x, dt2
t)
若弦只沿 y 轴振动，即: dx 0 dt
dy(x,t) y(x,t) ;
dt
t
d
2
y( x, t ) dt 2
2
y( x, t ) t 2
x : 0 F(x x)cos( ) F(x)cos
k1
m
k2
3
控 制 振 动
主 动 减 震
4
控 10 制8 振6
4
动2
工作频率
共振频率
0
0
0.5
1
1.5
2
2
t
1.75
工作频率
1.5
1.25
1
0.75
共振频率
0.5
0.25
0.6 0.8 1 1.2 1.4 1.6 1.8 2
t
ASME J. of Engineering for Gas Turbines and Power,
解的特性讨论 B
h
(02 2 )2 4 2 2
（1）当 0
B
h
02
H /m k/m
H k
（2）当 0
B
h
2
0
（3）当 0
（4）当
2 0
4
2
B h
2
B 取得极大值
22
例：已知：m0, m, e,，k,求滑块的动力学方程。
o
解：应用质心运动定理
m
x
理论力学中的动力学分析与运动方程的推导
理论力学中的动力学分析与运动方程的推导动力学是研究物体运动的学科，它通过分析力的作用和物体的运动状态，来推导出运动方程。
在理论力学中，动力学是一个重要的分支，它描述了力对物体运动的影响。
本文将从牛顿力学的角度，展示动力学分析和运动方程的推导过程。
一、牛顿第二定律的提出牛顿第二定律是描述力对物体运动的影响的基本定律。
它的数学表达式为：F=ma，其中F代表力的大小和方向，m代表物体的质量，a代表物体的加速度。
根据这个定律，我们可以得到运动方程。
二、运动方程的推导为了推导运动方程，我们需要首先建立坐标系。
假设一个物体在一维空间中运动，我们可以选取一个直角坐标系，将物体的位置用一个坐标x来表示。
接下来，我们需要考虑力对物体的作用情况。
1. 力的分析在动力学中，物体受到的力可以分为两类：约束力和非约束力。
约束力是由物体与其他物体之间的相互作用引起的，比如弹簧的张力、绳子的拉力等。
非约束力则是物体受到的其他力，如重力、摩擦力等。
根据牛顿第二定律，非约束力的合力乘以物体的质量就等于物体的加速度。
2. 运动方程的推导假设物体受到一个非约束力F，根据牛顿第二定律可以得到：F=ma。
将加速度a用速度v的导数表示，即a=dv/dt。
将速度v用位置x的导数表示，即v=dx/dt。
将以上三个式子代入F=ma中，可以得到F=m(dv/dt)=md^2x/dt^2。
这个方程就是物体在非约束力作用下的运动方程。
三、应用举例通过上述的运动方程推导，我们可以解决许多与动力学相关的问题，下面通过一个简单的应用举例来说明。
假设有一个质量为m的物体在水平面上运动，受到一个恒定的非约束力F。
根据上面推导的运动方程F=md^2x/dt^2，我们可以解得物体的运动方程为d^2x/dt^2 = F/m。
如果我们知道物体初始位置x0和初始速度v0，以及非约束力F的具体数值，那么我们可以通过求解运动方程来确定物体的运动轨迹。
首先对方程两边进行积分，得到dx/dt = v = (F/m)t + C1，其中C1为积分常数。
理论力学_动力学ppt课件
x
质点系中所有质点对于点O的 动量矩的矢量和，称为质点系 对点O的动量矩。
[LO ]z Lz
19
3. 定轴转动刚体对转轴的动量 矩
z
Lz M z (mivi ) mivi ri
miri2 miri2
ri
vi
mi
令：
mi
ri
2
Jz
Jz——刚体对 z 轴的转动惯量
y
x
Lz Jz
z
Mo(mv)
B
mv
O
r
h
A(x,y,z)
x
MO (mv) r mv
MO(mv) =mvh=2△OAB
MO(mv)
定位矢量
y
[MO (mv)]z M z (mv)
18
2. 质点系的动量矩
z
vi
LO MO (mivi )
m2
mi
ri
ri mvi
m1
O
y Lz M z (mivi )
aC g sin 0 FN mg cos
圆盘作平动
37
(b) 斜面足够粗糙
Σ Fx mg sin F maC
Σ Fy mg cos FN 0
J C FR
aC R
C
aC
F
mg
FN
aC
2 3
g sin
2 g sin
3R
F 1 mg sin
3
FN mg cos
由 F ≤ f F N 得：
自然轴系 轴, n轴和b轴上的投影)
dv m dt F
v2
m Fn
0 Fb
质点运动微分方程还可有极坐标形式, 柱坐标形式等等。 应用质点运动微分方程，可以求解质点动力学的两类问题。
理论力学课件 12动力学基本量
28
基本量
计算下列各物体的动能。
均质圆轮质量为m，半径为r；绕O轴转动，
角速度为ω，求其动能。
T
1 2
JO 2
ωr
m
O
C
1 2
(Jc
m r2
)
2
1 ( 1 m r2 m r2 ) 2
22
3 m r2 2
4 29
基本量
• 均质圆轮质量为m， 半径为r；在水平面 上纯滚动，轮心速 度为v，求其动能。
ω2 m2
O2
？
m
C
m1 ω1
O1
∵系统对称于两轮轴心连线，
∴系统质心必在该连线上， 系统质心的速度始终为零，
∴系统的动量 p = Mvc = 0 。 26
基本量
⑺ 两均质轮质量均为m1，半径均为R，两轮间距离为 d，履 带质量为m，长为 L，求 (1)系统的动量；(2)除去与地面
接触的履带以外的履带的动量。
动能等 ）和力的相关量 （ 冲量、力 矩、功等 ） —— 之间的 关系，从不同侧面对物体的机械运动进行深入的研究。
2
基本量
§12-1 基本动力学量的计算
一、动量的计算 一个质点的动量： mi , vci
1. 质点系的动量：质点系的动量等于质点系中每个质 点的动量的矢量合。
p
mi vi M vC
m2 R2 2
v2
D
2
TB
1 2
J
B
D
2 2
m2 2
( R22
R22
)
2 2
m2
R22
2 2
22
求图示均质物体或物体系统的动量。
⑴均质轮质量为m，半径为R，绕质心轴C 转动，角速度为ω， 则其动量为
基本量
计算下列各物体的动能。
均质圆轮质量为m，半径为r；绕O轴转动，
角速度为ω，求其动能。
T
1 2
JO 2
ωr
m
O
C
1 2
(Jc
m r2
)
2
1 ( 1 m r2 m r2 ) 2
22
3 m r2 2
4 29
基本量
• 均质圆轮质量为m， 半径为r；在水平面 上纯滚动，轮心速 度为v，求其动能。
ω2 m2
O2
？
m
C
m1 ω1
O1
∵系统对称于两轮轴心连线，
∴系统质心必在该连线上， 系统质心的速度始终为零，
∴系统的动量 p = Mvc = 0 。 26
基本量
⑺ 两均质轮质量均为m1，半径均为R，两轮间距离为 d，履 带质量为m，长为 L，求 (1)系统的动量；(2)除去与地面
接触的履带以外的履带的动量。
动能等 ）和力的相关量 （ 冲量、力 矩、功等 ） —— 之间的 关系，从不同侧面对物体的机械运动进行深入的研究。
2
基本量
§12-1 基本动力学量的计算
一、动量的计算 一个质点的动量： mi , vci
1. 质点系的动量：质点系的动量等于质点系中每个质 点的动量的矢量合。
p
mi vi M vC
m2 R2 2
v2
D
2
TB
1 2
J
B
D
2 2
m2 2
( R22
R22
)
2 2
m2
R22
2 2
22
求图示均质物体或物体系统的动量。
⑴均质轮质量为m，半径为R，绕质心轴C 转动，角速度为ω， 则其动量为
理论力学-静力学、动力学、运动学
它对刚体的作用效应。
1、静力学基本概念
（2）力偶
[ 例题 ]
从力偶的性质知，力偶 无合力，故一个力不能与 力偶平衡。为什么图示的 轮子上作用的力偶矩M = PR的力偶能与重物的重 力P相平衡？
M OR
P
1、静力学基本概念
力系：作用在物体上的一群力。
A
平衡力系：物体在力系作用下处于平衡。
F
（3） 刚体 在力的作用下，大小和形状都不改变的物体。
阻碍物体运动的限制条件称为约 束，约束对被约束物体的机械作用称 为约束力。
4、受力分析和受力图
4、受力分析和受力图
[ 例题 ]
试确定图示结构A、O处约束力的方向
FA
A
B
Cm
FO
D
E
O
D
FOO
E
4、受力分析和受力图
[ 例题 ]
试确定图示结构A、B、C处约束力的方向
m1
C
m2 已知：m1 = m2
作用于刚体上的力可沿其作用线移到同一刚体内 的任一点，而不改变该力对刚体的效应。
对于刚体，力的三要素为：大小，方向，作用线
2、 静力学基本公理
推论2：三力平衡汇交定理 刚体受三力作用而平衡，若其中两力作用
线汇交于一点，则另一力的作用线必汇交于 同一点，且三力的作用线共面。
1
1
3
3
2
2
3、 约束与约束反力
A
FA
FB
C
B
FC
m2
FB
B
4、受力分析和受力图
[ 例题 ]
试确定图示结构A、B处约束力的方向
B F
B m
A
C
D
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x
F
O
R
v
v0
vdv
Rx
1 x2
gR2dx
v02
v2
(1 R
1 )2gR2 x
要实现脱离地球引力作宇宙飞行，条件是：
x
x , v 0
v0 2gR 11.2km/s
工程动力学的研究模型
质点：质点是具有一定质量而几何形状和尺寸大小可以 忽略不计的物体。
广义的质点系统：系统内包含有限或无限个质点，这些 质点都具有惯性，并占据一定的空间；质点之间，质点 与边界之间，以不同的方式连接，或者附加以不同的约 束与物理条件。
刚体：是质点系的一种特殊情形，其中任意两个质点间 的距离保持不变。
ma F
★ 第三定律（作用与反作用定律）
牛顿及其在力学发展中的贡献
牛顿出生于林肯郡伍尔索朴城的一个中等农户家中。 在他出生之前父亲即去世，他不到三岁时母亲改嫁了， 他不得不靠他的外祖母养大。
1661年牛顿进入了剑桥大学的三一学院，1665年获文 学学士学位。在大学期间他全面掌握了当时的数学和光 学。1665-1666的两年期间，剑桥流行黑热病，学校暂 时停办，他回到老家。这段时间中他发现了二项式定律， 开始了光学中的颜色实验，即白光由7种色光构成的实 验，而且由于一次躺在树下看到苹果落地开始思索地心 引力问题。在30岁时，牛顿被选为皇家学会的会员，这 是当时英国最高科学荣誉。
工程动力学的研究模型
广义的质点系统
简单刚体系统－由1、2个刚体组成，每个刚体都作 二维运动，或者单个刚体作三维运动。
多刚体系统－由作大范围相对运动的多个相互约束 的刚体组成的系统。
第11章 质点动力学的基本方程
§11-1 动力学的基本定律
★ 第一定律（惯性定律） ★ 第二定律（力与加速度之间的关系的定律）
§11-2 质点的运动微分方程
n
ma Fi i 1
直角坐标形式
mx
m
d2x dt 2
i
Fix
my
m
d2y dt 2
i
Fiy
mz
m
d2z dt 2
i
Fiz
m
d 2r dt 2
n
Fi i 1
弧坐标形式
m
dv dt
Fiτ i
m v2
Fin i
0 Fib i
§11-3 质点动力学的两类基本问题
牛顿及其在力学发展中的贡献
★ 牛顿在光学上的主要贡献是发现了太阳光是由7种不 同颜色的光合成的，他提出了光的微粒说。
★ 牛顿在数学上的主要贡献是与莱布尼兹各自独立地 发明了微积分，给出了二项式定理。
★ 牛顿在力学上最重要的贡献，也是牛顿对整个自然 科学的最重要贡献是他的巨著《自然哲学的数学原理》。 这本书出版于1687年，书中提出了万有引力理论并且系 统总结了前人对动力学的研究成果，后人将这本书所总 结的经典力学系统称为牛顿力学。
动力学的两类基本问题
动力学第一类问题－已知系统的运动，求作用 在系统上的力。
动力学第二类问题－已知作用在系统上的力，求 系统的运动。
例 题 1 已知：P， 。求 fmin。
a
解: （1） 取物块为研究对象
（2） 研究对象受力分析
（3） 研究对象运动分析
（4） 列方程求解求知量
Fx
F
P sin
P g
m2
mn mi
工程动力学的研究模型
广义的质点系统
封闭质点系－既无外部质点进 入，又无内部质点流出的质点系 统。
开放质点系－有质点进入或流 出，或者二者兼而有之的质点系 统。
m1 m2 mi
mn m1 m2 mi mn
工程动力学的研究模型
广义的质点系统
开放质点系－有质点进入 或流出，或者二者兼而有之 的质点系统。
gl
v0
P
动荷系数
Fmax
P(1 v02 ) gl
Kd
Fd Fj
1 v02 gl
Hale Waihona Puke 例 题 3 求第二宇宙速度.。
解: 取卫星为研究对象
F m dv dt
F f mM , mg f mM F mg R2
x2
R2
x2
m
dv dt
mg x2
R2
dv dv dx v dv dt dx dt dx
a
Fy FN P cos 0
y
x
a
F
F
P(sin
a g ), FN
P cos
P
FN
F f FN
f min
a
g cos
tan
例 题 2 已知：P, l,v0 . 求 Fmax.。
O
解: 取物块为研究对象
F
P sin
P g
a
O1
F
Fn
F
P cos
P g
v2 l
v
F P cos P v2
● 高等动力学、机械动力学、结构动力学等等 新兴学科领域的重要理论基础。
工程动力学的研究方法
工程动力学的演绎方法
★ 根据研究对象和所研究的问题，经过合理的抽象和 简化，建立用于理论分析的模型。 ★ 建立相关的基本概念。 ★ 根据物质运动规律的有关定律和定理，应用数学分 析与演绎，导出与所研究的问题有关的定理或方程。
动力学
动力学研究物体的机械运动 与作用力之间的关系
工程实际中的动力学问题
舰载飞机在发动机和弹射器推力 作用下从甲板上起飞
工程实际中的动力学问题
若已知推力和跑道可能长 度，则需要多大的初速度和 一定的时间隔后才能达到飞 离甲板时的速度。
若已知初速度、一定的 时间间隔后飞离甲板时的速 度，则需要弹射器施加多大 推力，或者确定需要多长的 跑道。
工程动力学的研究模型
广义的质点系统
m1 m2 mi
mn
m1 m2 mi
mn
m1 m2 mi
mn
自由质点系统
非自由质点系统－ 非自由质点系统－ 质点之间刚性连接 质点之间弹性连接
工程动力学的研究模型
广义的质点系统
连续质点系－具有无穷多个 自由度的质点系统。
离散质点系－具有有限多个 m1
自由度的质点系统。
★ 系统的运动轨迹、速度、加速度、角速度、 角加速度等描述运动的量。
★ 系统的动量、冲量、动量矩、动能等描述运 动效应的量。
★ 系统的质量与描述运动的量和描述运动效应 的量之间的关系。
动力学涉及的内容与重要性
动力学在工程分析与工程设计中的重要作用
● 航空航天、交通运输、高速机械、军事工程、 体育运动等等诸多工程领域实现正常功能的重要分 析基础与设计基础。
工程实际中的动力学问题
v1
F
v2
棒球在被球棒 击打后，其速度 的大小和方向发
生了变化。如果 已知这种变化即 可确定球与棒的
相互作用力。
工程实际中的动力学问题 载人飞船的交会与对接
v2 v1
B A
工程实际中的动力学问题
航空航天器 的姿态控制
工程实际中的动力学问题 高速列车的振动问题
动力学涉及的内容与重要性