第八章 方差分析
医学统计学 -第08章 方差分析

第一节 方差分析的基本思想
看一个例子
例8-1 为研究钙离子对体重的影响作用,某研究者将36 只肥胖模型大白鼠随机分为三组,每组12只,分别给 予高脂正常剂量钙(0.5%)、高脂高剂量钙(1.0%)和高 脂高剂量钙(1.5%)三种不同的饲料,喂养9周,测其 喂养前后体重的差值。问三组不同喂养方式下大白鼠 体重改变是否不同?
• 三种喂养方式体重改变的平均值各不相同,这种变异 称为组间变异
•
是组内均值
X
与总均值
i
X
之差的平方和
360
340
组间变异反映了:
320
三种喂养方式的差异(影响), 300
同时也包含了随机误差。
280
260
240
k ni
220
SS组间
(Xi X )2
200
i1 j
180
X甲
X
X乙
X丙
甲
乙
丙
3、组内变异(SS组内,variation within groups)
0.05
2、根据公式计算SS、MS及F值,列于方差分析表内(计 算过程省略)
变异来源 总变异 组间 组内(误差)
完全随机设计的方差分析表
平方和 SS 自由度
均方MS
47758.32
35
31291.67
2
15645.83
16466.65
33
498.99
F值
31.36
3、确定P值,作出判断
分子自由度=k-1=2,分母自由度=n-k=33,查F 界值表(方差分析用)
表 8-1 三种不同喂养方式下大白鼠体重喂养前后差值(g)
正常钙(0.5%) 高剂量钙(1.0%) 高剂量钙(1.5%)
单向方差分析

F 分布曲线
17
F 界值表
5
附表5 F界值表(方差分析用,单侧界值) 上行:P=0.05 下行:P=0.01
分母自由度 υ2
•
分子旳自由度,υ1
1
2
3
4
5
6
161 200 216 225 230 234 1
4052 4999 5403 5625 5764 5859
18.51 19.00 19.16 19.25 19.30 19.33 2
t Yi Yh Se
Yi Yh
,
MS组内(
1 n1
1 n2
)
N a 组内
29
例四个均值旳Bonferroni法比较
设α=α’/c=0.1/6=0.0167,由此t旳临 界值为t(0.0167/2,20)=2.6117
18.5 28.0
t(A: B)
3.48 2.6117, 24 4 20
以F命名,故方差分析 又称 F 检验 (F
test)。用于推断两 个或多种总体均数有 无差别 。
3
方差分析旳优点: 不受比较组数旳限制,可比较多组均数 可同步分析多种原因旳作用 可分析原因间旳交互作用
4
完全随机设计资料(单原因)方差分析 One-way analysis of variance 第一节 方差分析旳基本思想
deviations from mean,SS)反应变异旳大小
10
1. 总变异: 全部测量值之间总
旳变异程度,计算公式
a ni
SS总
Yij Y
2
Y a ni 2 ij
C
i1 j1
i1 j1
N
第八章:方差分析

SSE xij xi
k ni i 1 j 1
2
计算结果为: SSE = 2708
三个离差平方和的关系
总离差平方和(SST)、组内离差平方和(SSE) 、组间离差平方和 (SSA) 之间的关系:
x
k i 1 j 1
ni
ij
x ni xi x xij x
外包装底色对产品销量是否有显著影响?
市场 北京 上海 深圳 西安 成都 红色 36 35 27 29 38 橙色 28 26 31 30 24 紫色 30 32 28 26 35 蓝色 22 27 20 21 29
什么是方差分析?
【 例 】为了对几个行业的服务质量进行评价,消费者协会 在4个行业分别抽取了不同的企业作为样本。最近一年中消 费者对总共23家企业投诉的次数如下表:
2.
方差分析的基本假定
1. 每个总体都服从正态分布 (每个行业被投诉的次数必须服从正态分布) 2. 各个总体的方差相同 ( 4个行业被投诉次数的方差都相等) 3. 观测值是独立的 (每个行业被投诉的次数与其他行业被投诉的次数独立)
方差分析的基本假设
H 0 : m1 m2 mk H1 : m1 , m2 , , mk 不全相等
2.计算误差
计算全部观测值的均值以及各水平下的组均值 计算总误差 计算组内误差 计算组间误差
计算总误差( SST)
1. 全部观察值 xij 与总平均值 x 的离差平方和 2. 反映全部观察值的离散状况 3. 其计算公式为
SST xij x
k ni i 1 j 1 2
方差分析
差异源
组间 组内
SS
1456.609 2708
第08章+单因素方差分析

方差分析的基本原理
在一个多处理试验中,可以得出一系列不同的观测值。 造成观测值不同的原因是多方面的,有的是处理不同引起 的,处理效应或条件变异,有的是试验过程中偶然性因素 的干扰和测量误差所致,既试验误差。方差分析的基本思 想是将测量数据的总变异按照变异原因不同分解为处理效 应和试验误差,并作出其数量估计。 通过方差比较以确 定各种原因在总变异中所占的重要程度,即用处理效应和 试验误差在一定意义下进行比较,如二者相差不大,说明 试验处理对指标影响不大,如二者相差较大,处理效应比 试验误差大得多,说明试验处理影响是很大的,不可忽视。 从而作为统计推断。
变差na来源5 5 平方和 自由度
均方每一个xij都F减去65
SST
处= 理a
误差i=1
n j =1
xi2j 13C1.7=4277 .28 4129 .96
25.58
20
=3124.794.32
0.78
42.23**
S*S*A
总1和 a = α=n0.i0=11
xi2.
1C47=.312308 5
计之前就要明确关于模型的基本假设。对于单因素方差分析 来说,两种模型无多大区别。
第八章 单因素方差分析
三、单因素方差分析的检验及例题验算
(得样一本固)的定方方效差式应分不模同型析,与的致随检使机验所效程得应结模序论型不方同差。分随析机的效程应序模完型全适一用样于,水但平由的于总获 体1,、而正固规定检效验应模程型序只适用于所选定的α个水平。也就是说,随机效应 模2型、Ⅰ可单推因方断素差总方齐体状差性况分检,析验而的固实定效战应检模验型程不序能推断总体状况。
卫生统计学第八章正交试验方差分析

WENKU DESIGN
正交试验设计定义与原理
正交试验设计定义
正交试验设计是研究多因素多水平的一种设计方法,它是根 据正交性从全面试验中挑选出部分有代表性的点进行试验, 这些有代表性的点具备了“均匀分散,齐整可比”的特点。
正交试验设计原理
正交试验设计是利用正交表来安排与分析多因素试验的一种 设计方法。它是由试验因素的全部水平组合中,挑选部分有 代表性的水平组合进行试验的,通过对这部分试验结果的分 析,了解全面试验的情况。
THANKS
感谢观看
REPORTINGΒιβλιοθήκη https://VS
正交表特点
每列中不同数字出现的次数相等;任意两 列中数字的排列方式齐全而且均衡。
正交试验设计步骤
挑因素,选水平
根据试验的目的和专业知识,挑选出与考察指标有关的因素。对选出的因素要分清主次,合理安排。 选取的水平数应根据实际情况而定,过少会导致结果不准确,过多则可能数据分布的规律性较差,代 表性差;
通过建立线性模型来描述各因素 与结果之间的关系,从而进行方 差分析和参数估计。
PART 03
正交试验方差分析步骤
REPORTING
WENKU DESIGN
数据整理与描述性统计
整理试验数据
按照试验因素和水平整理数据,列出试验指标的观察值。
计算总均值和总变异
计算所有观察值的总和、均值、离差平方和等描述性统计量。
选正交表,进行表头设计
根据确定的列数(C)与水平数(t)选择相应的正交表。选择的原则是首先满足列数,其次是水平数。若 有2个或2个以上正交表满足条件时则应选取行数最少的一个;
正交试验设计步骤
明确试验方案,进行试验;
第八章 方差分析与相关分析
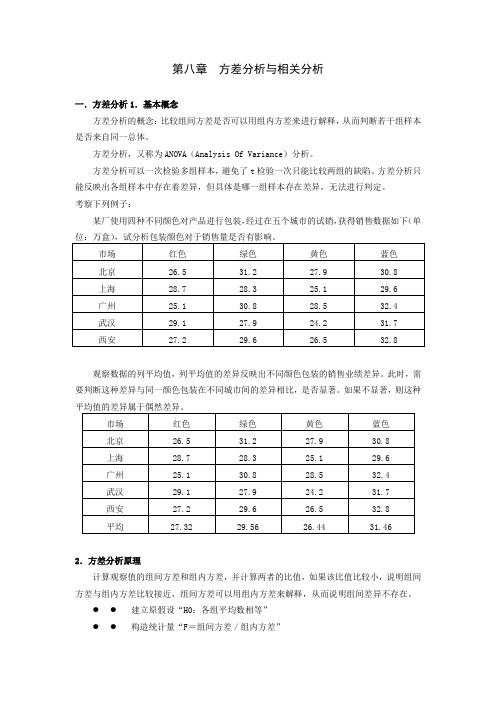
第八章方差分析与相关分析一.方差分析1.基本概念方差分析的概念:比较组间方差是否可以用组内方差来进行解释,从而判断若干组样本是否来自同一总体。
方差分析,又称为ANOVA(Analysis Of Variance)分析。
方差分析可以一次检验多组样本,避免了t检验一次只能比较两组的缺陷。
方差分析只能反映出各组样本中存在着差异,但具体是哪一组样本存在差异,无法进行判定。
考察下列例子:某厂使用四种不同颜色对产品进行包装,经过在五个城市的试销,获得销售数据如下(单观察数据的列平均值,列平均值的差异反映出不同颜色包装的销售业绩差异。
此时,需要判断这种差异与同一颜色包装在不同城市间的差异相比,是否显著。
如果不显著,则这种2.方差分析原理计算观察值的组间方差和组内方差,并计算两者的比值,如果该比值比较小,说明组间方差与组内方差比较接近,组间方差可以用组内方差来解释,从而说明组间差异不存在。
●●建立原假设“H0:各组平均数相等”●●构造统计量“F=组间方差/组内方差”●●在计算组间方差时,使用自由度为(r-1),计算组内方差时,使用自由度为(n-r)。
●●F满足第一自由度为(r-1),第二自由度为(n-r)的F分布。
●●查表,若F值大于0.05临界值,则拒绝原假设,认为各组平均数存在差异。
根据方差计算的原理,生成方差分析表如下:其中:组间离差平方和 SSA (Sum of Squares for factor A) =39.084误差项离差平方和 SSE (Sum of Squares for Error) =76.8455总离差平方和 SST (Sum of Squares for Total)=115.9295P-value值为0.000466,小于0.05,所以拒绝原假设。
3.双因素方差分析观察下列销售数据,欲了解包装方式和销售地区是否对于销售业绩有影响,涉及到双因素的方差分析。
此时需分别计算SSA、SSB与SSE之间的比值是否超过临界值。
生物统计-8第八章单因素方差分析
01
确定因子和水平
确定要分析的因子(独立变量) 和因子水平(因子的不同类别或 条件)。
建立模型
02
03
模型假设
根据因子和水平,建立方差分析 模型。模型通常包括组间差异和 组内误差两部分。
确保满足方差分析的假设条件, 包括独立性、正态性和同方差性。
方差分析的统计检验
01
F检验
进行F检验,以评估组间差异是否 显著。F检验的结果将决定是否拒
生物统计-8第八章单因素方差分析
目录
• 引言 • 方差分析的原理 • 单因素方差分析的步骤 • 单因素方差分析的应用 • 单因素方差分析的局限性 • 单因素方差分析的软件实现
01
引言
目的和背景
目的
单因素方差分析是用来比较一个分类变量与一个连续变量的关系的统计分析方法。通过此分析,我们可以确定分 类变量对连续变量的影响是否显著。
VS
多元性
单因素方差分析适用于单一因素引起的变 异,如果存在多个因素引起的变异,单因 素方差分析可能无法准确反映实际情况。 此时需要考虑使用其他统计方法,如多元 方差分析或协方差分析等。
06
单因素方差分析的软件 实现
使用Excel进行单因素方差分析
打开Excel,输入数据。
点击“确定”,即可得到单因素方差分析 的结果。
输出结果,并进行解释和 解读。
谢谢观看
背景
在生物学、医学、农业等领域,经常需要研究一个分类变量对一个或多个连续变量的影响。例如,研究不同品种 的玉米对产量的影响,或者不同治疗方式对疾病治愈率的影响。
方差分析的定义
定义
方差分析(ANOVA)是一种统计技术,用于比较两个或更多组数据的平均值 是否存在显著差异。在单因素方差分析中,我们只有一个分类变量。
第八章 方差分析
xij (i 1,2,, r , j 1,2,, s)
1 r s 1 s 记= ij 表示总平均值, i .= ij 表示因素A的第i个水平的平均值, . rs i 1 j 1 s j 1
1 r . j= ij 表示因素B的第j个水平的平均值 . r i 1
行业类型 计算机
3.94 2.76 8.95 3.23
每股净收益
3.04 4.69 1.52 5.05
医药
公用
2.89
-2.26
1.65
0.66
2.59
2.22
1.09
1.77
-1.07
-0.15
2.30
2.10
-3.10
2.89 1.12 -3.21 2.11
例8.3:某汽车销售商欲了解三种品牌的汽车X,Y,Z和四种标
ANOVA过程简介
ANOVA过程用于均衡数据的方差分析。
对非均衡数据的方差分析问题,SAS系统要求用GLM(一般 线性模型)来处理(单因素时也可以用ANOVA).
GLM过程也可以处理均衡数据的方差分析问题,但效率低于 ANOVA.
ANOVA过程简介
ANOVA过程的一般格式:
PROC ANOVA<options>; CLASS variables; MODEL dependents=effects</options>; BY variables; FREQ variable; MEANS effects</options>;
一、单因素方差分析模型
设因素X有k个水平,每个水平可视为一个小总体,分别用
X1 , X 2 ,, X k 来表示。记 j的总体均值为 j , X
第八章 方差分析
X ij = m j eij
2
SS t 总变异 df t = N 1
SS b 组间(处理)变异 df b = k 1
SS w 组内(误差)变异 df w = N k
均方
平方和 均方 = 自由度 SS e 组内(误差)均方 MS w = MS e = df e SS b 组间(处理)均方 MSb = MStr = df b
2 e 2 e
m =
j m
2
k 1
=
2 j
k 1
2
当H 0为真时,E MS error = E MStreatm ent 当H 0为假时,E MS error E MStreatm ent
平方和的分解 sum of squares
• 平方和的优越性在于其可加性
– 过程:包含27个词的表过3遍后要求被试写下 记住的词
因素“加工方式”有 5 个水平 j= 1 ,2 ,… ,k (k = 5 )
co unting i= 1 ,2 ,… ,n n= 1 0 9 8 6 8 10 4 6 5 7 7 To ta l(Tj) M e an SD V a ria nce 70 7 .0 0 1 .8 3 3 .3 3 rhy ming 7 9 6 6 6 11 6 3 8 7 69 6 .9 0 2 .1 3 4 .5 4 a dje ctiv e 11 13 8 6 14 11 13 13 10 11 110 1 1 .0 0 2 .4 9 6 .2 2 ima g e ry 12 11 16 11 9 23 12 10 19 11 134 1 3 .4 0 4 .5 0 2 0 .2 7 inte ntio na l 10 19 14 5 10 11 14 15 11 11 120 1 2 .0 0 3 .7 4 1 4 .0 0 503 =∑ X 1 0 .0 6 4 .0 1 1 6 .0 6 to ta l
第八讲-方差分析
x2 ij
j 1i 1
xij
N
k
2
SS B n j X j X t
i 1
2
k
j 1
nj
2
( xij)
i 1
nj
k nj
j 1i 1
xij
N
SSW SST SSB
2
nj
x k nj
x n j1 i1
k
2
ij j 1
ij i 1
j
3、确定自由度
df k 1 B
df N k W
二、(单因素)随机区组实验设计
1、模型
处理1
处理2 ……
区组1 被试1 x11 被试1 x21 ……
区组2 被试2 x12 被试2 x22 ……
处理k
被试1 xk1
被试2
xk
2
……… ……… ……
区组a 被试a x1a 被试a x2a ……
……
被试a xka
■注:每个区组内被试分配方式可以是以下 三种
T1
T2
8
39
20
26
12
31
14
45
10
40
T3
T4
17
32
工创问 具造题
21 20
23 28
教 程
丰 富 教
性 思 维
解 决 模
17
25
程教式 程教
20
29
程
T1: T2: T3: T4:CoRT
变异来源 自由度 平方和
处理 误差
总
3
1553.7
16 378.80
19 1932.55
均方
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上例全部15个数据掺差不齐,它们的差异叫总变差。产生总变差 的原因有两个
1) 随机误差 2) 系统误差
方差分析解决这类问题的思想是:
l 由数据的总变差中分离出随机误差和系统误差。 l 用系统误差和随机误差在一定条件下进行比较,如差异不大 则认为系统误差对指标的影响不大,如系统误差比随机误差大的 多,则说明条件的影响很大。以上面的例子说明即温度的变化对 得率的影响很大,因此调整温度对产量的影响很大。
A i B j C k ijk
AB ij
a
BC jk
a
AC ik
)
2
在假设之下,可得估计量。
三因素方差分析各影响得估计量
最小二乘估计
a iA
aB j
X ...
Xi .. X ...
X . j . X ... X .. k X ...
Xij. Xi .. X . j . X ...
A i AC ik
xijk a a a a
A i B j C k
AB ij
a
BC jk
a
AC ik
ijk
这里,
ijk ~ N (0, )
2
独立同分布。
我们的
H0
假设为:
C aiA a B ak 0 j H 0 : AB BC AC aij a jk aik 0
X:是二维数组
proup:为分组 P: 为F统计量的上侧概率 Table:为方差分析表 Stats:为F统计量
load hogg
% 调牛奶含菌量数据
[p,tbl,stats] = anova1(hogg) % 进行单因素方差分析 结果的方差分析表为:
接受域
例8.2.2 设单因素有三水平,每个水平下实验的次数不同。
i 1 i 1 i 1
M
M
M
2
S E X ij X i
i 1 j 1
M
N
2 M N i 1 j 1
ij i
2
对它们取期望值,利用
E i E 0
有
E S A N ai2 M 1 2
i 1
M
i
(6.2.2)
ai i
i 1,2,, m
X ij i ai ij
显然{ai}之间有关系
i 1,2, m; j 1,2,, n
0
a
i 1
M
i
Ai 表示水平 Ai 对实验结果产生的影响,它称做水平 Ai 的效应。
方差分析模型就是建立在以下假定之下:
E S E N M 2
令
则有
1 SA SA M 1
N E S A NM
M
1 SE Se NM
2 ai2 2 N A 2 i 1
E SE 2
如果H0:成立,则
2 A 0 ,从而 S A 与 S E
之比应近于1,
基本思想是将总变差进行分离,即系统误差和随机误差。 设:Stotal 总变差,即
Stotal X ij X
i 1 j 1
M
N
X
2 M N i 1 j 1
ij
Xi Xi X
2
X ij X i
i 1 j 1
M
N
2
( X i X )2 2( X ij X i )( X i X )
1) 2) 3)
X ij i ai ij
i 1,2, m; j 1,2,, n
a
i 1
M
i
0
ij ~ N 0,1
(一)参数估计 即通过实验估计μ和{ai},其估计量记为和μ和{ai} 。令
1 i N
则
j 1
M
ij
1 MN
i 1 j 1
ˆ ai X i X
此时方差分析模型可以改写为:
ˆ X ij X ai l ij
l ij
反映了误差
ij 。由于 X ij ,X
,
ˆ ai
均为已知故
l ij
可以通过样本求得。
(二)统计检验 如果因素A对指标有显著的影响,效应{ai}不全部为零,反之 则全为零。因此我们假设
H 0 : a1 a2 am
物与治愈率有否明显不同,这里我们考查的对象,原
料,药物称为因素,当考查的因素只有一个时我们称
为单因素问题。如果同时考虑两个或更多的因素问题,
则称多因素方差分析(这时计算起来很复杂)。
例:考查温度对某一化工厂产品得率的影响,选了五种不 同温度,同一温度做了三次试验,测得结果如下:
现在分析温度的变化对得率的影响。从平均得率来看,好象温度 对得率是有一定的影响,但详细观察一下数据就会发现问题,表现 在:
X ij X i
i 1 j 1
M
N
X
M N 2 i 1 j 1
i X
2
SE S A
注:交叉项在线性假设下为 0。这里统计量
SA N Xi X
i 1
M
2
N ai i
i 1
M
2
N ai 2 N ai i N i
2
其中 S 为残差平方和项,我们可以得到三因素方差分析表 E
两因素方差分析anova2语法:
Two-way Analysis of Variance (ANOVA)
p = anova2(X,reps) p = anova2(X,reps,'displayopt') [p,table] = anova2(...) [p,table,stats] = anova2(...) 这里: X:数据矩阵 reps:重复次数
xijk ( i 1,2,a; j 1,2,b;
令
k 1,2,, c )
B j C k
a , a , a 分别表示三 AB BC 个因素各自的效应,而 aij , a jk , a 分别表示因素A,B,C
表示实验数据的总体均值, 两两的混合效应,则多因素方差分析线性模型可表示为:
一般对 r 个因素( r 2 )的多因素方差分析中, 对于观察值
x i1i2 ir
的线性模型,有 交互效应,…, 项之和。 平方和分解
C
C
r 1 r
1 r
个各因素主效应, C r2 个两两不同因素的 个(r-1)个因素的交互效应以及随机误差
min x ijk ( a a a a
服从(N—M)个自由的
2(N M )
分布,且两者独立,从而
F S A / SB
服从以(M-1),(N-M)为自由度的F分布。
方差分析表的一般形式为:
例8.2.1 设五个不同国家船运来港的牛奶,分别抽取六桶,检验每 桶的细菌含量,即单因素五水平的实验数据为: 数据来自Hogg and Ledolter (1987) 。 组间(国家) 24 14 11 15 组内 7 9 7 21 12 7 19 7 24 4 19 7 15
M
N
ij
1 Xi N
1 X ij N j 1
N
a
i
ij ai i
1 M N X ai ij r i 1 j f
这里
r NM
取
X
是μ的一个无偏估计。
类似地可以推出
ai
的无偏估计是
ˆ ai
l 选择较好的工艺条件或确定进一步的实验方案。
这里介绍几个方差分析术语: 因素:实验中的每一个条件,如上例的温度便是一个因素。 水平:因素在实验中的等级称为水平,如上例中因素温度分为五 个水平:60℃65℃,70℃,75℃,80℃。如果把因素记为A, 则相应地把水平记为A1, A2, A3, A4, A5. 样本:在同样条件下得到不同的实验结果每个结果称为样本。
因素
I
0.365 0.255 0.195 0.215
II
0.27 0.275 0.240 0.265
III
0.305 0.250 0.225
0.185
问三水平下的结果是否有显著区别?注意group的使用。 data = [0.365 0.255 0.195 0.215 0.27 0.275 0.24 0.265 ... 0.185 0.305 0.25 0.225]; group = {'1','1','1','1','2','2','2','2',...
8.2 单因素方差分析
设因素A取了M个水平,每个水平重复了N次实验得到MN个样本, 在水平Ai下的第 j 次实验结果(样本)Xij 可以分解为:
X ij i ij
这响的大小,将 Xij 再进行分解, 令
1 M
令
第八章 方差分析
一、方差分析的基本概念 二、单因素方差分析 三、 多因素方差分析(MNOVA) 四、 案例分析 五、习题
8.1 方差分析的基本概念
经常遇到这样的问题,有几种不同的原料,要考
查它们对产品质量有没有显著的影响。某种新药与其 它一些传统药物对病人进行分组实验来考查不同的药
