悬索桥主缆线形计算和绘图实用方法
悬索桥结构计算理论

悬索桥结构计算理论悬索桥结构计算理论主要内容☞概述☻悬索桥的近似分析☞悬索桥主塔的计算☞悬索桥成桥状态和施工状态的精确计算1.概述1.1悬索桥的受力特征悬索桥是由主缆、加劲梁、主塔、鞍座、锚碇、吊索等构件构成的柔性悬吊体系,其主要构成如下图所示。
成桥时,主要由主缆和主塔承受结构自重,加劲梁受力由施工方法决定。
成桥后,结构共同承受外荷作用,受力按刚度分配。
悬索桥各部分的作用主缆是结构体系中的主要承重构件,受拉为主;主塔是悬索桥抵抗竖向荷载的主要承重构件,受压为主;加劲梁是悬索桥保证车辆行驶、提供结构刚度的二次结构,主要承受弯曲内力;吊索是将加劲梁自重、外荷载传递到主缆的传力构件,是连系加劲梁和主缆的纽带,受拉。
锚碇是锚固主缆的结构,它将主缆中的拉力传递给地基。
1.概述(续)✶悬索桥计算理论的发展与悬索桥自身的发展有着密切联系早期,结构分析采用线弹性理论(由于桥跨小,索自重较轻,结构刚度主要由加劲梁提供。
中期(1877), 随着跨度的增加,梁的刚度相对降低,采用考虑位移影响的挠度理论。
现代悬索桥分析采用有限位移理论的矩阵位移法。
✹跨度不断增大的同时,加劲梁相对刚度不断减小,线性挠度理论引起的误差已不容忽略。
因此,基于矩阵位移理论的有限元方法应运而生。
应用有限位移理论的矩阵位移法,可综合考虑体系节点位移影响、轴力效应,把悬索桥结构非线性分析方法统一到一般非线性有限元法中,是目前普遍采用的方法。
▪弹性理论(1)悬索为完全柔性,吊索沿跨密布;(2)悬索线性及座标受载后不变;(3)加劲梁悬挂于主缆,截面特点不变;仅有二期恒载、活载、温度、风力等引起的内力。
计算结果:悬索内力及加劲梁弯距随跨经的增大而增大。
▪挠度理论与弹性理论不同之处仅在于:考虑悬索竖向变形对内力的影响(不考虑剪力变形、吊杆倾斜及伸缩变形,影响较小)。
线性挠度理论:忽略挠度理论中活载引起的主缆水平分力与竖向位移之间的非线性关系。
计算结果:加劲梁弯距铰弹性理论结果要小。
主缆
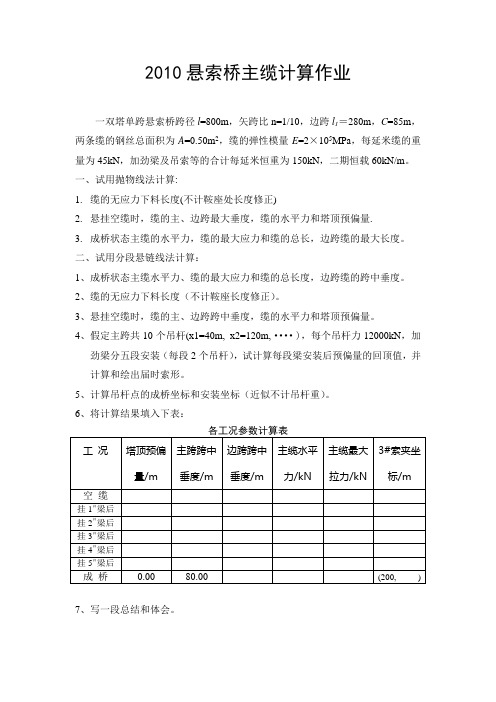
2010悬索桥主缆计算作业一双塔单跨悬索桥跨径l=800m,矢跨比n=1/10,边跨l1=280m,C=85m,两条缆的钢丝总面积为A=0.50m2,缆的弹性模量E=2×105MPa,每延米缆的重量为45kN,加劲梁及吊索等的合计每延米恒重为150kN,二期恒载60kN/m。
一、试用抛物线法计算:1.缆的无应力下料长度(不计鞍座处长度修正)2.悬挂空缆时,缆的主、边跨最大垂度,缆的水平力和塔顶预偏量.3.成桥状态主缆的水平力,缆的最大应力和缆的总长,边跨缆的最大长度。
二、试用分段悬链线法计算:1、成桥状态主缆水平力、缆的最大应力和缆的总长度,边跨缆的跨中垂度。
2、缆的无应力下料长度(不计鞍座长度修正)。
3、悬挂空缆时,缆的主、边跨跨中垂度,缆的水平力和塔顶预偏量。
4、假定主跨共10个吊杆(x1=40m, x2=120m,····),每个吊杆力12000kN,加劲梁分五段安装(每段2个吊杆),试计算每段梁安装后预偏量的回顶值,并计算和绘出届时索形。
5、计算吊杆点的成桥坐标和安装坐标(近似不计吊杆重)。
6、将计算结果填入下表:各工况参数计算表工况塔顶预偏量/m 主跨跨中垂度/m边跨跨中垂度/m主缆水平力/kN主缆最大拉力/kN3#索夹坐标/m空缆挂1#梁后挂2#梁后挂3#梁后挂4#梁后挂5#梁后成桥0.00 80.00 (200, ) 7、写一段总结和体会。
一、抛物线法计算1.1、缆的无应力下料长度(不计鞍座处长度修正) 1.1.1理论推导 抛物线主缆形状方程:()24fx Cy L x x L L=--+ 抛物线主缆形状长度:122221122112220221111ln 161LC C dy L S dx C C C C dx f C C ⎡⎤⎡⎤++⎛⎫⎢⎥=+=+-++⎢⎥ ⎪⎝⎭⎢⎥++⎢⎥⎣⎦⎣⎦⎰抛物线主缆的弹性伸长量为:2222220111616L Tds H dy HL C f Cf S dx EA EA dx EA L L L ⎡⎤⎛⎫⎛⎫∆==+=++-⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎣⎦⎰⎰ 无应力长度:0S S S =-∆ 成桥状态下,对于中跨:1244800,80,0,0.4,0.4C f C fL f C C C L L+-=======- 582250.5210 1.010255800H= 2.55108880EA kN L kNf ω=⨯⨯=⨯⨯==⨯⨯ 对于边跨22545280 1.72988 2.5510L f m H ω⨯===⨯⨯ 1244280,85,0.328,0.279C f C fL C C C L L+-====== 1.1.2无应力下料长度的计算用matlab 编写子函数【wuyingli.m 】%---------------------------------------------------------------------- function [S0,S1]=wuyingli(w,L,H,C) EA=1.0e8; f=w*L^2/8/H; C1=(C+4*f)/L; C2=(C-4*f)/L;S1=L^2/16/f*(C1*sqrt(1+C1^2)-C2*sqrt(1+C2^2)+log((C1+sqrt(1+C1^2))/(C2+sqrt(1+C2^2)))); %伸长后长度DS=H*L/EA*(1+C^2/L^2+16*f^2/L^2-16*f*C/L^2); %伸长量S0=S1-DS; %无应力长度1.1.3计算主程序【paowuxian_main.m】%----------------------------------------------------------------------p1=45;L1=800;C1=0;f1=80;p2=150;L2=280;C2=85;p3=60;EA=1.0e8;A=0.5;H1=(p1+p2+p3)*L1^2/8/80; %成桥状态下主缆水平力[SM0,SM1]=wuyingli(p1+p2+p3,L1,H1,C1); %函数计算成桥状态下中跨无应力索长[SS0,SS1]=wuyingli(p1,L2,H1,C2); %函数计算成桥状态下边跨无应力索长S0=SM0+2*SS0;disp(['中跨无应力下料长度:',num2str(SM0),'m'])disp(['边跨无应力下料长度:',num2str(SS0),'m'])disp(['主缆无应力下料长度:',num2str(S0),'m'])1.1.4计算结果中跨无应力下料长度:818.4821m边跨无应力下料长度:291.8836m主缆无应力下料长度:1402.2494m1.2、悬挂空缆时,缆的主、边跨最大垂度,缆的水平力和塔顶预偏量.1.2.1理论推导空缆时塔顶预偏量和主缆水平力,可转化为未知量为水平力H和预偏YP的二元非线性方程组。
大跨径悬索桥主缆成桥线形计算方法研究及应用

大跨径悬索桥主缆成桥线形计算方法研究及应用大跨径悬索桥是一种建筑结构工程中常见的桥梁形式,它的主要特点是利用悬索的拉力来支撑桥梁的自重和荷载。
而主缆则是悬索桥中起到主要承载作用的部分。
本文将研究大跨径悬索桥主缆的成桥线形计算方法,并探讨其在实际应用中的相应应用。
在进行大跨径悬索桥主缆成桥线形计算方法研究之前,首先需要了解大跨径悬索桥的基本概念和构造。
大跨径悬索桥由悬索、主缆、主塔等组成。
其中,主缆被悬挂在主塔上,作为悬索的延伸,并用于支撑桥面板。
主缆的成桥线形是指主缆在自重和荷载的情况下所形成的曲线形状。
大跨径悬索桥主缆成桥线形计算方法的研究是基于力学原理和结构力学的分析。
首先,需要确定主缆的初始线形,通常可以假设为一定的曲线形状,如悬链线形。
然后,根据桥面板的自重和荷载情况,通过数值计算或解析计算的方法,确定主缆的悬挂点位置以及推力大小。
对于大跨径悬索桥主缆成桥线形计算方法的应用,可以分为以下几个方面。
首先,主缆成桥线形的计算可以用于确定主缆的几何参数,包括主缆的长度、形状和初始线形等。
这些参数的确定对于设计和施工是非常重要的。
其次,主缆成桥线形的计算可以用于确定主缆的受力情况,包括主缆的张力和弯矩等。
这些受力情况的计算可以用于判断主缆是否满足设计要求,以及确定主缆的安全性和可靠性。
最后,主缆成桥线形的计算也可以用于对已建成的大跨径悬索桥进行检测和监测,以保证桥梁的正常使用和运行。
在实际应用中,大跨径悬索桥主缆成桥线形的计算涉及到多种计算工具和方法。
其中,常用的方法包括有限元方法、近似解法和经验公式等。
这些方法各有优缺点,在具体应用中需要综合考虑工程的实际情况和计算精度的要求,选择合适的计算方法。
综上所述,大跨径悬索桥主缆成桥线形计算方法的研究及应用是一项重要的工作。
通过对主缆成桥线形计算方法的研究,可以为大跨径悬索桥的设计、施工和监测提供重要的理论依据和技术支持。
在实际应用中,需要综合考虑多种计算方法和工具,以确保计算结果的准确性和可靠性。
大跨径悬索桥主缆线形分析

大跨径悬索桥主缆线形分析目录第一章绪论 (1)1.1概述 (1)1.2国内外研究现状 (3)1.3本文主要研究目的及内容 (5)1.3.1 本文研究目的 (5)1.3.2 本文研究的主要内容 (5)1.3.4 本文研究的技术路线 (7)第二章悬索桥分析理论和主缆线形计算方法 (8) 2.1悬索桥分析理论 (8)2.1.1 弹性理论 (8)2.1.2 挠度理论 (9)2.1.3 非线性有限元理论 (10)2.2主缆成桥线形计算方法 (11)2.2.1 抛物线法 (11)2.2.2 分段悬链线法 (15)2.2.3 有限元法 (20)2.3主缆空缆线形计算方法 (26)2.3.1 悬链线法 (26)2.3.2 有限元法 (28)2.4本章小结 (29)第三章悬索桥主缆线形计算分析 (30)3.1工程概况 (30)3.1.1 依托工程简介 (30)3.1.2 主要材料特性 (38)3.1.3 主缆设计点坐标 (38)3.1.4 主缆下料长度 (41)3.2主缆成桥线形计算分析 (43)3.2.1 抛物线法 (43)3.2.2 分段悬链线法 (44)3.2.3 有限元法 (45)3.2.4 成桥线形对比分析 (47)3.3主缆空缆线形计算分析 (52)3.3.1 悬链线法 (52)3.3.2 有限元法 (53)3.3.3 空缆线形对比分析 (55)3.4主缆施工阶段线形分析 (59)3.4.1 施工过程模拟 (59)3.4.2 施工阶段主缆控制点变化分析 (61) 3.5主缆线形计算方法适用性分析 (65) 3.5.1 主缆成桥线形计算方法适用性 (65) 3.5.2 主缆空缆线形计算方法适用性 (67) 3.6本章小结 (69)第四章主缆无应力索长计算分析 (71) 4.1抛物线法 (71)4.2分段悬链线法 (72)4.3有限元法 (73)4.4索鞍无应力索长修正 (76)4.4.1 计算理论 (76)4.4.2 修正结果 (78)4.5无应力索长对比分析 (78)4.6本章小结 (81)第五章主缆线形参数影响分析 (82)5.1主缆线形影响参数 (82)5.2主缆弹性模量影响 (83)5.2.1 弹性模量方案选取 (83)5.2.2 弹性模量对主缆线形影响分析 (84) 5.3索股自重影响 (88)5.3.1 索股自重荷载集度方案选取 (88)5.3.2 索股自重对主缆线形影响分析 (88)5.4主缆跨度影响 (92)5.4.1 主缆跨度方案选取 (92)5.4.2 主缆跨度对主缆线形影响分析 (93)5.5温度影响 (95)5.5.1 温度效应计算原理 (95)5.5.2 温度变化方案选取 (96)5.5.3 温度变化对主缆线形影响分析 (97)5.6本章小结 (101)结论与展望 (102)参考文献 (104)攻读学位期间取得的研究成果 (107)致谢 (108)第一章绪论第一章绪论1.1 概述悬索桥以悬索结构为主要承重构件,主缆、吊杆、锚碇、主塔、加劲梁和桥面铺装为悬索桥主要组成部分,自古以来这种悬索状的桥型就存在,通常被称作吊桥[1]。
第四章悬索桥精确计算

真实索形的迭代计算(续)
根据IP点处实际的H和V,可计算边跨主缆的成桥索形;根 据主索鞍、转索鞍的设计半径,可计算主缆与鞍座的切点座 标;根据吊杆在主缆和桥面上的y座标,可计算吊索在成桥 态的长度。至此,整个悬吊部分的受力与几何形态都被唯一 确定。 否则设误差向量为:
e f hi f
i 1
悬索桥索形力学模型简化图
真实索形的迭代计算
已知:主缆恒载集度 q ,中跨吊杆间距和矢高 f ,鞍座上IP点 坐标,求主缆索形。
公式准备1:取主缆吊杆间任一段无伸长自由悬索,其竖坐标
为y,向下为正,单位缆长重为q,任一点处的Lagrange坐 标为s ,相应的迪卡尔坐标为(x,y),则任意索自由索段
悬索桥 结构精确计算理论
悬索桥成桥状态和施工状态的精确计算
什么是成桥状态和施工状态精确计算? 计算思路:确定悬索桥成桥和施工状态的关键是确定主 缆成桥时的线型,即计算主缆与吊索交点位置及主缆与 鞍座的切点座标。将悬索桥简化成图示的力学模型。
悬索桥索形力学模型简化图
悬索桥成桥状态和施工状态的精确计算
m
e y hi y
i 1
n+1
(54)
实际的H,V可通过影响矩阵法迭代计算按如下步骤迭代求解:
悬索桥施工状态的计算
悬索桥施工状态是指从挂主缆开始到成桥各阶段悬索桥的构 形和受力状态。确定施工状态主要解决三方面问题:
1) 主缆各索段无应力索长
2) 挂索初始状态 3) 吊梁阶段的结构状态
V )T
c11 c 21
c12 H e f V e c 22 y
(56)
H,V通过影响矩阵法迭代计算步骤(续)
3.修正索端力H=H+ H,V=V+ V ,重新计算hi和ef,ey。 由于方程是非线性的,整个计算可以按1-3步进行迭代。当 式(54)的误差值落入收敛范围时,迭代计算结束。这样,不
基于MATLAB的悬索桥主索成桥线形计算

坐标为 (8 , .2 , 10 2 4 ) 第一根吊索距 离索塔 7 5 其 它 4 . m,
吊杆间距为 5 钢丝绳弹性模量 E=19 5×1 la m, .8 0I , V P 主缆面积 A= .5 m 主缆 自重集度 q 35 N m, 0 19 =1. k / 加
劲梁及行车道板恒载荷 载集 度 P= 5 N m, 顶主索 3k / 塔
妻 一) 一 ) = ( = ,
( ) qs s = '
不考虑主缆 弹性伸 长对主缆线 比重 的影 响 , 根据 质量守恒定律 :
q =q , ( =q q s) ' = s s
法确定的初始线形 为基 础 , 使用悬链 线索 单元做更精
确的分析。
( 2 MA L B程序编制 TA )
一 ) +
如图 1 所示 , 柔性 索段 A 沿索 自重均 布荷载为 B, q 弹性模 量为 , , 横断面积为 A 索段 两端点跨度 为 Z , , 高差为 h 索段 的无应力长 度为 S , 变形 后的形状 , 。S为 长度 。索段 A端 的水平分力为 日, 向分力为 , 竖 B端 的竖 向分力为 , 向张力为 。索段上一点 c在索 切 段变形前的无 应力索 长轮廓线上 的拉格 朗 日坐标为 s
『 T 窖 =—, ) (d q = 一) s s
( s)=
可得 x d
H
Y s 积分得 : 对 ’
Y ÷(/ ( —s + =一  ̄ / V q)) c +
由) 0 0得 : = ( , )= ( c
图1 索单元示意图
)
y = ÷ () 一 s 口 (
4 结 语
[ ] 文曙东 , 2 郑凯峰 , 栗怀广.空间索 自 锚式悬索桥线形精确计算
大跨度悬索桥丝股架设线形计算的精确方法

【大跨度悬索桥丝股架设线形计算的精确方法】1. 引言大跨度悬索桥作为工程中的一项重要建筑,其设计和构建中的悬索桥丝股架设线形计算显得尤为重要。
本文将深入探讨大跨度悬索桥丝股架设线形计算的精确方法,帮助读者全面了解该领域的相关知识。
2. 分类精确方法在大跨度悬索桥丝股架设线形计算中,精确方法可以分为几种不同的分类:2.1 几何精确法2.2 数值精确法2.3 实验精确法3. 几何精确法的原理和应用几何精确法是一种通过几何学方法,以解析性的手段进行丝股架设线形计算的方法。
其原理是...在实际工程中,几何精确法常常应用于...4. 数值精确法的原理和应用数值精确法是一种通过数值计算的方法,以数字模拟的手段进行丝股架设线形计算的方法。
其原理是...在实际工程中,数值精确法常常应用于...5. 实验精确法的原理和应用实验精确法是一种通过实际实验和测试的方法,以试验验证的手段进行丝股架设线形计算的方法。
其原理是...在实际工程中,实验精确法常常应用于...6. 精确方法的优缺点比较在大跨度悬索桥丝股架设线形计算中,不同的精确方法都有其优缺点。
几何精确法在...,数值精确法在...,实验精确法在...,因此在实际应用中,需要综合考虑并选择最合适的方法。
7. 个人观点和理解在我看来,大跨度悬索桥丝股架设线形计算的精确方法是一个综合性的问题,需要结合几何、数值和实验方法来进行综合分析。
每种方法都有其局限性,但相互结合可以得到更加精确和可靠的结果。
8. 总结和回顾通过本文的探讨,我们对大跨度悬索桥丝股架设线形计算的精确方法有了更深入的理解。
在实际应用中,需要充分考虑每种方法的特点,并综合运用,才能取得最优的效果。
通过以上论述,可以看出大跨度悬索桥丝股架设线形计算的精确方法是一个复杂而又具有挑战性的问题。
只有站在更加深入和广泛的角度来审视,才能在这个领域做到真正的精通。
希望本文能够帮助读者更好地理解大跨度悬索桥丝股架设线形计算的精确方法,为相关工程提供支持和指导。
自锚式悬索桥缆索分析计算

自锚式悬索桥缆索分析计算摘要:对于自锚式悬索桥结构来讲,主要承重构件是两根主缆。
由于主缆是不可更换构件,所以当主缆架设完毕以后,其空缆和成桥状态下的线形和无应力长度是不可调整的,或者说调整量甚微。
因此在施工过程中,必须准确的计算缆索系统的各项参数,以指导现场施工。
关键词:自锚式悬索桥;主缆;线形;无应力长度;缆索系统;参数Abstract: For the self-anchored suspension bridge, the main load-bearing components are two main cables. As the main cable can not be replaced, so after the main cable is built, the linear and non-stress length under empety and bridge formed is not adjusted, or the adjust is minimal. Therefore, in the construction process, the various parameters of cable system must be accurate calculated to guide the site construction.Key words: self-anchored suspension bridge; the main cable; linear; non-stress length; cable system; parameters1 工程概况江阴新沟河大桥起止桩号为K17+006.18~K17+763.22,全桥长757.04m,跨径组合为3×30+4×30+(30+40+100+40+30)+4×30+2×(3×30)m,其中主桥为混凝土自锚式悬索桥,东西引桥为混凝土连续箱梁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第43卷 第 1 期 2 0 17 年 1 月
S山HANXI西ARC建HITEC筑TURE
JVaonl..432N01o7.1
文章编号:1009-6825 (2017) 01-0172-02
悬索桥主缆线形计算和绘图实用方法
熊安书
(广州地铁设计院有限公司,广 东 广 州 510010)
摘 要 :以 悬 索 桥 设 计 为 研 究 对 象 ,介绍了悬索桥主缆中跨与边跨悬链线的理论公式,并阐述了悬索桥主缆线形的计算及绘图方
其
中 ,k = T0/pg。
24
4.185
24,4.185 6 0.259 6,0.259
23
3.84
23,3.84 5 0.18
5,0.18
22
3.511
22,3.511 4 0.115 4,0.115
2 悬索桥中跨主缆线形计算与绘图实用方法
21
3.197
21,3.197 3 0.065 3,0.065
收稿日期:2016-10-30 作 者 简 介 :熊 安 书 (1 9 73-),男 ,高级工程师
法 ,指出实际工程中,在吊索集中荷载作用下,主缆线形会发生变化,为防止变形过大,设计应考虑主缆的重力刚度要求。
关 键 词 :悬 索桥,悬 链线,主缆线形,绘图方法
中图分类号:U 448.25
文献标识码:A
悬 索 桥 设 计 首 先 要 画 出 主 缆 线 形 才 能 进 行 建 模 试 算 ,而根 据 悬 链 线 理 论 公 式 直 接 画 出 主 缆 线 形 并 不 容 易 ,尤 其 是 三 跨 悬 索 桥 边跨主缆受边界条件影响,线 形 计 算 更 加 复 杂 ,悬链线理论公式 需 要 重 新 推 导 ,以 下 从 易 到 难 逐 步 介 绍 主 缆 线 形 计 算 和 绘 图 实 用 方法。
16,1.85
33
7.982
33,7.982 15 1.625 15,1.625
32
7.497
32,7.497 14 1.415 14,1.415
31
7.029
31,7.029 13 1.219 13,1.219
30
6.576
30,6.576 12 1.038 12,1.038
29
6.138
29,6.138 11 0. 872 11,0.872
20
2.897
20,2.897 2 0.029 2,0.029
悬索桥中跨主缆无应力线形为悬链线,实际工程设计方案之
19
初 ,由于尚未计算, 未 知 ,甚至主缆粗细待定、主缆线密 度 未 知 ,
18
参 数 ^ 未 知 ,则 无 法 直 接 利 用 悬 链 线 公 式 计 算 悬 链 线 坐 标 ,但通
画出中跨半跨悬链线。
3 边跨悬链线方程
3)
示 例 :结 合 某 25 m +70 m +25 m 三 跨 人 行 悬 索 桥 ,主缆中 悬 索 桥 边 跨 主 缆 由 于 边 界 条 件 变 化 ,是 非 标 准 的 悬 链 线 方
跨 垂 度 9 m ,以主缆中跨中点为坐标系原点,中跨主缆与塔理论交 程 ,详细推导过程如下:
E X C E L 计算表格如表1 所示。
表 1 EXCEL计算表(一)
以点(3 0 ,9 )单变量求解fc = 69.504 590 51
X
k
c
o
s
h
r {
x=/
k
)
—k
X
y - kcosh
{x/k) —k
35
9
35,9
17 2.089 17,2.089
34
8.483
34,8.483 16 1.85
28
5.717
28,5.717 10 0.721 10,0.721
27
5.311
27,5.311 9 0.584 9,0.584
26
4.92
26,4.92 8 0.461 8,0.464.545 7 0.353 7,0.353
图 1 1/2中跨悬链线计算示意图
经推导(过 程 略 )可 得 :悬 链 线 方 程 为 y =
命 令 ,输人栏粘贴坐标,即可自动连续画出中跨半跨主缆线形图,
1)
以主缆中跨中点为坐标系原点,已知主缆与桥塔理论交点如 图 2 所 示 。
为 (a a ),即为悬链线方程的一组解,在 e x c e l 中 以 & 为 变 量 ,
先 任 意 输 人 一 常 数 (如 1. 〇),按 悬 链 线 公 式 求 出 %= & 时 对 应 的 然 后 利 用 e x c e l 中单变量求解功能,设 定 y 目 标 值 为 ^ ,以 &
为 变 量 ,即 可 求 出 ^值 。
2)
按 第 一 步 求 出 的 &值 ,在 E X C E L 中 X 以 任 意 间 距 (如 1 m )
为步长增加,求 出 对 应 ^ 值 ,形 成 坐 标 点 ,并 复 制 到 剪 贴 板 ,打开
C A D ,利 用 P L I N E 命 令 ,在输人栏“粘 贴 ”坐标数据,即可自动连续
1 悬链线方程 一质量均匀分布的绳两端悬挂时绳子所表示的曲线为悬链
线 ,假设一个无限长的质量均匀分布的绳子在重力作用下自然下 垂 。设 绳 底 端 受 到 拉 力 为 r。,线 密 度 为 p ,重 力 加 速 度 为 g。如图 1 所示建立直角坐标系,设 绳 对 应 的 函 数 为 y =/(幻 ,对于横坐标 从 〇~ % 这 一段的绳,设 质 量 为 m ,长 度 为 i ,受 重 力 为 c ,受顶端拉 力 大 小 为 r ,该 力 倾 斜 角 为 0 ,该段绳受三力平衡:r ,c ,r„,画出受 力 示 意 图 ,有 G/77。= tan0。
2.613 2.344
19,2.613 1 18,2.344 0
0.007 0
1,0.007 0,0
过 设 定 塔 高 、主 缆 垂 度 ,则 主 缆 线 形 是 确 定 的 ,即 此 时 悬 链 线 方 程
将 E X C E L 中坐标数据复制到剪贴板,打 开 C A D ,利 用 PLINE
中为常数。
点 为 (35,9 ) ,在 E X C E L 中 以 为 变 量 ,先任意输人一常数(如1.0), 按悬链线公式求出%= 3 5 对 应 的 y ,然 后 利 用 E X C E L 中单变量求 解功能,设 定 y 目标值为9,以 为 变 量 ,即可求出& = 69.5M 590 51; 在 E X C E L 中 %以 1 m 间 距 ,求 出 对 应 y 值 ,形成坐标点。
