安徽新高考数学理科二轮复习作业精练精析专题限时集训(十四)A(含答案详析)
安徽新高考数学理科二轮复习作业精练精析专题限时集训(二)B(含答案详析)
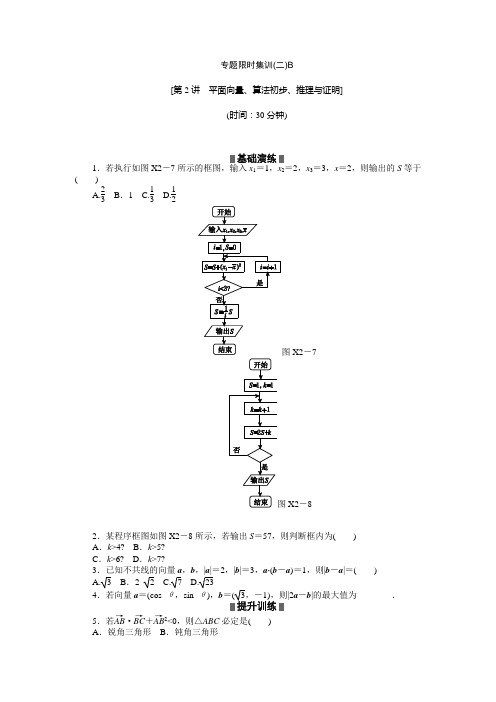
专题限时集训(二)B[第2讲 平面向量、算法初步、推理与证明](时间:30分钟)1.若执行如图X2-7122,x 3=3,x =2,则输出的S 等于( )A.23 B .1 C.13 D.12X2-7X2-82.某程序框图如图X2-8所示,若输出S =57,则判断框内为( ) A .k >4? B .k >5? C .k >6? D .k >7?3.已知不共线的向量a ,b ,|a |=2,|b |=3,a·(b -a )=1,则|b -a |=( ) A. 3 B .2 2 C.7 D.234.若向量a =(cos θ,sin θ),b |2a -b |的最大值为________.5.若AB →·BC →+AB →2<0,则△ABC 必定是( ) A .锐角三角形 B .钝角三角形C .直角三角形D .等腰直角三角形6.△ABC 外接圆的圆心为O ,半径为1,若AB →+AC →=2AO →,且|OA →|=|AC →|,则向量BA →在向量BC →方向上的投影为( )A.32B.32 C .3 D .-327.已知a 为执行如图X2-9所示的程序框图输出的结果,则二项式a x -1x6的展开式中含x 2项的系数是( )A .192B .32C .96D .-1928.已知△ABC 的面积为2,在△ABC 所在的平面内有两点P ,Q ,满足P A →+PC →=0,QA →=2BQ →,则△APQ 的面积为( )A.12B.23C .1D .2 9.在平面直角坐标系中,O 是坐标原点,两定点A ,B 满足|OA →|=|OB →|=OA →·OB →=2,则点集{P |OP →=λOA →+μOB →,|λ|+|μ|≤1,λ,μ∈R }所表示的区域的面积是( )A .2 2B .2 3C .4 2D .4 310.已知2+23=2 23,3+38=3 38,4+415=4 415,…,若6+at=6at(a ,t 均为正实数),则类比以上等式,可推测a ,t 的值,a +t =________. 11.在Rt △ABC 中,两直角边分别为a ,b ,设h 为斜边上的高,则1h 2=1a 2+1b2.由此类比:三棱锥S -ABC 中的三条侧棱SA ,SB ,SC 两两垂直,且长度分别为a ,b ,c ,设棱锥底面ABC 上的高为h ,则________________________________________________________________________.12.如图X2-10所示,表中的数阵为“森德拉姆素数筛”,其特点是每行每列都成等差数列.记第i 行第j 列的数为a ij (i ,j ∈N ),则a 99=________;表中数82共出现________次.专题限时集训(二)B1.A [解析] 输出的结果是(1-2)2+(2-2)2+(3-2)23=23.2.A [解析] 逐次运行的结果是k =2,S =4;k =3,S =11;k =4,S =26;k =5,S =57.当k =5时输出结果,故选A.3.A [解析] 由a ·(b -a )=1,得a·b -a 2=1,则a·b =5.所以|b -a |=b 2+a 2-2ab =9+4-10= 3.4.4 [解析] 因为向量a =(cos θ,sin θ),b =(3,-1),所以|a |=1,|b |=2,a·b =3cos θ-sin θ.又因为|2a -b |2=4a 2+b 2-4a ·b =8-4(3cos θ-sin θ)=8-8cos ⎝⎛⎭⎫θ+π6,所以|2a -b |2的最大值为16,因此|2a -b |的最大值为4.5.B [解析] AB →·BC →+AB →2<0,即AB →·(BC →+AB →)=AB →(BC →-BA →)=AB →·AC →<0,故角A 为钝角,所以△ABC 为钝角三角形.6.A [解析] 由AB →+AC →=2AO → 知,点O 在BC 上且为BC 的中点,如图所示,由于|OA →|=|AC →|,故△AOC 为正三角形,则∠ABC =30°.故BA →在向量BC →方向的投影为|BA →|cos 30°=3×32=32.7.D [解析] 由程序框图可知,第一次循环,a =11-a=-1,i =i +1=2,不满足条件i <2 011,再次循环;第二次循环,a =11-a =12,i =i +1=3,不满足条件i <2 011,再次循环;第三次循环,a =11-a =2,i =i +1=4,不满足条件i <2 011,再次循环;第四次循环,a =11-a=-1,i =i +1=5,不满足条件i <2 011,再次循环;…….由此可知a 的值为-1,12,2,三个数循环,所以输出的a 的值为2.又因为二项式的通项T r +1=C r 6(a x )6-r ⎝⎛⎭⎫-1x r=(-1)r C r 6a 6-r x 3-r,令3-r =2,解得r =1,所以二项式⎝⎛⎭⎫a x -1x 6的展开式中含x 2项的系数是(-1)C 1625=-192. 8.B [解析] P ,Q 的位置如图所示,根据三角形面积公式则S △APQ S △ABC =12|AP ||AQ |sin A12|AB ||AC |sin A =23×12=13,所以△APQ 的面积为23. 9.D [解析] 由|OA →|=|OB →|=OA →·OB →=2,可得点A ,B 在圆x 2+y 2=4上且∠AOB =60°.在平面直角坐标系中,设A (2,0),B (1,3),P (x ,y ),则(x ,y )=λ(2,0)+μ(1,3),所以x =2λ+μ,y =3μ,解得μ=y 3,λ=12x -12 3y .由于|λ|+|μ|≤1,则12x -12 3y +13y≤1,即|3x -y |+|2y |≤23,所以①⎩⎨⎧3x -y ≥0,y ≥0,3x +y ≤2 3或②⎩⎨⎧3x -y ≥0,y <0,3x -3y ≤23或③⎩⎨⎧3x -y <0,y ≥0,-3x +3y ≤2 3或 ④⎩⎨⎧3x -y <0,y <0,-3x -y ≤2 3.上述四个不等式组在平面直角坐标系中表示的区域如图所示阴影10.41 [解析] 4 415,… 照此规律,第511.1h 2=1a 2+1b 2+1c2 [解析] 方法一:过S 作△ABC 所在平面的垂线,垂足为O ,联结CO 并延长交AB 于D ,联结SD .∵SO ⊥平面ABC ,∴SO ⊥AB .∵SC ⊥SA ,SC ⊥SB ,∴SC ⊥平面ABC .∴SC ⊥AB ,SC ⊥SD ,∴AB ⊥平面SCD .则AB ⊥SD .∴在Rt △ABS 中,有1SD 2=1a2+1b 2,在Rt △CDS 中,有1h 2=1SD 2+1c 2=1a 2+1b 2+1c2. 方法二:根据等体积关系16abc =13S △ABC h ,则1h 2=4(S △ABC )2a 2b 2c2.∵4(S △ABC )2=|AB |2|AC |2sin 2A =|AB |2|AC |2(1-cos 2A )=|AB |2|AC |2⎣⎡⎦⎤1-(|AB |2+|AC |2-|BC |2)24|AB |2|AC |2=|AB |2|AC |2-(|AB |2+|AC |2-|BC |2)24=(a 2+b 2)(a 2+c 2)-(a 2+b 2+a 2+c 2-b 2-c 2)24=b 2c 2+a 2c 2+a 2b 2,∴1h 2=4(S △ABC )2a 2b 2c 2=b 2c 2+a 2c 2+a 2b 2a 2b 2c 2=1a 2+1b 2+1c2. 12.82 5 [解析] 第9行的第一个数为10,该行的公差为9,故第9个数是10+(9-1)×9=82.因为第n 行的通项公式是a nk =(n +1)+(k -1)n =kn +1,所以kn +1=82,解得kn =81.所以n =1,k =81;n =3,k =27;n =9,k =9;n =27,k =3;n =81,k =1.。
安徽新高考数学理科二轮复习作业精练精析专题限时集训(十九)(含答案详析)

专题限时集训(十九)[第19讲 坐标系与参数方程](时间:45分钟)1.极坐标方程ρ=cos θ和参数方程⎩⎪⎨⎪y =2+t (t 为参数)所表示的图形分别是( ) A .直线、直线 B .直线、圆C .圆、圆D .圆、直线2.二次曲线⎩⎪⎨⎪⎧x =5cos θ,y =3sin θ(θ是参数)的左焦点的坐标是________. 3.点P 的直角坐标为(-2,2),那么它的极坐标可表示为________.4.若曲线的极坐标方程为ρ=2sin θ+4cos θ,以极点为原点,极轴为x 轴正半轴建立直角坐标系,则该曲线的直角坐标方程为________________.5.在极坐标系中,直线l 的方程为ρsin θ=3,则点⎝⎭⎫2,π6到直线l 的距离为________. 6.若直线⎩⎪⎨⎪⎧x =1-2t ,y =2+3t(t 为实数)与直线4x +ky =1垂直,则常数k =________. 7.在极坐标系中,过圆ρ=6cos θ-2 2sin θ的圆心且与极轴垂直的直线的极坐标方程为________.8.在极坐标系中,点M ⎝⎛⎭⎫4,π3到曲线ρcos ⎝⎛⎭⎫θ-π3=2上的点的距离的最小值为________.9.直线3x +4y -7=0截曲线⎩⎪⎨⎪⎧x =cos α,y =1+sin α(α为参数)的弦长为________. 10.已知直线l 1:⎩⎪⎨⎪⎧x =1-2t ,y =2+kt (t 为参数),l 2:⎩⎪⎨⎪⎧x =s ,y =1-2s (s 为参数).若l 1∥l 2,则k =________;若l 1⊥l 2,则k =________.11.参数方程⎩⎪⎨⎪⎧x =3+3cos θ,y =-3+3sin θ(θ为参数)表示的图形上的点到直线y =x 的最短距离为________.12.已知直线l 的参数方程是⎩⎨⎧x =22t ,y =22t +4 2(t 是参数),圆C 的极坐标方程为ρ=2cos ⎝⎛⎭⎫θ+π4.由直线l 上的点向圆C 引切线,则切线长的最小值为________. 13.已知在直角坐标系xOy 中,圆锥曲线C 的参数方程为⎩⎨⎧x =2cos θ,y =3sin θ(θ为参数),定点A (0,-3),F 1,F 2是曲线C 的左,右焦点.(1)以原点为极点,x 轴正半轴为极轴建立极坐标系,求经过点F 1且平行于直线AF 2的直线l 的极坐标方程;(2)在(1)的条件下,设直线l 与曲线C 交于E ,F 两点,求弦EF 的长.14.以直角坐标系的原点O 为极点,x 轴的正半轴为极轴建立极坐标系,已知点P 的直角坐标为(1,-5),点M 的极坐标为4,π2,若直线l 过点P ,且倾斜角为π3,圆C 以M 为圆心,4为半径.(1)求直线l 的参数方程和圆C 的极坐标方程;(2)试判定直线l 与圆C 的位置关系.15.在直角坐标系xOy 中,直线的参数方程为⎩⎨⎧x =t ,y =3t (t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系.已知曲线C 的极坐标方程为ρ2cos 2θ+ρ2sin 2θ-2ρsin θ-3=0.(1)求直线的极坐标方程;(2)若直线与曲线C 相交于A ,B 两点,求|AB |.专题限时集训(十九)1.D [解析] ∵ρcos θ=x ,∴将cos θ=x ρ代入到ρ=cos θ中,得ρ=x ρ,∴ρ2=x ,∴x 2+y 2=x ,表示圆.∵⎩⎪⎨⎪⎧x =-1-t ,y =2t ,消去参数t 得2x +y +2=0,表示直线. 2.(-4,0) [解析] 该曲线的普通方程为x 225+y 29=1,左焦点为(-4,0). 3.⎝⎛⎭⎫2,3π4 [解析] 直接利用极坐标与直角坐标的互化公式可得极坐标为⎝⎛⎭⎫2,3π4+2k π(k ∈Z ). 4.x 2+y 2-4x -2y =0 [解析] ∵ρ=2sin θ+4cos θ,∴ρ2=2ρsin θ+4ρcos θ,∴x 2+y 2=2y +4x ,即x 2+y 2-2y -4x =0.5.2 [解析] 将直线l 的极坐标方程化为直角坐标方程y =3,点⎝⎛⎭⎫2,π6化为直角坐标为(3,1),∴点⎝⎛⎭⎫2,π6到直线l 的距离为2. 6.-6 [解析] 参数方程⎩⎪⎨⎪⎧x =1-2t ,y =2+3t 所表示的直线方程为3x +2y =7,由此直线与直线4x +ky =1垂直可得⎝⎛⎭⎫-32×⎝⎛⎭⎫-4k =-1,解得k =-6. 7.ρcos θ=3 [解析] 由ρ=6cos θ-2 2sin θ得ρ2=6ρcos θ-2 2ρsin θ,所以圆的直角坐标方程为x 2+y 2-6x +2 2y =0,将其化为标准方程为(x -3)2+(y +2)2=11,故圆心的坐标为(3,-2),所以过圆心且与x 轴垂直的直线的方程为x =3,将其化为极坐标方程为ρcos θ=3.8.2 [解析] 依题意知,点M 的直角坐标是(2,2 3),曲线的直角坐标方程是x +3y -4=0,因此所求的距离的最小值等于点M 到该直线的距离,即为|2+2 3×3-4|12+(3)2=2. 9.85[解析] 曲线的普通方程为x 2+(y -1)2=1.由圆心(0,1)到直线3x +4y -7=0的距离d =|0+4-7|32+42=35,则弦长L =2 r 2-d 2=85. 10.4 -1 [解析] 将l 1,l 2的方程化为一般方程,得l 1:kx +2y -4-k =0,l 2:2x +y-1=0.由l 1∥l 2,得k 2=21⇒k =4;由l 1⊥l 2,得2k +2=0⇒k =-1. 11.3(2-1) [解析] 参数方程⎩⎪⎨⎪⎧x =3+3cos θ,y =-3+3sin θ化为普通方程为(x -3)2+(y +3)2=9,圆心坐标为(3,-3),半径r =3,则圆心到直线y =x 的距离d =|3-(-3)|2=3 2,所以圆上点到直线y =x 的最短距离为d -r =3 2-3=3(2-1).12.2 6 [解析] ∵ρ=2cos θ-2sin θ,∴ρ2=2ρcos θ-2ρsin θ,∴圆C 的直角坐标方程为x 2+y 2-2x +2y =0,即⎝⎛⎭⎫x -222+⎝⎛⎭⎫y +222=1,∴圆心的直角坐标为⎝⎛⎭⎫22,-22,半径为1. 直线l 上的点向圆C 引切线所得的切线长是⎝⎛⎭⎫22t -222+⎝⎛⎭⎫22t +22+4 22-1=t 2+8t +40=(t +4)2+24≥2 6, ∴直线l 上的点向圆C 引切线,切线长的最小值是2 6.13.解:(1)圆锥曲线C 的参数方程为⎩⎨⎧x =2cos θ,y =3sin θ(θ为参数), 所以普通方程为C :x 24+y 23=1. ∵A (0,-3),F 2(1,0),F 1(-1,0),∴k =3,l :y =3(x +1),∴直线l 的极坐标方程为ρsin θ=3ρcos θ+3,即2ρsin ⎝⎛⎭⎫θ-π3= 3. (2)设E (x 1,y 1),F (x 2,y 2),由⎩⎪⎨⎪⎧x 24+y 23=1y =3(x +1)⇒5x 2+8x =0, ∴x 1+x 2=-85,x 1·x 2=0, ∴|EF |=1+k 2(x 1+x 2)2-4x 1x 2=165. 14.解:(1)直线l 的参数方程为⎩⎨⎧x =1+cos π3·t ,y =-5+sin π3·t ⇒⎩⎨⎧x =1+12t ,y =-5+32t (t 为参数). 因为M 点的直角坐标为(0,4),所以圆C 的方程为x 2+(y -4)2=16,将⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ,代入得圆C 的极坐标方程为ρ=8sin θ. (2)直线l 的普通方程为3x -y -5-3=0,圆心M 到l 的距离为d =|-4-5-3|2=9+32>4. 则直线l 与圆C 相离. 15.解:(1)消去参数得直线的普通方程为:y =3x ,由⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ,代入得ρsin θ=3ρcos θ. 则直线的极坐标方程为θ=π3. (2)由⎩⎪⎨⎪⎧ρ2cos 2θ+ρ2sin 2θ-2ρsin θ-3=0,θ=π3,得ρ2-3ρ-3=0, 设A ⎝⎛⎭⎫ρ1,π3,B ⎝⎛⎭⎫ρ2,π3,则有ρ1+ρ2=3,ρ1·ρ2=-3. 则|AB |=|ρ1-ρ2|=(ρ1+ρ2)2-4ρ1·ρ2=15.。
安徽新高考数学理科二轮复习作业精练精析专题限时集训(十)(含答案详析)

专题限时集训(十)[第10讲 数列求和及数列的简单应用](时间:45分钟)1.已知正项数列{a n }中,a 1=1,a 2n n -1a 2n +1(n ≥2),则a 6等于( )A .16B .8C .2 2D .42.已知数列{a n }为等比数列,且a 4·a 6=2a 5,设等差数列{b n }的前n 项和为S n ,若b 5=2a 5,则S 9=( )A .36B .32C .24D .223.设等比数列{a n }的各项均为正数,其前n 项和为S n .若a 1=1,a 3=4,S k =63,则k =________.4.设直线nx +(n +1)y =2(n ∈N *)与两坐标轴围成的三角形的面积为S n ,则S 1+S 2+…+S 2012=________.5(1101)2表示二进制的数,将它转化成十进制数的形式是1×23+1×22+0×21+1×20=13,那么将二进制数111…1(2)(共16位)转换成十进制数的值是( )A .217-2B .217-1C .216-1D .215-16.已知函数f (x )=1x +1,点O 为坐标原点,点A n (n ,f (n ))(n ∈N *).若记直线OA n 的倾斜角为θn ,则tan θ1+tan θ2+…+tan θn =( )A.1nB.1n +1C.n n +1D.n -1n 7.数列{a n }的前n 项和为S n ,已知a 1=15,且对任意的正整数m ,n ,都有a m +n =a m ·a n ,若S n <t 恒成立,则实数t 的最小值为( )A.14B.34C.43D .4 8.在数列{a n }中,若对任意的n ∈N *均有a n +a n +1+a n +2为定值,且a 7=2,a 9=3,a 98=4,则数列{a n }的前100项的和S 100=( )A .132B .299C .68D .999.定义n p 1+p 2+…+p n为n 个正数p 1,p 2,…,p n 的“均倒数”.若已知数列{a n }的前n 项的“均倒数”为12n +1,又b n =a n +14,则1b 1b 2+1b 2b 3+…+1b 10b 11=________. 10.已知数列{a n }中,a 1=1,a n +1=(-1)n (a n +1),记S n 为数列{a n }的前n 项和,则S 2013=________.11.已知数列{a n }的各项均为正整数,其前n 项和为S n .若a n +1=⎩⎪⎨⎪⎧a n 2,a n 是偶数,3a n +1,a n 是奇数,且S 3=29,则a 1=________;S 3n =________. 12.对于一切实数x ,令[x ]为不大于x 的最大整数,则函数f (x )=[x ]称为高斯函数或取整函数.若a n =f n 3,n ∈N *,S n 为数列{a n }的前n 项和,则S 3n =________. 13.已知等差数列{a n }满足a 3=10,a 5-2a 2=6.(1)求数列{a n }的通项公式;(2)数列{b n }满足b n =⎩⎪⎨⎪⎧2n -1(n 为奇数),12a n -1(n 为偶数),T n 为数列{b n }的前n 项和,求T 2n .14.等差数列{a n }中,2a 1+3a 2=11,2a 3=a 2+a 6-4,其前n 项和为S n .(1)求数列{a n }的通项公式;(2)设数列{b n }满足b n =1S n +1-1,其前n 项和为T n ,求证:T n <34(n ∈N *).15.环保刻不容缓,或许人类最后一滴水将是自己的泪水.某地水资源极为紧张,且受工业污染严重,预计20年后该地将无洁净的水可用.当地决定重新选址建设新城区,同时对旧城区进行拆除.已知旧城区的住房总面积为64a m 2,每年拆除的数量相同;新城区计划第一年建设住房面积a m 2,前四年每年以100%的增长率建设新住房,从第五年开始,每年都比上一年增加a m 2.设第n (n ≥1,且n ∈N )年新城区的住房总面积为a n m 2,该地的住房总面积为b n m 2.(1)求数列{a n }的通项公式;(2)若每年拆除4a m 2,比较a n +1与b n 的大小.专题限时集训(十)1.D [解析] 根据2a 2n =a 2n -1+a 2n +1知,数列{a 2n }为等差数列,首项为1,公差为3,所以a 2n =1+(n -1)×3=3n -2,又a n >0,所以a n =3n -2,所以a 6=18-2=4.2.A [解析] 由a 4·a 6=2a 5,得a 25=2a 5,即a 5=2,所以b 5=4,S 9=9(b 1+b 9)2=9b 5=36.3.6 [解析] 设公比为q ,因为a n >0,所以q >0,则a 3=4=a 1q 2=q 2,所以q =2,又S k =63=1-2k1-2,即2k =64,所以k =6. 4.20122013 [解析] 直线与两坐标轴的交点坐标分别为⎝⎛⎭⎫2n ,0,⎝ ⎛⎭⎪⎫0,2n +1,故S n =1n (n +1)=1n -1n +1,所以S 1+S 2+…+S 2012=1-12013=20122013. 5.C [解析] 即215+214+…+2+1=216-1. 6.C [解析] A n ⎝⎛⎭⎫n ,1n +1,tan θn =1n (n +1)=1n -1n +1,所以tan θ1+tan θ2+…+tan θn =1-1n +1=n n +1. 7.A [解析] 令m =1可得a n +1=15a n ,所以{a n }为首项为15,公比为15的等比数列,所以S n =15⎣⎡⎦⎤1-⎝⎛⎭⎫15n 1-15=14⎣⎡⎦⎤1-⎝⎛⎭⎫15n <14,故实数t 的最小值为14. 8.B [解析] 设a n +a n +1+a n +2=M ,则a n +1+a n +2+a n +3=M ,后式减去前式得a n +3=a n ,即数列{a n }是以3为周期的周期数列,a 7=a 1=2,a 9=a 3=3,a 98=a 2=4,所以在一个周期内的三项之和为9,所以S 100=33×9+2=299.9.1011 [解析] 由已知得n a 1+a 2+…+a n =12n +1, ∴a 1+a 2+…+a n =n (2n +1)=S n .当n ≥2时,a n =S n -S n -1=4n -1,当n =1时也成立,∴a n =4n -1,∴b n =a n +14=n ,∴1b n b n +1=1n -1n +1, ∴1b 1b 2+1b 2b 3+…+1b 10b 11=⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝⎛⎭⎫110-111=1011. 10.-1005 [解析] a 1=1,a 2=-2,a 3=-1,a 4=0,a 5=1,…,由此可得该数列的周期为4,一个周期内四项之和为-2,2013=503×4+1,a 2013=a 1,所以S 2013=503×(-2)+1=-1005.11.5 7n +22 [解析] 若a 1=4k ,则a 2=2k ,a 3=k ,此时S 3=7k =29,由于k 为整数,此时无解;若a 1=4k +1,则a 2=12k +4,a 3=6k +2,此时S 3=22k +7=29,解得k =1,即a 1=5; 若a 1=4k +2,则a 2=2k +1,a 3=6k +4,此时S 3=12k +7=29,由于k 为整数,此时无解;若a 1=4k +3,则a 2=12k +10,a 3=6k +5,此时S 3=22k +18=29,由于k 为整数,此时无解.综上可知a 1=5.由于a 1=5,则a 2=16,a 3=8,a 4=4,a 5=2,a 6=1,a 7=4,a 8=2,a 9=1,a 10=4,a 11=2,a 12=1.a 1=4+1,a 2=2+14,a 3=1+7,则a 1+a 2+a 3=22+7,其余每连续三项之和为7,故S 3n =22+7n .12.32n 2-12n [解析] 当n =3k ,n =3k +1,n =3k +2时均有a n =f ⎝⎛⎭⎫n 3=⎣⎡⎦⎤n 3=k ,所以 S 3n =0+0+1+1+1,\s \do 4(3个))+2+2+2,\s \do 4(3个))+…+(n -1)+(n -1)+(n -1),\s \do 4(3个))+n =3×1+n -12×(n -1)+n =32n 2-12n . 13.解:(1)设数列{a n }的公差为d ,则a 1+2d =10,a 1+4d -2(a 1+d )=6,解得a 1=2,d =4,所以a n =a 1+(n -1)d =4n -2.(2)数列{b n }的前2n 项和中,奇数项和偶数项各有n 项.奇数项是首项为1,公比为4的等比数列,其和为1×(1-4n )1-4=4n -13;偶数项是首项为1,公差为4的等差数列,其和为n +n (n -1)2×4=2n 2-n . 所以T 2n =4n -13+2n 2-n . 14.解:(1)设数列{a n }的公差为d ,则2a 1+3a 2=2a 1+3(a 1+d )=5a 1+3d =11, 2a 3=a 2+a 6-4,即2(a 1+2d )=a 1+d +a 1+5d -4,得d =2,a 1=1,所以a n =a 1+(n -1)d =1+(n -1)×2=2n -1.(2)证明:S n =na 1+12n (n -1)d =n ×1+12n (n -1)×2=n 2, b n =1S n +1-1=1(n +1)2-1=1n 2+2n =1n (n +2)=121n -1n +2, 所以T n =1211-13+12-14+13-15+…+1n -1-1n +1+1n -1n +2=1211+12-1n +1-1n +2<34(n ∈N *). 15.解:(1)设第n 年新城区的住房建设面积为λn m 2,则当1≤n ≤4时,λn =2n -1a ;当n ≥5时,λn =(n +4)a .所以,当1≤n ≤4时,a n =(2n -1)a ,当n ≥5时,a n =a +2a +4a +8a +9a +…+(n +4)a =n 2+9n -222a , 故a n =⎩⎪⎨⎪⎧(2n -1)a ,1≤n ≤4,n 2+9n -222a ,n ≥5. (2)当1≤n ≤3时,a n +1=(2n +1-1)a ,b n =(2n -1)a +64a -4na ,显然有a n +1<b n ,当n =4时,a n +1=a 5=24a ,b n =b 4=63a ,此时a n +1<b n .当5≤n ≤16时,a n +1=n 2+11n -122a ,b n =n 2+9n -222a +64a -4na . a n +1-b n =(5n -59)a .所以,当5≤n ≤11时,a n +1<b n ;当12≤n ≤16时,a n +1>b n .当n ≥17时,显然a n +1>b n , 故当1≤n ≤11时,a n +1<b n ;当n ≥12时,a n +1>b n .。
安徽新高考数学理科二轮复习作业精练精析专题限时集训(二)A(含答案详析)
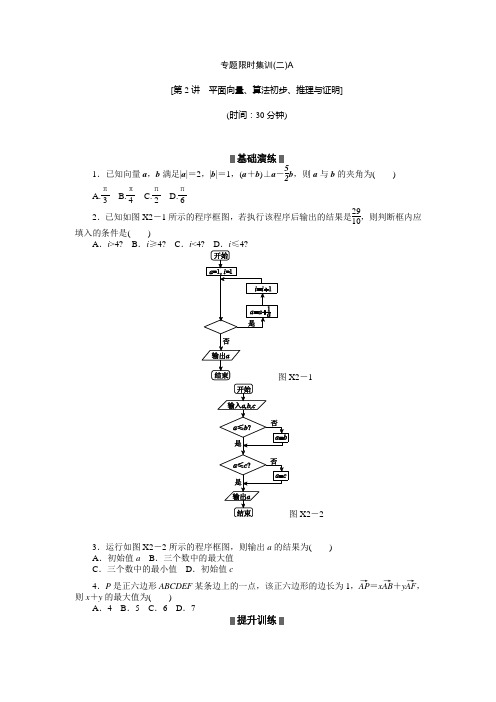
专题限时集训(二)A[第2讲 平面向量、算法初步、推理与证明](时间:30分钟)1.已知向量a ,b 满足|a |=2,|b |=1,(a +b )⊥a -52b ,则a 与b 的夹角为( )A.π3B.π4C.π2D.π62.已知如图X2-1所示的程序框图,若执行该程序后输出的结果是2910,则判断框内应填入的条件是( )A .i >4?B .i ≥4?C .i-1X2-23.运行如图X2-2所示的程序框图,则输出a 的结果为( ) A .初始值a B .三个数中的最大值 C .三个数中的最小值 D .初始值c4.P 是正六边形ABCDEF 某条边上的一点,该正六边形的边长为1,AP →=xAB →+yAF →,则x +y 的最大值为( )A .4B .5C .6D .75.已知平面上不共线的四点O ,A ,B ,C ,若OA →-4OB →+3OC →=0,则|AB →||BC →|=( )A .3B .4C .5D .66.已知向量a =(-1,1),b =(3,m ),a ∥(a +b ),则m =( ) A .2 B .-2 C .-3 D .37.若程序框图如图X2-3所示,则该程序运行后输出的k 值是( ) A .4 B .5 C .6 D .78.设M 是平行四边形ABCD 的对角线的交点,O 为任意一点,则OA →+OB →+OC →+OD →=( )A.OM → B .2OM →C .3OM →D .4OM →X2-3X2-49.如图X2-4给出的是计算1+13+15+…+12013的值的一个程序框图,则判断框内应填入的条件是( )A .i ≤1006?B .i >1006?C .i ≤1007?D .i >1007?10.如图X2-5所示,四边形ABCD 是正方形,延长CD 至E ,使得DE =CD .若动点P从点A 出发,沿正方形的边按逆时针方向运动一周回到A 点,其中AP →=λAB →+μAE →,下列判断正确..的是( ) A .满足λ+μ=2的点P 必为BC 的中点B .满足λ+μ=1的点P 有且只有一个C .λ+μ的最大值为3D .λ+μ的最小值不存在11.已知21×1=2,22×1×3=3×4,23×1×3×5=4×5×6,24×1×3×5×7=5×6×7×8,…依此类推,第n 个等式为X2-5X2-612.在平面直角坐标系中,若点P (x ,y )的坐标x ,y 均为整数,则称点P 为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S ,其内部的格点数记为N ,边界上的格点数记为L .例如图X2-6中△ABC 是格点三角形,对应的S =1,N =0,L =4.(1)图中格点四边形DEFG 对应的S ,N ,L 分别是________;(2)已知格点多边形的面积可表示为S =aN +bL +c ,其中a ,b ,c 为常数,若某格点多边形对应的N =71,L =18,则S =________(用数值作答).专题限时集训(二)A 1.A [解析] 因为(a +b )⊥⎝⎛⎭⎫a -52b ,所以(a +b )·⎝⎛⎭⎫a -52b =0,则|a |2-32a ·b -52|b |2=0,即|a |2-32|a |·|b |cos 〈a ,b 〉-52|b |2=0.又因为|a |=2,|b |=1,所以cos 〈a ,b 〉=12.由于0≤〈a ,b 〉≤π,故〈a ,b 〉=π3.2.C [解析] 逐次计算的结果是a =2,i =2;a =52,i =3;a =2910,i =4,此时满足条件输出.故选C.3.C [解析] 题中程序框图的运算功能是求三数中的最小数.另外,也可以取特殊值验证.4.A [解析] 如图,以A 为坐标原点,AD 为x 轴,与AD 垂直的直线为y 轴建立平面直角坐标系得,B ⎝⎛⎭⎫12,32,F ⎝⎛⎭⎫12,-32⇒AP →=⎝⎛⎭⎫12(x +y ),32(x -y ),由P 点的横坐标的最大值为2,得x +y 的最大值为4.5.A [解析] 由OA →-4OB →+3OC →=0,得A ,B ,C 三点共线.又因为OA →-4OB →+3OC →=0⇔BA →=3CB →,所以|AB →||BC →|=3.6.C [解析] 由向量a =(-1,1),b =(3,m ),得a +b =(2,m +1).因为a ∥(a +b ),所以-(m +1)=2,解得m =-3.7.B [解析] 逐次运行的结果依次是n =16,k =1;n =8,k =2;n =4,k =3;n =2,k =4;n =1,k =5.当n =1时,循环终止,输出k =5.8.D [解析] 如图所示,设P ,Q 分别为AB ,CD 的中点.因为OA →+OB →=2OP →,OC →+OD →=2OQ →,OP →+OQ →=2OM →,所以→→→→→.9.C [解析] i =1,S =0→S =12×1-1,i =2;i =2,S =12×1-1→S =12×1-1+12×2-1,i =3;……i =1007,S =12×1-1+12×2-1+12×3-1+…+12×1006-1→S =12×1-1+12×2-1+12×3-1+…+12×1007-1,i =1008.此时终止循环,故选C.10.C [解析] 由题意可知,λ≥0,μ≥0,当λ=μ=0时,λ+μ的最小值为0,此时P 点与点A 重合,故D 错误;当λ=1,μ=1时,P 点也可以在D 点处,故A 错误;当λ=1,μ=0,λ+μ=1时,P 点在B 处,当点P 在线段AD 中点时,λ=μ=12,即λ+μ=1,所以B错误.11.2n ×1×3×5…×(2n -1)=(n +1)×(n +2)×(n +3)×…×(n +n ) [解析] 根据等式两端的特点可得.12.(1)3,1,6 (2)79 [解析] (1)把四边形面积分割,其中四个面积为12的三角形,一个面积为1的正方形,故其面积S =3;四边形内部只有1个整点;边界上有6个整点,故答案为3,1,6.(2)根据图中的格点三角形和四边形可得1=4b +c ,3=a +6b +c ,再选顶点为(0,0),(2,0),(2,2),(0,2)的格点正方形可得4=a +8b +c .由上述三个方程解得a =1,b =12,c=-1,所以S =N +12L -1,将已知数据代入得S =71+9-1=79.。
安徽高考数学文科二轮复习作业精练精析专题限时集训(二)A(含答案详析)

专题限时集训(二)A[第2讲算法初步、推理与证明](时间:30分钟)1.某程序框图如图X2-1x的值是()A.3 B.4C.6 D.8X2-1X2-22.执行如图X2-2所示的程序框图,若输出结果为3,则可输入的实数x值的个数为()A.1 B.2C.3 D.43.观察下列等式:2+23=2 23,3+38=338,4+415=4415,…,照此规律,第五个等式为________.4.观察下列算式:13=1,23=3+5,33=7+9+11,43=13+15+17+19,……若某数n3按上述规律展开后,发现等式右边含有“2013”这个数,则n=________.5.阅读如图X2-3所示的程序框图,输出的S等于________.X2-3X2-46.在如图X2-4所示的数阵中,第________.7.某程序框图如图X2-5( )A .3B .4C .5D .6X2-5X2-68.某程序框图如图X2-6所示,则该程序运行后输出的值是( )A .2011B .2012C .2013D .20149.已知数列{a n }为11,21,12,31,22,13,41,32,23,14,…,依它的前10项的规律,则a 99+a 100的值为________.10.观察下列等式:1 3+23=1,73+83+103+113=12,16 3+173+193+203+223+233=39,…则当m<n且m,n∈N时,3m+13+3m+23+3m+43+3m+55+…+3n-23+3n-13=________(最后结果用m,n表示).11.用火柴棒摆“金鱼”,如图X2-7所示,按照规律,第n个“金鱼”图需要火柴棒的根数为________(用n表示).-712.根据下面一组等式:S1=1;S2=2+3=5;S3=4+5+6=15;S4=7+8+9+10=34;S5=11+12+13+14+15=65;S6=16+17+18+19+20+21=111;S7=22+23+24+25+26+27+28=175;……可得S1+S3+S5+…+S2n-1=________.13.“无字证明”,就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.请利用图X2-8中甲、乙两图阴影部分的面积关系,写出该图所验证的一个三角恒等变换公式:________________________________________________________________________.图X2-8专题限时集训(二)A1.D [解析] 第一次循环结束时,S =4,k =2;第二次循环结束时,S =22,k =3;第三次循环结束时,S =103,k =4,此时103>100,不满足S<100,则输出的x 的值为8.故选D.2.C [解析] 由题意知y =⎩⎪⎨⎪⎧x 2-1,x ≤2,log 2x ,x>2.当x ≤2时,由x 2-1=3,得x 2=4,解得x =±2.当x>2时,由log 2x =3,得x =8,所以可输入的实数x 值的个数为3,选C.3.6+635=6 635 [解析] 注意到2+222-1=2·222-1,3+332-1=3·332-1,4+442-1=4·442-1,…,由此归纳得知,第五个等式是6+662-1=6·662-1,即6+635=6·635. 4.45 [解析] 观察所给算式的规律,我们发现:第一个式子的最后一个数为12+0,第二个式子的最后一个数为22+1,第三个式子的最后一个数为32+2,…,所以第n 个式子的最后一个数为n 2+n -1,而2013介于442+43和452+44之间,所以n =45.5.50 [解析] S =-1+2-3+4-…-99+100=50.6.66 [解析] 每行的第2个数构成一个数列{a n },由题意知a 2=3,a 3=6,a 4=11,a 5=18,所以a 3-a 2=3,a 4-a 3=5,a 5-a 4=7,…,a n -a n -1=2(n -1)-1=2n -3,等式两边同时相加得a n -a 2=[(2n -3)+3]×(n -2)2=n 2-2n , 所以a n =n 2-2n +a 2=n 2-2n +3(n ≥2),所以a 9=92-2×9+3=66.7.B [解析] 第一次循环得S =0+20=1,k =1;第二次循环得S =1+21=3,k =2;第三次循环得S =3+23=11,k =3,第四次循环得S =11+211=2059,k =4,此时S>1000,不满足条件,输出k =4,所以选B.8.B [解析] 在循环中S 的值具有周期性:2012→2013→2012→2013→…,当i =0时,输出结果为2012.9.3724 [解析] 据题意分组得⎝⎛⎭⎫11,⎝⎛⎭⎫21,12,⎝⎛⎭⎫31,22,13,…,(n 1,n -12,…,2n -1,1n),第1组有1项,第2组有2项,…,第n 组有n 项.令n (n +1)2>99,当n =14时,n (n +1)2=105,比99大6,故a 1,a 2,a 105分别为⎝⎛⎭⎫11,⎝⎛⎭⎫21,12,⎝⎛⎭⎫31,22,13,…,(141,132,…,78,69,510,411,312,213,114),故a 99+a 100=78+69=3724. 10.n 2-m 2[解析] 据已知可得73+83+103+113=3×2+13+3×2+23+3×4-23+3×4-13=42-22=12,同理163+173+193+203+223+233=3×5+13+3×5+23+3×5+43+3×5+53+3×8-23+3×8-13=82-52=39,据此规律可得3m +13+3m +23+…+3n -23+3n -13=n 2-m 2.11.6n +2 [解析] 根据图形可知,当n =1时,S 1=6+2;当n =2时,S 2=6×2+2;当n =3时,S 3=6×3+2,…,依此推断,S n =6n +2.12.n 4 [解析] S 1=1;S 1+S 3=1+15=16;S 1+S 3+S 5=1+15+65=81,由归纳推理可知S 1+S 3+S 5+…+S 2n -1=n 4.13.sin(α+β)=sin αcos β+cos αsin β[解析] 由题意知甲图的阴影部分为菱形,其面积为S=1×1×sin(α+β),乙图阴影部分的面积为sin αcos β+cos αsin β=sin(α+β).。
安徽新高考数学理科二轮复习作业精练精析专题限时集训(二十)(含答案详析)

专题限时集训(二十)[第20讲 不等式选讲]时间:45分钟)1.下列各式中,最小值等于2A.x y +y x B.x 2+5x 2+4C .tan +1tan θD .2x +2-x2.不等式1<|x +1|<3的解集为______________________________________. 3.不等式|x -8|-|x -4|>2的解集为________.4.若不等式|x +1|+|x -2|≥a 对任意a 的取值范围是________.5.不等式|x -5|+|x +3|≥10A .[-5,7] B .[-4,6]C .(-∞,-5]∪[7,+∞)D .(-∞,-4]∪[6,+∞)6.若x ,y ∈R 且满足x +3y =2,则3x +27y +1的最小值是( )A .3 39 B .1+2 2 C .6 D .77.设x >0,y >0,A =x +y 1+x +y ,B =x 1+x +y1+y,则A ,B 的大小关系是( )A .A =B B .A <BC .A ≤BD .A >B8.已知关于x 的不等式|x -1|+|x |≤k 无解,则实数k 的取值范围是________.9.若不等式|x +1|+|x -3|≥a +4a对任意的实数x 恒成立,则实数a 的取值范围是________.10.已知h >0,a ,b ∈R ,条件甲:|a -b |<2h ,条件乙:|a -1|<h 且|b -1|<h ,则甲是乙的________条件.(填“必要不充分”“充分不必要”“充要”或“既不充分也不必要”).11.若对任意的x >0,xx 2+3x +1≤a 恒成立,则a 的取值范围是________.12.已知函数f (x )=|2x -a |+a .若不等式f (x )≤6的解集为{x |-2≤x ≤3},则实数a 的值为________.13.已知关于x 的不等式|ax -2|+a |x -1|≥2(a >0). (1)当a =1时,求不等式的解集;(2)若不等式的解集为R ,求实数a 的取值范围.14.(1)设x ≥1,y ≥1,证明:x +y +1xy ≤1x +1y+xy ;(2)设1<a ≤b ≤c ,证明:log a b +log b c +log c a ≤log b a +log c b +log a c .15.设数列{a n }满足a 1=0,a n +1=ca 3n +1-c ,c ∈N *,其中c 为实数.证明: (1)a n ∈[0,1]对任意n ∈N *成立的充分必要条件是c ∈[0,1];(2)若0<c <13,则a n ≥1-(3c )n -1,n ∈N *且n ≥2;(3)若0<c <13,则a 21+a 22+…+a 2n>n +1-21-3c,n ∈N *.专题限时集训(二十)1.D [解析] A ,C 中不满足正值条件.B 中x 2+5x 2+4=x 2+4+1x 2+4=x 2+4+1x 2+4≥2,当且仅当x 2+4=1即x 2=-3时等号成立,因此x 2+5x 2+4>2,B 不正确,D 正确,∵2x >0,2-x >0,∴2x +2-x ≥22x ·2-x =2,当且仅当2x =12x ,即x =0时等号成立.2.(-4,-2)∪(0,2) [解析] 由1<|x +1|<3可知⎩⎪⎨⎪⎧|x +1|<3,|x +1|>1⇒⎩⎪⎨⎪⎧-4<x <2,x >0或x <-2,故x 的取值范围是(-4,-2)∪(0,2).3.{x |x <5} [解析] 令f (x )=|x -8|-|x -4|=⎩⎪⎨⎪⎧4,x ≤4,-2x +12,4<x ≤8,-4,x >8.当x ≤4时,f (x )=4>2;当4<x ≤8时,f (x )=-2x +12>2,得x <5,故4<x <5;当x >8时,f (x )=-4>2不成立.故原不等式的解集为{x |x <5}.4.(-∞,3] [解析] 因为|x +1|+|x -2|≥|(x +1)-(x -2)|=3,所以a ≤3. 5.D [解析] ①当x ≥5时,不等式化为x -5+x +3≥10,解得x ≥6. ②当-3<x <5时,不等式化为5-x +x +3≥10,不等式不成立. ③当x ≤-3时,不等式化为5-x -(x +3)≥10,解得x ≤-4. 由①②③得x ≤-4或x ≥6.6.D [解析] 由基本不等式得,3x +33y +1≥2 3x ·33y +1=2 3x +3y +1=7,当且仅当3x =33y ,即x =1,y =13时,等号成立.7.B [解析] 因为x >0,y >0,所以B =x 1+x +y 1+y >x 1+x +y +y1+y +x =x +y 1+x +y=A ,即A <B .8.k <1 [解析] ∵|x -1|+|x |≥|x -1-x |=1,∴当k <1时,不等式|x -1|+|x |≤k 无解,故k <1.9.(-∞,0)∪{2} [解析] 当a <0时,显然成立;当a >0时,∵|x +1|+|x -3|≥|x +1-(x -3)|=4,∴a +4a≤4,∴a =2.综上可知a 的取值范围是(-∞,0)∪{2}.10.必要不充分 [解析] |a -b |=|a -1+1-b |≤|a -1|+|b -1|<2h ,故由乙能推出甲成立,但甲成立不能推出乙成立,所以甲是乙的必要不充分条件.11.⎣⎡⎭⎫15,+∞ [解析] ∵a ≥x x 2+3x +1=1x +1x+3对任意的x >0恒成立,设u =x +1x +3,∴只需a ≥⎝⎛⎭⎫1u max 即可.∵x >0,∴u ≥5(当且仅当x =1时取等号).由u ≥5知,0<1u ≤15,∴a ≥15.12.1 [解析] 由|2x -a |+a ≤6得|2x -a |≤6-a ,所以a -6≤2x -a ≤6-a ,即a -3≤x ≤3,所以a -3=-2,所以a =1.13.解:(1)当a =1时,不等式为|x -2|+|x -1|≥2.当x ≤1时,不等式为-(x -2)-(x -1)≥2,解得x ≤12;当1<x <2时,不等式为-(x -2)+(x -1)≥2,解得x ∈∅;当x ≥2时,不等式为(x -2)+(x -1)≥2,解得x ≥52.综上可知,不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≥52或x ≤12. (2)∵|ax -2|+a |x -1|≥|(ax -2)-(ax -a )|=|a -2|,∴|a -2|≥2,解得a ≥4或a ≤0,又a >0,∴实数a 的取值范围是[4,+∞).14.证明:(1)由于x ≥1,y ≥1,所以x +y +1xy ≤1x +1y+xy ⇔xy (x +y )+1≤y +x +(xy )2.将上式中的右式减左式,得 [y +x +(xy )2]-[xy (x +y )+1] =[(xy )2-1]-[xy (x +y )-(x +y )] =(xy +1)(xy -1)-(x +y )(xy -1) =(xy -1)(xy -x -y +1) =(xy -1)(x -1)(y -1).已知x ≥1,y ≥1,所以(xy -1)(x -1)(y -1)≥0, 从而所要证明的不等式成立.(2)设log a b =x ,log b c =y ,由对数的换底公式得log c a =1xy ,log b a =1x ,log c b =1y,log a c=xy .于是所要证明的不等式即为x +y +1xy ≤1x +1y+xy ,其中x =log a b ≥1,y =log b c ≥1,故由(1)成立知所要证明的不等式成立.15.证明:(1)先证必要性.∵a 1=0,∴a 2=1-c , 又∵a 2∈[0,1],∴0≤1-c ≤1,即c ∈[0,1].再证充分性.设c ∈[0,1],用数学归纳法证明a n ∈[0,1]. 当n =1时,a 1=0∈[0,1].假设a k ∈[0,1](k ≥1),则a k +1=ca 3k +1-c ≤c +1-c =1,且a k +1=ca 3k +1-c ≥1-c ≥0, 所以a k +1∈[0,1].由数学归纳法知a n ∈[0,1]对所有n ∈N *成立.综上可知a n ∈[0,1]对任意n ∈N *成立的充分必要条件是c ∈[0,1]. 当n ≥2时,(2)∵a n =ca 3n -1+1-c ,∴1-a n =c (1-a n -1)(1+a n -1+a 2n -1).∵0<c <13,由(1)知a n -1∈[0,1],所以1+a n -1+a 2n -1≤3且1-a n -1≥0, ∴1-a n ≤3c (1-a n -1),∴1-a n ≤3c (1-a n -1)≤(3c )2(1-a n -2)≤…≤(3c )n -1(1-a 1)=(3c )n -1,∴a n ≥1-(3c )n -1(n ∈N *且n ≥2).(3)设0<c <13,当n =1时,a 21=0>2-21-3c,结论成立. 当n ≥2时,由(2)知a n ≥1-(3c )n -1>0,∴a 2n ≥[1-(3c )n -1]2=1-2(3c )n -1+(3c )2(n -1)>1-2(3c )n -1, ∴a 21+a 22+…+a 2n =a 22+…+a 2n >n -1-2[3c +(3c )2+…+(3c )n -1]=n +1-2[1-(3c )n]1-3c >n +1-错误!.。
2024年安徽省高考数学真题及参考答案
2024年安徽省高考数学真题及参考答案一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求。
1.已知集合{}553<<-=x x A ,{}3,2,0,13--=,B ,则=B A ()A.{}0,1-B.{}32, C.{}0,13--, D.{}2,0,1-2.若i z z+=-11,则=z ()A.i --1B.i +-1C.i -1D.i +13.已知向量()1,0=a,()x b ,2= ,若()a b b 4-⊥,则=x ()A.2- B.1- C.1D.24.已知()m =+βαcos ,2tan tan =βα,则()=-βαcos ()A.m3- B.3m -C.3m D.m35.已知圆柱和圆锥的底面半径相等,侧面积相等,且它们的高均为3,则圆锥的体积为()A.π32 B.π33 C.π36 D.π396.已知函数()()⎪⎩⎪⎨⎧≥++<---=0,1ln 0,22x x e x a ax x x f x 在R 上单调递增,则a 的取值范围是()A.(]0,∞-B.[]0,1-C.[]1,1-D.[)∞+,07.当[]π2,0∈x 时,曲线x y sin =与⎪⎭⎫⎝⎛-=63sin 2πx y 的交点个数为()A.3B.4C.6D.88.已知函数()x f 定义域为R ,()()()21-+->x f x f x f ,且当3<x 时,()x x f =,则下列结论中一定正确的是()A.()10010>fB.()100020>fC.()100010<f D.()1000020<f二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,由选错的得0分.9.为了解推动出口后的亩收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值1.2=x ,样本方差01.02=S ,已知该种植区以往的亩收入X 服从正态分布()21.08.1,N ,假设失去出口后的亩收入Y 服从发正态分布()2,S x N ,则()(若随机变量Z 服从正态分布()2,σμN ,则()8413.0≈+<σμZ P )A.()2.02>>X PB.()5.0<>Z X PC.()5.0>>Z Y P D.()8.0<>Z Y P 10.设函数()()()412--=x x x f ,则()A.3=x 是()x f 的极小值点B.当10<<x 时,()()2xf x f <C.当21<<x 时,()0124<-<-x f D.当01<<-x 时,()()x f x f >-211.造型可以看作图中的曲线C 的一部分,已知C 过坐标原点O ,且C 上的点满足横坐标大于2-,到点()02,F 的距离与到定直线()0<=a a x 的距离之积为4,则()A .2-=aB .点()022,在C 上C .C 在第一象限的点的纵坐标的最大值为1D .当点()00,y x 在C 上时,2400+≤x y三、填空题:本题共3小题,每小题5分,共15分.12.设双曲线()0,012222>>=-b a by a x C :的左右焦点分别为21,F F ,过2F 作平行于y 轴的直线交C 于B A ,两点,若131=A F ,10=AB ,则C 的离心率为.13.若曲线x e y x+=在点()1,0处的切线也是曲线()a x y ++=1ln 的切线,则=a .14.甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片分别标有数字1,3,5,7,乙的卡片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两个各自从自己特有的卡片中随机选一张,并比较所选卡片的数字的大小,数字大的人得1分,数字小的人得0分,然后各自弃置此轮所选的卡片(弃置的卡片在此后的轮次中不能使用).则四轮比赛后,甲的总得分小于2的概率为.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)记ABC ∆的内角C B A ,,的对边分别为c b a ,,.已知B C cos 2sin =,ab c b a 2222=-+.(1)求B ;(2)若ABC ∆的面积为33+,求c .16.(15分)已知()30,A 和⎪⎭⎫⎝⎛233,P 为椭圆()012222>>=+b a b y a x C :上两点.(1)求C 的离心率;(2)若过P 的直线l 交C 于另一点B ,且ABP ∆的面积为9,求l 的方程.17.(15分)如图,四棱锥ABCD P -中,⊥P A 底面ABCD ,2==PC P A ,1=BC ,3=AB .(1)若PB AD ⊥,证明:∥AD 平面PBC ;(2)若DC AD ⊥,且二面角D CP A --的正弦值为742,求AD .18.(17分)已知函数()()312ln-++-=x b ax xx x f .(1)若0=b ,且()0≥'x f ,求a 的最小值;(2)证明:曲线()x f y =是中心对称图形;(3)若()2->x f ,当且仅当21<<x ,求b 的取值范围.19.(17分)设m 为正整数,数列242.1,,,+m a a a 是公差不为0的等差数列,若从中删去两项i a 和()j i <后剩余的m 4项可被平均分为m 组,且每组的4个数都能构成等差数列,则称数列242.1,,,+m a a a 是()j i ,一一可分数列.(1)写出所有的()j i ,,61≤<≤j i ,使数列62.1,,,a a a 是()j i ,一一可分数列;(2)当3≥m 时,证明:数列242.1,,,+m a a a 是()13,2一一可分数列;(3)从242,1+m ,, 中一次任取两个数i 和j ()j i <,记数列242.1,,,+m a a a 是()j i ,一一可分数列的概率的概率为m P ,证明:81>m P .参考答案一、单项选择题1.A解析:∵553<<-x ,∴3355<<-x .∵2513<<,∴1523-<-<-.∴{}0,1-=B A .2.C解析:∵i z z +=-11,∴()()i i i z i iz z i z -=+=⇒+=⇒-+=11111.3.D 解析:()4,24-=-x a b ,∵()a b b4-⊥,∴()044=-+x x ,∴2=x .4.A解析:∵()m =+βαcos ,2tan tan =βα,∴()()32121tan tan 1tan tan 1sin sin cos cos sin sin cos cos cos cos -=-+=-+=-+=+-βαβαβαβαβαβαβαβα.∴()m 3cos -=-βα.5.B解析:由32⋅==r rl S ππ侧可得32=l ,∴3=r .∴ππ33393131=⋅⋅==Sh V .6.B由()()0,1ln ≥++=x x e x f x为增函数,故此分段函数在R 上递增,只需满足:⎪⎩⎪⎨⎧≤-≥-=--1022a a a,解得01≤≤-a .7.C解析:∴32π=T .8.B解析:()()()123f f f +>,()22=f ,()11=f .()()()()()122234f f f f f +>+>,()()()()()1223345f f f f f +>+>,……()()()8912123410>+>f f f ,……,()()()9871233237715>+>f f f ,()()()15971377261016>+>f f f .∴()100020>f .二、多项选择题9.BC 解析:已知()21.08.1~,N X ,由题目所给条件:若随机变量Z 服从正态分布,()8413.0≈+<σμZ P ,则()8413.09.1≈<X P ,易得()1587.08413.012≈-<>X P .故A 错误,B 正确;对于C:()21.01.2~,N Y ,∴()5.01.2=>Y P ,即()()5.01.22=>>>Y P Y P ,故C正确;对于D:同上易得()8413.02.2≈<Y P .由正态密度曲线的对称性可知()()8.08412.02.22>≈<=>Y P Y P .故D 错误.10.ACD解析:对于A:()()()()()()31314122--=-+--='x x x x x x f .令()0='x f ,解得11=x ,32=x .x 变化时,()x f '与()x f 变化如下表:故A 正确;对于B:当10<<x 时,102<<<x x ,又()x f 在()1,0上单调递增,所以()()x f xf <2,故B 错误;对于C :令()2112<<-=x x t ,则31<<x .()x f 在()3,1上单调递减,()()()13f t f f <<,()43-=f ,()11=f ,即()0121<-<-x f .故C 正确;对于D:()()()412--=x x x f ,()()()()()21421222---=---=-x x x x x f .∴()()()()()32122212-=--=--x x x x f x f .当01<<-x 时,()013<-x ,∴()()x f x f -<2成立.故D 正确.11.ABD解析:对于A:O 点在曲线C 上,O 到F 的距离和到a x =的距离之积为4,即42=⨯a ,解得2±=a .又∵0<a ,∴2-=a ,故A 正确;对于B:由图象可知曲线C 与x 轴正半轴相交于一点,不妨设B 点.设()0,m B ,其中2>m ,由定义可得()()422=+-m m ,解得22±=m .又∵2>m ,∴22=m ,故B 正确;对于C:设C 上一点()y x P ,,()()42222=++-x y x ,其中2->x .化简得曲线C 的轨迹方程为()()2222216--+=x x y ,其中2->x .已知2=x 时,12=y ,对x 求导()()2223232--+-=x x y .2122-==x y ,则在2=x 是下降趋势,即存在2<x 时,1>y 成立,故C 错误;对于D:()()2222216--+=x x y ,∵()022≥-x ,∴()22216+≤x y .∴240+≤x y .又∵20->x ,2400+≤x y ,则24000+≤≤x y y ,故D 正确.三、填空题12.23解析:作图易得131=A F ,52=AF ,且212F F AF ⊥,12222121=-=AF A F F F .由双曲线定义可得:8221=-=AF A F a ,6221==F F c ,则23==a c e .13.2ln 解析:1+='xe y ,20='==x y k ,切线l 的方程:12+=x y .设l 与曲线()a x y ++=1ln 的切点横坐标为0x ,110+='x y ,则2110=+=x k ,解得210-=x .代入12+=x y 可得切点为⎪⎭⎫⎝⎛-021,,再代入()a x y ++=1ln ,a +=21ln 0,即2ln =a .14.21解析:不妨确定甲的出牌顺序为7,5,3,1.乙随机出牌有2444=A 种基本事件.甲的数字1最小,乙的数字8最大.若数字1和数字8轮次不一致,乙最少得2分,甲最多2分.站在甲的视角下,分四种情况:①8对1,则7必得分(1)若得3分:3,5都得分,3对2,5对4(1种情况)(2)若得2分:3,5只有一个得分(ⅰ):5得分,3不得分:5对2,3对4或6(2种情况);5对4,3对6(1种情况);(ⅱ):3得分,5不得分:3对2,5对6(1种情况);②8对3,7必得分5得分:5对2,4,7对应2种情况,共有422=⨯种情况;③8对5,7必得分3得分:3对2,7对应2中情况,共有221=⨯种情况;④8对7,最多得2分3得分,5得分:3对2,5对4(1种情况).共有12种情况,甲总得分不小于2的概率为212412=.四、解答题15.解:(1)∵ab c b a 2222=-+,∴22222cos 222==-+=ab ab ab c b a C .∴22cos 1sin 2=-=C C .又∵B C cos 2sin =,∴22cos 2=B ,∴21cos =B ,∴3π=B .(2)∵33sin 21+==∆Bac S ABC ,∴333sin 21+=ac π.即434+=ac ……①由(1)易知4π=C ,3π=B .由正弦定理C c A a sin sin =,()CcC B a sin sin =+.∴4sin43sin πππc a =⎪⎭⎫ ⎝⎛+,∴224269c =+,∴c a 213+=.代入①式解得22=c .16.解:(1)将()30,A ,⎪⎭⎫⎝⎛233,P 代入椭圆12222=+b y a x 得:⎪⎪⎩⎪⎪⎨⎧=+=149919222b a b ,可得⎪⎩⎪⎨⎧==91222b a ,∴3222=-=b a c ,∴32=a ,3=c .∴离心率21323===a c e .(2)①当l 斜率不存在时,29332121=⨯⨯=-⋅=∆A P ABP x x PB S ,不符,舍去.②当l 斜率存在时,设l 方程:()323-=-x k y .联立()⎪⎪⎩⎪⎪⎨⎧=+-=-191232322y x x k y 可得:()()()02736212342222=--++-++k k x k k x k.由韦达定理:()34273622+--=⋅k k k x x B P ,又3=P x ,∴()3491222+--=k k k x B .∵BP 与y 轴交点⎪⎭⎫ ⎝⎛+-233,0k ,∴()9349123323213232122=+---⋅+=-+⋅=∆k k k k x x k S B P ABP 解得21=k 或23,∴l 方程x y 21=或0623=--y x .17.解:(1)证明:∵⊥P A 底面ABCD ,∴AD P A ⊥.又∵PB AD ⊥,∴⊥AD 平面P AB ,则AB AD ⊥.又∵1,32===BC AB AC ,,∴222BC AB AC +=,则BC AB ⊥,∴BC AD ∥.∵⊄AD 平面PBC ,⊂BC 平面PBC ,∴∥AD 平面PBC .(2)以D 为原点,DA 为x 轴正方向建立如图所示空间直角坐标系.设0,0,,>>==q p q DC p DA ,满足4222==+AC q p ,则()()()()0,0,0,0,,0,20,0,0,D q C p P p A ,,.设平面APC 法向量为()111,,z y x m =,∴()()0,,200q p AC AP -==,,,.∴⎪⎩⎪⎨⎧=+-=⋅==⋅002111qy px m AC z m AP ,取()0,,p q m = .设平面DPC 法向量为()()()0,,0,2,0,,,,222q DC p DP z y x n ===.∴⎪⎩⎪⎨⎧==⋅=+=⋅002222qy n DC z px n AP ,取()p n -=,0,2 .∴2222742142,cos ⎪⎪⎭⎫⎝⎛-=+⋅+=p q p qn m .∴7142=+p q .又∵422=+q p ,∴3=p ,即3=AD .18.解:(1)0=b 时,()ax x x x f +-=2ln,∴()()022≥+-⋅='a x x x f .∴()22-≥x x a .又∵()2,0∈x ,设()()22-=x x x h ,当()2,0∈x 时,()2max -=x h ,∴2-≥a .∴a 的最小值为2-.(2)由题意可知()x f 的定义域为()20,.()()()()()a x b x a xx bx x a x x x f x f 2111ln 111ln1133=-+-++-++++-+=-++.∴()x f 关于()a ,1中心对称.(3)()212ln 3->-++-x b ax xx ,即()0212ln3>+-++-x b ax x x 即()()02112ln 3>++-+-+-a x b x a xx.令1-=x t ,则()1,0∈t ,()0211ln 3>++++-+=a bt at tt t g .()t g 关于()a +2,0中心对称,则当且仅当()1,0∈t 时,()0>t g 恒成立.需02=+a ,即2-=a ,()0≥'t g 在()1,0恒成立.()()()()22222212231223032112t t t b t bt bt t t t g --≥⇒--≥⇒≥+--+='.令2t m =,则()1,0∈m ,()()12122-=--=m m m m m h .()2max -=m h ,∴23-≥b ,即32-≥b .∴⎪⎭⎫⎢⎣⎡+∞-∈,32b .19.解:(1)从1,2,3,4,5,6中删去()j i ,剩下的四个数从小到大构成等差数列,记为{}k b ,41≤≤k .设{}k b 公差为d ,已知1=d ,否则,若2≥d ,则6314≥=-d b b ,又51614=-≤-b b ,故矛盾,∴1=d ,则{}k b 可以为{}4,3,2,1,{}5,4,3,2,{}6,5,4,3,则对应()j i ,分别为()()()2,16,16,5,,.(2)证明:只需考虑前14项在去掉()13,2后如何构成3组4项的等差数列,后面剩下的()34124-=-m m 可自然依序划分为3-m 组等差数列.则只需构造{}14,12,11,10,9,8,7,6,5,4,3,1的一组划分,使划分出的3组数均成等差数列,取{}{}{}14,11,8,512,9,6,310,7,4,1,,,这单租数均为公差为3的等差数列,对于剩下的()34-m 个数,按每四个相邻数一组,划分为3-m 组即可.由此可见去掉()13,2后,剩余的m 4个数可以分为m 组,每组均为等差数列,故3≥m 时,24,2,1+m 是()13,2可分数列,即2421,,,+m a a a 是()13,2可分数列.(3)证明:用数学归纳法证明:共有不少于12++m m 中()j i ,的取法使24,2,1+m 是()j i ,可分数列,①当1=m 时,由(1)知,有11132++=种()j i ,的取法,②假设当n m =时,有至少12++n n 种()j i ,的取法,则当1+=n m 时,考虑数列{}64,,2,1+n 下对于()j i ,分三种情况讨论:1°当1=i 时,取()1,,,2,1,0,24+=+=n n k k j 则j i ,之间(不含j i ,)有k k 41124=--+个连续的自然数,可按形如{}{}{}14,4,14,249,8,7,65,4,3,2+--k k k k ,,, 划分,剩下的64,,44,34+++n k k ,也可按每四个连续自然数划分得到相应的等差数列,∵1,,,2,1,0+=n n k ,∴这种情况有2+n 种()j i ,的取法.2°当2=i 时,取()1,,,2,14+=+=n n k k j ,现以k 为公差构造划分为:{}13,12,11+++k k k ,,{}33,32,3,3+++k k k ,……{}14,13,12,1----k k k k ,{}k k k k 4,3,22,,{}24,23,22,2++++k k k k (注意当2=k 时,只有{}{}10,8,6,47,5,3,1,这两组)剩下的64,,44,34+++n k k ,也可按每四个连续自然数划分得到相应的等差数列,∵1,,,2+=n n k ,∴这种情况有n 种()j i ,的取法.3°当2>i 时,考虑{}64,,7,6,5+n 共24+n 个数,由归纳假设里n m =时,有至少12++n n 种()j i ,的取法.综合1°2°3°,当1+=n m 时,至少有()()()()1111222++++=+++++n n n n n n 中取法,由①②及数学归纳法原理,值共有不少于12++m m 种()j i ,的取法使24,2,1+m 为()j i ,可分数列,那么()()8188811681121411222222242=++++>++++=++++=++≥+m m m m m m m m m m m m C m m P m m ,∴81>m P .。
安徽新高考数学文科二轮复习作业精练精析专题限时集训(十四)(含答案详析)
专题限时集训(十四)[第14讲 直线与圆](时间:45分钟)1.过点A(1,2)且垂直于直线2x +( ) A .x -2y +4=0 B .2x +y -7=0 C .x -2y +3=0 D .x -2y +5=02.经过圆x 2-2x +y 2=0的圆心且与直线x +2y =0平行的直线方程是( ) A .x +2y -1=0 B .x -2y -2=0 C .x -2y +1=0 D .x +2y +2=03.若直线(1+a)x +y +1=0与圆x 2+y 2-2x =0相切,则a 的值是( ) A .1或-1 B .2或-2 C .1 D .-1 4.已知圆C :x 2+y 2=2与直线l :x +y +2=0,则圆C 被直线l 所截得的弦长为( ) A .1 B. 3 C .2 D .2 35.设过点(0,b)且斜率为1的直线与圆x 2+y 2+2x =0相切,则b 的值为( ) A .2± 2 B .2±2 2 C .1±2 D.2±16.若直线3x +y +a =0过圆x 2+y 2+a 的值为________.7.已知直线l 1:x +(a -2)y -2=02+ay -1=0,则“a =-1”是“l 1⊥l 2”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.圆C 1:x 2+y 2-1=0与圆C 2:x 2+y 2-4x -5=0的位置关系是( ) A .相交 B .外切 C .内切 D .外离9.若直线ax -by +1=0过圆C :x 2+y 2+2x -4y +1=0的圆心,则ab 的取值范围是( )A.⎝⎛⎦⎤-∞,14 B.⎝⎛⎦⎤-∞,18C.⎝⎛⎦⎤0,14D.⎝⎛⎦⎤0,18 10.若直线ax +2by -2=0(a>0,b>0)始终平分圆x 2+y 2-4x -2y -8=0的周长,则1a +2b的最小值为( ) A .1 B .5C .3+4 2D .3+2 211.直线x -3y +2=0被圆x 2+y 2=4截得的劣弧长为________.12.若直线l 与圆x 2+(y +1)2=4相交于A ,B 两点,且线段AB 的中点坐标是(1,-2),则直线l 的方程为________.13.已知圆C :(x -a)2+(y -b)2=8(ab>0)过坐标原点,则圆心C 到直线l :x b +ya=1的距离的最小值等于________.14.在平面直角坐标系xOy 中,设点P 为圆C :(x -1)2+y 2=4上的任意一点,点Q(2a ,a -3)(a ∈R ),则线段PQ 长度的最小值为________.15.已知圆C :x 2+y 2=1,过点P(0,2)作圆C 的切线,交x 轴正半轴于点Q ,若M(m ,n)为线段PQ 上的动点,求3m +1n的最小值.16.过原点O 且以点C ⎝⎛⎭⎫t ,2t (t ∈R ,t ≠0)为圆心的圆与x 轴,y 轴分别交于点A 和点B.(1)求证:△OAB 的面积为定值;(2)设直线y =-2x +4与圆C 交于点M ,N ,若OM =ON ,求圆C 的方程.专题限时集训(十四)1.C [解析] 直线2x +y -5=0的斜率为-2,因此所求直线的斜率为12,方程为y -2=12(x -1),化为一般式为x -2y +3=0. 2.A [解析] 圆x 2-2x +y 2=0的圆心为(1,0),所求直线方程为y -0=-12(x -1),即x +2y -1=0.3.D [解析] x 2+y 2-2x =0化为标准方程为(x -1)2+y 2=1,由|1+a +1|(1+a )2+12=1得a =-1.4.C [解析] 因为d =|2|2=1,所以弦长为2 (2)2-12=2.5.C [解析] 设直线的方程为y =x +b ,圆心(-1,0)到直线的距离等于半径1,即|-1+b|2=1,解得b =1±2. 6.1 [解析] x 2+y 2+2x -4y =0化为标准方程为(x +1)2+(y -2)2=5,则有3×(-1)+2+a =0,解得a =1.7.A [解析] 由1×(a -2)+(a -2)a =0得a =-1或a =2,因此“a =-1”是“l 1⊥l 2”的充分不必要条件.8.C [解析] 两圆标准方程分别为x 2+y 2=1和(x -2)2+y 2=9,(0-2)2+(0-0)2=2=3-1,所以两圆位置关系为内切.9.B [解析] 因为直线ax -by +1=0过圆C 的圆心(-1,2),所以a +2b =1.由(a +2b )28≥ab ab ≤18. 10.D [解析] 圆x 2+y 2-4x -2y -8=0的圆心为(2,1),由题知直线过圆心,所以2a +2b -2=0,即a +b =1.故1a +2b =a +b a +2(a +b )b =3+b a +2ab≥3+2 2.11.4π3 [解析] 圆心为(0,0),半径为2,圆心到直线的距离d =|2|12+(3)2=1,直线l 与圆C 相交所得的弦长为2 22-12=2 3,该弦所对的圆心角为π3×2=2π3,所以劣弧长为2π3×2=4π3.12.x -y -3=0 [解析] 圆心坐标为(0,-1),则直线l 的斜率为k =-1-2-(-1)1-0=1,所以直线l 的方程为y +2=x -1,即x -y -3=0.13.2 [解析] 由题意得a 2+b 2=8,x b +ya=1可化为ax +by -ab =0,所以d =|a 2+b 2-ab|a 2+b2=|8-ab|8≥⎪⎪⎪⎪⎪⎪8-a 2+b 228=|8-4|8= 2.14.5-2 [解析] 点Q 在直线x -2y -6=0上,圆心(1,0)到该直线的距离为d =|1-2×0-6|12+22=5,因此线段PQ 长度的最小值为5-2.15.解:如图所示,设直线PQ 联结OA ,则OA ⊥PQ.因为OA =1, OP =2,所以∠OPA =30°,所以∠OQP =60°.故直线PQ 的斜率为tan 120°=-3,直线PQ 的方程为y =-3x +2⎝⎛⎭⎫0≤x ≤2 33.因为点M(m ,n)在线段PQ 上,所以3m +n =2,故3m +1n =12⎝⎛⎭⎫3m +1n (3m +n)=12(4+3n m +3m n )≥ 12(4+2 3)=2+3,当且仅当m =n =3-1时取等号. 16.解:(1)证明:因为圆C 过原点O ,OC 2=t 2+4t2.所以圆C 的方程为(x -t)2+⎝⎛⎭⎫y -2t 2=t 2+4t2,令x =0得y =0或4t ;令y =0得x =0或2t ,故A(2t ,0),B ⎝⎛⎭⎫0,4t . 所以S △OAB =12OA ·OB =12×⎪⎪⎪⎪4t ×|2t|=4,即△OAB 的面积为定值.(2)因为OM =ON ,CM =CN ,所以OC 垂直平分线段MN.因为k MN =-2,所以k OC =12,所以直线OC 的方程为y =12x.因为C 为圆心,所以2t =12t ,解得t =±2.当t =2时,点C(2,1),OC =5,此时点C 到直线y =-2x +4的距离为d =|2×2+1-4|22+1=55<5,直线与圆交于两点;当t =-2时,点C(-2,-1),OC =5,此时点C 到直线y =-2x +4的距离为 d =|-2×2-1-4|22+1=9 55>5,直线与圆相离,所以t =-2不符合题意,舍去.所以圆C 的方程为(x -2)2+(y -1)2=5.。
新课标新高考数学理科二轮复习作业精练精析专题限时集训(六)A(含答案详析)
专题限时集训(六)A[第6讲 导数及其应用](时间:45分钟)1.曲线y =2x 3-3x +1在点(1,0) ) A .y =4x -5 B .y =-3x +2 C .y =-4x +4 D .y =3x -32.函数f (x )=2ln x +x 2-bx +a (b >0,a ∈R )在点(b ,f (b ))处的切线斜率的最小值是( ) A .2 2 B .2 C. 3 D .13.已知函数f (x )=x +1,g (x )=a ln x ,若在x =14处函数f (x )与g (x )的切线平行,则实数a 的值为( )A.14B.12 C .1 D .44.已知函数f (x )=⎩⎨⎧x +1(-1≤x ≤0),1-x 2(0<x ≤1),则⎠⎛-11f (x )d x 的值为( ) A .1+π2 B .12+π4C .1+π4D .12+π25.函数f(x)=x +sin x(x ∈R )( A .是偶函数且为减函数 B .是偶函数且为增函数 C .是奇函数且为减函数 D .是奇函数且为增函数6.若y =f (x )既是周期函数,又是奇函数,则其导函数y =f ′(x )( ) A .既是周期函数,又是奇函数 B .既是周期函数,又是偶函数 C .不是周期函数,但是奇函数 D .不是周期函数,但是偶函数7.设函数f (x )=|sin x |的图像与直线y =kx (k >0)有且仅有三个公共点,这三个公共点的横坐标的最大值为α,则α等于( )A .-cos αB .tan αC .sin αD .π8.已知函数f (x )及其导数f ′(x ),若存在x 0,使得f (x 0)=f ′(x 0),则称x 0是f (x )的一个“巧值点”,下列函数中,有“巧值点”的是( )①f (x )=x 2;②f (x )=e -x ;③f (x )=ln x ;④f (x )=tan x ;⑤f (x )=x +1x.A .①③⑤B .③④C .②③④D .②⑤9.⎠⎛1(1-x2-x)d x=________.10.函数y=f(x)的导数记为f′(x),若f′(x)的导数记为f(2)(x),f(2)(x)的导数记为f(3)(x),…,已知f(x)=sin x,则f(2013)(x)=________.11.由曲线y=2x2,直线y=-4x-2,直线x=1围成的封闭图形的面积为________.12.函数f(x)=x3+2xf′(-1),则函数f(x)在区间[-2,3]上的值域是________.13.已知函数f(x)=x,g(x)=x4x-a.函数g(x)在(1,+∞)上单调递减.(1)求实数a的取值范围;(2)设函数h(x)=f(x)·g(x),x∈[1,4],求函数y=h(x)的最小值.14.已知函数f(x)=x2-(a+2)x+a ln x+2a+2,其中a≤2.(1)求函数f(x)的单调区间;(2)若函数f(x)在(0,2]上有且只有一个零点,求实数a的取值范围.15.已知函数f(x)=(2-a)ln x-1,g(x)=ln x+ax2+x(a∈R),令φ(x)=f(x)+g′(x).(1)当a=0时,求φ(x)的极值;(2)当-3<a<-2时,若对∀λ1,λ2∈[1,3],使得|φ(λ1)-φ(λ2)|<(m+ln 2)a-2ln 3恒成立,求实数m的取值范围.专题限时集训(六)A1.D [解析] y ′=6x 2-3,当x =1时y ′=3,即曲线y =2x 3-3x +1在点(1,0)处的切线方程的斜率为3,故切线方程为y =3(x -1),即y =3x -3.2.A [解析] f ′(x )=2x +2x -b ,故曲线y =f (x )在点(b ,f (b ))的切线斜率是f ′(b )=2b+2b -b =b +2b≥2 2,当b =2时等号成立.3.A [解析] 由题意,在x =14处,两个函数的导数值相等.又f ′(x )=12 x,g ′(x )=a x ,所以1=4a ,即a =14. 4.B [解析] 根据定积分的几何意义可得所求的定积分为12+π4.5.D [解析] f (x )满足f (-x )=-f (f ′(x )=1+cos x ≥0,函数f (x )是增函数.6.B [解析] 因为y =f (x )是周期函数,则有f (x +T )=f (x ),两边同时求导,得f ′(x +T )(x +T )′=f ′(x ),即f ′(x +T )=f ′(x ),所以导函数为周期函数.因为y =f (x )是奇函数,所以f (-x )=-f (x ),两边同时求导,得f ′(-x )(-x )′=-f ′(x ),即-f ′(-x )=-f ′(x ),所以f ′(-x )=f ′(x ),即导函数为偶函数.选B.7.B [解析] 直线y =kx 与曲线y =-sin x (x ∈[π,2π])相切,设切点为(α,-sin α),则-sin α=kα且k =-cos α,所以α=tan α.8.A [解析] ①即x 2=2x ,这个方程显然有解,故①符合要求;②即e -x =-e -x ,此方程无解,故②不符合要求;③即ln x =1x,数形结合可知这个方程也存在实数解,故③符合要求;④中,f ′(x )=cos 2x +sin 2x cos 2x =1cos 2x ,若f (x )=f ′(x ),即1cos 2x=tan x ,化简得sin x cos x =1,即sin 2x =2,方程无解,故④不符合要求;⑤中,f ′(x )=1-1x 2,1-1x 2=x +1x,即x 3-x 2+x+1=0,令g (x )=x 3-x 2+x +1,则g (-1)=-2,g (0)=1,所以必存在x 0∈(-1,0)使g (x 0)=0,故⑤符合要求.9.π4-12 [解析] ⎠⎛01(1-x 2-x)d x =⎠⎛01 1-x 2d x -⎠⎛01x d x =π4-⎪⎪⎝⎛⎭⎫12x 210=π4-12. 10.cos x [解析] f′(x)=cos x ,f (2)(x)=-sin x ,f (3)(x)=-cos x ,f (4)(x)=sin x ,以4为周期,故f (2013)(x)=f′(x)=cos x.11.163[解析] 联立直线方程与抛物线方程得x 2+2x +1=0,解得x =-1,即直线y =-4x -2为抛物线y =2x 2的一条切线(如图),因此所求的面积为定积分⎠⎛-11(2x 2+4x +2)d x =23(x +1)3错误!错误!-1=错误!.12.[-4 2,9] [解析] f′(x)=3x 2+2f′(-1),令x =-1可得f ′(-1)=-3,所以f(x)=x 3-6x ,f′(x)=3x 2-6.令f′(x)=0得x =±2,根据三次函数的性质,可得x =-2为其极大值点,x =2为其极小值点.又f(-2)=4,f(-2)=4 2,f(2)=-4 2,f(3)=9,所以函数f(x)在区间[-2,3]上的最小值为f(2)=-4 2,最大值为f(3)=9,所以其值域为[-4 2,9].13.解:(1)g(x)=x 4x -a =14(4x -a )+14a 4x -a=14+a4(4x -a ).因为g(x)在(1,+∞)上单调递减,所以⎩⎪⎨⎪⎧a>0,a 4≤1,即0<a ≤4.(2)h(x)=x ·x4x -a =(x )34x -a ,h ′(x)=32x 12(4x -a )-4x 32(4x -a )2=2 x ⎝⎛⎭⎫x -3a 4(4x -a )2, 因为0<a ≤4,所以0<3a4≤3.当0<3a 4≤1,即0<a ≤43时,h(x)在[1,4]上单调递增,所以h(x)min =h(1)=14-a;当1<3a 4≤3,即43<a ≤4时,h(x)在⎣⎡⎭⎫1,3a 4上单调递减,在⎣⎡⎦⎤3a 4,4上单调递增,所以h(x)min =h ⎝⎛⎭⎫3a 4=3 3a 16.14.解:(1)函数定义域为{x|x>0},且f′(x)=2x -(a +2)+a x =(2x -a )(x -1)x.①当a ≤0,即a2≤0时,令f′(x)<0,得0<x<1,所以函数f(x)的单调递减区间为(0,1);令f′(x)>0,得x>1,所以函数f(x)的单调递增区间为(1,+∞).②当0<a 2<1,即0<a<2时,令f′(x)>0,得0<x<a2或x>1,所以函数f(x)的单调递增区间为⎝⎛⎭⎫0,a2,(1,+∞); 令f′(x)<0,得a2<x<1,所以函数f(x)的单调递减区间为⎝⎛⎭⎫a 2,1. ③当a2=1,即a =2时,f′(x)≥0恒成立,所以函数f(x)的单调递增区间为(0,+∞).(2)①当a ≤0时,由(1)可知,函数f(x)的单调递减区间为(0,1),f(x)在(1,2]单调递增.所以f(x)在(0,2]上的最小值为f(1)=a +1.由于f ⎝⎛⎭⎫1e 2=1e 4-2e 2-a e 2+2=⎝⎛⎭⎫1e 2-12-a e2+1>0,要使f(x)在(0,2]上有且只有一个零点,需满足f(1)=0或⎩⎪⎨⎪⎧f (1)<0,f (2)<0,解得a =-1或a<-2ln 2.②当a =2时,由(1)可知,函数f(x)在(0,2]上单调递增,且f(e -4)=1e 8-4e4-2<0,f(2)=2+2ln 2>0,所以f(x)在(0,2]上有且只有一个零点.③当0<a<2时,由(1)可知,函数f(x)在⎝⎛⎭⎫a 2,1上单调递减,在⎝⎛⎭⎫0,a2,(1,2]上单调递增,又因为f(1)=a +1>0,所以当x ∈⎝⎛⎦⎤a 2,2时,总有f(x)>0.因为0<e -2a +2a<1<a +2,所以f ⎝⎛⎭⎫e -2a +2a =e -2a +2a ⎣⎡⎦⎤e -2a +2a -(a +2)+⎝⎛⎭⎫a ln e -2a +2a +2a +2=e -2a +2a ⎣⎡⎦⎤e -2a +2a -(a +2)<0.所以f(x)在区间⎝⎛⎭⎫0,a 2内必有零点.又因为f(x)在⎝⎛⎭⎫0,a 2内单调递增,从而当0<a ≤2时,f(x)在(0,2]上有且只有一个零点.综上所述,0<a ≤2或a<-2ln 2或a =-1时,f(x)在(0,2]上有且只有一个零点.15.解:因为g′(x)=1x +2ax +1,所以φ(x)=(2-a)ln x +1x+2ax ,x ∈(0,+∞).(1)a =0时,φ(x)=2ln x +1x ,x ∈(0,+∞),φ′(x)=2x -1x 2=2x -1x2.令φ′(x)=0,得x =12.当0<x<12时,φ′(x)<0;当x>12时,φ′(x)>0.所以函数φ(x)在⎝⎛⎭⎫0,12上单调递减,在⎝⎛⎭⎫12,+∞上单调递增,所以函数φ(x)在x =12处取得极小值φ⎝⎛⎭⎫12=2-2ln 2,无极大值.(2)φ′(x)=2-a x -1x 2+2a =2ax 2+(2-a )x -1x 2=2a ⎝⎛⎭⎫x -12⎝⎛⎭⎫x +1a x 2,x ∈(0,+∞).当a<-2时,0<-1a <12,所以在⎝⎛⎭⎫0,-1a 和⎝⎛⎭⎫12,+∞上φ′(x)<0.所以函数的单调递减区间是⎝⎛⎭⎫0,-1a ,⎝⎛⎭⎫12,+∞. 所以当-3<a<-2时,φ(x)在[1,3]上单调递减,所以φ(x)min =φ(3)=(2-a)ln 3+13+6a ,φ(x)max =φ(1)=2a +1.对∀λ1,λ2∈[1,3],使得|φ(λ1)-φ(λ2)|<(m +ln 2)a -2ln 3恒成立等价于|φ(λ1)-φ(λ2)|max=φ(1)-φ(3)<(m +ln 2)a -2ln 3恒成立,即(2a +1)-⎣⎡⎦⎤(2-a )ln 3+13+6a =23-2ln 3+(ln 3-4)a<(m +ln 2)a -2ln 3恒成立,即⎝⎛⎭⎫m +4+ln 23a -23>0在-3<a<-2时恒成立. 令h(a)=⎝⎛⎭⎫m +4+ln 23a -23,则h(a)是a 的一次函数,故只要h(-3)≥0且h(-2)≥0即可.h(-3)=⎝⎛⎭⎫m +4+ln 23(-3)-23≥0,解得m ≤-389-ln 23; h(-2)=⎝⎛⎭⎫m +4+ln 23(-2)-23≥0,解得m ≤-133-ln 23.所以m ≤-133-ln 23.所以所求的m 的取值范围是⎝⎛⎦⎤-∞,-133-ln 23. (也可使用分离参数的方法)。
安徽新高考数学理科二轮复习作业精练精析专题限时集训(四)B(含答案详析)
专题限时集训(四)B[第4讲 函数、基本初等函数Ⅰ的图像与性质](时间:30分钟)1.已知f (x )=⎩⎪⎨⎪⎧2x +3(x ≤0),f (x -1)-f (x -2)(x >0),则f (2)=( ) A .1 B .2 C .0 D .-12.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后来为了赶时间加快速度行驶,与以上事件吻合得最好的图像是( )图X4-2 3.已知函数f (x )=⎩⎪⎨⎪⎧log 2x ,x >0,log 12(-x ),x <0,若af (-a )>0,则实数a 的取值范围是( ) A .(-1,0)∪(0,1)B .(-∞,-1)∪(1,+∞)C .(-1,0)∪(1,+∞)D .(-∞,-1)∪(0,1)4.已知函数f (x )的图像如图X4-3所示,则f (x )的解析式可以是( )A .f (x )=ln|x |xB .f (x )=e x xC .f (x )=1x 2-1D .f (x )=x -1x5.设函数f (x )=⎩⎪⎨⎪⎧x 2-6x +6,x ≥0,3x +4,x <0,若互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3),则x 1+x 2+x 3的取值范围是( )A.203,263B.203,263C.113,6D.113,66.函数f (x )=ln |x |( )图X4-47.函数y =f (x ),x ∈D ,若存在常数C ,对任意的x 1∈D ,存在唯一的x 2∈D ,使得f (x 1)f (x 2)=C ,则称函数f (x )在D 上的几何平均数为C .已知f (x )=x 3,x ∈[1,2],则函数f (x )在[1,2]上的几何平均数为( )A. 2 B .2 C .4 D .2 28.定义在R 上的函数y =f (x ),在(-∞,a )上是增函数,且函数y =f (x +a )是偶函数,当x 1<a ,x 2>a ,且|x 1-a |<|x 2-a |时,有( )A .f (x 1)>f (x 2)B .f (x 1)≥f (x 2)C .f (x 1)<f (x 2)D .f (x 1)≤f (x 2)9.设定义在R 上的奇函数y =f (x ),满足对任意t ∈R 都有f (t )=f (1-t ),且x ∈0,12时,f (x )=-x 2,则f (3)+f -32的值等于( ) A .-12 B .-13 C .-14 D .-1510.定义区间(a ,b ),[a ,b ),(a ,b ],[a ,b ]的长度均为d =b -a ,多个区间并集的长度为各区间长度之和,例如,(1,2)∪[3,5)的长度d =(2-1)+(5-3)=3.用[x ]表示不超过x 的最大整数,记{x }=x -[x ],其中x ∈R .设f (x )=[x ]·{x },g (x )=x -1,当0≤x ≤k 时,若不等式f (x )< g (x )的解集区间的长度为5,则k 的值为( )A .6B .7C .8D .911.已知函数f (x )=⎩⎪⎨⎪⎧log 2x ,x >0,2x ,x ≤0,若f (a )=12,则a 等于________. 12.设a ,b ∈R ,且a ≠2,若定义在区间(-b ,b )内的函数f (x )=lg 1+ax 1+2x 是奇函数,则a +b 的取值范围是________.13.设函数f (x )=|x -a |-ax ,其中a 为常数.若函数f (x )存在最小值的充要条件是a ∈A ,则(1)集合A =________;(2)当a ∈A 时,函数f (x )的最小值为________.专题限时集训(四)B1.D [解析] f (2)=f (1)-f (0)=[f (0)-f (-1)]-f (0)=-f (-1)=-1.2.C [解析] 由题意可知函数图像最开始为“斜率为负的线段”,接着为“与x 轴平行的线段”,最后为“斜率为负值,且小于之前斜率的线段”.观察选项中图像可知,C 项符合,故选C.3.A [解析] 若a >0,则f (-a )>0,即log 12a >0,解得0<a <1;若a <0,则f (-a )<0,即log 2(-a )<0,解得-1<a <0.故实数a 的取值范围是(-1,0)∪(0,1).4.A [解析] 从图像可知,函数是奇函数且以±1为零点,且随着x →+∞,函数值逐步趋近于0,故选项A 中的函数符合.5.D [解析] 设x 1<0,x 2≥0,x 3≥0,根据抛物线的对称性可得x 2+x 3=6,函数f (x )在[0,+∞)最小值为-3,当x ∈(-∞,0)时,函数f (x )<4.所以x 1满足-3<3x 1+4<4,即-73<x 1<0.由此得113<x 1+x 2+x 3<6. 6.B [解析] 函数是非奇非偶函数,排除选项A ,C.当x >0时f (x )=sin 2x +x ,f ′(x )=2cos 2x +1,此时函数f (x )在⎝⎛⎭⎫0,π6上单调递增,只能是选项B 中的函数图像. 7.D [解析] 由于x 1∈[1,2],所以2x 1∈[1,2],取x 2=2x 1即得f (x 1)f (x 2)=8,所以f (x 1)f (x 2)=2 2.8.A [解析] 由于函数y =f (x +a )是偶函数,其图像关于y 轴对称,把这个函数图像平移|a |个单位(a <0左移、a >0右移)可得函数y =f (x )的图像,因此可得函数y =f (x )的图像关于直线x =a 对称,此时函数在(a ,+∞)上是减函数,由于x 1<a ,x 2>a 且|x 1-a |<|x 2-a |,说明x 1离对称轴的距离比x 2离对称轴的距离小,故f (x 1)>f (x 2).9.C [解析] 由于函数f (x )是奇函数,且对任意t ∈R f (t )=f (1-t ),所以f (x )=-f (x -1)⇒f (x +1)=-f (x )⇒f (x +2)=f (x ),所以f (x )是以2为周期的周期函数,故f (3)=f (1)=f (1-1)=f (0)=0,f ⎝⎛⎭⎫-32=f ⎝⎛⎭⎫12=-14. 所以f (3)+f ⎝⎛⎭⎫-32=-14. 10.B [解析] 当n ≤x <n +1,n 为自然数,[x ]=n ,{x }=x -[x ]=x -n ,不等式f (x )<g (x ),即n (x -n )<x -1,即(n -1)x <n 2-1.当n =0时,不等式(n -1)x <n 2-1,即x >1,此时无解;当n =1时,不等式(n -1)x <n 2-1,即0<0,此时不等式也无解;当n ≥2时,不等式(n -1)x <n 2-1,即x <n +1,此时不等式f (x )<g (x )的解集为[n ,n +1). 综上可知不等式f (x )<g (x )在0≤x ≤k 上只有k >2时有解,且其解集为[2,k ),故当解区间的长度为5时k =7. 11.2或-1 [解析] 若a >0,则log 2a =12,得a =2;若a ≤0,则2a =12,得a =-1. 12.⎝⎛⎦⎤-2,-32 [解析] f (-x )+f (x )=lg 1-ax 1-2x +lg 1+ax 1+2x =lg 1-a 2x 21-4x 2=0,∴1-a 2x 21-4x 2=1,∴(a 2-4)x 2=0,∵x 2不恒为0,∴a 2=4,又a ≠2,故a =-2,∴f (x )=lg 1-2x 1+2x. 由1-2x 1+2x>0,得-12<x <12,由题意(-b ,b )⊆⎝⎛⎭⎫-12,12,∴0<b ≤12,故-2<a +b ≤-32. 13.[-1,1] -a 2 [解析] (1)当x ≥a 时,f (x )=(1-a )x -a ;当x <a 时,f (x )=a -(1+a )x .要使f (x )有最小值,需满足1-a ≥0,且1+a ≥0,即-1≤a ≤1时,f (x )存在最小值.(2)当x =a 时,f (x )取得最小值-a 2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题限时集训(十四)A[第14讲 圆锥曲线的热点问题](时间:45分钟)1.已知椭圆C :x 24+y2b=1,直线l :y =mx +1,若对任意的m ∈R ,直线l 与椭圆C 恒有公共点,则实数b 的取值范围是( )A .[1,4)B .[1,+∞)C .[1,4)∪(4,+∞)D .(4,+∞)2.与两圆x 2+y 2=1及x 2+y 2-8x +12=0都外切的圆的圆心在( ) A .一个椭圆上 B .双曲线的一支上 C .一条抛物线上 D .一个圆上3.已知两定点A (1,1),B (-1,-1),动点P 满足P A →·PB →=x22,则点P 的轨迹是( )A .圆B .椭圆C .双曲线D .拋物线4.已知椭圆C 1:x 2m +2+y 2n=1与双曲线C 2:x 2m -y 2n =1共焦点,则椭圆C 1的离心率e的取值范围为( )A.⎝⎛⎭⎫22,1B.⎝⎛⎭⎫0,22C .(0,1) D.⎝⎛⎭⎫0,125.以抛物线y 2=8x x +2=0相切,这些圆必过一定点,则这一定点的坐标是( )A .(0,2)B .(2,0)C .(4,0)D .(0,4) 6.已知圆柱的底面半径为2,高为3,用一个平面去截该圆柱,若所截得的截面为椭圆,则椭圆的离心率的取值范围为( )A.⎝⎛⎭⎫0,22 B.⎝⎛⎦⎤0,25 C.⎝⎛⎦⎤0,35 D.⎝⎛⎦⎤0,45 7.过椭圆x 29+y 24=1上一点M 作圆x 2+y 2=2的两条切线,A ,B 为切点,过A ,B 的直线l 与x 轴,y 轴分别交于P ,Q 两点,则△POQ 的面积的最小值为( )A.12B.23 C .1 D.438.抛物线y 2=2px (p >0)的焦点为F ,点A ,B 在此抛物线上,且∠AFB =90°,弦AB的中点M 在该抛物线准线上的射影为M ′,则|MM ′||AB |的最大值为( )A. 3B.32 C .1 D.229.双曲线x 2a 2-y2b 2=1(a ,b >0)的一条渐近线的倾斜角为π3,离心率为e ,则a 2+e b的最小值为________.10.过抛物线y 2=x 的焦点F 的直线m 的倾斜角θ≥π4,直线m 交抛物线于A ,B 两点,且A 点在x 轴上方,则|F A |的取值范围是________.11.设椭圆x 2a 2+y 2b 2=1(a >b >0)的中心、右焦点、右顶点分别为O ,F ,G ,且直线x =a 2c与x 轴相交于点H ,则|FG ||OH |最大时椭圆的离心率为________.12.抛物线y 2=8x 的准线为l ,点Q 在圆C :x 2+y 2+6x +8y +21=0上,设抛物线上任意一点P 到直线l 的距离为m ,则m +|PQ |的最小值为________.13.已知E (2,2)是抛物线C :y 2=2px 上一点,经过点(2,0)的直线l 与抛物线C 交于A ,B 两点(不同于点E ),直线EA ,EB 分别交直线x =-2于点M ,N .(1)求抛物线方程及其焦点坐标;(2)已知O 为原点,求证:∠MON 为定值.14.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为53,定点M 的坐标为(2,0),椭圆短轴的端点分别是B 1,B 2,且MB 1⊥MB 2.(1)求椭圆C 的方程;(2)设过点M 且斜率不为0的直线交椭圆C 于A ,B 两点.试问x 轴上是否存在定点P ,使PM 平分∠APB ?若存在,求出点P 的坐标;若不存在,说明理由.15.设双曲线C 以椭圆x 225+y 29=1的两个焦点为焦点,且双曲线C 的焦点到其渐近线的距离为2 3.(1)求双曲线C 的方程;(2)若直线y =kx +m (k ≠0,m ≠0)与双曲线C 交于不同的两点E ,F ,且点E ,F 都在以点P (0,3)为圆心的圆上,求实数m 的取值范围.专题限时集训(十四)A1.C [解析] 直线恒过定点(0,1),只要该点在椭圆内部或椭圆上即可,故只要b ≥1且b ≠4.2.B [解析] 圆x 2+y 2-8x +12=0的圆心为(4,0),半径为2,动圆的圆心到(4,0)的距离减去到(0,0)的距离等于1,由此可知,动圆的圆心在双曲线的一支上.3.B [解析] 设点P (x ,y ),则P A →=(1-x ,1-y ),PB →=(-1-x ,-1-y ),所以P A →·PB →=(1-x )(-1-x )+(1-y )(-1-y )=x 2+y 2-2.由已知可知x 2+y 2-2=x 22,即x 24+y 22=1,所以点P 的轨迹为椭圆,故选B.4.A [解析] 根据已知得m >0,n >0,且m +2-n =m +n ,即n =1,所以椭圆的离心率为e =m +1m +2=1-1m +2.又m >0,所以1-1m +2>12,所以22<e <1.5.B [解析] 直线x +2=0为抛物线y 2=8x 的准线,根据抛物线的定义可知圆心到准线的距离等于圆心到焦点的距离,故与直线x +2=0相切的圆恒过定点(2,0).6.C [解析] 无论怎么截取,所得椭圆的短轴长为2b =4,而圆柱底面直径为4,高为3,所以所得椭圆的长轴长的范围为4<2a ≤5,故45≤b a <1,于是椭圆的离心率0<e =1-b 2a2≤35. 7.B [解析] 设M (x 0,y 0),根据圆的切线知识可得过A ,B 的直线l 的方程为x 0x +y 0y=2,由此得P ⎝⎛⎭⎫2x 0,0,Q ⎝⎛⎭⎫0,2y 0,故△POQ 的面积为12×⎪⎪⎪⎪2x 0×⎪⎪⎪⎪2y 0=2||x 0y 0.因为点M 在椭圆上,所以x 209+y 204=1≥2⎪⎪⎪⎪x 03·⎪⎪⎪⎪y 02,由此得|x 0y 0|≤3,所以2|x 0y 0|≥23,当且仅当|x 0|3=|y 0|2时等号成立.8.D [解析] |MM ′|=12(|AF |+|BF |)≤|AF |2+|BF |22=|AB |22=22|AB |,故|MM ′||AB |≤22.9.2 63 [解析] 由已知可得b a =3,b =3a 且双曲线的离心率为e =1+⎝⎛⎭⎫b a 2=2,所以a 2+e b =a 2+23a ≥2 2a 3a=2 63,当且仅当a =2时等号成立.10.⎝⎛⎦⎤14,1+22 [解析] 当θ→π时,|F A |取值趋于p 2,故|F A |的取值范围的左端点是p 2=14;当直线m 的倾斜角等于π4时,|F A |取值最大,此时直线方程是y =x -14,代入抛物线方程得x 2-32x +116=0,由此可得点A 的横坐标是x =32+⎝⎛⎭⎫322-142=34+22.根据抛物线定义可知该点到焦点的距离等于其到准线的距离,故这个距离是34+22+14=1+22.故|F A |的取值范围是⎝⎛⎦⎤14,1+22.11.12[解析] 已知O (0,0),F (c ,0),G (a ,0),H ⎝⎛⎭⎫a 2c ,0,所以|FG ||OH |=a -c a 2c =ac -c 2a 2=e -e 2=-⎝⎛⎭⎫e -122+14≤14,所以当|FG ||OH |最大时,e =12.12.41-2 [解析] 由抛物线的定义可知,点P 到直线l 的距离m 即为点P 到抛物线的焦点F (2,0)的距离.设线段FC 与圆交于点E ,则|FE |即为m +|PQ |的最小值.将圆C :x 2+y 2+6x +8y +21=0化为标准方程是(x +3)2+(y +4)2=4,其半径r =2,故|FE |=|FC |-r =(-3-2)2+(-4-0)2-2=41-2.13.解:(1)将E (2,2)代入y 2=2px ,得p =1,所以抛物线方程为y 2=2x ,其焦点坐标为⎝⎛⎭⎫12,0.(2)证明:设A ⎝⎛⎭⎫y 212,y 1,B ⎝⎛⎭⎫y 222,y 2,M (x M ,y M ),N (x N ,y N ).方法一:因为直线l 不经过点E ,所以直线l 一定有斜率,设直线l 的方程为y =k (x -2),与抛物线方程联立,⎩⎪⎨⎪⎧y =k (x -2),y 2=2x ,消去x ,得ky 2-2y -4k =0,由韦达定理得y 1y 2=-4,y 1+y 2=2k.直线AE 的方程为y -2=y 1-2y 212-2(x -2),即y =2y 1+2(x -2)+2,令x =-2,得y M =2y 1-4y 1+2,同理可得y N =2y 2-4y 2+2.又OM →=(-2,y M ),ON →=(-2,y N ),所以OM →·ON →=4+y M y N =4+2y 1-4y 1+2·2y 2-4y 2+2=4+4[y 1y 2-2(y 1+y 2)+4]y 1y 2+2(y 1+y 2)+4=4+4⎝⎛⎭⎫-4-4k +4-4+4k+4=0,所以OM ⊥ON ,即∠MON 为定值π2.方法二:设直线l 的方程为x =my +2,与抛物线方程联立⎩⎪⎨⎪⎧x =my +2,y 2=2x ,消去x ,得y 2-2my -4=0,由韦达定理得y 1y 2=-4,y 1+y 2=2m .直线AE 的方程为y -2=y 1-2y 212-2(x -2),即y =2y 1+2(x -2)+2,令x =-2,得y M =2y 1-4y 1+2,同理可得y N =2y 2-4y 2+2.又OM →=(-2,y M ),ON →=(-2,y N ),OM →·ON →=4+y M y N =4+4(y 1-2)(y 2-2)(y 1+2)(y 2+2)=4+4[y 1y 2-2(y 1+y 2)+4]y 1y 2+2(y 1+y 2)+4=4+4(-4-4m +4)-4+4m +4=0,所以OM ⊥ON ,即∠MON 为定值π2.14.解:(1)由e 2=59=a 2-b 2a 2=1-b 2a 2,得b a =23.依题意可知△MB 1B 2是等腰直角三角形,从而b =2,故a =3,所以椭圆C 的方程是x 29+y 24=1.(2)设A (x 1,y 1),B (x 2,y 2),直线AB 的方程为x =my +2.将直线AB 的方程与椭圆C 的方程联立,消去x 得(4m 2+9)y 2+16my -20=0,所以y 1+y 2=-16m 4m 2+9,y 1y 2=-204m 2+9.若PM 平分∠APB ,则直线P A ,PB 的倾斜角互补,所以k P A +k PB =0.设P 点的坐标为(a ,0),则有y 1x 1-a +y 2x 2-a=0.将x 1=my 1+2,x 2=my 2+2代入上式,整理得2my 1y 2+(2-a )(y 1+y 2)(my 1+2-a )(my 2+2-a )=0,所以2my 1y 2+(2-a )(y 1+y 2)=0,将y 1+y 2=-16m 4m 2+9,y 1y 2=-204m 2+9代入上式,整理得(-2a +9)·m =0.由于上式对任意实数m 都成立,所以a =92.综上可知,存在定点P ⎝⎛⎭⎫92,0,使PM 平分∠APB .15.解:(1)设双曲线C 的方程为x 2a 2-y 2b2=1,(a ,b >0).依题可知双曲线C 的两个焦点分别为F 1(-4,0),F 2(4,0),∴c =4.又∵双曲线C 的焦点到渐近线的距离为2 3,∴|4b |a 2+b2=|4b |c =2 3,即b =2 3,∴a 2=c 2-b 2=4,∴双曲线C 的方程为x 24-y 212=1.(2)设E (x 1,y 1),F (x 2,y 2),由⎩⎪⎨⎪⎧y =kx +m ,x 24-y 212=1消去y 整理得(3-k 2)x 2-2kmx -(m 2+12)=0, 依题意得⎩⎪⎨⎪⎧3-k 2≠0,Δ=4k 2m 2+4(3-k 2)(m 2+12)>0.(*) 设EF 的中点为G (x 0,y 0),则x 0=x 1+x 22=km3-k 2,又∵点G 在直线y =kx +m 上,∴y 0=kx 0+m =3m 3-k2,∴G 点的坐标为⎝⎛⎭⎫km 3-k 2,3m 3-k 2. ∵E ,F 两点都在以P (0,3)为圆心的同一圆上,∴GP ⊥EF ,即k GP ·k =3m3-k 2-3km 3-k 2·k =-1,整理得k 2=9-4m3,代入(*)式得⎩⎨⎧3-9-4m 3≠0Δ=4m 2·9-4m 3+4⎝⎛⎭⎫3-9-4m 3(m 2+12)>0,解得m >0或m <-163.又k 2=9-4m 3>0,∴m <94.故所求m 的取值范围是⎝⎛⎭⎫-∞,-163∪⎝⎛⎭⎫0,94.。
