六年级数学反比例解决问题练习题
部编新人教版小学六年级数学下册《用反比例解决问题》学霸作业及答案

用反比例解决问题第1关练速度1.下面每题中的两种量是否成比例?如果成比例,成什么比例?(1)装配一批电池,每天的装配数量与所需天数。
()(2)正方形的面积与边长。
()(3)水池的容积一定,水管每小时的注水量与所用的时间。
()(4)在一定的时间内,加工每个零件所用的时间与加工的零件数。
()(5)体积一定,圆柱的底面积和高。
()(6)书的总页数一定,看过的页数与未看过的页数。
()(7)每天修路200m,修路的天数与修完路的长度。
()2.填表。
一种圆锥,它的体积(V)一定。
(1)根据表中数据判断,平行四边形的底和高成什么比例?为什么?(2)如果小红画的平行四边形的底是7.2cm,那么高是多少厘米?4.同学们排队做广播操,如果每行站24人,正好站15行;如果每行站20人,可以站几行?(1)我会分析:本题中,每行人数和行数是两种相关联的量。
()是一定的。
每行人数和行数成()比例。
(2)我会解答:第2关练准确率5.下面是铺一间房屋的地面所用地砖的规格和块数的关系示意图。
(1)从图中可以看出,所需地砖的块数是随着()的变化而变化的,这两种量成()比例。
(2)当用每块面积为0.6m²的地砖铺地时,需要这种地砖()块。
(3)当用每块面积为()m²的地砖铺地时,需要这种地砖120块。
6.某工厂生产一种零件,现在生产每个零件所用的时间由技术革新前的8分钟减少到了5分钟,原来生产60个零件的时间现在能生产多少个?7.有一个班的同学到公园去划船,他们已提前租好了若干条船,现在如果增加一条船,正好每条船坐6人;如果减少一条船,正好每条船坐9人。
这个班共有多少人?8.甲、乙两人骑自行车从A、B两地同时相向而行,甲行完全程要6小时,甲、乙相遇时所行的路程比是3∶2,乙行完全程要多少时间?9.如图,平行四边形ABCD的周长为75cm,以BC为底时,高是14cm;以CD为底时,高是16cm。
那么平行四边形ABCD的面积是多少?10.制作一批零件,甲单独完成要8小时,已知甲、乙的工作效率比是4∶3,那么乙单独完成要多长时间?第3关练思维11.一架飞机所带的燃料最多可以用6小时,飞机去时顺风每小时可以飞行1500km,返回时逆风每小时可以飞行1200km。
六年级数学下册 试题-提优训练5(正、反比例) (含答案)(苏教版)

提优训练(5)(正、反比例) 班级 姓名一、填空1. 甲乙两人共同加工一批零件,完成任务时,甲乙完成零件个数的比是3:5,他们的工作效率之比是( );用同样多的钱,可以买A 种书12本,可以买B 种书18本, 两种书的单价之比是( );客货两车同时从AB 两地相向而行,客车速度与货车速度的比是3:5,相遇时,客货两车所行的路程之比是( )。
2.有一只汽船,在静水中航行每小时20千米。
汽船往返于甲、乙两个码头,逆水航行花费的时间等于顺水航行的1.5倍。
水的流速每小时( )千米。
3.某校买来A 、B 两种篮球共100个,已知甲种篮球每个30元,乙种篮球每个20元,且甲、乙两种篮球所用钱数一样多。
甲种篮球买了( )个。
4.小明从甲地到乙地,去时每小时行6千米,回来时每小时行9千米,来回一共用5小时。
甲、乙两地相距( )千米。
5.一辆汽车从A 城开往B 城,去时用了9小时,返回时速度快了10%,返回时需要( )小时。
6.甲、乙两辆汽车同时从两个城市相对开出,2小时后,两车在距离中点20千米处相遇,这时甲车与乙车的路程比是3:4,甲车每小时行( )千米。
7. 李平骑自行车从家到县城,原计划用5小时30分。
由于途中有3.6千米的道路不平,走这段路时的速度相当于原来的34,因此,晚到了12分钟。
李平家到县城有( )千米。
8. 一个车间改革后,人员减少20﹪,产量却增加了20﹪,工作效率提高了( )﹪。
9. 客车和货车同时从甲、乙两地的中间向相反的方向行驶,3小时后,客车到达甲地,货车离乙地还有42千米。
已知货车和客车的速度比是5 :7,甲、乙两地相距( )千米。
10.甲乙两列火车的速度比是5∶4,乙车先出发,从B 站开往A 站,当行到离B 站72千米的地方时,甲车从A 站出发开往B 站,两列火车相遇的地方离A 、B 两站距离的比是3∶4,A 、B 两站相距( )千米。
二、应用题1. 甲、乙两辆汽车同时从A 、B 两个城市相对开出,经过8小时相遇后,甲车继续向前开到B 城还要4小时。
小学六年级数学比例和反比例 测试题含答案及知识点
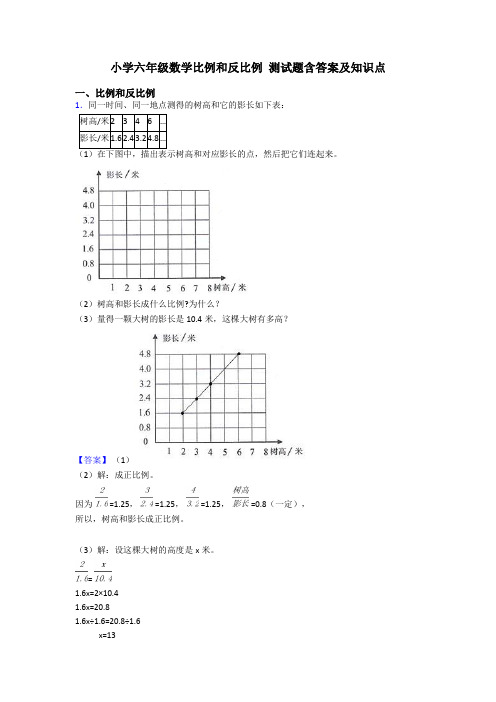
小学六年级数学比例和反比例测试题含答案及知识点一、比例和反比例1.同一时间、同一地点测得的树高和它的影长如下表:树高/米2346…影长/米1.62.43.24.8…(2)树高和影长成什么比例?为什么?(3)量得一颗大树的影长是10.4米,这棵大树有多高?【答案】(1)(2)解:成正比例。
因为 =1.25, =1.25, =1.25, =0.8(一定),所以,树高和影长成正比例。
(3)解:设这棵大树的高度是x米。
=1.6x=2×10.41.6x=20.81.6x÷1.6=20.8÷1.6x=13答:这棵大树的高度是13米。
【解析】【分析】(1)观察统计图可知,横轴表示树高,竖轴表示影长,据此先描点,再连线,据此作图;(2)分别用树高:影长,求出比值,当比值一定时,成正比例,据此判断;(3)根据题意可知,设这棵大树的高度是x米,用树高:影长=树高:影长,据此列正比例解答.2.把一瓶果汁平均分成若干杯,分的杯数和每杯的果汁量如下表。
分的杯数/杯6543每杯的果汁量/mL100120()200(2)分的杯数和每杯的果汁量有什么关系?为什么?(3)如果把这些果汁平均分成10杯,每杯的果汁量是多少毫升?【答案】(1)150(2)解:成反比例,因为每杯的果汁量×分的杯数=果汁总量。
(3)解:6×100÷10=60(毫升)答:每杯的果汁量是60毫升。
【解析】【解答】解:(1)100×6÷4=150(mL)【分析】(1)这瓶果汁的总量不变,用总量除以4即可求出每杯的容量;(2)根据正反比例关系的意义确定这两个量的关系;(3)用果汁总量除以10即可求出每杯果汁的容量。
3.甲乙两地相距440千米,一辆汽车从甲地开往乙地,3时行了240千米,照这样计算,几小时可以到达乙地?(用比例解)【答案】解:设小时可以到达乙地,答:5.5小时可以到达乙地。
小学六年级数学比例和反比例 测试题含答案及知识点
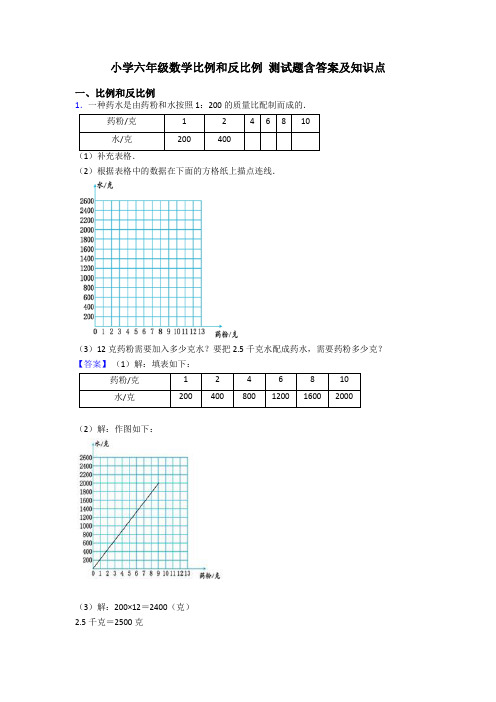
小学六年级数学比例和反比例测试题含答案及知识点一、比例和反比例1.一种药水是由药粉和水按照1:200的质量比配制而成的.药粉/克1246810水/克200400(1)补充表格.(2)根据表格中的数据在下面的方格纸上描点连线.(3)12克药粉需要加入多少克水?要把2.5千克水配成药水,需要药粉多少克?【答案】(1)解:填表如下:药粉/克1246810水/克200400800120016002000(2)解:作图如下:(3)解:200×12=2400(克)2.5千克=2500克2500× =12.5(克)答:12克药粉需要加水2400克,要把2.5千克水配成药水,需要药粉12.5克.【解析】【分析】(1)根据条件“ 一种药水是由药粉和水按照1:200的质量比配制而成的”可知,用药粉:水=1:200,据此列比例解答,然后填表即可;(2)根据统计表中的数据,在统计图中先描点,然后再连线,图中的统计图纵轴每格代表200克,据此作图;(3)根据条件可知,1克药粉要加入200克水,用药粉的质量×200=水的质量,据此用乘法计算;要把2.5千克水配成药水,需要药粉多少克,先统一单位,1千克=1000克,然后用水的质量×药粉占水的分率=药粉的质量,据此列式解答。
2.如果10千克菜籽可以榨6.5千克菜油,那么有这种菜籽360千克,可以榨多少千克油?(用比例解)【答案】解:设可以榨x千克油。
10:6.5=360:x10x=6.5×360x=2340÷10x=234答:可以榨油234千克。
【解析】【分析】菜籽的重量和榨油的质量的比值是不变的,二者成正比例,设出未知数,根据正比例关系列出比例,解比例求出可以榨油的重量即可。
3.把一瓶果汁平均分成若干杯,分的杯数和每杯的果汁量如下表。
分的杯数/杯6543每杯的果汁量/mL100120()200(2)分的杯数和每杯的果汁量有什么关系?为什么?(3)如果把这些果汁平均分成10杯,每杯的果汁量是多少毫升?【答案】(1)150(2)解:成反比例,因为每杯的果汁量×分的杯数=果汁总量。
六年级数学下册典型例题系列之第六单元正比例和反比例在图表中的应用专项练习(解析版)(苏教版)

2021-2022学年六年级数学下册典型例题系列之第六单元正比例和反比例在图表中的应用专项练习(解析版)一、填空题。
1.(2021·河北邯郸·小升初真题)如图表示一辆汽车在公路上行驶的时间与路程的关系,这辆汽车行驶的时间与路程成()比例。
照这样计算,2.2小时行驶()千米。
【解析】(1)根据图可知:路程÷时间=速度(一定),商一定,所以路程和时间成正比例关系;(2)100÷1×2.2=100×2.2=220(千米)2.(2021·河北保定·小升初真题)观察关于购买衣服的统计表:购买衣服的数量和总价成( )比例。
【解析】70÷2=35105÷3=35140÷4=35175÷5=35210÷6=35总价÷数量=35(一定),商一定,所以购买衣服的数量和总价成正比例。
3.(2021·云南玉溪·六年级期末)如图表示一辆汽车在公路上行驶的时间与路程的关系,这辆汽车行驶的时间与路程成( )比例。
照这样计算,该汽车6.6时行驶( )km。
【解析】6.6×100=660(千米)这辆汽车行驶的时间与路程成正比例。
照这样计算,该汽车6.6时行驶660km。
4.(2021·陕西·延安市宝塔区蟠龙镇初级中学六年级期末)莎莎骑车到相距5千米的书店买书,买完书立刻返回家中。
如图是她离开家的距离与时间的统计图。
(1)莎莎去书店每小时行( )千米,用了( )分钟,这段时间内她骑车的路程和时间成( )比例。
(2)莎莎从书店返回家中的速度是每小时( )千米,用了( )分钟。
(3)莎莎返回时的速度比去时慢( )%。
【解析】(1)5÷0.5=10(千米),所以,莎莎去书店每小时行10千米,用了30分钟,这段时间内她骑车的路程和时间成正比例;(2)5÷1.25=4(千米),所以,莎莎从书店返回家中的速度是每小时4千米,用了75分钟;(3)(10-4)÷10=6÷10=60%所以,莎莎返回时的速度比去时慢60%。
《反比例》数学六年级教案练习题详解与答案

反比例是数学中的一个重要概念,它在实际生活中也有广泛的应用。
在六年级的数学教学中,反比例的学习是必不可少的。
今天,我们将为大家详细讲解数学六年级教案中的练习题,以及答案解析。
一、选择题1.一个矩形的长和宽成反比例,如果它的长为5,则宽为多少?A.1B.2C.3D.4答案:D。
解析:由于长和宽成反比例,长与宽呈现出一定的规律。
当长为5时,宽应该为原来的1/5,即5×1/5=1,宽为4。
2.有一条路程,如果两名工人同时开始走,第一名工人的速度是第二名工人的1.5倍,他们走到终点的时间是相同的。
如果第二名工人用了4小时,第一名工人用了多长时间?A.2.5小时B.3小时C.4.5小时D.6小时答案:A。
解析:设第二名工人的速度为v,则第一名工人的速度为1.5v。
设路程为S,则根据路程=速度×时间可以得到:v×4=1.5v×t。
解得:t=2.5小时。
3.一个需要从A地到达B地,已知需要走的路程是20米,走的最快速度为8m/s。
需要多长时间到达B地?A.2.5秒B.2.8秒C.3.0秒D.4秒答案:C。
解析:根据路程=速度×时间,可以得到时间为20÷8=2.5秒。
4.小红每天早上骑自行车去学校,行程固定为6公里。
如果她增加了速度,需要2分钟才能到达学校。
如果小红减速,需要5分钟才能到达学校。
求小红原来每小时的骑车速度是多少?A.20公里/小时B.25公里/小时C.30公里/小时D.35公里/小时答案:B。
解析:设小红原来的速度为v,则根据路程=速度×时间,可以得到6=vt。
已知小红增加速度后的时间为2/60=1/30小时,可以得到6=v×1/30,即v=6×30=180公里/小时。
同理,小红减速时的速度为6÷(5/60)=72公里/小时。
根据反比例的定义可知,速度与时间呈反比例关系,速度越快,所用时间越短。
小红原来的速度应该在这两个速度之间,取平均值即可得出答案:(180+72)÷2=126公里/小时,约等于25公里/小时。
六年级数学反比例习题

一、选择题。
1. 成反比例的量是()。
A.A和B互为倒数
B.圆柱的高一定,体积和底面积
C.被减数一定,减数与差
D.除数一定,商和被除数
2. 如果=那么和()。
A.成正比例
B.成反比例
C.不成比例
3. 互为倒数的两个数()。
A.成正比例
B.成反比例
C.不成比例
4. 在同一个圆里,周长与直径()
A.成正比例
B.成反比例
C.不成比例
5. 路程一定,速度和时间()。
A.成正比例
B.成反比例
C.不成比例
二、下面两种量成什么比例,并说明理由。
①时间一定,每小时织布的米数和织布总米数。
②平行四边形面积一定,它的底和高。
③分子一定,分母和分数值。
④报纸的单价一定,总价与订阅的份数。
六下数学 正比例与反比例 应用题训练30题 带答案

相同时间内,路程和速度成正比例,速度之比=路程之比
(2x-130):(x+130)=3:2 解得x=650
8、一辆卡车与一辆小轿车同时从甲、乙两城相对开出,相遇后两 车继续向前行驶.当小轿车到达甲地、卡车到达乙地后.立即返回 ,第二次相遇点距甲城120千米,已知:卡车与小轿车的速度比是3 :4,甲、乙两城相距多少千米?
13、用方砖铺一间教室的地面,如果用边长为2dm的方砖 ,需要用60块,如果改用边长为3dm的方砖,需要用多少 块? 27块 解析:解设需要用x块砖 教室的面积一定,所用的方砖的块数和每块方砖的面积成 反比例
2×2×60=3×3×x 解得 x=80/3 进一法,所以需要27块
14、有甲乙丙三个相互咬合的齿轮,当甲齿轮转动2圈时, 乙齿轮转动3圈,丙齿轮转动4圈,这三个齿轮的齿数之比 是( ):( ):( )。 6:4:3 解析:相互咬合的齿轮转动的总齿数是相同的,那么一圈 的齿数和转动的圈数是成反比例的,设三个齿轮的齿数分 别为x y z 则2x=3y=4z 得x:y :z=6:4:3
16、学校组织同学参观爱国主义纪念展,每60名同学配2
X=18
4、某修路队修一条公路,前6天修了180米,照这样的速度,修路 队又修了5天才全部修完,这条公路全长是多少米?
解设这条公路的全长是x米 每天修的长度一定,路的全长和时间成正比例关系 180:6=x:(6+5)
X=330
5、甲乙丙三人进行200米赛跑(他们的速度保持不变),甲到 终点时,乙还差20米,丙离终点还有25米,问乙到达终点时, 丙还差多少米?
解设:甲乙两城相距x千米 则第二次相遇时,卡车经过的路程为:x+x-120=2x-120 小轿车经过的路程为:x+120
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例解决问题
例1:小华读一本书,每天读6页,4天可以读完。
如果每天读8页,几天可以读完?
1、修路队修一段公路,每天修50米,6天修完。
如果每天修100米,几天可以修完?
2、一头牛每天吃草20千克,吃了6天。
如果每天吃了30千克,这些草可以吃几天?
3、一批零件,工人师傅每小时工7个,8小时加工完成。
如果每小时加工8个,几小时可以完成?
4、张老师打印一份文件,如果每行排24个字,需要排21行。
如果每行排28个字,需要排多少行?
5、小华每天读24页书,12天读完了《红岩》一书。
小明每天读36页书,几天可以读完《红岩》?
例2:食堂运来一批蔬菜,原计划每天吃50千克,30天慢慢消费完这批蔬菜。
后来根据大家的意见,每天比原计划多吃10千克,这批蔬菜可以吃多少天
6、某厂运来一批煤,计划每天用5吨,40天用完,如果改进锅炉,每天节约1吨,这批煤可以用多少天?
7、一堆煤,每天烧0.8吨,可以烧42天。
现在每天节约0.1吨,可以烧多少天?
8、一堆煤,计划每天烧0.6吨,30天烧完,实际多烧了6天,实际每天烧多少吨?
9、某机床厂计划每天生产6台机床,40天可完成一批任务。
由于技术革新,实际提前10天完成了任务,实际每天生产多少台机床?
例3:车队向灾区运送一批救灾物资,去时每小时行60千米,6.5小时到达。
回来时用了6小时,回来时比去时每小时多行多少
千米?
10、一辆汽车从甲地去乙地,每小时行驶60去千米,5.5小时到达。
返回时只用了5小时,返回时每小时行驶多少千米?。
