伯努利定律
伯努利吸盘原理

伯努利吸盘原理
伯努利吸盘原理是指在流体力学中,当流体通过管道或流经物体表面时,流速增大,压力就会减小,这就是伯努利定律。
而伯努利吸盘就是利用这一原理制成的一种吸盘装置,它可以通过气流的流动产生负压,从而实现吸附物体的目的。
伯努利吸盘主要由吸盘体、进气口、出气口等部分组成。
当气流通过进气口进入吸盘内部时,由于吸盘内部的形状设计和出气口的设置,气流在流动过程中会加速,从而使得吸盘内部的压力降低。
根据伯努利定律,流速增大,压力就会减小,因此在吸盘的作用下,外部大气压力就会将物体压附在吸盘上。
伯努利吸盘广泛应用于工业生产中,比如在自动化生产线上,可以利用伯努利吸盘来进行物料的吸取和传送。
由于伯努利吸盘不需要额外的能源,只需要通过气流就能产生负压,因此在一些特殊环境下,比如易燃易爆的场所,伯努利吸盘就显得更加安全可靠。
另外,伯努利吸盘也被广泛应用于机器人领域。
在一些需要进行物体抓取和搬运的场合,机器人可以通过安装伯努利吸盘来实现对物体的抓取和固定。
由于伯努利吸盘对物体表面的要求并不高,因此可以适用于各种不同材质和形状的物体,这为机器人的灵活应用提供了可能。
此外,伯努利吸盘还可以应用于一些特殊的领域,比如在医疗器械上,可以利用伯努利吸盘来实现对一些脆弱的组织或器官的抓取和固定,从而为医生的手术操作提供更大的便利和安全保障。
总的来说,伯努利吸盘作为一种利用流体力学原理制成的吸附装置,具有结构简单、使用方便、安全可靠等优点,在工业生产、机器人领域以及医疗器械等领域都有着广泛的应用前景。
随着科学技术的不断发展,相信伯努利吸盘在未来会有更多的创新和应用,为人们的生产和生活带来更多的便利和效益。
伯努利定律和伯努利定理

伯努利定律和伯努利定理
一、伯努利定律
伯努利定律是流体力学中的基本原理,由瑞士物理学家丹尼尔·伯努利于1738年提出。
定律指出,在理想流体中,流速大的地方压力小,流速小的地方压力大。
这是因为流体的压力与流速和重力之间存在相互关系。
在不可压缩的稳定流中,流体的动能和势能之和保持不变,即总机械能守恒。
这个定律可以用来解释和分析很多流体动力学现象,如飞机的升力、管道中的水流等。
二、伯努利定理
伯努利定理是热力学中的一个基本定理,由瑞士物理学家丹尼尔·伯努利于1757年提出。
定理指出,在没有外部力量作用的情况下,流体内部各点的速度和压力是连续变化的,但在同一水平面上,流体的速度和压力具有相同的值。
这个定理可以用来分析流体在管道中的流动和扩散现象,以及流体在容器中的等压和等温变化等。
总结:
伯努利定律和伯努利定理是两个不同的物理原理,分别应用于流体力学和热力学领域。
尽管它们的应用范围不同,但它们都涉及到流体的速度和压力之间的关系。
在实际应用中,需要根据具体的物理环境和现象选择合适的原理进行分析和计算。
伯努利定理的意义

伯努利定理的意义伯努利定理是流体力学中的一个基本定律,描述了流体在运动过程中压力和速度之间的关系。
这个定理的重要性在于它能够解释很多现象,例如飞机起飞、水泵工作等,同时也为设计和控制流体系统提供了基础和指导。
伯努利定理简单来说,就是在不考虑粘性阻力和外力作用的情况下,当流体沿着管道或容器中的不同位置流动时,其速度和压力之间存在一个反比例关系。
也就是说,当速度增大时,压力降低,反之亦然。
这个规律可以通过物理方程式来表达,即P + ½ρv² = 常数,其中 P 表示压力、ρ 表示流体密度、v 表示流体速度。
这个定理的应用非常广泛。
在空气动力学中,飞机的升力是由空气在机翼上流动、速度变化和压力产生的。
伯努利定理可以用来说明机翼上下表面所受到的压强不平衡是导致升力产生的原因之一。
在水力工程中,水泵的工作原理也是基于该定理:当水从进水口进入泵中,随着流速增加,压力会降低,从而产生一个向上的力,将水送至出水口。
伯努利定理还可以用来解释很多其他的现象,例如爬山气球的升力、船行驶时的动力、喷气式发动机的推力等。
此外,该定理也为工程设计提供了理论基础。
在流体系统的设计中,提高流速可以降低管道或容器的截面积,从而节约材料和成本。
此外,根据该定理,流体的速度和压力变化可以实现流量控制、氧气传输、空气过滤等应用。
综上所述,伯努利定理是流体力学中的一个重要定理,不仅能够解释很多现象,而且为工程设计和流体系统的控制提供了基础和指导。
通过深入研究和应用伯努利定理,我们可以更好地理解流体的运动规律,优化流体系统的设计和运作,从而促进科技进步和社会发展。
伯努利定律内容

伯努利定律内容
伯努利定律是流体力学中的一个基本定律,它描述了在不同截面积上的流速不同的流体,其压力和动能之间的关系。
伯努利定律是流体力学的基础,对于理解流体运动和流体机械的设计有着重要的意义。
伯努利定律的内容可以简单地概括为:在流体运动过程中,当流体通过不同截面积时,流速的变化会引起压力和动能的变化,压力和动能之间的变化是相互关联的,即当流体速度增加时,压力就会降低,反之亦然。
伯努利定律的数学表达式为:P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2,其中P1和P2分别表示流体通过不同截面积的压力,ρ为流体密度,v1和v2分别表示流体通过不同截面积的速度,h1和h2分别表示流体通过不同截面积的高度。
伯努利定律的实际应用非常广泛,例如在流体机械中,伯努利定律可以用于设计流量计、涡轮机、喷气发动机等;在气象学中,伯努利定律可以用于解释风的形成和变化;在生物学中,伯努利定律可以用于研究血流动力学等。
伯努利定律的应用还可以帮助我们理解一些日常生活中的现象。
例如,当我们在喝吸管饮料时,吸管内的压力会降低,而外部的大气压力会将液体推向吸管内,这就是伯努利定律的应用;当我们在开车行驶时,车前方的空气会流经车身,形成气流,而车身的形状和速度会影响气流的流速和压力分布,这也是伯努利定律的应
用。
总之,伯努利定律是流体力学中的一个基本定律,它描述了流体在不同截面积上的压力和动能之间的关系,具有广泛的应用价值。
对于工程技术、气象学、生物学等领域的研究和应用,伯努利定律都有着重要的作用。
伯努利定律表达式

伯努利定律表达式
伯努利定律是流体力学中的一个基本定律,描述了在流体中沿流线上流速变化和压力变化之间的关系。
伯努利定律的数学表达式如下:
P + 1/2ρv²+ ρgh = 常数
其中:
- P 表示流体的压力(单位:帕斯卡,Pa),
-ρ表示流体的密度(单位:千克/立方米,kg/m³),
- v 表示流体的速度(单位:米/秒,m/s),
- g 表示重力加速度(单位:米/秒²,m/s²),
- h 表示流体在重力场中的高度(单位:米,m)。
上述表达式中的每一项分别代表了流体的压力能、动能和重力势能,它们在沿流线上的不同位置可能会发生变化,但总和保持不变。
这意味着当流体在流动过程中速度增加时,压力会下降;反之,当速度减小时,压力会增加。
伯努利定律适用于理想流体(无粘性和无压缩性)在稳态流动条件下的情况。
它可以用于解释多种现象,例如飞机升力产生、水管中水流速度和压力的关系等。
需要注意的是,伯努利定律的适用范围有限,
对于涉及湍流、粘性流体或复杂流动情况的问题,可能需要考虑其他因素和扩展模型。
伯努利方程三种公式
伯努利方程三种公式
伯努利方程三种公式如下:
P1/ρg+h1+ν²1/2g=C(constant value)。
ρg(P1/ρg+h1+ν²1/2g)=C(another constant value)。
i.e.P1+h1ρg+1/2ρv^2=C。
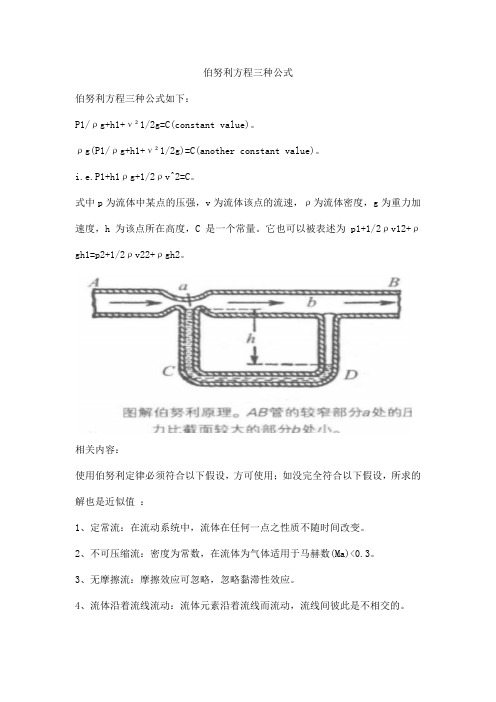
式中p为流体中某点的压强,v为流体该点的流速,ρ为流体密度,g为重力加速度,h为该点所在高度,C是一个常量。
它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。
相关内容:
使用伯努利定律必须符合以下假设,方可使用;如没完全符合以下假设,所求的解也是近似值:
1、定常流:在流动系统中,流体在任何一点之性质不随时间改变。
2、不可压缩流:密度为常数,在流体为气体适用于马赫数(Ma)<0.3。
3、无摩擦流:摩擦效应可忽略,忽略黏滞性效应。
4、流体沿着流线流动:流体元素沿着流线而流动,流线间彼此是不相交的。
伯努利试验公式

伯努利试验公式
伯努利试验公式是描述管道或管道中流体流动的基本物理定律之一。
其公式表示为:
P + 1/2ρv^2 + ρgh = 常数
其中,P为流体静压力,ρ为流体密度,v为流体流速,g为重力加速度,h为流体高度。
这个公式说明了在管道或管道中,流体静压力、动能和位能之和是一个常数。
换句话说,当流速增加时,静压力会下降,而动能和位能则会增加,以保持总能量不变。
这个公式在航空、汽车、液压和水力工程等领域中都得到了广泛应用。
例如,它可以用来计算飞机、汽车或船只的速度、液压系统的压力、水力发电厂的效率等等。
需要注意的是,伯努利试验公式只适用于稳态流动的情况,即流体的速度和压力分布不随时间变化。
在非稳态流动或湍流中,该公式的适用性可能会受到限制。
伯努利 反比定律

伯努利反比定律伯努利反比定律是流体力学中的重要定律之一,它描述了在静止流体中,速度和压力之间的关系。
该定律是由瑞士数学家丹尼尔·伯努利在18世纪提出的,基于能量守恒的原理。
伯努利反比定律可以用以下公式表示:P + 1/2ρv² + ρgh = 常量其中,P是流体的压力,ρ是流体的密度,v是流体的速度,g是重力加速度,h是流体的高度。
该公式表示了在流体沿着流动路径上的某一点的总压力,即静压、动压和势能之和是一个常量。
通过伯努利反比定律,可以得出以下结论:1. 当速度增加时,压力降低。
根据公式可知,速度的增加导致动压项1/2ρv²的增加,而压力的减小则是为了保持总压力不变。
这就解释了为什么当流体通过管道缩窄或通过障碍物时,流体速度增加,而压力降低。
2. 当高度增加时,压力增加。
根据公式可知,高度的增加导致势能项ρgh的增加,而压力的增加则是为了保持总压力不变。
这就解释了为什么在山上气温较低、气压较高,而在山下气温较高、气压较低。
3. 当密度增加时,压力增加。
根据公式可知,密度的增加会导致静压项ρ的增加,而压力的增加则是为了保持总压力不变。
这就解释了为什么在深海中,水的压力比在海平面上更高,因为水的密度在深海中更大。
4. 伯努利反比定律适用于理想流体。
理想流体是指没有粘性和黏滞性的流体,实际流体在一些情况下可能不完全符合伯努利反比定律。
例如,在流体通过狭窄管道或穿过小孔时会产生湍流,这就会使得流体的速度和压力分布不均匀。
伯努利反比定律在许多实际应用中都有重要的意义。
例如,在航空工程中,该定律可以用来解释飞机上升或下降时的气动性能变化。
在涡轮机械中,该定律可以用来分析流体的能量转换和传输过程。
在建筑工程中,该定律可以用来设计水力工程和通风系统。
总之,伯努利反比定律是流体力学中一条基本原理,通过它可以理解速度和压力之间的关系。
这个定律对于解释和设计许多实际问题具有重要意义,是流体力学研究中的基础之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
伯努利定律
简介:
在一个流体系统,比如气流、水流中,流速越快,流体产生的压力就越小,这就是被称为“流体力学之父”的丹尼尔·伯努利1738年发现的“伯努利定律”。
这个压力产生的力量是巨大的,空气能够托起沉重的飞机,就是利用了伯努利定律。
飞机机翼的上表面是流畅的曲面,下表面则是平面。
这样,机翼上表面的气流速度就大于下表面的气流速度,所以机翼下方气流产生的压力就大于上方气流的压力,飞机就被这巨大的压力差“托住”了。
当然了,这个压力到底有多大,一个高深的流体力学公式“伯努利方程”会去计算它。
定律假设
1.非粘滞——流体无需抵抗与容器壁之间的粘滞力
2.不可压缩——气体因其可压缩性多不依循此定律;不可压缩性可维持密度不变
3.稳定——高速流动会导致紊流的出现
历史
伯努利开辟并命名了流体动力学这一学科,区分了流体静力学与动力学的不同概念。
1738年,他发表了十年寒窗写成的《流体动力学》一书。
他用流体的压强、密度和流速等作为描写流体运动的基本概念,引入了“势函数”“势能”(“位势提高”)来代替单纯用“活力’讨论,从而表述了关于理想流体稳定流动的伯努利方程,这实质上是机械能守恒定律的另一形式。
他还用分子与器壁的碰撞来解释气体压强,并指出,只要温度不变,气体的压强总与密度成正,与体积成反比,用此解释了玻意耳定律。
伯努利方程
设在右图的细管中有理想流体在做定常流动,且流动方向从左向右,我们在管的a1处和a2处用横截面截出一段流体,即a1处和a2处之间的流体,作为研究对象.设a1处的横截面积为S1,流速为V1,高度为h1;a2处的横截面积为S2,流速为V2,高度为h2.
思考下列问题:
①a1处左边的流体对研究对象的压力F1的大小及方向如何
②a2处右边的液体对研究对象的压力F2的大小及方向如何
③设经过一段时间Δt后(Δt很小),这段流体的左端S1由a1移到b1,右端S2由a2移到b2,两端移动的距离分别为ΔL1和ΔL2,则左端流入的流体体积和右端流出的液体体积各为多大它们之间有什么关系为什么
④求左右两端的力对所选研究对象做的功
⑤研究对象机械能是否发生变化为什么
⑥液体在流动过程中,外力要对它做功,结合功能关系,外力所做的功与流体的机械能变化间有什么关系
推导过程:
如图所示,经过很短的时间Δt,这段流体的左端S1由a1移到b1,右端S2由a2移到b2,两端移动的距离为ΔL1和ΔL2,左端流入的流体体积为ΔV1=S1ΔL1,右端流出的体积为ΔV2=S2ΔL2.
因为理想流体是不可压缩的,所以有
ΔV1=ΔV2=ΔV
作用于左端的力F1=p1S2对流体做的功为
W1=F1ΔL1 =p1·S1ΔL1=p1ΔV
作用于右端的力F2=p2S2,它对流体做负功(因为右边对这段流体的作用力向左,而这段流体的位移向右),所做的功为
W2=-F2ΔL2=-p2S2ΔL2=-p2ΔV
两侧外力对所选研究液体所做的总功为
W=W1+W2=(p1-p2)ΔV
又因为我们研究的是理想流体的定常流动,流体的密度ρ和各点的流速V没有改变,所以研究对象(初态是a1到a2之间的流体,末态是b1到b2之间的流体)的动能和重力势能都没有改变.这样,机械能的改变就等于流出的那部分流体的机械能减去流入的那部分流体的机械能,即
E2-E1=ρ()ΔV+ρg(h2-h1)ΔV
又理想流体没有粘滞性,流体在流动中机械能不会转化为内能
∴W=E2-E1
(p1-p2)ΔV=ρ(-))ΔV+ρg(h2-h1)ΔV
整理后得:整理后得:
又a1和a2是在流体中任取的,所以上式可表述为
上述两式就是伯努利方程.
当流体水平流动时,或者高度的影响不显著时,伯努利方程可表达为
该式的含义是:在流体的流动中,压强跟流速有关,流速V大的地方压强p小,流速V小的地方压强p大。
