2019年中考数学几何基础知识汇总
初三数学几何知识点归纳

初三数学几何知识点归纳初三数学几何知识点归纳1 同角或等角的余角相等2 过一点有且只有一条直线和已知直线垂直3 过两点有且只有一条直线4 两点之间线段最短5 同角或等角的补角相等6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行初中几何公式:角9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补初中几何公式:三角形15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于18018 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理有两边和它们的夹角对应相等的两个三角形全等23 角边角公理有两角和它们的夹边对应相等的两个三角形全等24 推论有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理有三边对应相等的两个三角形全等26 斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合初中几何公式:等腰三角形30 等腰三角形的性质定理等腰三角形的两个底角相等31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于6034 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论 2 有一个角等于60的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a+b=c47勾股定理的逆定理如果三角形的三边长a、b、c有关系a+b=c,那么这个三角形是直角三角形初中几何公式:四边形48定理四边形的内角和等于36049四边形的外角和等于36050多边形内角和定理 n边形的内角的和等于(n-2)18051推论任意多边的外角和等于36052平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形初中几何公式:菱形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(ab)267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形初中几何公式:正方形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称初中几何公式:等腰梯形74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形初中几何公式:等分78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半 L=(a+b)2 S=Lh83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84 (2)合比性质如果a/b=c/d,那么(ab)/b=(cd)/d85 (3)等比性质如果a/b=c/d==m/n(b+d++n0),那么(a+c++m)/(b+d++n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的.余切值等于它的余角的正切值初中几何公式:圆101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三个点确定一条直线110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111推论1 ①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧112推论2 圆的两条平行弦所夹的弧相等113圆是以圆心为对称中心的中心对称图形114定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等115推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116定理一条弧所对的圆周角等于它所对的圆心角的一半117推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等118推论2 半圆(或直径)所对的圆周角是直角;90的圆周角所对的弦是直径119推论3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形120定理圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角121①直线L和⊙O相交 d﹤r②直线L和⊙O相切 d=r③直线L和⊙O相离 d﹥r122切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123切线的性质定理圆的切线垂直于经过切点的半径124推论1 经过圆心且垂直于切线的直线必经过切点125推论2 经过切点且垂直于切线的直线必经过圆心126切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角127圆的外切四边形的两组对边的和相等128弦切角定理弦切角等于它所夹的弧对的圆周角129推论如果两个弦切角所夹的弧相等,那么这两个弦切角也相等130相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等131推论如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项132切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项133推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等134如果两个圆相切,那么切点一定在连心线上135①两圆外离 d﹥R+r ②两圆外切 d=R+r③两圆相交 R-r﹤d﹤R+r(R﹥r)④两圆内切 d=R-r(R﹥r) ⑤两圆内含d﹤R-r(R﹥r)136定理相交两圆的连心线垂直平分两圆的公共弦137定理把圆分成n(n3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138定理任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆139正n边形的每个内角都等于(n-2)180/n140定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141正n边形的面积Sn=pnrn/2 p表示正n边形的周长142正三角形面积3a/4 a表示边长143如果在一个顶点周围有k个正n边形的角,由于这些角的和应为360,因此k(n-2)180/n=360化为(n-2)(k-2)=4144弧长计算公式:L=nR/180145扇形面积公式:S扇形=nR/360=LR/2146内公切线长= d-(R-r) 外公切线长= d-(R+r)。
2019中考数学知识点:中考数学几何知识点精品教育.doc

中考数学知识点:中考数学几何知识点从某种意义上来说中考数学中几何做的如何直接决定了中考数学是否能够拿到高分,是否能够拉开差距。
由此看来,数学中几何对于中考数学来说非常重要。
得几何者得中考数学天下。
通常情况下,几何在中考中呈现方式为:选择题中小题计算相应的角度、线段,填空题中也以相应的计算为基础。
选择填空每题各四分。
接下来在解答题中,通常会考查简单的全等三角形、圆中的切线证明以及圆中计算和证明、第22题动手操作或者几何变通思维能力题目、24题代几综合题目、25题几何综合压轴题。
其中,第22、24、25通常被称为中考数学压轴题,这三道题目做的好与坏直接关系到中考数学分数的高与低。
在23题中一般考查几何辅助线思维能力锻炼,考查学生空间想象能力以及动手操作能力;24一般考查二次函数与四边形、三角形乃至于圆的综合,题目难度系数较大,是每一届中考考生的绊脚石之一(2019年24题考查几何综合思维能力,主题考查旋转变换思想)。
25题一般考查几何综合变换,常常和几何中的几何变换之旋转、平移、轴对称。
这三大变换足以让很多学生扣分,如2019年北京中考25题考查几何轴对称导致当年满分和高分分数剧降!那么面对几何的重要性,在刚进入初三的孩子们来说,我们需要注意如下几点:1、重视新课中的基础。
在学校学习新课的时候就一定要打扎实基础,把每一个基础的知识点弄清楚。
把每一个定理和定理的证明方法弄明白,从而联想到相关的知识点。
上课勤做笔记,记住每一个闪光的思路。
2、注重归纳。
把自己在课本辅导书上做到的相关的题型总结在一起,经常回顾,同时标记重要题型。
3、保持四边形、三角形中辅助线添加熟练。
特别是几何三大变换,旋转、平移、轴对称要熟练,多练习这类型的题目。
4、多练习题目。
5、熟练掌握初中阶段数学模型。
掌握模型,熟练运用阶梯技巧。
中考数学几何知识点总结(专题汇总)

2019中考数学几何知识点总结(专题汇总)1 同角或等角的余角相等2 过一点有且只有一条直线和已知直线垂直3 过两点有且只有一条直线4 两点之间线段最短5 同角或等角的补角相等6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理有两边和它们的夹角对应相等的两个三角形全等23 角边角公理有两角和它们的夹边对应相等的两个三角形全等24 推论有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理有三边对应相等的两个三角形全等26 斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论 2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a+b=c47勾股定理的逆定理如果三角形的三边长a、b、c有关系a+b=c,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理 n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形本文导航 1、首页2、角3、三角形4、等腰三角形5、四边形6、矩形7、菱形8、正方形9、等腰梯形10、等分》》》菱形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等。
初中几何知识点梳理

初中几何知识点梳理在初中数学的学习中,几何是一个重要的组成部分。
它不仅能够培养我们的空间想象力和逻辑思维能力,还为我们今后学习更高级的数学知识打下坚实的基础。
下面就让我们一起来梳理一下初中几何的主要知识点。
一、线段与角线段是几何中最基本的元素之一。
两点之间的距离就是连接这两点的线段的长度。
线段的中点将线段分为长度相等的两部分。
角是由两条有公共端点的射线组成的图形。
角的度量单位是度、分、秒。
直角为 90 度,平角为 180 度,周角为 360 度。
同角或等角的余角相等,同角或等角的补角相等。
对顶角相等。
二、相交线与平行线相交线中最重要的概念是邻补角和对顶角。
两条直线相交,形成的四个角中,有公共顶点且有一条公共边的两个角互为邻补角;有公共顶点但没有公共边的两个角互为对顶角。
平行线的判定方法有:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行。
平行线的性质包括:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补。
三、三角形三角形是由不在同一直线上的三条线段首尾顺次相接所组成的封闭图形。
三角形按边分类可分为不等边三角形和等腰三角形(等边三角形是特殊的等腰三角形);按角分类可分为锐角三角形、直角三角形和钝角三角形。
三角形的内角和为 180 度。
三角形的一个外角等于与它不相邻的两个内角的和。
三角形的三边关系是:任意两边之和大于第三边,任意两边之差小于第三边。
三角形的中位线平行于第三边,且等于第三边的一半。
全等三角形的判定方法有:SSS(边边边)、SAS(边角边)、ASA(角边角)、AAS(角角边)、HL(斜边、直角边,仅适用于直角三角形)。
相似三角形的判定方法有:两角对应相等,两三角形相似;两边对应成比例且夹角相等,两三角形相似;三边对应成比例,两三角形相似。
四、四边形四边形包括平行四边形、矩形、菱形、正方形和梯形。
平行四边形的性质有:对边平行且相等,对角相等,对角线互相平分。
初三数学几何知识点归纳总结

初三数学几何知识点归纳总结除了课堂上的学习外,数学知识点也是学生提高数学成绩的重要途径,本文为大家提供了初三数学几何知识点归纳总结,希望对大家的学习有一定帮助。
1 同角或等角的余角相等2 过一点有且只有一条直线和已知直线垂直3 过两点有且只有一条直线4 两点之间线段最短5 同角或等角的补角相等6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行初中几何公式:角9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补初中几何公式:三角形15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于18018 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理有两边和它们的夹角对应相等的两个三角形全等23 角边角公理有两角和它们的夹边对应相等的两个三角形全等24 推论有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理有三边对应相等的两个三角形全等26 斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合初中几何公式:等腰三角形30 等腰三角形的性质定理等腰三角形的两个底角相等31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于6034 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论 2 有一个角等于60的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a+b=c47勾股定理的逆定理如果三角形的三边长a、b、c有关系a+b=c,那么这个三角形是直角三角形初中几何公式:四边形48定理四边形的内角和等于36049四边形的外角和等于36050多边形内角和定理 n边形的内角的和等于(n-2)18051推论任意多边的外角和等于36052平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形初中几何公式:菱形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(ab)267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形初中几何公式:正方形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称初中几何公式:等腰梯形74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形初中几何公式:等分78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半 L=(a+b)2 S=Lh83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84 (2)合比性质如果a/b=c/d,那么(ab)/b=(cd)/d85 (3)等比性质如果a/b=c/d==m/n(b+d++n0),那么(a+c++m)/(b+d++n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值初中几何公式:圆101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三个点确定一条直线110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111推论1 ①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧112推论2 圆的两条平行弦所夹的弧相等113圆是以圆心为对称中心的中心对称图形114定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等115推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116定理一条弧所对的圆周角等于它所对的圆心角的一半117推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等118推论2 半圆(或直径)所对的圆周角是直角;90的圆周角所对的弦是直径119推论3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形120定理圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角121①直线L和⊙O相交 d﹤r②直线L和⊙O相切 d=r③直线L和⊙O相离 d﹥r122切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123切线的性质定理圆的切线垂直于经过切点的半径124推论1 经过圆心且垂直于切线的直线必经过切点125推论2 经过切点且垂直于切线的直线必经过圆心126切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角127圆的外切四边形的两组对边的和相等128弦切角定理弦切角等于它所夹的弧对的圆周角129推论如果两个弦切角所夹的弧相等,那么这两个弦切角也相等130相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等131推论如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项132切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项133推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等134如果两个圆相切,那么切点一定在连心线上135①两圆外离 d﹥R+r ②两圆外切 d=R+r③两圆相交 R-r﹤d﹤R+r(R﹥r)④两圆内切 d=R-r(R﹥r) ⑤两圆内含d﹤R-r(R﹥r)136定理相交两圆的连心线垂直平分两圆的公共弦137定理把圆分成n(n3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138定理任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆139正n边形的每个内角都等于(n-2)180/n140定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141正n边形的面积Sn=pnrn/2 p表示正n边形的周长142正三角形面积3a/4 a表示边长143如果在一个顶点周围有k个正n边形的角,由于这些角的和应为360,因此k(n-2)180/n=360化为(n-2)(k-2)=4 144弧长计算公式:L=nR/180145扇形面积公式:S扇形=nR/360=LR/2146内公切线长= d-(R-r) 外公切线长= d-(R+r)小编为大家整理的初三数学几何知识点归纳总结相关内容大家一定要牢记,以便不断提高自己的数学成绩,祝大家学习愉快!。
中考数学总复习《几何初步》专题基础知识回顾三
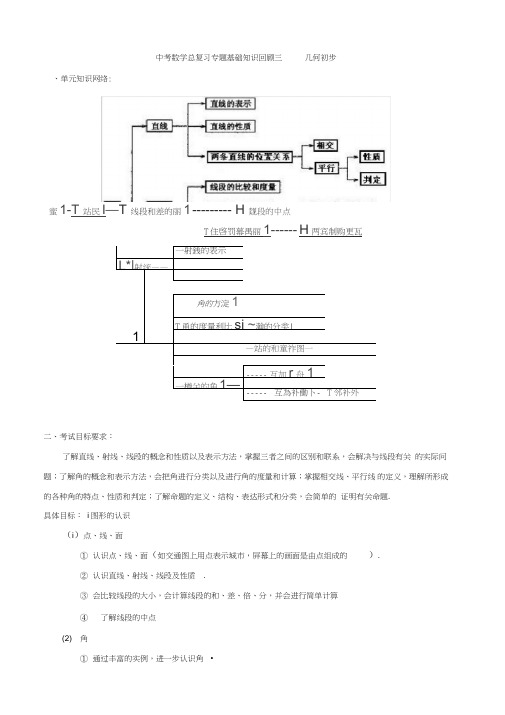
中考数学总复习专题基础知识回顾三几何初步、单元知识网络:蜜1-T 站民I—T 线段和差的丽1--------- H 觌段的中点T住啓罚幕禺丽1 ------ H两宾制购更瓦一射銭的表示L*|射统——角的方淀1T甬的度量利比si ~瀚的分类|1>—站的和童祚图一----- 互加r舟1一樽关的角1—----- 互為补働卜-T邻补外二、考试目标要求:了解直线、射线、线段的概念和性质以及表示方法,掌握三者之间的区别和联系,会解决与线段有关的实际问题;了解角的概念和表示方法,会把角进行分类以及进行角的度量和计算;掌握相交线、平行线的定义,理解所形成的各种角的特点、性质和判定;了解命题的定义、结构、表达形式和分类,会简单的证明有关命题.具体目标:i图形的认识(i)点、线、面①认识点、线、面(如交通图上用点表示城市,屏幕上的画面是由点组成的).②认识直线、射线、线段及性质.③会比较线段的大小,会计算线段的和、差、倍、分,并会进行简单计算④了解线段的中点(2) 角②会比较角的大小,能估计一个角的大小,会计算角度的和与差,认识度、分、秒,会进行简单换算.③了解角平分线及其性质(3)相交线与平行线①了解补角、余角、对顶角,知道等角的余角相等、等角的补角相等、对顶角相等②了解垂线、垂线段等概念,了解垂线段最短的性质,体会点到直线距离的意义③知道过一点有且仅有一条直线垂直于已知直线,会用三角尺或量角器过一点画一条直线的垂线④了解线段垂直平分线及其性质•⑤知道两直线平行同位角相等,进一步探索平行线的性质⑥知道过直线外一点有且仅有一条直线平行于已知直线,会用三角尺和直尺过已知直线外一点画这条直线的平行线•⑦体会两条平行线之间距离的意义,会度量两条平行线之间的距离2、尺规作图①完成以下基本作图:作一条线段等于已知线段,作一个角等于已知角,作角的平分线,作线段的垂直平分线•②了解尺规作图的步骤,对于尺规作图题,会写已知、求作和作法(不要求证明)•3、命题与证明①理解证明的定义和必要性•②通过具体的例子,了解定义、命题、定理的含义,会区分命题的条件(题设)和结论•③结合具体例子,了解逆命题的概念,会识别两个互逆命题,并知道原命题成立其逆命题不一定成立④掌握用综合法证明的格式,体会证明的过程要步步有据三、知识考点梳理知识点一、直线的概念和性质1.直线的定义:代数中学习的数轴和一张纸对折后的折痕等都是直线,直线可以向两方无限延伸.( 直线的概念是一个描述性的定义,便于理解直线的意义)2.直线的两种表示方法:(1) 用表示直线上的任意两点的大写字母来表示这条直线,如直线AB,其中A B是表示直线上两点的字母;(2) 用一个小写字母表示直线,如直线a.3.直线和点的两种位置关系(1) 点在直线上( 或说直线经过某点) ;(2) 点在直线外( 或说直线不经过某点).4.直线的性质:过两点有且只有一条直线( 即两点确定一条直线).5.同一平面内两条不同直线的位置关系:(1) 两条直线无公共点,即平行;(2) 两条直线有一个公共点,即两条直线相交,这个公共点叫做两条直线的交点( 两条直线相交,只有个交点).知识点二、射线、线段的定义和性质1.射线的定义:直线上一点和它一旁的部分叫做射线. 射线只向一方无限延伸.2.射线的表示方法:(1) 用表示射线的端点和射线上任意一点的大写字母来表示这条射线,如射线是射线上一点;OA其中O是(2)用一个小写字母表示射线,如射线 a.3. 线段的定义:直线上两点和它们之间的部分叫做线段,两个点叫做线段的端点4. 线段的表示方法:(1) 用表示两个端点的大写字母表示,如线段AB, A B是表示端点的字母;(2) 用一个小写字母表示,如线段 a.5. 线段的性质:所有连接两点的线中,线段最短(即两点之间,线段最短).6. 线段的中点:线段上一点把线段分成相等的两条线段,这个点叫做线段的中点7. 两点的距离:连接两点间的线段的长度,叫做两点的距离•知识点三、角1. 角的概念:(1) 定义一:有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,两条射线分别叫做角的边•(2) 定义二:一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角•射线旋转时经过的平面部分是角的内部,射线的端点是角的顶点,射线旋转的初始位置和终止位置分别是角的两条边•2. 角的表示方法:(1) 用三个大写字母来表示,注意将顶点字母写在中间,如/ AOB(2) 用一个大写字母来表示,注意顶点处只有一个角用此法,如/ A;(3) 用一个数字或希腊字母来表示,如/ 1,/ ^ •3•角的分类:(1) 按大小分类:锐角----小于直角的角(0 °v v 90° )直角----平角的一半或90 °的角(壮=90° )钝角----大于直角而小于平角的角(90 °v®v 180°)(2) 平角:一条射线绕着端点旋转,当终止位置与起始位置成一条直线时,所成的角叫做平角,平角于180 ° .(3) 周角:一条射线绕着端点旋转,当终止位置又回到起始位置时,所成的角叫做周角,周角等于360° .(4) 互为余角:如果两个角的和是一个直角(90 ° ),那么这两个角叫做互为余角.⑸互为补角:如果两个角的和是一个平角(180 ° ),那么这两个角叫做互为补角.4. 角的度量:(1) 度量单位:度、分、秒;(2) 角度单位间的换算:1 ° =60T =60〃(即:1度=60分,1分=60秒);(3) 1 平角=180°, 1 周角=360°, 1 直角=90° .5. 角的性质:同角或等角的余角相等,同角或等角的补角相等6. 角的平分线:如果一条射线把一个角分成两个相等的角,那么这条射线叫做这个角的平分线知识点四、相交线1.对顶角(1)定义:如果两个角有一个公共顶点,而且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫对顶角(2)性质:对顶角相等2 •邻补角(1) 定义:有一条公共边,而且另一边互为反向延长线的两个角叫做邻补角(2) 性质:邻补角互补.3. 垂线(1)两条直线互相垂直的定义:当两条直线相交所得的四个角中,有一个角是直角时,就说这两条直线是互相垂直的,它们的交点叫做垂足.垂直用符号“丄”来表示(2) 垂线的定义:互相垂直的两条直线中,其中的一条叫做另一条的垂线,如直线垂直于直线b,垂足为0,则记为a丄b,垂足为O.其中a是b的垂线,b也是a的垂线.(3) 垂线的性质:①过一点有且只有一条直线与已知直线垂直②连接直线外一点与直线上各点的所有线段中,垂线段最短•简单说成:垂线段最短(4) 点到直线的距离定义:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离4•同位角、内错角、同旁内角(1) 基本概念:两条直线(如a、b)被第三条直线(如c)所截,构成八个角,简称三线八角,如右图所示:/ 1和/ 8、/ 2和/ 7、/ 3和/6、/ 4和/ 5是同位角;/ 1和/ 6、/ 2和/5是内错角;/ 1和/5、 /2和/ 6是同旁内角.(2) 特点:同位角、内错角、同旁内角都是由三条直线相交构成的两个角.两个角的一条边在同一直线(截线)上,另一条边分别在两条直线(被截线)上.知识点五、平行线1 •平行线定义:在同一平面内,不相交的两条直线叫做平行线.平行用符号“//”来表示,•如直线a与b平行,记作a // b.在几何证明中,“//”的左、右两边也可能是射线或线段2.平行公理及推论:(1) 经过直线外一点,有且只有一条直线与这条直线平行 .(2) 平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行 如果 b // a , c // a ,那么 b // c.3.性质:(1) 平行线永远不相交; (2) 两直线平行,同位角相等; (3) 两直线平行,内错角相等; (4) 两直线平行,同旁内角互补;(5) 如果两条平行线中的一条垂直于某直线,那么另一条也垂直于这条直线,可用符号表示为: 若 b / c , b ± a ,贝U c 丄a.4.判定方法:(1) 定义(2) 平行公理的的推论(3) 同位角相等,两直线平行; (4) 内错角相等,两直线平行; (5) 同旁内角互补,两直线平行; (6) 垂直于同一条直线的两条直线平行 .知识点六、命题、定理、证明 1.命题:(1) 定义:判断一件事情的语句叫命题 . (2) 命题的结构:题设 +结论 =命题(3) 命题的表达形式:如果……那么……;若……则……; (4) 命题的分类:真命题和假命题(5) 逆命题:原命题的题设是逆命题的结论,原命题的结论是逆命题的题设.2.公理、定理:(1) 公理:人们在长期实践中总结出来的能作为判断其他命题真假依据的真命题叫做公理.即:3•证明:用推理的方法证实命题正确性的过程叫做证明四、规律方法指导1数形结合思想禾U用线段的长度、角的角度、对顶角、三线八角等基本几何图形,会求线段的长,以及角的度数,禾U 用图形的直观性解决数的抽象性,能在一定条件下形数互化,由数构形,以形破数2 •分类讨论思想直线的交点个数及位置关系,角的大小等需要有分类讨论的思想,包含多种可能的情况时,应根据可能出现的所有情况来分别讨论得出各种情况下相应的结论,不重不漏3. 化归与转化思想在解决利用几何图形求线段长度和角的度数的问题时,常常是将需要解决的问题,通过做辅助线、求和差等转化手段,归结为另一个相对较容易解决的或者已经有解决模式的问题,化繁为简、化难为易,由复杂与简单的转化•4. 注意观察、分析、总结结合近几年中考试卷,几何基本图形中的角的计算、与线段和平行有关的实际问题是当前命题的热点,常以填空和选择形式出现,以考查基础为主;尺规作图通常结合计算和证明出现,要注意弄清概念,认真观察,总结规律,并做到灵活应用•经典例题精析考点一、直线、射线、线段的概念和性质1. (1) (2010江苏宿迁)直线上有2010个点,我们进行如下操作:在每相邻两点间插入1个点,经过3次这样的操作后,直线上共有____________ 个点•答案:16073(2)下列语句正确的是()解析:选项A 中直线是向两方无限延伸的, 不能延长,所以A 错;选项B 中射线是向一方无限延伸的, 而延长射线0A 就是指由0向A 延长,射线只能反向延长,所以 B 错;选项C 中AC 只能大于BC,线段延长应有方向,而且要符合实际意义,所以C 错.所以选D.举一反三【变式1】下列语句正确的是() A.如果PA=PB 那么P 是线段AB 的中点 B .线段有一个端点 C.直线AB 大于射线ABD.反向延长射线 0P(0为端点)考点:直线、射线、线段的性质 •解析:在只用几何语言表达而没有图形的情况下,要注意图形的不同情形,象 A 中往往容易考虑不到 P 、A 、B 三点可能不在同一直线上,要注意线段的中点首先应为线段上一点,而误选A ;线段有两个端点,所以B 错;直线可以向两方无限延伸,射线可以向一方无限延伸,所以直线与射线都无法度量长度,不能 比较大小,所以 C 错.答案选D.⑴数轴上有两点A 、B 分别表示实数a 、b 则线段AB 的长度是()考点:数轴上两点间的距离和线段的加减•思路点拨:本类题目注意线段长度是非负数,若有字母注意使用绝对值 •根据题意,画图解:(1)中数轴上两点间的距离公式为:|a-b |或|b-a | .(2)如图,因为 CA=3AB 所以CB=4AB 则线段CA 与线段CB 之比为3AB:4AB=3:4.答案:(1)C ; (2)A总结升华:解决本例类型的题目应结合图形,即数形结合,这样做起来简捷 举一反三C.延长线段 AB 至U C,使AC=BC 考点:直线、射线、线段的性质 •D.延长线段AB 到C,使AC=3ABA.a-bB.a+bC. | a-b |D. | a+b |(2)已知线段AB 在BA 的延长线上取一点C,使CA=3AB 则线段CA 与线段CB 之比为()A.3 : 4B.2 : 3C.3 : 5D.1 : 2【变式1】如图,点A、B、C在直线』上,则图中共有________ 条线段.―*—*--------------- ;A B C I答案:3【变式2】有一段火车路线,含这段铁路的首尾两站在内共有5个车站(如图),图中共有几条线段?在这段线路上往返行车,需印制几种车票(每种车票要印出上车站与下车站)?I ________ I_______ | _________ I_____ |A E C D E解:线段有10条;车票需要2X 10=20种.总结升华:在直线上确定线段的条数公式为:(其中n为直线上点的个数).在求从一个顶点引出的n条射线所形成的小于平角的角的个数也可用此公式【变式3】已知线段AB=8cm延长AB至C,使AC=2AB D是AB中点,则线段CD= __________ .思路点拨:解决本例类型的题目应结合图形,即数形结合,本题考查延长线段的方向和线段的中点的概念.I d 3 ■A DB C解:如图,••• AB=8cm AC=2AB「. AC=2X 8=16cmI■/ D是AB中点/• AD=8X - =4cm /• CD=AC-AD=16-4=12cm考点二、角AH3.下列说法正确的是()A. 角的两边可以度量.B. 角是由有公共端点的两条射线构成的图形.C. 平角的两边可以看成直线.D. —条直线可以看成是一个平角.考点:角的定义解析:角的两边是射线,不能度量,所以A错;平角的两边也是射线,不能是直线,所以C错;了解直线和平角两者之间的区别,角有顶点,所以 D 错•故选B.b 4 .已知 0C 平分/ AOB 则下列各式:⑴ / AOC= / AOB (2) / A0C 2 COB ⑶ / AOB=Z AOC 其中正确的是() A.只有(1)B.只有 ⑴(2)C.只有⑵(3)D.(1)(2)(3)思路点拨:角平分线定义的的三种表达形式•答案:D(A ) 30° ( B ) 40° (C ) 60°( D ) 70°考点:平行线的性质、三角形外角定理 答案:A(2)已知/凸与/ ◎互余,且/已=40 °,则/ Q 的补角为 ___________________ 度• 考点:角互余和互补定义 •思路点拨:本题考查互余、互补两角的定义,互余、互补只与两角度数和有关,与角的位置无关 解:•••/ 门与/ * 互余,•••/ ^ +/ ' =90°;:/ & =40 °,•••/ ': =90 ° - Z =90° -40 ° =50° . •••/ ';的补角=180 ° -50 ° =130° .举一反三【变式1】如图,已知/ COE N BOD 2 AOC=90,则图中互余的角有 ____________ 对,互补的角有 ________5.( 1)(2010山东德州)如图,直线,则/ E 等于()/ C = 40考点:互为余角和互为补角的定义•思路点拨:在本题目中,当图中角比较多时,就将图形的角进行归类,找出每种相等的角,按照同角或等角的余角相等,同角或等角的补角相等的性质解决问题,注意要不重不漏解:互余的角有:/ COD^/ DOE / COD和/ BOC / AOB和/ DOE / AOB和/ BOC 共4 对; 互补的角有:/ EOD 和/ AOD / BOC和/AOD / AOB和/ BOE/ COD和/ BOE / AOC和/ COE / AOC和/ BOD / COE和/ BOD 共7 对.【变式2】已知:如图,ACL BC,垂足为C,/ BCD是/ B的余角•求证:/ ACD=/ B.证明:••• ACL BC(已知)•••/ ACB=90 ()•••/ BCD是/ DCA的余角()•••/ BCD是/ B的余角(已知)• / ACD/ B()•会用所学的定理、公理、推论等真命题概括几何语言思路点拨:会根据所给的语句写出正确的根据答案:垂直定义;余角定义,同角的余角相等* 6.⑴已知/ 1=43° 27',则/ 1的余角是___________________ ,补角是 ________ ;(2)18.32 ° =18° ( ) ' ( ) 〃,216° 42' = __________ ° .考点:掌握角的单位之间的换算关系• 1 ° =60', 1 ' =60〃.解:(1) / 1 的余角=90° -43 ° 27' =89° 60' -43 ° 27' =46° 33';/ 1 的补角=180° -43 ° 27' =179° 60' -43 ° 27' =136° 33';(2) 0.32 ° =0.32 X 60' =19.2 ' 0.2 ' =0.2 X 60〃=12〃所以18.32 ° =18° 19' 12〃;42' =0.7 ° 所以216 ° 42' =216.7举一反三 【变式1】计算• ①—②.1 2.f 5考点:会计算角之间的和、差、倍、分,注意相邻单位之间是 解:①I -二‘1,=68° 70' =69° 10'② 亠/ ■_ =62°X 3+25'X 3=186° +75' =187° 15' ③J 7 1丁=67° 80' -37 ° 33' =30° 47'④ 二 2 =69° 60'- 3=23° 20'6” 7. (1) (2010内蒙呼和浩特)8点30分时,钟表的时针与分针的夹角为 _____________________ 答案:75(2)时钟在1点30分时,时针与分针的夹角为 __________ 度. 解析:时钟上时针和分针是实际生活中常见的角,分针1小时旋转360度,1分钟旋转6度;时针1小时旋转30度,1分钟旋转0.5度.在相同时间下,分针旋转的角度是时针的12倍.钟表上1和6的夹角为150°,过了半小时,时针转了 15°,所以1点30分时,时针与分针的夹角为 150° -15 ° =135° .举一反三【变式1】某火车站的时钟楼上装有一个电子报时钟,在钟面的边界上,每一分钟的刻度处都装有只小彩灯,晚上9时35分20秒时,时针与分针所夹的角内装有多少只小彩灯?格,中间有12个分钟刻度处,而每一个分钟刻度处有一只小彩灯,所以它们之间有12个小彩灯.” &表示O 点南偏东15°方向和北偏东25°方向的两条射线组成的角等于 ___________________ 度. 考点:方位角60进制的,相同单位互相加减解析:9时35分20秒时,时针与分针的夹角间的小格数为45+35— +个小所以/ AOB=180 -25 ° -15 ° =140举一反三【变式1】如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°,甲、乙两地间同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西________ 度.考点:方位角在实际中的应用思路点拨:结合图形,在求方位角时,掌握甲和乙之间方向相反的规律,甲观察乙是北偏东 48°,乙观察甲就是南偏西 48° .答案:48OAL 0B / BOC=40 , 0D 平分/ AOC 则/ BOD=思路点拨:通过观察图形,找出各角之间的联系,关键是看清角所在的位置,结合图形进行计算 解:••• OA1OB •••/ AOB=90 ,•••/ BOC=40 ,•••/ AOC 2 AOB+Z BOC=90 +40° =130°,丄 丄•/ OD 平分/ AOCCOD= / AOC= X 130° =65•••/ BOD 2 COD-/ BOC=65 -40 ° =25 ° .解析:如图,南北方向上的线与OA 0B 的夹角分别为 25°和159.如图,]匕-A总结升华:用尺规作图中直尺只起到画线(直线、射线、线段)的作用•而不能用来量取举一反三【变式1】用一副三角板画角,不能画出的角的度数是 ()A.15 °B.75 °C.145 °D.165 °思路点拨:了解一副三角板中各角的度数,总结规律:用一副三角板画角,能画出的角都是 15°的整数倍•答案:C【变式2】以/ AOB 的顶点 0为端点作射线 OC 使/ AOC:/ BOC=5:4.(1)若/ AOB=18,求/ AOC 与/ BOC 的度数;(2)若/ AOB=m ,求/ AOC 与/ BOC 的度数•思路点拨:当题目中包含多种可能的情况时,应根据可能出现的所有情况进行分类,要做到无遗漏、 无重复• 答案:⑴ 第一种情形:OC 在/ AOB 的外部,可设/ AOC=5x / BOC=4x则/ AOB=/ AOC-Z BOC=x ?即 x=18° . •••/ AOC=90,/ BOC=72 .第二种情形:OC 在/ AOB 的内部, 可设/ AOC=5x / BOC=4x 则/ AOB=/ AOC 丄 BOC=9x • 9x=18。
2019年中考数学几何公式定理汇总
2019年中考数学几何公式定理汇总1.过两点有且只有一条直线2.两点之间线段最短3.同角或等角的补角相等4.同角或等角的余角相等5.过一点有且只有一条直线和已知直线垂直6.直线外一点与直线上各点连接的所有线段中,垂线段最短7.平行公理经过直线外一点,有且只有一条直线与这条直线平行8.如果两条直线都和第三条直线平行,这两条直线也互相平行9.同位角相等,两直线平行10.内错角相等,两直线平行11.同旁内角互补,两直线平行12.两直线平行,同位角相等13.两直线平行,内错角相等14.两直线平行,同旁内角互补15.定理三角形两边的和大于第三边16.推论三角形两边的差小于第三边17.三角形内角和定理三角形三个内角的和等于180°18.推论1直角三角形的两个锐角互余19.推论2三角形的一个外角等于和它不相邻的两个内角的和20.推论3三角形的一个外角大于任何一个和它不相邻的内角21.全等三角形的对应边、对应角相等22.边角边公理有两边和它们的夹角对应相等的两个三角形全等23.角边角公理有两角和它们的夹边对应相等的两个三角形全等24.推论有两角和其中一角的对边对应相等的两个三角形全等25边边边公理有三边对应相等的两个三角形全等26斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等27.定理1:在角的平分线上的点到这个角的两边的距离相等28.定理2:到一个角的两边的距离相同的点,在这个角的平分线上29.角的平分线是到角的两边距离相等的所有点的集合30.等腰三角形的性质定理等腰三角形的两个底角相等31.推论1:等腰三角形顶角的平分线平分底边并且垂直于底边32.等腰三角形的顶角平分线、底边上的中线和高互相重合33.推论3:等边三角形的各角都相等,并且每一个角都等于60°34等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35.推论1:三个角都相等的三角形是等边三角形36.推论2:有一个角等于60°的等腰三角形是等边三角形37.在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38.直角三角形斜边上的中线等于斜边上的一半39.定理线段垂直平分线上的点和这条线段两个端点的距离相等40.逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41.线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42.定理1:关于某条直线对称的两个图形是全等形43.定理2:如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44.定理3:两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45.逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46.勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即ab=c47.勾股定理的逆定理如果三角形的三边长a、b、c有关系ab=c,那么这个三角形是直角三角形48.定理四边形的内角和等于360°49.四边形的外角和等于360°50.多边形内角和定理n边形的内角的和等于(n-2)×180°51.推论任意多边的外角和等于360°52.平行四边形性质定理1平行四边形的对角相等53.平行四边形性质定理2平行四边形的对边相等54.推论夹在两条平行线间的平行线段相等55.平行四边形性质定理3平行四边形的对角线互相平分56.平行四边形判定定理1两组对角分别相等的四边形是平行四边形57.平行四边形判定定理2两组对边分别相等的四边形是平行四边形58.平行四边形判定定理3对角线互相平分的四边形是平行四边形59.平行四边形判定定理4一组对边平行相等的四边形是平行四边形60.矩形性质定理1矩形的四个角都是直角61.矩形性质定理2矩形的对角线相等62.矩形判定定理1有三个角是直角的四边形是矩形63.矩形判定定理2对角线相等的平行四边形是矩形64.菱形性质定理1菱形的四条边都相等65.菱形性质定理2菱形的对角线互相垂直,并且每一条对角线平分一组对角66.菱形面积=对角线乘积的一半,即S=(a×b)÷267.菱形判定定理1:四边都相等的四边形是菱形68.菱形判定定理2:对角线互相垂直的平行四边形是菱形69.正方形性质定理1:正方形的四个角都是直角,四条边都相等70.正方形性质定理2:正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71.定理1关于中心对称的两个图形是全等的72.定理2关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73.逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74.等腰梯形性质定理等腰梯形在同一底上的两个角相等75.等腰梯形的两条对角线相等76.等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77.对角线相等的梯形是等腰梯形78.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79.推论1:经过梯形一腰的中点与底平行的直线,必平分另一腰80.推论2:经过三角形一边的中点与另一边平行的直线,必平分第三边81.三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82.梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(ab)÷2S=L×h83.(1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84.(2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85.(3)等比性质如果a/b=c/d=…=m/n(bd…n≠0),那么(ac…m)/(bd…n)=a/b86.平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87.推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88.定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89.平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90.定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91.相似三角形判定定理1:两角对应相等,两三角形相似(ASA)92.直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93.判定定理2:两边对应成比例且夹角相等,两三角形相似(SAS)94.判定定理3:三边对应成比例,两三角形相似(SSS)95.定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96.性质定理1:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97.性质定理2:相似三角形周长的比等于相似比98.性质定理3:相似三角形面积的比等于相似比的平方99.任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100.任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101.圆是定点的距离等于定长的点的集合102.圆的内部可以看作是圆心的距离小于半径的点的集合103.圆的外部可以看作是圆心的距离大于半径的点的集合104.同圆或等圆的半径相等105.到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106.和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107.到已知角的两边距离相等的点的轨迹,是这个角的平分线108.到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109.定理不在同一直线上的三个点确定一条直线110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111.推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧弦的垂直平分线经过圆心,并且平分弦所对的两条弧平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧112.推论2:圆的两条平行弦所夹的弧相等113.圆是以圆心为对称中心的中心对称图形114.定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等115.推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116.定理一条弧所对的圆周角等于它所对的圆心角的一半117.推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等118.推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径119.推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形120.定理圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角121.直线L和O相交d﹤r直线L和O相切d=r直线L和O相离d﹥r122.切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123.切线的性质定理圆的切线垂直于经过切点的半径124.推论1:经过圆心且垂直于切线的直线必经过切点125.推论2:经过切点且垂直于切线的直线必经过圆心126.切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角127.圆的外切四边形的两组对边的和相等128.弦切角定理弦切角等于它所夹的弧对的圆周角129.推论如果两个弦切角所夹的弧相等,那么这两个弦切角也相等130.相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等131.推论如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项132.切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项133.推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等134.如果两个圆相切,那么切点一定在连心线上135.两圆外离d﹥Rr两圆外切d=Rr两圆相交R-r﹤d﹤Rr(R﹥r)两圆内切d=R-r(R﹥r)两圆内含d﹤R-r(R﹥r)136.定理相交两圆的连心线垂直平分两圆的公共弦137.定理把圆分成n(n≥3):依次连结各分点所得的多边形是这个圆的内接正n边形经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138.定理任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆139.正n边形的每个内角都等于(n-2)×180°/n140.定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141.正n边形的面积Sn=pnrn/2p表示正n边形的周长142.正三角形面积√3a/4a表示边长143.如果在一个顶点周围有k个正n边形的角,由于这些角的和应为360°,因此k×(n-2)180°/n=360°化为(n-2)(k-2)=4144.弧长计算公式:L=nπR/180145.扇形面积公式:S扇形=nπR/360=LR/2146.内公切线长=d-(R-r)外公切线长=d-(Rr)。
初中数学几何知识点总结5篇
初中数学几何知识点总结初中数学几何知识点总结(精选10篇)总结是对某一特定时间段内的学习和工作生活等表现情况加以回顾和分析的一种书面材料,通过它可以全面地、系统地了解以往的学习和工作情况,不妨坐下来好好写写总结吧。
那么你真的懂得怎么写总结吗?以下是小编整理的初中数学几何知识点总结,希望对大家有所帮助。
初中数学几何知识点总结 11、四边形的.面积公式⑴、S□ABCD=a·h⑵、S菱形=1/2a·b(a、b为对角线)⑶、S梯形=1/2(a+b)·h=m·h(m为中位线)2、三角形的面积公式⑴、S△=1/2·a·h⑵、S△=1/2·P·r(P为三角形周长,r为三角形内切圆的半径)3、S正多边形=1/2·Pn·rn=1/2·nan·rn4、S圆=πR25、S扇形=nπ=1/2LR6、S弓形=S扇-S△初中数学几何知识点总结 21、三角形、平行四边形和梯形的计算用到的定理主要有三角形全等定理,中位线定理,等腰三角形、直角三角形、正三角形及各种平行四边形的性质等定理。
关于梯形中线段计算主要依据梯形中位线定理及等腰梯形、直角梯形的性质定理等。
2、有关圆的线段计算的主要依据⑴、切线长定理⑵、圆切线的性质定理。
⑶、垂径定理。
⑷、圆外切四边形两组对边的和相等。
⑸、两圆外切时圆心距等于两圆半径之和,两圆内切时圆心距等于两半径之差。
3、直角三角形边的`计算直角三角形边长的计算应用最广,其理论依据主要是勾股定理和特殊角三角形的性质及锐角三角函数等。
4、成比例线段长度的求法⑴、平行线分线段成比例定理;⑵、相似形对应线段的比等于相似比;⑶、射影定理;⑷、相交弦定理及推论,切割线定理及推论;⑸、正多边形的边和其他线段计算转化为特殊三角形。
初中数学几何知识点总结 31、过两点有且只有一条直线2、两点之间线段最短3、同角或等角的补角相等4、同角或等角的余角相等5、过一点有且只有一条直线和已知直线垂直6、直线外一点与直线上各点连接的'所有线段中,垂线段最短7、平行公理经过直线外一点,有且只有一条直线与这条直线平行8、如果两条直线都和第三条直线平行,这两条直线也互相平行9、同位角相等,两直线平行10、内错角相等,两直线平行11、同旁内角互补,两直线平行12、两直线平行,同位角相等13、两直线平行,内错角相等14、两直线平行,同旁内角互补15、定理三角形两边的和大于第三边16、推论三角形两边的差小于第三边17、三角形内角和定理三角形三个内角的和等于180°18、推论1直角三角形的两个锐角互余19、推论2三角形的一个外角等于和它不相邻的两个内角的和20、推论3三角形的一个外角大于任何一个和它不相邻的内角初中数学几何知识点总结 41、掌握最基本的五种尺规作图⑴、作一条线段等于已知线段。
山东各2019年中考数学分类解析-专项8:平面几何基础
山东各2019年中考数学分类解析-专项8:平面几何基础专题8:平面几何基础一、选择题1. 〔2018山东滨州3分〕借助一副三角尺,你能画出下面哪个度数的角【】A、65°B、75°C、85°D、95°【答案】B。
【考点】角的计算。
【分析】利用一副三角板可以画出75°角,用45°和30°的组合即可。
应选B。
2. 〔2018山东滨州3分〕一个三角形三个内角的度数之比为2:3:7,这个三角形一定是【】A、等腰三角形B、直角三角形C、锐角三角形D、钝角三角形【答案】D。
【考点】三角形内角和定理,比例的计算。
【分析】按比例计算出各角的度数即可作出判断:三角形的三个角依次为180°×22+3+7=30°,180°×32+3+7=45°,180°×72+3+7=105°,所以这个三角形是钝角三角形。
应选D。
3. 〔2018山东德州3分〕不一定在三角形内部的线段是【】A、三角形的角平分线B、三角形的中线C、三角形的高D、三角形的中位线【答案】C。
【考点】三角形的角平分线、中线、高和中位线。
【分析】因为在三角形中,它的中线、角平分线和中位线一定在三角形的内部,而钝角三角形的高在三角形的外部。
应选C。
4. 〔2018山东东营3分〕以下图形中,是中心对称图形的是【】A、 B、 C、 D、【答案】B。
【考点】中心称对形。
【分析】根据中心对称图形的概念,中心对称图形是图形沿对称中心旋转180度后与原图重合。
因此,A、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形;B、将此图形绕圆心旋转180度正好与原来的图形重合,所以这个图形是中心对称图形;C、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形;D、将此图形绕任一点旋转180度都不能与原来的图形重合,所以这个图形不是中心对称图形。
2019年中考数学总复习:几何图形证明专题(超详细,经典!!!)
B中考数学总复习 几何图形证明专题【题型一】考察概念基础知识点型例1如图1,等腰△ABC 的周长为21,底边BC = 5,AB 的垂直平分线是DE ,则△BEC 的周长为 。
例2 如图2,菱形ABCD 中,60A ∠=°,E 、F 是AB 、AD 的中点,若2EF =,菱形边长是______.例3 (切线)已知AB 是⊙O 的直径,PB 是⊙O 的切线,AB =3cm ,PB =4cm ,则BC = . 【题型二】折叠题型:折叠题要从中找到对就相等的关系,然后利用勾股定理即可求解。
例4(09绍兴)D E ,分别为AC ,BC 边的中点,沿DE 折叠,若48CDE ∠=°,则APD ∠等于 。
例5如图4.矩形纸片ABCD 的边长AB =4,AD =2.将矩形纸片沿 EF 折叠, 使点A 与点C 重合,折叠后在其一面着色(图),则着色部分的面积为( ) A . 8 B .112C . 4D .52【题型三】涉及计算题型:常见的有应用勾股定理求线段长度,求弧长,扇形面积及圆锥体积,侧面积,三角函数计算等。
例6如图3,P 为⊙O 外一点,PA 切⊙O 于A ,AB 是⊙O 的直径,PB 交⊙O 于C ,PA =2cm ,PC =1cm,则图中阴影部分的面积S 是 ( ) A.2235cm π- B 2435cm π- C 24235cm π- D 2232cm π-D C B AE FG 【题型四】证明题型:三角形全等【判定方法1:SAS 】例1 (2011广州)如图,AC 是菱形ABCD 的对角线,点E 、F 分别在边AB 、AD 上,且 AE=AF 。
求证:△ACE ≌△ACF例2 (2010长沙)在正方形ABCD 中,AC 为对角线,E 为AC 上一点,连接EB 、ED . (1)求证:△BEC ≌△DEC ;(2)延长BE 交AD 于F ,当∠BED =120°时,求∠EFD 的度数.【判定方法2:AAS (ASA )】例3 如图,ABCD 是正方形,点G 是BC 上的任意一点,DE AG ⊥于 E ,BF DE ∥,交 AG 于F ,求证:AF BF EF =+.例4 (2011浙江台州)如图,在□ABCD 中,分别延长BA ,DC 到点E ,使得AE=AB , CH=CD 连接EH ,分别交AD ,BC 于点F,G 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学几何基础知识汇总
(名师总结知识点汇总,绝对精品,值得下载)
中考几何证明(三角形、四边形、圆)
考察形式:
①、证明线段相等或证全等;
②、在①结论的基础上给出一定条件求值或判断说明
初中几何证明线段或角度相等思路:
1、证明三角形全等(5个判定条件);
2、看题目是否有“平分”存在,若有,则利用角平分线的性质证明;
3、看题目中是否存在若干个线段中点的条件,若有,则想办法构造或利用中位线,利用中位线的性质证明;
4、利用已知图形的性质证明(特殊的平行四边形、等腰三角形三线合一)
三角形相关知识点汇总
1、与三角形有关的线段:
三角形任意两边之和大于第三边,a
为△三角形的中位线平行
于第三边且等于第三
边的一半
且
1
离与重心到对边中点
的距离之比为
2
个顶点组成的
角形面积相等。
3
个顶点距离平方的和
最小。
有两边相等,且底角相等的三角形1
等角对等边;
合一
中线)
AB
直角三角形中的两直角边的平方之两直角边的平方之和
等
(
2、与三角形有关的角
三角形的三个内角和∠
直角三角形的两个锐∠
三角形的外角等于与
∠
它不相邻的两个内角
三边相等,三角相等
∠,
AC
3、三角形面积计算
4、三角形全等
全等三角形判定条件:
1、_______:三边对应相等的两个三角形全等(可简写成“SSS”)
2、________:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)
3、_________:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)
4、_________:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)
5、__________:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”)
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等
(4):时刻注意图形中的隐含条件,如“公共角”、“公共边”、“对顶角”
5、四边形相关知识点汇总
1、平行四边形的概念、性质及判定
2、特殊平行四边形的概念、性质及判定
①矩形
②菱形
③正方形。
