强连通分量的定义
强连通分量——精选推荐

强连通分量写在前⾯:我是⼀只蒟蒻今天,我们来介绍⼀下强连通分量这个玩意⼉有向图的DFS:与⽆向图的差别就在于,搜索时只能顺边。
所以,有时的搜索树会不⽌⼀个根,因为,从⼀点出发不⼀定能⾛完所有点。
在⼀个搜索图中,每条有向边(x,y)⼀定是以下三(四)种之⼀:⽗⼦边——具有⽗⼦关系返祖边——指向其祖先横叉边——dfn[y]<dfn[x]强连通图定义给定⼀张有向图。
若对于图中任意两节点x,y,既存在x到y的路径,也存在y到x的路径,则称该有向图是“强连通图”。
强连通分量(SCC)即有向图中的极⼤强连通⼦图。
思想实现Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的⼀棵⼦树。
搜索时,把当前搜索树中未处理的节点加⼊⼀个堆栈,回溯时可以判断栈顶到栈中的节点是否为⼀个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的⼦树能够追溯到的最早的栈中节点的次序号。
当DFN(u)=Low(u)时,以u为根的搜索⼦树上所有节点是⼀个强连通分量。
下⾯我们对这个图进⾏⼀下模拟这样,我们就完成了找强连通分量的过程,下⾯我们来看⼀下核⼼代码,1void tarjan(int x){2 dfn[x]=low[x]=++num;//更新3 s[++top]=x;in[x]=1;//当前元素⼊栈4for(int i=head[x];i;i=e[i].next){5int y=e[i].to;6if(!dfn[y]){7 tarjan(y);8 low[x]=min(low[x],low[y]);9 }else{10if(in[y])low[x]=min(low[x],dfn[y]);//如果被访问过且还在栈中,更新11 }12 }13if(dfn[x]==low[x]){//是强连通分量14 cnt++;int c;//颜⾊块加⼀15do{16 c=s[top--];17 a[c]=cnt;//进⾏染⾊处理18 v[cnt]++;//当前连通块的数量统计19in[c]=0;//出栈标记20 }while(x!=c);21 }22 }OK,我们就结束了基本讲解,下⾯是两道基本栗题。
数据结构课设有向图强连通分量求解

数据结构课设有向图强连通分量求解强连通分量(Strongly Connected Components)是有向图中的一种特殊的连通分量,指的是图中任意两个顶点之间都存在有向路径。
求解有向图的强连通分量可以使用Tarjan算法,该算法基于深度优先搜索(DFS)。
具体步骤如下:1. 初始化一个栈,用于存储已访问的顶点;2. 对于图中的每一个顶点v,如果v未访问,则进行DFS遍历;3. 在DFS遍历中,对于当前访问的顶点v,设置v的索引号和低链接号为当前索引值,并将v入栈;4. 遍历v的所有邻接顶点w,如果w未访问,则进行DFS遍历,并将w的低链接号更新为min(当前顶点的低链接号, w的低链接号);5. 如果当前顶点v的低链接号等于索引号,则将v出栈,并将v及其出栈的顶点组成一个强连通分量。
示例代码如下:```pythonclass Graph:def __init__(self, vertices):self.V = verticesself.adj = [[] for _ in range(vertices)]self.index = 0self.lowlink = [float("inf")] * verticesself.onStack = [False] * verticesself.stack = []self.scc = []def addEdge(self, u, v):self.adj[u].append(v)def tarjanSCC(self, v):self.index += 1self.lowlink[v] = self.indexself.stack.append(v)self.onStack[v] = Truefor w in self.adj[v]:if self.lowlink[w] == float("inf"):self.tarjanSCC(w)self.lowlink[v] = min(self.lowlink[v], self.lowlink[w]) elif self.onStack[w]:self.lowlink[v] = min(self.lowlink[v], self.lowlink[w]) if self.lowlink[v] == self.index:scc = []w = -1while w != v:w = self.stack.pop()self.onStack[w] = Falsescc.append(w)self.scc.append(scc)def findSCC(self):for v in range(self.V):if self.lowlink[v] == float("inf"): self.tarjanSCC(v)return self.scc```使用示例:```pythong = Graph(5)g.addEdge(1, 0)g.addEdge(0, 2)g.addEdge(2, 1)g.addEdge(0, 3)g.addEdge(3, 4)print("Strongly Connected Components:") scc = g.findSCC()for component in scc:print(component)```输出结果:```Strongly Connected Components:[4][3][0, 2, 1]```以上代码实现了有向图的强连通分量的求解,通过Tarjan算法进行DFS遍历和低链接号的更新,最终得到所有的强连通分量。
强连通分量(超详细!!!)

强连通分量(超详细)⼀、定义在有向图G中,如果两个顶点u,v间有⼀条从u到v的有向路径,同时还有⼀条从v到u的有向路径,则称两个顶点强连通。
如果有向图G的每两个顶点都强连通,称G是⼀个强连通图。
有向⾮强连通图的极⼤强连通⼦图,称为强连通分量。
图中,⼦图{1,2,3,4}为⼀个强连通分量,因为顶点1,2,3,4两两可达。
{5},{6}也分别是两个强连通分量。
⼆、tarjan算法时间复杂度是O(N+M)四条边:树枝边:DFS时经过的边,即DFS搜索树上的边。
前向边:与DFS⽅向⼀致,从某个结点指向其某个⼦孙的边。
后向边:与DFS⽅向相反,从某个结点指向其某个祖先的边。
(返祖边)横叉边:从某个结点指向搜索树中的另⼀⼦树中的某结点的边。
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的⼀棵⼦树。
搜索时,把当前搜索树中未处理的节点加⼊⼀个堆栈,回溯时可以判断栈顶到栈中的节点是否为⼀个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的⼦树能够追溯到的最早的栈中节点的次序号。
由定义可以得出,Low(u)=Min {Low(u), Low(v) } (u,v)为树枝边,u为v的⽗节点 . Low(u)=Min {Low(u), DFN(v) } DFN(v),(u,v)为指向栈中节点的后向边(指向栈中结点的横叉边) }当结点u搜索结束后,若DFN(u)=Low(u)时,则以u为根的搜索⼦树上所有还在栈中的节点是⼀个强连通分量。
算法过程:从节点1开始DFS,把遍历到的节点加⼊栈中。
搜索到节点u=6时,DFN[6]=LOW[6],找到了⼀个强连通分量。
退栈到u=v为⽌,{6}为⼀个强连通分量。
初始化时Low[u]=DFN[u]=++index返回节点5,发现DFN[5]=LOW[5],退栈后{5}为⼀个强连通分量。
返回节点3,继续搜索到节点4,把4加⼊堆栈。
发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。
求强连通分量的Kosaraju算法和Tarjan算法的比较 by ljq
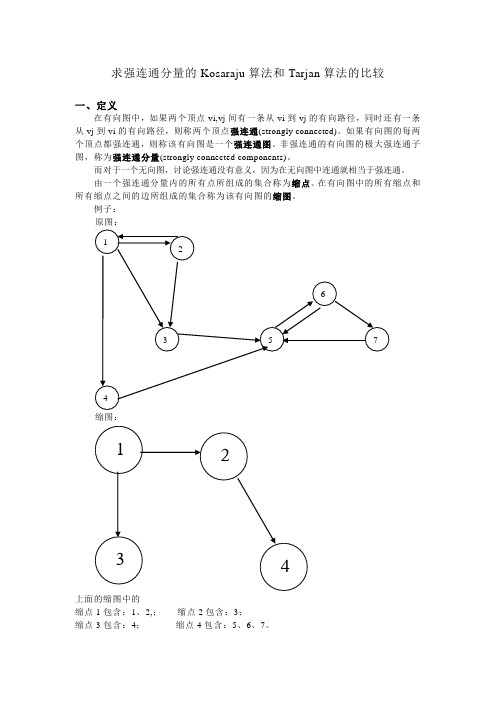
求强连通分量的Kosaraju算法和Tarjan算法的比较一、定义在有向图中,如果两个顶点vi,vj间有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。
如果有向图的每两个顶点都强连通,则称该有向图是一个强连通图。
非强连通的有向图的极大强连通子图,称为强连通分量(strongly connected components)。
而对于一个无向图,讨论强连通没有意义,因为在无向图中连通就相当于强连通。
由一个强连通分量内的所有点所组成的集合称为缩点。
在有向图中的所有缩点和所有缩点之间的边所组成的集合称为该有向图的缩图。
例子:原图:缩图:上面的缩图中的缩点1包含:1、2,;缩点2包含:3;缩点3包含:4;缩点4包含:5、6、7。
二、求强连通分量的作用把有向图中具有相同性质的点找出来,形成一个集合(缩点),建立缩图,能够方便地进行其它操作,而且时间效率会大大地提高,原先对多个点的操作可以简化为对它们所属的缩点的操作。
求强连通分量常常用于求拓扑排序之前,因为原图往往有环,无法进行拓扑排序,而求强连通分量后所建立的缩图则是有向无环图,方便进行拓扑排序。
三、Kosaraju算法时间复杂度:O(M+N)注:M代表边数,N代表顶点数。
所需的数据结构:原图、反向图(若在原图中存在vi到vj的有向边,在反向图中就变成为vj到vi的有向边)、标记数组(标记是否遍历过)、一个栈(或记录顶点离开时间的数组)。
算法描叙:步骤1:对原图进行深度优先遍历,记录每个顶点的离开时间。
步骤2:选择具有最晚离开时间的顶点,对反向图进行深度优先遍历,并标记能够遍历到的顶点,这些顶点构成一个强连通分量。
步骤3:如果还有顶点没有遍历过,则继续进行步骤2,否则算法结束。
hdu1269(Kosaraju算法)代码:#include<cstdio>#include<cstdlib>const int M=10005;struct node{int vex;node *next;};node *edge1[M],*edge2[M];bool mark1[M],mark2[M];int T[M],Tcnt,Bcnt;void DFS1(int x)mark1[x]=true;node *i;for(i=edge1[x];i!=NULL;i=i->next) {if(!mark1[i->vex]){DFS1(i->vex);}}T[Tcnt]=x;Tcnt++;}void DFS2(int x){mark2[x]=true;node *i;for(i=edge2[x];i!=NULL;i=i->next) {if(!mark2[i->vex]){DFS2(i->vex);}}}int main(){int n,m;while(scanf("%d%d",&n,&m)){if(n==0&&m==0){break;}int i,a,b;for(i=1;i<=n;i++){mark1[i]=mark2[i]=false;edge1[i]=NULL;edge2[i]=NULL;}node *t;while(m--){scanf("%d%d",&a,&b);t=(node *)malloc(sizeof(node));t->vex=b;t->next=edge1[a];edge1[a]=t;t=(node *)malloc(sizeof(node));t->vex=a;t->next=edge2[b];edge2[b]=t;}Tcnt=0;for(i=1;i<=n;i++){if(!mark1[i]){DFS1(i);}}Bcnt=0;//Bcnt用于记录强连通分量的个数for(i=Tcnt-1;i>=0;i--){if(!mark2[T[i]]){DFS2(T[i]);Bcnt++;}}if(Bcnt==1)//如果强连通分量的个数为1则说明该图是强连通图{printf("Yes\n");}else{printf("No\n");}}return 0;}四、Tarjan算法时间复杂度:O(M+N)注:M代表边数,N代表顶点数。
求有向图的强连通分量个数(kosaraju算法)

求有向图的强连通分量个数(kosaraju算法)求有向图的强连通分量个数(kosaraju算法)1. 定义连通分量:在⽆向图中,即为连通⼦图。
上图中,总共有四个连通分量。
顶点A、B、C、D构成了⼀个连通分量,顶点E构成了⼀个连通分量,顶点F,G和H,I分别构成了两个连通分量。
强连通分量:有向图中,尽可能多的若⼲顶点组成的⼦图中,这些顶点都是相互可到达的,则这些顶点成为⼀个强连通分量。
上图中有三个强连通分量,分别是a、b、e以及f、g和c、d、h。
2. 连通分量的求解⽅法对于⼀个⽆向图的连通分量,从连通分量的任意⼀个顶点开始,进⾏⼀次DFS,⼀定能遍历这个连通分量的所有顶点。
所以,整个图的连通分量数应该等价于遍历整个图进⾏了⼏次(最外层的)DFS。
⼀次DFS中遍历的所有顶点属于同⼀个连通分量。
下⾯我们将介绍有向图的强连通分量的求解⽅法。
3. Kosaraju算法的基本原理我们⽤⼀个最简单的例⼦讲解Kosaraju算法显然上图中有两个强连通分量,即强连通分量A和强连通分量B,分别由顶点A0-A1-A2和顶点B3-B4-B5构成。
每个连通分量中有若⼲个可以相互访问的顶点(这⾥都是3个),强连通分量与强连通分量之间不会形成环,否则应该将这些连通分量看成⼀个整体,即看成同⼀个强连通分量。
我们现在试想能否按照⽆向图中求连通分量的思路求解有向图的强连通分量。
我们假设,DFS从强连通分量B的任意⼀个顶点开始,那么恰好遍历整个图需要2次DFS,和连通分量的数量相等,⽽且每次DFS遍历的顶点恰好属于同⼀个连通分量。
但是,我们若从连通分量A中任意⼀个顶点开始DFS,就不能得到正确的结果,因为此时我们只需要⼀次DFS就访问了所有的顶点。
所以,我们不应该按照顶点编号的⾃然顺序(0,1,2,……)或者任意其它顺序进⾏DFS,⽽是应该按照被指向的强连通分量的顶点排在前⾯的顺序进⾏DFS。
上图中由强连通分量A指向了强连通分量B。
强连通分量与模拟链表

强联通分量与模拟链表作者:逸水之寒1.强连通分量强连通分量的定义是:在有向图中,u可以到达v,但是v不一定能到达u,如果u,v 到达,则他们就属于一个强连通分量。
求强连通分量最长用的方法就是Kosaraju算法,比较容易理解而且效率很高,本文对强连通分量的求法均采用Kosaraju算法。
其主要思想:首先对原图G进行深搜形成森林(树),然后选择一棵树进行第二次深搜,注意第一次是要判断节点A能不能通向节点B,而第二次要判断的是节点B能不能通向A,能遍历到的就是一个强连通分量。
(附录给出伪代码)Kosaraju算法如果采用了合适的数据结构,它的时间复杂度是O(n)的。
相关题目有很多,例如USACO 5.3.3,2009NOIP Senior No.3。
下面将以USACO 5.3.3 schlnet 举例说明。
Preblem 1. Network of Schools (USACO 5.3.3 schlnet\IOI96 No.3)A number of schools are connected to a computer network. Agreements have been developed among those schools: each school maintains a list of schools to which it distributes software (the "receiving schools"). Note that ifB is in the distribution list of school A, then A does not necessarily appear in the list of school B.You are to write a program that computes the minimal number of schools that must receive a copy of the new software in order for the software to reach all schools in the network according to the agreement (Subtask A). As a further task, we want to ensure that by sending the copy of new software to an arbitrary school, this software will reach all schools in the network. To achieve this goal we may have to extend the lists of receivers by new members. Compute the minimal number of extensions that have to be made so that whatever school we send the new software to, it will reach all other schools (Subtask B). One extension means introducing one new member into the list of receivers of one school.INPUT FORMATThe first line of the input file contains an integer N: the number of schools in the network (2<=N<=100). The schools are identified by the first N positive integers. Each of the next N lines describes a list of receivers. The line i+1 contains the identifiers of the receivers of school i. Each list ends with a 0. An empty list contains a 0 alone in the line.SAMPLE INPUT (file schlnet.in)52 43 04 5 01 0OUTPUT FORMATYour program should write two lines to the output file. The first line should contain one positive integer: the solution of subtask A. The second line should contain the solution of subtask B.SAMPLE OUTPUT (file schlnet.out)12分析:本题需要将强连通分量进行缩点,具体做法可以先求出所有的强连通分量,然后重新建立图,将一个强连通分量用一个点在新图中表示出来。
强连通分量个数的最小值
强连通分量个数的最小值1. 引言在图论中,强连通分量是指图中的一组顶点,其中任意两个顶点都存在一条有向路径。
强连通分量个数的最小值是指在一个有向图中,最少需要将多少个顶点组成一个强连通分量。
本文将介绍强连通分量的概念、计算方法以及如何求解强连通分量个数的最小值。
2. 强连通分量的定义在有向图中,如果从顶点A到顶点B存在一条有向路径,同时从顶点B到顶点A也存在一条有向路径,则称顶点A和顶点B是强连通的。
如果一个有向图中的每个顶点都与其他所有顶点强连通,则该有向图被称为强连通图。
而强连通分量则是指有向图中的一组顶点,其中任意两个顶点都是强连通的,且不与其他顶点强连通。
3. 强连通分量的计算方法为了计算一个有向图的强连通分量,可以使用强连通分量算法,其中最常用的是Tarjan算法和Kosaraju算法。
3.1 Tarjan算法Tarjan算法是一种深度优先搜索算法,用于寻找有向图的强连通分量。
算法的基本思想是通过DFS遍历图中的每个顶点,并记录每个顶点的遍历次序和能够到达的最小顶点次序。
通过这些信息,可以判断顶点是否属于同一个强连通分量。
具体步骤如下:1.初始化一个空栈和一个空的遍历次序数组。
2.对于每个未遍历的顶点,进行深度优先搜索。
3.搜索过程中,记录每个顶点的遍历次序和能够到达的最小顶点次序,并将顶点加入栈中。
4.当搜索完成后,根据遍历次序和能够到达的最小顶点次序,可以确定每个顶点所属的强连通分量。
3.2 Kosaraju算法Kosaraju算法是另一种用于计算有向图强连通分量的算法。
算法的基本思想是通过两次深度优先搜索来确定强连通分量。
具体步骤如下:1.对原始图进行一次深度优先搜索,记录顶点的遍历次序。
2.对原始图的转置图(即将所有边的方向反转)进行一次深度优先搜索,按照遍历次序对顶点进行访问。
3.访问过程中,可以确定每个顶点所属的强连通分量。
4. 求解强连通分量个数的最小值要求解强连通分量个数的最小值,可以使用以下方法:1.使用Tarjan算法或Kosaraju算法计算有向图的强连通分量。
强连通分量是无向图的极大强连通子图
强连通分量是无向图的极大强连通子图
进行描述
强连通分量是指连接图中任意两个顶点之间均存在有向路径的最大连通子图,也就是说只要我们从图中的任何顶点出发,都无论是正方向还是逆方向,都可以到达图中的任何其余的顶点。
它是一种比较有代表性的子图模式,主要具有以下4个特点:
1.强连通分量是一个强连通的极大子图,它体现着图的最强的连通性;
2. 强连通分量的子图之间不再相互连接;
3. 强连通分量子图与子图之间均不相互连接;
4. 强连通分量子图中所有顶点均相互连接。
强连通分量最主要的应用就是拓扑排序,它是图论中一种重要的算法,主要用于完成有向图的拓扑排序。
在完成拓扑排序之前我们可以先找出图中的强连通分量,有了强连通分量的信息之后就可以处理的更加细致,从而节省大量时间。
因此,在实际应用中,我们要深入思考如何更好的利用强连通分量,对之后的处理来说是一种重要的算法工具。
图论_连通_连通分量
图论_连通_连通分量 强连通图 : 强连通分量就是本⾝ 有向图 ---> ⾮强连通图 : 多个强连通分量图---> 连通图 : 连通分量就是本⾝ ⽆向图 ---> ⾮连通图 : 多个连通分量路径 : 顾名思义.路径长度 : 路径上边的数量.路径 : 顾名思义.路径长度 : 路径上边的数量.连通 : ⽆向图顶点A可以到顶点B,则称A,B连通.强连通 : 有向图中,两个顶点间⾄少存在⼀条互相可达路径,则两个顶点强连通连通图 : 图中任意两点都连通的图.强连通图 : 有向图的任意两点都强连通.连通分量 : ⽆向图的极⼤连通⼦图称为连通分量.连通图只有⼀个连通分量,即⾃⾝强连通分量: 强连通图有向图的极⼤强连通⼦图.强连通图的强连通分量只有⼀个,即强连通图本⾝.基图 : 将有向图的所有边替换成⽆向边形成的图.弱连通图 : 基图是连通图的有向图.(即,连通的有向图)求图的连通分量的⽬的,是为了确定从图中的⼀个顶点是否能到达图中的另⼀个顶点,也就是说,图中任意两个顶点之间是否有路径可达。
求强连通分量有多种算法.我⽤的Tarjan算法. 复杂度O(V+E)这两个博客写得不错:https:///reddest/p/5932153.htmlhttps:///shadowland/p/5872257.htmlint dfn[16]; // 时间戳int dfn_num = 0; // 时间int low[16]; // 节点u所能访问到的最⼩时间戳int inSt[16]; // 节点u是否在栈中.int st[16];int top = 0;// 我们维护的信息.int col[16]; // 给节点染⾊, 同⼀个连通块的节点应该是同⼀个颜⾊的.int col_num = 0; // 颜⾊值.int size[16]; // 每个颜⾊值所拥有的块数./*第⼀步: 访问当前节点的所有⼦节点: ⼦节点有三种第⼀种: 未访问过的, 我们对它进⾏访问, 同时设置它的时间戳dfn[u]和low[u]为++ndfn_num,以及进栈.第⼆种: 访问过的,并且在栈中,我们直接更新我们当前节点的low[] --> 注意应该⽤low[u] 和 dfn[v]⽐较.第三种: 访问过的,并且不在栈中的, 我们直接跳过.因为这个时候,所以它已经染⾊了,属于⼀个连通块了.第⼆步: 如果dfn[u] == low[u] 说明已经找到⼀个连通块了.这时候我们要将栈顶元素弹出,直到当前节点. 记得也要修改inSt, 同时维护我们需要的信息.*/void Tarjan(int u) {int v, i;dfn[u] = low[u] = ++dfn_num; //添加时间戳.st[++top] = u; // 进栈inSt[u] = true; // 标⽰在栈for (i=head[u]; i; i=edge[i].lst) {v = edge[i].to;if (!dfn[v]) {Tarjan(v);low[u] = min(low[u], low[v]);} else if (inSt[v]) {low[u] = min(low[u], dfn[v]);}}if (dfn[u] == low[u]) {col_num++;do {inSt[st[top]] = false;col[st[top]] = col_num;size[col_num]++;} while (st[top--] != u);}}View Code加上2个板⼦题./problem/1332/题⽬很简单: 要你求出最⼤的强连通块,如果有多个则输出字典序最⼩的⼀个.#include <cstdio>#include <cstring>#include <algorithm>using namespace std;const int maxn = 5e4+500;struct Edge {int lst;int to;}edge[maxn<<1];int head[maxn];int qsz = 1;inline void add(int u, int v) {edge[qsz].lst = head[u];edge[qsz].to = v;head[u] = qsz++;}int dfn[maxn]; // 时间戳int dfn_num = 0; // 时间int low[maxn]; // 节点u所能访问到的最⼩时间戳int inSt[maxn]; // 节点u是否在栈中.int st[maxn];int top = 0;// 我们维护的信息.int col[maxn]; // 给节点染⾊, 同⼀个连通块的节点应该是同⼀个颜⾊的.int col_num = 0; // 颜⾊值.int size[maxn]; // 每个颜⾊值所拥有的块数.int id[maxn];void Tarjan(int u) {int v, i;dfn[u] = low[u] = ++dfn_num; //添加时间戳.st[++top] = u; // 进栈inSt[u] = true; // 标⽰在栈for (i=head[u]; i; i=edge[i].lst) {v = edge[i].to;if (!dfn[v]) {Tarjan(v);low[u] = min(low[u], low[v]);} else if (inSt[v]) {low[u] = min(low[u], dfn[v]);}}if (dfn[u] == low[u]) {col_num++;id[col_num] = u;do {inSt[st[top]] = false;col[st[top]] = col_num;size[col_num]++;id[col_num] = min(id[col_num], st[top]);} while (st[top--] != u);}}int main(){memset(id, 0x3f, sizeof(id));int n, i, u, v, m, t;scanf("%d%d", &n, &m);for (i=1; i<=m; ++i) {scanf("%d%d%d", &u, &v, &t);add(u, v);if (t==2) add(v, u);}for (i=1; i<=n; ++i)if (!dfn[i]) Tarjan(i);int mm = 0, tcol = -1;for (i=1; i<=col_num; ++i)if (mm < size[i]) {mm = size[i];tcol = i;} else if (m == size[i]) {if (id[tcol] > id[i])tcol = i;}// printf("%d \n", tcol);printf("%d\n", mm);for (i=1; i<=n; ++i)if (col[i] == tcol) printf("%d ", i);printf("\n");return0;}View Codehttps:///problem/HYSBZ-1051题⽬: 求出所有⽜都欢迎的⽜的个数. 我们可以把所有连通块求出,然后把⼀个连通块看成⼀个点,即缩点. 然后找到出度为零的点(连通块), 如果有且只有⼀个,那么连通块的点数就是答案,否则答案为零.#include <cstdio>#include <algorithm>using namespace std;struct Edge {int lst;int to;}edge[50500];int head[10100];int qsz = 1;inline void add(int u, int v) {edge[qsz].lst = head[u];edge[qsz].to = v;head[u] = qsz++;}int dfn[10100]; // 时间戳int dfn_num = 0; // 时间int low[10100]; // 节点u所能访问到的最⼩时间戳int inSt[10100]; // 节点u是否在栈中.int st[10100];int top = 0;// 我们维护的信息.int col[10100]; // 给节点染⾊, 同⼀个连通块的节点应该是同⼀个颜⾊的.int col_num = 0; // 颜⾊值.int size[10100]; // 每个颜⾊值所拥有的块数./*第⼀步: 访问当前节点的所有⼦节点: ⼦节点有三种第⼀种: 未访问过的, 我们对它进⾏访问, 同时设置它的时间戳dfn[u]和low[u]为++ndfn_num,以及进栈.第⼆种: 访问过的,并且在栈中,我们直接更新我们当前节点的low[] --> 注意应该⽤low[u] 和 dfn[v]⽐较. 第三种: 访问过的,并且不在栈中的, 我们直接跳过.因为这个时候,所以它已经染⾊了,属于⼀个连通块了. 第⼆步: 如果dfn[u] == low[u] 说明已经找到⼀个连通块了.这时候我们要将栈顶元素弹出,直到当前节点. 记得也要修改inSt, 同时维护我们需要的信息.*/void Tarjan(int u) {int v, i;dfn[u] = low[u] = ++dfn_num; //添加时间戳.st[++top] = u; // 进栈inSt[u] = true; // 标⽰在栈for (i=head[u]; i; i=edge[i].lst) {v = edge[i].to;if (!dfn[v]) {Tarjan(v);low[u] = min(low[u], low[v]);} else if (inSt[v]) {low[u] = min(low[u], dfn[v]);}}if (dfn[u] == low[u]) {col_num++;do {inSt[st[top]] = false;col[st[top]] = col_num;size[col_num]++;} while (st[top--] != u);}}bool ou[10010];int main(){// freopen("E:\\input.txt", "r", stdin);int n, i, j, u, v, m;scanf("%d%d", &n, &m);for (i=1; i<=m; ++i) {scanf("%d%d", &u, &v);add(u, v);}for (i=1; i<=n; ++i)if (!dfn[i])Tarjan(i);// 缩点操作int cnt = 0, res = 0;for (i=1; i<=n; ++i) {if (ou[col[i]]) continue;for (j=head[i]; j; j=edge[j].lst) {v = edge[j].to;if (col[i] != col[v]) {ou[col[i]] = true;break;}}}for (i=1; i<=col_num; ++i) {if (!ou[i]) {res = size[i];cnt++;}if (cnt > 1) {res = 0;break;}}printf("%d\n", res);return0;}View Code。
强连通分量
强连通分量【引言】本文讲述了求强连通分量的T arjan算法的思想以及一般过程,鉴于T arjan算法比较抽象,很多人明白怎么做但不理解为什么,所以本文以作者对T arjan算法的理解为主,供读者参考。
【正文】一、强连通分量的概念及性质。
概念:对于一个有向图G,存在点集P使得P中任意两点可以互相到达,则称P为一个强连通分量。
性质:如果对于一个点v,在v可以到达的点中,可以回到v的点和v一定属于同一个强连通分量;不可以回到v的点和v一定不属于一个强连通分量。
二、T arjan思想1.初步思想:利用搜索算法找到点v可以到达的所有点,再判断这些点中哪些可以回到v,并对符合条件的点进行染色,染成同色的点组成一个强连通分量。
2.深搜性质的利用:首先对点来做一些定义:白色点:表示该点还没有被访问过。
灰色点:表示正在处理该点发出的边,还没处理完。
黑色点:表示该点发出的所有边都处理完了。
深搜序:表示所有点由白变灰的顺序。
附属点:某点v从刚刚变成灰色到刚刚变成黑色这段时间内访问并处理过的所有点(不包括那些在v之前变灰或变黑的点,那些点在这段时间内只访问但没处理)性质1:从开始处理点v到处理完点v,所有的附属点都从白变黑。
性质2:在开始处理点v之前的那个时刻,所有的灰色点都可以到达点v,称这些灰色点为祖先点,并且这些祖先点构成一条链。
性质3:对于性质2所述的那些灰色点,在深搜序中靠前的点一定可以到达靠后的点。
这些性质有助于理解后面的思想。
3.引入进一步思想:首先是想法:对于当前点v,和它在同一个强连通分量里的点一定可以到达它。
这些点可以分为两部分:(1)性质2中那些灰色的点(祖先点) (2)其他可以到达v的点对于(2)那部分点,又可以分为两部分:和v在同一个强连通分量里的:这部分点将会变成v的附属点,所以不必考虑。
不和v在同一个强连通分量里的:这部分点显然不在考虑范畴内,但一会儿要用到。
所以,我们只需要考虑性质2中的祖先点!!!也就是说,v的附属点中,可以直接或间接到达那些祖先点的点,和v一定属于同一个强连通分量(通俗点说,就是v可以到它,它可以到 v的祖先,v的祖先又可以到v)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
强连通分量的定义
强连通分量是图论中的一个概念,指的是在有向图中,若任意两个顶点都存在一条有向路径,则这个有向图就是强连通的。
而强连通分量则指的是有向图中的极大强连通子图,即在该子图中任意两个顶点都是强连通的,并且该子图不能再加入其他的顶点或边使其仍然保持强连通。
在实际应用中,强连通分量有着广泛的应用。
比如在电路设计中,可以将电路看作一个有向图,每个元件看作一个顶点,元件之间的电线则看作一条有向边。
那么在这个电路中,如果存在一个强连通分量,则说明这些元件可以构成一个独立的电路模块,可以方便地进行测试和维护。
此外,在社交网络分析、路网规划等领域,强连通分量也有着重要的应用。
在实际应用中,我们可以通过深度优先搜索(DFS)或者Tarjan算法来求解一个有向图的强连通分量。
具体来说,DFS 算法可以通过遍历有向图来寻找所有的强连通分量;而Tarjan 算法则是一种更高效的算法,可以在O(V+E)的时间复杂度内求解一个有向图的所有强连通分量。
总之,强连通分量是图论中一个重要的概念,在实际应用中有着广泛的应用。
通过深入学习和理解这个概念,我们可以更好地应用它来解决实际问题。
