求强连通分量的Kosaraju算法和Tarjan算法的比较 by ljq
复杂网络中的社团发现算法对比和性能评估

复杂网络中的社团发现算法对比和性能评估在复杂网络的研究中,社团发现算法对于揭示网络中隐含的组织结构和功能模块具有重要意义。
社团发现算法目的是将网络的节点划分为不同的社团或群集,使得同一个社团内的节点之间具有紧密的连接,而不同社团之间的连接则相对较弱。
本文将对几种常见的复杂网络社团发现算法进行对比和性能评估。
1. 强连通性算法强连通性算法主要关注网络中的强连通分量,即其中的节点之间互相可达。
常见的强连通性算法有Tarjan算法和Kosaraju算法。
这些算法适用于有向图和无向图,并且能够有效地识别网络中的全部强连通分量。
2. 谱聚类算法谱聚类算法是一种基于图谱理论的社团发现算法,通过将网络表示为拉普拉斯矩阵,使用特征值分解或近似方法提取主要特征向量,从而实现节点的划分。
常见的谱聚类算法包括拉普拉斯特征映射(LE)和归一化谱聚类(Ncut)。
谱聚类算法在复杂网络中表现出色,尤其在分割不规则形状的社团时效果较好。
3. 模块度优化算法模块度优化算法通过最大化网络的模块度指标,寻找网络中最优的社团划分。
常见的模块度优化算法有GN算法(Girvan-Newman)和Louvain算法。
这些算法通过迭代删除网络中的边或合并社团,以最大化模块度指标。
模块度优化算法具有较高的计算效率和准确性,广泛应用于实际网络的社团发现中。
4. 层次聚类算法层次聚类算法通过基于节点之间的相似度或距离构建层次化的社团结构。
常见的层次聚类算法有分裂和合并(Spectral Clustering,SC)和非重叠连通(Non-overlapping Connector,NC)算法。
这些算法通过自顶向下或自底向上的方式逐步划分或合并社团。
层次聚类算法能够全面地刻画网络中的社团结构,但在大规模网络上的计算复杂度较高。
5. 基于物理模型的算法基于物理模型的算法通过模拟物理过程来发现网络中的社团结构。
常见的基于物理模型的社团发现算法有模拟退火算法(Simulated Annealing,SA)和蚁群算法(Ant Colony Algorithm,ACA)。
离散数学试题及答案

离散数学试题及答案一、选择题1. 在集合论中,下列哪个选项表示两个集合A和B的并集?A. A ∩ BB. A ∪ BC. A - BD. A × B答案:B2. 命题逻辑中,下列哪个符号表示逻辑非?A. ∧B. ∨C. ¬D. →答案:C3. 在有向图中,如果存在一条从顶点u到顶点v的路径,那么称顶点v为顶点u的:A. 祖先B. 后代C. 邻居D. 连接点答案:B二、填空题1. 一个命题函数P(x)表示为“x是偶数”,那么其否定形式为________。
答案:x是奇数2. 在关系R上,如果对于所有的a和b,如果(a, b)∈R且(b, a)∈R,则称R为________。
答案:自反的三、简答题1. 简述什么是等价关系,并给出其三个基本性质。
答案:等价关系是一种特殊的二元关系,它满足自反性、对称性和传递性。
自反性指每个元素都与自身相关;对称性指如果a与b相关,则b也与a相关;传递性指如果a与b相关,b与c相关,则a与c也相关。
2. 解释什么是图的连通分量,并给出如何判断一个图是否是连通图。
答案:连通分量是指图中最大的连通子图,即图中任意两个顶点之间都存在路径。
判断一个图是否是连通图,可以通过深度优先搜索或广度优先搜索算法遍历整个图,如果所有顶点都被访问,则图是连通的。
四、计算题1. 给定命题公式P:((p → q) ∧ (r → ¬p)) → (q ∨ ¬r),证明P是一个重言式。
答案:通过使用命题逻辑的等价规则和真值表,可以证明P在所有可能的p, q, r的真值组合下都为真,因此P是一个重言式。
2. 给定一个有向图G,顶点集合V(G)={1, 2, 3, 4},边集合E(G)={(1, 2), (2, 3), (3, 4), (4, 1), (2, 4)}。
找出所有强连通分量。
答案:通过Kosaraju算法或Tarjan算法,可以找到图G的强连通分量,结果为{1, 4}和{2, 3}。
求强连通分量的几种算法的实现与分析

求强连通分量的几种算法的实现与分析作者:陈燕,江克勤来源:《电脑知识与技术》2011年第09期摘要:有向图的强连通性是图论中的经典问题,有着很多重要的应用。
该文给出了求强连通分量的Kosaraju、Tarjan和Gabow三个算法的具体实现,并对算法的效率进行了分析。
关键词:强连通分量;深度优先搜索;Kosaraju算法;Tarjan算法;Gabow算法中图分类号:TP312文献标识码:A文章编号:1009-3044(2011)09-2140-03The Implementation and Analysis of Several Algorithms About Strongly Connected Components CHEN Yan1, JIANG Ke-qin2(1.Nanjing Health Inspection Bureau, Nanjing 210003, China; 2.School of Computer and Information, Anqing Teachers College, Anqing 246011, China)Abstract: Digraph of strong connectivity is the classic problems in graph theory, which arises in many important applications. In this paper, the detailed implementation of Kosaraju, Tarjan and Gabow algorithms is discussed for solving strongly connected components, and the efficiency of three algorithms is analyzed.Key words: strongly connected components; depth first search; Kosaraju; Tarjan; Gabow图的连通性是图论中的经典问题,所谓连通性,直观地讲,就是“连成一片”。
Kosaraju算法

求有向图的强连通分量的经典算法——Kosaraju算法一、Kosaraju算法步骤:Step1、对有向图G做dfs(深度优先遍历),记录每个结点结束访问的时间Step2、将图G逆置,即将G中所有弧反向。
Step3、按Step1中记录的结点结束访问时间从大到小对逆置后的图做dfs Step4、得到的遍历森林中每棵树对应一个强连通分量。
相关概念:在dfs(bfs)算法中,一个结点的开始访问时间指的是遍历时首次遇到该结点的时间,而该结点的结束访问时间则指的是将其所有邻接结点均访问完的时间。
二、Kosaraju算法求解过程实例下面结合实例说明Kosaraju算法的基本策略。
图1给出了一个有向图G。
图1 有向图GStep1:假设从DFS在遍历时按照字母顺序进行,根据Kosaraju算法,在步骤1中我们得到的遍历顺序可以表达为[A,[C,[B,[D,D],B],C],A][E,[F,[G,[H,H],G],F],E]在遍历序列中每一个结点出现了两次,其中第一次出现的时间为该结点的开始访问时间,第二次出现的时间为该结点的结束访问时间。
Step2:根据算法第2步,将图G逆置,得到对应的反向图G’如图2所示。
Step3:根据步骤1得到的遍历序列,按照结点结束访问时间递减排序后的结果为EFGHACBD下面,按照该结点序列顺序对逆置图G ’所深度优先遍历,得到的深度优先遍历森林如图3所示。
森林中共有4棵树,其中(a)和(d)只有一个结点,这里认为单结点也是一个强联通分量(在实际应用中可以根据实际需要将这种情况过滤掉)。
三、算法讨论问题1:以上图为例,第一遍搜索得到以A 为根的子序列(设为S1)和以E 为根的子树序列(设为S2),图反向后,再从E 开始搜索,能搜到的元素肯定不会包含S1的元素,为什么?答:因为S1中的点都不能到达E ,而第二遍搜索就是看哪些点能到达E ,所以搜不到S1中的点。
问题2:图反向后对A 进行深搜,尽管E 能到达A ,为什么搜不到E ?因为第一遍深搜时,A 不能达到E ,所以E 肯定位于A 的右边,而第二遍深搜是按照结束时间进行搜索的,在搜索A 之前,已经搜完E ,对E 设置了已经遍历标志,所以不会把E 并入A 的强联通分量。
强连通算法--Tarjan个人理解+详解

强连通算法--Tarjan个⼈理解+详解⾸先我们引⼊定义:1、有向图G中,以顶点v为起点的弧的数⽬称为v的出度,记做deg+(v);以顶点v为终点的弧的数⽬称为v的⼊度,记做deg-(v)。
2、如果在有向图G中,有⼀条<u,v>有向道路,则v称为u可达的,或者说,从u可达v。
3、如果有向图G的任意两个顶点都互相可达,则称图 G是强连通图,如果有向图G存在两顶点u和v使得u不能到v,或者v不能到u,则称图G 是强⾮连通图。
4、如果有向图G不是强连通图,他的⼦图G2是强连通图,点v属于G2,任意包含v的强连通⼦图也是G2的⼦图,则乘G2是有向图G的极⼤强连通⼦图,也称强连通分量。
5、什么是强连通?强连通其实就是指图中有两点u,v。
使得能够找到有向路径从u到v并且也能够找到有向路径从v到u,则称u,v是强连通的。
然后我们理解定义:既然我们现在已经了解了什么是强连通,和什么是强连通分量,可能⼤家对于定义还是理解的不透彻,我们不妨引⼊⼀个图加强⼤家对强连通分量和强连通的理解:标注棕⾊线条框框的三个部分就分别是⼀个强连通分量,也就是说,这个图中的强连通分量有3个。
其中我们分析最左边三个点的这部分:其中1能够到达0,0也能够通过经过2的路径到达1.1和0就是强连通的。
其中1能够通过0到达2,2也能够到达1,那么1和2就是强连通的。
.........同理,我们能够看得出来这⼀部分确实是强连通分量,也就是说,强连通分量⾥边的任意两个点,都是互相可达的。
那么如何求强连通分量的个数呢?另外强连通算法能够实现什么⼀些基本操作呢?我们继续详解、接着我们开始接触算法,讨论如何⽤Tarjan算法求强连通分量个数:Tarjan算法,是⼀个基于Dfs的算法(如果⼤家还不知道什么是Dfs,⾃⾏百度学习),假设我们要先从0号节点开始Dfs,我们发现⼀次Dfs 我萌就能遍历整个图(树),⽽且我们发现,在Dfs的过程中,我们深搜到了其他强连通分量中,那么俺们Dfs之后如何判断他喵的哪个和那些节点属于⼀个强连通分量呢?我们⾸先引⼊两个数组:①dfn【】②low【】第⼀个数组dfn我们⽤来标记当前节点在深搜过程中是第⼏个遍历到的点。
求强连通分量的Kosaraju算法和Tarjan算法的比较 by ljq
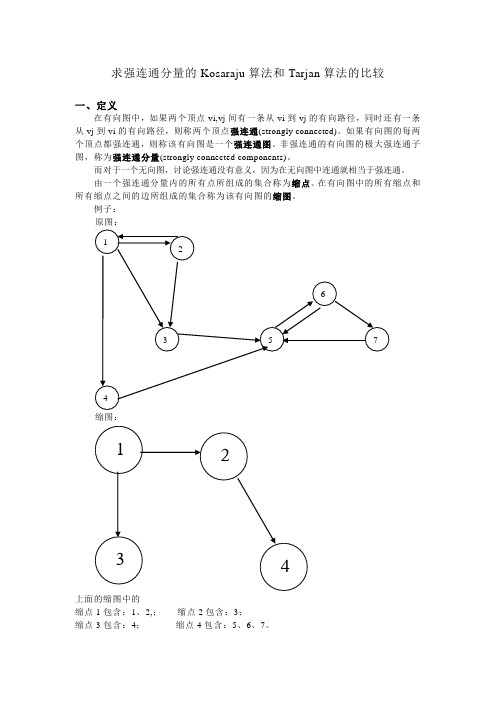
求强连通分量的Kosaraju算法和Tarjan算法的比较一、定义在有向图中,如果两个顶点vi,vj间有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。
如果有向图的每两个顶点都强连通,则称该有向图是一个强连通图。
非强连通的有向图的极大强连通子图,称为强连通分量(strongly connected components)。
而对于一个无向图,讨论强连通没有意义,因为在无向图中连通就相当于强连通。
由一个强连通分量内的所有点所组成的集合称为缩点。
在有向图中的所有缩点和所有缩点之间的边所组成的集合称为该有向图的缩图。
例子:原图:缩图:上面的缩图中的缩点1包含:1、2,;缩点2包含:3;缩点3包含:4;缩点4包含:5、6、7。
二、求强连通分量的作用把有向图中具有相同性质的点找出来,形成一个集合(缩点),建立缩图,能够方便地进行其它操作,而且时间效率会大大地提高,原先对多个点的操作可以简化为对它们所属的缩点的操作。
求强连通分量常常用于求拓扑排序之前,因为原图往往有环,无法进行拓扑排序,而求强连通分量后所建立的缩图则是有向无环图,方便进行拓扑排序。
三、Kosaraju算法时间复杂度:O(M+N)注:M代表边数,N代表顶点数。
所需的数据结构:原图、反向图(若在原图中存在vi到vj的有向边,在反向图中就变成为vj到vi的有向边)、标记数组(标记是否遍历过)、一个栈(或记录顶点离开时间的数组)。
算法描叙:步骤1:对原图进行深度优先遍历,记录每个顶点的离开时间。
步骤2:选择具有最晚离开时间的顶点,对反向图进行深度优先遍历,并标记能够遍历到的顶点,这些顶点构成一个强连通分量。
步骤3:如果还有顶点没有遍历过,则继续进行步骤2,否则算法结束。
hdu1269(Kosaraju算法)代码:#include<cstdio>#include<cstdlib>const int M=10005;struct node{int vex;node *next;};node *edge1[M],*edge2[M];bool mark1[M],mark2[M];int T[M],Tcnt,Bcnt;void DFS1(int x)mark1[x]=true;node *i;for(i=edge1[x];i!=NULL;i=i->next) {if(!mark1[i->vex]){DFS1(i->vex);}}T[Tcnt]=x;Tcnt++;}void DFS2(int x){mark2[x]=true;node *i;for(i=edge2[x];i!=NULL;i=i->next) {if(!mark2[i->vex]){DFS2(i->vex);}}}int main(){int n,m;while(scanf("%d%d",&n,&m)){if(n==0&&m==0){break;}int i,a,b;for(i=1;i<=n;i++){mark1[i]=mark2[i]=false;edge1[i]=NULL;edge2[i]=NULL;}node *t;while(m--){scanf("%d%d",&a,&b);t=(node *)malloc(sizeof(node));t->vex=b;t->next=edge1[a];edge1[a]=t;t=(node *)malloc(sizeof(node));t->vex=a;t->next=edge2[b];edge2[b]=t;}Tcnt=0;for(i=1;i<=n;i++){if(!mark1[i]){DFS1(i);}}Bcnt=0;//Bcnt用于记录强连通分量的个数for(i=Tcnt-1;i>=0;i--){if(!mark2[T[i]]){DFS2(T[i]);Bcnt++;}}if(Bcnt==1)//如果强连通分量的个数为1则说明该图是强连通图{printf("Yes\n");}else{printf("No\n");}}return 0;}四、Tarjan算法时间复杂度:O(M+N)注:M代表边数,N代表顶点数。
求有向图的强连通分量个数(kosaraju算法)

求有向图的强连通分量个数(kosaraju算法)求有向图的强连通分量个数(kosaraju算法)1. 定义连通分量:在⽆向图中,即为连通⼦图。
上图中,总共有四个连通分量。
顶点A、B、C、D构成了⼀个连通分量,顶点E构成了⼀个连通分量,顶点F,G和H,I分别构成了两个连通分量。
强连通分量:有向图中,尽可能多的若⼲顶点组成的⼦图中,这些顶点都是相互可到达的,则这些顶点成为⼀个强连通分量。
上图中有三个强连通分量,分别是a、b、e以及f、g和c、d、h。
2. 连通分量的求解⽅法对于⼀个⽆向图的连通分量,从连通分量的任意⼀个顶点开始,进⾏⼀次DFS,⼀定能遍历这个连通分量的所有顶点。
所以,整个图的连通分量数应该等价于遍历整个图进⾏了⼏次(最外层的)DFS。
⼀次DFS中遍历的所有顶点属于同⼀个连通分量。
下⾯我们将介绍有向图的强连通分量的求解⽅法。
3. Kosaraju算法的基本原理我们⽤⼀个最简单的例⼦讲解Kosaraju算法显然上图中有两个强连通分量,即强连通分量A和强连通分量B,分别由顶点A0-A1-A2和顶点B3-B4-B5构成。
每个连通分量中有若⼲个可以相互访问的顶点(这⾥都是3个),强连通分量与强连通分量之间不会形成环,否则应该将这些连通分量看成⼀个整体,即看成同⼀个强连通分量。
我们现在试想能否按照⽆向图中求连通分量的思路求解有向图的强连通分量。
我们假设,DFS从强连通分量B的任意⼀个顶点开始,那么恰好遍历整个图需要2次DFS,和连通分量的数量相等,⽽且每次DFS遍历的顶点恰好属于同⼀个连通分量。
但是,我们若从连通分量A中任意⼀个顶点开始DFS,就不能得到正确的结果,因为此时我们只需要⼀次DFS就访问了所有的顶点。
所以,我们不应该按照顶点编号的⾃然顺序(0,1,2,……)或者任意其它顺序进⾏DFS,⽽是应该按照被指向的强连通分量的顶点排在前⾯的顺序进⾏DFS。
上图中由强连通分量A指向了强连通分量B。
求强连通分量
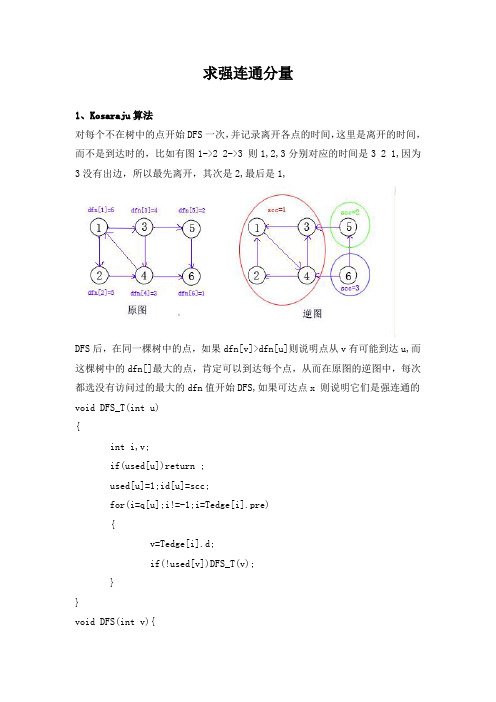
求强连通分量1、Kosaraju算法对每个不在树中的点开始DFS一次,并记录离开各点的时间,这里是离开的时间,而不是到达时的,比如有图1->2 2->3 则1,2,3分别对应的时间是3 2 1,因为3没有出边,所以最先离开,其次是2,最后是1,DFS后,在同一棵树中的点,如果dfn[v]>dfn[u]则说明点从v有可能到达u,而这棵树中的dfn[]最大的点,肯定可以到达每个点,从而在原图的逆图中,每次都选没有访问过的最大的dfn值开始DFS,如果可达点x 则说明它们是强连通的void DFS_T(int u){int i,v;if(used[u])return ;used[u]=1;id[u]=scc;for(i=q[u];i!=-1;i=Tedge[i].pre){v=Tedge[i].d;if(!used[v])DFS_T(v);}}void DFS(int v){int i,u;if(used[v])return ;used[v]=1;for(i=p[v];i!=-1;i=edge[i].pre){u=edge[i].d;if(!used[u])DFS(u);}order[++num]=v;}int Kosaraju(){int i,j,k,v,u;memset(used,0,sizeof(used));num=0;for(i=1;i<=n;++i)if(!used[i])DFS(i);memset(used,0,sizeof(used));memset(id,0,sizeof(id));scc=0;for(i=num;i>=1;--i)if(!used[order[i]])scc++,DFS_T(order[i]);}2、Tarjan算法dfn[v]记录到达点v的时间,跟上面的离开不同,low[v]表示通过它的子结点可以到达的所有点中时间最小值,即low[i]=min(low[i],low[u]),u为v的了孙,初始化时low[v]=dfn[u]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求强连通分量的Kosaraju算法和Tarjan算法的比较一、定义在有向图中,如果两个顶点vi,vj间有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。
如果有向图的每两个顶点都强连通,则称该有向图是一个强连通图。
非强连通的有向图的极大强连通子图,称为强连通分量(strongly connected components)。
而对于一个无向图,讨论强连通没有意义,因为在无向图中连通就相当于强连通。
由一个强连通分量内的所有点所组成的集合称为缩点。
在有向图中的所有缩点和所有缩点之间的边所组成的集合称为该有向图的缩图。
例子:原图:缩图:上面的缩图中的缩点1包含:1、2,;缩点2包含:3;缩点3包含:4;缩点4包含:5、6、7。
二、求强连通分量的作用把有向图中具有相同性质的点找出来,形成一个集合(缩点),建立缩图,能够方便地进行其它操作,而且时间效率会大大地提高,原先对多个点的操作可以简化为对它们所属的缩点的操作。
求强连通分量常常用于求拓扑排序之前,因为原图往往有环,无法进行拓扑排序,而求强连通分量后所建立的缩图则是有向无环图,方便进行拓扑排序。
三、Kosaraju算法时间复杂度:O(M+N)注:M代表边数,N代表顶点数。
所需的数据结构:原图、反向图(若在原图中存在vi到vj的有向边,在反向图中就变成为vj到vi的有向边)、标记数组(标记是否遍历过)、一个栈(或记录顶点离开时间的数组)。
算法描叙:步骤1:对原图进行深度优先遍历,记录每个顶点的离开时间。
步骤2:选择具有最晚离开时间的顶点,对反向图进行深度优先遍历,并标记能够遍历到的顶点,这些顶点构成一个强连通分量。
步骤3:如果还有顶点没有遍历过,则继续进行步骤2,否则算法结束。
hdu1269(Kosaraju算法)代码:#include<cstdio>#include<cstdlib>const int M=10005;struct node{int vex;node *next;};node *edge1[M],*edge2[M];bool mark1[M],mark2[M];int T[M],Tcnt,Bcnt;void DFS1(int x)mark1[x]=true;node *i;for(i=edge1[x];i!=NULL;i=i->next) {if(!mark1[i->vex]){DFS1(i->vex);}}T[Tcnt]=x;Tcnt++;}void DFS2(int x){mark2[x]=true;node *i;for(i=edge2[x];i!=NULL;i=i->next) {if(!mark2[i->vex]){DFS2(i->vex);}}}int main(){int n,m;while(scanf("%d%d",&n,&m)){if(n==0&&m==0){break;}int i,a,b;for(i=1;i<=n;i++){mark1[i]=mark2[i]=false;edge1[i]=NULL;edge2[i]=NULL;}node *t;while(m--){scanf("%d%d",&a,&b);t=(node *)malloc(sizeof(node));t->vex=b;t->next=edge1[a];edge1[a]=t;t=(node *)malloc(sizeof(node));t->vex=a;t->next=edge2[b];edge2[b]=t;}Tcnt=0;for(i=1;i<=n;i++){if(!mark1[i]){DFS1(i);}}Bcnt=0;//Bcnt用于记录强连通分量的个数for(i=Tcnt-1;i>=0;i--){if(!mark2[T[i]]){DFS2(T[i]);Bcnt++;}}if(Bcnt==1)//如果强连通分量的个数为1则说明该图是强连通图{printf("Yes\n");}else{printf("No\n");}}return 0;}四、Tarjan算法时间复杂度:O(M+N)注:M代表边数,N代表顶点数。
所需的数据结构:原图、标记数组(与Kosaraju算法的标记不同,这里的标记数组是标记顶点是否在栈内)、一个栈、dfn数组(记录顶点被遍历的时间)、low数组(记录顶点或顶点的子树能够追溯到的最早的栈中顶点的遍历时间)。
算法描叙:步骤1: 找一个没有被遍历过的顶点v,进行步骤2(v)(遍历时间由1开始累加,若是非连通图,则须重复进行步骤1)。
否则,算法结束。
步骤2(v): 初始化dfn[v]和low[v]的值为当前的遍历时间,并且v进栈;对于v所有的邻接顶点u:(1)如果u没有被遍历过,则进行步骤2(u),同时维护low[v]。
(2)如果u已经被遍历过,但还在栈中(即还不属于任一强连通分量),则维护low[v],否则不做任何操作。
如果有dfn[v]==low[v],则把栈中的顶点弹出(直到把v都弹出为止),这些顶点组成一个强连通分量。
hdu1269(Tarjan算法)代码:#include<cstdio>#include<cstring>#include<cstdlib>const int MAX=10005;struct node{int vex;node *next;};node *g[MAX];bool ins[MAX];int dfn[MAX],low[MAX],s[MAX],sn,belong[MAX],out[MAX]; int cnt,time;void dfs(int i){time++;dfn[i]=low[i]=time;s[sn]=i;sn++;ins[i]=true;int j;node *t;for(t=g[i];t!=NULL;t=t->next){j=t->vex;if(dfn[j]==0)//处理树枝边{dfs(j);if(low[j]<low[i]){low[i]=low[j];}}else if(ins[j]&&dfn[j]<low[i])//处理后向边{low[i]=dfn[j];}}if(dfn[i]==low[i]){cnt++;do{j=s[sn-1];sn--;ins[j]=false;}while(j!=i);}}void tarjan(int n){int i;for(i=1;i<=n;i++){if(dfn[i]==0){dfs(i);}}}int main(){int n,m;while(scanf("%d%d",&n,&m)){if(n==0&&m==0){break;}memset(g+1,NULL,n*sizeof(node *));int a,b;node *t;while(m--){scanf("%d%d",&a,&b);t=(node *)malloc(sizeof(node));t->vex=b;t->next=g[a];g[a]=t;}cnt=0;//cnt用于记录强连通分量的个数time=0;sn=0;memset(ins+1,false,n*sizeof(bool));memset(dfn+1,0,n*sizeof(int));tarjan(n);if(cnt==1)//如果强连通分量的个数为1则说明该图是强连通图{printf("Yes\n");}else{printf("No\n");}}return 0;}五、Kosaraju算法和Tarjan算法比较举例子比较两个算法:Kosaraju算法:原图:建立反向图:对原图进行深度优先遍历后,顶点的离开时间分别为:1离开时间为7,2离开时间为5,3离开时间为4,4离开时间为6,5离开时间为3,6离开时间为2,7离开时间为1。
则按顶点按离开时间从大到小排列的序列为:1、4、2、3、5、6、7,按上述序列对反向图进行深度优先遍历,属于同一次深度优先遍历的顶点则属于同一个强连通分量(即缩点),结果:1、2属于同一个强连通分量,3自己为一个强连通分量,4自己为一个一个强连通分量,5、6、7属于同一个强连通分量。
Tarjan算法:原图:对原图进行深度优先遍历(无须回溯):下面分析整个dfs过程中的ins数组、dfn数组和low数组的变化情况(遍历前先清0):遍历顶点1:遍历顶点3:遍历顶点5:离开顶点5时有dfn[5]==low[5],所以5、6、7组成一个强连通分量:离开顶点3时有dfn[3]==low[3],所以3自己为一个强连通分量:离开顶点2:离开顶点4时有dfn[4]==low[4],所以4自己为一个强连通分量:离开顶点1时有dfn[1]==low[1],所以1、2组成一个强连通分量:结果:1、2属于同一个强连通分量,3自己为一个强连通分量,4自己为一个一个强连通分量,5、6、7属于同一个强连通分量。
两个算法的执行步骤不同,但得出的结果都是一致正确的。
时间复杂度比较:两个算法的时间复杂度都是O(M+N)(M代表边数,N代表顶点数),但是Kosaraju 算法须要进行两次dfs,并且要建立反向图,而Tarjan算法只须就进行一次dfs,在实际的应用中Tarjan算法的时间效率的确比Kosaraju算法要高(网上资料统计出Tarjan算法的时间效率要比Kosaraju算法要高30%左右)。
空间复杂度比较:Tarjan算法虽然比Kosaraju算法多用两个一维数组,但虽然Kosaraju算法比Tarjan算法多浪费建立一个反向图的空间,所以总体来说在空间复杂度上还是Tarjan算法比Kosaraju 算法要占优势。
理解难易程度比较:Kosaraju算法单纯的两次深搜的做法显然比Tarjan算法要容易理解。
代码量比较:两个算法的代码量差距不大。
Kosaraju算法的优势:该算法依次求出的强连通分量已经符合拓扑排序了。
Tarjan算法的优势:该算法相比Kosaraju算法拥有时间和空间上的优势。
使用范围:在稀疏图中差别不明显,而在稠密图中Kosaraju算法建立反向图和两次dfs的操作显然比Tarjan算法的一次dfs要慢的多,所以在稠密图中尽量使用Tarjan算法;而涉及求图的拓扑性质时则选用Kosaraju算法较优。
