梯子的倾斜角度.ppt
合集下载
北师大版九年级数学下册1.1.2从梯子的倾斜程度谈起第二课时教学课件

倾斜角的邻边与斜边比值越小,梯子变陡.
B
求sin∠ACD,cos∠ACD和tan∠ACD. 自学检测1:(8分钟)
∠A的对边 什么是锐角A的正弦与余弦?
sinA= (2019•荆门)如图,在Rt△ABC中,∠ACB=90°.
sinA=
.
④若AC=5,AD=4,则DB= .
斜边
则cosA= .
BC AB
则AB的长为 ,BC的长为 .
sinA=
.
梯子在上升过程中,倾斜角变大,
A
练习:(2019•乐山)如图,已知△ABC的三个顶点均在格点上,则cosA的值为 .
13m 斜边
5m∠A的对边 12m ┌ ∠A的邻边 C
如图:在Rt△ABC中,∠C=900,AC=10,
注意解题格式;
梯子在上升过程中,倾斜角变大, BC=6,sinA= ,则DE= .
5m ∠A的对边
┌ C
12 cosA= 13
.cosB= 5 . 13
小结: ∠A的对边
tanA=
BC
∠A的邻边 AC
∠A的对边
sinA= 斜边
BC AB
A
cosA= ∠A的邻边 AC 斜边 AB
B
斜边5m 4m
∠A的邻边
3m
∠A的对边
┌ C
锐角A的正切,正弦,余弦都叫做∠A的三角函数.
求∠B的各三角函数值.
① sin
B
((BCCD))((AACB))
(AD) (AC)
② sin
A
((ACCD))((ABCB))
(BD) (BC)
A
③若BD=6,CD=8.则cosA= 4 .
5
梯子的倾斜程度与正切

即学即用 如图,梯子AB的倾斜程度与tanA有关吗?
梯子AB越陡,tanA的值越大. tanA的值越大,梯子AB越陡.
B
A
C
初试牛 刀
1、鉴宝专家—是真是假:
(1).如图 ① tan A BC (错).
AC
(2).如图 ② tan A AC (错).
BC
A
(3).如图 ② tan A BC (错).
(4)四人小组合作,观察梯子在下 降变缓过程中,倾斜角,铅直高度与 水平宽度的比发生了什么变化?
在实践中探索新知
(4)梯子在下降变缓过程中, 倾斜角,铅直高度与水平宽度 的比发生了什么变化?
铅 直 高 度
水平宽度
在实践中探索新知
(4)梯子在下降变缓过程中, 倾斜角,铅直高度与水平宽度 的比发生了什么变化?
tan B
(
BC)
(BD )
(CD)
.
A
C
┌ DB
3.在上图中,若BD=6,CD=12.求tanA的值. 1
tanA=
2
1、在初中阶段,正切是在直角三角形中定义 的,∠A是一个锐角。
2、tanA是一个完整的符号,它表示∠A的正切,记号里
习惯省去角的符号“∠”.但∠BAC的正切表示为
tan∠BAC
即∠A的大小确定, 它的对边与
邻边的比值是确定的,与直角
A
C2C2C2CC21 三角形的大小无关。
深入探究:如果改变∠A 的大小, ∠A的对边与邻边的
比值会随之改变吗?
∠A的大小改变, ∠A的对边与邻边的比值随 之改变。
B B1 B2
A
C2
C1
当直角三角形的锐角确定后,它的
初中九年级数学从梯子的倾斜程度谈起(第1课时)

∠A的对边与邻边的比值会
随之改变吗?
A
C2
C1
∠A的大小改变, ∠A的对边与邻边的比值随之改变。
由此你得出什么结论?
当直角三角形的锐角确定后,它的对边与邻边的比
值也随之唯一确定;比值和三角形的大小无关,只
和倾斜角的大小有关。
在Rt△ABC中, 如果 锐角A确定, 那么 ∠A的对边与邻边的比 随之确定,
***************************************** 找课件,来莎莎课件站!
(免费课件,免费教案,免费试卷)
国内著名的免费课件交流平台!
*****************************************
第一章:直角三角形的边角关系
(2) B1C1 和 B2C2 有什么关系?
C1
AC1 AC2
∵∠A=∠A ∠AC1B1=∠AC2B2 ∴Rt△AC1B1∽Rt△AC2B2 B1C1 B2C2 AC1 AC2
B
如果任意改变B2在梯子上的位置呢? 你有什么想法?
B1
∠A的大小确定, ∠A的对边与
邻边的比值不变。
B2
3
如果改变∠A 的大小,
么? 3.什么是坡度?
三、学生自学:老师巡视 (8分钟)
四、自学检测:( 10分钟)
1、
2 、
五、点拨:(10分钟)
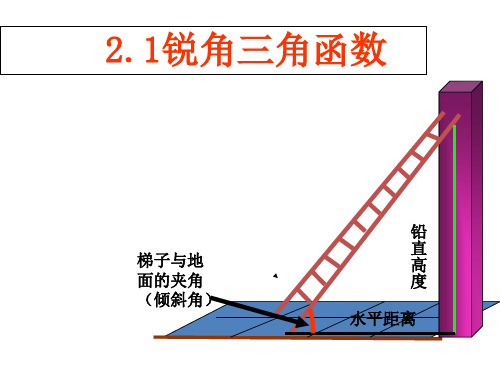
梯子与地面的 夹角(倾斜角)
铅 直 高 度 水平距离
梯子在上升变陡过程中,倾斜角 的大小发生了什么变化?
倾
可以用梯子与地面
斜 的夹角(倾斜角)的大
角 小来判断两架梯子哪个
越 更陡些。
ቤተ መጻሕፍቲ ባይዱ
大
备选:从梯子的倾斜程度谈起

合适的倾斜角度应确保地面接触点之 间的距离足够大,以分散梯子的重量, 提高稳定性。
梯子倾斜角度与使用者的舒适度
梯子倾斜角度过大或过小都可能影响 使用者的舒适度。角度过大会使使用 者感到不稳定,角度过小则可能使使 用者感到疲劳和不适。
使用者应根据实际需要调整梯子的倾 斜角度,以找到一个既安全又舒适的 平衡点。
梯子的防滑设计及其重要性
01
防滑材质
采用防滑材料制作踏板能够有效 增加使用者的安全性,降低滑倒 的风险。
防滑纹路
02
03
防滑把手
在踏板上设计防滑纹路可以增加 脚底与踏板的摩擦力,防止使用 者在上下梯子时滑倒。
在梯子的两端设置防滑把手有助 于增加使用者的稳定性,提供额 外的支撑力。
03 梯子的使用与维护
05 梯子安全事故案例分析
家用梯使用中的安全事故案例
案例一
某家庭主妇在使用家用梯子时不慎摔倒,导致腰部受伤。经调查发现,该梯子倾斜角度过大,稳定性不足。
案例二
一户人家在装修时,工人因梯子滑动而跌落,导致腿部骨折。事后发现,该梯子底部防滑垫损坏,未及时更换。
工业用梯的安全事故案例
案例一
某工厂在使用工业用梯时,一名工人失足从梯子上跌落,造成头部受伤。经调查,该梯子设计不合理 ,安全防护措施不足。
02 梯子的设计因素与安全性 能
梯子的材质与结构对稳定性的影响
材质
金属、木质、塑料等不同材质的梯子 在稳定性方面存在差异。金属梯子通 常最为稳固,木质梯子次之,而塑料 梯子较轻便但可能不太稳固。
结构
直梯、折叠梯、伸缩梯等不同结构的 梯子对稳定性也有影响。直梯通常较 为稳定,折叠梯和伸缩梯在打开或收 起过程中可能存在摇晃的风险。
梯子倾斜角度与使用者的舒适度
梯子倾斜角度过大或过小都可能影响 使用者的舒适度。角度过大会使使用 者感到不稳定,角度过小则可能使使 用者感到疲劳和不适。
使用者应根据实际需要调整梯子的倾 斜角度,以找到一个既安全又舒适的 平衡点。
梯子的防滑设计及其重要性
01
防滑材质
采用防滑材料制作踏板能够有效 增加使用者的安全性,降低滑倒 的风险。
防滑纹路
02
03
防滑把手
在踏板上设计防滑纹路可以增加 脚底与踏板的摩擦力,防止使用 者在上下梯子时滑倒。
在梯子的两端设置防滑把手有助 于增加使用者的稳定性,提供额 外的支撑力。
03 梯子的使用与维护
05 梯子安全事故案例分析
家用梯使用中的安全事故案例
案例一
某家庭主妇在使用家用梯子时不慎摔倒,导致腰部受伤。经调查发现,该梯子倾斜角度过大,稳定性不足。
案例二
一户人家在装修时,工人因梯子滑动而跌落,导致腿部骨折。事后发现,该梯子底部防滑垫损坏,未及时更换。
工业用梯的安全事故案例
案例一
某工厂在使用工业用梯时,一名工人失足从梯子上跌落,造成头部受伤。经调查,该梯子设计不合理 ,安全防护措施不足。
02 梯子的设计因素与安全性 能
梯子的材质与结构对稳定性的影响
材质
金属、木质、塑料等不同材质的梯子 在稳定性方面存在差异。金属梯子通 常最为稳固,木质梯子次之,而塑料 梯子较轻便但可能不太稳固。
结构
直梯、折叠梯、伸缩梯等不同结构的 梯子对稳定性也有影响。直梯通常较 为稳定,折叠梯和伸缩梯在打开或收 起过程中可能存在摇晃的风险。
梯子的安全使用培训课件

保持冷静,迅速撤离危险区域
及时报警或联系救援人员,说明 情况并保持沟通
添加标题
添加标题
添加标题
添加标题
确保自身安全,避免造成二次伤 害
如有伤者,先进行急救处理,等 待救援人员到来
遇到人员受伤或被困时的救援措施
保持冷静,立即拨打急救电话 观察梯子周围环境,确保安全 如有出血,立即止血 如有骨折,不要随意移动伤者
公司
梯子的安全使用培 训课件
单击此处添加副标题
汇报人:
目录
单击添加目录项标题
01
梯子的基本知识
02
梯子的安全使用方法
03
梯子的保养和维护
04
梯子的安全注意事项
05
应急处理和救援措施
06
01
添加章节标题
01
梯子的基本知识
梯子的种类和用途
伸缩梯:可调节高度, 适合不同场合使用
铝合金梯:轻便耐用, 适合户外使用
梯子稳定 性:确保 梯子有足 够的稳定 性,防止 在使用过 程中发生 倾倒或滑 落
01
梯子的安全使用方法
正确放置梯子
选择稳固的地面, 避免在湿滑、松 软或倾斜的地面 上放置梯子
梯子应与地面保 持垂直,不得倾 斜
梯子脚应踩实, 不得悬空
梯子顶部不得超 过最高承重限制, 不得超过梯子长 度的1/4
保持梯子稳定
梯子应放置在坚实、平整的地面上 梯子与地面的夹角应为75度左右 梯子应有防滑措施,如防滑垫或防滑条 梯子应有足够的支撑,避免倾斜或倒塌
避免超载
梯子承载能力: 根据梯子的材质、 结构、长度等因 素确定
超载危害:可能 导致梯子损坏、 倒塌,造成人员 伤亡
避免超载措施: 使用前检查梯子 承载能力,确保 不超过其最大承 载量
山东省九年级鲁教版(五四制)数学上册课件:21锐角三角函数(1)(共13张PPT)
例1下图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
A
ቤተ መጻሕፍቲ ባይዱ
E
4m 甲
乙
┐ 8mα
C甲
B
F
解:甲梯中 梯 tan 4 1 .
82
13 m
β
乙 梯
5m
┌
D
乙梯中 tan 5 5 .
132 52 12
∵ tanα> tanβ ∴甲梯更陡
知识点 3 坡度和坡角
如图,正切也经常用来描述山坡的坡度.例如, 有一山坡在水平方向上每前进100m就升高60m,那 么山坡的坡度i(即tanα)就是:
的值始终不变,等于
BC . AC
正切的定义:
如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边
与邻边的比便随之确定,这个比叫做 ∠A的正切,记作tan A,
A的对边
即tan A= A的邻边
说明:tan A表示锐角A的正切,一般省略“∠”,但 当用三个字母表示角时,不能省略“∠”.如tan ∠ABC.
总结
1、正切的定义:
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的 比便随之确定,这个比叫做 ∠A的正切,记作tan A,
A的对边 即tan A= A的邻边
2、倾斜程度,其本意指倾斜角的大小,一般来说,倾斜角较大 的物体,就说它放得更“陡”.
3、利用物体与地面夹角的正切值来判断物体的倾斜程度,夹角 的正切值越大,则夹角越大,物体放置得越“陡”.
α
β
梯子的顶端到地面的高度与 其底端到墙的水平距离的比 值相同时,梯子就一样陡。
4m
3m
3m
2m
比值大的梯子陡。
知识点 1 正切的定义
从梯子的倾斜程度谈起 (上课用的)

1
1、今天我们学习从梯子的倾斜程度谈起 的第一课时,大家知道梯子是我们常见的 物体,而使用梯子的时候,梯子的倾斜程 度又是至关重要的。
2
2
3
你能比较两个 梯子哪个更陡吗?
我们可以把斜靠在 墙壁上的梯子看成 什么图形呢?当学 生回答是直角三角 形时,老师引入下 一张图片。
4
(1)如图,梯子AB和EF哪个更陡?
对 tanA是一个比值(直角边之比, 是一个比值 3、tanA是一个比值(直角边之比, 注意比的顺 邻 );且tanA﹥ 无单位; 序);且tanA﹥0,无单位;
4、tanA的大小只与∠A的大小有关,而与直角三 tanA的大小只与∠ 的大小有关, 的大小只与 角形的边长无关。 角形的边长无关。 5、角相等,则正切值相等;两锐角的正切值相等, 角相等,则正切值相等;两锐角的正切值相等, 则这两个锐角相等。 则这两个锐角相等。
梯子EF更陡 梯子 更陡
A E 3.5m F 1.3m D
4m B 1.5m C
在实例3中,引导学生仿照前面两个例子进行变形,逐步引导学生 会说出用比值来比较。当学生说出用比值是,老师可以问“如何 “ 用比值来比较”“为什么比值大的陡” ”“为什么比值大的陡 用比值来比较”“为什么比值大的陡” 总结:我们大家通过这么多的讨论,咱们明确了, 总结:我们大家通过这么多的讨论,咱们明确了,要想比较两个 梯子哪个陡,我们可以通过什么来刻画(比值), ),也就是说可以 梯子哪个陡,我们可以通过什么来刻画(比值),也就是说可以 通过两条直角边的比值来刻画梯子哪个更陡。 通过两条直角边的比值来刻画梯子哪个更陡。马上引入下个话题
(√ )
13
定义中应该注意的几个问题: 定义中应该注意的几个问题:
1、tanA是在直角三角形中定义的,∠A是一个锐角 tanA是在直角三角形中定义的,∠A是一个锐角 是在直角三角形中定义的,∠A 注意数形结合,构造直角三角形) (注意数形结合,构造直角三角形) 2、tanA是一个完整的符号,表示∠A的正切,习 tanA是一个完整的符号,表示∠ 的正切, 是一个完整的符号 惯省去“ 惯省去“∠”;
1、今天我们学习从梯子的倾斜程度谈起 的第一课时,大家知道梯子是我们常见的 物体,而使用梯子的时候,梯子的倾斜程 度又是至关重要的。
2
2
3
你能比较两个 梯子哪个更陡吗?
我们可以把斜靠在 墙壁上的梯子看成 什么图形呢?当学 生回答是直角三角 形时,老师引入下 一张图片。
4
(1)如图,梯子AB和EF哪个更陡?
对 tanA是一个比值(直角边之比, 是一个比值 3、tanA是一个比值(直角边之比, 注意比的顺 邻 );且tanA﹥ 无单位; 序);且tanA﹥0,无单位;
4、tanA的大小只与∠A的大小有关,而与直角三 tanA的大小只与∠ 的大小有关, 的大小只与 角形的边长无关。 角形的边长无关。 5、角相等,则正切值相等;两锐角的正切值相等, 角相等,则正切值相等;两锐角的正切值相等, 则这两个锐角相等。 则这两个锐角相等。
梯子EF更陡 梯子 更陡
A E 3.5m F 1.3m D
4m B 1.5m C
在实例3中,引导学生仿照前面两个例子进行变形,逐步引导学生 会说出用比值来比较。当学生说出用比值是,老师可以问“如何 “ 用比值来比较”“为什么比值大的陡” ”“为什么比值大的陡 用比值来比较”“为什么比值大的陡” 总结:我们大家通过这么多的讨论,咱们明确了, 总结:我们大家通过这么多的讨论,咱们明确了,要想比较两个 梯子哪个陡,我们可以通过什么来刻画(比值), ),也就是说可以 梯子哪个陡,我们可以通过什么来刻画(比值),也就是说可以 通过两条直角边的比值来刻画梯子哪个更陡。 通过两条直角边的比值来刻画梯子哪个更陡。马上引入下个话题
(√ )
13
定义中应该注意的几个问题: 定义中应该注意的几个问题:
1、tanA是在直角三角形中定义的,∠A是一个锐角 tanA是在直角三角形中定义的,∠A是一个锐角 是在直角三角形中定义的,∠A 注意数形结合,构造直角三角形) (注意数形结合,构造直角三角形) 2、tanA是一个完整的符号,表示∠A的正切,习 tanA是一个完整的符号,表示∠ 的正切, 是一个完整的符号 惯省去“ 惯省去“∠”;
九年级数学下册第一章直角三角形的边角关系1从梯子的倾斜程度谈起第1课时习题课件北师大版

2.(2013·聊城中考)河堤横断面如图所示,堤高BC=6 m,迎水 坡AB的坡比为 1∶ 3,则AB的长为( )
A.12 mB.4 3 m C.5 3 mD.6 3 m
【解析】选A.在Rt△ABC中, tan A 1 BC , BC 6 m,
3 AC
AC 6 3 m,AB BC2 AC2 12 m.
提示:四边形BFEC是正方形,则EF=BF=BC=4 m.
3.可求出AF的长是多少?那么即可求出坝底宽AD.
提示:在Rt△ABF中,由勾股定理可得:AF 52-42 3m.
根据以上探究,可得坝底AD=AF+FE+ED =3+4+8=15(m).
【互动探究】在上题中,斜坡AB的坡度是多少? 提示:在Rt△AFB中,因BF=4,AF=3,所以斜坡AB的坡度 为 4.
BF 5
【总结提升】利用定义求锐角的正切值的“三步法” 1.观察:观察所给的锐角是否在直角三角形中. 2.转化:如果所给的锐角不在直角三角形中,可通过作辅助线 构造直角三角形或利用等量关系代换将锐角“转移”到直角三 角形中. 3.求解:在直角三角形中求出这个角的对边与邻边的比值,就 是这个角的正切值.
∴梯形ABCD 的周长为AB+BC+CD+DA
6 10 32 3 13 5 37 6 10 3 13 m.
答:梯形ABCD 的周长为(37 6 10 3 13)m.
【想一想错在哪?】如图,△ABC中,∠C=90°,BC=6 cm, tan B 3,△ABC的面积是多少?
2
谢谢 观看
知识点 2 正切的应用 【例2】如图,一段河坝的横断面为梯形ABCD,试根据图中的 数据,求出坝底宽AD.(i=CE∶ED,单位:m)
