线性代数期末试题A
线性代数试题A及答案
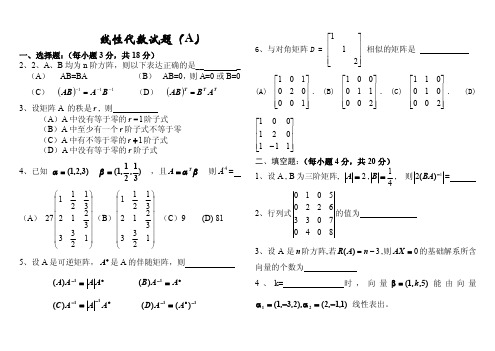
线性代数试题(A )一、选择题:(每小题3分,共18分)2、2、A 、B 均为n 阶方阵,则以下表达正确的是__ _ (A ) AB=BA (B ) AB=0,则A=0或B=0 (C ) ()111---=B A AB (D ) ()T T TA B AB =3、设矩阵A 的秩是r , 则(A )A 中没有等于零的1-r 阶子式 (B )A 中至少有一个r 阶子式不等于零 (C )A 中有不等于零的1+r 阶子式 (D )A 中没有等于零的r 阶子式4、已知 )3,2,1(=a )31,21,1(=b ,且b a T A = 则4A =(A ) 27÷÷÷÷÷÷øöççççççèæ1233321231211(B )÷÷÷÷÷÷øöççççççèæ1233321231211 (C )9 (D) 81 5、设A 是可逆矩阵,*A 是A 的伴随矩阵,则*-=A A A A 1)( *-=A A B 1)( *--=A AA C 11)( 11)()(-*-=A A D6、与对角矩阵D = úúúûùêêêëé211 相似的矩阵是 (A) úúúûùêêêëé100020101. (B) úúúûùêêêëé200110001. (C) úúúûùêêêëé200010011. (D) úúúûùêêêëé-111021001 二、填空题:(每小题4分,共20分)1、设A , B 为三阶矩阵, 2=A ,41=B , 则12-)(BA = 2、行列式8040703362205010的值为 3、设A 是n 阶方阵,若3-=n A R )(,则0=AX 的基础解系所含向量的个数为4、k= 时,向量)5,,1(k =b 能由向量)1,1,2(),2,3,1(21-=a -=a 线性表出。
线性代数期末考试题及答案

线性代数期末考试题及答案一、选择题1. 下列哪个不是线性代数的基本概念?A. 矩阵B. 向量C. 函数D. 行列式答案:C. 函数2. 矩阵A的转置记作A^T,则(A^T)^T等于A. AB. -AC. A^TD. 2A答案:A. A3. 对于矩阵A和B,满足AB = BA,则称A和B是A. 相似矩阵B. 对角矩阵C. 线性无关D. 对易矩阵答案:D. 对易矩阵4. 行列式的性质中,不能成立的是A. 行列式交换行B. 行列式某一行加上另一行不变C. 行列式等于数乘其中某一行对应的代数余子式的和D. 行列式的某一行的系数乘以另一行不变答案:D. 行列式的某一行的系数乘以另一行不变5. 给定矩阵A = [3, -1; 4, 2],则A的秩为A. 0B. 1C. 2D. 3答案:C. 2二、填空题1. 给定矩阵A = [2, 1; -3, 5],则A的行列式为______答案:132. 设矩阵A的逆矩阵为A^-1,若AA^-1 = I,其中I是单位矩阵,则A的逆矩阵为______答案:I3. 若矩阵的秩为r,且矩阵的阶数为n,若r < n,则该矩阵为______矩阵答案:奇异三、简答题1. 解释什么是线性相关性和线性无关性?答案:若存在不全为零的数k1, k2,...,kn,使得方程组中的向量k1v1 + k2v2 + ... + knvn = 0成立,则称向量组{v1, v2, ..., vn}线性相关;若该方程仅在k1 = k2 = ... = kn = 0时成立,则称向量组{v1, v2, ..., vn}线性无关。
2. 如何判断一个矩阵是对称矩阵?答案:若矩阵A的转置等于自身,即A^T = A,则称矩阵A是对称矩阵。
四、计算题1. 给定矩阵A = [1, 2; 3, 4],求A的逆矩阵。
答案:A的逆矩阵为1/(-2)[4, -2; -3, 1]2. 求向量v = [1, 2, 3]的模长。
线性代数期末考试试题A及解答

3、此二次型矩阵特征值有负值,,故二次型不正定。--------------------(14分)
六、
1、证明: -------------(3分)
,故 可逆,且 ----(5分)
2、证明:因为 为正交矩阵且 , ------------(1分)
-------(4分)
,故 -----------------(5分)
六 证明题
1、若 阶矩阵 满足 ,求证 可逆,并求 。
2、设五阶正交矩阵 满足 ,求证:矩阵 的秩 。
线性代数A参考答案及评分标准
一、填空
1、负;46。2、4;2; 与 。
3、 ; 。4、 。
5、 6、 。
7、0; 。8、 ;2; 。
二、计算
1、 --(3分)=
--------------(5分)= ------------------(6分)
得到齐次线性方程组的基础解系
三、 --------(2分)
故 时, ,方程组有解---------(4分)
此时方程组的一般解为: ,得一个特解
导出组的一个基础解系, -----------------(10分)
通解为 ( , 为任意常数)…(12分)
四、 ,
得到 的特征值 ---------------(4分)
三(12 )设线性方程组 ,当 为何值时 能与对角形矩阵相似,求参数 的值。
五(14 )二次型
(1)写出二次型的矩阵 。
(2)用正交变换法将此二次型化为标准形并写出所做的正交变换 以及二次型的标准形。
(3)此二次型是否正定,说明理由。
5.四阶矩阵 的行列式 则 , , 的列向量组线性关。
线性代数A-期末模拟试卷(无答案)

线性代数A 期末模拟试卷(无答案)一、选择题(本大题共5小题,每题3分,共15分)1.设A是p×s矩阵,C是m×n矩阵,如果AB T C有意义,则B是什么矩阵()(A)p×n (B)p×m (C) s×m (D)m×s2.设A,B均为n阶可逆矩阵,则下列各式中不正确的是-------()(A)(A+B)T=A T+B T(B) (A+B)-1=A-1+B-1(C)(AB)-1=B-1A-1(D)(AB)T=B T A T3.线性方程组2020ax zx ay zax y z+=⎧⎪++=⎨⎪-+=⎩只有零解,则a的取值为---()(A)a=2 (B)a≠2 (C)a=1 (D)a≠14.设A是n阶方阵,|A|=0,则下列结论中错误的是------()(A) R(A)<n(B)A有两行元素成比例(C)A的n个列向量线性相关(D)A有一个行向量是其余n个行向量的线性组合5.已知3阶矩阵A相似于B,A的特征值为2、3、4,E为3阶单位矩阵,则|B-E|=---------()(A)6;(B)12;(C)24;(D)48二、填空题(本大题共5小题,每题3分,共15分)1.已知0333231232221131211≠=k a a a a a a a a a ,则=---32323331121213112222232141062532125321a a a a a a a a a a a a . 2.若A,B 为3阶方阵,且|A|=2,|B|=2,则|-2A|= ,|A -1B T |= .3.设A 是三阶方阵,A 的特征值为2,3,λ,且|2A|=48,则=λ , R(A)= 。
4.已知⎪⎪⎪⎭⎫ ⎝⎛=130120005A ,则A -1= . 5.设A 为n 阶矩阵,|A|=-2,求|3(A )-1A *|= 。
三、计算题(本大题共5小题,每题10分,共50分)1.(1)计算行列式3 (22)............2 (322)...23=n D (2)设3351110243152113------=D ,D 的(i ,j )元的代数余子式记作A ij 。
线性代数a期末考试题及答案

线性代数a期末考试题及答案一、选择题(每题5分,共20分)1. 以下哪个矩阵是可逆的?A. 零矩阵B. 单位矩阵C. 对角矩阵D. 奇异矩阵答案:B2. 矩阵的秩是指:A. 矩阵的行数B. 矩阵的列数C. 矩阵中非零行的最大数目D. 矩阵中非零列的最大数目答案:C3. 如果一个矩阵A的行列式为0,则:A. A是可逆的B. A是不可逆的C. A是正定的D. A是负定的答案:B4. 以下哪个选项不是线性方程组解的性质?A. 唯一性B. 存在性C. 零解D. 非零解答案:D二、填空题(每题5分,共20分)1. 矩阵的________是矩阵中所有元素的和。
答案:迹2. 如果一个向量组线性无关,则该向量组的________等于向量的个数。
答案:秩3. 对于一个n阶方阵A,如果存在一个非零向量x使得Ax=0,则称x为矩阵A的________。
答案:零空间4. 一个矩阵的________是指矩阵中所有行向量或列向量的最大线性无关组的个数。
答案:秩三、解答题(每题10分,共60分)1. 已知矩阵A=\[\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\],求A的行列式。
答案:\[ \text{det}(A) = 1*4 - 2*3 = 4 - 6 = -2 \]2. 设A=\[\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\],B=\[\begin{pmatrix} 2 & 0 \\ 1 & 3 \end{pmatrix}\],求AB。
答案:\[ AB = \begin{pmatrix} 1*2 + 2*1 & 1*0 + 2*3 \\ 3*2 +4*1 & 3*0 + 4*3 \end{pmatrix} = \begin{pmatrix} 4 & 6 \\ 10 & 12 \end{pmatrix} \]3. 已知矩阵A=\[\begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix}\],求A的特征值。
《线性代数》期末考试题及详细答案(本科A、B试卷)

XXX 学年期末考试试卷《线性代数》期末考试题及详细答案(本科A 、B 试卷)A 卷一、填空题 (将正确答案填在题中横线上。
每小题2分,共10分)。
1、设1D =3512, 2D =345510200,则D =12DD OO=_____________。
2、四阶方阵A B 、,已知A =116,且=B ()1-12A 2A --,则B =_____________。
3、三阶方阵A 的特征值为1,-1,2,且32B=A -5A ,则B 的特征值为_____________。
4、若n 阶方阵A 满足关系式2A -3A-2E O =,若其中E 是单位阵,那么1A -=_____________。
5、设()11,1,1α=,()21,2,3α=,()31,3,t α=线性相关,则t=_____________。
二、单项选择题 (每小题仅有一个正确答案,将正确答案的番号填入下表内,每小题2分,共20分)。
1、若方程13213602214x x xx -+-=---成立,则x 是:课程代码: 适用班级:命题教师:任课教师:(A )-2或3; (B )-3或2; (C )-2或-3; (D )3或2; 2、设A 、B 均为n 阶方阵,则下列正确的公式为: (A )()332233A B+3AB +B A B A +=+; B )()()22A B A+B =A B --; (C )()()2A E=A E A+E --; (D )()222AB =A B ; 3、设A 为可逆n 阶方阵,则()**A=?(A )A E ; (B )A ; (C )nA A ; (D )2n A A -;4、下列矩阵中哪一个是初等矩阵:(A )100002⎛⎫ ⎪⎝⎭; (B )100010011⎛⎫⎪⎪ ⎪⎝⎭; (C )011101001-⎛⎫ ⎪- ⎪ ⎪⎝⎭; (D )010002100⎛⎫⎪- ⎪ ⎪⎝⎭;5、下列命题正确的是:(A )如果有全为零的数1,k 2k 3,,,m k k 使1122m m k k k αααθ+++=,则1,α2α,,m α 线性无关; (B )向量组1,α2α,,m α 若其中有一个向量可由向量组线性表示,则1,α2α,,m α线性相关;(C )向量组1,α2α,,m α 的一个部分组线性相关,则原向量组本身线性相关; (D )向量组1,α2α,,m α线性相关,则每一个向量都可由其余向量线性表示。
线性代数期末考试试题及答案
线性代数期末考试试题及答案一、选择题(每题5分,共20分)1. 若矩阵A是可逆的,则下列哪个选项是正确的?A. A的行列式为0B. A的行列式不为0C. A的逆矩阵不存在D. A的逆矩阵是其转置矩阵答案:B2. 线性方程组有唯一解的充分必要条件是:A. 系数矩阵的行列式为0B. 系数矩阵的行列式不为0C. 增广矩阵的秩等于系数矩阵的秩D. 增广矩阵的秩大于系数矩阵的秩答案:B3. 设A是n阶方阵,若A的特征值均为1,则A可能是:A. 零矩阵B. 单位矩阵C. 任意对角矩阵D. 任意方阵答案:B4. 向量空间中,若两个向量组等价,则它们:A. 包含相同数量的向量B. 包含相同数量的线性无关向量C. 可以相互线性表出D. 具有相同的维数答案:D二、填空题(每题5分,共20分)1. 设矩阵A的秩为r,则矩阵A的行向量组和列向量组的最大线性无关组包含的向量数量均为______。
答案:r2. 若向量组α1, α2, ..., αn线性无关,则向量组α1+β,α2+β, ..., αn+β线性相关,其中β为非零向量,这说明向量组α1, α2, ..., αn的线性相关性与向量β的______有关。
答案:选择3. 设A是3×3矩阵,且A的行列式|A|=2,则矩阵A的逆矩阵的行列式|A^(-1)|等于______。
答案:1/24. 若线性方程组的系数矩阵A和增广矩阵B具有相同的秩,则该线性方程组的解集的维数为n-r,其中n是矩阵A的阶数,r是矩阵A的秩,则该线性方程组的解集的维数为______。
答案:n-r三、解答题(每题15分,共40分)1. 已知矩阵A=\[\begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix}\],求矩阵A的特征值和特征向量。
答案:特征值λ1 = 5,对应的特征向量为\[\begin{pmatrix}-2 \\1\end{pmatrix}\];特征值λ2 = 1,对应的特征向量为\[\begin{pmatrix}1 \\1.5\end{pmatrix}\]。
线性代数期末试题及答案
线性代数期末试题及答案一、选择题(每题5分,共20分)1. 设矩阵A为3阶方阵,且|A|=2,则|2A|等于:A. 4B. 8C. 16D. 32答案:C2. 若向量α=(1, 2, 3),β=(2, 1, 0),则α·β等于:A. 4B. 5C. 6D. 7答案:B3. 设A为n阶方阵,且A^2=I,则A的行列式|A|等于:A. 1B. -1C. 0D. 2答案:A4. 若矩阵A的秩为2,则矩阵A的行向量线性相关还是线性无关?A. 线性相关B. 线性无关C. 线性独立D. 不能确定答案:A二、填空题(每题5分,共20分)1. 设矩阵B为2阶方阵,且B^2=0,则称矩阵B为______。
答案:幂零矩阵2. 若矩阵A和B可交换,即AB=BA,则称矩阵A和B为______。
答案:可交换矩阵3. 设向量α=(1, 2),β=(3, 4),则向量α和β的夹角的余弦值为______。
答案:3/54. 设矩阵A为3阶方阵,且A的特征值为1, 2, 3,则矩阵A的迹为______。
答案:6三、简答题(每题10分,共30分)1. 简述矩阵的转置矩阵的定义。
答案:矩阵A的转置矩阵记为A^T,其元素满足A^T_{ij}=A_{ji},即A^T的第i行第j列的元素是A的第j行第i列的元素。
2. 什么是线性方程组的齐次解?答案:线性方程组的齐次解是指当方程组的常数项全为零时,方程组的解,通常表示为零向量。
3. 说明矩阵的相似对角化的条件。
答案:矩阵A相似对角化的条件是矩阵A有n个线性无关的特征向量,其中n是矩阵A的阶数。
四、计算题(每题15分,共30分)1. 已知矩阵A=\[\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\],求矩阵A的行列式。
答案:|A| = 1*4 - 2*3 = -22. 设线性方程组为:\[\begin{matrix} x + 2y - z = 1 \\ 3x - y + 2z = 2 \\ x + y + z = 3 \end{matrix}\]求方程组的解。
线代A期末考试题及答案
线代A期末考试题及答案一、选择题(每题4分,共20分)1. 向量组 \(\alpha_1, \alpha_2, \ldots, \alpha_n\) 线性无关的充分必要条件是:A. 向量组中任意向量不能由其他向量线性表示B. 向量组中任意向量不能由其他向量线性组合得到C. 向量组中任意向量不能由其他向量线性组合得到,且向量组中向量个数等于空间的维数D. 向量组中向量个数等于空间的维数答案:A2. 矩阵 \(A\) 可逆的充分必要条件是:A. \(A\) 的行列式不为零B. \(A\) 的秩等于其行数C. \(A\) 的秩等于其列数D. \(A\) 的秩等于其行数且等于其列数答案:D3. 对于实对称矩阵 \(A\),下列说法正确的是:A. \(A\) 一定可以对角化B. \(A\) 一定可以正交对角化C. \(A\) 的所有特征值都是实数D. \(A\) 的所有特征值都是正数答案:C4. 矩阵 \(A\) 和 \(B\) 相似的充分必要条件是:A. \(A\) 和 \(B\) 有相同的特征多项式B. \(A\) 和 \(B\) 有相同的特征值C. \(A\) 和 \(B\) 有相同的秩D. \(A\) 和 \(B\) 有相同的迹答案:B5. 矩阵 \(A\) 为正定矩阵的充分必要条件是:A. \(A\) 的所有特征值都大于零B. \(A\) 的所有特征值都大于等于零C. 对于任意非零向量 \(x\),都有 \(x^TAx > 0\)D. 对于任意非零向量 \(x\),都有 \(x^TAx \geq 0\)答案:C二、填空题(每题4分,共20分)6. 若向量 \(\alpha = (1, 2, 3)^T\) 和 \(\beta = (4, 5, 6)^T\),则向量 \(\alpha + \beta\) 等于 \(\boxed{(5, 7, 9)^T}\)。
7. 矩阵 \(A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\)的行列式为 \(\boxed{-2}\)。
线性代数期末考试考核试卷
4.以下哪个向量组构成一个基?
A. (1, 0, 0), (0, 1, 0), (0, 0, 0)
B. (1, 2, 3), (4, 5, 6), (7, 8, 9)
C. (1, 2, 3), (2, 4, 6), (1, 1, 1)
D. (1, 1, 0), (0, 1, 1), (1, 0, 1)
...
20.(根据实际题目内容填写答案)
二、多选题
1. BCD
2. ABCD
3. ABC
4. AB
5. ABC
...
20.(根据实际题目内容填写答案)
三、填题
1. 1
2.线性无关
3.主
...
10.(根据实际题目内容填写答案)
四、判断题
1. √
2. √
3. √
...
10. ×
五、主观题(参考)
1.向量组线性无关,可以通过计算行列式不为零来证明。一个可以由给定向量组线性表示的向量可以是它们的线性组合,例如\(a\vec{v}_1 + b\vec{v}_2 + c\vec{v}_3\),其中\(a, b, c\)是适当的系数。
D. (1, 1), (1, -1)
(答题括号:________)
5.在求解线性方程组时,以下哪些情况下可以使用高斯消元法?
A.系数矩阵是方阵
B.系数矩阵是非奇异的
C.方程组中方程的个数等于未知数的个数
D.方程组可能有无穷多解
(答题括号:________)
(以下题目类似,省略以节约空间)
6. ...
A.若A为m×n矩阵,则A的转置为n×m矩阵
B.若A为m×n矩阵,则A的转置为m×n矩阵
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东财政学院
2004--2005学年第一学期期末考试《线性代数》试卷A
(考试时间为120分钟)
学院_________ 班级 ___________ 姓名__________ 学号__________
注意:请将所有试题的答案均写在答题纸上!
一.判断题(2分×5=10分)
1.若O B A n n n n =⨯⨯,且O A ≠,则B 奇异.( )
2.若n n n n n n n I C B A =⨯⨯⨯,则C B A ,,均可逆,且AB C AC B BC A ===---111,,.( )
3.若向量组s ααα,,,21 线性无关,且可由向量组s βββ,,,21 线性表出,则s βββ,,,21 也线性无关.( )
4.若方程组)0(≠=b b Ax 有唯一解,则方程组0=Ax 仅有零解.( )
5.若向量α与任意同维的向量均正交,则0=α.( ) 二.单项选择题(2分×5=10分)
1.若0)(=*
⨯n n A r ,2≥n ,则)(A r 不可能...是( ) (注:)(A r 表示矩阵A 的秩,下同.)
A .0;
B .1;
C .2-n ;
D .1-n .
2.若n n A ⨯为对称矩阵,n n B ⨯为反对称矩阵,则下列矩阵中为反对称...矩阵的是( ) A .BA AB +; B .BA AB -; C .AB ; D .BAB .
3.若B A ,分别为m n n m ⨯⨯,矩阵,则( )
A .当n m >时,0≠A
B ; B .当n m >时,0=AB ;
C .当m n >时,0≠AB ;
D .当m n >时,0=AB . 4.若矩阵)(n m A n m <⨯的行向量组线性无关,则( )
A .方程组0=Ax 仅有零解;
B .方程组b Ax =有唯一解;
C .方程组b Ax =有无穷多解;
D .方程组b Ax =无解.
5.下列矩阵中可.
相似于对角矩阵的是( ) A .⎪⎪⎪⎭⎫ ⎝
⎛20
0010021; B .⎪⎪⎪⎭⎫ ⎝
⎛10
0020
201; C .⎪⎪⎪⎭⎫ ⎝
⎛10
0020
021
; D .⎪⎪⎪⎭
⎫
⎝
⎛20
0010
111
. 三.填空题(3分×5=15分) 1.设3,2-==⨯⨯n n n n B A ,则_________21
=-*
B
A .
2.若C B A ,,均为n 阶方阵,且n I CA BC AB ===,则________222=++C B A .
3.若矩阵n n n n B A ⨯⨯~,A 的特征值为
1
1,
1,,,31,21+n n ,则________||1
=--n I B .
4.若齐次线性方程组⎪⎩⎪
⎨⎧=++=++=++0
2020
2321321321ax x x
x x x x x x 存在基础解系,则a 的取值为___________.
5.若γβα,,为单位正交向量组,c b a ,,为实常数,
则
_____________=++γ
βαc b a .
四.计算题(10分×5=50分)
1.计算行列式n
n
n n n n x a x x a x a x x a x x a D 0
00000000001113322211
1
------+=
的值.
2.设向量)2
1
,0,2
1
(=α,ααT
I A -=3,ααT
I B 23+=,求AB .
3.设矩阵n n ij a A ⨯=)(,3≥n ,011≠a ,ij A 为ij a 的代数余子式,且ij ij a A =,
n j i ,,2,1, =,求A 的值.
4.求a 为何值时,向量组)3,1,1,1(1=α,)1,5,3,1(2--=α,)2,1,2,3(3+-=a α,
),10,6,2(4a --=α线性相关?当4321,,,αααα线性相关时,求其秩和一个极大无关组,
并将其余向量用此极大无关组线性表出.
5.设实对称矩阵⎪⎪⎪⎭
⎫
⎝
⎛----=32
0222
021A ,(1)求一个可逆矩阵P ,使得AP P 1
-为对角矩阵;(2)求一个正交矩阵Q ,使得AQ Q 1-为对角矩阵. 五.证明题(5分×3=15分)(任选三.题即可) 1.求证:若O B A n n n n =⨯⨯,则n B r A r ≤+)()(.
2.求证:若r A r n m =⨯)(,则存在可逆矩阵n n m m Q P ⨯⨯,,使得⎪⎪⎭
⎫ ⎝
⎛=O O
O I PAQ r
. 3.求证:若向量β可由向量组s ααα,,,21 线性表出,则表出方式唯一的充要..条件是s ααα,,,21 线性无关.
4.求证:齐次线性方程组0=⨯x A n n 仅有零解的充要..
条件是矩阵A 无零特征值.。
