弹簧减震器选型公式
弹簧设计的计算公式

弹簧设计的计算公式
常见的弹簧设计绝大部分是压缩螺旋弹簧或拉伸螺旋弹簧。
这两种弹簧设计,涉及下面的项目。
在这里将关于a),b),c)进行解说。
a)在使用范围内,弹簧负载和形变量:弹簧常数
b)安装弹簧的空间:长度x外形
c)弹簧的固定方法:弹簧的两端形状和固定方法
d)其他:弹簧刚度(永久变形),疲劳度
(1)弹簧常数和弹簧形状尺寸的关系式
弹簧的形变量和负载(力)的关系。
P =k x δ
P:弹簧负载
k:弹簧常数
δ:弹簧挠度(形变量)
(k:弹簧常数)用弹簧材料特性和弹簧形状可以用下述公式表达。
这个公式压缩螺旋弹簧和拉伸螺旋弹簧都适用。
k =P/δ=G x d4/8 x n x D3 ・・・(A)
G:横向弹性系数(杨氏模量)
d:线径
n:有效匝数
D:平均线圈直径
通过使公式(A)变形,暂时设定D(平均线圈直径),d(线径),
k(弹簧常数)来计算有效匝数:n,或者根据已知的P,D,d,n ,来计算形变量:δ。
(2)弹簧的长度、外形的设计
弹簧长度是根据(允许形变量)与弹簧载荷之间的关系来选择和设计的。
(允许形变量)是会使弹簧变形或损坏的最大变形量(参考图1)。
风机弹簧减震器的效率计算

风机弹簧减震器的效率计算曹静;谭浩华;荣光伟【摘要】本文阐述风机弹簧减震器的选型与校核计算.利用隔振效率得出当弹簧减震器的工作频率大于5倍的固有频率时,弹簧减震器的减震效果可以达到95.8%以上.通过简单的计算可以验证所选的弹簧减震器是否合理.如果验算未能达到预期要求,可以采取加大基座重量或增加弹簧减震器的数量以及选取较低弹簧减震器的刚性系数等措施来达到期望的减震效果.【期刊名称】《机械研究与应用》【年(卷),期】2018(031)006【总页数】4页(P96-99)【关键词】风机弹簧减震器;隔振效率;刚度【作者】曹静;谭浩华;荣光伟【作者单位】英格索兰亚太技术工程中心,上海 200051;英格索兰亚太技术工程中心,上海 200051;英格索兰亚太技术工程中心,江苏太仓 215400【正文语种】中文【中图分类】O2620 引言新项目是新一代屋顶机产品的设计,其主要零部件之一室内风机是重新选型的,新选择的后倾式离心风机具有风量大、压力低但效率高的特点,在暖通行业应用十分广泛。
新的风机选定之后相应的配件要重新选择,支撑结构也要重新设计,测试等工作任务艰巨。
如果测试过程中发现风机有问题还需要修改重来,很是费时;如果在前期能准确选择某些零部件并确保他们的可靠性,那测试时出现问题的概率会小并能及时排除某些确定的因素找到问题的根本原因。
弹簧减震器是风机结构中不可缺少的一部分,它具有性能稳定、承载能力强、寿命长、抗环境污染能力强、计算可靠和固有频率低等优点。
笔者结合Creo软件,通过这一简单快速的计算方法来校核弹簧减震器的选型是否合理,使其达到期望的减震效果,在实践中有重要的意义。
1 理论分析在许多工程问题中,我们并不希望产生机械振动,而在诸如搅拌机、振动器等系统中,却又希望产生振动。
由于振动系统是具有一定质量且其中部件能相对运动的系统,因此具有弹性构件可以储存弹性能,系统的阻尼可以把部分能量转化为热能以及通过基座激励可使能量转化为系统的能量。
弹簧减震计算

弹簧减震计算弹簧减震是一种常见的减震装置,广泛应用于汽车、摩托车、自行车等交通工具,以及工业机械设备中。
它的作用是通过弹簧的弹性来减少震动和冲击,保护车辆或设备的稳定性和乘坐舒适度。
弹簧减震的原理是利用弹簧的弹性来吸收和消散外部的震动能量。
当车辆或设备遇到不平路面或外部冲击时,弹簧会被挤压或拉伸,吸收和储存能量。
当外部力量消失时,弹簧会释放储存的能量,使车辆或设备回到原来的平衡状态。
这个过程中,弹簧会起到缓冲和减震的作用,有效地降低震动和冲击的影响。
弹簧减震的设计考虑到了多个因素,如载荷、行驶速度、路面条件等。
对于不同的应用场景,需要选择合适的弹簧类型和参数。
常见的弹簧类型有螺旋弹簧、气弹簧和液压弹簧等。
螺旋弹簧是最常见的一种,它通过螺旋形状的弹簧线圈来提供弹性。
气弹簧利用气体的可压缩性来提供弹性,具有较好的减震效果。
液压弹簧则利用液体的不可压缩性来提供弹性,适用于高负荷和高速运动的场景。
除了弹簧的选择,减震效果还与减震器的设计和调校有关。
减震器是安装在弹簧上的一个装置,它通过内部的阻尼器来控制弹簧的振动。
阻尼器可以通过调整阻尼力的大小和调校阻尼力的变化规律,来实现对弹簧振动的控制。
较好的减震器设计能够在保证舒适性的同时,有效地抑制车辆或设备的震动。
弹簧减震的优势在于其结构简单、可靠性高、成本较低。
相比于其他减震装置,弹簧减震更容易维修和更换。
此外,弹簧减震还可以根据实际需求进行调整和改进,以适应不同的工况和路况。
然而,弹簧减震也存在一些局限性。
由于弹簧的弹性系数是固定的,无法根据实际情况进行调整。
这意味着在不同的工况下,弹簧减震可能无法提供最佳的减震效果。
此外,弹簧减震在处理较大冲击力时效果有限,需要配合其他减震装置来实现更好的效果。
弹簧减震是一种常见且有效的减震装置。
通过合理选择弹簧类型和参数,并结合减震器的设计和调校,可以实现良好的减震效果。
然而,弹簧减震也有其局限性,需要在实际应用中进行综合考虑和优化设计。
弹簧系数k的计算公式

弹簧系数k的计算公式
弹簧系数k的计算公式是F=kx。
劲度系数,即倔强系数(弹性系数),它描述单位形变量时所产生弹力的大小,k值大,说明形变单位长度需要的力越大。
劲度系数又称刚度系数或者倔强系数。
劲度系数在数值上等于弹簧伸长(或缩短)单位长度时的弹力。
弹簧是一种利用弹性来工作的机械零件。
用弹性材料制成的零件在外力作用下发生形变,除去外力后又恢复原状。
亦作“弹簧”。
一般用弹簧钢制成。
弹簧的种类复杂多样,按形状分,主要有螺旋弹簧、涡卷弹簧、板弹簧、异型弹簧等。
F=kx,F为弹力,k为劲度系数(或倔强系数),x为弹簧拉长(或压短)的长度。
例1:用5N力拉劲度系数为100N/m的弹簧,则弹簧被拉长5cm。
按受力性质,弹簧可分为拉伸弹簧、压缩弹簧、扭转弹簧和弯曲弹簧,按形状可分为碟形弹簧、环形弹簧、板弹簧等。
1。
弹簧计算公式

弹簧计算公式弹簧计算公式是用来计算弹簧的弹力的数学公式。
弹簧是一种用来存储和释放能量的弹性元件,广泛应用于各种机械装置和工具中。
根据弹簧的形状和用途,可以分为压簧、拉簧和扭簧。
下面将分别介绍这三种弹簧的弹力计算公式。
1.压簧弹力计算公式压簧是一种用于承受压缩力的弹簧,通常由钢丝绕成螺旋形。
压簧的弹力与其形状、材料的物理性质以及受到的压缩力有关。
压簧的弹力计算公式如下:F=k*x其中,F表示弹簧的弹力,k是一个常数,称为簧系数,x是压簧的变形量。
压簧的弹力与其变形量呈线性关系,即弹簧的弹力与其压缩或拉伸的距离成正比。
簧系数k的大小取决于弹簧的材料和几何形状。
2.拉簧弹力计算公式拉簧是一种用于承受拉力的弹簧,通常由钢丝绕成螺旋形。
拉簧的弹力与其形状、材料的物理性质以及受到的拉力有关。
拉簧的弹力计算公式如下:F=k*x其中,F表示弹簧的弹力,k是一个常数,称为拉簧的刚度系数或簧系数,x是拉簧的变形量。
拉簧的弹力与其变形量呈线性关系,即弹簧的弹力与其拉伸或压缩的长度成正比。
簧系数k的大小取决于弹簧的材料和几何形状。
3.扭簧弹力计算公式扭簧是一种用于承受扭转力的弹簧,通常由钢丝绕成螺旋形。
扭簧的弹力与其形状、材料的物理性质以及受到的扭转力矩有关。
扭簧的弹力计算公式如下:T=k*φ其中,T表示弹簧的扭力,k是弹簧的刚度系数或簧系数,φ是弹簧的扭转角度。
扭簧的弹力与其扭转角度成正比。
簧系数k的大小取决于弹簧的材料和几何形状。
需要注意的是,以上的公式都是基于线性弹性假设的情况下推导出来的。
实际上,弹簧的变形行为通常是非线性的,因此在计算弹力时需要考虑非线性效应,例如在变形量较大或载荷较高的情况下。
除了弹力的计算公式,还可以根据实际需要计算弹簧的弹性系数、刚度系数、临界长度等参数。
这些参数对于设计和选择弹簧具有重要意义,可以保证弹簧在工作过程中具有足够的弹性和耐力。
(完整版)减震器选型方法

隔振器自身的刚度作用是在振动时会产生一个与振动位移成正比的恢复力,同时隔振器自身阻尼的作用是在振动时会产生一个和振动速度成正比的阻尼力。
在被动隔振中, 良好的隔振设计可使大部分的基座或基础运动都由隔振器来吸收,即隔振的目的就是减少振动的传递率使基座或基础的运动干扰尽量不向被保护的仪器或设备传播,并使仪器或设备的振动响应尽量保持最小。
隔振器最终的设计应该使隔振系统的固有频率低,有可变的阻尼特性,使系统既不会有显著的共振放大,同时又有良好的隔振效率,而且抗冲击性能和稳定性要好,因此, 在设计隔振器的阻尼时应同时考虑隔振系统的隔振效率和共振放大率,而隔振器的设计就是要适当选择系统隔振器的阻尼及刚度橡胶垫由于自身安装比较方便,形状可以根据需求制作,因此,微捷联惯组的隔振器尺寸是根据惯组的实际安装尺寸来设计车栽环境中振动噪声上妾是臬屮在10 Hz -120 Hz以及吏跖的频率驗根据减版原理,墓想隔离詠的抿动噪声,就必须使陌掘系统的固有频率在THz以下,即由隔振传递率曲线nJ甸当就提频率与園有鮒率的比大于时才会有隔振效果.而在实际工程中-股取该频率比为25^4,5・听以系统的固仃频率的范围兄2H2^4H2.同样隔离10Hz以上的推动嗥声时累统的训肓頤举确定的方法同上.即在一定范嵐内.所设计的隔振系统的固角频咿的偵越低,族动噪声被隔离的频段就越竜,因此,庄设计隔振系统时应使隔振丟统的固有频率辱凰偏低,微捷联惯组和其安驶支架的总质呈大约足50倔左彩,因此,耍采用四级对称式的安装方式,每组隔抿褂的平均承重质駄应该足1N以上,即每俎的隔扼器承重的质煨是在125g以上*通过以上分析.结薛微捶联惯组的宴际尺寸展终确定的隔振索统ffi隔撮器的結构歷卖际尺寸如图3.5所示,为r便惯组在各个方向上b耦,逸择r四组硅橡股垫,毎组棟由仿貞结果術报结构的同冇频净来看•隔振糸统的一阶同冇频率为65.204Hz.孙沖如图4.4 (a)所示,惯性組合在垂直方向上却沿Y轴产生了线振动,隔振系统的:阶固有频率为66.796Hz,振型如上图4.4(b)所示,惯性组合沿X轴产生了线振动;隔振系统的二阶固〃频率为66.8671k, fti型如上IW4.4 (c)所示,惯性组合沿乙轴心生了线振动•由丁振动耦合容易给系统引入伪运幼倍号,从而会彩响惯导系统的测量稻度,因此避免或尽吊•减小报动耦介通常是捷联惯导系统術抿设计的V耍耍求,仿真结果农明:在线般动输入的情况下,隔扳系统的前三阶固有频率为66Hz左右即在三轴匕儿乎不存任按动朗介,川以实现对岛频拓动的仃效袁减。
压缩弹簧设计计算公式

压缩弹簧设计计算公式
常见的弹簧刚度计算公式有以下几种:
1. Hooke定律:
弹簧刚度(K)=受力(F)/变形量(ΔL)
弹簧刚度也可以表示成:K=Gd^4/8ND^3,其中G为弹簧材料的剪切模量,d为弹簧线径,D为弹簧的均衡直径,N为弹簧的圈数。
2.圈数公式:
弹簧刚度(K)=Gd^4/8ND^3
弹簧圈数(N)=(Gd^4/8KD^3)+1
弹簧线径(d)=(8NKD^3)/(G)
3.线径公式:
弹簧刚度(K)=Gd^4/8ND^3
弹簧线径(d)=((8NKF)/(πG))^0.25
弹簧圈数(N)=(Gd^4/8KD^3)+1
以上的公式是根据Hooke定律和圈数公式、线径公式推导得出的。
其中,G为弹簧材料的剪切模量,d为弹簧线径,D为弹簧的均衡直径,N为弹簧的圈数,K为弹簧刚度,F为受力,ΔL为变形量。
在实际应用中,根据不同的设计需求和实际情况,可以选择合适的公式进行计算。
同时,由于弹簧经常在循环载荷下工作,还需考虑弹簧的疲劳寿命等因素,以保证弹簧的使用安全和可靠性。
因此,在进行压缩弹簧
设计时,应结合实际情况和经验进行综合考虑,并且需要进行相关的试验和验证。
此外,弹簧设计还需要考虑其他因素,如预缩量、自由长度、受力方式等。
因此,以上给出的公式只是设计中的一部分,还需要根据具体情况进行综合考虑和修改。
总结起来,压缩弹簧设计计算公式主要包括Hooke定律、圈数公式和线径公式,这些公式基于弹簧刚度的定义,用于计算弹簧的物理性能。
在实际应用中,需要根据具体情况选择和修改适合的公式,并结合其他因素进行综合设计。
蝶形弹簧schnorr的选型和计算
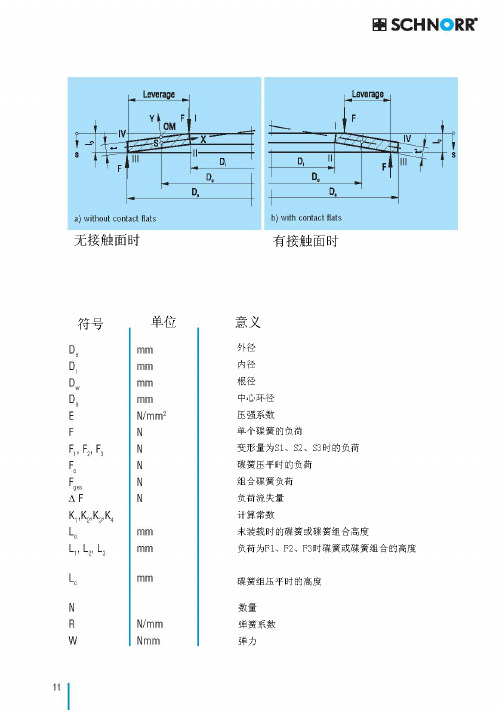
3.1单个碟簧的组合方式休诺碟簧独特的结构使得组合使用碟簧变得极为方便。
多种组合碟簧可以满足各种不同的工况。
原则上可以使用如下的组合方式(figure21):串联组合碟簧并联组合碟簧多片多组串联组合碟簧组合碟簧的特性由单个碟簧的特性和组合方式所决定3.2串联组合碟簧Figure21 中b型图即3片串联组合碟簧,此种组合形式计算公式如下:碟簧载荷量:F ges=F碟簧偏斜:S ges=i*s未装载时碟簧长度:L0=i*I03.3并联组合碟簧(并联请勿超过4片)Figure21 中c型图即双片并联组合碟簧,此种组合形式计算公式如下:碟簧载荷量:F ges=n*F碟簧组偏斜:S ges=i*s未装载时碟簧组长度:L0=I0+(n-1)*t多片并联使用时,由于摩擦起负荷变化如下图:3.4多片多组串联组合碟簧Figure21 中d型图即双片3组串联组合碟簧,此种组合形式计算公式如下:碟簧载荷量:F ges=n*F碟簧组偏斜:S ges=i*s未装载时碟簧组长度:L0=i*[I0+(n-1)*t]注:最佳排列方式为单片少量,串联外径选择越大越好由于摩擦,位移不稳定性随串联片数增加而扩大我们推荐串联总长度L0为:L0<=3*De若实际运用总长度必须超过时,请利用平垫圈均分为2-3段。
3.5碟簧的累进特性当随着碟簧偏移增加时,在许多场合对碟簧有这样一个要求,碟簧的载荷也会累进增加。
碟簧的增加特性比率(对碟簧它是典型的)会代替减少的(如图22所示)。
这样的特性曲线会通过众多方法获得。
用碟簧堆如图23.a所显示将碟簧1,2,3叠加使用,随着载荷的施加,碟簧1,2,3折叠的阶层会变平,这样的一个碟簧堆的特性是由每单个的碟簧特性导致的,如图23所示。
同样的效果也可(图23.b)由不同厚度结合性的碟簧来构成的碟簧堆来获得。
在这个事例中,根据德标2093或SCANORR工厂标准来选择,必须考虑碟簧堆1或2的折叠或薄的单个碟簧被选用在非常高的压力情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
隔振率: T
A
0.90.950.95
传递率: η
0.10.050.05
激励源频率: fn Hz
24.1666666724.1666666710
弹簧固有频率:fo Hz
7.2865241615.2735990142.182178902
弹簧压缩量:h mm
4.6802167838.93495931452.18264433
弹簧刚度:K kg/mm
85.4661265744.767971063.832691934
弹簧承重:W kg
400400200
风机转速:N RPM
14501450600
弹簧减震选型公式使用方法:
输入隔振率TA,风机转速N,弹簧承重W就
可以计算出压缩量h,刚度K,就可以得到
弹簧选型了!
