第八课 SPSS logistic回归分析
Spss软件之logistic回归分析
…
n
0
1
Xn01
X n02
…
1
0
X n11
X n12
…
2
0
Xn21
X n22
…
Xk X 10k X 11 k X 12k
X iMk
X n0k X n1 k X n2k
M
0
XnM1
XnM2
…
X nMk
Conditional logistic regression
用Pi表示第i层在一组危险因素作用下发病的概率, 条 件 logistic 模型可表示为
n
L
1
i1 1
M
k exp
j (X itj X i0 j )
t 1
j1
可以看出，条件logistic 回归分析只估计了表示危 险因素作用的βj值，表示匹配组效应的常数项βi0 则被自动地消去了。
Conditional logistic regression
对上述条件似然函数L取自然对数后，用非线性 迭代法求出参数的估计值bi及其标准误Sbi。回归 系数的假设检验及分析方法与非条件logistic回归 完全相同。
c1 1, c0 0,
Xj
1， 暴露
0，非暴露
ORj exp( j )
Logistic regression analysis
0,
ORj
1
无作用
ORj exp( j ), j >0, ORj 1 危险因子
0, ORj 1 保护因子
二、模型的参数估计
在logistic回归模型中，回归系数的估计通常用最大 似然法（MLE）。其基本思想是先建立一个样本 的似然函数，求似然函数达到最大值时参数的取 值，即为参数的极大似然估计值。
多因素logistic回归分析spss
多因素logistic回归分析spssLogistic回归分析是一种用来研究影响离散变量的因素的方法，该方法的输出是一个logistic模型，这一模型可以用于预测变量的值，即预测该变量的值有多高的概率会取各种可能的取值。
简言之，logistic回归分析的主要目的是把客观的结果（例如，是否改变某个政策，是否感染某种疾病等）变成可预测的离散变量，以便分析影响客观结果的各种因素。
Spss可以提供多因素logistic回归分析，这种分析可用于识别影响离散变量（例如，是否改变某个政策，是否感染某种疾病等）的多个因素之间的关联。
该分析需要有一个组合变量作为自变量，以及一个离散变量作为因变量。
例如，如果您要研究性别和年龄两个因素如何影响某种疾病的发生率，那么性别和年龄两个因素就是组合变量，而疾病的发生率则是因变量。
1.建立变量和分类（上述示例中需要建立性别和年龄两个变量，以及分类变量的可能的取值）。
2.执行logistic回归分析。
打开spss，并在“分析”菜单中打开多元分析，然后点击“逻辑回归”，并选择您要研究的变量和分类。
3.生成回归模型和检验其统计学意义。
在spss中，您可以使用类似“回归系数”之类的描述性统计学方法来估算回归模型，并可以使用“p-值”来判断回归模型中各变量的统计学意义。
4.Interpret模型。
根据p值判断各变量的统计学意义，进而分析影响离散变量的多个因素之间的关联。
四、总结Logistic回归分析是一种用来研究影响离散变量的因素的方法，spss可以提供多因素logistic回归分析，这种分析可用于识别影响离散变量的多个因素之间的关联，spss中步骤：建立变量和分类，执行logistic回归分析，生成回归模型和检验其统计学意义，Interpret模型。
SPSS做Logistic回归步骤
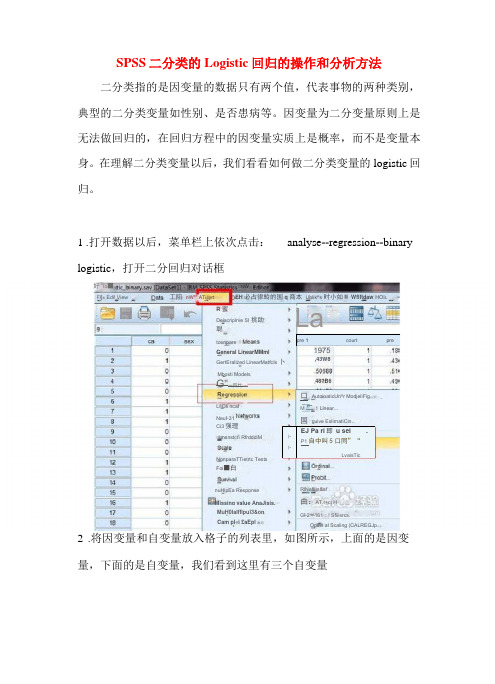
SPSS 二分类的Logistic 回归的操作和分析方法二分类指的是因变量的数据只有两个值，代表事物的两种类别， 典型的二分类变量如性别、是否患病等。
因变量为二分变量原则上是 无法做回归的，在回归方程中的因变量实质上是概率，而不是变量本 身。
在理解二分类变量以后，我们看看如何做二分类变量的logistic 回归。
1 .打开数据以后，菜单栏上依次点击： analyse --regression --binary logistic ，打开二分回归对话框2 .将因变量和自变量放入格子的列表里，如图所示，上面的是因变 量，下面的是自变量，我们看到这里有三个自变量pre 1courtpre卜 卜EJ Pa ri 即 u sei.P1自中叫5口同”“LvaisTic好 Io ■网 □N W□imsnstcri RfrdddiMNonparaTTietrtc Tests Foi ■白MuH0lalfflpul3&on Deiscriplrve SI 挑助聪LfiOli ncaf - Neuf-31 nuHlpEa ResponseMissing value AnaJisis. EH 必占律蛉的国q 商本 Ublik^s 时小如M Wflftdaw HOI LFl[« Edi! View工陷 nW"" ATiilyrtCam pl«i £aEpl 骷与Opsin al Scaling (CALREGJp..R 蜜GertEralized LinearMatfcIs 卜 Mbosti ModelsRlNafllin&af .曲：AT.r+ci HC] 2^^161；! Sfiiisrcs.tosnpareGeneral LinearMMml 48?B6Ci3强理 G"一四忙—一 3 La,43W8口 AutoioaticUn^r ModjeliFig..M 二1 Linear...国 guive EslirnatiCin...C>ep«n (lferit3 .设置回归方法，这里选择最简单的方法：enter ,它指的是将所有的 变量一次纳入到方程。
SPSS中logistics回归分析哑变量设置及结果解读
SPSS中logistics回归分析哑变量设置及结果解读
SPSS中logistics回分析哑变量设置及结果解读
⼀、SPSS 两分类logistics回归分析：分析—回归—⼆元logistic
⼆、在进⾏回归分析时，如果要分析的变量为分类变量（尤其是⽆序多分类变量）
时，通常会将原始的多分类变量转化为哑变量，通过构建回归模型，每⼀个哑变量都能得出⼀个估计的回归系数，从⽽使得回归的结果更易于解释，更具有实际意义。
在SPSS中的实现过程如下：
默认的参考值为最后⼀个，即：赋值最⼤的数；如果想要更改将第⼀个作为参照则需要点击：“第⼀个（F）” –“变化量（H）”，
如下图：出现“x7（指⽰符（first））”时，则说明x7变量是以第⼀个（最⼩的）作为参照。
三、结果：
在输出结果中有“分类变量编码”，即展⽰了分类变量设置为哑变量的编码；
最后结果中，需对照“分类变量编码”进⾏结果解释，在“⽅程中变量” 的“铂种类（1）”则代表的是“顺铂”相对于“其他”的OR值是0.483；“铂种类（2）”则代表的是“奥沙利铂”相对于“其他”的OR值是0.852；…… “肝功能（1）”则代表肝功能异常相对于正常
的OR是3.634。
(完整版)spss的logistic分析教程
Logistic回归主要分为三类，一种是因变量为二分类得logistic回归，这种回归叫做二项logistic回归，一种是因变量为无序多分类得logistic回归，比如倾向于选择哪种产品，这种回归叫做多项logistic回归。
还有一种是因变量为有序多分类的logistic回归，比如病重的程度是高，中，低呀等等，这种回归也叫累积logistic回归，或者序次logistic回归。
二值logistic回归：选择分析——回归——二元logistic，打开主面板，因变量勾选你的二分类变量，这个没有什么疑问，然后看下边写着一个协变量。
有没有很奇怪什么叫做协变量？在二元logistic回归里边可以认为协变量类似于自变量，或者就是自变量。
把你的自变量选到协变量的框框里边。
细心的朋友会发现，在指向协变量的那个箭头下边，还有一个小小的按钮，标着a*b，这个按钮的作用是用来选择交互项的。
我们知道，有时候两个变量合在一起会产生新的效应，比如年龄和结婚次数综合在一起，会对健康程度有一个新的影响，这时候，我们就认为两者有交互效应。
那么我们为了模型的准确，就把这个交互效应也选到模型里去。
我们在右边的那个框框里选择变量a，按住ctrl，在选择变量b，那么我们就同时选住这两个变量了，然后点那个a*b的按钮，这样，一个新的名字很长的变量就出现在协变量的框框里了，就是我们的交互作用的变量。
然后在下边有一个方法的下拉菜单。
默认的是进入，就是强迫所有选择的变量都进入到模型里边。
除去进入法以外，还有三种向前法，三种向后法。
一般默认进入就可以了，如果做出来的模型有变量的p值不合格，就用其他方法在做。
再下边的选择变量则是用来选择你的个案的。
一般也不用管它。
选好主面板以后，单击分类（右上角），打开分类对话框。
在这个对话框里边，左边的协变量的框框里边有你选好的自变量，右边写着分类协变量的框框则是空白的。
你要把协变量里边的字符型变量和分类变量选到分类协变量里边去（系统会自动生成哑变量来方便分析，什么事哑变量具体参照前文）。
spss logistic回归分析
Log
P 1− P
= 1.358 −1.832x1
−
2.140x3
应用Logistic回归分析时的注意事项
1. Logistic回归是乘法模型，这一点，在结果解释时需 要慎重。
对于自变量（X1，X2），OR12=EXP(β1+β2)=OR1×OR2
例：某研究调查胃癌发病的危险因素，得到“有不良饮食习 惯”相对于“无不良饮食习惯”的OR=2.6， “喜吃卤食和盐渍 食物”相对于“不吃卤食和盐渍食物”的OR=2.4。那么根据 Logistic回归，“有不良饮食习惯且喜吃卤食和盐渍食物”相 对于“无不良饮食习惯且不吃卤食和盐渍食物”的 OR=2.6×2.4=6.24，得出此结论时需要考虑：从专业知识上 是否合理？
另法：将X1、X3指定为分类变量。
另法：将X1、X3指定为分类变量。
注：变量编码发生 了变化：0→ 0.5， 1→ -0.5
与前述结果相比，X1与X3的回归系数符号发生了变化，结果解释有 所不同：病情不严重组相对于严重组，OR＝4.928（病情不严重的 患者，其治愈的概率是病情严重的患者的4.928倍）；新疗法组相对 于旧疗法组， OR＝9.707， （接受新疗法的患者，其治愈的概率是 接受旧疗法的患者的9.707倍）。 注：对于二分类变量，可以当作连续变量处理，也可以指定为 分类变量，但要注意结果解释。
2. 通常情况下，自变量为二分类变量时，可以当作连续变 量进入模型（常用0、1或者1、2赋值），也可以通过 “categorical”来指定哑变量。但是，对多分类变量应该 通过“categorical”来指定哑变量，而不宜直接作为连续 变量处理。
多元线性回归分析与Logistic回归分析都是实际工作中 常用的方法，用于影响因素分析时，多元线性回归的因 变量是连续变量，而Logistic回归的因变量是分类变 量；两种方法的自变量可为连续变量或分类变量，当为 分类变量时，均需相应的哑变量（二分类变量例外）。
如何用SPSS做logistic回归分析报告解读汇报
如何用spss17.0进行二元和多元logistic回归分析一、二元logistic回归分析二元logistic回归分析的前提为因变量是可以转化为0、1的二分变量，如：死亡或者生存，男性或者女性，有或无，Yes或No，是或否的情况。
下面以医学中不同类型脑梗塞与年龄和性别之间的相互关系来进行二元logistic回归分析。
（一）数据准备和SPSS选项设置第一步，原始数据的转化：如图1-1所示，其中脑梗塞可以分为ICAS、ECAS和NCAS三种，但现在我们仅考虑性别和年龄与ICAS的关系，因此将分组数据ICAS、ECAS和NCAS转化为1、0分类，是ICAS赋值为1，否赋值为0。
年龄为数值变量，可直接输入到spss中，而性别需要转化为（1、0）分类变量输入到spss当中，假设男性为1，女性为0，但在后续分析中系统会将1，0置换（下面还会介绍），因此为方便期间我们这里先将男女赋值置换，即男性为“0”，女性为“1”。
图1-1第二步：打开“二值Logistic 回归分析”对话框：沿着主菜单的“分析（Analyze）→回归（Regression）→二元logistic （Binary Logistic）”的路径（图1-2）打开二值Logistic 回归分析选项框（图1-3）。
如图1-3左侧对话框中有许多变量，但在单因素方差分析中与ICAS 显著相关的为性别、年龄、有无高血压，有无糖尿病等（P<0.05），因此我们这里选择以性别和年龄为例进行分析。
在图1-3中，因为我们要分析性别和年龄与ICAS的相关程度，因此将ICAS选入因变量（Dependent）中，而将性别和年龄选入协变量（Covariates）框中，在协变量下方的“方法（Method）”一栏中，共有七个选项。
采用第一种方法，即系统默认的强迫回归方法（进入“Enter”）。
接下来我们将对分类（Categorical），保存（Save），选项（Options）按照如图1-4、1-5、1-6中所示进行设置。
SPSS实验8_ 二项Logistic回归分析报告
SPSS作业8：二项Logistic回归分析为研究和预测某商品消费特点和趋势，收集到以往胡消费数据。
数据项包括是否购买，性别，年龄和收入水平。
这里采用Logistic回归的方法，是否购买作为被解释变量（0/1二值变量），其余各变量为解释变量，且其中性别和收入水平为品质变量，年龄为定距变量。
变量选择采用Enter方法，性别以男为参照类，收入以低收入为参照类。
（一）基本操作：（1）选择菜单Analyze－Regression－Binary Logistic;（2）选择是否购买作为被解释变量到Dependent框中，选其余各变量为解释变量到Covariates框中，采用Enter方法，结果如下：消费的二项Logistic分析结果（一）（强制进入策略）. 专业专注.分析：上表显示了对品质变量产生虚拟变量的情况，产生的虚拟变量命名为原变量名（编码）。
可以看到，对收入生成了两个虚拟变量名为Income （1）和Income（2），分别表示是否中收入和是否高收入，两变量均为0时表示低收入；对性别生成了一个虚拟变量名为Gedder（1），表示是否女，取值为0时表示为男。
. 专业专注.消费的二项Logistic分析结果（二）（强制进入策略）Block 0: Beginning Block分析：上表显示了Logistic分析初始阶段（第零步）方程中只有常数项时的错判矩阵。
可以看到：269人中实际没购买且模型预测正确，正确率为. 专业专注.100％；162人中实际购买了但模型均预测错误，正确率为0%。
模型总的预测正确率为62.4％。
消费的二项Logistic分析结果（三）（强制进入策略）分析：上表显示了方程中只有常数项时的回归系数方面的指标，各数据项的含义依次为回归系数，回归系数标准误差，Wald检验统计量的观测值，自由度，Wald检验统计量的概率p值，发生比。
由于此时模型中未包含任何解释变量，因此该表没有实际意义。
如何用SPSS做logistic回归分析解读
如何⽤SPSS做logistic回归分析解读如何⽤spss17.0进⾏⼆元和多元logistic回归分析⼀、⼆元logistic回归分析⼆元logistic回归分析的前提为因变量是可以转化为0、1的⼆分变量，如：死亡或者⽣存，男性或者⼥性，有或⽆，Yes或No，是或否的情况。
下⾯以医学中不同类型脑梗塞与年龄和性别之间的相互关系来进⾏⼆元logistic回归分析。
（⼀）数据准备和SPSS选项设置第⼀步，原始数据的转化：如图1-1所⽰，其中脑梗塞可以分为ICAS、ECAS和NCAS三种，但现在我们仅考虑性别和年龄与ICAS的关系，因此将分组数据ICAS、ECAS和NCAS转化为1、0分类，是ICAS 赋值为1，否赋值为0。
年龄为数值变量，可直接输⼊到spss中，⽽性别需要转化为（1、0）分类变量输⼊到spss当中，假设男性为1，⼥性为0，但在后续分析中系统会将1，0置换（下⾯还会介绍），因此为⽅便期间我们这⾥先将男⼥赋值置换，即男性为“0”，⼥性为“1”。
图1-1第⼆步：打开“⼆值Logistic回归分析”对话框：沿着主菜单的“分析（Analyze）→回归（Regression）→⼆元logistic（Binary Logistic）”的路径（图1-2）打开⼆值Logistic 回归分析选项框（图1-3）。
如图1-3左侧对话框中有许多变量，但在单因素⽅差分析中与ICAS 显著相关的为性别、年龄、有⽆⾼⾎压，有⽆糖尿病等（P<0.05），因此我们这⾥选择以性别和年龄为例进⾏分析。
在图1-3中，因为我们要分析性别和年龄与ICAS的相关程度，因此将ICAS选⼊因变量（Dependent）中，⽽将性别和年龄选⼊协变量（Covariates）框中，在协变量下⽅的“⽅法（Method）”⼀栏中，共有七个选项。
采⽤第⼀种⽅法，即系统默认的强迫回归⽅法（进⼊“Enter”）。
接下来我们将对分类（Categorical），保存（Save），选项（Options）按照如图1-4、1-5、1-6中所⽰进⾏设置。
SPSS-配对条件 Logistic 回归分析
SPSS配对调查资料的条件 Logistic 回归分析（1:1或1:n）1. 1:1 病例对照研究的基本概念在管理工作中，我们也经常要开展对照调查。
例如为什么有的人患了胃癌，有的人却不会患胃癌？如果在同一居住地选取同性别、年龄相差仅±2 岁的健康人作对照调查，调查他们与患胃癌有关的各种影响因素，这就是医学上很常用的所谓“1:1 病例对照研究”。
病例对照研究资料常用条件Logistic 回归分析。
条件Logistic 回归模型（conditional logistic regression model,CLRM)，下称CLRM 模型。
2. 条件Logistic 回归模型的一个实例某地在肿瘤防治健康教育、社区干预工作中做了一项调查，内容是三种生活因素与胃癌发病的关系。
调查的三种生活因素取值见表 11-6。
请拟合条件Logistic 回归模型，说明胃癌发病的主要危险因素。
表 11-6 三种生活因素与胃癌发病关系的取值------------------------------------------------------------------------------------------ 变量名取值范围------------------------------------------------------------------------------------------ X1 (不良生活习惯) 0，1，2，3，4 表示程度（0 表示无，4 表示很多）X2 (喜吃卤食和盐腌食物) 0，1，2，3，4 表示程度（0 表示不吃，4 表示喜欢吃、吃很多） X3 (精神状况) 0 表示差，1 表示好------------------------------------------------------------------------------------------表 11-7 50 对胃癌病例（S=1）与对照（S=0）三种生活习惯调查结果------------------------------------------------------------------------------------------ 病例对照病例对照-----------------------------------------------------------------------------No S X1 X2 X3 No S X1 X2 X3 No S X1 X2 X3 No S X1 X2 X3------------------------------------------------------------------------------------------1 12 4 0 1 03 1 0 26 1 2 2 0 26 0 1 1 02 13 2 1 2 0 0 1 0 27 1 2 0 1 27 0 0 2 13 1 3 0 0 3 0 2 0 1 28 1 1 1 1 28 0 3 0 14 1 3 0 0 4 0 2 0 1 29 1 2 0 1 29 0 4 0 05 1 3 0 1 5 0 0 0 0 30 1 3 1 0 30 0 0 2 16 1 2 2 0 6 0 0 1 0 31 1 1 0 1 31 0 0 0 07 1 3 1 0 7 0 2 1 0 32 1 4 2 1 32 0 1 0 18 1 3 0 0 8 0 2 0 0 33 1 4 0 1 33 0 2 0 19 1 2 2 0 9 0 1 0 1 34 1 2 0 1 34 0 0 0 110 1 1 0 0 10 0 2 0 0 35 1 1 2 0 35 0 2 0 111 1 3 0 0 11 0 0 1 1 36 1 2 0 0 36 0 2 0 112 1 3 4 0 12 0 3 2 0 37 1 0 1 1 37 0 1 1 013 1 1 1 1 13 0 2 0 0 38 1 0 0 1 38 0 4 0 014 1 2 2 1 14 0 0 2 1 39 1 3 0 1 39 0 0 1 015 1 2 3 0 15 0 2 0 0 40 1 2 0 1 40 0 3 0 116 1 2 4 1 16 0 0 0 1 41 1 2 0 0 41 0 1 0 117 1 1 1 0 17 0 0 1 1 42 1 3 0 1 42 0 0 0 118 1 1 3 1 18 0 0 0 1 43 1 2 1 1 43 0 0 0 019 1 3 4 1 19 0 2 0 0 44 1 2 0 1 44 0 1 0 020 1 0 2 0 20 0 0 0 0 45 1 1 1 1 45 0 0 0 121 1 3 2 1 21 0 3 1 0 46 1 0 1 1 46 0 0 0 022 1 1 0 0 22 0 2 0 1 47 1 2 1 0 47 0 0 0 023 1 3 0 0 23 0 2 2 0 48 1 2 0 1 48 0 1 1 024 1 1 1 1 24 0 0 1 1 49 1 1 2 1 49 0 0 0 125 1 1 2 0 25 0 2 0 0 50 1 2 0 1 50 0 0 3 1------------------------------------------------------------------------------------------- 3. 条件Logistic 回归模型的拟合原理与方法本例以 SPSS 软件包来拟合 CLRM 模型。
详解利用SPSS进行Logistic_回归分析
第8 章利用SPSS 进行Logistic 回归分析现实中的很多现象可以划分为两种可能，或者归结为两种状态，这两种状态分别用0和1 表示。
如果我们采用多个因素对0－1 表示的某种现象进行因果关系解释，就可能应用到logistic 回归。
Logistic 回归分为二值logistic 回归和多值logistic 回归两类。
首先用实例讲述二值logistic 回归，然后进一步说明多值logistic 回归。
在阅读这部分内容之前，最好先看看有关SPSS 软件操作技术的教科书。
§8.1 二值logistic 回归8.1.1 数据准备和选项设置我们研究2005 年影响中国各地区城市化水平的经济地理因素。
城市化水平用城镇人口比重表征，影响因素包括人均GDP、第二产业产值比重、第三产业产值比重以及地理位置。
地理位置为名义变量，中国各地区被分别划分到三大地带：东部地带、中部地带和西部地带。
我们用各地区的地带分类代表地理位置。
第一步：整理原始数据。
这些数据不妨录入Excel 中。
数据整理内容包括两个方面：一是对各地区按照三大地带的分类结果赋值，用0、1 表示，二是将城镇人口比重转换逻辑值，变量名称为“城市化”。
以各地区2005 年城镇人口比重的平均值45.41%为临界值，凡是城镇人口比重大于等于45.41%的地区，逻辑值用Yes 表示，否则用No 表示（图8-1-1）图8-1-1 原始数据（Excel 中，局部）将数据拷贝或者导入SPSS 的数据窗口（Data View）中（图8-1-2）。
图8-1-2 中国31 个地区的数据（SPSS 中，局部）第二步：打开“聚类分析”对话框。
沿着主菜单的“Analyze→Regression→Binary Logistic K”的路径（图8-1-3）打开二值Logistic 回归分析选项框（图8-1-4）。
图8-1-3 打开二值Logistic 回归分析对话框的路径对数据进行多次拟合试验，结果表明，像二产比重、三产比重等对城市化水平影响不显著。
SPSS课件logistic回归分析
Logistic回归分析
Log.sav
关于考试
考试时间：下周的上课时间
每人准备一张软盘，在软盘上注明姓名、学 号
Logistic回归分析
数据背景（data13-02） 北京医科大学附属人民医院内分泌科卢纹凯教授课题。 颈总动脉中层厚度imt>0.8mm或有斑块定义为动脉硬 化，因变量type值为1；非硬化imt＜0.8mm且无斑块， 因变量type值为0。糖尿病患者123例数据。研究哪 些指标可以判断糖尿病患者是否动脉硬化。自变量 AGE年龄、ALB尿白蛋白、BMI体重指数、ISI胰岛素 敏感指数、SBP收缩压、TG甘油三脂、CHO胆固醇、 DURA糖尿病程。其中尿白蛋白、甘油三脂、胆固醇 三项生化指标在回归估计过程中均使用他们的对数变 量：ALBLN、TGLN、CHOLN。
级分组资料或是计量资料，此时，可以使用logistic
回归来分析பைடு நூலகம்变量（二值变量）与自变量的关系。
三、 Logistic回归分析
Categorical 多分类变量的比较
Save 功能按钮
Option 功能按钮
Logistic回归分析
为研究急性肾衰（AFR）患者死亡的危险因素，经回顾性
调查分析，获得某医院1999～2000年中所有发生AFR的
422名患者的临床资料见数据文件logistic.sav。本资料共涉 及29个变量，分别是：sex, age, 社会支持，慢性病，手术，
肿瘤，糖尿病，动脉硬化，器官移植，cr（血肌酐），hg
（血红蛋白），肾毒性，少尿，lbp，黄疸，昏迷，辅助呼 吸，心衰，肝衰，出血，呼衰，器官衰竭，胰腺炎，dic， 败血症，感染，hbp，透析方式，死亡。其中器官衰竭、和 透析方式为多分类变量，分别有6个和4个水平，定量变量 有age，cr，hg；其余为二分类变量。
如何用spss实现配比的条件logistics回归分析
如何用spss实现配比的条件logistics回归分析孙大鹏sundapeng87@仅以此篇献给那些专注于使用spss而不会使用sas、R、epiinfo 等统计软件的同志，spss是大家用的非常广泛的统计工具，它的数据管理非常直观，但是有一点就是它的回归分析中没有条件logistics回归分析模块。
而这个分析模块在后三个软件中可以轻松实现。
下面就给大家介绍一下如何使用spss进行条件logistics回归分析。
原理就是利用生存分析中的cox回归模型。
一、变量准备。
（一）首先我们准备好的数据应该有个因变量y，为0，1格式的，0代表对照或未发病，1代表病例或已发病。
（二）我们要分析的自变量x1，x2，一般为二分类变量，1或0，是否。
当然也可以是多组的分类变量，这个比较麻烦（一般不推荐，后面结果分析会说一下）。
（三）分组变量标注分组的代码group。
假设1：4配比，这5个个案为一组，共用一个group号。
（四）Cox回归模型，需要一个time的生存时间变量，这个变量我们这样设置，首先有个因变量y，为0，1格式的，计算time=2-y。
这样子就是设置成病例生存时间为1，对照生存时间为2。
病例发病对照不发病，对照的生存时间必然要长于病例。
数据见附件1二、操作步骤（一）数据导入spss。
不会的回家自己学去。
（二）分析----生存函数----Cox回归打开对话框（三）选取变量，第一时间选入time变量；第二个状态选入y 即病例和对照，定义事件为为1；协变量选择X，你要分析的因素方法选择向前条件分层选择group；重要选项中可以设置计算可信区间（四）结果判读Sig 为P值；B为系数；Exp（B）为OR值，后面为OR值可信区间三、关于x为分类变量，并且为多组时的问题（一）需要对协变量设置分类，选择第一个后，记得要点击更改。
如果选入变量，分类按钮为灰色，这是请点击分层的变量，移出再移入，分类按钮就变换过来了。
（二）这个样子就可以计算分析了，但是结果的显示数据正确，但是结果表格OR值和X分类变量的对应关系混乱。
Logistic回归spss
4、回归系数βi的意义
流行病学的常用指标优势比（odds ratio,OR)或称比数比，定义为：暴露 人群发病优势与非暴露人群发病优势 之比。 P1 /(1 P1 ) 即Xi的优势比为： OR P0 /(1 P0 )
Ln(OR) log it[ P(1)] log it[ P(0)] ( 0 i 1) ( 0 i 0) i
a
N 121 0 121 0 121
Pe rce nt 100.0 .0 100.0 .0 100.0
a. If weight is in effect, see classification t able for th e total numb er of case s.
2. 因变量的编码
De pendent Variable Encoding Original Value Intern al Val ue 无 0 有 1
经数学变换得
ln[ p /(1 p)] 0 1 X 1 p X p
定义Logistic变换
log it ( p) ln[ p /(1 p)]
Logistic回归方程
Logit( p) 0 1 X 1 p X p
逐步Logistic回归分析
（1）向前法(forward selection)
开始方程中没有变量，自变量 由少到多一个一个引入回归方程。 按自变量对因变量的贡献（P值的大 小）由小到大依次挑选，变量入选 的条件是其P值小于规定进入方程的 P界值Enter, 缺省值 P(0.05)。
（2）后退法(backward selection) 开始变量都在方程中，然后 按自变量因变量的贡献（P值的大 小）由大到小依次剔除，变量剔 除的条件是其P值小于规定的剔除 标准Remove, 缺省值 p(0.10)。
如何用SPSS做logistic回归分析
如何用spss17.0进行二元和多元logis tic回归分析一、二元logis tic回归分析二元logis tic回归分析的前提为因变量是可以转化为0、1的二分变量，如：死亡或者生存，男性或者女性，有或无，Yes或No，是或否的情况。
下面以医学中不同类型脑梗塞与年龄和性别之间的相互关系来进行二元logist ic回归分析。
（一）数据准备和SP SS选项设置第一步，原始数据的转化：如图1-1所示，其中脑梗塞可以分为ICAS、ECAS和NC AS三种，但现在我们仅考虑性别和年龄与ICAS的关系，因此将分组数据ICAS、ECAS和NC AS转化为1、0分类，是ICAS赋值为1，否赋值为0。
年龄为数值变量，可直接输入到s pss中，而性别需要转化为（1、0）分类变量输入到spss当中，假设男性为1，女性为0，但在后续分析中系统会将1，0置换（下面还会介绍），因此为方便期间我们这里先将男女赋值置换，即男性为“0”，女性为“1”。
图1-1第二步：打开“二值Logis tic 回归分析”对话框：沿着主菜单的“分析（Analyze）→回归（Regress ion）→二元logis tic （BinaryLogisti c）”的路径（图1-2）打开二值Log istic回归分析选项框（图1-3）。
如图1-3左侧对话框中有许多变量，但在单因素方差分析中与IC AS 显著相关的为性别、年龄、有无高血压，有无糖尿病等（P<0.05），因此我们这里选择以性别和年龄为例进行分析。
在图1-3中，因为我们要分析性别和年龄与ICAS的相关程度，因此将ICAS选入因变量（Depende nt）中，而将性别和年龄选入协变量（Covaria tes）框中，在协变量下方的“方法（Method）”一栏中，共有七个选项。
利用SPSS进行Logistic回归分析
利用SPSS进行Logistic回归分析第8章利用SPSS进行Logistic回归分析现实中的很多现象可以划分为两种可能，或者归结为两种状态，这两种状态分别用0和1表示。
如果我们采用多个因素对0－1表示的某种现象进行因果关系解释，就可能应用到logistic回归。
Logistic回归分为二值logistic回归和多值logistic回归两类。
首先用实例讲述二值logistic回归，然后进一步说明多值logistic回归。
在阅读这部分内容之前，最好先看看有关SPSS软件操作技术的教科书。
§8.1 二值logistic回归8.1.1 数据准备和选项设置我们研究2005年影响中国各地区城市化水平的经济地理因素。
城市化水平用城镇人口比重表征，影响因素包括人均GDP、第二产业产值比重、第三产业产值比重以及地理位置。
地理位置为名义变量，中国各地区被分别划分到三大地带：东部地带、中部地带和西部地带。
我们用各地区的地带分类代表地理位置。
第一步：整理原始数据。
这些数据不妨录入Excel中。
数据整理内容包括两个方面：一是对各地区按照三大地带的分类结果赋值，用0、1表示，二是将城镇人口比重转换逻辑值，变量名称为“城市化”。
以各地区2005年城镇人口比重的平均值45.41%为临界值，凡是城镇人口比重大于等于45.41%的地区，逻辑值用Yes表示，否则用No表示（图8-1-1）。
图8-1-1 原始数据（Excel中，局部）将数据拷贝或者导入SPSS的数据窗口（Data View）中（图8-1-2）。
图8-1-2 中国31个地区的数据（SPSS中，局部）第二步：打开“聚类分析”对话框。
沿着主菜单的“Analyze→Regression→Binary LogisticK”的路径（图8-1-3）打开二值Logistic回归分析选项框（图8-1-4）。
图8-1-3 打开二值Logistic回归分析对话框的路径对数据进行多次拟合试验，结果表明，像二产比重、三产比重等对城市化水平影响不显著。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ln P 1 P
=
0
1 X1
2
X
2
m
X
m
检验方法（讲义260-261页） 1）似然比检验 (likelihood ratio test) 2）Wald检验
例表16-1吸烟、饮酒与食管癌资料 （SAS软件计算）
1.对建立的整个模型做检验。
Testing Global Null Hypothesis: BETA=0
包括 l 个自变量的 对数似然函数
G服从自由度（d）=p-l的χ2分布
似然比检验对β做检验
例：X1为吸烟，X2为饮酒，检验饮酒与食 管癌关系，H0：β2=0，H1：β2≠0
log it( p) 0 1x1 2x2
log it( p) 0 1x1
G ＞3.84，p＜0.05，说明调整吸烟因素 后，饮酒与食管癌有关系。
比发生Y事件的对数优势比。
回归系数β与ORi
X与Y的关联
β=0，OR=1，
无关
β＞1，OR＞1 ， 有关，危险因素
β＜1，OR＜1， 有关，保护因子
事件发生率很小，OR≈RR。
二、logistic回归模型的参数估计
1. 模型中的参数（βi）估计
，
ln P 1 P
=
0
1 X1
2
X
2
m
X
m
通常用最大似然函数 (maximum likelihood estimate， MLE)估计β， 由统计软件包完成。
成不一致干扰疗效分析，通过该法可控制 非处理因素，正确评价疗效。
3.预测与判别 预测个体在某因素存在条件下，发生某事件
（发病）的概率，为进一步治疗提供依据。
例1
例：
表5-4甲乙两疗法某病治愈率%比较
病型
甲疗法
病人 治愈 治愈
数
数
率
普通型 重型 合计
300 100 400
180 35 215
60.0 35.0 53.8
Test Chi-Square DF Pr 似然比 68.5457 2 <.0001 计分检验 67.0712 2 <.0001 Wald检验 64.2784 2 <.0001
2.检验二：
检验模型中某β是否对Y有作用。
检验假设： H 0 : j 0 H1 : j 0
检验统计量：主要为Wald检验（SAS软件）
2 ( bj )2 ν=1的χ2
例；
S2 bj (0.8856)2 33.86
0.15
在大样本时，三方法结果一致。
例表16-1资料，对各x的β做检验（wald检验） 参数 β估计值 标准误 Chi-Squa Pr 常数-0.9099 0.1358 44.8699 .0001 吸烟 0.8856 0.1500 34.8625 .0001 饮酒 0.5261 0.1572 11.2069 .0008
方程如下：
线形 关系
y log it( p) 0 1x1 Y～（-∞至+∞）
截距（常数）
回归系数
在有多个危险因素（Xi）时
多个变量的logistic回归模型方程的线性表达：
logit(p)
ln
1
P P
=
0
1
X1
2
X
2
m
X
m
或
p( y 1/ x1, x2
x ) 1 e 1 k
( 0 1xk ....k xk )
乙疗法
病人 治愈
数
数
治愈 率
100 300 400
65 65.0 125 41.7 190 47.5
表5-5直接法计算标准化治愈率
病型 标准
甲疗法
乙疗法
治疗 原治 预期
原治 预期
人数 愈率 治愈数 愈率 治愈数
普通型 400 60.0 240
65.0 260
重型 400 35.0 140
41.7 167
例：暴露因素 高血压史(x1)：有 或无 高血脂史(x2)： 有 或 无 吸烟(x3)： 有或无
冠心病结果 有 或无
研究问题可否用多元线性回归方法？
yˆ a b1x1 b2x2 bmxm
1.多元线性回归方法要求 Y 的取值为计量 的连续性随机变量。
2.多元线性回归方程要求Y与X间关系为线 性关系。
exp(0.5261) OR 1.6923
OR的可信区间估计
吸烟与不吸烟患食管癌OR的95%可信区间：
饮酒与不饮酒OR的95%可信区间：
三、Logistic 回归模型的假设检验
1.检验一：对建立的整个模型做检验。
说明自变量对Y的作用是否有统计意义。
H0 : 1 2 m 0
H1 : 各（j j 1，2，，m)不全为0
Intercept -0.6453 0.1653 15.24 <.0001
疗法
0.2482 0.1699 2.13 0.1442
病情
0.9900 0.1699 33.93 <.0001
Odds Ratio Estimate
Point 95% Wald
Effect Estimate Confidence Limits
变量 β
Sb Waldχ2 P
标准β’ OR
常数 -4.705 1.54 9.30 年龄 0.924 0.477 3.76 X5 1.496 0.744 4.04 X6 3.136 1.249 6.30 X8 1.947 0.847 5.29
0.0023 0.0525 0.0443 0.0121 0.0215
饮酒 不饮酒
经logistic回归计算后得 b0 =-0.9099， b1 =0.8856， b2
=l0n.(52p61) ：
exp( ) OR
exp(0.8856) OR 2.4244
控制饮酒因素后， 吸烟与不吸烟相比 患食管癌的优势比 为2.4倍
Odds Ratio Estimates Point 95% Wald
Effect Estimate Confidence Limits 吸烟x1 2.424 1.807 3.253 饮酒x2 1.692 1.244 2.303
似然比检验（讲义）
对某个β做检验，检验统计量（G）
包括p个自变量的对 数似然函数
p( y 1)
1
P概率
1
1 exp[(0 x)]
z 0 1x
0.5
Β为正值，x越 大，结果y=1发 生的可能性（p） 越大。
-3 -2 -1 0 1
Z值 23
图16-1 Logistic回归函数的几何图形
几个logistic回归模型方程
e0 x p1 P( y 1/ x 1) 1 e0 x
P( y
0/ x
1)
1
1
e0 x e0
x
1
p1
e0 p0 P( y 1/ x 0) 1 e0
e0 P( y 0 / x 0) 1 1 e0 1 p0
logistic回归模型方程的线性表达
对logistic回归模型的概率（p）做logit变
换， log it( p) ln( p ) 1 p
疗法 1.282
0.919 1.788
病情 2.691
1.929 3.755
例2 性别、两种药物对某病疗效的研究
性别
治疗方法
疗效
有效
无效 合计
（y=1） （y=0）
女
新药（x2=1） 21
6
27
X1=1 对照（x2=0） 13
19
32
男
新药（x2=1） 7
7
14
X1=0 对照（x2=0） 1
10
11
logistic回归分析
logistic回归为概率型非线性 回归模型，是研究分类观察 结果(y)与一些影响因素(x) 之间关系的一种多变量分析 方法
问题提出：
医学研究中常研究某因素存在条件下某结果是否 发生？以及之间的关系如何？
因素（X）
疾病结果（Y）
x1，x2，x3…XK
发生
Y=1
不发生 Y=0
成组（未配对）设计的病例对照研究资料，计算的 Logistic回归模型为非条件Logistic回归。
例：见265页 区别： 条件Logistic回归的参数估计无常数项（β0），主
要用于危险因素的分析。
第三节 logistic回归的应用及注意事 项
一、logistic回归的应用
1.疾病（某结果）的危险因素分析和筛选 用回归模型中的回归系数（βi）和OR说明
Y 发病=1 不发病=0
危险因素
x= 1 x= 0
30（a） 10（ b）
70（c） 90（d）
a+c
b+d
危险因素
x= 1 x= 0
p1 1-p1
p0 1-p0
a p1 a c
有暴露因素人群中发病的比例
多元回归模型的的 i概念
logit(p)
ln
1
P P
=
0
1
X1
mXm
i 反映了在其他变量固定后，X=1与x=0相
第一节 logistic回归
1.基本概念 logistic回归要求应变量（Y）取值为分类变量
（两分类或多个分类）
1 Y 0
出现阳性结果 (发病、有效、死亡等） 出现阴性结果 (未发病、无效、存活等）
自变量（Xi）称为危险因素或暴露因素，可为连续变 量、等级变量、分类变量。 可有m个自变量X1， X2，… Xm
OR e
如X=1，0两分类，则OR的1-α可信区间 估计公式