标号法求最短路径例题详解
标数法: 用来解决计算最短路线问题的方法,在给出的图形中

“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
7.
一只密蜂从 A 处出发, A 回到家里 B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而 不准逆行,共有多少种回家的方法?
1 A 2 3 4 5 6 7 8 9 B
8. 在图中,用水平或垂直的线段连接相邻的字母,当沿着这些线段行走时,正好拼出 “ APPLE ”的路线共有多少条?
“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
有问题跟我联系哦!wutong@ 【数学加油站答案】
1.
A E1 1 C 1 F2 3 1 D
3G 6 B
H
I
2. 首先明确三天所走的路线有什么不同?每天的路线有无限制条件?若有, 是什么?搞清 楚这些问题后,仍然用标数法求解.第一天(无限制条件)共有 16 条;第二天(必须 经过公园)共有 8 条;第三天(必须不经过公园)共有 8 条. 3. 因为 B 在 A 的右下方,由标号法可知,从 A 到 B 的最短路径上,到达任何一点的走法 数都等于到它左侧点的走法数与到它上侧点的走法数之和. 有积水的街道不可能有路线 经过,可以认为积水点的走法数是 0.接下来,可以从左上角开始,按照加法原理,依 次向下向右填上到各点的走法数.如右上图,从 A 到 B 的最短路线有 22 条.
“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
标数法: 用来解决计算最短路线问题的方法,在给出的图形中 的每一个结点标出到达该点的方法 数,最后利用相加的原则求出到达目 的地的方法数。
从 A 到 B 的最短路线有多少条?
“为什么蜈蚣出门要这么长时间呢?” “因为它要穿鞋呀… …”
5. 用“标数”求出:从学校到养老院共 126 条.必经过市中心的 60 条,所以可行的路有: 126 60 66 (条) .
仓储习题
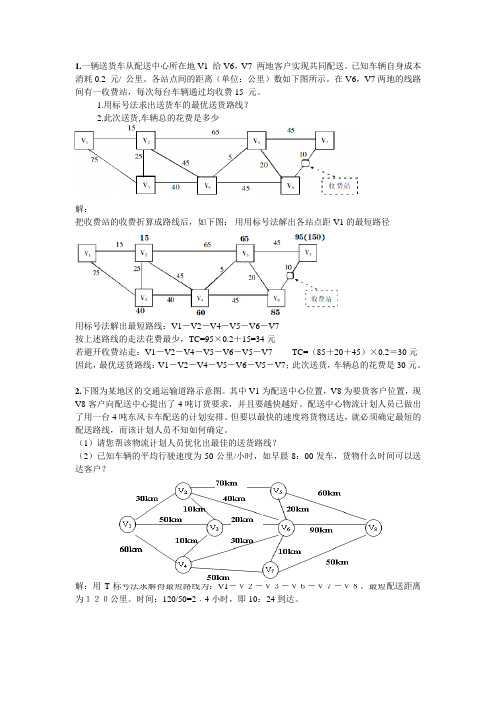
1.一辆送货车从配送中心所在地V1 给V6,V7 两地客户实现共同配送。
已知车辆自身成本消耗0.2 元/ 公里。
各站点间的距离(单位:公里)数如下图所示。
在V6,V7两地的线路间有一收费站,每次每台车辆通过均收费15 元。
1.用标号法求出送货车的最优送货路线?2.此次送货,车辆总的花费是多少解:把收费站的收费折算成路线后,如下图:用用标号法解出各站点距V1的最短路径用标号法解出最短路线:V1-V2-V4-V5-V6-V7按上述路线的走法花费最少,TC=95×0.2+15=34 元若避开收费站走:V1-V2-V4-V5-V6-V5-V7 TC=(85+20+45)×0.2=30 元因此,最优送货路线:V1-V2-V4-V5-V6-V5-V7;此次送货,车辆总的花费是30 元。
2.下图为某地区的交通运输道路示意图。
其中V1为配送中心位置,V8为要货客户位置,现V8客户向配送中心提出了4吨订货要求,并且要越快越好。
配送中心物流计划人员已做出了用一台4吨东风卡车配送的计划安排。
但要以最快的速度将货物送达,就必须确定最短的配送路线,而该计划人员不知如何确定。
(1)请您帮该物流计划人员优化出最佳的送货路线?(2)已知车辆的平均行驶速度为50公里/小时,如早晨8:00发车,货物什么时间可以送达客户?解:用T标号法求解得最短路线为:V1-V2-V3-V6-V7-V8。
最短配送距离为120公里。
时间:120/50=2﹒4小时,即10:24到达。
3.某物流公司拟建一仓库负责向四个工厂进行物料供应配送,各工厂的具体位置与年物料配送量于下表,请利重心法(91页)确定物流公司的仓库位置,设拟建物流公司仓库对各工厂的单位运输成本相等。
4.随着业务的发展,该公司在四个城市都设置了配送中心,并在城市4设置了一个总仓库为四个配送中心送货,各配送中心的位置(Xi,Yi)及其日常送货数量qi(车)如表3所示。
由于需求增加过快和成本过高等原因,该公司正在设想将仓库从城市C4搬出,另外选址建设一个仓库。
标号法

标号法标号法是一种最佳算法,多用于求图的最短路问题。
一、标号法的概念:所谓标号,是指与图的每一个顶点相对应的一个数字。
标号法可以说是动态规划,它采用顺推的方法,对图的每一边检测一次,没有重复的回溯搜索,因此标号法是一种最佳算法。
二、标号法的算法流程:现有一图G,求从起点Vs到终点Ve的最短距离。
设:Sum(j)───顶点Vj的标号,代表的是Vs到Vj的最短距离。
Vj•已标味着Vs到Vj的最短路以及这条路径的长度已求出。
M(i,j)───Vi到Vj的非负长度。
H(j)───顶点Vj的前趋结点。
标号法的算法流程如下:sum(s)←0↓Vs进入队列L↓-----→移出队列L的队首Vk←-----| ↓ || Vk是不是Ve------------------|---→计算结束打印路径| N∣ Y || ↓ || 由Vk扩展出结点Vj || (Vk与Vj之间相连) || Sj←Sum(k)+M(k,j) || ↓ || Sj小于Sum(j) || | || Y | N || | --------------------| || ↓| Sum(j)←Sj| H(j)← Vk| Vj加入队列L并对队列L按Sum值由小到大排序| ↓---------------注意:1.只有两个顶点间的距离为非负时,才可用标号法。
2.只有队列的首结点是目标结点时,才可停止计算。
•否则得出的不一定是最优解。
三、例题解析:1.相邻项序列(GDOI97第四题)问题描述:对于一个N*N(<=100)的正整数矩阵M,存在从M[A1,•B1] •开始到M[A2,B2]结束的相邻项序列.两个项M[I,J]和M[K,L]•相邻的件是指满足如下情况之一:(1)I=K+-1和J=L(2)I=K和J=L+-1。
任务:从文件中输入矩阵M,再读入K(K<=4)组M[A1,B1]和M[A2,B2]的值。
对于每一组M[A1,B1]和M[A2,B2],求一相邻项序列,使得相邻项之差的绝对值之和为最小。
最短路径与标号法

最短路径与标号法前面我们学习过动态规划的应用,图中没明显阶段求最短路径的问题属于无明显阶段的动态规划,通常用标号法求解,求最短路径问题是信息学奥赛中很重要的一类问题,许多问题都可转化为求图的最短路径来来解,图的最短路径在图论中有经典的算法,本章介绍求图的最短路径的dijkstra算法、Floyed算法,以及标号法。
一、最短路径的算法1、单源点最短路径(dijkstra算法)给定一个带权有向图G=(V,E),其中每条边的权是一个非负实数,另外,还给定V中的一个顶点,称为源点。
求从源点到所有其他各顶点的最短路径长度。
这个问题称为单源最短路径问题。
求单源最短路径可用dijkstra算法求解。
(dijkstra算法)算法思想:设源点为x0,dist[i]表示顶点i到源点x0的最短路径长度,map[i,j]表示图中顶点i到顶点j的长度,用数组mark对所有的顶点作标记,已求出源点到达该点J的最短路径的点J记为mark[j]=true,否则标记为false。
初始时,对源点作标记,然后从未作标记的点中找出到源点路径长度最短的顶点minj,对该顶点作标记,并对其它未作标记的点K作判断:if dist[minj]+map[minj,k]<dist[k] then dist[k]= dist[minj]+map[minj,k]。
重复处理,直到所有的顶点都已作标记,这时求出了源点到所有顶点的最短路径。
算法过程:const maxn=100;varmap: array[1..maxn,1..maxn] of integer;dist: array[1..maxn] of integer;mark: array[1..maxn] of Boolean;n,k: integer;procedure dijkstra;var I,j,min,minj,temp:integer;beginfillchar(mark,sizeof(mark),0);for I:=1 to n do dist[i]:=maxint;dist[k]:=0;for I:=1 to n-1 dobeginmin:=maxint;for j:=1 to n doif (not mark[j]) and (dist[j]<min) thenbeginmin:=dist[j]; minj:=j;end;mark[minj]:=true;for j:=1 to n doif (not mar[j]) and (map[minj,j]>0) thenbegintemp:=dist[minj]+map[minj,j];if temp<dist[j] then dist[j]:=temp;end;end;end;以上只是求出了从源点到其它所有点的最短路径长度,所经过的具体路径没有保存,如果要求出具体的路径来,那么在求最短路径的过程中要将经过的中间点记录下来。
dijkstra标号法例题

dijkstra标号法例题
Dijkstra标号法是一种用于求解带权图中单源点最短路径的算法。
以下是一个Dijkstra标号法的例题:
题目:已知一个带权图,求顶点A到其他所有顶点的最短路径。
图中的顶点及其权重如下:
顶点:A(0),B(4),C(3),D(2),E(1)
边权:AB(1),AC(2),AD(3),AE(4),BC(1),BD(2),BE(3),CD(1),DE(1)
以下是使用Dijkstra标号法求解的过程:
1. 初始化:将起点A的标号设为0,其他顶点的标号设为无限大。
2. 将起点A加入优先队列中。
3. 从优先队列中取出距离起点最近的点,这里是最小权值为0的A。
将A的邻接顶点B、C、D、E的标号更新为1(即距离A的最短路径长度为1)。
4. 修改从A出发到集合V-S(已找到最短路径的顶点)上任一顶点K 的最短路径长度。
如果d[K]大于d[A] + a[A,K],则修改为d[K] = d[A] + a[A,K]。
在本例中,修改B、C、D、E到其他顶点的距离。
5. 重复步骤3和4,直到所有顶点都获得最短路径。
最终得到的最短路径如下:
A -> B(1) -> E(2) -> D(3) -> C(4)
需要注意的是,Dijkstra标号法得到的最短路径是单源点A到其他顶点的最短路径,而非A到B、A到C等两点之间的最短路径。
如需求解两点之间的最短路径,可以分别以两个顶点为起点,重复上述过程。
最短路径问题的求解PPT精选文档

.
3
最短路径问题的求解
三、等代价搜索法 等代价搜索法也是在宽度优先搜索的基础上进行了部分优化的一种算法,它与
启发式搜索的相似之处都是每次只展开某一个结点(不是展开所有结点),不同之 处在于:它不需要去另找专门的估价函数,而是以该结点到A点的距离作为估价值, 也就是说,等代价搜索法是启发式搜索的一种简化版本。它的大体思路是:
.
2
最短路径问题的求解
二、 启发式搜索 在宽度优先搜索算法的基础上,每次并不是把所有可展开的结点展开,
而是对所有没有展开的结点,利用一个自己确定的估价函数对所有没展开 的结点进行估价,从而找出最应该被展开的结点(也就是说我们要找的答 案最有可能是从该结点展开),而把该结点展开,直到找到目标结点为止。
.
12
最短路径问题的求解
八、Dijkstra算法(从一个顶点到其余各顶点的最短路径,单源最短路径) 例3、如下图,假设C1,C2,C3,C4,C5,C6是六座城市,他们之间的连线表示两 城市间有道路相通,连线旁的数字表示路程。请编写一程序,找出C1到Ci 的最短路径(2≤i≤6),输出路径序列及最短路径的路程长度。
3、由数轴可见,A与A'点相比,A点离原点近,因而保留A点,删除A'点,相应的,B、B'点保留B点, D、D'保留D',E、E'保留E',得到下图:
.
11
最短路径问题的求解
4、此时再以离原点最近的未展开的点B联接的所有点,处理后,再展开离原点最近未展开的D点, 处理后得到如下图的最终结果:
matlab最短路径问题标号法

一、介绍MATLAB是一种非常流行的数学建模和仿真软件,被广泛应用于工程、科学和金融领域。
在MATLAB中,最短路径问题是一个常见的优化问题,通常会涉及到图论、线性代数和优化算法等知识。
在解决最短路径问题时,我们常常需要使用标号法来求解,本文将对MATLAB中最短路径问题的标号法进行介绍。
二、什么是最短路径问题最短路径问题是指在一个加权有向图或无向图中寻找两个顶点之间的最短路径。
在实际应用中,最短路径问题通常涉及到网络规划、路线规划、物流配送等方面。
我们需要求解城市之间的最短路径来设计公交线路,或者求解货物在仓库之间的最短路径来优化物流方案。
三、最短路径问题的标号法在MATLAB中,我们可以使用标号法(Label Correcting Algorithm)来求解最短路径问题。
标号法是一种基于节点标号的启发式算法,它通过不断更新节点的标号信息来逐步搜索最短路径。
下面是标号法的基本思路:1. 初始化:我们需要对图中的节点进行初始化,设置起点的标号为0,其他节点的标号为无穷大。
2. 标号更新:我们开始不断更新节点的标号。
对于每个节点,我们计算通过它能够到达的节点的距离,并将这些距离与当前节点的标号进行比较。
如果通过当前节点到达某个邻居节点的路径距离更短,则更新该邻居节点的标号为当前节点的标号加上当前节点到邻居节点的距离。
3. 节点选择:在标号更新的过程中,我们需要选择一个未加入最短路径的节点,并将其标记为已加入最短路径。
这个过程通常会涉及到优先级队列等数据结构的使用,以便快速找到最短路径的下一个节点。
4. 终止条件:当所有节点都已加入最短路径,或者找到目标节点时,算法终止,最短路径即为标号信息所指示的路径。
四、MATLAB实现最短路径问题的标号法在MATLAB中,我们可以利用图论工具箱和优化工具箱来实现最短路径问题的标号法。
下面是一个简单的MATLAB示例:```matlab创建图N = 5; 节点数E = [1, 2; 1, 3; 2, 3; 2, 4; 3, 4; 3, 5; 4, 5]; 边集L = [1, 2, 3, 4, 5]; 标号W = [1, 2, 3, 4, 5, 6, 7]; 权重G = digraph(E(:, 1), E(:, 2), W);最短路径求解[s, t] = deal(1, N); 起点和终点[P, D] = graphshortestpath(G, s, t, 'Method', 'positive');```在这个例子中,我们首先创建了一个有向图G,并指定了节点数N、边集E、节点标号L和边权重W。
最短路径:标号校正算法

前驱图
假设我们Update(5) 且pred(5)=4
27
前驱图
假设我们Update(4) 且pred(4) := 8. 那么4-8-5-4 有负代价.
在Update(4)前, 以下为 真: d(5) = d(4) + c45 d(8) = d(5) + c58 d(4) > d(8) + c84
d(j) ≤d(i) + cij ,i ∈N ,j ≠1.
(1)
d(1) = 0.
(2)
那么对于每个 j 有 d(j) ≤d*(j).
证明:令 P 是任何一从结点 1 到结点 j的路径,其长度 是c(P),且假设 P 有 k 条弧.
断言: d(j) ≤c(P). 注释: 如果 P 是从 1 到 j的最短路径,那么
当k遍以后,dk(j) ≤dk-1(i) + cij= d*(j).
14
证明结束
定理 FIFO 标号纠正算法对于所有的在N中的j,在 O(nm)步找到从路径1到j的最小路径长度,或者说明 存在一个负代价圈.
证明:如果没有负代价圈,从 1 到j 的最短通路有至多有 n-1条弧,因此n-1遍后,对于所有的j 有d(j) = d*(j).
通过前面的定理得到: d(j) = d*(j).
9
更多关于有限性
如果数据不被要求是整数,将发生什么? 算法仍然是有限的,但是需要使用不同的证明.
如果有一个负代价圈,将会发生什么? 算法也许不再有限. 可能,d(j)保持减小到 -∞ 但是当 d(j)<-nC的时候,我们可以停止它,既然这保 证存在一个负代价圈.
证明. d(j) ≤d*(j). 且, d(j) ≥d*(j), d(j) 是从结点 1 到 结点 j 的某路径的长度. 因此 d(j) = d*(j).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法: 1. v1获p标号: l i( 0 )=0, P0={v1}, T0=V-{v1}, vj(j=2,3,,n)获t 标
号: l j =wij. 令r1.
( r 1 ) min{l (j r 1) } , vi获得p标号: li( r ) li( r 1) . 2. 设 l i v T
5
标号法求最短路径 第三步:
标号法求v0到v5的最短路径
r 0 1 2 vi v0 v1 v2 v3 v4 v5
0
1 1/v0
4 3 3/v0
8 8
6 4
因为第二步得到的数字当中3最小,v2最短为3。 因为通过v2不能直接到达v3,所以v3下面还是8。 通过v2到达v4需要4 到达不了v5
w()=6
9
同理得到第五行,只是得到第五行以后所有都标红了,也就是所有都结束 了,最后加一行,把所有标红的数字重新写一遍,这些数字就是到达相应 vi所需要的最短路径
第六步:
求v0到v5的最短路径
r 0 1 2 3 4 5 w vi
v0
0
v1
1 1/v0
v2
4 3 3/v1
v3
8 8 7 7/v4 7
6
标号法求最短路径 第四步:
标号法求v0到v5的最短路径
r 0 1 2 3 vi v0 v1 v2 v3 v4 v5
0
1 1/v0
4 3 3/v0
8 8 7
6 4 4/v2
10
7
标号法求最短路径 第五步:
标号法求v0到v5的最短路径
r 0 1 2 3 4 vi v0 v1 v2 v3 v4 v5
0
1
4
因为第一步v0只能够到达v1和v2,所以v1和v2下面写到达 的权重,而v3~v5写无穷大。
4
标号法求最短路径 第二步:
标号法求v0到v5的最短路径
r 0 1 vi v0 v1 v2 v3 v4 v5
0
1 1/v0
4 3
8
6
因为第一步得到的数字当中除了已经确定的0以外,1最小, 所以到达v1的最短路径确定了,为1,并且通过v0。 因为通过v1到达v2需要3步,比4小,所以v2处写3。 同理,因为通过v1到达v3和v4的权重和小于正无穷。
0
1 1/v0
4 3 3/v0
8 8 7 7/v4
6 4 4/v2
10 9
8
r 0 1 2 3 4 5 w
vi 0
v0
v1
1 1/v0 4
v2
4 4/v0
v3
v4
v5
6 6/v4 6
0
1
4
8 6 8 5 8 5/v2 8 8/v1 8 5
=v0v1v2v4v3v5,
v4
6 4 4/v2
v5
10 9 9/v3 9
0
1
3
4
=v0v1v2v4v3v5,
w()=9
10
(0)
令 Pr=Pr-1{vi}, Tr=Tr-1-{vi}. 若Tr=, 则结束. 3. vjTr, 令 l (j r ) min {l (j r 1) , l i( r ) wij }
j
r 1
令r=r+1, 转2.
3
标号法求最短路径 第一步:
标号法求v0到v5的最短路径
r 0 vi v0 v1 v2 v3 v4 v5
1
标号法(E.W.Dijkstra, 1959)
设带权图G=<V,E,w>, 其中eE, w(e)0. 设V={v1,v2,,vn}, 求v1到其余各顶点的最短路径 p标号(永久性标号)l i( r ): 第r步获得的v1到vi最短路径的 权 t标号(临时性标号) l i( r ) : 第r步获得的v1经过p标号顶点 到达vi的路径的最小权, 是v1到vi的最短路径的权的上 界 第r步通过集Pr={v | v在第r步已获得永久性标号} 第r步未通过集Tr=V-Pr
最短路径
带权图G=<V,E,w>, 其中w:ER. eE, w(e)称作e的权. e=(vi,vj), 记w(e)=wij . 若vi,vj不 相邻, 记wij =. 设L是G中的一条路径, L的所有边的权之和称作L的 权, 记作w(L). u和v之间的最短路径: u和v之间权最小的通路. 例1 L1=v0v1v3v5, w(L1)=10, L2=v0v1v4v5, w(L2)=12, L3=v0v2v4v5, w(L3)=11.
