信号与系统matlab作业
信号与系统matlab实验报告

信号与系统MATLAB实验报告实验目的本实验旨在通过MATLAB软件进行信号与系统的相关实验,探究信号与系统的特性与应用。
实验步骤1. 准备工作在正式进行实验之前,我们需要做一些准备工作。
首先,确保已经安装好MATLAB软件,并且熟悉基本的操作方法。
其次,准备好实验所需的信号与系统数据,可以是已知的标准信号,也可以是自己采集的实际信号。
2. 信号的生成与显示使用MATLAB编写代码,生成不同类型的信号。
例如,可以生成正弦信号、方波信号、三角波信号等。
通过绘制信号波形图,观察不同信号的特点和变化。
t = 0:0.1:10; % 时间范围f = 1; % 信号频率s = sin(2*pi*f*t); % 正弦信号plot(t, s); % 绘制信号波形图3. 系统的建模与分析根据实验需求,建立相应的系统模型。
可以是线性时不变系统,也可以是非线性时变系统。
通过MATLAB进行模型的建立和分析,包括系统的时域特性、频域特性、稳定性等。
sys = tf([1, 2], [1, 3, 2]); % 系统传递函数模型step(sys); % 绘制系统的阶跃响应图4. 信号与系统的运算对于给定的信号和系统,进行信号与系统的运算。
例如,进行信号的卷积运算、系统的响应计算等。
通过MATLAB实现运算,并分析结果的意义与应用。
x = [1, 2, 3]; % 输入信号h = [4, 5, 6]; % 系统响应y = conv(x, h); % 信号的卷积运算plot(y); % 绘制卷积结果的波形图5. 实验结果分析根据实验数据和分析结果,对实验进行结果总结与分析。
可以从信号的特性、系统的特性、运算结果等方面进行综合性的讨论和分析。
实验总结通过本次实验,我们学习了如何在MATLAB中进行信号与系统的实验。
通过生成信号、建立系统模型、进行运算分析等步骤,我们深入理解了信号与系统的基本原理和应用方法。
通过实验数据和结果分析,我们对信号与系统有了更深刻的认识,并掌握了MATLAB在信号与系统实验中的应用技巧。
信号与系统MATLAB实验课后习题答案
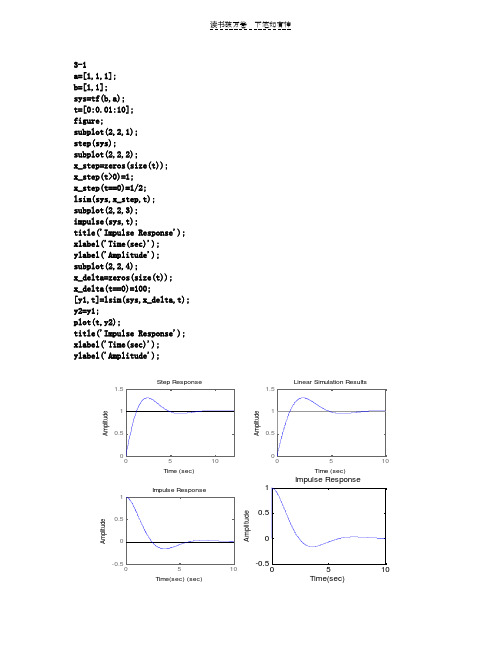
a=[1,1,1]; b=[1,1]; sys=tf(b,a); t=[0:0.01:10]; figure;subplot(2,2,1); step(sys);subplot(2,2,2);x_step=zeros(size(t)); x_step(t>0)=1; x_step(t==0)=1/2; lsim(sys,x_step,t); subplot(2,2,3); impulse(sys,t);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude'); subplot(2,2,4);x_delta=zeros(size(t)); x_delta(t==0)=100;[y1,t]=lsim(sys,x_delta,t); y2=y1;plot(t,y2);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude');00.511.5Step ResponseTime (sec)A m p l i t u d e0.511.5Linear Simulation ResultsTime (sec)A m p l i t u d e510-0.500.51Impulse ResponseTime(sec) (sec)A m p l i t u d e510-0.50.51Impulse ResponseTime(sec)A m p l i t u d e函数int1如下:function [F,tF]=int1(f,tf,a)T=tf(2)-tf(1);F=zeros(size(tf)); tF=zeros(size(tf)); tF=tf; for n=1:length(tf)-1;F(n+1)=F(n)+T*f(n); end验证如下:t=[-1:0.01:4]; e=zeros(size(t)); e=(t>-1/2&t<1);[z,zz]=int1(e,t,-1); figure;plot(zz,z);-1-0.500.51 1.52 2.53 3.5400.511.5T1=1;N1=10000; t1=linspace(0,T1-T1/N1,N1)';f1=1-2*t1;OMG=32*pi;K1=100;omg=linspace(-OMG/2,OMG/2-OMG/K1,K1)';X1=T1/N1*exp(-j*kron(omg,t1.'))*f1;fs1=OMG/2/pi/K1*exp(j*kron(t1,omg.'))*X1;T2=5;N2=10000;t2=linspace(0,T2-T2/N2,N2)';fs2=0*t2;f2=sawtooth(t2*2*pi,0);X2=T2/N2*exp(-j*kron(omg,t2.'))*f2;fs2=fs2+OMG/2/pi/K1*exp(j*kron(t2,omg.'))*X2;figure;subplot(2,2,1);plot(omg,abs(X1),'r');xlabel('Frequency'),ylabel('Amplitude')title('单个锯齿周期幅频特性曲线');subplot(2,2,2);plot(t1,fs1,'r');xlabel('Time'),ylabel('Amplitude')title('Function after recovered');subplot(2,2,3);plot(omg,abs(X2),'r');xlabel('Frequency'),ylabel('Amplitude')title('五个锯齿周期幅频特性曲线');subplot(2,2,4);plot(t2,fs2,'r');xlabel('Time'),ylabel('Function after recovered')title('Function after recovered');-100-5005000.20.40.60.8FrequencyA m p l i t u d e单个锯齿周期幅频特性曲线00.51-1-0.500.51TimeA m p l i t u d eFunction after recovered-100-5005000.511.52FrequencyA m p l i t u d e五个锯齿周期幅频特性曲线246-2-1012TimeF u n c t i o n a f t e r r e c o v e r e dFunction after recovered4-2fsana 函数如下:function F=fsana(t,f,N)omg1=2*pi/(max(t)-min(t)); k=[-N:N]';F=1/length(t)*exp(-j*kron(k*omg1,t.'))*f; fssyn 函数如下:function f=fssyn(F,t)omg1=2*pi/(max(t)-min(t)); N=floor(length(F)/2); k=[-N:N];f=exp(j*kron(t,k*omg1))*F; 验证如下: clc clearclose allT1=1;N1=256; t=linspace(0,T1-T1/N1,N1)'; f=1-2*t;subplot(3,1,1); plot(t,f);title('验证原函数') N=25;F1=fsana(t,f,N); subplot(3,1,2); stem(abs(F1),'s');title('前N 项傅立叶级数系数幅度曲线') f2=fssyn(F1,t) ;subplot(3,1,3); plot(t,f2);xlabel('time[s]'),ylabel('Amplitude'); title('傅立叶逆变换后时域函数');00.10.20.30.40.50.60.70.80.91-101验证原函数00.20.4前N 项傅立叶级数系数幅度曲线00.10.20.30.40.50.60.70.80.91-202time[s]A m p l i t u d e傅立叶逆变换后时域函数。
信号与系统matlab实验2
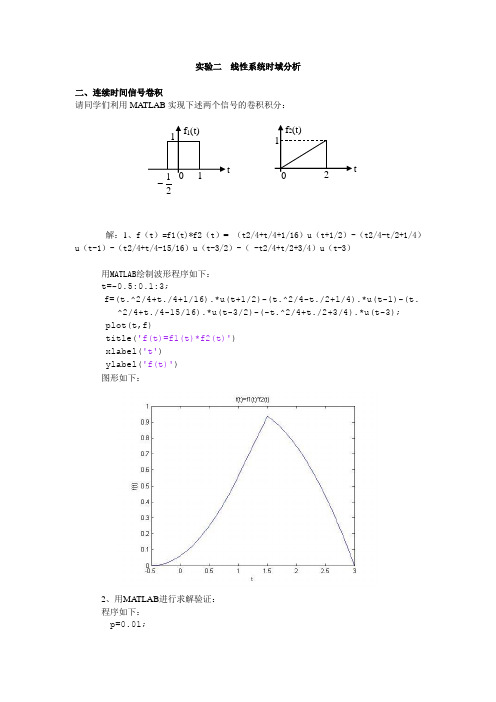
实验二 线性系统时域分析二、连续时间信号卷积请同学们利用MA TLAB 实现下述两个信号的卷积积分:解:1、f (t )=f1(t)*f2(t )= (t2/4+t/4+1/16)u (t+1/2)-(t2/4-t/2+1/4)u (t-1)-(t2/4+t/4-15/16)u (t-3/2)-( -t2/4+t/2+3/4)u (t-3)用MATLAB 绘制波形程序如下:t=-0.5:0.1:3;f=(t.^2/4+t./4+1/16).*u(t+1/2)-(t.^2/4-t./2+1/4).*u(t-1)-(t.^2/4+t./4-15/16).*u(t-3/2)-(-t.^2/4+t./2+3/4).*u(t-3);plot(t,f)title('f(t)=f1(t)*f2(t)')xlabel('t')ylabel('f(t)')图形如下:2、用MA TLAB 进行求解验证:程序如下:p=0.01;k1=-0.5:p:1;f1=0.*k1+1;k2=0:p:2;f2=0.5.*k2;[f,k]=sconv(f1,f2,k1,k2,p);图形如下:三、线性系统时域分析1、连续系统的冲激响应、阶跃响应及MATLAB实现解:(a)该系统的冲激响应h(t)=(2/√65)*sin(√65t/4)e-t/4,阶跃响应g(t)=(1/8)*[1-e-t/4cos(√65t/4)-(1/√65)*e t/4sin(√65t/4)]绘制波形的程序如下:syms tf1=sym('2/65^0.5*exp(-1/4*t)*sin(65^0.5/4*t)');f2=sym('1/8*(1-exp(-1/4*t)*cos(65^0.5/4*t)-1/65^0.5*exp(-1/4*t)* sin(65^0.5/4*t))');subplot(1,2,1)ezplot(f1,[0 8]);subplot(1,2,2)ezplot(f2,[0 8]);图形如下:(b)用MA TLAB进行验证:冲激响应程序如下:a=[2 1 8];b=[0 1];impulse(b,a);图形如下:阶跃响应程序如下:a=[2 1 8];b=[0 1];step(b,a);图形如下:2、LTI连续系统的求解解:(a)系统的零状态响应r(t)=(2e-t-2e-2t-te-2t)u(t)绘制波形的程序如下:f=sym('2*exp(-t)-2*exp(-2*t)-t*exp(-2*t)'); ezplot(f1,[0 5])图形如下:(b)用MA TLAB进行验证:程序如下:a=[1 4 4];b=[1 3];p=0.01;t=0:p:5;x=exp(-1*t);lsim(b,a,x,t);图形如下:。
matlab软件仿真实验(信号与系统)(1)
matlab软件仿真实验(信号与系统)(1)《信号与系统实验报告》学院:信息科学与⼯程学院专业:物联⽹⼯程姓名:学号:⽬录实验⼀、MATLAB 基本应⽤实验⼆信号的时域表⽰实验三、连续信号卷积实验四、典型周期信号的频谱表⽰实验五、傅⽴叶变换性质研究实验六、抽样定理与信号恢复实验⼀MATLAB 基本应⽤⼀、实验⽬的:学习MATLAB的基本⽤法,了解 MATLAB 的⽬录结构和基本功能以及MATLAB在信号与系统中的应⽤。
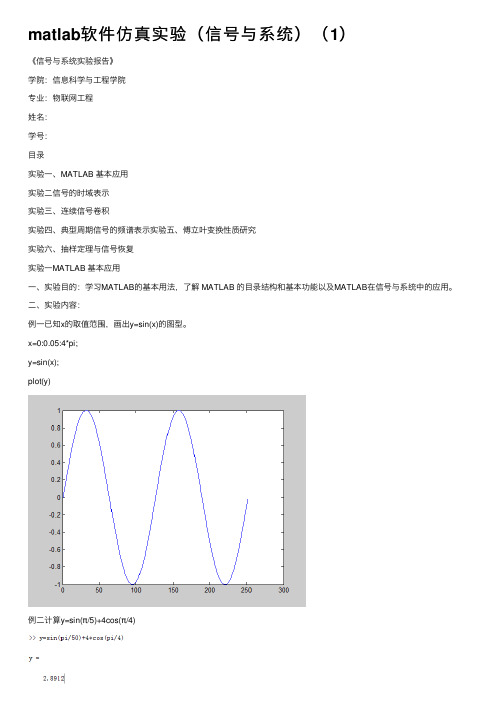
⼆、实验内容:例⼀已知x的取值范围,画出y=sin(x)的图型。
x=0:0.05:4*pi;y=sin(x);plot(y)例⼆计算y=sin(π/5)+4cos(π/4)例三已知z 取值范围,x=sin(z);y=cos(z);画三维图形。
z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)xlabel('x')ylabel('y')zlabel('z')例四已知x的取值范围,⽤subplot函数绘图。
参考程序:x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(2,2,1),plot(x,y1),title('sin(x)')subplot(2,2,2),plot(x,y2),title('1.5*cos(x)')subplot(2,2,3),plot(x,y3),title('sin(2*x)')subplot(2,2,4),plot(x,y4),title('5*cos(2*x)')连续信号的MATLAB表⽰1、指数信号:指数信号Ae at在MATLAB中可⽤exp函数表⽰,其调⽤形式为:y=A*exp(a*t) (例取 A=1,a=-0.4)参考程序:A=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;2、正弦信号:正弦信号Acos(w0t+?)和Asin(w0t+?)分别由函数cos和sin表⽰,其调⽤形式为:A*cos(w0t+phi) ;A*sin(w0t+phi) (例取A=1,w0=2π,?=π/6) 参考程序:A=1;w0=2*pi; phi=pi/6; t=0:0.001:8;ft=A*sin(w0*t+phi);plot(t,ft);grid on ;3、抽样函数:抽样函数Sa(t)在MATLAB中⽤sinc函数表⽰,其定义为:sinc(t)=sin(πt)/( πt)其调⽤形式为:y=sinc(t)参考程序:t=-3*pi:pi/100:3*pi;ft=sinc(t/pi);plot(t,ft);grid on;4、矩形脉冲信号:在MATLAB中⽤rectpuls函数来表⽰,其调⽤形式为:y=rectpuls(t,width),⽤以产⽣⼀个幅值为1,宽度为width,相对于t=0点左右对称的矩形波信号,该函数的横坐标范围由向量t决定,是以t=0为中⼼向左右各展开width/2的范围,width的默认值为1。
信号与系统matlab程序

信号与系统是通信和信息工程领域的基础课程,涉及到信号的表示、处理和分析。
在MATLAB中,我们可以使用各种函数和工具箱来实现信号与系统的各种操作。
以下是一个简单的MATLAB程序,用于生成和绘制一个简单的正弦波信号。
这个程序首先生成了一个时间向量,然后使用sin函数生成了一个频率为1Hz的正弦波信号。
最后,使用plot函数将信号绘制出来。
这只是MATLAB在信号与系统领域的一个简单应用,实际上MATLAB提供了许多其他工具和函数,可用于更复杂的信号处理和分析任务。
matlab信号与系统实验报告

matlab信号与系统实验报告Matlab信号与系统实验报告引言:信号与系统是电子工程、通信工程等领域中的重要基础课程,对于理解和应用各种信号处理技术具有重要意义。
本实验报告旨在通过使用Matlab软件,对信号与系统的基本概念和实验进行探讨和分析。
实验一:信号的基本特性分析在信号与系统的研究中,我们首先需要了解信号的基本特性。
通过Matlab软件,我们可以方便地对不同类型的信号进行分析和处理。
在本实验中,我们选择了常见的正弦信号和方波信号进行分析。
首先,我们生成了一个频率为1kHz,幅度为2V的正弦信号,并绘制了其时域波形图和频谱图。
通过观察时域波形图,我们可以看到正弦信号具有周期性和连续性的特点。
而通过频谱图,我们可以看到正弦信号在频域上只有一个峰值,说明其是单频信号。
接下来,我们生成了一个频率为1kHz,幅度为2V,占空比为50%的方波信号,并绘制了其时域波形图和频谱图。
与正弦信号不同,方波信号具有分段常值的特点。
通过频谱图,我们可以看到方波信号在频域上存在多个谐波分量,说明其是由多个频率的正弦信号叠加而成。
实验二:系统的时域响应分析在信号与系统中,系统的时域响应是描述系统对输入信号进行处理的重要指标。
通过Matlab软件,我们可以方便地分析和绘制系统的时域响应。
在本实验中,我们选择了一个一阶低通滤波器作为系统,输入信号为一个频率为1kHz,幅度为2V的正弦信号。
通过绘制输入信号和输出信号的时域波形图,我们可以观察到系统对输入信号进行了滤波处理,输出信号的幅度和相位发生了变化。
此外,我们还可以通过改变系统的参数,如截止频率和阶数,来观察系统的时域响应的变化。
通过对比不同参数下的输出信号波形图,我们可以得出不同参数对系统响应的影响。
实验三:系统的频域响应分析除了时域响应,频域响应也是描述系统特性的重要指标。
通过Matlab软件,我们可以方便地进行系统的频域响应分析。
在本实验中,我们选择了一个二阶巴特沃斯低通滤波器作为系统,输入信号为一个频率为1kHz,幅度为2V的正弦信号。
信号与系统实验MATLAB实验代码
1-1clear all;close all;t=0:0.01:10;A= 1;a=-0.4;ft=A*exp(a*t); plot(t,ft);1-2clear all;close all;t=-3:0.001:3;ft=tripuls(t,4,0.5); plot(t,ft);ft1=tripuls(t,4,1); figure,plot(t,ft1);1-3clear all;close all;t=0:0.001:4;T= 1;Ft=rectpuls(t-2*T,T); plot(t,Ft);1-4clear all;close all;k=-50:50;delta=[zeros(1,50),1,zeros(1,50)]; stem(k,delta);1-5clear all;close all;k=-50:50;uk=[zeros(1,50),ones(1,51)]; stem(k,uk);2-1clear all;close all;t=-3:0.001:3;ft=tripuls(t,4,0.5); subplot(3,1,1);plot(t,ft);title('f(t)');ft1=tripuls((2*t),4,0.5); subplot(3,1,2);plot(t,ft1);title('f(2t)');ft2=tripuls((2-2*t),4,0.5); subplot(3,1,3);plot(t,ft2);title('f(2-2t)');2-2clear all;close all;h=0.001;t=-3:h:3;ft=tripuls(t,4,0.5);subplot(3,1,1);plot(t,ft);title('f(t)');y1=diff(ft)*1/h;subplot(3,1,2);plot(t(1:length(t)-1),y1);title('the differentiation of f(t)');3-1clear all;close all;t=-10:0.01:10;A= 1;a=-0.4;ft=A*exp(a*abs(t)); plot(t,ft);3-2clear all;close all;r=0.02;t=-5:r:5;f1=1/2*exp(-2*t).*stepfun(t,0);f2=1/2*exp(-2*(t-1)).*stepfun(t-1,0); ft1=diff(f1)*1/r;ft2=diff(f2)*1/r;subplot(3,1,1);plot(t,f1);grid on;xlabel('t');ylabel('f(t)');title('f(t)');subplot(3,1,2);plot(t(1:length(t)-1),ft1);title('diff1');subplot(3,1,3);plot(t(1:length(t)-1),ft2);title('diff2');4-1clear all;close all;syms t f;f= fourier(exp((-2)*abs(t))); ezplot(f);4-2clear all;close all;syms t w;f=ifourier(1/(1+(w^2)),t); ezplot(f);a ns1/2*exp(-t)*heaviside(t)+1/2*exp(t)*heaviside(-t) 4-3clear all;close all;r=0.02;t=-5:r:5;N=200;w=2*pi;k=-N:N;w=k*w/N;f1=1/2*exp(-2*t).*stepfun(t,0);F=r*f1*exp(-j*t'*w);F1=abs(F);P1=angle(F);subplot(3,1,1);plot(t,f1);grid on;xlabel('t');ylabel('f(t)');title('f(t)');subplot(3,1,2);plot(w,F1);xlabel('w');grid on;ylabel('F(jw)');subplot(3,1,3);plot(w,P1*180/pi);grid;xlabel('w');ylabel('W');4-4clear all;close all;R=0.02;t=-2:R:2;f=stepfun(t,-1)-stepfun(t,1); f1=f.*exp(-j*5*t);f2=f.*exp(j*5*t);W1=pi*5;N=500;k=-N:N;W=k*W1/N;F1=f1*exp(-j*t'*W)*R;F2=f2*exp(-j*t'*W)*R;F1=real(F1);F2=real(F2); subplot(2,1,1); plot(W,F1); xlabel('w'); ylabel('F1(jw)'); title('频谱F1(jw)'); subplot(2,1,2); plot(W,F2); xlabel('w'); ylabel('F2(jw)'); title('频谱F2(jw)');。
基于MATLAB的信号与系统试验指导编程练习
2连续时间信号在MATLAB中的表示2-1.利用MATLAB命令画出下列连续信号的波形图(1)>> t=0:0.01:3;>> ft=2*cos(3*t+pi/4);>> plot(t,ft),grid on;>> axis([0 3 -2.2 2.2]);>> title('2cos(3t+pi/4)')(2)>> t=0:0.01:3;>> ft=2-exp(-t);>> plot(t,ft),grid on;>> title('(2-exp(-t))u(t)')(3)>> t=-1:0.01:1;>> ft=t.*(uCT(t)-uCT(t-1));>> plot(t,ft),grid on>> axis([-1 1 -0.2 1.2]);>> title('t[u(t)-u(t-1)]')(4)>> t=-1:0.01:3;>> ft=(1+cos(pi*t)).*(uCT(t)-uCT(t-2));>> plot(t,ft),grid on>> axis([-1 3 -0.2 2.2]);>> title('[1+cos(pi*t)][u(t)-u(t-2)]')2-2.利用MATLAB命令画出下列复信号的实部、虚部、模和辐角(1)>> t=0:0.01:3;>> ft=2+exp(i*(pi/4)*t)+exp(i*(pi/2)*t);>> subplot(2,2,1);plot(t,real(ft));title('实部');axis([0 3 0 4]);grid on;>> subplot(2,2,2);plot(t,imag(ft));title('虚部');axis([0 3 0 2]);grid on;>> subplot(2,2,3);plot(t,abs(ft));title('模');axis([0 3 0 4]);grid on;>> subplot(2,2,4);plot(t,angle(ft));title('相角');axis([0 3 0 2]);grid on;(2)t=0:0.01:3;>> ft=2*exp(i*(t+pi/4));>> subplot(2,2,1);plot(t,real(ft));title('实部');axis([0 3 0 2]);grid on;');axis([0 3 0 2]);grid on; 虚部>> subplot(2,2,2);plot(t,imag(ft));title('>> subplot(2,2,3);plot(t,abs(ft));title('模');axis([0 3 0 4]);grid on;>> subplot(2,2,4);plot(t,angle(ft));title('相角');axis([0 3 0 4]);grid on;2-3.利用MATLAB命令产生幅度为1、周期为1、占空比为0.5的一个周期矩形脉冲信号>> t=-0.5:0.01:3;>> ft=square(2*pi*t,50);>> plot(t,ft);grid on;axis([-0.5 3 -1.2 1.2]);>> title('幅度为1、周期为1、占空比0.5的周期举行脉冲信号')3连续时间信号在MATLAB中的运算3-1.试用MATLAB命令绘出以下信号的波形图(1)>> syms x t;>> t=-1:0.01:1;>> x=exp(-t).*sin(10*pi*t)+exp(-0.5*t).*sin(9*pi*t);>> plot(t,x)(2)>> syms x t;>> t=-1:0.01:1;>> x=sinc(t).*cos(10*pi*t);>> plot(t,x)3-2.已知连续时间信号f(t)的波形如图3-6所示,试用MATLAB 命令画出下列信号的波形图先画出图3-6:>> t=-2:0.01:2;>>f=(-t-1).*(-uCT(t+2)+uCT(t+1))+uCT(t+1)+uCT(t)-uCT(t-1)-(t-1).*(uCT(t-1)-uCT(t-2))-uCT(t-2);>> plot(t,f)>> axis([-4 4 -1 2])>> title('图3-6')>> t=-2:0.01:2;>> f1=funct2(t-1);>> f2=funct2(2-t);>> f3=funct2(2*t+1);>> f4=funct2(4-t/2);>> f5=(funct2(t)+funct2(-t)).*uCT(t);>> subplot(231);plot(t,f1);grid on;title('f(t-1)');axis([-3 3 -1 2]);>> subplot(232);plot(t,f2);grid on;title('f(2-t)');axis([-3 3 -1 2]);>> subplot(233);plot(t,f3);grid on;title('f(2t-1)');axis([-3 3 -1 2]);>> subplot(234);plot(t,f4);grid on;title('f(4-t/2)');axis([-3 3 -1 2]);>> subplot(235);plot(t,f5);grid on;title('(f(t)+f(-t))u(t)');axis([-3 3 -1 2]);3-3.试用MATLAB命令绘出如图3-7所示信号的偶分量和奇分量>> t=0:0.01:2;>> f=(uCT(t)-uCT(t-2)).*(-t+1);>> plot(t,f);title('图3-7')>> f1=fliplr(f);>> fe=(f+f1)/2;fo=(f-f1)/2;>> subplot(211),plot(t,fe);grid on>> title('fe')>> subplot(212),plot(t,fo);grid on;title('fo')4连续时间信号的卷积计算命令绘出下列信号的卷积积分的时域4-1用MATLAB 波形图>>dt=0.001;t1=-0.5:dt:3.5;>> f1=uCT(t1)-uCT(t1-2);>> t2=t1;>> f2=uCT(t2)+uCT(t2-1)-uCT(t2-2)-uCT(t2-3);>> [t,f]=ctsconv(f1,f2,t1,t2,dt);6周期信号的傅里叶级数及频谱分析6-1已知周期三角信号如图6-5所示,试求出该信号的傅里叶级数,利用MATLAB编程实现其各次谐波的叠加,并验证其收敛性。
信号与系统Matlab实验报告
实验一MATLAB 程序入门和基础应用一、实验名称MATLAB 程序入门和基础应用二、实验目的1.学习Matlab软件的基本使用方法;2.了解Matlab的数值计算,符号运算,可视化功能;3. Matlab程序设计入门四、实验设备计算机MATLAB软件六、实验内容及具体步骤1、打开MATLAB的系统界面,对其功能做一个大致了解;2、学习变量的描述方法,掌握几个固定变量:I,j,pi,inf的使用。
注意,变量描述以字母开头,可以由字母、数字和下划线混合组成,区分字母大,小写字符长度不超过31个。
3、学习数值,矩阵,运算符,向量的矩阵运算,数组运算的描述方法。
(1)用一个简单命令求解线性系统3x1+ x2 - x3 =3.6x1+2x2+4x3 = 2.1-x1+4x2+5x3 = -1.4A=[3 1 -1;1 2 4;-1 4 5];b=[3.6;2.1;-1.4];x=A\b结果:x = 1.4818 -0.4606 0.3848(2)用简短命令计算并绘制在0≤x≤6范围内的sin(2x)、sinx2、sin2x。
x=linspace(0,6)y1=sin(2*x),y2=sin(x.^2),y3=(sin(x)).^2;plot(x,y1,x, y2,x, y3)4、Matlab符号运算功能(1)符号运算的过程在符号运算的整个过程中,所有的运算均是以符号进行的,即使以数字形式出现的量也是字符量。
做一个对sin(x/2)求导的过程。
在命令窗口中输入如下符号表达式按回车:f='sin(x/2)';dfdx=diff(f)显示结果如下:dfdx = 1/2*cos(1/2*x)整个求导的过程都是由符号变量和符号表达式完成,没有涉及到具体的数值运算,其中1/2也被当作是字符量。
注意:符号变量前先要进行定义,定义语句是:sym 或syms 变量名列表。
前者定义一个单一的符号变量,后者可以一次定义多个符号变量。
信号与系统matlab仿真实验报告
题号
1、对于一般的正弦信号、复指数信号、指数信号能够画出其波形图,分析其有
无周期,有周期的给出周期值;
2、能够画出任意输入信号的时域波形图;
注:请区别CT和DT信号。
3、能够画出信号的频谱图,包括幅度谱和相位谱;
4、能够实现信号卷积,并画出卷积后信号的波形图;
1.我把前四个要求集成在了一个主面板里,通过面板platform调用四个不同的功能。
2.第一个分界面general_signal用于实现题目1,由用户选择信号类型并输入信号相关参数。
3.第二个分界面any_signal用于实现题目1、2,同时显示出信号的时域波形以及频谱图、相位图。
4.第三、四个界面signal_ct_conv、signal_dt_conv分别用于实现连续和离散的卷积,对应题目4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《信号与系统》matlab作业 M2-1(1)t=0:0.001:4
f=rectpuls(t-1,2) plot(t,f) xlabel('t');ylabel('f(t)'); axis([0,4,0,2])
00.511.522.533.5400.20.40.60.811.21.41.61.82
tf(t)
(2)t=-2:0.02:6;
x=(t>=0); plot(t,x); axis([-1 3 0 2]);
-1-0.500.511.522.5300.20.40.60.811.21.41.61.82
(3)t=-2:0.02:6;
x=10*exp(-1*t)-5*exp(-2*t); plot(t,x); xlabel('t');ylabel('x'); -2-10123456-200-150-100-50050
tx
(4)t=-2:0.02:6
x=(t>=0); y=t.*x; plot(t,y);
-2-101234560123456
(5)t=-0.1*pi:0.001:0.1*pi;
x=2*abs(sin(10*pi*t+pi/3)); xlabel('t');ylabel('x(t)'); plot(t,x); axis([-0.1*pi,0.1*pi,0,2]) -0.3-0.2-0.100.10.20.300.20.40.60.811.21.41.61.82 (6)t=-2:0.002:2;
x=cos(t)+sin(2*pi*t); xlabel('t');ylabel('x'); plot(t,x);
-2-1.5-1-0.500.511.52-1.5-1-0.500.511.52
(7)t=-20:0.02:20;
x=4*exp(-0.5*t).*cos(2*pi*t); xlabel('t');ylabel('x'); plot(t,x); -20-15-10-505101520-8-6-4-20246810x 104 (8)t=-2:0.02:2;
x=sinc(t).*cos(30*t); xlabel('t');ylabel('x'); plot(t,x);
-2-1.5-1-0.500.511.52-1-0.8-0.6-0.4-0.200.20.40.60.81
M2-3(1)function yt=x2_3(t)
yt=t.*(t>0&t<=2)+2*(t>2&t<=3)-1*(t>3&t<=5) (2)t=-20:0.001:20
subplot(3,1,1) plot(t,x2_3(t)) title('x(t)') axis([-12,12,-2,4]) subplot(3,1,2) plot(t,x2_1(0.5*t)) title('x(0.5t)') axis([-12,12,-2,4]) subplot(3,1,3) plot(t,x2_1(2-0.5*t)) title('x(2-0.5t)') axis([-12,12,-2,4])
-10-50510-2024x(t)
-10-50510-2024x(0.5t)
-10-50510-2024x(2-0.5t)
M2-9 (1) k=-4:7;
x=[-3 -2 3 1 -2 -3 -4 2 -1 4 1 -1]; stem(k,x)
-4-202468-4-3-2-101234 (2) 插值: k=-12:21; x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; N=length(x); y=zeros(1,3*N-2); y(1:3:end)=x; stem(k,y)
-15-10-50510152025-4-3-2-101234
抽值: x=[0,0,-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; y=x(1:3:end); k=-1:3; stem(k-1,y) -2-1.5-1-0.500.511.52-2-1.5-1-0.500.511.52 (3) k=-4:7; m=k-2; xm=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; n=k+4; xn=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; subplot(2,1,1) stem(m,xm) axis([-3,6,-5,5]) title('x[k+2]') subplot(2,1,2) stem(n,xn) title('x[k+4]') axis([-2,12,-5,5]) -3-2-10123456-505x[k+2]-2024681012-505x[k+4] (4) k=-7:4; x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; y=fliplr(x); stem(k,y) -8-6-4-2024-4-3-2-101234 M3-1 (1) t=0:0.01:10
sys=tf([2,1],[1,3,2]) x=exp(-3*t).*(t>=0) y=lsim(sys,x,t) plot(t,y)
0246810-0.0500.050.10.150.20.250.3
(2) M3-4 k=-2:3 x=[0.85 0.53 0.21 0.67 0.84 0.12] m=-1:3 h=[0.68 0.37 0.83 0.52 0.71] y=conv(x,h) N=length(y) stem(0:N-1,y)
012345678900.20.40.60.811.21.41.61.82
M3-8 k=0:30 a=[1 0.7 -0.45 -0.6] b=[0.8 -0.44 0.36 0.02] impz(b,a,k) stem(k,h) 051015202530-1-0.500.511.5n (samples) AmplitudeImpulse Response
M4-1 (1) N=20; n1= -N:-1; c1= 1/2.*sinc(n1/2).*exp(-j*n1*pi*1/2); c0=(1/2.*sinc(0/2)).*exp(-1*j*0*pi*1/2)-1/2; n2=1:N; c2= 1/2.*sinc(n2/2).*exp(-1*j*n2.*pi*1/2); cn=[c1 c0 c2]; n= -N:N; subplot(2,1,1); stem(n,abs(cn));ylabel(' Cn的幅度'); subplot(2,1,2); stem(n,angle(cn)); ylabel(' Cn的相位');xlabel('\omega/\omega0'); -20-15-10-50510152000.10.20.30.4Cn的幅度
-20-15-10-505101520-4-2024Cn的相位
/0 (2) N=8;
n1= -N:-1; c1= -2*j*sin(n1*pi/2)/pi^2./n1.^2.*exp(-j*n1*1/2); c0=-2*j*sin(0*pi/2)/pi^2./0.^2.*exp(-j*0*1/2)+2*pi; n2=1:N; c2= -2*j*sin(n2*pi/2)/pi^2./n2.^2.*exp(-j*n2*1/2); cn=[c1 c0 c2]; n= -N:N; subplot(2,1,1); stem(n,abs(cn));ylabel(' Cn的幅度'); subplot(2,1,2); stem(n,angle(cn)); ylabel(' Cn的相位');xlabel('\omega/\omega0');
