材料力学课件第五章 平面图形的几何性质
合集下载
附录1 平面图形的几何性质PPT课件

截面对于一个构件或者结构来说是非常重要的,下面我 们列举一下工程当中常见的几种截面:
槽钢 工字型
角钢
1
标题添加
点击此处输入相 关文本内容
标题添加
点击此处输入相 关文本内容
总体概述
点击此处输入 相关文本内容
点击此处输入 相关文本内容
2
平面图形的几何性质
杆件的和截面是平面图形,它的几何性 质与强度、刚度计算密切相关,必须很好掌 握。拉压中的面积A,扭转中的极惯性矩 都 属于截面图形的几何性质。在附录1中我们I P还 要学到静矩、惯性矩和惯性积。
的,但惯性矩恒为正。 (2)组合截面对某一轴的惯性矩等于各部分对
该轴的惯性矩之代数和。
n
n
Iz
i1
I
zi
Iy
i 1
I
yi
13
例1 试计算图(a)所示矩形截面对于其对称轴
(即形心轴)z 和 y 的惯性矩。
y
解: 取平行于x轴的狭长条,
则 dA=b dy
IzAy2dAh 2h 2by2dyb1h23
A
单位:m 4
o
y
11
惯性矩 z
y A o
图形对z轴的惯性矩
Iz
y2dA
A
dA
z
图形对y轴的惯性矩
y
Iy
z2dA
A
单位:m 4
极惯性矩和对轴惯性矩之间的关系:Ip 2dAIz Iy
A
12
惯性半径
截面图形对y轴的惯性半径:i y
Iy A
截面图形对z轴的惯性半径:iz
Iz A
惯性矩的性质 (1)截面图形对不同坐标轴的惯性矩是不同
a
槽钢 工字型
角钢
1
标题添加
点击此处输入相 关文本内容
标题添加
点击此处输入相 关文本内容
总体概述
点击此处输入 相关文本内容
点击此处输入 相关文本内容
2
平面图形的几何性质
杆件的和截面是平面图形,它的几何性 质与强度、刚度计算密切相关,必须很好掌 握。拉压中的面积A,扭转中的极惯性矩 都 属于截面图形的几何性质。在附录1中我们I P还 要学到静矩、惯性矩和惯性积。
的,但惯性矩恒为正。 (2)组合截面对某一轴的惯性矩等于各部分对
该轴的惯性矩之代数和。
n
n
Iz
i1
I
zi
Iy
i 1
I
yi
13
例1 试计算图(a)所示矩形截面对于其对称轴
(即形心轴)z 和 y 的惯性矩。
y
解: 取平行于x轴的狭长条,
则 dA=b dy
IzAy2dAh 2h 2by2dyb1h23
A
单位:m 4
o
y
11
惯性矩 z
y A o
图形对z轴的惯性矩
Iz
y2dA
A
dA
z
图形对y轴的惯性矩
y
Iy
z2dA
A
单位:m 4
极惯性矩和对轴惯性矩之间的关系:Ip 2dAIz Iy
A
12
惯性半径
截面图形对y轴的惯性半径:i y
Iy A
截面图形对z轴的惯性半径:iz
Iz A
惯性矩的性质 (1)截面图形对不同坐标轴的惯性矩是不同
a
材料力学 第五章ppt课件

A A
s
A
(对称面)
2 Ey E2 EI z M ( d A ) y d A y d A M z A A
s
A
EIz
A
2 Iz y A 轴 惯 性矩 d
1 Mz EI z
M y s x I z
… …(3)
杆的抗弯刚度。
. . . . . . ( 4 )
d4
64
d
Iz d3 W z ym a x 32
4 D 4 空心圆 I ( 1 a ) z
d D
ad
64
D
3 I D 4 z W ( 1 a ) z y max 32
11
三、常见截面的IZ和WZ:
3 bh 矩形 Iz 12
b b
2 Iz bh W z y 6 m ax
§5-3 横力弯曲时梁横截面上的正应力 一、正应力近似公式:
M y s x I z . . . . . . ( 4 )
二、横截面上最大正应力:
M s max Wz
… …(5)
I z W z 抗 弯 截 面 模 量 。 y m a x
10
三、常见截面的IZ和WZ:
圆 Iz
M 60 4 1 s 10 92 . 6 MP 1 max
M 67 . 5 4 max s 10 104 . 2 MP max W 6 . 48 z
120 M
求曲率半径
qL 8
+
2
EI 5 . 832 z 200 10 194 . 4 m 1 M 60 1
力状态。
s
A
(对称面)
2 Ey E2 EI z M ( d A ) y d A y d A M z A A
s
A
EIz
A
2 Iz y A 轴 惯 性矩 d
1 Mz EI z
M y s x I z
… …(3)
杆的抗弯刚度。
. . . . . . ( 4 )
d4
64
d
Iz d3 W z ym a x 32
4 D 4 空心圆 I ( 1 a ) z
d D
ad
64
D
3 I D 4 z W ( 1 a ) z y max 32
11
三、常见截面的IZ和WZ:
3 bh 矩形 Iz 12
b b
2 Iz bh W z y 6 m ax
§5-3 横力弯曲时梁横截面上的正应力 一、正应力近似公式:
M y s x I z . . . . . . ( 4 )
二、横截面上最大正应力:
M s max Wz
… …(5)
I z W z 抗 弯 截 面 模 量 。 y m a x
10
三、常见截面的IZ和WZ:
圆 Iz
M 60 4 1 s 10 92 . 6 MP 1 max
M 67 . 5 4 max s 10 104 . 2 MP max W 6 . 48 z
120 M
求曲率半径
qL 8
+
2
EI 5 . 832 z 200 10 194 . 4 m 1 M 60 1
力状态。
材料力学第五章平面弯曲.ppt

5.2 平面弯曲时梁横截面上的正应力 与正应力强度条件
一、纯弯曲与横力弯曲
Q→τ M →σ
CD段 — 纯弯曲(Q = 0)
AC、DB段 — 横力弯曲 (Q ≠ 0)
回顾与比较:
内力
应力
N
A
T
IP
M ?
YA
Q
?
二、梁的纯弯曲实验 变形现象:
1)各纵向线均变成了圆弧曲线,且上面部分纵向线缩短,下 面纵向线伸长,但各纵向线间距不变; 2)各横向线仍保持为直线,只是相邻横向线相对转了一个角 度,变形后的横向线仍与纵线垂直; 3)矩形截面的宽度变形后上宽下窄。
= 2b,讨论梁立置与倒置两种情况哪一种更好?
注意:Z 轴为中 性轴
q
b
h
h
b
根据弯曲强度条件
M
WZ
同样载荷条件下,工作应力越小越好 因此,WZ 越大越好
梁立置时:
WZ
bh2 6
b 2b2
6
4b3 6
2 b3 3
梁倒置时:
WZ
hb2 6
2b b2 6
2b3 6
1 b3 3
立置比倒 置好。
E Ey (2)
My
IZ
该截面弯矩
My
Iz
横截面上 某点正应力
该点到中性p 2)平面弯曲
中性轴以下σ为拉应力
M > 0时 中性轴以上σ为压应力
中性轴上各点σ=0
下边缘各点
max
上边缘各点
max
M < 0时 相反。
(四)最大正应力:
140MPa, 试选择工字钢的型号。
分析:
(1)确定危险截面
(2) max
力学附录I_平面图形的几何性质2形心主轴和形心主惯性矩

材料力学 附录I 平面图形的几何性质
§I-1 静矩和形心 §I-2 惯性矩和惯性半径 §I-3 惯性积 §I-4 平行移轴公式 §I-5 转轴公式 主惯性轴
材料力学 附录I 平面图形的几何性质
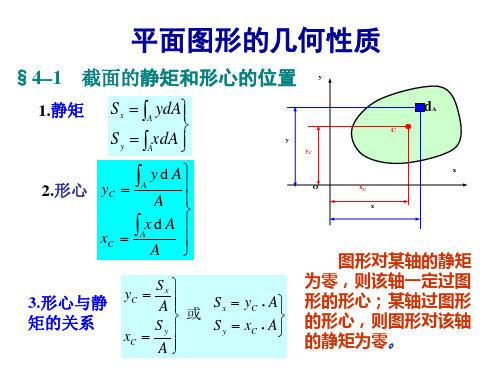
§I-1 静矩和形心
1.静矩 2.形心
注意
Sz
A
ydA
Sy
zdA
A
yd A
解: I y
z 2 dA
A
h/2
z2bdz
h / 2
bh 3
12
dz
z
材料力学 附录I 平面图形的几何性质
例I-2-2:求图示圆平面对y、z轴的惯性矩。
d4
I p 32
Iy Iz Ip
Iy Iz
Iy
Iz
1 2
Ip
d 4
64
材料力学 附录I 平面图形的几何性质
yC zC
• •
A A
可知,静矩的几何意义:形心位置与轴的距
离大小。
当一个平面图形是由几个简单平面图形组成,称为组合平面图
形,其静矩和形心坐标分别为
S z
n
Szi
i 1
ห้องสมุดไป่ตู้
n
Ai yCi
i 1
S
y
n
Syi
i 1
n
Ai zCi
i 1
组合图形对某一轴的静矩等于各 组成部分对同一轴静矩的代数和
19.7mm
zC
Sy A
10120 60 70105 1200 700
39.7mm
材料力学 附录I 平面图形的几何性质
§I-1 静矩和形心 §I-2 惯性矩和惯性半径 §I-3 惯性积 §I-4 平行移轴公式 §I-5 转轴公式 主惯性轴
材料力学 附录I 平面图形的几何性质
§I-1 静矩和形心
1.静矩 2.形心
注意
Sz
A
ydA
Sy
zdA
A
yd A
解: I y
z 2 dA
A
h/2
z2bdz
h / 2
bh 3
12
dz
z
材料力学 附录I 平面图形的几何性质
例I-2-2:求图示圆平面对y、z轴的惯性矩。
d4
I p 32
Iy Iz Ip
Iy Iz
Iy
Iz
1 2
Ip
d 4
64
材料力学 附录I 平面图形的几何性质
yC zC
• •
A A
可知,静矩的几何意义:形心位置与轴的距
离大小。
当一个平面图形是由几个简单平面图形组成,称为组合平面图
形,其静矩和形心坐标分别为
S z
n
Szi
i 1
ห้องสมุดไป่ตู้
n
Ai yCi
i 1
S
y
n
Syi
i 1
n
Ai zCi
i 1
组合图形对某一轴的静矩等于各 组成部分对同一轴静矩的代数和
19.7mm
zC
Sy A
10120 60 70105 1200 700
39.7mm
材料力学 附录I 平面图形的几何性质
材料力学PPT截面几何性质)
解:首先求对圆心的极惯性矩。 在离圆心O为处作宽度为d的薄圆环,其面 积dA=2pd,则
I p
2 d A
A
d /2 2 (2p d ) pd 4
0
32
由于圆形对任意直径轴都是对称的,故Ix=Iy 注意到Iρ=Ix+Iy,得到
Ix
Iy
1 2
I
pd 4
64
y d
x
C
d
§4-3 惯性矩和惯性积的平行移轴公式 组合截面的惯性矩和惯性积
y0 y 10
例4-7 计算图示截面的形心主轴和形心主惯性矩
图形的对称中心C为形心,在C点建立坐标
II
系xCy如图
将整个图形分成I、II、III三个矩形,如图
I x0 整个图形对x、y轴的惯性矩和惯性积分别
120
0 x 为
C 10
IIII Ix IIx IIIx IIIIx
10
101203 12
60103 12
(60-
5)2
(6010)2
70
5.08106 mm4
Iy IIy IIIy IIIIy 1.84106 mm 4 Ixy IIxy IIIxy IIIIxy -2.31106 mm 4
tg20
-
2I xy Ix -Iy
1.4260
27o 28'
00 p/4,Ix Iy,自x轴逆时针旋转 27o28'转到主轴x0,Ix0 Imax,Iy0 Imin
2.惯性矩:
Ix Iy
AAxy22ddAA
分别为图形对x、y轴 的惯性矩;
y O
x
3.惯性积:
dA x
I xy A xydA为图形对x、y一对正交轴的惯性积;
材料力学附录I 平面图形的几何性质2形心主轴和形心主惯性矩

材料力学 附录I 平面图形的几何性质
y
1.先求截面的 形心轴
A2
取参考坐标系如图,则:
A1
zc
yc
60100 50 60 100
202 202
70
44.7mm
yc z 2.求截面对形心轴的惯性矩:
I yc
Iy
100 603 12
404 64
1.67 106 mm4
I zc
I A1 zc
zC
Sy A
2h 5
材料力学 附录I 平面图形的几何性质
4.组合平面图形的形心与静矩
由
Sz Sy
yC zC
• •
A A
可知,静矩的几何意义:形心位置与轴的距
离大小。
当一个平面图形是由几个简单平面图形组成,称为组合平面图
形,其静矩和形心坐标分别为
S z
n
Szi
i 1
n
Ai yCi
i 1
S
y
n
I
x
I 2
y
)2
I
2 xy
材料力学 附录I 平面图形的几何性质
2.形心主轴和形心主惯性矩:
主轴过形心时,称其为形心主轴。平面图形对形心主轴之
惯性矩,称为形心主惯性矩
tg
2
0
2I xC yC I xC I yC
形心主惯性矩:
I I
xC0 yC0
I
xC
I 2
yC
(
I
xC
I 2
yC
)2
I
2 xCyC
材料力学 附录I 平面图形的几何性质
iy 、iz 分别称为平面图形对y轴和z轴的惯性半径
平面图形性质

③ 建立形心坐标系;求:IyC , IxC , I xCy
I xC I矩xC I圆xC I矩x A矩 y 2 [ I圆x1A圆 (0.5d y)2 ]
1.5d(2d )3 d 4 d 2 3d 2 (0.177d ) 2 [ (0.5d 0.177d ) 2 ]0.685d 4 12 64 4
dS y dAx
or
微面积dA对Y轴的静矩
x dA
S x dS x ydA
A A
S y Ax S x Ay
x
C y
y
x
S y dS y xdA
A A
量钢:L3 如S=0 ↔ 轴过形心
二、组合截面的静矩与形心: 整个图形对某轴的静矩, 等于图形各部分对同轴静矩的 代数和(由静矩定义可知)
y 2d
d
yC O
(1.5d )32d d 4 I yC I 矩xC I圆xC 0.513d 4 12 64
x1
I xCyC 0
( yC为对称轴 )
x xC b
xC yC 轴便是形心主轴 I xC , I yC便是形心主惯性矩
如 : A Ai
i 1
n
S x Ai yi Ay
则
i 1 n
n
S y Ai xi Ax
i 1
∴
x y
x A
i
i
A yi Ai A
例1 试确定下图的形心坐标。
10
解 : 1.用正面积法求解,图形分割
y
120 C2 C1(0,0) C2(-35,60)
3.求截面形心主惯性矩的方法 ①建立坐标系 ②计算面积和面积矩 ③求形心位置
附录Ⅰ 平面图形的几何性质5-1纯弯曲5-2.5-3

σ c max
σ c max
My c max IZ
ycmax
M
z
yt max
y
σ t max
但工程中常用的梁,纯弯曲时的正应力计算公式可以精确的
计算横力弯曲时横截面上的正应力 。 等直梁横力弯曲(nonuniform bending)时横截面上的最大正应 力公式为
smax
M ( x) WZ
z
dA
zdA S z
A
y
c
z
z
A
A
y
A
ydA A
S
o
z
y y
y
A
S
y
Az
S
z
Ay
z
S
y
Az
dA
S
z
பைடு நூலகம்
Ay
z
c
z
o
y y
y
若截面对某一轴的静矩等于零,则该轴必过形心。 截面对形心轴的静矩等于零。
三、 组合截面的静矩和形心 由几个简单图形组成的截面称为组合截面
截面各组成部分对于某一轴的静矩之代数和,就等于该
z
I z π d 64 Wz d 2 d 2
y d
4
= d 32
3
2)对于中性轴不是对称轴的横截面 应分别以横截面上受拉和 受压部分距中性轴最远的 距离
yc max
M
yt max
和
yc max
直
接代入公式 z
yt max
y
My s Iz
求得相应的最大正应力
σ t max
My t max IZ
neutral axis of the beam to the fibers)
σ c max
My c max IZ
ycmax
M
z
yt max
y
σ t max
但工程中常用的梁,纯弯曲时的正应力计算公式可以精确的
计算横力弯曲时横截面上的正应力 。 等直梁横力弯曲(nonuniform bending)时横截面上的最大正应 力公式为
smax
M ( x) WZ
z
dA
zdA S z
A
y
c
z
z
A
A
y
A
ydA A
S
o
z
y y
y
A
S
y
Az
S
z
Ay
z
S
y
Az
dA
S
z
பைடு நூலகம்
Ay
z
c
z
o
y y
y
若截面对某一轴的静矩等于零,则该轴必过形心。 截面对形心轴的静矩等于零。
三、 组合截面的静矩和形心 由几个简单图形组成的截面称为组合截面
截面各组成部分对于某一轴的静矩之代数和,就等于该
z
I z π d 64 Wz d 2 d 2
y d
4
= d 32
3
2)对于中性轴不是对称轴的横截面 应分别以横截面上受拉和 受压部分距中性轴最远的 距离
yc max
M
yt max
和
yc max
直
接代入公式 z
yt max
y
My s Iz
求得相应的最大正应力
σ t max
My t max IZ
neutral axis of the beam to the fibers)
