2020高考数学考点突破—计数原理、概率与统计1:分类加法计数原理与分步乘法计数原理
1.1 分类计数原理和分步计数原理

(3)有不同颜色的5件上衣与3件不同颜色的长裤,如果一条长裤与一件上衣配 成一套,则不同的配法有多少种? 分步问题 (4)从一个装有4个不同白球的盒子里或装有3个不同黑球的盒子里取1个球, 共有多少种不同的取法? 分类问题 (5)从一个装有4个不同白球的盒子里和装有3个不同黑球的盒子里各取1个 球,共有多少种不同的取法? 分步问题 (6)某商场有6个门,某人从其中的任意一个门进入商场,再从其他的门出去, 共有多少种不同的进出商场的方式? 分步问题
问题剖析
小明要完成的一件事是什么
北京→重庆
完成这件事情要分几步
2步
每步中的任一方法能否独立完成这 件事
不能
每步方案中分别有几种不同的方法 4种 3种
完成这件事共有多少种不同的方法 4✕3=12种
想一想:
(1)用前6个大写英文字母和1~9九个阿拉伯数字,以 A1,A2,···,B1,B2,···的方式给教室里的座 位编号,总共能够编出多少种不同的号码? (2)从班上30名男生、25名女生中选男生、女生各1名 担任数学课代表,一共有多少种不同的选法?
现有5幅不同的国画,2幅不同的油画,7幅不同的水彩画
事件1:从中任选一幅画布置房间 事件2:从这些国画、油画、水彩画中各选一幅布置房间 事件3:从这些画中选出两幅不同种类的画布置房间
问题2:以上三个事件各有多少种不同的选法
1.解决计数问题的基本方法:
列举法、两个计数原理
2.选择两个原理解题的关键是: 根据题目,弄清完成一件事的要求至关重要, 只有这样才能正确区分“分类”和“分步”.
数,只需将各类方法数相加,因此分类计数原理又称加法原理
2)首先要根据具体的问题确定一个分类标准,分类 要做到类类独立,不重不漏。
2020-2021学年高考数学(理)考点:分类加法计数原理与分步乘法计数原理

考点梳理
一般形式
区别
完成一件事有 n 类不同方案,
分类加法计数原理 分步乘法计数原理
在第 1 类方案中有 m1 种不同的
方法,在第 2 类方案中有 m2 种 不同的方法,…,在第 n 类方 案中有 mn 种不同的方法,那么 完成这件事共有 N=m1+m2+…+mn 种不同的 方法 完成一件事需要 n 个步骤,做 第 1 步有 m1 种不同的方法,做 第 2 步有 m2 种不同的方法, …,做第 n 步有 mn 种不同的方 法,那么完成这件事共有
概念方法微思考 1.在解题过程中如何判定是用分类加法计数原理还是分步乘法计数原理? 提示 如果已知的每类办法中的每一种方法都能完成这件事,应该用分类加法计数原理;如果每类 办法中的每一种方法只能完成事件的一部分,就用分步乘法计数原理. 2.两种原理解题策略有哪些? 提示 ①明白要完成的事情是什么; ②分清完成该事情是分类完成还是分步完成,“类”间互相独立,“步”间互相联系; ③有无特殊条件的限制; ④检验是否有重复或遗漏.
被 5 整除的个数有 ( )
A.512
B.192
C.240
D.108
【答案】D
【解析】能被 5 整除的四位数末位是 0 或 5 的数,因此分两类
第一类,末位为 0 时,其它三位从剩下的数中任意排 3 个即可,有 A53 60 个,
第二类,米位为 5 时,首位不能排 0,则首位只能从 1,3,4,5 选 1 个,第二位和第三位从剩
C.72
D.108
【答案】B
【解析】第一步从 4 名实习教师中选出 2 名组成一个复合元素,共有 C42 6 种,
第二步把 3 个元素(包含一个复合元素)安排到三个班实习有 A33 6 种, 根据分步计数原理不同的分配方案有 6 6 36 种. 故选 B . 12.(2019•河南模拟)某省示范高中将 6 名教师分配至 3 所农村学校支教,每所学校至少分配一名
高三理科数学第一轮复习§12.1:分类加法计数原理与分步乘法计数原理

第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
解析
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
解析
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
解析
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
解析
第十二章:计数原理、概率、 随机变量及其分布 §12.1:分类加法计数原理与 分步乘法计数原理
6.1分类加法计数原理与分步乘法计数原理课件(人教版)

6.1 分类加法计数原理 与分步乘法计数原理
1.理解分类加法计数原理与分步乘法 计数原理.(重点) 2.会用这两个原理分析和解决一些简 单的实际计数问题.(难点)
1.核糖核酸(RNA)分子有碱基按一定顺序排列而成。 已知碱基有4种,但由成百上千个碱基组成的RNA分 子的种数非常巨大。为什么?
B 果将这 2 个新节目插人节目单中,那么不同的插法种数为( )
A.12
B.20
C.36
D.120
解析:利用分步计数原理,第一步插入第一个新节目,有 4 种方法,第二步插 入第二个新节目,此时有 5 个空,故有 5 种方法.因此不同的插法共有 45 20 种.故选 B.
2.如图,用 4 种不同的颜色对 A,B,C,D 四个区域涂色,要求相邻的两个区
工程学
如果这名同学只能选一个专业,那么他共有多少种选择?
解:这名同学可以选择 A,B 两所大学中的一所. 在 A 大学中有 5 种专业选择方法,在 B 大学中有 4 种专业选择方法. 因为没有一个强项专业是两所大学共有的, 所以根据分类加法计数原理, 这名同学可能的专业选择种数为 N 5 4 9 .
完成一件事需要两个步骤,做第 1 步有 m 种不同的方
法,做第 2 步有 n 种不同的方法,那么完成这件事共有 N
=m×n种不同的方法.
例 1 在填写高考志愿表时,一名高中毕业生了解到,A,B
两所大学各有一些自己感兴趣的强项专业,如下表.
A 大学
B 大学
生物学
数学
化学
会计学
医学
信息技术学
物理学
法学Biblioteka 例5 给程序模块命名,需要用3个字符,其中首字符要求用字母 A~G或U~Z,后两个字符要求用数字1~9,最多可以给多少个程 序模块命名?
( 人教A版)分类加法计数原理与分步乘法计数原理课件 (共27张PPT)

3.商店里有上衣 15 种,裤子 18 种,某人要买一件上衣或一条裤子,共有________ 种不同的选法,要买上衣、裤子各一件,共有________种不同的选法. 解析:要买一件上衣或一条裤子只有 15+18=33 种;要买上衣、裤子各一件共有 15×18=270 种. 答案:33 270
探究一 分类加法计数原理
分类讨论思想解决排数问题 [典例] 用 0,1,2,3,4,5 可以组成多少个无重复数字且比 2 015 大的四位偶数? [解析] 解法一 按末位是 0,2,4 分为三类: 第一类,末位是 0 的有 4×4×3=48 个; 第二类,末位是 2 的有 3×4×3=36 个; 第三类,末位是 4 的有 3×4×3=36 个. 其中 2 014 不合题意,应去除, 由分类加法计数原理,得 N=48+36+36-1=119 个.
[双基自测] 1.一个科技小组有 3 名男同学,5 名女同学,从中任选一名同学参加学科竞赛,不同 的选派方法共有________种. 解析:任选一名同学参加学科竞赛不同的选派方法有 3+5=8 种. 答案:8
2.2016 年猴年春节晚会上,某一舞蹈节目共有 6 名男演员,6 名女演员.现选一男 演员,一女演员作为领舞演员,不同的选法种数为________. 解析:共有 6×6=36 种. 答案:36
选法;第 2 步,选长裤,从 3 条长裤中任选一条,有 3 种不同选法.故共有 4×3=
12 种不同的配法.
答案:B
3.已知集合 M={1,-2,3},N={-4,5,6,7},从两个集合中各取一个元素作为点的
坐标,则这样的坐标在直角坐标系中可表示第一、二象限内不同的点的个数是( )
A.18
B.17
应用分类加法计数原理的关键: 用分类加法计数原理计数,关键在于根据问题的特点确定一个适合它的分类标准在这 个分类标准下,完成这件事的任何一种方法只属于某一类,并且分别属于不同种类的 两种方法是不同的.
高考数学第十章计数原理、概率、随机变量及其分布10.1分类加法计数原理与分步乘法计数原理理

2021/12/12
第十六页,共四十二页。
解法 2:a=b 时有 4 种情况,故椭圆个数为 4×8-4=28 个. (2)根据“凸数”的特点,中间的数字只能是 3,4,5,故分三 类,第一类,当中间数字为“3”时,此时有 2 种(132,231); 第二类,当中间数字为“4”时,从 1,2,3 中任取两个放在 4 的 两边,故有 6 种; 第三类,当中间数字为“5”时,从 1,2,3,4 中任取两个放在 5 的两边,故有 12 种; 根据分类加法计数原理,得到由 1,2,3,4,5 可以组成无重复数 字的三位“凸数”的个数是 2+6+12=20.
有 1 个;a=4 时,有 3 个;a=6 时,有 5 个;a=8 时,有 7 个,
共有 1+3+5+7=16 个.
若焦点在 y 轴上,则 b>a,b=3 时,有 1 个;b=4 时,有 1 个;b=5 时,有 2 个;b=6 时,有 2 个;b=7 时,有 3 个;b =8 时,有 3 个.共有 1+1+2+2+3+3=12 个.故共有 16+ 12=28 个.
2021/12/12
第十页,共四十二页。
4.已知某公园有 5 个门,从任一门进,另一门出,则不同的走法
的种数为 __2_0___(用数字作答).
解析:分两步,第一步选一个门进有 5 种方法,第二步再 选一个门出有 4 种方法,所以共有 5×4=20 种走法.
2021/12/12
第十一页,共四十二页。
一个旅游景区的游览线路如图所示,某人从 P 点处进,Q 点处出, 沿图中线路游览 A,B,C 三个景点及沿途风景,则不同(除交汇点 O 外)
的游览线路有____4_8____种.(用数字作答)
2021/12/12
分类加法计数原理与分步乘法计数原理

解法三(分类法):完成涂色的方法分为两类, 2011高考导航 第一类:四个区域涂四种不同的颜色共有 =120种 第二类:四个区域涂三种不同的颜色,由于A、D不相 邻只能是A、D两区域颜色一样,将A、D看做一个区 域,共 =60种涂法. 由分类计数原理知共有涂法120+60=180(种). 方法总结:对涂色问题,有两种解法: 法1是逐区图示法,注意不相邻可同色.
点也有2种染色方法. 则有5×4×3(1×3+2×2)=420种.
方法二、按所用颜色种数分类.
第一类,5种颜色全用,共有
A5
5
种不同的方法;
第二类,只用4种颜色,则必有某两个顶点同色 (A与C,或B与D),共有2× A 4 种不同的方法; 5
第三类,只用3种颜色,则A与C、B与D必定同色,
3 共有A 5 种不同的方法.
4、有无特殊条件的限制;
5、检验是否有重漏.
1.如图所示的阴影部分由方格纸上3个小方格组成,我
们称这样的图案为L型(每次旋转90°仍为L型图案), 那么在由4×5个小方格组成的方格纸上可以画出不同 位置的L型图案的个数是( ) A.16 C.48 B.32 D.64 C
解析、每四个小方格(2×2型)中有“L”型图案4个, 共 有 2×2 型 小 方 格 12 个 , 所 以 共 有 “ L” 型 图 案 4×12=48个.
分类计数原理
与 分步计数原理
1、分类加法计数原理:完成一件事,有n类办法,在 第1类办法中有m1种不同的方法,在第2类办法中有m2 种不同的方法……在第n类办法中有mn种不同的方法. 那么 完成这件事共有 N m1 m2 mn 种不同的方 法.
2、分步乘法计数原理:完成一件事,需要分成n个步 骤,做第1步有m1种不同的方法,做第2步有m2种不同的 方法……,做第n步有mn种不同的方法.那么完成这件 事共有N m1 m2 mn 种不同的方法.
第六章 高考数学 计数原理知识总结
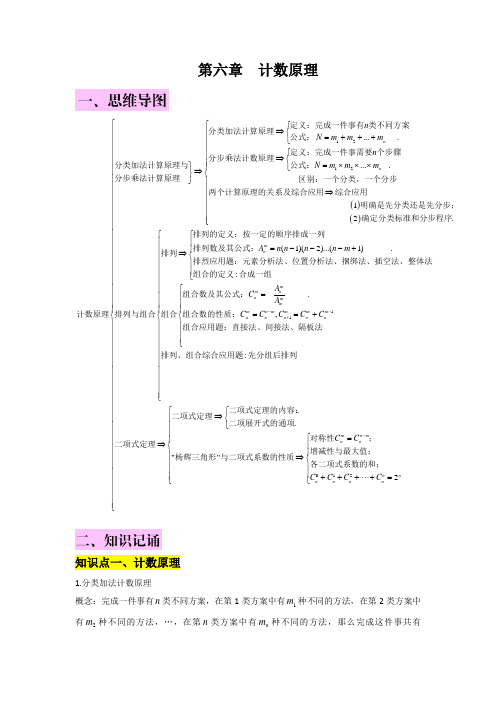
第六章 计数原理()()1212_...__...._.12.n n n N m m m n N m m m ⎧⎧⇒⎪⎨=+++⎩⎪⎪⎧⎪⇒⎨⎪=⨯⨯⨯⎫⎪⎩⇒⎬⎨⎭⎪⎪⇒⎪⎪⎪⎪⎩⇒定义:完成一件事有类不同方案分类加法计算原理公式:定义:完成一件事需要个步骤分步乘法计数原理公式:分类加法计算原理与分步乘法计算原理区别:一个分类,一个分步两个计算原理的关系及综合应用综合应用明确是先分类还是先分步;确定分类标准和分步程序排列排列计数原理排列与组合11(1)(2)...(1)______.:______.,:mn mmn n m m m n m m m m n n n n nA n n n n m A C A C C C C C --+⎧⎪=---+⎪⎨⎪⎪⎩⎧=⎪⎪⎪==+⎨⎪⎪⎪⎩的定义:按一定的顺序排成一列排列数及其公式:排烈应用题:元素分析法、位置分析法、捆绑法、插空法、整体法组合的定义合成一组组合数及其公式:组合组合数的性质:组合应用题:直接法、间接法、隔板法排列、组合综合应用题先分组后012..""2m n mn n n n n n n n C C C C C C -⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎧⎧⇒⎪⎪⎨⎩⎪⎪⎪⎪⎧=⎪⎪⇒⎨⎪⎪⎪⎪⎪⇒⎨⎪⎪⎪⎪⎪⎪⎪+++⋅⋅⋅+=⎩⎩⎪⎪⎪⎪⎩排列二项式定理的内容:二项式定理二项展开式的通项对称性;二项式定理增减性与最大值;杨辉三角形与二项式系数的性质各二项式系数的和;知识点一、计数原理1.分类加法计数原理概念:完成一件事有n 类不同方案,在第1类方案中有1m 种不同的方法,在第2类方案中有2m 种不同的方法,…,在第n 类方案中有n m种不同的方法,那么完成这件事共有12n N m m m =++⋅⋅⋅+种不同的方法(也称加法原理)特征:(1)任何一类方案都能完成这件事;(2)各类方案之间相互独立;(3)分类要做到“不重不漏”2.分步乘法计数原理概念:完成一件事需要n 个步骤,做第1步有1m 种不同的方法,做第2步有2m 种不同的方法,…,做第n 步有n m 种不同的方法,那么,完成这件事共有12n N m m m =⨯⨯⋅⋅⋅⨯种不同的方法(也称乘法原理)特征:(1)任何一步都不能单独完成这件事;(2)各步之间相互依存;(3)分步要做到“步骤完整”知识点二、排列1.排列:一般地,从n 个不同元素中取出()m m n ≤个元素,按照一定的顺序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列2.排列数:从n 个不同元素中取出()m m n ≤个元素的所有不同排列的个数叫做从n 个不同元素中取出m 个元素的排列数,用符号mn A 表示 3.排列数公式:()()()()!121!mn n A n n n n m n m =--⋅⋅⋅-+=-(*,m n N ∈,且m n ≤)知识点三、组合1.组合:一般地,从n 个不同的元素中取出()m m n ≤个元素合成一组,叫做从n 个不同元素中取出m 个元素的一个组合2.组合数:从n 个不同元素中取出()m m n ≤个元素的所有不同组合的个数,叫做从n 个不同元素中取出m 个元素的组合数,用符号mn C 表示3.组合数公式:()()()()121!!!!mmn nm n n n n n m A n C A m m n m --⋅⋅⋅-+===-(*,m n N ∈,且m n ≤)4.组合数的性质:(1)m n m n n C C -=;(2)11m m m n n n C C C -+=+知识点四、二项式定理1.二项式定理概念:一般地,对于任意的正整数n , 都有()()01102*nnn n k n k k n nn n n n n a b C a C aC a b C a b C b n N ---+=+++⋅⋅⋅++⋅⋅⋅+∈. 这个公式称为二项式定理,等号右边的式子称为()n a b +的二项展开式,()na b +的二项展开式共有1n +项,其中各项的系数{}()0,1,2,,kn C k n ∈⋅⋅⋅叫做二项式系数,k n k k n C a b -称为二项展开式的第1k +项,又称为二项展开式的通项 2.二项展开式的特征: (1)二项展开式共有1n +项;(2)二项式系数依次为组合数012,,,,,,knn n n n n C C C C C ⋅⋅⋅⋅⋅⋅; (3)各项次数都等于二项式的幂指数n ;(4)字母a 的指数由n 开始按降幂排列到0,b 的指数由0开始按升幂排列到n 3.二项式系数与项的系数的区别:二项式系数为项的系数指该项中除字母外的部分 4.二项式系数的性质对称性:与首末两端“等距离”的两个二项式系数相等 增减性:当12n k +<时,二项式系数是逐渐增大的,由对称性知它的后半部分是逐渐减小的最大值:当n 是偶数时,中间一项的二项式系数2n nC 取得最大值;当n 是奇数时,中间两项的二项式系数1122,n n nnCC-+相等,且同时取得最大值5.二项式系数和:(1)二项展开式中各二项式系数之和为2n;(2)在二项展开式中奇数项的二项式系数之和与偶数项的二项式系数之和相等且都等于12n -.类型一:两个基本计数原理的实际应用问题例1 在某种信息传输过程中,4个数字组成的一个排列 (数字允许重复)表示一个信息,不同的排列表示不同的信息.若所用数字只有0和1,则与信息0110至多有2个对位置上的数字相同的信息个数为( )A .10B .11C .12D .15解析:方法1:分有0个时应位置上的数字相同、1个对应位显上的数字相同、2个时应位五上的数字相同讨论:(1)若有0个对应位五上的数字相同.则信息为1001,共有1个. (2)若有1个叶应位丑上的数字相同1101,1011,1000.共有4个. (3)若有2个时应位置上的数字相同,又分为以下情况①若位笠一与二对应相同,则信息为0101; ②若位五一与三时应相同,则信息为0011; ③若位五一与四对应相同,则信忽为0000; ④若位且二与三对应相同,则信息为1111; ⑤若位里二与四时应相同,则信忠为1100;⑥若位置三与四时应相同、则信.息为1010.共有6个.故与信息0110至多有2个对应位置上的数字相同的信息个数为14611.++= 方法2:若有0个对应位置上的数字相同.共有1个;若有1个对应位置上的数字相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020高考数学考点突破之计数原理、概率与统计(1)
第1讲分类加法计数原理与分步乘法计数原理【考点梳理】
1.分类加法计数原理
完成一件事有两类不同的方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法.
2.分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法.
3.分类加法和分步乘法计数原理,区别在于:分类加法计数原理针对“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事;分步乘法计数原理针对“分步”问题,各个步骤相互依存,只有各个步骤都完成了才算完成这件事.
【考点突破】
考点一、分类加法计数原理
【例1】(1)三个人踢毽,互相传递,每人每次只能踢一下,由甲开始踢,经过4次传递后,毽又被踢回给甲,则不同的传递方式共有( )
A.4种
B.6种
C.10种
D.16种
(2)满足a,b∈{-1,0,1,2},且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为()
A.14
B.13
C.12
D.10
[答案] (1)B(2)B
[解析] (1)分两类:甲第一次踢给乙时,满足条件有3种方法(如图),甲乙丙乙
甲甲乙甲丙甲
同理,甲先传给丙时,满足条件有3种踢法.
由分类加法计数原理,共有3+3=6种传递方法.
(2)①当a=0,有x=-b
2,b=-1,0,1,2有4种可能;
②当a≠0时,则Δ=4-4ab≥0,ab≤1,
(ⅰ)若a=-1时,b=-1,0,1,2有4种不同的选法;
(ⅱ)若a=1时,b=-1,0,1有3种可能;
(ⅲ)若a=2时,b=-1,0,有2种可能.
∴有序数对(a,b)共有4+4+3+2=13(个).
【类题通法】
分类标准是运用分类加法计数原理的难点所在,应抓住题目中的关键词、关键元素、关键位置.
1.根据题目特点恰当选择一个分类标准.
2.分类时应注意完成这件事情的任何一种方法必须属于某一类,并且分别属于不同种类的两种方法是不同的方法,不能重复.
3.分类时除了不能交叉重复外,还不能有遗漏,如本例(2)中易漏a=0这一类.
【对点训练】
1.如图,从A到O有________种不同的走法(不重复过一点).
[答案] 5
[解析] 分3类:第一类,直接由A到O,有1种走法;第二类,中间过一个点,有A→B→O和A→C→O共2种不同的走法;第三类,中间过两个点,有A→B→C→O 和A→C→B→O共2种不同的走法,由分类加法计数原理可得共有1+2+2=5种不同的走法.
2.从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列的个数为( )
A.3
B.4
C.6
D.8
[答案] D
[解析]以1为首项的等比数列为1,2,4;1,3,9;
以2为首项的等比数列为2,4,8;
以4为首项的等比数列为4,6,9;
把这4个数列的顺序颠倒,又得到另外的4个数列,
∴所求的数列共有2(2+1+1)=8个.
考点二、分步乘法计数原理
【例2】(1)教学大楼共有五层,每层均有两个楼梯,由一层到五层的走法有( )
A.10种
B.25种
C.52种
D.24种
(2)定义集合A与B的运算A*B如下:A*B={(x,y)|x∈A,y∈B},若A={a,b,c},B={a,c,d,e},则集合A*B的元素个数为________(用数字作答).
[答案] (1)D(2)12
[解析] (1)每相邻的两层之间各有2种走法,共分4步.
由分步乘法计数原理,共有24种不同的走法.
(2)显然(a,a),(a,c)等均为A*B中的关系,确定A*B中的元素是A中取一个元素来确定x,B中取一个元素来确定y,由分步计数原理可知A*B中有3×4=12个元素.
【类题通法】
1.在第(1)题中,易误认为分5步完成,错选B.
2.利用分步乘法计数原理应注意:①要按事件发生的过程合理分步,即分步是有先后顺序的.②各步中的方法互相依存,缺一不可,只有各步骤都完成才算完成这件事.
【对点训练】
1.某学校开设“蓝天工程博览课程”,组织6个年级的学生外出参观包括甲博物馆在内的6个博物馆,每个年级任选一个博物馆参观,则有且只有两个年级选择甲博物馆的情况有( )
A.C26·45种
B.A26·54种
C.C26·A45种
D.C26·54种
[答案] D
[解析] 有两个年级选择甲博物馆共有C26种情况,其余四个年级每个年级各有5种选择情况.故有且只有两个年级选择甲博物馆的情况有C26×54种.
2.设集合A={-1,0,1},B={0,1,2,3},定义A*B={(x,y)|x∈A∩B,y∈A∪B},则A*B中元素的个数为________(用数字作答).
[答案] 10
[解析]易知A∩B={0,1},A∪B={-1,0,1,2,3},
∴x有两种取法,y有5种取法.
由分步乘法计数原理,A*B的元素有2×5=10(个).
考点三、两个计数原理的综合应用
【例3】(1)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有()
A.144个
B.120个
C.96个
D.72个
(2)如图所示,用4种不同的颜色对图中5个区域涂色(4种颜色全部使用),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色种数为________(用数字作答).
[答案] (1)B(2)96
[解析](1)由题意,首位数字只能是4,5,若万位是5,则有3×A34=72(个);若万位是4,则有2×A34个=48(个),故比40 000大的偶数共有72+48=120(个).选B.
(2)按区域1与3是否同色分类:
①区域1与3同色:先涂区域1与3有4种方法,再涂区域2,4,5(还有3种颜色)有A33种方法.
∴区域1与3涂同色,共有4A33=24种方法.
②区域1与3不同色:先涂区域1与3有A24种方法,第二步涂区域2有2种涂色方法,第三步涂区域4只有一种方法,第四步涂区域5有3种方法.
∴这时共有A24×2×1×3=72种方法.
由分类加法计数原理,不同的涂色种数为24+72=96.
【类题通法】
1.①注意在综合应用两个原理解决问题时,一般是先分类再分步.在分步时可能又用到分类加法计数原理.②注意对于较复杂的两个原理综合应用的问题,可恰当地列出示意图或列出表格,使问题形象化、直观化.
2.解决涂色问题,可按颜色的种数分类,也可按不同的区域分步完成.第(2)题中,相邻区域不同色,是按区域1与3是否同色分类处理.
【对点训练】
1.如果一个三位正整数如“a1a2a3”满足a1<a2,且a2>a3,则称这样的三位数为凸数(如120,343,275等),那么所有凸数的个数为()
A.240
B.204
C.729
D.920
[答案] A
[解析]若a2=2,则百位数字只能选1,个位数字可选1或0“凸数”为120与121,共2个.若a2=3,则“凸数”有2×3=6(个).若a2=4,满足条件的“凸数”有3×4=12(个),…,若a2=9,满足条件的“凸数”有8×9=72(个).
∴所有凸数有2+6+12+20+30+42+56+72=240(个).
2.从一架钢琴挑出的十个音键中,分别选择3个,4个,5个,…,10个键同时按下,可发出和声,若有一个音键不同,则发出不同的和声,则这样的不同的和声数为________(用数字作答).
[答案] 968
[解析]由题意知本题是一个分类计数问题,共有8种不同的类型,
当有3个键同时按下,有C310种结果,
当有4个键同时按下,有C410种结果,
…,
以此类推,根据分类加法计数原理得到共有C310+C410+C510+…+C1010
=C010+C110+C210+…+C1010-(C010+C110+C210)=210-(1+10+45)=968.。
