Eviews之变系数回归模型
Eviews的logistic回归分析

预测应用
利用建立的模型进行预测,比较预测结果与 实际观测值的差异。
06
结论与展望
研究结论
01
Logistic回归分析在eviews中 的实现方法已经得到了验证, 并且具有较高的预测精度和稳 定性。
02
通过eviews进行Logistic回归 分析可以有效地解决分类问题 ,尤其在二分类问题中表现优 异。
03
EViews软件介绍
软件概述
EViews是一款专门用于经济学、金融 学、统计学等领域的数据分析和预测 软件,具有强大的数据处理、回归分 析和时间序列分析功能。
EViews具有友好的用户界面和灵活的 操作方式,使得用户可以轻松地进行 数据处理、模型建立和预测分析。
EViews提供了丰富的数据接口,支持 多种数据格式,可以方便地导入各种 数据源,如Excel、CSV、数据库等。
变量选择
根据研究目的和理论背景,选择与购买行为相关 的自变量。
3
模型估计
使用EViews软件进行模型参数估计,得到回归 系数、置信区间等。
结果解读与讨论
结果解读
根据回归结果,解释各个自变量对因变量的 影响程度和方向。
模型评估
使用似然比检验、AIC等统计量评估模型的 拟合优度。
结果讨论
根据回归结果,探讨自变量之间的交互作用 和模型假设的合理性。
03
在实际应用中,Logistic回归 分析可以帮助我们更好地理解 数据之间的关系,为决策提供 有力支持。
研究不足与展望
目前的研究主要集中在Logistic回归 分析的算法实现和预测精度方面,对 于其理论基础和应用场景的研究还不 够深入。
在实际应用中,Logistic回归分析对 于异常值的敏感度较高,需要进一步 研究如何降低其对模型稳定性的影响 。
《计量经济学》eviews实验报告一元线性回归模型详解

计量经济学》实验报告一元线性回归模型-、实验内容(一)eviews基本操作(二)1、利用EViews软件进行如下操作:(1)EViews软件的启动(2)数据的输入、编辑(3)图形分析与描述统计分析(4)数据文件的存贮、调用2、查找2000-2014年涉及主要数据建立中国消费函数模型中国国民收入与居民消费水平:表1年份X(GDP)Y(社会消费品总量)200099776.339105.72001110270.443055.42002121002.048135.92003136564.652516.32004160714.459501.02005185895.868352.62006217656.679145.22007268019.493571.62008316751.7114830.12009345629.2132678.42010408903.0156998.42011484123.5183918.62012534123.0210307.02013588018.8242842.82014635910.0271896.1数据来源:二、实验目的1.掌握eviews的基本操作。
2.掌握一元线性回归模型的基本理论,一元线性回归模型的建立、估计、检验及预测的方法,以及相应的EViews软件操作方法。
三、实验步骤(简要写明实验步骤)1、数据的输入、编辑2、图形分析与描述统计分析3、数据文件的存贮、调用4、一元线性回归的过程点击view中的Graph-scatter-中的第三个获得在上方输入Isycx回车得到下图DependsntVariable:Y Method:LeastSquares□ate:03;27/16Time:20:18 Sample:20002014 Includedobservations:15VariableCoefficientStd.Errort-StatisticProb.C-3J73.7023i820.535-2.1917610.0472X0416716 0.0107S838.73S44 a.ooao R-squared0.991410 Meandependentwar119790.2 AdjustedR.-squared 0.990750 S.D.dependentrar 7692177 S.E.ofregression 7J98.292 Akaike infocriterion20.77945 Sumsquaredresid 7;12E^-08 Scliwarz 匚「爬伽20.37386 Loglikelihood -1&3.3459Hannan-Quinncriter. 20.77845 F-statistic 1I3&0-435 Durbin-Watsonstat0.477498Prob(F-statistic)a.oooooo在上图中view 处点击view-中的actual ,Fitted ,Residual 中的第一 个得到回归残差打开Resid 中的view-descriptivestatistics 得到残差直方图/icw Proc Qtjject PrintN^me FreezeEstimateForecastStatsResids凹Group:UNIIILtD Worktile:UN III LtLJ::Unti1DependentVariablesMethod;LeastSquares□ate:03?27/16Time:20:27Sample(adjusted):20002014Includedobservations:15afteradjustmentsVariable Coefficient Std.Errort-Statistic ProtJ.C-3373.7023^20.535-2.191761 0.0472X0.4167160.01075S38.735440.0000R-squared0.991410 Meandependeniwar1-19790.3 AdjustedR-squa.red0990750S.D.dependentvar 76921.77 SE.ofregre.ssion 7J98.292 Akaike infacriterion20.77945 Sumsquaredresid 7.12&-0S Schwarzcriterion 20.S73S6 Laglikelihood -153.84&9Hannan-Quinncrite匚20.77545 F-statistic1I3&0.435Durbin-Watsonstat 0.477498 ProbCF-statistic) a.ooaooo在回归方程中有Forecast,残差立为yfse,点击ok后自动得到下图roreestYFM J訓YForea空巾取且:20002015 AdjustedSErmpfe:2000231i mskJddd obaerratire:15Roof kter squa red Error理l%2Mean/^oLteError畐惯啟iJean Afe.PereersErro r5.451SSQThenhe鼻BI附GKWCE口.他腐4Prop&niwi□ooooooVactaree Propor^tori0.001^24G M『倚■底Props^lori09®475在上方空白处输入lsycs…之后点击proc中的forcase根据公式Y。
第13章 EVIEWS 基本回归模型

第十三章基本回归模型单方程回归是最丰富多彩和广泛使用的统计技术之一。
本章介绍EViews中基本回归技术的使用:说明并估计一个回归模型,进行简单的特征分析并在深入的分析中使用估计结果。
随后的章节讨论了检验和预测,以及更高级,专业的技术,如加权最小二乘法、二阶段最小二乘法(TSLS)、非线性最小二乘法、ARIMA/ARIMAX模型、GMM(广义矩估计)、GARCH模型, 和定性的有限因变量模型。
这些技术和模型都是建立在本章介绍的基本思想的基础之上的。
§13.1 方程对象EViews中的单方程回归估计是用方程对象来完成的。
为了创建一个方程对象:从主菜单选择Object/New Object/Equation或Quick/Estimation Equation…,或者在命令窗口中输入关键词equation。
在随后出现的方程说明对话框中说明要建立的方程,并选择估计方法。
下面我们详细介绍在EViews中如何说明方程。
EViews将在方程窗口中估计方程并显示结果。
估计结果会作为方程对象的一部分存储起来以便随时提取。
这样我们只需打开方程对象来显示简要结果,或者利用EViews工具来处理方程对象的结果。
例如,可以使用估计方程作为联立方程模型的一部分。
§13.2 在EViews中对方程进行说明当创建一个方程对象时,会出现如下对话框:在这个对话框中需要说明三件事:方程说明,估计方法,和该估计使用的样本。
在最上面的编辑框中,可以说明方程:因变量(左边)和自变量(右边)以及函数形式。
有两种说明方程的基本方法:列表法和公式法。
列表法简单但是只能用于§13.2.1列表法说明线性方程的最简单的方法是列出方程中要使用的变量列表。
首先是因变量或表达式名,然后是自变量列表。
例如,要说明一个线性消费函数CS,用一个常数和inc对其作回归,在方程说明对话框上部输入:cs c inc注意回归变量列表中的序列c。
EVIEWS回归结果的理解

EVIEWS回归结果的理解在经济学和统计学中,回归分析是一种常用的方法,用于研究变量之间的关系。
EVIEWS是一款常用的计量经济学软件,通过进行回归分析,可以得到一系列统计结果。
本文将介绍EVIEWS回归结果的理解,并解释这些结果对研究的意义和解释。
一、回归方程在进行回归分析后,EVIEWS将给出一个回归方程。
回归方程表示了自变量与因变量之间的关系。
通常,回归方程的形式为:Y = β0 + β1X1 + β2X2 + ... + βkXk + ε其中,Y代表因变量,X1、X2、...、Xk代表自变量,β0、β1、β2、...、βk代表回归系数,ε代表误差项。
回归系数可以理解为自变量对因变量的影响程度,而误差项表示了模型无法解释的部分。
二、回归系数的解释EVIEWS给出的回归结果中,包含了回归方程中自变量的回归系数。
这些回归系数可以帮助我们理解自变量对因变量的影响。
回归系数的正负值表示变量间的正相关或负相关关系,绝对值大小表示相关关系的强弱程度。
需要注意的是,回归系数的统计显著性非常重要。
EVIEWS会给出回归系数的t值和p值,用于判断回归系数是否显著。
如果p值小于设定的显著性水平(通常为0.05),则认为回归系数是显著的,即表明自变量对因变量的影响是存在的。
三、决定系数(R-squared)在EVIEWS回归结果中,还会给出一个被称为决定系数的统计量,用于衡量回归模型对因变量的解释程度。
决定系数的取值范围在0到1之间,越接近1表示回归模型对因变量的解释能力越强。
需要注意的是,决定系数并不代表回归模型的好坏。
一个决定系数较高的回归模型并不一定是更好的模型,因为决定系数受到样本大小、变量选择等多个因素的影响。
因此,在解读决定系数时,需要结合实际问题和模型的适用性进行综合评估。
四、残差分析在EVIEWS回归结果中,还会给出一系列统计指标,用于评估回归模型的拟合优度和模型的合理性。
其中,残差是一项重要指标。
eviews实验报告一元线形回归模型
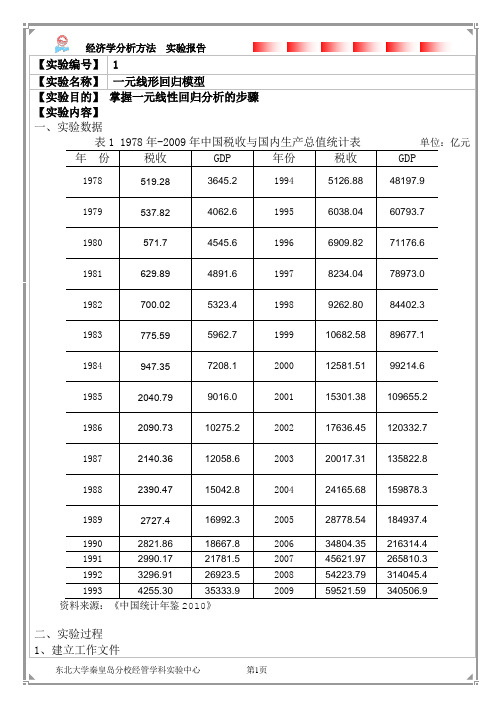
【实验编号】 1【实验名称】一元线形回归模型【实验目的】掌握一元线性回归分析的步骤【实验内容】一、实验数据表1 1978年-2009年中国税收与国内生产总值统计表单位:亿元年份税收GDP 年份税收GDP1978 519.28 3645.2 1994 5126.88 48197.91979 537.82 4062.6 1995 6038.04 60793.71980 571.7 4545.6 1996 6909.82 71176.61981 629.89 4891.6 1997 8234.04 78973.01982 700.02 5323.4 1998 9262.80 84402.31983 775.59 5962.7 1999 10682.58 89677.11984 947.35 7208.1 2000 12581.51 99214.61985 2040.79 9016.0 2001 15301.38 109655.21986 2090.73 10275.2 2002 17636.45 120332.71987 2140.36 12058.6 2003 20017.31 135822.81988 2390.47 15042.8 2004 24165.68 159878.31989 2727.4 16992.3 2005 28778.54 184937.41990 2821.86 18667.8 2006 34804.35 216314.41991 2990.17 21781.5 2007 45621.97 265810.31992 3296.91 26923.5 2008 54223.79 314045.41993 4255.30 35333.9 2009 59521.59 340506.9 资料来源:《中国统计年鉴2010》二、实验过程1、建立工作文件(1)点击桌面Eviews5.0图标,运行Eviews软件。
经验分享使用eviews做回归分析

[经验分享] 使用eview s做线性回归分析Glossa ry:ls(least square s)最小二乘法R-sequar ed样本决定系数(R2):值为0-1,越接近1表示拟合越好,>0.8认为可以接受,但是R2随因变量的增多而增大,解决这个问题使用来调整Adjust R-seqaur ed()S.E of regression回归标准误差Log likelihood对数似然比:残差越小,L值越大,越大说明模型越正确Durbin-Watson stat:DW统计量,0-4之间Mean dependent var因变量的均值S.D. dependent var因变量的标准差Akaike info criter ion赤池信息量(AIC)(越小说明模型越精确)Schwar z ctiter ion:施瓦兹信息量(SC)(越小说明模型越精确)Prob(F-statis t ic)相伴概率fitted(拟合值)线性回归的基本假设:1.自变量之间不相关2.随机误差相互独立,且服从期望为0,标准差为σ的正态分布3.样本个数多于参数个数建模方法:ls y c x1 x2 x3 ...x1 x2 x3的选择先做各序列之间的简单相关系数计算,选择同因变量相关系数大而自变量相关系数小的一些变量。
模型的实际业务含义也有指导意义,比如m1同g dp肯定是相关的。
模型的建立是简单的,复杂的是模型的检验、评价和之后的调整、择优。
模型检验:1)方程显著性检验(F检验):模型拟合样本的效果,即选择的所有自变量对因变量的解释力度F大于临界值则说明拒绝0假设。
Eviews给出了拒绝0假设(所有系统为0的假设)犯错误(第一类错误或α错误)的概率(收尾概率或相伴概率)p 值,若p小于置信度(如0.05)则可以拒绝0假设,即认为方程显著性明显。
eviews处理面板数据操作步骤(特别好)

File/New/ Workfile Workfile structure type : Balanced Panel
Start date 1935 End date 1954 Number of cross 1 OK Cross Section Identifiers:_GM _CH _GE _WE _US
.
10
思路一:变量之间是非同阶单整 :序列变换
◎变量之间是非同阶单整的指即面板数据中有些序列平稳而有些序列不平稳,
此时不能进行协整检验与直接对原序列进行回归。
◎对序列进行差分或取对数使之变成同阶序列
若变换序列后均为平稳序列可用变换后的序列直接进行回归
思路二 若变换序列后均为同阶非平稳序列,则请点
.
若拒绝H1 ,则模型为变参数模型(模型一)。 构建统计量:请点F统计量
.
26
假设检验的 F 统计量的计算方法
构建变参数模型得残差平方和S1 并考虑其自由度 请点
构建变截距模型得残差平方和S2并考虑其自由度 请点
构建不变参数模型得残差平方和S3并考虑其自由度 请点
计算 F2 统计量
F 2 ( S 3 S 1 S ( 1 N ) / N [ N T ( 1 k ( ) k 1 ) ( 1 ) ) ~ ] F [N ( 1 )k ( 1 )N , ( T k 1 )]
第十章 Panel Data模型
第一步 录入数据
第二步 分析数据的平稳性(单位根检验)
第三步 平稳性检验后分析路径选择
第四步 协整检验`
第五步 回归模型
.
1
第一步 录入数据
一 请点 实例数据 二 请点 录入数据软件操作
经验分享,使用eviews做回归分析

[经验分享] 使用eviews做线性回归分析Glossary:ls(least squares)最小二乘法R-sequared样本决定系数(R2):值为0-1,越接近1表示拟合越好,>0.8认为可以接受,但是R2随因变量的增多而增大,解决这个问题使用来调整Adjust R-seqaured()S.E of regression回归标准误差Log likelihood对数似然比:残差越小,L值越大,越大说明模型越正确Durbin-Watson stat:DW统计量,0-4之间Mean dependent var因变量的均值S.D. dependent var因变量的标准差Akaike info criterion赤池信息量(AIC)(越小说明模型越精确)Schwarz ctiterion:施瓦兹信息量(SC)(越小说明模型越精确)Prob(F-statistic)相伴概率fitted(拟合值)线性回归的基本假设:1.自变量之间不相关2.随机误差相互独立,且服从期望为0,标准差为σ的正态分布3.样本个数多于参数个数建模方法:ls y c x1 x2 x3 ...x1 x2 x3的选择先做各序列之间的简单相关系数计算,选择同因变量相关系数大而自变量相关系数小的一些变量。
模型的实际业务含义也有指导意义,比如m1同gdp肯定是相关的。
模型的建立是简单的,复杂的是模型的检验、评价和之后的调整、择优。
模型检验:1)方程显著性检验(F检验):模型拟合样本的效果,即选择的所有自变量对因变量的解释力度F大于临界值则说明拒绝0假设。
Eviews给出了拒绝0假设(所有系统为0的假设)犯错误(第一类错误或α错误)的概率(收尾概率或相伴概率)p 值,若p小于置信度(如0.05)则可以拒绝0假设,即认为方程显著性明显。
2)回归系数显著性检验(t检验):检验每一个自变量的合理性|t|大于临界值表示可拒绝系数为0的假设,即系数合理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
EVIEWS 之变系数回归模型
1 变系数回归模型
前面讨论的是变截距模型,并假定不同个体的解释变量的系数是相同的,然而在现实中变化的经济结构或者不同的经济背景等不可观测的反映个体差异的因素会导致经济结构的参数随着横截面个体的变化而变化,即解释变量对被解释变量的影响要随着截面的变化而变化。
这时要考虑系数随着横截面个体的变化而变化的变系数模型。
1.变系数回归模型原理
变系数模型一般形式如下:
,1,2,,,1,2,,it i it i it y x u i N t T αβ=++==(1) 其中:it y 为因变量,it x 为1k ⨯维解释变量向量,N 为截面成员个数,T 为每个截面成员的观测时期总数。
参数i α表示模型的常数项,i β为对应于解释变量的系数向量。
随机误差项it u 相互独立,且满足零均值、等方差的假设。
在式子(1)中所表示的变系数模型中,常数项和系数向量都是随着截面个体变化而变化,因此将该模型改写为:
it it i it y x u λ=+ (2)
其中:1(1)(1,)it it k x x ⨯+=,'(,)i
i i λαβ= 模型的矩阵形式为:
u X Y +∆= (3)
其中:11N NT y Y y ⨯⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦;121i i i iT T y y y y ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦;⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=N X X X X 00000021;1121112
22212i i ki i i ki i iT
iT kiT T k x x x x x x x x x x ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,12(1)1N N k λλλ+⨯⎡⎤⎢⎥⎢⎥∆=⎢⎥⎢⎥⎣⎦,11N NT u u u ⨯⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,121i i i iT T u u u u ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦
类似于变截距模型,根据系数变化的不同形式,变系数模型中系数的变化,即解释变量对被解释变量的影响也分固定影响和随机影响两类,相应的变系数模型也分为固定影响变系数模型和随机影响变系数模型两类,前者也被称为似不相关回归模型,后者包括Swamy 随机系数模型和Hsiao 模型等,本章只介绍Swamy 随机系数模型。
2.变系数模型分类及软件估计
1)模型分类
在Eviews 软件中pool 面板数据建立的方程组中,依据其解释变量的系数向量β对所有个体和时期的不同而有如下的三种极端情形:
(1)对所有的截面和时期,β是个常数且相同,其模型形式如下:
it it i t it y x αβδγε=++++ (4)
这里在β向量中有k 个系数,每个都对应一个解释变量x 。
在软件操作中,就是将所有解释变量都填入common coefficients 。
(2)β依据所有的截面的不同而不同,每个截面有一个系数,不同截面系数不一样,说明个体成员间的差异而导致各个解释变量的系数而不同,但这里不
随时期的不同而不同,模型形式如下:
it it i i t it y x αβδγε=++++ (5)
在软件操作中,就是将所有解释变量全部填入cross-section specific 。
然后点击“确定”,得到的估计结果如下:
(3)β依据所有时期的不同而不同,每个时期变量有一个不同的系数,不随截面不同而变化,说明结构变化而导致各个解释变量的系数而不同,模型形式
如下:
it it t i t it y x αβδγε=++++ (6)
(4)在实际的应用中,我们常常是将上面的三种情形混合着用,比如有的数据中某些变量既有结构的变化,但其他的变量却随个体而变化,我们就可以将
(2)和(3)混合着用。
因此面板数据的分类非常复杂,我们推广到更一般情形下,将解释变量分类上述三种(不随截面和时点变化的解释变量、只随截面变量的解释变量和只随时点变化的解释变量),模型为:
001122it it it i it t i t it y x x x αβββδγε=++++++ (7)
本章除了介绍一般的变系数模型外,后两节专门介绍似不相关回归和swamy 模型的相关理论。
3.似不相关回归模型
在固定影响变系数模型中,系数向量是跨截面变化的常数向量,引向当不同个体之间的随机误差项不相关时,固定影响变系数模型的估计就简化为对单个的截面分布估计各截面单方程的系数,但在实际生活中这样面板数据的建立也就没意义了。
因此,一般讨论最多的是不同个体之间的随机误差项相关的固定影响变系数模型。
1)模型理论
如果模型(1)满足如下的假设,我们则称之为似不相关回归模型(seemingly unrelated regression models ,SUR )。
①对于i=1,2,…,N ,()0i E u =;②对于i=1,2,…,N ,'2()i i i T E u u I σ=;
③对于i ,j=1,2,…,N ,'
()i j ij T E u u I σ=;④对于i=1,2,…,N ,i X 在重复抽
样中是固定的。
随机误差项的方差协方差矩阵为:
T I Ω=∑⊗ (8)
其中,2112122122212N N N N N σσσσσσσσσ⎡⎤⎢⎥⎢⎥∑=⎢⎥⎢⎥⎢⎥⎣⎦
,且11T I --Ω=∑⊗ 因此,在同一时刻,不同个体的被解释变量只受到共同不可观测或不可度量的因素的影响时,可以利用似不相关回归模型估计。
一般称个体间的这种相关性为同期相关性(contemporaneous correlation )。
在实际经济生活中,有许多经济问题具有同期相关性。
例如,由于货币政策、要素价格和地缘经济因素等不易观测或度量的因素的共同影响,同一个国家不同商品的需求量、不同企业的投资和和不同地区的消费水平等经济变量表现出显著的同期相关性。
在处理这类经济问题时,可以将模型设定为似不相关回归模型。
(1)误差项的协方差矩阵Ω已知
模型系数可以利用GLS 方法估计,即
[][]Y X X X SUR 1
11ˆ---Ω'Ω'=λ (9) 在上面的假设下,如果模型使得11)(lim --∞→Ω'X X T 是有限非退化矩阵,则估计
量SUR λ是λ的最佳线性无偏一致渐近正态分布的估计量。
并且,如果误差项向量服从多元正态分布,则SUR λ是λ的最小方差线性无偏的和渐近有效的估计量。
(2)协方差矩阵Ω未知
当误差项协方差矩阵Ω未知时,首先要先对Ω进行估计。
Zellner (1962)提出了两种估计Ω的方法,其一是利用模型(3)中每个个体的独立回归模型的残差it u 估计ij σ和2i σ,其二是利用模型(3)系统的OLS 残差it u 估计ij σ和2i σ。
∑=-=T t it i u
K T 1
22
ˆ1σ (10) ∑=-=T
t jt it ij u u K
T 1ˆˆ1σ (11)
于是,若1-Ω存在,则λ的FGLS 方法估计量,即
[][]Y X X X SUR 111---Ω'Ω'=λ (12)
通常,将该估计量称为ZEF 估计。
另外,Zellner 还提出了一种迭代算法,称为ITERZEF 估计。
其计算过程是:根据式子(12)计算模型(3)的ZEF 估计量SUR λ;然后依据ZEF 估计量SUR λ,利用(10)和(11)再次估计Ω;利用Ω的新估计量,根据(12)再次进行计算模型(3)的ZEF 估计量。
重复上面三个步骤,直到ZEF 估计量SUR λ相对误差较小时,结束迭代过程,最终得到的ZEF 估计量SUR λ即为λ的ITERZEF 估计量。
2)Eviews 估计过程
(1)在pool 窗口中,点击object ,建立名为SUR 的新系统(system ):
(2)点击OK ,设定如下的SUR 模型系统
(3)点击Estimate,估计SUR模型系统(如图所示),在Estimation method 中选择seemingly Unrelated Regression方法,其他保持Eviews默认的设置,
(4)点击“确定”,估计SUR模型,结果输出如下:。
