四年级数学三角形的面积计算PPT优秀课件
合集下载
《三角形的面积》数学ppt课件
平行四边形的面积是其相邻两边之积，而三角形的面积是平行四边形面
积的一半，因为三角形占据了平行四边形的一半空间。
03
推导公式
同样设三角形底边长为a，高为h，则三角形面积S = 1/2 * a * h。
两者方法比较与联系
比较
矩形法和平行四边形法都是通过构造一个与三角形 相邻且等高的图形来推导三角形面积公式。两种方 法在构造图形和分析关系上略有不同，但最终得出 的公式是一致的。
直角三角形性质
有一个角为90°；勾股定 理（直角三角形的两条直 角边的平方和等于斜边的 平方）。
等边三角形性质
三边相等，三个角都是 60°；三线合一（每条边 上的中线、高线和所对角 的平分线互相重合）。
02
三角形面积计算公式推导
Chapter
矩形法推导三角形面积公式
构造矩形
推导公式
在三角形的一边上作一个与之相邻且 等高的矩形。
实例演示：如何减小误差
实例一
01
通过多次测量取平均值的方法，减小测量误差对三角形边长和
角度的影响。
实例二
02
针对已知三边长的三角形，采用海伦公式进行精确计算，避免
使用其他近似公式带来的误差。
实例三
03
在进行数值计算时，增加有效数字位数，例如使用双精度浮点
数进行计算，以减小舍入误差对计算结果的影响。
联系
两种方法都利用了“等底等高”的原理，即两个图 形如果底边相等且高相等，则它们的面积之比等于 其对应的高之比。这也是三角形面积公式推导的关 键所在。
03
具体应用：求解不同类型三角 形面积
Chapter
已知两边及夹角求面积
公式介绍
S = 1/2 * a * b * sinC，其中a、 b为已知两边长度，C为两边夹角
四年级数学三角形的面积计算1
平行四边形的面积=底×高
（两个三角形的面积）
（一个）三角形的面积=底×高÷2
S=ah ÷2Βιβλιοθήκη 平行四边形的面积是它等底等高 的三角形的面积的2倍。 三角形的面积是它等底等高的平 行四边形的面积的一半。
例1 一种零件有一面是三角 形，三角形的底是5.6 厘米， 高是4 厘米。这个三角形的 面积是多少平方厘米？
三、判断题
1、三角形的面积是平行四边形面积的一半。
… …（ ） 2、有两个形状不同的三角形，它们的底、 高都相等，那么它们的面积一定相等。 ……（ ） 3、三角形的底越长，它的面积就越大。 ……（ ） 4、两个三角形的高相等，它们的面积就相 等。 … …（ ）
×
√
× ×
四、应用题
一块三角形菜地，底2.1米，高是底的
五年级数学教学课件
三角形的面积计算
授课老师 林耀奎 课件制作 林耀奎
长方形的面积=长×宽 正方形的面积=边长×边长 平行四边形的面积=底×高
» 复习
计算下面长方形和平行四边形的面积。
7米 4 米 4 米 7米
7×4=28（平方米）
2 厘 米 3厘米
三角形的面积计算
思考与讨论：
拼成的平行四边形的底和高与原来 的三角形的底和高有什么关系？平行四 边形的面积是怎样的？得出的三角形的 面积又是怎样的？
3、有一个三角形，它的面积是50平方厘米， 如果把它的底扩大4倍，那么它的面积应是 （ 200 ）平方厘米。
二、选择题
1、有一块三角形铁皮，底4.2米，高2米，它 的面积是（ C ） A、8.4平方米 B 、4.2米 C、4.2平方米 2、右图平行四边形的面 积是12平方厘米，那么画 斜线部分的面积是（ ） B A、12平方厘米 B、6平方厘米 C、无法解答
等边三角形优秀PPT课件
数学研究中
等边三角形是数学研究中的重要对 象之一，与三角函数、数列等领域 有密切联系。
03
等边三角形面积与周长计算
面积计算公式推导
等边三角形面积公式
S = (a^2 * sqrt(3)) / 4，其中a为等边三角形的边长。
公式推导
等边三角形可以划分成两个等腰直角三角形，每个直角三角形的面积为(1/2) * a * (a * sqrt(3) / 2)，因此等边三角形面积为2 * (1/2) * a * (a * sqrt(3) / 2) = (a^2 * sqrt(3)) / 4。
05
等边三角形相关数学问题探讨
等腰直角三角形与等边三角形关系探讨
定义与性质 等腰直角三角形是两边相等的直角三角形，等边三角形则 是三边都相等的三角形。两者都属于特殊三角形，具有一 些独特的性质。
关联与转化 等腰直角三角形可以通过添加辅助线转化为等边三角形， 从而利用等边三角形的性质解决问题。反之，等边三角形 也可以转化为等腰直角三角形进行求解。
三边相等判定法
定义
判定方法
三边长度相等的三角形称为等边三角 形。
通过测量三角形的三边长度，判断是 否相等来确定是否为等边三角形。
判定定理
若三角形三边长度分别为a、b、c， 且满足a=b=c，则该三角形为等边三 角形。
两角相等判定法
定义
有两个内角相等的三角形 称为等腰三角形，若这两 个内角均为60度，则为等 边三角形。
特点
等边三角形的三个内角均为60°， 具有对称性。
与其他三角形关系
01
02
03
与等腰三角形关系
等边三角形是特殊的等腰 三角形，其中两腰长度相 等且等于第三边。
与直角三角形关系
等边三角形是数学研究中的重要对 象之一，与三角函数、数列等领域 有密切联系。
03
等边三角形面积与周长计算
面积计算公式推导
等边三角形面积公式
S = (a^2 * sqrt(3)) / 4，其中a为等边三角形的边长。
公式推导
等边三角形可以划分成两个等腰直角三角形，每个直角三角形的面积为(1/2) * a * (a * sqrt(3) / 2)，因此等边三角形面积为2 * (1/2) * a * (a * sqrt(3) / 2) = (a^2 * sqrt(3)) / 4。
05
等边三角形相关数学问题探讨
等腰直角三角形与等边三角形关系探讨
定义与性质 等腰直角三角形是两边相等的直角三角形，等边三角形则 是三边都相等的三角形。两者都属于特殊三角形，具有一 些独特的性质。
关联与转化 等腰直角三角形可以通过添加辅助线转化为等边三角形， 从而利用等边三角形的性质解决问题。反之，等边三角形 也可以转化为等腰直角三角形进行求解。
三边相等判定法
定义
判定方法
三边长度相等的三角形称为等边三角 形。
通过测量三角形的三边长度，判断是 否相等来确定是否为等边三角形。
判定定理
若三角形三边长度分别为a、b、c， 且满足a=b=c，则该三角形为等边三 角形。
两角相等判定法
定义
有两个内角相等的三角形 称为等腰三角形，若这两 个内角均为60度，则为等 边三角形。
特点
等边三角形的三个内角均为60°， 具有对称性。
与其他三角形关系
01
02
03
与等腰三角形关系
等边三角形是特殊的等腰 三角形，其中两腰长度相 等且等于第三边。
与直角三角形关系
《三角形的面积》PPT课件
.
29
.
30
三角形，可以拼成一
个平行四边形。
.
8
钝角三角形
.
9
钝角三角形
.
10
钝角三角形
两个完全一样的钝角
三角形，可以拼成一
个平行四边形。
角形
.
13
直角三角形
两个完全一样的直角三角形，
可以拼成一个平行四边形。
.
14
直角三角形
两个完全一样的直角三角形，
可以拼成一个平行四边形。
＝1650（cm2）
答：它的面积是1650cm2。
.
19
学以致用
指出下面三角形的底和高，并口算出它们的
面积。( 单位：厘米）
4
4
1.5
2.5
3
3
.
20
典题精讲
图中三角形ABC的面积
是24cm2,BD=DC,阴影部分
的面积是多少平方厘米?
.
21
典题精讲
解题思路：
BD=DC,也就是三角形ABD和ADC
等于平行四边形面积的一半。
.
25
易错提醒
判断:三角形的面积等
于平行四边形面积的一半。
(
)
√
判断:三角形的面积等
于平行四边形面积的一半。
(
)
×
.
26
学以致用
A
D
B
C
E
上图是一个平行四边形，看图填空。
平行四边形的面积是12平方厘米，三角形
ABC的面积是(
)平方厘米。
6
.
27
学以致用
你能在图中再画出与涂颜色的三角
等底、等高,即阴影部分三角形的面积
29
.
30
三角形，可以拼成一
个平行四边形。
.
8
钝角三角形
.
9
钝角三角形
.
10
钝角三角形
两个完全一样的钝角
三角形，可以拼成一
个平行四边形。
角形
.
13
直角三角形
两个完全一样的直角三角形，
可以拼成一个平行四边形。
.
14
直角三角形
两个完全一样的直角三角形，
可以拼成一个平行四边形。
＝1650（cm2）
答：它的面积是1650cm2。
.
19
学以致用
指出下面三角形的底和高，并口算出它们的
面积。( 单位：厘米）
4
4
1.5
2.5
3
3
.
20
典题精讲
图中三角形ABC的面积
是24cm2,BD=DC,阴影部分
的面积是多少平方厘米?
.
21
典题精讲
解题思路：
BD=DC,也就是三角形ABD和ADC
等于平行四边形面积的一半。
.
25
易错提醒
判断:三角形的面积等
于平行四边形面积的一半。
(
)
√
判断:三角形的面积等
于平行四边形面积的一半。
(
)
×
.
26
学以致用
A
D
B
C
E
上图是一个平行四边形，看图填空。
平行四边形的面积是12平方厘米，三角形
ABC的面积是(
)平方厘米。
6
.
27
学以致用
你能在图中再画出与涂颜色的三角
等底、等高,即阴影部分三角形的面积
2024年宝藏PPT分享303小学数学《三角形的面积》
数学竞赛题目解析与拓展
2024/3/1
典型题目解析
在数学竞赛中，经常出现与三角形面 积相关的题目。通过分析典型题目的 解题思路和方法，可以帮助学生掌握 解题技巧，提高数学竞赛的应对能力 。
拓展题目挑战
除了典型题目，还可以提供一些拓展 题目供学生挑战。这些题目可以涉及 更复杂的三角形形状和面积计算方法 ，激发学生的探索精神和创新思维。
等边三角形面积计算
等边三角形是三边长度都相等的三角形。其面积计算公式为：面积 = (边长^2 × √3) / 4。这个公式利用了等边三角形的高与边长的固定比例关系。
2024/3/1
16
直角三角形面积计算技巧分享
直角三角形面积计算
直角三角形是一个角为90度的三角形。其面积计算公式为： 面积 = (底 × 高) / 2，其中底和高分别是直角三角形的两个 直角边。
7
三角形基本性质回顾
三角形有三条边和三个角，任意两边之和大于第三边。
三角形内角和为180度。
2024/3/1
三角形具有稳定性，即三边长度确定后，三角形的形状和大小就唯一确定了。
8
平行四边形面积公式复习
平行四边形的面积可以通过底和高来 计算，即面积 = 底 × 高。
在计算平行四边形面积时，需要确保 底和高的单位一致。
学生自我评价报告分享
学生能够熟练掌握三角形面积的计算 方法，并能够在实际问题中加以应用 。
部分学生在理解三角形面积与底和高 之间的关系时存在困难，需要进一步 加强练习和指导。
学生在课堂上积极参与讨论和实验， 表现出浓厚的学习兴趣和探究精神。
2024/3/1
25
下节课预告及预习建议
下节课将学习梯形的面积计算，学生需要提前预习相关知识。
四年级数学三角形的面积计算7课件
这套幻灯片所设计的是五年级第一学期三角形面积的计算公式 一节内容，目的在于通过动画演示使学生对于三角形面积和与其等 底等高三角形之间的转换关系有更加生动感性的认识。
编号1：出示长方形，复习长方形的面积，知道平行线间的垂 线有无数条。
编号2：经对角线的划分后直角三角形的面积是长方形的一半。 编号3：长方形中的锐角三角形 经做高分割后两个小三角形的 面积是两个小长方形的一半，从而可以知道大三角形的面积是大三 角形的一半。 编号4：钝角三角形的面积是长方形的一半，出示课题及公式。 编号5：比较第一个图中的三角形经过位置变化后什么变了什 么没变。 这套幻灯片的设计宗旨是从实际出发为教学服务，尽量达到 易操做和实用的效果。
4cm
10cm
长方形面积 = 长 × 宽
长方形面积的一半=长×宽 ÷2
4cm
10cm
4cm 10cm
三角形面积的计算公式
三角形的面积=底×高÷ 2 S=ah ÷ 2
长方形面积的一半=长×宽÷2
高
宽
长ห้องสมุดไป่ตู้
(底)
12cm
5cm 12cm
5cm
5cm
12cm
5cm 12cm
多媒体制作
编号：66
制作说明：
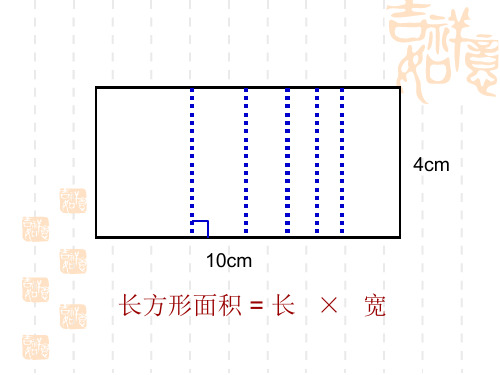
编号1：出示长方形，复习长方形的面积，知道平行线间的垂 线有无数条。
编号2：经对角线的划分后直角三角形的面积是长方形的一半。 编号3：长方形中的锐角三角形 经做高分割后两个小三角形的 面积是两个小长方形的一半，从而可以知道大三角形的面积是大三 角形的一半。 编号4：钝角三角形的面积是长方形的一半，出示课题及公式。 编号5：比较第一个图中的三角形经过位置变化后什么变了什 么没变。 这套幻灯片的设计宗旨是从实际出发为教学服务，尽量达到 易操做和实用的效果。
4cm
10cm
长方形面积 = 长 × 宽
长方形面积的一半=长×宽 ÷2
4cm
10cm
4cm 10cm
三角形面积的计算公式
三角形的面积=底×高÷ 2 S=ah ÷ 2
长方形面积的一半=长×宽÷2
高
宽
长ห้องสมุดไป่ตู้
(底)
12cm
5cm 12cm
5cm
5cm
12cm
5cm 12cm
多媒体制作
编号：66
制作说明：
北师大版数学《三角形的面积》课件
2024/1/25
三角形的面积可以用公式 S = (1/2) × 底 × 高 来计算，其中 S 表示面积，底和高都是长度 单位。
在计算三角形面积时，需要注 意高和底的对应关系，以及单 位的一致性。
9
平行四边形的面积公式
平行四边形是两组对边分别平行的四边 形。
2024/1/25
平行四边形的面积可以用公式 S = 底 × 高 来计算，其中 S 表示面积，底和
北师大版数学《三角形 的面积》课件
2024/1/25
1
目录
• 课程介绍与目标 • 基础知识回顾 • 三角形面积的计算方法 • 三角形面积的应用举例 • 课堂活动与互动环节 • 课后作业与拓展延伸
2024/1/25
2
01
课程介绍与目标
2024/1/25
3
三角形面积的概念
2Hale Waihona Puke 24/1/25三角形面积的定义
情感态度与价值观
通过探究三角形面积的计算方法， 培养学生的数学思维和解决问题的 能力，同时让学生感受到数学在生 活中的广泛应用。
5
教材版本与特点
教材版本
本课程采用北师大版数学教材，该教材注重数学知识的系统性和逻辑性，强调数学与生活的联系。
教材特点
本教材在编排上采用了“问题情境—建立模型—解释、应用与拓展”的模式，引导学生从实际问题出 发，通过观察、比较、分析、归纳等方法，逐步建立数学模型，理解数学概念和方法。同时，教材中 还配备了大量的例题和练习题，帮助学生巩固所学知识，提高解题能力。
2024/1/25
25
阅读相关数学史料，了解三角形面积的发展历程
阅读古希腊数学家海伦的著作， 了解海伦公式的发现和应用。
2024/1/25
三角形的面积可以用公式 S = (1/2) × 底 × 高 来计算，其中 S 表示面积，底和高都是长度 单位。
在计算三角形面积时，需要注 意高和底的对应关系，以及单 位的一致性。
9
平行四边形的面积公式
平行四边形是两组对边分别平行的四边 形。
2024/1/25
平行四边形的面积可以用公式 S = 底 × 高 来计算，其中 S 表示面积，底和
北师大版数学《三角形 的面积》课件
2024/1/25
1
目录
• 课程介绍与目标 • 基础知识回顾 • 三角形面积的计算方法 • 三角形面积的应用举例 • 课堂活动与互动环节 • 课后作业与拓展延伸
2024/1/25
2
01
课程介绍与目标
2024/1/25
3
三角形面积的概念
2Hale Waihona Puke 24/1/25三角形面积的定义
情感态度与价值观
通过探究三角形面积的计算方法， 培养学生的数学思维和解决问题的 能力，同时让学生感受到数学在生 活中的广泛应用。
5
教材版本与特点
教材版本
本课程采用北师大版数学教材，该教材注重数学知识的系统性和逻辑性，强调数学与生活的联系。
教材特点
本教材在编排上采用了“问题情境—建立模型—解释、应用与拓展”的模式，引导学生从实际问题出 发，通过观察、比较、分析、归纳等方法，逐步建立数学模型，理解数学概念和方法。同时，教材中 还配备了大量的例题和练习题，帮助学生巩固所学知识，提高解题能力。
2024/1/25
25
阅读相关数学史料，了解三角形面积的发展历程
阅读古希腊数学家海伦的著作， 了解海伦公式的发现和应用。
2024/1/25
三角形的面积优秀课件
课件名称：三角形的面积一、教学目标1.学生能理解三角形的面积公式，并能够运用公式计算三角形的面积。
2.通过实践活动，学生增强合作学习的意识，提高解决问题的能力。
3.通过数学历史和数学趣闻的介绍，激发学生对数学学习的兴趣和热情。
二、教学内容及过程1.引入（5分钟）教师展示三角形模型，引导学生回答三角形的定义，并提出问题：“你们知道这个三角形的面积怎么计算吗？”鼓励学生积极回答，引入课题。
2.知识点讲解（20分钟）（1）三角形面积公式的推导。
通过PPT演示将三角形转化为平行四边形，引导学生理解公式的推导过程。
（2）公式及实例分析。
讲解公式形式及含义，举一些实际例子，如已知底和高的情况，让学生加深对公式的理解和记忆。
3.课堂练习（15分钟）（1）基础练习。
根据公式计算一些简单三角形的面积，让学生练习并口头回答结果。
（2）综合练习。
给出一个实际问题，如“已知三角形底边长为6cm，高为4cm，求该三角形的面积”，让学生运用公式解决。
4.小组讨论（10分钟）将学生分成小组，让他们互相讲解解题思路和方法，加强学生对三角形面积计算的理解。
5.总结与拓展（5分钟）（1）总结。
回顾本节课学习的重点和难点，加深学生对三角形的面积计算的理解。
（2）拓展。
介绍更多关于三角形面积计算的方法和应用，如海伦公式等，并引入数学历史和趣闻，激发学生对数学学习的兴趣和热情。
三、教学评价1.针对教学目标进行评价，观察学生是否能够理解三角形的面积公式，并能够运用公式计算三角形的面积。
2.通过课堂练习和小组讨论等活动，观察学生是否能够积极参与，合作解决问题。
3.在拓展环节，观察学生是否对数学历史和趣闻产生兴趣，是否有进一步的探索欲望。
四、教学材料1.PPT课件，包含三角形定义、公式推导过程、实例分析等内容。
2.三角形模型、直尺、三角板等教学工具。
3.练习题和拓展材料。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
=30 ×36÷ 2 =540(dm2)
B、解：S = a h ÷ 2
=39 ×36÷ 2 =702(dm2)
判断： 三角形的面积都等于长方形面积的一半 （×）一组对应的底和高都是2米源自三角形，它的面积恰好是2米。
（×）
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
否
是
是
否
宽高 高
宽
宽
底（长）
底（长）
高 底（长）
• 三角形的面积=它相应长方形的面积÷2 =长×宽÷2
三角形的面积=底 ×高 ÷2
S = a h ÷2
同学自学例1书115-116页
一条红领巾的底边长100厘米，它的 高33厘米。求红领巾的面积。
解：S = a h ÷2 =100 × 33 ÷2 =1650(cm2)
三角形面积的计算
初步设计：其中有一块绿地是长方形的，要植上
每平方米3元的草皮，这块地需投入多少钱？
经讨论设计：在长方形地当中的这个直角三角形 上植草皮，那么它的面积是长方形面积的多少 呢？
下图每个小方格边长1厘米，面积是1平方厘米。
高 高
高
底
底
底
• 三角形的面积=它相应长方形的面积÷2
判断下列图形中的绿色三角形面 积是否是该长方形面积的一半？
答：红领巾的面积是1650平方厘米。
计算下面三角形的面积：(单位:cm)
6
10
15
解：S = a h ÷ 2 =15 × 10÷ 2
=75(cm2)
8
解：S = a h ÷ 2 =8 × 6÷ 2 =24(cm2)
选择：计算下面三角形的面积 正确的是（ A ）。
单位(dm)
A、解：S = a h ÷ 2
B、解：S = a h ÷ 2
=39 ×36÷ 2 =702(dm2)
判断： 三角形的面积都等于长方形面积的一半 （×）一组对应的底和高都是2米源自三角形，它的面积恰好是2米。
（×）
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
否
是
是
否
宽高 高
宽
宽
底（长）
底（长）
高 底（长）
• 三角形的面积=它相应长方形的面积÷2 =长×宽÷2
三角形的面积=底 ×高 ÷2
S = a h ÷2
同学自学例1书115-116页
一条红领巾的底边长100厘米，它的 高33厘米。求红领巾的面积。
解：S = a h ÷2 =100 × 33 ÷2 =1650(cm2)
三角形面积的计算
初步设计：其中有一块绿地是长方形的，要植上
每平方米3元的草皮，这块地需投入多少钱？
经讨论设计：在长方形地当中的这个直角三角形 上植草皮，那么它的面积是长方形面积的多少 呢？
下图每个小方格边长1厘米，面积是1平方厘米。
高 高
高
底
底
底
• 三角形的面积=它相应长方形的面积÷2
判断下列图形中的绿色三角形面 积是否是该长方形面积的一半？
答：红领巾的面积是1650平方厘米。
计算下面三角形的面积：(单位:cm)
6
10
15
解：S = a h ÷ 2 =15 × 10÷ 2
=75(cm2)
8
解：S = a h ÷ 2 =8 × 6÷ 2 =24(cm2)
选择：计算下面三角形的面积 正确的是（ A ）。
单位(dm)
A、解：S = a h ÷ 2