6.2.1多面体的表面积
多面体的体积和表面积计算公式大全

立 方 体
长 方 体 ∧ 棱 柱 ∨
三 棱 柱
棱 锥
棱 台
学大教育个性化教案模板
多面体的体积和表面积
尺寸符号
.1
圆 柱 和 空 心 圆 柱 ∧ 管 ∨
斜 线 直 圆 柱
直 圆 锥
圆 台
球
ห้องสมุดไป่ตู้
学大教育个性化教案模板
.2
球 扇 形 ∧ 球 楔 ∨
球 缺
圆 环 体 ∧ 胎 ∨
球 带 体
桶 形
学大教育个性化教案模板
.3
学大教育个性化教案模板
椭 球 体
a,b,c-半轴
交 叉 圆 柱 体
梯 形 体
正 方形
长 方形
三 角形
图形
常用图形求面积公式
尺寸符号
面积(F) 表面 积(S)
.4
平 行四 边形
任 意四 边形
正 多边 形
菱 形
梯 形
圆 形
椭 圆形
学大教育个性化教案模板
a· b-主轴
F= a· b
(π/4)
.5
扇 形
学大教育个性化教案模板
弓 形
圆 环
部 分圆 环
新 月形
L d/10 P 0.40
2d/10 4d/10
5d/10 3d/10
6d/10
7d/10
1.91 2.25 0.79 1.18 1.56
2.55
.6
抛 物线 形
等 多边 形
学大教育个性化教案模板
.7
多面体的表面积与体积

多面体的表面积与体积在几何学中,多面体指的是由多个平面多边形所围成的立体形状。
而多面体的表面积和体积则是对这种立体形状的重要数值描述。
本文将详细介绍多面体的表面积和体积的计算方法及其应用。
一、多面体的表面积多面体的表面积是指该立体形状所有的外表面积之和。
对于不同类型的多面体,其表面积的计算方法也有所不同。
下面将以常见的几种多面体为例来阐述其表面积的计算公式。
1. 三棱锥的表面积三棱锥是一种具有棱和一个尖顶的四面体。
它的表面积可以用以下公式来求解:表面积=底面积+4×侧面积其中底面积可以根据具体形状使用不同的计算公式,而侧面积则可以通过棱长和高的关系求解。
2. 正方体的表面积正方体是一种具有六个正方形面的多面体。
它的表面积可以表示为:表面积=6×边长×边长每个面都是正方形,所以表面积可以简单地通过边长进行计算。
3. 正六面体的表面积正六面体是一种具有六个正六边形面的多面体。
它的表面积可以表示为:表面积=6×边长×边长×√3/4其中√3/4是六边形(正六边形)的面积公式中的常数。
二、多面体的体积多面体的体积是指该立体形状所占据的空间大小。
与表面积不同,体积是一个三维的概念,因此计算方法也具有一定的复杂性。
下面将介绍几种常见多面体的体积计算公式。
1. 三棱锥的体积三棱锥的体积可以通过以下公式计算:体积=底面积×高/3其中底面积和高的计算方法与之前的表面积计算相同。
2. 正方体的体积正方体的体积可以表示为:体积=边长×边长×边长正方体的边长相等,因此体积可以通过边长的立方得到。
3. 正六面体的体积正六面体的体积可以表示为:体积=边长×边长×边长×√2/3其中√2/3是正六面体体积计算公式中的常数。
三、多面体的应用多面体的表面积和体积在现实生活中有着广泛的应用。
例如,建筑师需要计算建筑物的体积来确定所需的材料数量;工程师需要计算机械零件的表面积以确定其可行性和性能;科学家利用多面体的体积和表面积计算研究材料的物理特性等等。
几何中的多面体和圆锥体的表面积和体积

几何中的多面体和圆锥体的表面积和体积一、多面体的表面积和体积1.多面体:由四个或四个以上的多边形所围成的立体。
2.多面体的表面积:多面体所有面的面积之和。
3.多面体的体积:多面体所占空间的大小。
4.常见多面体:立方体、长方体、棱柱、棱锥等。
5.多面体表面积和体积的计算公式:–立方体:表面积 = 6a²,体积 = a³–长方体:表面积 = 2(ab + ac + bc),体积 = abc–棱柱:表面积 = 2(ah + bh),体积 =底面积×高–棱锥:表面积 = (底边长×周长)/2,体积 = (底边长×高)/3二、圆锥体的表面积和体积1.圆锥体:由一个圆面和一个顶点不在同一平面的直线(母线)所围成的立体。
2.圆锥体的表面积:圆锥侧面积加上底面积。
3.圆锥体的体积:圆锥所占空间的大小。
4.常见圆锥体:圆锥、圆台等。
5.圆锥体表面积和体积的计算公式:–圆锥:表面积= πrl + πr²,体积= πr²h/3–圆台:表面积= π(r+R)l + πr² + πR²,体积= (1/3)πh(r² + R² + rR)其中,a、b、c分别为长方体的三条棱长;h为棱柱的高;R为圆锥的底面半径;r为圆锥的母线长;l为圆锥的斜高。
三、多面体和圆锥体的性质1.多面体的性质:各面为平面,相邻面相交于直线,多面体的顶点数、边数和面数之间存在一定的关系。
2.圆锥体的性质:底面为圆,侧面为曲面,从顶点到底面圆心的线段称为高,圆锥的母线、斜高、高之间存在一定的关系。
四、多面体和圆锥体的应用1.在生活中,多面体和圆锥体广泛应用于建筑、家具、模具等领域。
2.在科学实验中,多面体和圆锥体可用于测量物体的体积和表面积,从而求得物体的密度、质量等参数。
3.在数学教育中,多面体和圆锥体的表面积和体积的计算有助于培养学生的空间想象能力和逻辑思维能力。
多面体的表面积公式

contents
目录
• 引言 • 多面体的基本概念 • 多面体的表面积公式 • 特殊多面体的表面积公式 • 表面积公式的实际应用 • 结论
01 引言
主题简介
• 多面体表面积公式:多面体表面积公式的推导和应用是多面体 几何学中的重要内容,它涉及到多面体的各个面的面积和形状。
重要性及应用
正多面体的表面积公式
正多面体的表面积公式
正多面体的每个面都是正多边形,其表面积由以下公式给出:A = (n*s^2)/a,其中 n是多面体的面数,s是多边形的边长,a是多边形的内角。
举例
正方体的表面积公式为6s^2,其中s是正方体的边长。
半正多面体的表面积公式
半正多面体的表面积公式
半正多面体是一个多面体,其每个面都是半正多边形,其表面 积由以下公式给出:A = (n*s^2)/2a,其中n是多面体的面数, s是多边形的边长,a是多边形的内角。
材料科学
在材料科学研究中,多面体的表面积公式可用于计算材料的表面积,这对于研究材料的 物理和化学性质具有重要意义。例如,在催化剂和电极材料的研究中,表面积的计算有
助于了解材料的活性、反应速率和性能。
06 结论
表面积公式的意义
内容,它对于理解多面 体的形状、结构和性质具有重要
多边形的面积公式
多边形的面积=边长×高,这 是由三角形面积公式推导而来。
多面体的表面积公式
多面体的表面积=2×(多面体 的底面积+多面体的侧面积)。
公式理解
多面体的底面积
多面体的底面是一个多边形,其面积为底边长度 乘高。
多面体的侧面积
多面体的侧面积是由底面和顶面的边长和对应的 高构成的三角形的面积之和。
多面体的体积和表面积公式大全
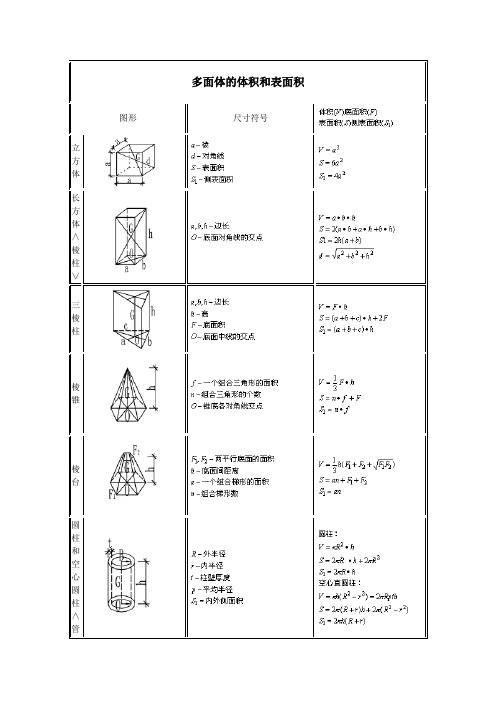
扇 形
弓 形
圆 环
部 分 圆 环
新 月 形
L d/10 P 0.40 抛 物 线 形
2d/10 3d/10 4d/10 0.79 1.18 1.56
5d/10 6d/10 7d/10 1.91 2.25 2.55
等 多 边 形
多面体的体积和表面积图形尺寸符号立方体长方体棱柱三棱柱棱锥棱台圆柱和空心圆柱管斜线直圆柱直圆锥圆台球球扇形球楔球缺圆环体胎球带体桶形椭球体abc半轴交叉圆柱体梯形体常用图形求面积公式图形尺寸符号面积f表面积s正方形长方形三角形平行四边形任意四边形正多边形菱形梯形圆形椭圆形ab主轴f4ab扇形弓形圆环部分圆环新月形ld102d103d104d105d106d107d10p040079118156191225255抛物线形等多边形
r-放坡系数,如 1:0.5 r=0.5
V=(a1+rh)(b1+rh)h+r h /3
2 3
常用图形求面积公式
图形
尺寸符号
面积(F) 表面积(S)
正 方 形 长 方 形 三 角 形 平 行 四 边 形 任 意 四 边 形
正 多 边 形
菱 形
梯 形
圆 形
椭 圆 形
a· b-主轴
F= (π/4) a·b
多面体的体积和表面积
图形 立 方 体 长 方 体 ∧ 棱 柱 ∨ 三 棱 柱 尺寸符号
棱 锥
棱 台
圆 柱 和 空 心 圆 柱 ∧ 管
∨
斜 线 直 圆 柱
直 圆 锥
圆 台
球
球 扇 形 ∧ 球 楔 ∨
球 缺
圆 环 体 ∧ 胎 ∨
球 带 体,c-半轴
交 叉 圆 柱 体
梯 形 体
认识多面体的表面积和体积

认识多面体的表面积和体积多面体是几何学中一个重要的概念,它是一个由多个平面多边形组成的立体图形。
学习多面体的表面积和体积,可以深入理解几何学的基本原理,并应用到实际生活中的问题中。
本文将介绍多面体的表面积和体积的概念、计算方法以及应用。
一、多面体的定义和特点多面体是由平面多边形连接而成的立体图形。
它有以下几个基本特点:1. 多面体的所有边都是线段,将两个顶点连接起来得到的结果。
2. 多面体的所有面都是平面多边形,由多个边围成的封闭图形。
3. 多面体的每个顶点都与其他若干个顶点相连,形成了多个面的交汇点。
多面体可以分为两类:凸多面体和凹多面体。
凸多面体的内部不包含任何角,所有的面都向外凸出。
而凹多面体的内部包含至少一个角,至少有一个面向内凹陷。
在计算多面体的表面积和体积时,需要根据具体情况选择合适的方法。
二、多面体的表面积计算方法计算多面体的表面积是为了了解立体图形的大小和形态。
下面介绍几个常见多面体的表面积计算方法:1. 立方体的表面积计算立方体是一种具有六个面都是正方形的多面体。
其表面积等于所有面的面积之和。
假设立方体的边长为a,则其表面积等于6*a^2。
2. 正四面体的表面积计算正四面体是一种具有四个全等的正三角形面的多面体。
其表面积等于底面积加上四个侧面的面积之和。
假设正四面体的边长为a,则其表面积等于√3*a^2。
3. 正六面体的表面积计算正六面体是一种具有六个全等的正方形面的多面体。
其表面积等于所有面的面积之和。
假设正六面体的边长为a,则其表面积等于6*a^2。
4. 正八面体的表面积计算正八面体是一种具有八个全等的正三角形面的多面体。
其表面积等于所有面的面积之和。
假设正八面体的边长为a,则其表面积等于2*√3*a^2。
通过以上几个常见多面体表面积的计算方法,我们可以了解到不同多面体的表面积公式及其计算过程。
这些计算方法可以帮助我们更好地理解立体图形的几何特征。
三、多面体的体积计算方法计算多面体的体积是为了了解立体图形所占有的空间大小。
多面体的体积与表面积计算
多面体的体积与表面积计算解答:多面体是一种几何体,它有很多种不同的形状,每种形状都有不同的计算体积和表面积的方法。
在这篇文章中,我们将介绍一些常见多面体的计算方法,并提供一些例子来帮助理解。
以下是多面体的体积与表面积计算方法:1. 立方体的计算方法:立方体是一种特殊的多面体,它的六个面是相等的正方形。
立方体的体积和表面积计算方法如下:- 体积:立方体的体积等于一边的长度的立方,即V = a^3,其中V 为体积,a为边长。
- 表面积:立方体的表面积等于六个面的面积之和,即S = 6a^2,其中S为表面积,a为边长。
例如,如果一个立方体的边长为5cm,那么它的体积为V = 5^3 = 125 cm^3,表面积为S = 6 \times 5^2 = 150 cm^2。
2. 正四面体的计算方法:正四面体是一种有四个面且每个面都是等边三角形的多面体。
正四面体的体积和表面积计算方法如下:- 体积:正四面体的体积等于边长的立方除以6的平方根乘以2,即V = (a^3 / 6) \times \sqrt{2},其中V为体积,a为边长。
- 表面积:正四面体的表面积等于底面积的四倍,即S = 4 \times\sqrt{3} \times a^2 / 4 = \sqrt{3} \times a^2,其中S为表面积,a为边长。
例如,如果一个正四面体的边长为6cm,那么它的体积为V = (6^3 / 6) \times \sqrt{2} ≈ 20.784 cm^3,表面积为S = \sqrt{3} \times 6^2 =36\sqrt{3} cm^2。
3. 正六面体的计算方法:正六面体是一种有六个面且每个面都是正方形的多面体。
正六面体的体积和表面积计算方法如下:- 体积:正六面体的体积等于一边的立方乘以根号2,即V = a^3\times \sqrt{2},其中V为体积,a为边长。
- 表面积:正六面体的表面积等于六个面的面积之和,即S = 6a^2,其中S为表面积,a为边长。
多面体体积和面积公式
S曲
=
2πrh
=π(d2 4
+ h2)
S = πh(4r − h)
d 2 = 4h(2r − h)
Go=3(2r-h)2/4(3r-h)
V = 2πr2R • r2 = 1 π 2Dd 2 4
S = 4πr2Rr = π 2Dd = 39.478Rr
在环中心上
R − 球半径 r1,r2 − 底面半径 h − 腰高 h1 − 球心O至带底圆心O1的距离
Go=h/2
V = πr2 • h1 + h2 2
S
=
πr(h1
+
h2 )
+
πr 2
•
(1 +
1 cosα
)
S1 = πr(h1 + h2)
G0
=
h1
+ h2 4
+
r2tg 2α 4(h1 + h2)
GK = 1 • r2 • tgα 2 h1 + h2
直圆锥
圆台
球 球扇形∧
球楔∨
r − 底面半径 h−高 l − 母线长
V
=
πh b
(3R12
+
3r22
+
h2
)
S1 = 2πRh
S = 2πRh + π (r12 + r22)
Go=h1+h/2
D −中间断面直径 d − 底直径 l − 桶高
对于抛物线形桶体
V = πl (2D2 + Dd + 3 d 2)
15
4
对于圆形桶体
V = πl (2D2 + d 2) 12
多面体的表面积和体积公式
多面体的表面积和体积公式
多面体是指由多个面组成的立体图形,常见的多面体有正方体、正六面体(立方体)、正四面体等。
对于多面体的表面积(S)和体积(V),它们的计算公式如下:
1. 表面积的计算公式:
对于任意一个多面体,其表面积等于各个面积之和。
多面体的面积可以按照不同的划分方式来计算。
例如,对于正方体和正六面体,可以分别计算每个面的面积,然后将其相加。
2. 体积的计算公式:
多面体的体积计算公式会根据不同的多面体而有所不同。
以下是一些常见多面体的体积计算公式:
- 正方体的体积公式:V = a^3,其中a为正方体的边长。
- 正六面体的体积公式:V = a^3,其中a为正六面体的边长。
- 正四面体的体积公式:V = (√2/12) * a^3,其中a为正四面体
的边长。
需要注意的是,这些公式仅适用于特定形状的多面体。
对于其他形状的多面体,可能需要使用不同的公式来计算表面积和体积。
多面体的体积和表面积计算公式
球 带 体
桶 形
椭 球 体
a,b,c-半轴
交 叉 圆 柱 体
第3页
多面体的体积和表面积计算表
梯 形 体
常用图形求面积公式
图形
尺寸符号
面积(F) 表面积(S)
正 方 形 长 方 形 三 角 形 平 行 四 边 形 任 意 四 边 形
正 多 边 形
第4页
多面体的体积和表面积计算表
菱 形
梯 形
圆 形
椭 圆 形 a· b-主轴 F= (π/4) a·b
扇 形
弓 形
圆 环
第5页
多面体的体积和表面积计算表
部 分 圆 环
新 月 形
L d/10 P 0.40 抛 物 线 形
2d/10 3d/10 4d/10 0.79 1.18 1.56
5d/10 6d/10 7d/10 1.91 2.25 2.55
等 多 边 形
第6页
多面体的体积和表面积计算表
多面体的体积和表面积
图形 立 方 体 长 方 体 ∧ 棱 柱 ∨ 三 棱 柱 尺寸符号
棱 锥
棱 台
圆 柱 和 空 心 圆 柱 ∧ 管
第1页
多面体的体积和表面积计算表
∨
斜 线 直 圆 柱
直 圆 锥
ቤተ መጻሕፍቲ ባይዱ
圆 台
球
球 扇 形 ∧ 球 楔 ∨
第2页
多面体的体积和表面积计算表
球 缺
圆 环 体 ∧ 胎 ∨
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表面积=侧面积+底面积
作业
课本129页第2、3题
多面体的表面积
填空
2 S a • (1)正方形面积公式:__________。 • (2)矩形面积公式: __________ S ab 。
1 S ah 。 • (3)三角形面积公式:_________ 2
•
3 2 a 正三角形面积公式:_______ 。 4 S
正方体的平面展开图
正方体的棱长为a,分别求它的侧面积和表面积。
S正方体侧=4a2
S正方体表=6a2
长方体的长、宽、高分别为a、b、 c,分别求它的侧面积和表面积。
S长方体侧=2(ac+bc) S长方体表=2(ab+ac+bc)
正方体和长方体的表面积
正方体表面积: 长方体的表面积:
a a
c
b
S 6a
2
S 2(ab ac bc)
• 用空间几何体的展开图来求它的侧面积
几何体的展开图 侧面展开图的构成
一组平行边形
一组三角形
直棱柱的侧面积
直棱柱的侧面展开图是矩形,这个矩形的 长是直棱柱的底面周长,宽是直棱柱的高。
h
c
S直棱柱侧=ch
正棱锥的侧面积
正棱锥的侧面展开图是全等的等腰三角形
h’
c
1 S正棱锥侧= ch’ 2
棱柱、棱锥的表面积
表面积=侧面积+底面积
例1、如图,一个正四棱锥S-ABCD的高SO和底 面边长都是4,求它的侧面积和表面积。
S D
O A E
C
B
设计一个正四棱锥形冷水塔塔顶,高是 练习 0.85m,底面的边长是1.5m,制造这种塔 顶需要多少平方米铁板?(保留两位有效 数字)
S
0.85
O 1.5
E
课堂小结
S直棱柱侧=ch
