2008级大学物理(II)期末试卷及解答
2008级大学物理2试卷解答

2008级大学物理2 A 卷解答一、选择题(共30分)C, B, D, E, D; D, B, C, B, A二、填空题(共30分)11. 66 1分;66 1分;0 1分 12.()32102281q q q R++πε 3分13. )/(21220d U r εε 3分14. aIB π=830μ 3分 15.t B r d /d 213分 16. x 轴正方向 1分;x 轴负方向 2分17. ∆x /v 1分2)/(1)/(c x v v -∆ 2分 18. θφννc o s )c o s (p ch c h +'= 3分 19. 2.55 3分20. 1.06×10-24 (或 6.63×10-24或0.53×10-24 或 3.32×10-24) 3分 根据 ≥∆∆y p y ,或 h p y y ≥∆∆,或 21≥∆∆y p y ,或h p y y 21≥∆∆,可得以上答案. 三、计算题(共40分)21.解:把所有电荷都当作正电荷处理. 在θ处取微小电荷d q = λd l = 2Q d θ / π 1分它在O 处产生场强θεεd 24d d 20220RQR q E π=π=2分 按θ角变化,将d E 分解成二个分量:θθεθd sin 2sin d d 202RQ E E x π== 1分θθεθd cos 2cos d d 202R Q E E y π-=-= 1分对各分量分别积分,积分时考虑到一半是负电荷⎥⎦⎤⎢⎣⎡-π=⎰⎰πππθθθθε2/2/0202d sin d sin 2R QE x =0 2分 2022/2/0202d cos d cos 2R QR Q E y εθθθθεππππ-=⎥⎦⎤⎢⎣⎡-π-=⎰⎰ 2分所以j R Q j E i E E y x202επ-=+= 1分22. 解:由安培环路定理:∑⎰⋅=iI l Hd 2分0< r <R 1区域: 212/2R Ir rH =π212R Ir H π=, 2102R Ir B π=μ 3分 R 1< r <R 2区域: I rH =π2r I H π=2, rIB π=2μ 2分R 2< r <R 3区域: 02IB rμ=π2分r >R 3区域: H = 0,B = 0 1分23. 解:Ob 间的动生电动势:⎰⎰=⋅⨯=5/405/401d d )v (L L l Bl l B ωε225016)54(21BL L B ωω== 4分 b 点电势高于O 点. Oa 间的动生电动势:⎰⎰⋅=⨯=5/05/02d d )v (L L l Bl l B ωε22501)51(21BL L B ωω== 4分 a 点电势高于O 点. ∴ 22125016501BL BL U U b a ωωεε-=-=-221035015BL BL ωω-=-= 2分24. 解:据相对论动能公式 202c m mc E K -= 1分 得 )1)/(11(220--=c c m E K v 即419.11)/(11202==--cm E c Kv 解得v = 0.91c 2分平均寿命为821031.5)/(1-⨯=-=c v ττ s 2分25. 解:远离核的光电子动能为 4.16.1315212=-==v e K m E eV 则==eKm E 2v 7.0×105 m/s 2分 光电子的德布罗意波长为===ve m h p h λ 1.04×10-9m =10.4 Å 3分。
07-08(二)大学物理Ⅱ重修班试卷及解答 (1)

07/08(二)大学物理Ⅱ 重修班试卷(A )一 选择题(共24分) 1.(本题3分)(2018)边长为L 的一个导体方框上通有电流I ,则此框中心的磁感强度 (A) 与L 无关. (B) 正比于L 2. (C) 与L 成正比. (D) 与L 成反比.(E) 与I 2有关. [ D ] 【提示】0O 124(cos cos )4I B r μθθπ=⨯-, =2Lr ,145θ=︒,2135θ=︒ 2.(本题3分)(2125)如图,长度为l 的直导线ab 在均匀磁场B中以速度v移动,直导线ab 中的电动势为 (A) Bl v .(B) Bl v sin α. (C) Bl v cos α. (D) 0. [ D ]【提示】没有切割磁感应线。
()B L ε=⨯⋅v ,()B ⨯v 的方向垂直于纸面,与L 点积后等于零。
3.(本题3分)(5138)在一自感线圈中通过的电流I 随时间t 的变化规律如图(a)所示,若以I 的正流向作为ε的正方向,则代表线圈内自感电动势ε随时间t 变化规律的曲线应为图(b)中(A)、(B)、(C)、(D)中的哪一个?[ D ]【提示】d d L I L t ε=-,d d It为I —t 曲线上的斜率;还有一负号。
4.(本题3分)(2420)在圆柱形空间内有一磁感强度为B 的均匀磁场,如图所示.B的大小以速率d B /d t 变化.在磁场中有A 、B 两点,其间可放直导线AB 和弯曲的导线AB ,则 (A) 电动势只在AB 导线中产生. (B) 电动势只在AB 导线中产生. (C) 电动势在AB 和AB 中都产生,且两者大小相等.(D) AB 导线中的电动势小于AB 导线中的电动势. [ D ] 【提示】作径向辅助线后构成一个回路,则AB 的电动势等于该回路的电动势,而回路的电vttt动势与回路的面积成正比。
所以,面积大的,电动势就大。
5.(本题3分)(3356) 在如图所示的单缝夫琅禾费衍射实验中,若将单缝沿透镜光轴方向向透镜平移,则屏幕上的衍射条纹 (A) 间距变大.(B) 间距变小.(C) 不发生变化. (D) 间距不变,但明暗条纹的位置交替变化. [ C ]6.(本题3分)(3361)某元素的特征光谱中含有波长分别为λ1=450 nm 和λ2=750 nm (1 nm =10-9 m)的光谱线.在光栅光谱中,这两种波长的谱线有重叠现象,重叠处λ2的谱线的级数将是 (A) 2 ,3 ,4 ,5 ...... (B) 2 ,5 ,8 ,11...... (C) 2 ,4 ,6 ,8 ...... (D) 3 ,6 ,9 ,12...... [ D ] 【提示】1122sin d k k θλλ==,2133,6,9,......5k k == 7.(本题3分)(3368)一束光强为I 0的自然光垂直穿过两个偏振片,且此两偏振片的偏振化方向成45°角,则穿过两个偏振片后的光强I 为 (A) 4/0I 2 . (B) I 0 / 4.(C) I 0 / 2. (D)2I 0 / 2. [ B ]【提示】自然光通过一个偏振片后,为光强2I 的线偏振光,再通过第二个偏振片后,光强为200cos 4524I I I ⎛⎫=︒=⎪⎝⎭8.(本题3分)(3544)一束自然光自空气射向一块平板玻璃(如图),设入射角等于布儒斯特角i 0,则在界面2的反射光 (A) 是自然光. (B) 是线偏振光且光矢量的振动方向垂直于入射面. (C) 是线偏振光且光矢量的振动方向平行于入射面. (D) 是部分偏振光. [ B ]【提示】0090=+γi ,r 为界面2上的布儒斯特角,所以,在界面2的反射光是线偏振光且光矢量的振动方向垂直于入射面.二 填空题(共26分) 9.(本题4分)(2065)两个带电粒子,以相同的速度垂直磁感线飞入匀强磁场,它们的质量之比是1∶4,电屏幕荷之比是1∶2,它们所受的磁场力之比是____________,运动轨迹半径之比是______________.1∶2 2分 1∶2 2分 【提示】磁场力F q B =v ,1212::1:2F F q q ==2q B m R =v v →m R qB =v ,112221121==412R m q R m q ⎛⎫⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭10.(本题3分)(2584)有一半径为a ,流过稳恒电流为I 的1/4圆弧形载流导线bc ,按图示方式置于均匀外磁场B中,则该载流导线所受的安培力大小为______ . aIB【提示】均匀外磁场中,弯曲导线的受力=从起点到终点通以同样电流的直导线的受力。
08大学物理Ⅱ习题集及解答
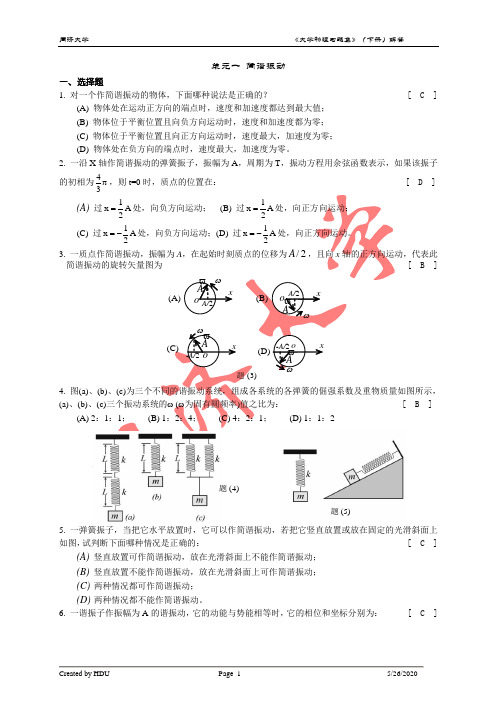
单元一 简谐振动一、 选择题1. 对一个作简谐振动的物体,下面哪种说法是正确的? [ C ](A) 物体处在运动正方向的端点时,速度和加速度都达到最大值; (B) 物体位于平衡位置且向负方向运动时,速度和加速度都为零; (C) 物体位于平衡位置且向正方向运动时,速度最大,加速度为零;(D) 物体处在负方向的端点时,速度最大,加速度为零。
2. 一沿X 轴作简谐振动的弹簧振子,振幅为A ,周期为T ,振动方程用余弦函数表示,如果该振子的初相为4π,则t=0时,质点的位置在: [ D ](A)(C)3. [ B ]4. 图(a)(a)、(b) [ B ]5. 一弹簧振子,当把它水平放置时,它可以作简谐振动,若把它竖直放置或放在固定的光滑斜面上如图,试判断下面哪种情况是正确的: [ C ](A) 竖直放置可作简谐振动,放在光滑斜面上不能作简谐振动;(B) 竖直放置不能作简谐振动,放在光滑斜面上可作简谐振动; (C) 两种情况都可作简谐振动; (D) 两种情况都不能作简谐振动。
6. 一谐振子作振幅为A 的谐振动,它的动能与势能相等时,它的相位和坐标分别为: [ C ]题215(A),or ;A;(B),;3326632(C),or ;(D),;4433ππ±±π±±±π±ππ±±π±±±π±7. 一质点沿x 轴作简谐振动,振动方程为 10.04cos(2)3x t ππ=+(SI ),从t = 0时刻起,到质点位置在x = -0.02 m 处,且向x 轴正方向运动的最短时间间隔为 [ D ](A)s 81; (B) s 61; (C) s 41; (D) s 218. 图中所画的是两个简谐振动的振动曲线,这两个简谐振动叠加后合成的余弦振动的初相为[ C ]T /12;0.5 s 后, 2112它们的合振动的初相为 0.60π 。
普通物理(下)08-09期末考试AB卷及答案

安徽大学2008—2009学年第1学期 《普通物理A(下)》考试试卷(A 卷)(闭卷 时间120分钟)一、单选题(每小题3分,共30分)1.如图所示,两个大小不同的容器用均匀的细管相连,管中有一水银滴作活塞,大容器装有氧气,小容器装有氢气.当温度相同时,水银滴静止于细管中央,则此时这两种气体中(A) 氧气的密度较大. (B) 氢气的密度较大.(C) 密度一样大. (D) 哪种的密度较大是无法判断的. [ ]2.一容器贮有某种理想气体,其分子平均自由程为0λ,若气体的热力学温度降到原来的一半,但体积不变,分子作用球半径不变,则此时平均自由程为 (A)02λ. (B) 0λ.(C)20λ. (D) 20λ. [ ]3.一摩尔单原子理想气体,从初态温度1T 、压强1p 、体积1V ,准静态地等温压缩至体积2V ,外界需作多少功? [ ] (A)121lnV V RT . (B)211ln V VRT . (C))(121V V p -. (D)1122V p V p -. 4.如图所示,质量为m 的物体由劲度系数为k 1和k 2的两个轻弹簧连接,在水平光滑导轨上作微小振动,则系统的振动频率为(A)m k k 212+π=ν. (B) mk k 2121+π=ν. (C) 212121k mk k k +π=ν. (D) )(212121k k m k k +π=ν. [ ]5.一质点作简谐振动,已知振动频率为f ,则振动动能的变化频率是 [ ] (A) 4f . (B) 2 f . (C) f . (D) 2/f . (E) f /46.图A 表示t = 0时的余弦波的波形图,波沿x 轴正向传播;图B 为一余弦振动曲线.则图A 中所表示的x = 0处振动的初相位与图By所表示的振动的初相位(A) 均为零. (B) 均为1π2(C) 均为1π2-(D) 依次分别为1π2与1π2-.(E) 依次分别为1π2-与1π2. [ ]7.某时刻驻波波形曲线如图所示,则a 、b 两点振动的相位差是(A) 0.(B) 1π2.(C) π. (D) π45.[ ]8.一薄透镜的焦距f = 20cm -.一物体放在p = 30 cm 处,物高h 0 = 5 cm .则像距q ,像高h i 分别为 (A) 12cm ,5cm. (B) 12cm -,5cm.(C) 12cm -,4cm. (D) 12cm -,2cm. [ ] 9.把一平凸透镜放在平玻璃上,构成牛顿环装置.当平凸透镜慢慢地向上平移时,由反射光形成的牛顿环(A) 向中心收缩,条纹间隔变小. (B) 向中心收缩,环心呈明暗交替变化. (C) 向外扩张,环心呈明暗交替变化.(D) 向外扩张,条纹间隔变大. [ ]10.在光栅光谱中,若所有偶数级次的主极大都恰好在单缝衍射的暗纹方向上,即实际上不出现,那么此光栅每个透光缝宽度a 和相邻两缝间不透光部分宽度b 的关系为 [ ] (A) a=21b . (B) a=b . (C) a=2b . (D) a=3b . 二、填空题(每小题3分,共30分) 11.对于单原子分子理想气体,23RT 代表的物理意义是_____________________________. (式中R 为普适气体常量,T 为气体的温度)12.设气体分子服从麦克斯韦速率分布律,v 代表平均速率,v ∆为一固定的速率区间,则速率在 v 到 v +v ∆范围内的分子数占分子总数的百分率随气体的温度升高而__________(增加、降低或保持不变).13.同一种理想气体的定压摩尔热容C p大于定体摩尔热容C V,其原因是____________________________________________________________________________.14.在一个孤立系统内,一切与热现象有关的实际的过程都是________________________.15.一水平弹簧简谐振子的振动曲线如图所示.当振子处在位移为零、速度为ω-A、加速度为零和弹性力为零的状态时,应对应于曲线上的________点.16.两个同方向的简谐振动,周期相同,振幅分别为A1 = 0.05 m和A2 = 0.07 m,它们合成为一个振幅为A = 0.09 m的简谐振动.则这两个分振动的相位差为___________rad.17.图为一种声波干涉仪,声波从入口E进入仪器,分BC两路在管中传播至喇叭口A汇合传出,弯管C可以移动以改变管路长度,当它渐渐移动时从喇叭口发出的声音周期性地增强或减弱,设C管每移动10 cm,声音减弱一次,则该声波的频率为(空气中声速为340 m/s)________________________.18.在如图所示的单缝夫琅禾费衍射装置示意图中,用波长为λ的单色光垂直入射在单缝上,若P点是衍射条纹中的中央明纹旁第二个暗条纹的中心,则由单缝边缘的A、B两点分别到达P点的衍射光线光程差是_________.19.应用布儒斯特定律可以测介质的折射率.今测得此介质的起偏振角i0=56.0,这种物质的折射率为_________________.20.有一凸球面镜,曲率半径为20 cm.如果将一点光源放在离镜面顶点14 cm远处,则像点在镜______________cm处.三、计算题(共35分)21.(本题10分)一定量的单原子分子理想气体,从A态出发经等压过程膨胀到B态,又经绝热过程膨胀到C态,如图所示.试求这全过程中气体对外所作的功,内能的增量以及吸收的热量.22.(本题10分)一横波沿绳子传播,其波的表达式为)2100cos(05.0xtyπ-π=(SI)-CλPp(Pa)1×104×10(1) 求此波的振幅、波速、频率和波长. (2) 求绳子上各质点的最大振动速度和最大振动加速度. (3) 求x 1 = 0.2 m 处和x 2 = 0.7 m 处二质点振动的相位差.23.(本题5分)在双缝干涉实验中,双缝与屏间的距离D =1.2 m ,双缝间距d =0.45 mm ,若测得屏上干涉条纹相邻明条纹间距为1.5 mm ,求光源发出的单色光的波长λ.24.(本题5分)三个偏振片P 1、P 2、P 3顺序叠在一起,P 1、P 3的偏振化方向保持相互垂直,P 1与2的夹角为α,P 2可以入射光线为轴转动.今以强度为I 0的单色自然光垂直入射在偏振片上.不考虑偏振片对可透射分量的反射和吸收.(1) 求穿过三个偏振片后的透射光强度I与α角的函数关系式; (2) 试定性画出在P 2转动一周的过程中透射光强I 随α角变化的函数曲线.25.(本题5分)功率为P 的点光源,发出波长为λ的单色光,在距光源为d 处,每秒钟落在垂直于光线的单位面积上的光子数为多少?若λ=663nm ,则光子的质量为多少?(普朗克常量h =6.63×10-34 J·s)四、证明题(共5分) 26.(本题5分)一束具有动量p的电子,垂直地射入宽度为a 的狭缝,若在狭缝后远处与狭缝相距为R 的地方放置一块荧光屏,试证明屏幕上衍射图样中央最大强度的宽度)(2ap Rh d /=,式中h 为普朗克常量.安徽大学2008—2009学年第1学期 《普通物理A(下)》考试试卷(B 卷)(闭卷 时间120分钟)一、单选题(每小题3分,共30分)1.一定量某理想气体按pV 2=恒量的规律膨胀,则膨胀后理想气体的温度(A) 将升高. (B) 将降低.(C) 不变. (D)升高还是降低,不能确定. [ ] 2.一瓶氦气和一瓶氮气密度相同,分子平均平动动能相同,它们都处于平衡状态,则它们(A) 温度相同、压强相同. (B) 温度、压强都不相同. (C) 温度相同,但氦气的压强大于氮气的压强.(D) 温度相同,但氦气的压强小于氮气的压强. [ ]3.一定量的理想气体,在体积不变的条件下,当温度升高时,分子的平均碰撞频率Z 和平均自由程λ的变化情况是:(A) Z 增大,λ不变. (B) Z 不变,λ增大.(C) Z 和λ都增大. (D) Z 和λ都不变. [ ]4.如图,当气缸中的活塞迅速向外移动使气体膨胀时,气体所经历的过程 [ ](A) 是平衡过程,它能用p ─V 图上的一条曲线表示. (B) 不是平衡过程,但它能用p ─V 图上的一条曲线表示. (C) 不是平衡过程,它不能用p ─V 图上的一条曲线表示. (D) 是平衡过程,但它不能用p ─V 图上的一条曲线表示5.一定量的理想气体,从a 态出发经过①或②过程到达b 态,acb 为等温线(如图),则①、②两过程中外界对系统传递的热量Q 1、Q 2是 [ ](A) Q 1>0,Q 2>0. (B) Q 1<0,Q 2<0. (C) Q 1>0,Q 2<0.(D) Q 1<0,Q 2>0.6.一劲度系数为k 的轻弹簧截成三等份,取出其中的两根,将它们并联,下面挂一质量为m 的物体,如图所示.则振动系统的频率为[ ] (A)m k32π1. (B)mk2π1 .p V(C)m k 32π1. (D)mk62π1. 7.一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的(A) 7/16. (B) 9/16. (C) 11/16.(D) 13/16. (E) 15/16. [ ]8.一长度为l 、劲度系数为k 的均匀轻弹簧分割成长度分别为l 1和l 2的两部分,且l 1 = n l 2,n 为整数. 则相应的劲度系数k 1和k 2为 [ ](A) 11+=n kn k , )1(2+=n k k . (B) n n k k )1(1+=, 12+=n kk . (C) n n k k )1(1+=, )1(2+=n k k . (D) 11+=n kn k , 12+=n kk . 9.如图所示,S 1和S 2为两相干波源,它们的振动方向均垂直于图面,发出波长为 的简谐波,P 点是两列波相遇区域中的一点,已知 λ21=P S ,λ2.22=P S ,两列波在P 点发生相消干涉.若S 1的振动方程为 )212cos(1π+π=t A y ,则S 2的振动方程为 [ ](A) )212cos(2π-π=t A y . (B) )2cos(2π-π=t A y . (C) )212cos(2π+π=t A y . (D) )1.02cos(22π-π=t A y . 10.两块平玻璃构成空气劈形膜,左边为棱边,用单色平行光垂直入射.若上面的平玻璃以棱边为轴,沿逆时针方向作微小转动,则干涉条纹的 [ ](A) 间隔变小,并向棱边方向平移.(B) 间隔变大,并向远离棱边方向平移. (C) 间隔不变,向棱边方向平移. (D) 间隔变小,并向远离棱边方向平移.二、填空题(每小题3分,共30分)11.一个容器内有摩尔质量分别为M mol1和M mol2的两种不同的理想气体1和2,当此混合气体处于平衡状态时,1和2两种气体分子的方均根速率之比是__________________.12.有1 mol 刚性双原子分子理想气体,在等压膨胀过程中对外作功W ,则其温度变化T =__________. 13. 沿弦线传播的一入射波在x = L 处(B 点)发生反射,反射点为自由端(如图).设波在传播和反射过程中振幅不变,且反射波的表达式为)(2cos 2λνxt A y +=π, 则入射波的表达式为Sy 1 = ______________________________. 14.设入射波的表达式为 1cos 2π()xy A t νλ=+.波在x = 0处发生反射,反射点为固定端,则形成的驻波表达式为____________________________________.15. 如图所示,假设有两个同相的相干点光源S 1和S 2,发出波长为的光.A 是它们连线的中垂线上的一点.若在S 1与A 之间插入厚度为e 、折射率为n 的薄玻璃片,则两光源发出的光在A 点的相位差=________.16. 平行单色光垂直入射于单缝上,观察夫琅禾费衍射.若屏上P 点处为第二级暗纹,则单缝处波面相应地可划分为_______ 个半波带.若将单缝宽度缩小一半,P 点处将是_________级__________纹.17. 用波长为的单色平行红光垂直照射在光栅常数d =2μm (1μm =10-6 m)的光栅上,用焦距f =0.500 m 的透镜将光聚在屏上,测得第一级谱线与透镜主焦点的距离l =0.1667m .则可知该入射的红光波长λ=_________________nm .18. 一束自然光垂直穿过两个偏振片,两个偏振片的偏振化方向成45°角.已知通过此两偏振片后的光强为I ,则入射至第二个偏振片的线偏振光强度为________________. 19.某光电管阴极,对于λnm 的入射光,其发射光电子的遏止电压为0.71 V .当入射光的波长为________nm 时,其遏止电压变为1.43 V . ( e =1.60×10-19 C ,h =6.63×10-34 J ·s )20.有一凸球面镜,曲率半径为20 cm .如果将一点光源放在离镜面顶点14 cm 远处,则像点在镜______________cm 处. 三、计算题(共35分)21.(本题10分)1 mol 单原子分子的理想气体,经历如图所示的可逆循环,联结ac 两点的曲线Ⅲ的方程为2020/V V p p =, a 点的温度为T 0(1)以T 0 , 普适气体常量R 表示Ⅰ、Ⅱ、Ⅲ过程中气体吸收的热量. (2)求此循环的效率.(提示:循环效率的定义式η=1- Q 2 /Q 1, Q 1为循环中气体吸收的热量,Q 2为循环中气体放出的热量.)22.(本题5分)两个物体作同方向、同频率、同振幅的简谐振动.在振动过程中,的位置向平衡位置运动时,第二个物体也经过此位置,但向远离平衡位置的方向运动.试利用旋转矢量p 9p V法求它们的相位差.23.(本题5分)已知波长为λ的平面简谐波沿x 轴负方向传播.x = λ/4处质点的振动方程为 ut A y ⋅=λπ2cos(SI)(1) 写出该平面简谐波的表达式. (2) 画出t = T 时刻的波形图.24.(本题10分)在如图所示的瑞利干涉仪中,T 1、T 2是两个长度都是l 的气室,波长为λ透镜L 1的前焦面上,在双缝S 1和S 2处形成两个同相位的相干光源,用目镜E 观察透镜L 2焦平面C 上的干涉条纹.当两气室均为真空时,观察到一组干涉条纹.在向气室T 2中充入一定量的某种气体的过程中,观察到干涉条纹移动了M 条.试求出该气体的折射率n (用已知量M ,λ和l 表示出来).25.(本题5分)假设电子绕氢核旋转的玻尔轨道的圆周长刚好为电子物质波波长的整数倍,试从此点出发解出玻尔的动量矩量子化条件.四、回答问题(共5分) 26.(本题5分)试述关于光的偏振的布儒斯特定律 .安徽大学2008—2009学年第一学期《普通物理A 》(A 卷)考试试题参考答案及评分标准 一、选项题(每题3分,共30分)1.A2.B3.D4.B5.B6.D7.C8.D9.B 10.B 二、填空题(每题3分,共30分)11.一摩尔理想气体的内能 3分 12.降低 3分13.在等压升温过程中,气体要膨胀而对外作功,所以要比气体等体升温过程多吸收一部分热量. 3分14.不可逆的 3分 15.b ,f 3分 16.1.47 3分 17.1.7×103 Hz 3分 参考解:两路声波干涉减弱条件是:λδ)12(21+=-=k EBA ECA ①当C 管移动x = 10 cm = 0.1 m 时,再次出现减弱,波程差为λδδ]1)1(2[212++=+='k x ②②-①得x 2=λ故 ===)2/(/x u u λν 1.7×103 Hz18.2 λ 3分 19.1.48 3分 20.后5.8(或者-5.8) 3分 三、计算题(35分) 21.(本题10分)解:由图可看出 p A V A = p C V C从状态方程 pV =νRT T A =T C ,因此全过程A →B →C∆E =0. 3分 B →C 过程是绝热过程,有Q BC = 0. A →B 过程是等压过程,有)(25)( A A B B A B p AB V p V p T T C Q -=-=ν=14.9×105 J . 故全过程A →B →C 的 Q = Q BC +Q AB =14.9×105 J . 4分 根据热一律Q =W +∆E ,得全过程A →B →C 的W = Q -∆E =14.9×105 J . 3分 22.(本题10分)解:(1) 已知波的表达式为)2100cos(05.0x t y π-π= 与标准形式)/22cos(λνx t A y π-π= 比较得A = 0.05 m , ν = 50 Hz , λ = 1.0 m 各1分 u = λν = 50 m/s 1分 (2) 7.152)/(max max =π=∂∂=A t y νv m /s 2分322max 22max 1093.44)/(⨯=π=∂∂=A t y a νm/s 2 2分(3) ππ=-=∆λφ/)(212x x ,二振动反相 2分 23.(本题5分)解:根据公式 x = k λ D / d 相邻条纹间距 ∆x =D λ / d则 λ=d ∆x / D 3分 =562.5 nm . 2分 24.(本题5分)解:(1) 连续穿过三个偏振片之后的光强为 I =0.5I 0cos 2α cos 2(0.5π-α ) 2分 =I 0sin 2(2α) / 8 1分 (2) 画出曲线 2分 25.(本题5分)解:设光源每秒钟发射的光子数为n ,每个光子的能量为h ν则由 λν/nhc nh P == 得: )/(hc P n λ= 令每秒钟落在垂直于光线的单位面积的光子数为n 0,则)4/()4/(/220hc d P d n S n n π=π==λ 3分光子的质量 )/()/(/22λλνc h c hc c h m ====3.33×10-36 kg 2分四 证明题(5分) 26.(本题5分)23. I 0证:单缝夫朗禾费衍射各级极小的条件为: λφk a ±=sin ( k = 1,2……)令 k = 1, 得 λφ=s i n a 1分 可见,衍射图形第一级极小离中心点距离 a f f R x /sin tg 1λφφ⋅=≈= 1分 又电子德布罗意波的波长 p h /=λ 2分 所以中央最大强度宽度 )/(221ap Rh x d == 1分安徽大学2008—2009学年第一学期《普通物理A 》(B 卷)考试试题参考答案及评分标准 一、选项题(每题3分,共30分)1. B2. C3. A4. C5. A6. D7. E8. C9. D 10. A 二、填空题(每题3分,共30分) 11.1mol 2mol /M M 3分12. W /R 3分 13.)2(2cos λλνLxt A +-π 3分14.)212cos(]212cos[2π+ππ-π=t xA y νλ 或)212cos(]212cos[2π-ππ+π=t x A y νλ 或 )2c o s (]212c o s [2t xA y νλππ+π=. 3分 15.2π (n -1) e / λ 3分 16.4 1分 第一 1分 暗 1分 17.632.6 或 633 3分 18.2I 3分 19.3.82×102 3分 20.后5.8(或者-5.8) 3分 三、计算题(35分) 21.(本题10分)解:设a 状态的状态参量为p 0, V 0, T 0,则p b =9p 0, V b =V 0, T b =(p b /p a )T a =9T 0 1分∵ 220V V p p c c = ∴ 0003V V p pV c == 1分∵ p c V c =RT c ∴ T c = 27T 0 1分 (1) 过程Ⅰ )9(23)(00T T R T T C Q a b V V -=-=012RT = 1分 过程Ⅱ Q p = C p (T c -T b ) = 45 RT 0 1分 过程Ⅲ ⎰+-=acV V c a V V V V p T T C Q 2020/d )()()(3)27(233320000c a V V V p T T R -+-=023030007.473)27(39RT V V V p RT -=-+-= 3分 (2) %3.1645127.471||1000=+-=+-=RT RT RT Q Q Q p V η 2分22.(本题5分)解:依题意画出旋转矢量图. 3分 由图可知两简谐振动的位相差为π21. 2分 23.(本题10分)解:(1) 如图A ,取波线上任一点P ,其坐标设为x ,由波的传播特性,P 点的振动落后于λ /4处质点的振动. 2分 该波的表达式为)]4(22cos[x ut A y -π-π=λλλ)222cos(x ut A λλπ+π-π= (SI) 3分(2)t = T 时的波形和 t = 0时波形一样. t = 0时22cos()cos()22y A x A x λλ=-+=-ππππ 2分按上述方程画的波形图见图B . 3分 24.(本题5分)解:当T 1和T 2都是真空时,从S 1和S 2来的两束相干光在O 点的光程差为零.当T 1中充入一定量的某种气体后,从S 1和S 2来的两束相干光在O 点的光程 差为(n – 1)l . 1分在T 2充入气体的过程中,观察到M 条干涉条纹移过O 点,即两光束在O 点的光程差改变了M λ.故有Ox P xλ/4u图A(n -1)l -0 = M λ 3分 n =1+M λ / l . 1分25.(本题5分)解:从题设可知,若圆周半径为r ,则有2πr = n λ,这里n 是整数,λ是电子物质 波的波长. 1分 根据德布罗意公式 )/(v m h =λ 得 )/(2v m nh r =π 于是 nh rm =πv 2 2分 这里m 是电子质量,v 是电子速度的大小,r m v 为动量矩,以L 表示, 则上式 为: )2/(π=nh L这就是玻尔的动量矩量子化条件. 2分 四 证明题(5分) 26.(本题5分)解:从题设可知,若圆周半径为r ,则有2πr = n λ,这里n 是整数,λ是电子物质 波的波长. 1分 根据德布罗意公式 )/(v m h =λ 得 )/(2v m nh r =π 于是 nh rm =πv 2 2分 这里m 是电子质量,v 是电子速度的大小,r m v 为动量矩,以L 表示, 则上式 为: )2/(π=nh L这就是玻尔的动量矩量子化条件. 2分。
08级普通物理期末考试题

一、填空题(30分)
1.用文字叙述法拉第电磁感应定律(),并写出其表达式()。
2.写出麦克斯韦方程组的积分形式。
3.已知两无穷大电荷面密度均为σ的平行平面,写出两平面左、两平面间、两平面右的电场强度()()()。
4.写出阴极射线在给定磁场中的偏转方向。
5.交流电中ψ=θu-θi(电压和电流的相位差),电阻的ψ=(),电感的ψ=()。
6.物镜直径为30mm的望远镜的有效放大率是()。
7.全息照相利用光的()记录,利用光的()重现。
8.某种玻璃的折射率是1.73,求其布儒斯特角()。
二、(20分)
两个同心带电金属球壳,半径分别是R1,R2(R1<R2),带电量分别是Q1,Q2,求这两个球壳把空间分为三个区域的电势分布。
三、(15分)
长为L的金属棒在垂直于纸面向里的匀强磁场B中绕其端点旋转,角速度为ω,求其感应电动势。
四、(12分)
杨氏干涉,已知Δx,d,D,求所用激光波长并画出试验装置的示意图。
五、(15分)
卫星能看清楚地上的车牌号
1.车牌号是10cm,卫星离地高度为200km,求其最小角分辨率
2.求镜头的最小直径。
(λ=500nm)
六、(8分)
有四分之一波长波片(1/4λ片)和偏振片两种光学仪器,问如何使自然光转化为圆偏振光。
画出装置图和图示。
2008-2009(2)基础物理1期末试卷A答案

08-09学年第2学期基础物理学(1)期末试卷A 卷参考答案一.选择题(每题3分, 共30分)1.[D]2.[C]3.[C]4.[D]5.[D]6.[A]7.[B]8.[C]9.[A] 10.[B]二.填空题(每题3分, 共30分,注:数量级错误各扣1分,单位错误总共扣1分) 1.02)cos 1(x t m F +-ωω (SI) 3分 2. 36 rad/s 3分参考解:系统对竖直轴的角动量守恒. r a d /s36/22210==r r ωω3. 18 J 2分 6 m/s 1分4.l g /sin 3θω= 3分5. 0.13m 2分 0.05m 1分6. 1.5×106 V 3分7. 1/εr 1分 1/εr 2分8. 铁磁质 1分 顺磁质 1分 抗磁质 1分9. 0 1分 )9/(22220a I πμ 2分10. 1 3分三.计算题(每题10分, 共40分)1. 解:以原子核为坐标原点,作用在质子上的力为有心力,故质子对O 点的角动量守恒s s r m b m v v =0 ① 4分 式中v s 是质子离原子核最近时的速度,由能量守恒有s S r K Z e m m /21212220+=v v ② 4分 由式①和②联立求解得2222202)(b m K Z e m K Z e r s ++=v v 2分2.解:取如图x 坐标,平衡位置为原点O ,向下为正,m 在平衡位置时弹簧已伸长x 00kx mg = ① 1分设m 在x 位置,分析受力, 这时弹簧伸长0x x +)(02x x k T += ② 1分由牛顿第二定律和转动定律列方程: ma T mg =-1 ③ 2分βJ R T R T =-21④ 1分βR a = ⑤ 1分 联立解得 mR J kxa +-=)/(22分 由于x 系数为一负常数,故物体做简谐振动,其角频率为 1分 222)/(mRJ kR mR J k+=+=ω 1分3. 解:(1) 在球内取半径为r 、厚为d r 的薄球壳,该壳内所包含的电荷为d q = ρd V = qr 4πr 2d r /(πR 4) = 4qr 3d r/R 4 2分则球体所带的总电荷为 ()q r rRq V Q r V===⎰⎰34d /4d ρ 3分(2) 在球内作一半径为r 1的高斯球面,按高斯定理有404102401211d 414Rqr r r R qr E r r εε=π⋅π=π⎰ 1分 得 402114R qr E επ= (r 1≤R),1E 方向沿半径向外. 2分在球体外作半径为r 2的高斯球面,按高斯定理有 0222/4εq E r =π得 22024r q E επ= (r 2 >R ),2E方向沿半径向外. 2分4.解:建立坐标(如图)21B B B+= 1分x I B π=201μ, )(202a x I B -π=μ 2分x I a x I B π--π=2)(200μμ, B 方向⊙ 2分 d x x a x I x B d )11(2d 0--π==v v μ 2分 ⎰⎰--π==+x x a x I ba d )11(2d 202a v μ b a b a I ++π=2)(2ln20v μ 2分感应电动势方向为C →D ,D 端电势较高.1分212a x +d x 2a +b I I C Dv xO x。
2007-2008(2)大学物理C类期末试卷答案
(A)F R2 ;
(B) 2F R2 ;
(C)3F R2 ;
(D) 4F R2。
y
R x
O
3. 如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴 O 旋转,初始状态为静
止悬挂.现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰
撞,则在碰撞过程中对细杆与小球这一系统
O
(A) 只有机械能守恒. (B) 只有动量守恒.
则该带电粒子满足的动力学方程是
。
答: m
d
2
r r
=
r qE
+
r qv
×
r B
dt 2
8. 一自感系数为 0.25H 的线圈,当线圈中的电流在 0.01s 内由 2A 均匀地减小到零。线圈中
的自感电动势的大小为
答案:50V
9. 一电偶极子放在场强大小为 2 ×103 V/m 的匀强电场中,其电偶极矩方向与场强方向相
(2)半径为 r (r > R) ,高为 h 圆柱体内包含的电荷量:
∫ ∫ q2 =
R ρ 2π r '2hdr ' =
0
R Ar ' 2π r 'hdr ' = 2πAhR3 / 3
0
――――― 1 分
(3)场强大小分布:
取半径为 r 、高为 h 的高斯圆柱面。面上各点场强大小为 E 并垂直于柱面。则穿过该柱面的
因此(1)下落距离
h= 1 at 2 =63.3 m
1分
2
(2) 张力
T =m(g-a)=37.9 N
2分
4. 一半径为 R 的“无限长”圆柱形带电体,其电荷体密度为: ρ = Ar (r ≤ R) 、
四川大学2008级物理化学I-2期末试题A(answer)
2008级化学学院物理化学(I)-2期末考试试题-A 卷一. 选择题(16分)1. 一个化学体系吸收了光子之后,将引起下列哪种过程 D .A. 引起化学反应B. 产生荧光C. 发生无辐射跃迁D. 过程不能确定2. 已知某二级反应 A +B → P 的活化能E a =100 kJ·mol -1,在定容条件下,在273K 和起始浓度c A ,0=c B ,0=a mol·dm -3时,测得其半衰期为t 1。
在相同的起始浓度和323K 时,半衰期为t 2, 则 A .A. t 2 < t 1B. t 2 = t 1C. t 2 > t 1D. 不能确定3. 在一定温度和较小的浓度情况下,增大强电解质溶液的浓度,则溶液的电导率κ与摩尔电导Λm 变化为B .A. κ增大,Λm 增大B. κ增大,Λm 减少C. κ减少,Λm 增大D. κ减少,Λm 减少4. 某原电池在298 K, p θ条件下可逆放电过程中,当Q R = -200 J 时,其电池反应的焓变ΔH 为 B .A. ΔH = -200 JB. ΔH < -200 JC. ΔH = 0D. ΔH > -200 J5. 已知298 K, p θ 时φθ(Zn 2+/Zn) = - 0.763V ,H 2在Zn 和光亮Pt 上的超电势分别约为0.7V 和0.3V ,若分别以Zn 和光亮Pt 为阴极电解1 mol·kg -1 的ZnSO4溶液(设为中性),在Zn 和光亮Pt 阴极上首先析出的物质将分别为 C .A. 均为H 2B. 均为ZnC. Zn 和H 2D. H 2和Zn6. 两液体A 和B 表面张力γA =2γB ,密度ρA =2ρB ,一毛细管插入A 中液面上升1.5cm ,若将此毛细管插入B 中,液面上升 D 。
A. 6.0cmB. 4.0cmC. 3.0cmD. 1.5cm7. 某表面活性剂的水溶液,表述不正确的是 A .A. 表面产生负吸附B. 能形成胶束C. 能在表面定向排列降低表面能D. 使溶液表面能力显著降低8. 当一束足够强的自然光通过一胶体溶液,在与光束垂直方向上一般可观察到 C .A. 橙红色光B. 黄光C. 兰紫色光D. 白光二、填空题(16分)1. 生物死亡后,因为不再吸收放射性碳原子,相应的放射性也逐渐降低。
2008级大学物理(II)期末试卷解答
2008级大学物理2 A 卷解答一、选择题(共30分)C, B, D, E, D; D, B, C, B, A二、填空题(共30分)11. 66 1分;66 1分;0 1分 12.()32102281q q q R++πε 3分13. )/(21220d U r εε 3分14. aIB π=830μ 3分 15.t B r d /d 213分 16. x 轴正方向 1分;x 轴负方向 2分17. ∆x /v 1分 2)/(1)/(c x v v -∆ 2分 18. θφννcos )cos (p c h c h +'= 3分19. 2.55 3分20. 1.06×10-24 (或 6.63×10-24或0.53×10-24 或 3.32×10-24) 3分 根据 ≥∆∆y p y ,或 h p y y ≥∆∆,或 21≥∆∆y p y ,或h p y y 21≥∆∆,可得以上答案. 三、计算题(共40分)21.解:把所有电荷都当作正电荷处理. 在θ处取微小电荷 d q = λd l = 2Q d θ / π 1分它在O 处产生场强θεεd 24d d 20220RQR q E π=π=2分 按θ角变化,将d E 分解成二个分量:θθεθd sin 2sin d d 202RQE E x π== 1分θθεθd cos 2cos d d 202R QE E y π-=-= 1分对各分量分别积分,积分时考虑到一半是负电荷⎥⎦⎤⎢⎣⎡-π=⎰⎰πππθθθθε2/2/0202d sin d sin 2R QE x =0 2分 2022/2/0202d cos d cos 2R QR Q E y εθθθθεππππ-=⎥⎦⎤⎢⎣⎡-π-=⎰⎰ 2分 所以j R Q j E i E E y x202επ-=+= 1分d qR Oyθd θθ22. 解:由安培环路定理: ∑⎰⋅=iI l Hd 2分0< r <R 1区域: 212/2R Ir rH =π212R Ir H π=, 2102R Ir B π=μ 3分R 1< r <R 2区域: I rH =π2r I H π=2, rIB π=2μ 2分R 2< r <R 3区域: 02IB rμ=π2分r >R 3区域: H = 0,B = 0 1分23. 解:Ob 间的动生电动势:⎰⎰=⋅⨯=5/405/401d d )v (L L l Bl l B ωε225016)54(21BL L B ωω== 4分b 点电势高于O 点. Oa 间的动生电动势:⎰⎰⋅=⨯=5/05/02d d )v (L L l Bl l B ωε22501)51(21BL L B ωω== 4分a 点电势高于O 点. ∴ 22125016501BL BL U Ub a ωωεε-=-=-221035015BL BL ωω-=-= 2分24. 解:据相对论动能公式 202c m mc E K -= 1分 得 )1)/(11(220--=c c m E K v 即419.11)/(11202==--cm E c Kv 解得v = 0.91c 2分平均寿命为821031.5)/(1-⨯=-=c v ττ s 2分25. 解:远离核的光电子动能为 4.16.1315212=-==v e K m E eV 则==eKm E 2v 7.0×105 m/s 2分 光电子的德布罗意波长为===ve m h p h λ 1.04×10-9 m =10.4 Å 3分。
08级物理学期末试卷(B)参考答案
08级物理学期末试卷(B )参考答案一.填空:每空2分,共38分1.^^7260j i V -=→, ^^7230j i a -=→2.dt dV a =τ 切线 RV a n 2= 圆心22τa a a n+= τθa a tg n= 3.^^cos sin j t b i t a ωωωω+- 4.角动量增量 5.线性恢复力, km π2 6.合外力等于零,外力的矢量合所作的功和非保内力的功等于零,合外力矩等于零,惯性。
7.0mv 竖直向下8.2221ωρϖA =二.选择:每题2分,共20分CDCCBDBCCB三.计算题:42分1.解:取质点为研究对象,由加速度定义有t dtdv a 4==(一维可用标量式)tdt dv 4=⇒ 2分由初始条件有:⎰⎰=tvtdt dv 04得: 22t v = 2分由速度定义得:22t dtdxv ==dt t dx 22=⇒ 2分由初始条件得:dt t dx tx⎰⎰=02102即10322+=t x m 4分 2.解:受力分析:A m :重力g m A,桌面支持力1N ,绳的拉力1T ;B m :重力g m B,绳的拉力2T ; c m :重力g m c,轴作用力2N , c m 绳作用力'1T 、'2T⎪⎪⎩⎪⎪⎨⎧=-=-=α2122121''R m R T R T a m T g m a m TcB B A 及11'T T =,22'T T =,αR a = 4分解得:⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧++⎪⎭⎫⎝⎛+=++=++=c B A B c A cB A B A c BA B m m m gm m m T m m m g m m T m m m g m a 2121212121 4分讨论:不计c m 时,⎪⎪⎩⎪⎪⎨⎧+==+=B A B A BA B m m gm m T T m m g m a 21 2分(即为质点情况)3.解:⑴研究对象:1m 、2m⑵受力分析:1m 、2m 各受两个力,即重力C图 4-9图 4-10gBB2N及绳拉力,如图2-7。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r,考试作弊将带来严重后果!华南理工大学期末考试《2008级大学物理(II )期末试卷A 卷》试卷1. 考前请将密封线内各项信息填写清楚; 所有答案请直接答在答题纸上; .考试形式:闭卷;4. 本试卷共25题,满分100分, 考试时间120分钟。
2010年1月18日9:00-----11:00 30分).(本题3分)在电荷为-Q 的点电荷A 的静电场中,将另一电荷为q 的B 从a 点移到b 点.a 、b 两点距离点电荷A 的距离 r 1和r 2,如图所示.则移动过程中电场力做的功为 (A)⎪⎪⎭⎫ ⎝⎛-π-21114r r Q ε. (B) ⎪⎪⎭⎫ ⎝⎛-π210114r r qQ ε. (C) ⎪⎪⎭⎫ ⎝⎛-π-210114r r qQ ε. (D) ()1204r r qQ-π-ε [ ] .(本题3分)一“无限大”均匀带电平面A ,其附近放一与它平行的有一定厚度的B ,如图所示.已知A 上的电荷面密度+σ ,则在导体板B 的两个表面1和2上的感生电荷面密度为: (A) σ 1 = - σ, σ 2 = + σ.(B) σ 1 = σ21-, σ 2 =σ21+. (C) σ 1 = σ21-, σ 2 = σ21-.(D) σ 1 = - σ, σ 2 = 0. [ ].(本题3分)在静电场中,作闭合曲面S ,若有0d =⎰⋅SS D (式中D为电位移矢量),则S 面内必定(A) 既无自由电荷,也无束缚电荷. (B) 没有自由电荷. (C) 自由电荷和束缚电荷的代数和为零. (D) 自由电荷的代数和为零. [ ]A +σ24.(本题3分)一个通有电流I 的导体,厚度为D ,横截面积为S ,放置在磁感强度为B 的匀强磁场中,磁场方向垂直于导体的侧表面,如图所示.现测得导体上下两面电势差为V ,则此导体的霍尔系数等于(A) IBVDS . (B) DS IBV.(C) IBD VS . (D) BD IVS.(E) IBVD . [ ]5.(本题3分)两个同心圆线圈,大圆半径为R ,通有电流I 1;小圆半径为r ,通有电流I 2,方向如图.若r << R (大线圈在小线圈处产生的磁场近似为均匀磁场),当它们处在同一平面内时小线圈所受磁力矩的大小为 (A)R r I I 22210πμ. (B)R r I I 22210μ.(C) rR I I 22210πμ. (D) 0.[ ]6.(本题3分)如图所示,两个线圈P 和Q 并联地接到一电动势恒定的电源上.线圈P 的自感和电阻分别是线圈Q 的两倍,线圈P 和Q 之间的互感可忽略不计.当达到稳定状态后,线圈P 的磁场能量与Q 的磁场能量的比值是(A) 4. (B) 2. (C) 1. (D)21. [ ] 7.(本题3分)把一个静止质量为m 0的粒子,由静止加速到=v 0.6c (c 为真空中光速)需作的功等于 (A) 0.18m 0c 2. (B) 0.25 m 0c 2.(C) 0.36m 0c 2. (D) 1.25 m 0c 2. [ ] 8.(本题3分)粒子在一维无限深方势阱中运动. 图为粒子处于某一能态上的波函数ψ(x )的曲线.粒子出现概率最大的位置为(A) a / 2.(B) a / 6,5 a / 6.(C) a / 6,a / 2,5 a / 6. (D) 0,a / 3,2 a / 3,a . [ ] 9.(本题3分)在原子的K 壳层中,电子可能具有的四个量子数(n ,l ,m l ,m s )是(1) (1,1,0,21). (2) (1,0,0,21). (3) (2,1,0,21-). (4) (1,0,0,21-).O r R I 1 I 2xaa31a 32ψ(x )O以上四种取值中,哪些是正确的? (A) 只有(1)、(3)是正确的. (B) 只有(2)、(4)是正确的. (C) 只有(2)、(3)、(4)是正确的.(D) 全部是正确的. [ ] 10.(本题3分)根据量子力学原理,氢原子中,电子的轨道角动量L 的最小值为 (A) 0. (B) . (C) 2/ . (D) 2. [ ]二、填空题(共30分)11.(本题3分)已知某静电场的电势函数U =6x -6x 2y -7y 2 (SI).由场强与电势梯度的关系式可得点(2,3,0)处的电场强度E =___________i +____________j+_____________k (SI).12.(本题3分)电荷分别为q 1,q 2,q 3的三个点电荷分别位于同一圆周的三个点上,如图所示.设无穷远处为电势零点,圆半径为R ,则b点处的电势U =___________ .13.(本题3分)一平行板电容器两极板间电压为U ,两板间距为d , 其间充满相对介电常量为εr 的各向同性均匀电介质,则电介质中的电场能量密度w =______________.14.(本题3分)一无限长载流直导线,通有电流I ,弯成如图形状.设各线段皆在纸面内,则P 点磁感强度B的大小为________________.15.(本题3分)无限长直通电螺线管的半径为R ,设其内部的磁场以d B / d t 的变化率增加,则在螺线管内部离开轴线距离为r (r < R )处的涡旋电场的强度为_______________________________________.16.(本题3分) 图示一充电后的平行板电容器,A 板带正电,B 板带负电.当将开关K 合上放电时,AB 板之间的电场方向为______________, 位移电流的方向为____________________。
(按图上所标x 轴正、负方向来回答) .17.(本题3分)在S 系中的x 轴上相隔为∆x 处有两只同步的钟A 和B ,读数相同.在S '系的x '轴上也有一只同样的钟A ',设S '系相对于S 系的运动速度为v , 沿x 轴方向, 且当A '与A 相遇时,刚好两钟的读数均为零.那么,当A '钟与B 钟相遇时,在S 系中B 钟的读数是__________;此时在S '系中A '钟的读数是______________.q 1q 3R18.(本题3分)如图所示,一频率为ν 的入射光子与初始静止的自由电子发生碰撞和散射.如果散射光子的频率为ν′,反冲电子的动量为p ,则在与入射光子平行的方向上的动量守恒定律的分量形式为___________________.19.(本题3分)氢原子由定态l 跃迁到定态k 可发射一个光子.已知定态l的电离能为0.85 eV ,又知从基态使氢原子激发到定态k 所需能量为10.2 eV ,则在上述跃迁中氢原子所发射的光子的能量为__________eV . 20.(本题3分)在电子单缝衍射实验中,若缝宽为a = 0.1 nm (1 nm = 10-9 m),电子束垂直射在单缝面上,则衍射的电子横向动量的最小不确定量∆p =______________N ·s .(普朗克常量h =6.63×10-34 J ·s)三、计算题(共40分)21.(本题10分)一个细玻璃棒被弯成半径为R 的半圆形,沿其上半部分均匀分布有电荷+Q ,沿其下半部分均匀分布有电荷-Q ,如图所示.试求圆心O 处的电场强度.22.(本题10分)一根同轴线由半径为R 1的实心长金属导线和套在它外面的半径为R 3的同轴导体圆筒组成.R 1与R 2之间充满磁导率为μ的各向同性均匀非铁磁介质,R 2与R 3之间真空,如图.传导电流I 沿实心导线向上流去,由圆筒向下流回,在它们的截面上电流都是均匀分布的.求同轴线内外的磁感强度大小B 的分布.23.(本题10分)如图所示,一根长为L 的金属细杆ab 绕竖直轴O 1O 2以角速度ω在水平面内旋转.O 1O 2在离细杆a 端L /5处.若已知地磁场在竖直方向的分量为B.求ab 两端间的电势差b a U U -.24.(本题5分)已知μ 子的静止能量为 105.7 MeV ,平均寿命为 2.2×10-8s .试求动能为 150 MeV 的μ 子的速度v 是多少?平均寿命τ 是多少? 25.(本题5分)能量为15 eV 的光子,被处于基态的氢原子吸收,使氢原子电离发射一个光电子,求此光电子的德布罗意波长.不考虑相对论效应。
(电子的质量m e =9.11×10-31 kg ,普朗克常量h =6.63×10-34 J ·s ,1 eV =1.60×10-19 J)b2008级大学物理2 A 卷解答一、选择题(共30分)C, B, D, E, D; D, B, C, B, A二、填空题(共30分)11. 66 1分;66 1分;0 1分 12.()32102281q q q R++πε 3分13. )/(21220d U r εε 3分14. aIB π=830μ 3分 15.t B r d /d 213分 16. x 轴正方向 1分;x 轴负方向 2分17. ∆x /v 1分2)/(1)/(c x v v -∆ 2分 18. θφννcos )cos (p ch c h +'= 3分 19. 2.55 3分20. 1.06×10-24 (或 6.63×10-24或0.53×10-24 或 3.32×10-24) 3分 根据 ≥∆∆y p y ,或 h p y y ≥∆∆,或 21≥∆∆y p y ,或h p y y 21≥∆∆,可得以上答案. 三、计算题(共40分)21.解:把所有电荷都当作正电荷处理. 在θ处取微小电荷d q = λd l = 2Q d θ / π 1分它在O 处产生场强θεεd 24d d 20220RQR q E π=π=2分 按θ角变化,将d E 分解成二个分量:θθεθd sin 2sin d d 202RQ E E x π== 1分θθεθd cos 2cos d d 202R Q E E y π-=-= 1分对各分量分别积分,积分时考虑到一半是负电荷⎥⎦⎤⎢⎣⎡-π=⎰⎰πππθθθθε2/2/0202d sin d sin 2R QE x =0 2分 2022/2/0202d cos d cos 2R QR Q E y εθθθθεππππ-=⎥⎦⎤⎢⎣⎡-π-=⎰⎰ 2分所以j R Q j E i E E y x202επ-=+= 1分22. 解:由安培环路定理:∑⎰⋅=i I l H d 2分0< r <R 1区域: 212/2R Ir rH =π212R Ir H π=, 2102R Ir B π=μ 3分 R 1< r <R 2区域: I rH =π2r I H π=2, rIB π=2μ 2分R 2< r <R 3区域: 02IB rμ=π2分r >R 3区域: H = 0,B = 0 1分23. 解:Ob 间的动生电动势:⎰⎰=⋅⨯=5/405/401d d )v (L L l Bl l B ωε225016)54(21BL L B ωω== 4分 b 点电势高于O 点. Oa 间的动生电动势:⎰⎰⋅=⨯=5/05/02d d )v (L L l Bl l B ωε22501)51(21BL L B ωω== 4分 a 点电势高于O 点. ∴ 22125016501BL BL U U b a ωωεε-=-=-221035015BL BL ωω-=-= 2分24. 解:据相对论动能公式 202c m mc E K -= 1分 得 )1)/(11(220--=c c m E K v 即419.11)/(11202==--cm E c Kv 解得v = 0.91c 2分平均寿命为821031.5)/(1-⨯=-=c v ττ s 2分25. 解:远离核的光电子动能为 4.16.1315212=-==v e K m E eV 则==eKm E 2v 7.0×105 m/s 2分 光电子的德布罗意波长为===ve m h p h λ 1.04×10-9 m =10.4 Å 3分。
