飞行器制导理论大作业
哈工大飞行器控制与制导考试题

哈工大《飞行器控制与制导》试题
1、求按照321转序转动的转换矩阵。
2、什么是纵向静稳定性?给出纵向静稳定性的条件。
3、侧向运动的微分方程为:β
ψψδβψψ
δβψ
+=---=+=v y y v a a a a a 32151 ,求y δ到侧向过载的传递函数,并给出一种XX 侧向过载的方案。
4、从物理层面说明为什么尾控型导弹的XX (好像是过载)是非最小相位,而攻角是最小相位。
5、假设惯性系到弹道系的转动是先转θ,后转v ψ,求转动矩阵以及加速度在弹道系上的投影。
6、推导比例导引的法向过载,并给出一种改进形式,使得命中时的法向过载与导弹和目标的相对速度无关。
7、给出一种导引头跟踪方案。
8、证明非机动目标的最优二次型导引律等价于比例导引。
飞行器总体设计 大作业第二章(2)
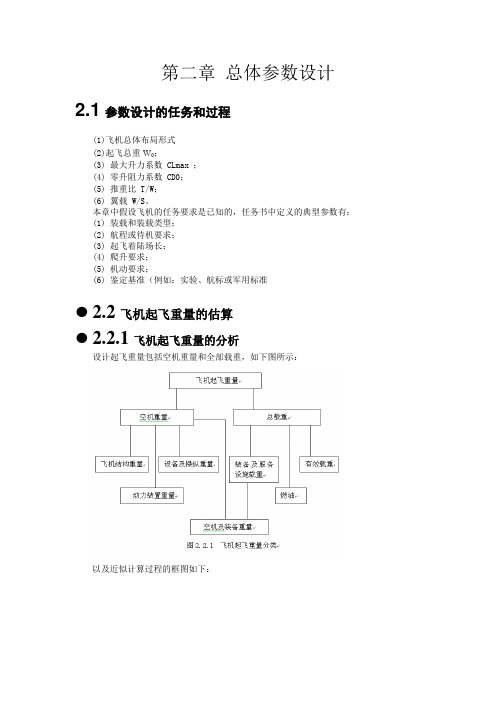
第二章总体参数设计2.1参数设计的任务和过程(1)飞机总体布局形式(2)起飞总重W0;(3) 最大升力系数 CLmax ;(4) 零升阻力系数 CD0;(5) 推重比 T/W;(6) 翼载 W/S。
本章中假设飞机的任务要求是已知的,任务书中定义的典型参数有:(1) 装载和装载类型;(2) 航程或待机要求;(3) 起飞着陆场长;(4) 爬升要求;(5) 机动要求;(6) 鉴定基准(例如:实验、航标或军用标准●2.2飞机起飞重量的估算●2.2.1飞机起飞重量的分析设计起飞重量包括空机重量和全部载重,如下图所示:以及近似计算过程的框图如下:W 0为飞机的起飞总重,它由以下几部分组成:e f p W W W W ++=0)(eq en st f p W W W W W ++++=Wp ——有效载荷(含乘员)重量;Wf ——燃油重量,包括任务燃油(可用燃油)、备份燃油(安全余油)及死油三部分; We ——空机重量,主要包括结构(机体、起落架、操纵系统等)重量、动力装置重量及设备重量三部分; 因为:e f p W W W W ++=00000)/()/(W W W W W W W e f p ++=e f p W W W W ++=0/(00)/W W所以:000//1W W W W W W e f p--=其中:0/w w f、0/w w e 分别称为燃油重量系数、空机重量系数。
在有效载重Wp 已知的情况下,求出空机重量系数0/w w e 和燃油重量系数 0/w w f (或燃油重量f W ),就可求出0W 。
2.2.2各重量系数的预测一、空机重量系数0/w w e的确定起飞重量中,空机重量可以用对应的空机重量系数乘以起飞重量而得到.空机空重:EE O OW W W W =⨯ 空机重量系数:C EO VS OW AW K W = 相对于O W 的经验空机重量系数统计值对于变后掠翼VS K =1.04, 正常机翼VS K =1.00 取 A=0.93, C=-0.07 VSK =1.00空机重量系数0.070.93ETO TOW W W -= 二、燃油重量系数0/w w f 的确定飞行任务中使用燃油重量为 (1)fused ff TO W m W =-任务燃油重量为 (1)F ff TO fres W m W W =-+ 其中 ff m 为任务燃油系数,fres W 为额外燃油重量, 任务燃油系数ff m = 710i i i iW W =+=∏ 这里注意取0W =TO W 典型飞行任务剖面图各任务段重量比的计算: 任务抛面 i i W W /1+发动机启动和暖机0.9900 取自AAA 典型的暖机段燃油系数 滑 跑 0.9950 取自AAA 典型的滑跑段燃油系数 起 飞 0.9950 取自AAA 典型的起飞段燃油系数爬升到巡航高度并加速到巡航速度0.9850 根据经验公式巡 航 0.8185 根据经验公式待 机 0.9323 根据经验公式取m in 30=ltr E施放有效载荷 1.0000待 机 0.9993 式取m in 5=ltr E根据经验公返 航 0.8185 根据经验公式下 降 0.9850 取自AAA 典型的下降段燃油系数 着陆、滑行和关机0.9950取自AAA 典型的着陆/滑行段燃油系数现在开始计算空中中巡航段和待机段的重量比 (1)巡航段54W W发动机耗油率C 发动机类型巡航耗油率待机耗油率2滑跑1发动机启动和暖机起飞4爬升并加速5巡航6待机7下降8着陆滑行并关机本运输机采用双转子,轴流式,高涵道比涡轮风扇发动机V2500这种发动机推力大、耗油率低。
简单飞行器设计大作业

简单飞行器设计大作业
**一、设计目标**
本次设计的目标是设计一个简单的飞行器,能够在空中稳定飞行,并具备一定的操控性能。
**二、设计要求**
1. 飞行器能够安全起飞和降落。
2. 具备简单的航向控制能力。
3. 能够在空中稳定飞行一段时间。
**三、设计方案**
1. 飞行器整体采用轻量化材料制作,以减小重量,提高飞行效率。
2. 采用电动马达作为动力源,驱动螺旋桨产生升力。
3. 飞行器的控制系统采用遥控器进行控制,通过调整马达的转速实现飞行器的升降和航向控制。
**四、技术实现**
1. 选择合适的材料制作飞行器的机架和外壳。
2. 安装电动马达和螺旋桨,并进行动力系统的调试。
3. 设计并制作遥控器,实现对飞行器的远程控制。
4. 进行飞行测试,对飞行器的性能进行评估和优化。
**五、总结与展望**
通过本次简单飞行器设计大作业,我们初步掌握了飞行器设计的基本流程和方法。
在未来的工作中,可以进一步优化飞行器的设计,提高其性能和可靠性,为实际应用提供更好的解决方案。
以上示例仅供参考,你可以根据具体的设计要求和实际情况进行修改和完善。
复旦 飞行力学与飞行控制大作业

ixt jyt kzt 。设飞机有一角速度 ix j y kz ,它会引起质量元 dm 产生一
t t t
牵连速度 Vdm 。牵连速度的向量值可按下式计算:
第3页
i Vdm xt xt
j
k
t
y
yt
z
zt
t
i ( yt zt zt yt ) j ( zt xt xt zt ) k ( xt yt yt xt ) iVdmx jVdmy kVdmz
R rt (t rt )t
上式除以 t ,并令 t 0 ,可得:
(A.1)
dr drt t rt dt dt
上式中
(A.2)
dr dr 为向量相对于地坐标系变化率 (即绝对运动) , t 为向量相对于动坐标系的 dt dt
变化率(即相对运动) ,t rt 为由动坐标系转动而引起的向量变化率(即牵连运动) 。上式 可以推广到任意向量的情况。对于 H t 、 Vt 向量有:
A.2 运动学方程组的建立 A.2.1 角位置运动学方程组
永远是沿垂直轴的, 永远是沿水平轴的。唯有 在飞机的三个姿态角的角速度中,
、 向机体三轴投影, xt 、 yt 、 是绕机体轴 OX t 的。 因些, 把 、 只有 xt 包含 的全部,
第4页
z 都会含有 、 的投影分量。因此,用坐标变换可得 x 、 y 、 z 和 、 、 之间
(A.21)
dH Vxt sin Vyt cos cos Vzt cos sin (A.22) dt dZ Vxt sin cos Vyt (sin sin sin cos cos ) Vzt (cos cos sin sin sin ) dt
《认识飞行器作业设计方案-2023-2024学年科学人教鄂教版》

《认识飞行器》作业设计方案第一课时一、设计目的:通过本次作业设计,使学生了解飞行器的种类、结构和原理,培养学生的观察、思考和分析能力,激发学生的学习兴趣,提高学生的创造性思维和动手能力。
二、作业内容:1. 研究类别:围绕飞行器展开,主要包括飞机、直升机、无人机等种类。
2. 结构分析:学生需要了解各种飞行器的结构组成,并画出简单的示意图。
3. 原理探究:学生需要探究飞行器的飞行原理,包括升力原理、动力原理等。
4. 创意设计:学生可以根据所学知识,设计一种自己的飞行器,并制作一个简单的模型。
5. 实践操作:学生可以选择一种飞行器进行实践操作,比如组装一个飞机模型或者操作一台无人机。
6. 实地考察:学生可以组织班级活动,前往机场等地进行实地考察,观察不同种类飞行器的起降过程。
三、作业要求:1. 学生需认真阅读相关学习资料,了解各种飞行器的基本知识。
2. 学生需根据设计要求,完成作业内容并按时提交。
3. 学生需积极参与课堂讨论,与同学分享自己的研究成果。
4. 学生需保持独立思考,勇于提出自己的见解,并尊重他人意见。
四、评估方式:1. 学生完成作业内容的质量(包括专业性、创意性等)。
2. 学生在课堂上积极参与讨论的程度。
3. 学生在实地考察中的观察记录和归纳能力。
4. 学生对于飞行器知识的理解和运用能力。
五、作业实施计划:1. 第一周:介绍飞行器基本知识,分组讨论各种飞行器的种类和结构。
2. 第二周:学生独立研究不同飞行器的飞行原理并做报告。
3. 第三周:学生完成创意设计并展示自己设计的飞行器模型。
4. 第四周:学生实地考察,观察不同种类飞行器的起降过程。
5. 第五周:学生总结本次作业,对所学知识进行归纳梳理。
通过以上设计方案,相信学生们将能够对飞行器有一个更加深入的了解,培养出对科技的热爱和对未来的探索精神。
同时,也能够激发学生的学习兴趣,提高他们的综合能力和创造力。
愿本次作业设计成为学生们知识海洋的一次冒险,让他们在探索中不断成长。
航天器制导与控制课后题答案(西电)
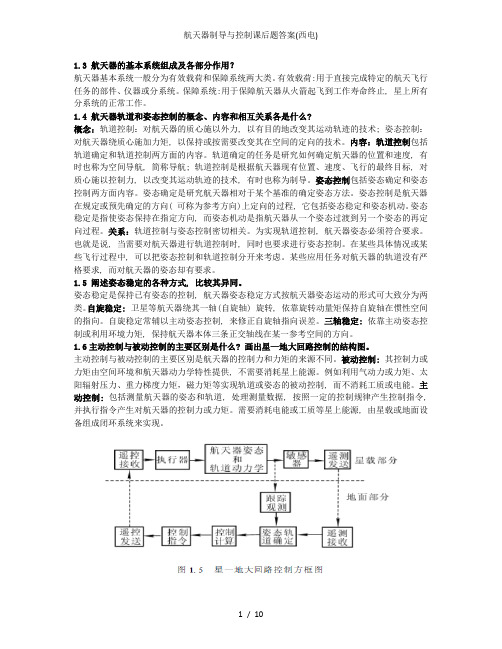
1.3 航天器的基本系统组成及各部分作用?航天器基本系统一般分为有效载荷和保障系统两大类。
有效载荷:用于直接完成特定的航天飞行任务的部件、仪器或分系统。
保障系统:用于保障航天器从火箭起飞到工作寿命终止, 星上所有分系统的正常工作。
1.4 航天器轨道和姿态控制的概念、内容和相互关系各是什么?概念:轨道控制:对航天器的质心施以外力, 以有目的地改变其运动轨迹的技术; 姿态控制:对航天器绕质心施加力矩, 以保持或按需要改变其在空间的定向的技术。
内容:轨道控制包括轨道确定和轨道控制两方面的内容。
轨道确定的任务是研究如何确定航天器的位置和速度, 有时也称为空间导航, 简称导航; 轨道控制是根据航天器现有位置、速度、飞行的最终目标, 对质心施以控制力, 以改变其运动轨迹的技术, 有时也称为制导。
姿态控制包括姿态确定和姿态控制两方面内容。
姿态确定是研究航天器相对于某个基准的确定姿态方法。
姿态控制是航天器在规定或预先确定的方向( 可称为参考方向)上定向的过程, 它包括姿态稳定和姿态机动。
姿态稳定是指使姿态保持在指定方向, 而姿态机动是指航天器从一个姿态过渡到另一个姿态的再定向过程。
关系:轨道控制与姿态控制密切相关。
为实现轨道控制, 航天器姿态必须符合要求。
也就是说, 当需要对航天器进行轨道控制时, 同时也要求进行姿态控制。
在某些具体情况或某些飞行过程中, 可以把姿态控制和轨道控制分开来考虑。
某些应用任务对航天器的轨道没有严格要求, 而对航天器的姿态却有要求。
1.5 阐述姿态稳定的各种方式, 比较其异同。
姿态稳定是保持已有姿态的控制, 航天器姿态稳定方式按航天器姿态运动的形式可大致分为两类。
自旋稳定:卫星等航天器绕其一轴(自旋轴) 旋转, 依靠旋转动量矩保持自旋轴在惯性空间的指向。
自旋稳定常辅以主动姿态控制, 来修正自旋轴指向误差。
三轴稳定: 依靠主动姿态控制或利用环境力矩, 保持航天器本体三条正交轴线在某一参考空间的方向。
制导飞行器概论小作业

制导飞行器概论小作业任课教师:马国梁1.海平面炮兵标准气象条件:气温 015N t =℃密度0 1.2063N ρ=kg/m 3气压01000N p =hPa相对湿度50%地面虚温 0288.9N τ=K(湿空气折合成干空气后的修正温度)音速0341.1N a =m/s2.空中标准气象条件在所有高度上无风,记y 为海拔高度。
A=230;B=−6.328×10-3;C=1.17210-6;(1) 对流层(9300y <m)温度(单位 K):0N By ττ=+ (1.1)气压函数:540 5.(1 2.190410)Np p y --=⨯ (1.2) (2) 亚同温层(930012000y ≤<m)温度(单位 K):2(9300)(9300)A B y C y τ=+-+- (1.3) 气压函数0 2.344(-9300)-63280.2922575exp -2.1206426arctan +0.1939252032221.057N p y p ⎛⎫⎛⎫⎛⎫=⨯⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ (1.4)(3) 同温层(1200030000y ≤<m)温度(单位 K):221.5τ= (1.5)气压函数:0120000.1937254exp 6483.305N p y p -⎛⎫=⨯- ⎪⎝⎭(1.6) 密度计算公式:000N N N p p τρρτ=⋅⋅ (1.7) 音速计算公式:a =(1.8)比热比 1.404k =,干空气气体常数287.05d R = J/(kg.K)作业内容:编制程序,根据我国炮兵的地面标准气象条件和空中标准气象条件绘制密度和音速随高度变化的曲线,高度范围030000y ≤<m ,高度取值间隔(≤50m)。
北航飞行力学大作业.

飞行力学大作业1理论推导方程在平面地球假设下,推导飞机质心在体轴系下的动力学方。
质心惯性加速度的基本方程是式(5.1.7),其中动点就是在转动参考系F E 中的O y 。
这样质心相r' 对于地球的速度,已用来表示。
这里假设地轴固定于惯性空间,且。
因此,的原点的E V 0ω= E F 加速度就是与地球转动有关的向心加速度。
数值比较表明,这一加速度和g 相比通常可以略去。
0a 而对于式(5.1.7)中的向心加速度项的情况也是一样的,,也通常省略。
在式(5.1.7)中剩下r ωω' 的两项中,而哥氏加速度为。
后者取决于飞行器速度的大小和方向,并且在轨道速E r V'= 2E E V ω 度时至多为10%g 。
当然在更高速度时可能更大。
所以保留此项。
最后质心的加速度可以简化为如下形式:2E E E CE EE E a V V ω=+ 有坐标转换知:(1)()()222()E E E E E E CB BE CE BE E E E BE E BE E E E B E E E E E E E B B B B B B B B Ba L a L V V L V L V V V V V V ωωωωωωω==+=+=+-+=++ 体轴系中的力方程为:f=m 而 f=+mg+TCB a B A 设飞机的迎角为,侧滑角为,则体轴系的气动力表示为:αβ cos cos cos sin sin ()()sin cos 0sin cos sin sin cos x y BW W y Z z A D D A L A L L C C A L a a a L αβαβααβββββ----⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==--=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦重力在牵连垂直坐标系下为:(3)00V g g ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦设发动机的安装角为,发动机的推力在机体坐标系的表示如下:τ (4)cos 0sin Z x y T T T T T ττ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦由坐标转换可知 :(5)sin sin cos cos cos B BV V mg mL g mg θφθφθ-⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦所以由上述公式可知:+= m = m [] (6)sin sin cos cos cos mg θφθφθ-⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦X Y Z ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦CB a ()E E E B B B V V ωω++ 其中:(7)cos cos cos sin sin cos cos 0sin cos 00sin 0sin cos sin sin cos 0sin cos E B BW u V V V v L V w a a a a αβαβααβββββββ--⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦(8)B p q r ω⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦E B EE B BE B p q r ω⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(9)带入原方程,可得其质心的动力学方程:cos sin [()()]cos sin [()()]sin cos cos [()()]EE x B B E Ey B B E Ez B B A T mg m u q q w r r v A mg m v r r u p p w A T mg m w p p v q q u τθθφτθφ+-=++-++=++-+-+=++-+ (10)(2)飞机的转动动力学方程:由G h = (11)且I I I h R R dm=⎰()I IB B B B R L R R ω=+ (12)由坐标变换知道:B BI I BI I IB B BI I IB B B h L h L R L R dm L R L R dmω==+⎰⎰ (13)由书上的(4.7,4)的规则知道:B BI I IB R L R L = (14)B B B B B B h R R dm R R dmω=+⎰⎰ (15)因为飞机一般认为是刚体飞机,故其变形分量一般认为为0,所以:(16)B B B B B B B B Bxxy zx B xyyyz zx yzz h R R dm R R dm I I I I I I I I I ωωκωκ==-=⎡⎤--⎢⎥=--⎢⎥⎢⎥--⎣⎦⎰⎰(17)22==0))()()()()x xy zx B xyyyz zx yzz xy yz r r x zx y z y yr ry zx z x xzr r z zx x y x y I I I I I I I I I I I L I p I r pq I I qr r h q h M I qI r p I I rp r h p h N I rI p qr I I pq q h p h κ⎡⎤--⎢⎥=--⎢⎥⎢⎥--⎣⎦=-+---+=----+-=-----+∑∑∑∑∑∑ ((考虑发动机转子的转动惯量,可得(18)r r r B B B h κω=(19)r r B B B BB B B B h R R dm h h ωκω=+=+∑∑⎰ 可知在体轴系下的各转矩为:r r B BI I B B B B B B B B B BB B B G L G h h h h ωκωκωωκωω==+=++++∑∑(20)000x xy zx x xy zx x xy zx xy yyz xy y yz xy yyz zxyz z zx yz z zx yz z L I I I p I I I p r q I I I p M I I I q I I I q r p I I I q N I I I r I I I r q p I I I r ⎡⎤⎡⎤⎡⎤-------⎡⎤⎡⎤⎡⎤⎡⎤⎡⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=--+--+---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-------⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 000r r xx r r y y r r z z h r q h h r p h h q p h ⎤⎢⎥⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥++-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦∑∑∑∑∑∑ (3)(21)()E V VB B B V L V W =+ ;(22)B u V v w ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦y x B z W W W W ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦()cos cos ()(sin sin cos cos sin )()(cos sin cos sin sin )E x y z xu W v W w W θψφθψφψφθψφψ=+++-+++ ()cos sin ()(sin sin sin cos cos )()(cos sin sin sin cos )E x y z yu W v W w W θψφθψφψφθψφψ=++++++-(23)()sin ()cos cos cos E x y zu W v W w θθφθ=++++ (4)由公式32V i j k ωωφθψ-=++ 再根据欧拉角的矩阵变化知(24)100i ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦30cos sin j φφ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦2sin cos sin cos cos k θθφθφ-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦当和均予忽略时,则[P ,Q ,R]=[p ,q ,r],即F B 相对于F I 的角速度,方程可写成如下形式:V ωE ω(25)10sin 0cos cos sin 0sin cos cos P Q R θφφθφθφθφψ⎡⎤-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦通过求逆,知:(26)1sin tan cos tan 0cos sin 0sin sec cos sec P Q R φφθφθθφφψφθφθ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ (5)当无风和具有对称面的刚体飞机,其六自由度运动方程为:质心动力学方程:(27)cos sin [()()]cos sin [()()]sin cos cos [()()]EE x B B E E y B B E Ez B B A T mg m u q q w r r v A mg m v r r u p p w A T mg m w p p v q q u τθθφτθφ+-=++-++=++-+-+=++-+ 若忽略地球的自转则可得:(28)cos sin []cos sin []sin cos cos []x y z A T mg m uqw rv A mg m vru pw A T mg m wpv qu τθθφτθφ+-=+-+=+--+=+- 绕质心转动的动力学方:由于具有对称面,且可以忽略有:B κ==0xy yz I I 根据(2)推出其简化的动力学方程为:(29)22))()()()()x zx y z y zx z x z zx x y L I p I r pq I I qrM I qI r p I I rp N I rI p qr I I pq =-+--=----=---- ((质心运动学方程:根据(3)可知,(30)()cos cos ()(sin sin cos cos sin )()(cos sin cos sin sin )()cos sin ()(sin sin sin cos cos )()(cos sin sin sin cos )()sin ()cos cos cos E x y z E x y z E x y xu W v W w W yu W v W w W zu W v W w θψφθψφψφθψφψθψφθψφψφθψφψθθφθ=+++-+++=++++++-=++++ 由于是无风,故(31)0x y z W W W ===(32)cos cos (sin sin cos cos sin )(cos sin cos sin sin )cos sin (sin sin sin cos cos )(cos sin sin sin cos )sin cos cos cos E E E xu v w yu v w zu v w θψφθψφψφθψφψθψφθψφψφθψφψθθφθ=+-++=+++-=++ 绕质心转动的运动学方程:根据(4)可知(33)sin tan cos tan cos sin sin sec cos sec P Q R Q R Q R φφθφθθφφψφθφθ=++=-=+ 二、小扰动线化设基准运动为对称定常直线水平飞行,假设飞机是具有对称面的刚体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
飞行器制导理论大作业(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--飞行器制导理论实报告课程名称:飞行器制导理论专业:飞行器设计与工程班级:姓名:学号:一、 实验目的掌握比例导引弹道的基本设计过程 二、 实验原理1、动力学方程(只考虑纵向平面):cos cos sin (sin )cos (cos sin )sin cos cos cos sin mV V m m V m m dV mP X G dt d mV P Y P Z G dtx V y V αβθθαγαβγθθψθ=--=++--==m V 为导弹速度,θ弹道倾角,V ψ弹道偏角,V γ速度滚转角,,,m m m x y z 为导弹位移,,,X Y Z 为气动力阻力、升力和侧向力,具体表达式为y ref z refY Y Y C qS Z Z Z C qS αααβββαβ====由此反推得到攻角α为(cos )cos cos sin V V VmV G mV P Yαθθγθψγα+-=+ 2、比例导引律的运动学方程:cos cos sin sin T T T T T T drV V dt dq r V V dt q q d dqk dt dtηηηηησησσ=-=-=+=+=3、导引头动态跟踪特性可考虑为一阶惯性环节11S c G s τ=+,这里c τ可取为。
4、先把自动驾驶仪简化,将自动驾驶仪考虑为一阶环节,其传递函数为A G 为110.1n A nc A A a G a s ττ==+=5、自动驾驶仪设计。
根据理想弹道数据,选取特征点,求解出动力系数2235~a a 。
由动力系数可以计算出弹体环节系数:2544334214141D D D D a a a a a a a K a a a T a T ζ***⎧⎪=-⎪⎪⎪=-⎪+⎪⎪=⎨⎪⎪=⎪⎪⎪⎪=⎪⎩进一步得到弹体环节传递函数:()()()()()122112157.31zzy z D D DD D nD K T s Gs Ts T s VG s g T s ωδωξ+=++=+控制回路可以参考下图进行设计:N具体控制律可写作:()z p yc y d z K N N K δω=--弹体环节部分参考数据如下,由于导引系数、计算方法以及气动数据有差异,数据可能有一些波动,数据仅供参考:设计控制系数p K 和d K ,并带入俯仰平面三自由度方程组中进行弹道验证:三、 实验过程1、计算理想弹道:根据动力学方程和比例导引律的运动学方程,计算理想弹道。
取比例系数K=3。
2、 将导引头,自动驾驶仪均视为一阶环节计算弹道:导引头传递函数为一阶惯性环节11S c G s τ=+,自动驾驶仪传递函数简化为11n A nc A a G a s τ==+。
将他们带入弹道计算过程,计算考虑导引头和自动驾驶仪后的弹道。
3、自动驾驶仪设计:根据理想弹道数据,每隔一个时间步长选取一个特征点,解出动力系数a22-a35,由动力系数可以算出弹体环节系数,进一步得到弹体环节传递函数。
用二阶环节模拟一阶环节,令二阶环节的时间常数等于一阶环节时间常数,即n 1/a ωτ=,依次解算Kp ,Kd 。
调整Kp 、Kd 的值,使考虑导引头及自动驾驶仪的导弹能够命中目标。
四、 实验结果1、 理想弹道:取时间步长dt=,导弹和目标的相对距离小于2为终止条件:最后相距r=,时间t=,速度v=s。
2、将导引头,自动驾驶仪均视为一阶环节计算弹道:取时间步长dt=,导弹和目标的相对距离小于20为终止条件:最后相距r= ,时间t= 。
3、自动驾驶仪设计:a、弹体环节传递函数及用二阶环节模拟一阶环节,即n 1/aωτ=,依次解算Kp,Kd如图:b、全程令Kp=,Kd=,比例系数增大为K=6,取dt=1,代入自动驾驶仪中得:取导弹和目标的相对距离小于20为终止条件:最后相距r= ,时间t= 15s。
五、结果分析考虑导引头和自动驾驶仪的动态跟踪特性之后,导弹的最高飞行高度增加,弹道的最高点右移,导弹飞行时间增加。
设计自动驾驶仪时,弹道轨迹右移严重,导弹下落困难,可适当增加比例系数K。
六、实验总结通过这次实验,我理解了弹道设计的基本流程。
航天是一门基于应用的学科,必须将理论知识应用于实践才有意义。
只有将书本上的知识应用于实践,才能更加深刻的掌握知识,反过来又能促进将来的实践。
七、程序1、理想弹道(python):import mathimport numpy as npimport as plt#解决中文显示问题['']=['SimHei'][''] = False#初始条件m = [];theta = []; (5*180)alpha = []; (0)v = []; (20)x = []; (0); y = []; (0)xt = 1500; yt = 0q = []; (0)r = []; (1500)S =P = 140; g =ms =rho =Cy_delta =L =Jz =mz_wz =#函数拟合Ma = [, , ]Cya_point = [, , ]Cya_line = (Ma, Cya_point, 2)#用2次多项式拟合Cya = (Cya_line)Cx_point = [, , ]Cx_line = (Ma, Cx_point, 2)#用2次多项式拟合Cx = (Cx_line)i = 0dt=k = 3ti = int(2/dt)while r[i]>2:if i*dt>=2:P = 0ms = 0(x[i]+(theta[i])*dt*v[i])(y[i]+(theta[i])*dt*v[i])((xt-x[i+1])/((x[i+1]-xt)**2+(y[i+1]-yt)**2)))(theta[i]+k*(q[i+1]-q[i]))Cxt =Cx(v[i]/340)Cyat = Cya(v[i]/340)qt = *rho*v[i]**2X = Cxt*qt*SY = Cyat*qt*S*alpha[i]dv = (P*(alpha[i])-X-m[i]*g*(theta[i]))/m[i](v[i]+dv*dt)#((m[i]*v[i]*k*(q[i+1]-q[i])/dt+m[i]*g*(theta[i])-Y)/P))((m[i]*v[i]*k*(q[i+1]-q[i])/dt+m[i]*g*(theta[i]))/(P+Cyat*qt*S))(m[i]-ms*dt)((x[i+1]-xt)**2+(y[i+1]-yt)**2))i = i+1print(r[i])print(i*dt)print(v[100])()(x, y)("理想弹道")("x/m")("y/m")()(x, v)("速度")("x(m)")("v(m/s)")()(x, theta)("弹道倾角")("x/m")("theta")()(x, alpha)("攻角")("x/m")("alpha")()2、将导引头,自动驾驶仪均视为一阶环节计算弹道:clcm(1) =;theta(1) =5*pi/180;alpha(1) = 0;v(1) = 20;x(1) = 0; y(1) = 0;xt = 1500; yt = 0;q(1) = 0;r(1) = 1500;S = ;P = 140; g = ;ms = ;rho = ;Cy_delta = ;L = ;Jz = ;mz_wz = ;%函数拟合Ma = [ ];Cya_point = [, , ];Cya_line = polyfit(Ma, Cya_point, 2);%#用2次多项式拟合Cx_point = [, , ];Cx_line = polyfit(Ma, Cx_point, 2);%#用2次多项式拟合i = 1;dt=;k = 3;ti = round(2/dt);while r(i)>20if i*dt>=2P = 0;ms = 0;endx(i+1)=(x(i)+cos(theta(i))*dt*v(i));y(i+1)=(y(i)+sin(theta(i))*dt*v(i));q(i+1)=(-acos((xt-x(i+1))/sqrt((x(i+1)-xt)^2+(y(i+1)-yt)^2)));%状态方程A=[0 1;-10 -15];B=[0;1];C=[50 0];ut=(q(i+1)-q(i))/dt;syms t tau;xtt=int(expm(A*(t-tau))*B*ut,tau,0,t);ytt=C*xtt;qtt=subs(ytt,t,;theta(i+1)=(theta(i)+k*qtt*dt);Cxt = polyval(Cx_line,v(i)/340);Cyat = polyval(Cya_line,v(i)/340);qt = *rho*v(i)^2;X = Cxt*qt*S;Y = Cyat*qt*S*alpha(i);dv = (P*cos(alpha(i))-X-m(i)*g*sin(theta(i)))/m(i);v(i+1)=(v(i)+dv*dt);%alpha(i+1)=(asin((m(i)*v(i)*k*(q(i+1)-q(i))/dt+m(i)*g*cos(theta(i))-Y)/P)) alpha(i+1)=((m(i)*v(i)*k*(q(i+1)-q(i))/dt+m(i)*g*cos(theta(i)))/(P+Cyat*qt*S));m(i+1)=(m(i)-ms*dt);r(i+1)=(sqrt((x(i+1)-xt)^2+(y(i+1)-yt)^2));i=i+1;endr(i)i*dtfigure()plot(x, y)title('弹道')xlabel('x/m')ylabel('y/m')figure()plot(x, v)title('速度')xlabel('x(m)')ylabel('v(m/s)')figure()plot(x,alpha)title('攻角')xlabel('x(m)')ylabel('alpha')figure()plot(x,theta)title('弹道倾角')xlabel('x(m)')ylabel('theta')3、自动驾驶仪设计:a、弹体环节传递函数及用二阶环节模拟一阶环节,即n 1/aωτ=,依次解算Kp,Kd如图:clc%#初始条件m(1) =;theta(1) =5*pi/180;alpha(1) = 0;v(1) = 20;x(1) = 0; y(1) = 0;xt = 1500; yt = 0;q(1) = 0;r(1) = 1500;S = ;P = 140; g = ;ms = ;rho = ;Cy_delta = ;L = ;Jz = ;mz_wz = ;%#函数拟合Ma = [ ];Cya_point = [, , ];Cya_line = polyfit(Ma, Cya_point, 2);%#用2次多项式拟合mz_a_point = [, , ];mz_a_line = polyfit(Ma, mz_a_point, 2);%#用2次多项式拟合mz_delta_point = [, , ];mz_delta_line = polyfit(Ma, mz_delta_point, 2);%#用2次多项式拟合Cx_point = [, , ];Cx_line = polyfit(Ma, Cx_point, 2);%#用2次多项式拟合%状态方程% A=[-5];% B=[1];% x0=[0];% ut=1;% t = 2;% syms tau;% xtt=expm(A*t)*x0+int(expm(A*(t-tau))*B*ut,tau,0,t);taua = ;ksi = ;i = 1;dt=;k = 3;ti = round(2/dt);while r(i)>20if i*dt>=2P = 0;ms = 0;endx(i+1)=(x(i)+cos(theta(i))*dt*v(i));y(i+1)=(y(i)+sin(theta(i))*dt*v(i));q(i+1)=(-acos((xt-x(i+1))/sqrt((x(i+1)-xt)^2+(y(i+1)-yt)^2)));theta(i+1)=(theta(i)+k*(q(i+1)-q(i)));% if i==1% theta(i+1)=(theta(i)+k*(q(i+1)-q(i)));% else% a=-((1+Kd(i-1)*KD(i-1))**g+Kp(i-1)*KD(i-1)*v(i-1))/*g*(TD(i-1)^2));% b= -(2*kxiD(i-1)*TD(i-1)+Kd(i-1)*KD(i-1))/(TD(i-1)^2);% A=[0 1;a b];% B=[0;1];% c=Kp(i-1)*KD(i-1)*v(i-1)/*g*TD(i-1)^2);% C=[c 0];% ut=(q(i+1)-q(i))/dt;% syms t tau;% xtt2=int(expm(A*(t-tau))*B*ut,tau,0,t);% ytt2=C*xtt2;% qtt2=subs(ytt2,t,;% theta(i+1)=(theta(i)+k*qtt2*dt);% endCxt = polyval(Cx_line,v(i)/340);Cyat = polyval(Cya_line,v(i)/340);qt = *rho*v(i)^2;X = Cxt*qt*S;Y = Cyat*qt*S*alpha(i);dv = (P*cos(alpha(i))-X-m(i)*g*sin(theta(i)))/m(i);v(i+1)=(v(i)+dv*dt);%alpha(i+1)=(asin((m(i)*v(i)*k*(q(i+1)-q(i))/dt+m(i)*g*cos(theta(i))-Y)/P)) alpha(i+1)=((m(i)*v(i)*k*(q(i+1)-q(i))/dt+m(i)*g*cos(theta(i)))/(P+Cyat*qt*S));m(i+1)=(m(i)-ms*dt);r(i+1)=(sqrt((x(i+1)-xt)^2+(y(i+1)-yt)^2));a1 = -(mz_wz*qt*S*L*L/v(i))/Jz;a2 = -(polyval(mz_a_line,v(i)/340)*qt*S*L*/Jz;a3 = -(polyval(mz_delta_line,v(i)/340)*qt*S*L*/Jz;a4 = (P+Cyat*qt*S*/(m(i)*v(i));a5 = (Cy_delta*qt*S*/(m(i)*v(i));a4_xing = a4-a2*a5/a3;KD(i)=(-a3*a4_xing/(a2+a1*a4));T1D(i)=(1/a4_xing);TD(i)=(1/sqrt(abs(a2+a1*a4)));kxiD(i)=((a1+a4)/(2*sqrt(abs(a2+a1*a4))));% syms Kp Kd;%[Kp,Kd]=solve((2*kxiD(i)*TD(i)+Kd*KD(i))/(TD(i)^2)=2*ksi/taua,((1+Kd*KD(i))**g +Kp*KD(i)*v(i))/*g*TD(i)^2)=(1/taua)^2);% Kp(i)=vpa(Kp,4);% Kd(i)=vpa(Kd,4);Kd(i)=(2*ksi/taua*TD(i)^2-2*kxiD(i)*TD(i))/(KD(i)*T1D(i));Kp(i)=((1/taua)^2**g*(TD(i))^2-(1+Kd(i)*KD(i))**g)/(Kd(i)*v(i)); i=i+1;endx(1)= [ ];figure()plot(x,KD)title('KD')xlabel('x/m')ylabel('KD')figure()plot(x,TD)title('TD')xlabel('x/m')ylabel('TD')figure()plot(x,kxiD)title('kxiD')xlabel('x/m')ylabel('kxiD')figure()plot(x,T1D)title('T1D')xlabel('x/m')ylabel('T1D')figure()plot(x, Kd)title('Kd')xlabel('x/m')ylabel('Kd')figure()plot(x, Kp)title('Kp')xlabel('x/m')ylabel('Kp')b、用解算的Kp,Kd计算弹道:clc%#初始条件m(1) =;theta(1) =5*pi/180;alpha(1) = 0;v(1) = 20;x(1) = 0; y(1) = 0;xt = 1500; yt = 0;q(1) = 0;r(1) = 1500;S = ;P = 140; g = ;ms = ;rho = ;Cy_delta = ;L = ;Jz = ;mz_wz = ;%#函数拟合Ma = [ ];Cya_point = [, , ];Cya_line = polyfit(Ma, Cya_point, 2);%#用2次多项式拟合mz_a_point = [, , ];mz_a_line = polyfit(Ma, mz_a_point, 2);%#用2次多项式拟合mz_delta_point = [, , ];mz_delta_line = polyfit(Ma, mz_delta_point, 2);%#用2次多项式拟合Cx_point = [, , ];Cx_line = polyfit(Ma, Cx_point, 2);%#用2次多项式拟合%状态方程% A=[-5];% B=[1];% x0=[0];% ut=1;% t = 2;% syms tau;% xtt=expm(A*t)*x0+int(expm(A*(t-tau))*B*ut,tau,0,t);taua = ;ksi = ;i = 1;dt=;k = 3;ti = round(2/dt);while r(i)>20if i*dt>=2P = 0;ms = 0;endx(i+1)=(x(i)+cos(theta(i))*dt*v(i));y(i+1)=(y(i)+sin(theta(i))*dt*v(i));q(i+1)=(-acos((xt-x(i+1))/sqrt((x(i+1)-xt)^2+(y(i+1)-yt)^2)));if i==1A=[-5];B=[1];C=[5];ut=(q(i+1)-q(i))/dt;syms t tau;xtt=int(expm(A*(t-tau))*B*ut,tau,0,t);ytt=C*xtt;qtt=subs(ytt,t,;theta(i+1)=(theta(i)+k*qtt*dt);elseA=[-5];B=[1];C=[5];ut=(q(i+1)-q(i))/dt;syms t tau;xtt=int(expm(A*(t-tau))*B*ut,tau,0,t);ytt=C*xtt;qtt=subs(ytt,t,;a=-((1+Kd(i-1)*KD(i-1))**g+Kp(i-1)*KD(i-1)*v(i-1))/*g*(TD(i-1)^2)); b= -(2*kxiD(i-1)*TD(i-1)+Kd(i-1)*KD(i-1))/(TD(i-1)^2);A2=[0 1;a b];B2=[0;1];c=Kp(i-1)*KD(i-1)*v(i-1)/*g*TD(i-1)^2);C2=[c 0];ut2=qtt;syms t2 tau2;xtt2=int(expm(A2*(t2-tau2))*B2*ut2,tau2,0,t2);ytt2=C2*xtt2;qtt2=subs(ytt2,t2,;theta(i+1)=(theta(i)+k*qtt2*dt);endCxt = polyval(Cx_line,v(i)/340);Cyat = polyval(Cya_line,v(i)/340);qt = *rho*v(i)^2;X = Cxt*qt*S;Y = Cyat*qt*S*alpha(i);dv = (P*cos(alpha(i))-X-m(i)*g*sin(theta(i)))/m(i);v(i+1)=(v(i)+dv*dt);%alpha(i+1)=(asin((m(i)*v(i)*k*(q(i+1)-q(i))/dt+m(i)*g*cos(theta(i))-Y)/P))alpha(i+1)=((m(i)*v(i)*k*(q(i+1)-q(i))/dt+m(i)*g*cos(theta(i)))/(P+Cyat*qt*S));m(i+1)=(m(i)-ms*dt);r(i+1)=(sqrt((x(i+1)-xt)^2+(y(i+1)-yt)^2));a1 = -(mz_wz*qt*S*L*L/v(i))/Jz;a2 = -(polyval(mz_a_line,v(i)/340)*qt*S*L*/Jz;a3 = -(polyval(mz_delta_line,v(i)/340)*qt*S*L*/Jz;a4 = (P+Cyat*qt*S*/(m(i)*v(i));a5 = (Cy_delta*qt*S*/(m(i)*v(i));a4_xing = a4-a2*a5/a3;KD(i)=(-a3*a4_xing/(a2+a1*a4));T1D(i)=(1/a4_xing);TD(i)=(1/sqrt(abs(a2+a1*a4)));kxiD(i)=((a1+a4)/(2*sqrt(abs(a2+a1*a4))));% syms Kp Kd;%[Kp,Kd]=solve((2*kxiD(i)*TD(i)+Kd*KD(i))/(TD(i)^2)=2*ksi/taua,((1+Kd*KD(i))**g +Kp*KD(i)*v(i))/*g*TD(i)^2)=(1/taua)^2);% Kp(i)=vpa(Kp,4);% Kd(i)=vpa(Kd,4);Kd(i)=(2*ksi/taua*TD(i)^2-2*kxiD(i)*TD(i))/(KD(i)*T1D(i));Kp(i)=((1/taua)^2**g*(TD(i))^2-(1+Kd(i)*KD(i))**g)/(Kd(i)*v(i));i=i+1endr(i)i*dtfigure()plot(x, y)title('理想弹道')xlabel('x/m')ylabel('y/m')c、全程令Kp=100,Kd=6,取dt=1,代入自动驾驶仪中得:取导弹和目标的相对距离小于20为终止条件:最后相距r= ,时间t= 15s。
