平移与旋转的练习题
旋转平移练习题五年级

旋转平移练习题五年级在小学五年级的数学课程中,旋转和平移是图形变换的两个基本类型。
旋转是指图形绕某一点旋转一定角度,而平移是指图形沿着某一直线方向移动一定距离。
以下是一些旋转和平移的练习题,供五年级学生练习使用:1. 平移练习题- 题目一:如果一个点A(2,3)沿着x轴正方向平移5个单位,求平移后的坐标。
- 题目二:一个长方形的长为4厘米,宽为3厘米,如果它沿着y轴负方向平移2厘米,求新长方形的四个顶点坐标。
- 题目三:一个三角形的顶点坐标分别为A(1,1),B(4,1),C(2,4)。
如果这个三角形沿着x轴正方向平移3个单位,求新三角形的顶点坐标。
2. 旋转练习题- 题目一:点P(-3,4)绕原点O(0,0)顺时针旋转90度,求旋转后的坐标。
- 题目二:一个正方形的四个顶点坐标分别为A(0,0),B(1,0),C(1,1),D(0,1)。
如果这个正方形绕点A顺时针旋转45度,求新正方形的四个顶点坐标。
- 题目三:一个圆心在O(0,0),半径为5的圆,绕原点O顺时针旋转30度,求旋转后圆上任意一点P(x,y)的新坐标。
3. 综合练习题- 题目一:一个平行四边形的顶点坐标分别为A(-2,-1),B(-1,2),C(3,3),D(2,-1)。
首先沿着x轴正方向平移4个单位,然后绕新平行四边形的中心点顺时针旋转60度,求旋转和平移后平行四边形的顶点坐标。
- 题目二:一个等边三角形的顶点坐标分别为A(0,0),B(3,0),C(1.5,3)。
首先绕原点O(0,0)顺时针旋转60度,然后沿着y轴正方向平移2个单位,求最终三角形的顶点坐标。
4. 应用题- 题目一:小明的房间有一个长为6米,宽为4米的矩形地毯。
如果地毯沿着房间的一边平移2米,求平移后地毯的长和宽。
- 题目二:一个时钟的时针从12点位置开始顺时针旋转了90度,求此时时针指向的数字。
这些练习题旨在帮助学生理解旋转和平移的基本概念,以及如何应用这些概念来解决实际问题。
初中数学图形的旋转与平移练习题及答案

初中数学图形的旋转与平移练习题及答案旋转与平移是数学中研究图形变换的重要概念,它们在几何图形的研究和解题中扮演着重要的角色。
下面将为大家提供一些初中数学图形的旋转与平移的练习题及答案,帮助大家更好地理解和掌握这一知识点。
练习题一:1. 将图形A绕点O逆时针旋转90度,得到图形B,如图所示。
请画出图形B,并标出其顶点坐标。
解答:根据题目所给条件,我们可以得知图形B是将图形A绕点O逆时针旋转90度得到的。
假设图形A的顶点坐标依次为A(x1, y1),B(x2,y2),C(x3, y3),则图形B的顶点坐标为A'(-y1, x1),B'(-y2, x2),C'(-y3, x3)。
练习题二:2. 将线段AB向右平移5个单位得到线段CD,如图所示。
如果A的坐标为(1, 2),请画出线段CD,并求出C点的坐标。
解答:根据题目所给条件,我们知道线段AB向右平移5个单位得到线段CD,那么坐标的改变量就是平移的距离。
假设A点的坐标为(x1, y1),则C点的坐标为(x1 + 5, y1)。
练习题三:3. 将线段EF绕点O顺时针旋转180度得到线段GH,如图所示。
请写出线段GH的坐标,并判断是否与线段EF相等。
解答:根据题目所给条件,我们知道线段EF绕点O顺时针旋转180度得到的线段GH。
假设E点的坐标为(x1, y1),F点的坐标为(x2, y2),则G 点的坐标为(-x1, -y1),H点的坐标为(-x2, -y2)。
通过对比可以发现,线段GH与线段EF在长度、形状上完全相同。
练习题四:4. 将正方形ABCD绕点O逆时针旋转90度得到正方形EFGH,如图所示。
若正方形ABCD的边长为5个单位,请计算正方形EFGH的边长。
解答:根据题目所给条件,我们知道正方形EFGH是将正方形ABCD绕点O逆时针旋转90度得到的。
假设正方形ABCD的边长为 a,则正方形EFGH的边长也为 a。
练习题五:5. 将图形P绕点O逆时针旋转270度得到图形Q,如图所示。
小学六年级平移与旋转练习题

小学六年级平移与旋转练习题一、填空题1. 点(3,4)关于原点顺时针旋转180°,得到新的点是(____,____)。
2. 图形A向右移动3个单位得到图形B,B再向上移动4个单位得到图形C。
图形A与C之间的平移距离是(____,____)。
3. 图形D相对于原点顺时针旋转90°,得到新的图形E。
图形D中的一个点是(3,2),那么在图形E中这个点的坐标是(____,____)。
4. 点(-2,5)相对于原点逆时针旋转270°后,得到新的点是(____,____)。
二、选择题1. 图形F相对于原点顺时针旋转180°,得到的图形是:A. 图形F'B. 图形GC. 图形HD. 图形I2. 图形J向右平移3个单位,再向下平移2个单位,得到的图形是:A. 图形KB. 图形LC. 图形MD. 图形N3. 图形P相对于原点顺时针旋转90°,再顺时针旋转90°,得到的图形是:A. 图形QB. 图形RC. 图形SD. 图形T4. 点(1,-3)相对于原点逆时针旋转270°后,得到的点是:A. (1,3)B. (3,-1)C. (-3,1)D. (-1,-3)三、应用题1. 图形U是一个正方形,边长为6个单位。
请你向右移动3个单位,再向下移动5个单位,得到新的图形V。
请问图形V的边长是多少?2. 图形W是一个矩形,长为8个单位,宽为4个单位。
请你将矩形W按顺时针方向旋转90°,得到新的图形X。
请问图形X的长和宽分别是多少?3. 图形Y是一个三角形,顶点为A(2,4),B(5,2),C(7,6)。
请你以点A为中心顺时针旋转90°,得到新的图形Z。
请写出图形Z的顶点坐标。
四、解答题1. 图形ABCD是一个菱形,A(1,4),B(4,1),C(7,4),D(4,7)。
请你以原点为中心顺时针旋转60°,得到新的图形。
请写出新的图形的顶点坐标。
【小学】小学三年级数学(下)《平移与旋转现象》练习题(含答案)
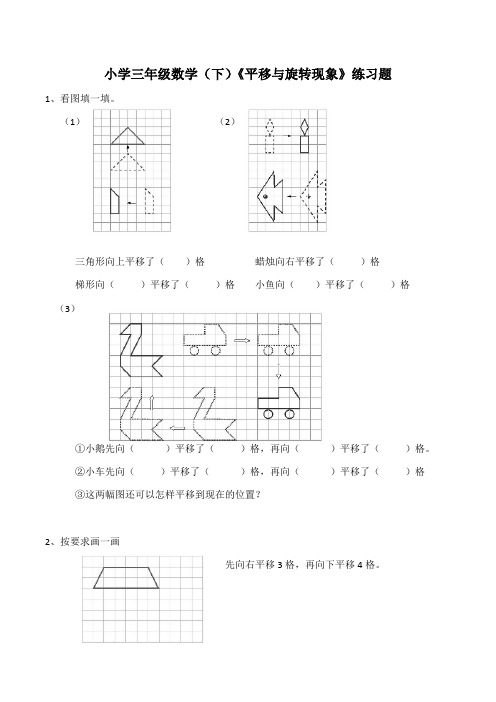
小学三年级数学(下)《平移与旋转现象》练习题1、看图填一填。
(1)(2)三角形向上平移了()格蜡烛向右平移了()格梯形向()平移了()格小鱼向()平移了()格(3)①小鹅先向()平移了()格,再向()平移了()格。
②小车先向()平移了()格,再向()平移了()格③这两幅图还可以怎样平移到现在的位置?2、按要求画一画先向右平移3格,再向下平移4格。
3、说一说,填一填。
分针顺时针旋转了()度。
逆时针旋转了()度。
4、下列图形中,不能由左图经过一次平移或亩得到的是()。
5、画一画。
(1)把图①绕O点顺时针旋转90°(2)把图②绕O点逆时针旋转90°。
6、旗帜上的图案哪些可以通过旋转得到,哪些可能通过平移得到?7、请你利用平衡或旋转的方法,将图2恢复到图一的样子。
说出变化的过程。
8、哪两个图形通过平移或旋转能够完全重合?(连一连)9、(1)上面的的哪些标志是轴对称的?(2)用旋转或平移的方法设计一个漂亮的标志。
附参考答案1、看图填一填。
(1)3格,左4格,(2)4格,左,5格。
(3)①左,7格,上,6格,②右,7格,下,6格,③小鹅向先上平移6格,再向左平移7格。
小车先向下平移6格,再向右平移7格。
2、画图。
略3、说、填。
图1:90°,图2:90°4、不能一次由旋转或平移得到的图形是②5、略6、由平移得到的是①④⑥,由旋转得到的是②③⑤7、把左下图向右平移1格,再向上平移格。
把右下图逆时针90°就恢复了原图。
8、通过平移重合的有:①和⑤,通过旋转重合的有:④和⑥,①和⑧,④和⑫,③和⑪,9、(1)轴对称图形有:上1,上2,上4,上5,下1,下3,下10;(2)略。
旋转平移练习题五年级

旋转平移练习题五年级1. 问题描述在数学课上,五年级的学生正在学习旋转和平移的概念。
为了巩固他们的理解,老师给了他们以下练习题。
2. 练习题一旋转:以点A为中心,逆时针旋转90度。
请根据题图信息回答以下问题:a) 在旋转之前,点B的坐标为(2, 3),在旋转之后,点B的坐标是多少?b) 旋转之后,线段AB的长度是否改变?为什么?c) 旋转之后,点C的位置如何变化?请说明原因。
3. 练习题二旋转:以点D为中心,顺时针旋转180度。
请根据题图信息回答以下问题:a) 旋转之后,点E的坐标是多少?b) 旋转之后,线段DE的长度是否改变?为什么?c) 旋转之后,点F的位置如何变化?请说明原因。
4. 练习题三平移:将图形G沿x轴正方向平移5个单位,请根据题图信息回答以下问题:a) 平移之后,点H的坐标是多少?b) 平移之后,线段GH的长度是否改变?为什么?c) 平移之后,点I的位置如何变化?请说明原因。
5. 练习题四平移:将图形J沿y轴负方向平移3个单位,请根据题图信息回答以下问题:a) 平移之后,点K的坐标是多少?b) 平移之后,线段JK的长度是否改变?为什么?c) 平移之后,点L的位置如何变化?请说明原因。
6. 练习题五旋转和平移:先将图形M以点N为中心进行逆时针旋转90度,再将旋转之后的图形沿x轴正方向平移4个单位。
请根据题图信息回答以下问题:a) 完成旋转后,点O的坐标是多少?b) 完成平移后,点P的坐标是多少?c) 完成旋转和平移后,线段MN的长度是否改变?为什么?d) 完成旋转和平移后,点Q的位置如何变化?请说明原因。
7. 总结回顾通过这些练习题,你能清晰地理解旋转和平移对点和线段的影响了吗?在旋转时,点的坐标会发生怎样的变化?线段的长度会保持不变吗?在平移时,点的坐标会如何变化?线段的长度会发生改变吗?通过反复练习,相信你已经掌握了旋转和平移的基本概念与技巧,能够灵活运用它们解决各种几何问题了!以上是旋转平移练习题五年级的内容。
初二平移与旋转练习题

初二平移与旋转练习题题目一:平移练习题1. 在平面直角坐标系中,顶点坐标分别是 (2,4)、(4,4)、(4,6)、(2,6)的正方形ABCD,向右平移3 个单位,求平移后的正方形的顶点坐标。
2. 在平面直角坐标系中,顶点坐标分别是 (-3,1)、(-2,5)、(-5,6)、(-6,2) 的四边形 EFGH,向下平移 4 个单位,求平移后的四边形的顶点坐标。
3. 在平面直角坐标系中,点 P 的坐标为 (1,3),将点 P 向右平移 2 个单位、向上平移 5 个单位,求平移后点 P 的坐标。
题目二:旋转练习题1. 将直角坐标系中的点 A(2,3) 逆时针旋转 90 度,求旋转后点的坐标。
2. 将直角坐标系中的点 B(-5,2) 顺时针旋转 180 度,求旋转后点的坐标。
3. 将直角坐标系中的点 C(-1,4) 逆时针旋转 270 度,求旋转后点的坐标。
题目三:平移与旋转综合练习题1. 以直角坐标系中的点 D(3,2) 为中心,将正方形 ABCD 逆时针旋转 90 度并向上平移 4 个单位,求旋转和平移后正方形的顶点坐标。
2. 以直角坐标系中的点 E(-2,5) 为中心,将四边形 EFGH 顺时针旋转 180 度并向右平移 3 个单位,求旋转和平移后四边形的顶点坐标。
3. 以直角坐标系中的点 F(0,-3) 为中心,将点 P(1,1) 逆时针旋转 120 度并向上平移 2 个单位,求旋转和平移后点 P 的坐标。
以上为初二平移与旋转练习题。
通过解答这些练习题,可以帮助你巩固平移与旋转的知识,提升解题能力。
希望你能认真思考并准确回答每个问题,加深对这两个概念的理解。
祝你学习进步!。
平移旋转练习题三年级

平移旋转练习题三年级一、选择题1. 平移是指图形在平面内沿某一方向移动一定的距离,以下哪个图形发生了平移?A. 一个正方形旋转90度B. 一个三角形向右移动5厘米C. 一个圆形绕着它的中心点旋转2. 下列哪个操作不是平移?A. 将一个长方形沿着水平方向移动B. 将一个圆沿着垂直方向移动C. 将一个正方形绕着一个点旋转3. 旋转是指图形绕着一个点或一条线旋转一定角度,以下哪个图形发生了旋转?A. 一个长方形向右平移B. 一个圆形绕着它的中心点旋转180度C. 一个三角形沿着对角线平移4. 一个图形经过平移后,下列哪个属性不会改变?A. 形状B. 大小C. 位置5. 如果一个图形绕着它的中心点旋转了90度,那么它的哪个属性发生了变化?A. 形状B. 大小C. 方向二、填空题6. 平移不改变图形的________和________。
7. 旋转改变图形的________,但图形的________和________保持不变。
8. 如果一个图形向右平移了3个单位,那么它的对应点也会向右平移________个单位。
9. 一个图形绕着一个点旋转后,这个点被称为图形的________。
三、判断题10. 平移和旋转都是图形的变换方式。
()11. 平移后的图形与原图形全等。
()12. 旋转后的图形与原图形相似。
()13. 平移可以改变图形的方向。
()14. 旋转不可以改变图形的大小。
()四、简答题15. 请解释什么是平移,并给出一个生活中的例子。
16. 请解释什么是旋转,并给出一个生活中的例子。
五、应用题17. 一个长方形的长是8厘米,宽是5厘米,如果这个长方形向右平移了4厘米,它的新位置是什么?18. 一个时钟的时针在12点位置,如果时针顺时针旋转了90度,它指向的数字是多少?六、绘图题19. 画出一个正方形,然后将其向右平移3厘米。
20. 画出一个圆形,然后将其绕着中心点顺时针旋转90度。
七、计算题21. 如果一个图形的平移距离是5厘米,那么它的对应点的移动距离是多少?22. 如果一个图形绕着它的中心点旋转了180度,那么它旋转了多少个直角?八、拓展题23. 假设有一个图形,它先向右平移了2厘米,然后绕着它的中心点顺时针旋转了90度,最后再向上平移了3厘米。
旋转与平移练习题

旋转与平移练习题旋转与平移练习题旋转与平移是数学中常见的几何变换操作,它们在解决实际问题和培养学生的空间想象力方面起着重要的作用。
在学习过程中,通过练习题的形式,学生可以更好地理解和掌握旋转与平移的概念和运算方法。
本文将通过一些具体的练习题,帮助读者更好地理解旋转与平移。
1. 旋转练习题题目一:将一个正方形顺时针旋转90度,求旋转后的图形。
解析:正方形的每个顶点都会按照相同的角度进行旋转。
顺时针旋转90度意味着每个顶点都向右移动一个单位,并且顺序变为右上、右下、左下、左上。
因此,旋转后的图形是一个新的正方形,其顶点为(1, 1)、(1, -1)、(-1, -1)、(-1, 1)。
题目二:将一个长方形逆时针旋转45度,求旋转后的图形。
解析:逆时针旋转45度意味着每个顶点都向左上移动一个单位,并且顺序变为左上、左下、右下、右上。
因此,旋转后的图形是一个新的长方形,其顶点为(-√2, √2)、(-√2, -√2)、(√2, -√2)、(√2, √2)。
2. 平移练习题题目一:将一个三角形向右平移3个单位,向上平移2个单位,求平移后的图形。
解析:平移操作是将图形的每个点都按照相同的位移向某个方向移动。
向右平移3个单位意味着每个点的x坐标都增加3,向上平移2个单位意味着每个点的y坐标都增加2。
因此,平移后的三角形的顶点坐标分别为(3, 2)、(4, 2)、(3, 3)。
题目二:将一个矩形向左平移5个单位,向下平移4个单位,求平移后的图形。
解析:向左平移5个单位意味着每个点的x坐标都减少5,向下平移4个单位意味着每个点的y坐标都减少4。
因此,平移后的矩形的顶点坐标分别为(-5, -4)、(-5, -6)、(-3, -6)、(-3, -4)。
通过以上练习题,我们可以看到旋转与平移的基本原理。
旋转是将图形绕某个点旋转一定角度,而平移是将图形沿着某个方向移动一定距离。
在实际应用中,旋转与平移常常用于建筑设计、机械制造、计算机图形学等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平移与旋转的练习题
平移与旋转的练习题
平移和旋转是几何学中常见的基本操作,它们在解决各种问题时起着重要作用。
本文将给出一些关于平移和旋转的练习题,以帮助读者更好地理解和掌握这两
个概念。
一、平移练习题
1. 将一个正方形沿着横轴向右平移3个单位,再向上平移4个单位,最后沿着
纵轴向下平移2个单位。
求平移后正方形的坐标。
2. 已知点A(2, 3)和B(-1, 5),将线段AB沿着横轴向右平移5个单位,再向上平
移2个单位。
求平移后线段AB的两个端点坐标。
3. 将一个三角形ABC沿着纵轴向下平移3个单位,再向右平移4个单位。
已知
点A(1, 2),B(3, 4),C(5, 6),求平移后三角形ABC的三个顶点坐标。
二、旋转练习题
1. 将一个正方形绕原点逆时针旋转90°,再沿着横轴向右平移2个单位。
已知
正方形的一个顶点坐标为(1, 1),求旋转后正方形的四个顶点坐标。
2. 将一个矩形绕点(2, 3)逆时针旋转180°,再沿着纵轴向下平移4个单位。
已知
矩形的四个顶点坐标分别为A(1, 2),B(3, 2),C(3, 4),D(1, 4),求旋转后矩形的
四个顶点坐标。
3. 将一个三角形绕点(0, 0)逆时针旋转60°,再沿着横轴向右平移3个单位。
已
知三角形的三个顶点坐标为A(1, 1),B(2, 3),C(3, 2),求旋转后三角形的三个顶点坐标。
通过以上练习题,我们可以巩固平移和旋转的基本概念,并理解它们在几何学
中的应用。
平移是指将图形在平面上沿着指定的方向移动一定的距离,而旋转是指将图形围绕某一点旋转一定角度。
这两个操作在计算机图形学、机器人控制、航空航天等领域都有广泛的应用。
在解决实际问题时,我们需要根据具体情况确定平移和旋转的坐标变换公式,以便准确地描述和计算图形的位置和形状变化。
通过练习题的训练,我们可以提高对平移和旋转的理解和运用能力,为解决更复杂的几何问题打下基础。
需要注意的是,在进行平移和旋转操作时,我们要注意坐标系的选择和变换的顺序,以确保结果的准确性。
同时,我们还可以通过数学软件或几何绘图工具来验证和可视化平移和旋转的结果,加深对这两个概念的理解。
总之,通过练习平移和旋转的相关题目,我们可以提高对几何学中这两个重要操作的掌握程度,并且为解决实际问题打下坚实的基础。
希望读者能够通过这些练习题,加深对平移和旋转的理解,并能够在实际应用中灵活运用它们。
