三角形内外角典型练习题

合集下载

三角形内、外角平分线专题练习

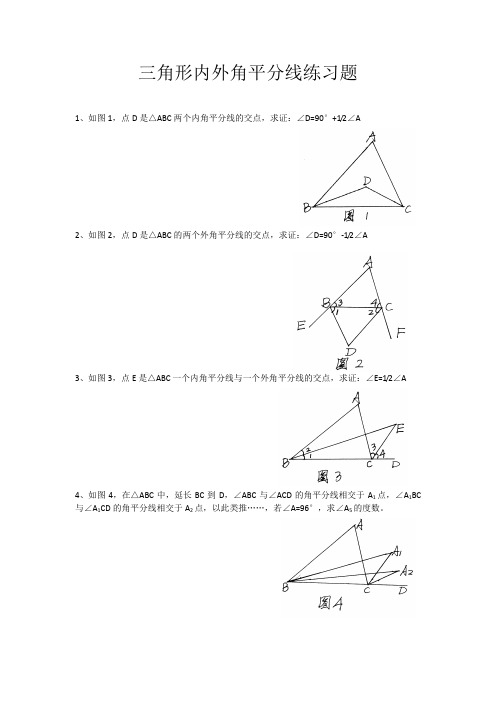
三角形内外角平分线练习题
1、如图1，点D是△ABC两个内角平分线的交点，求证：∠D=90°+1/2∠A
2、如图2，点D是△ABC的两个外角平分线的交点，求证：∠D=90°-1/2∠A
3、如图3，点E是△ABC一个内角平分线与一个外角平分线的交点，求证：∠E=1/2∠A
4、如图4，在△ABC中，延长BC到D，∠ABC与∠ACD的角平分线相交于A1点，∠A1BC 与∠A1CD的角平分线相交于A2点，以此类推……，若∠A=96°，求∠A5的度数。

5、如图5所示，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P，若∠BPC=40°，求∠CAP的度数。

6、如图6，在△ABC中，∠B＜∠C，AQ平分∠BAC，AQ交BC于点Q，点T是AQ延长线上的一点，TH⊥BC于点H，证明：∠HTA=1/2（∠C—∠B）。

7、如图7，D是△ABC的BC边上的一点，且∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数。

8、如图8，在直角坐标系中，点A、B分别在x轴、y轴正半轴上移动，
BE是∠ABO的外角平分线，BE的反向延长线与∠OAB的平分线相交于点C，试问∠ACB的大小是否发生变化？如果保持不变，请给出证明。

9、已知三角形的三个外角的度数之比2：3：4，则它的最大内角的度数为（）A．90°B．110°C．100°D．120°。

11.2.3三角形内角和与外角复习题

三角形内角和与外角练习题
1．已知：如图，E是△ABC的边CA延长线上一点，F是AB上一点，D点在BC 的延长线上．试证明∠1＜∠2．
2．如图，在△ABC中，AD，AE分别是△ABC的高线和角平分线．
（1）若∠B=30°，∠C=50°，求∠DAE的度数；
（2）若∠B=α，∠C=β，用含α，β的式子表示∠DAE．
3．已知如图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：_________；（2）仔细观察，在图2中“8字形”的个数：_________个；（3）在图2中，若∠D=40°，∠B=36°，试求∠P的度数；
4．如图，在△ABC中，已知∠B=60°，∠C=30°，AE是△ABC角平分线，求：（1）作BC边上的高AD；
（2）∠DAE的度数．
5．如图，在△ABC中，已知∠B=40°，∠C=60°，AE⊥BC于E，AD平分∠BAC，求∠DAE的度数．
6．如图，在△ABC中，D是BC上的一点，∠1=∠2，∠3=∠4，∠B=48°，求∠BAC 的度数．。

《三角形的内角和及外角定理》热点专题高分特训(含答案)

A.40° B.24° C.50° D.45° 答案：A 解题思路：
试题难度：三颗星知识点：三角形外角定理 8.如图，已知∠A=35°，∠B=20°，∠C=25°，则∠BDC 的度数为()
A.30° B.45° C.60° D.75° 答案：A 解题思路：
试题难度：三颗星知识点：角度的计算 6.如图，一个直角三角形纸片 ABC，剪去直角后，得到一个四边形 GBCH，则∠1+∠2=( )
A.90° B.180° C.240° D.270° 答案：D 解题思路：
试题难度：三颗星知识点：三角形的内角和 7.如图，在四边形 ABCD 中，∠A=62°，∠B=38°，∠BCD=140°，则∠D 的度数为) (
三角形的内角和及外角定理(人教版)
一、单选题(共 12 道，每道 8 分) 1.已知△ABC 中，∠B 是∠A 的 2 倍，∠C 比∠A 大 20°，则∠A 等于( ) A.30° B.40° C.60° D.80° 答案：B 解题思路：
试题难度：三颗星知识点：三角形内角和 2.如图，在△ABC 中，∠B=67°，∠C=33°，AD 是△ABC 的角平分线，则∠CAD 的度数为( )
试题难度：三颗星知识点：三角形的内角和 4.如图，在△ABC 中，∠B=∠C，FD⊥BC 于点 D，DE⊥AB 于点 E，∠AFD=158°，则∠EDF=( )
A.79° B.68° C.44° D.42° 答案：B 解题思路：
试题难度：三颗星知识点：角度的计算 5.如图，在△ABC 中，∠BAC=4∠1=4∠C，BD⊥CA 于点 D，则∠DBA=) (
A.40° B.45° C.50° D.55° 答案：A 解题思路：
试题难度：三颗星知识点：三角形的内角和 3.如图，在△ABC 中，AE 平分∠BAC，AD⊥BC 于点 D，若∠BAC=128°，∠C=36°，பைடு நூலகம்则∠DAE 的度数为( )

三角形的内角及外角和试题

6.如图3，下列说法错误的是（）
A、∠A ＜∠1 ＞∠2 B、∠2 ＞∠1 ＞∠AC、∠1 ＞∠2 ＞∠A D、无法确定
7.以下命题中正确的是（）
A、三角形的三个内角与三个外角的和为540°B、三角形的外角大于它的内角
C、三角形的外角都比锐角大D、三角形中的内角没有小于60°的
8.如图4，∠B =∠C，则∠ADC与∠AEB的大小关系（）
S阴＝1/2S矩形ABCD；
（2）在图3中，E、F分别为平行四边形ABCD的边AD、BC的中点，则S阴和S平行四边形ABCD之间满足的关系式为S阴＝1/2S平行四边形ABCD
（3）在图4中，E、F分别为任意四边形ABCD的边AD、BC的中点，则S阴和S四边形ABCD之间满足的关系式为S阴＝1/2S四边形ABCD；
解决问题：
（4）在图5中，E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点，并且图中阴影部分的面积为20平方米，求图中四个小三角形的面积和，即S1+S2+S3+S4= 2020．
5．探索发现：（1）如图1，在△ABC中，AD是BC边上的中线，若△ABC的面积为S，则△ACD的面积为1/2S
18．已知BD是△ABC的中线，△ABD的周长比△BCD的周长大2cm，若△ABC的周长为18cm，且AC=4cm，求AB和BC的长．
19．△ABC中，AB：AC=3：2，BC=AC+1，若△ABC的中线BD把△ABC的周长分成两部分的比是8：7，求边AB，AC的长．
20．若△ABC中两边长之比为2：3，三边都是整数且周长为18cm，求各边的长．
A∠ADC＞∠AEB B、∠ADC = ∠AEB C、∠ADC＜∠AEB D、大小关系不能确定

三角形内角与外角和典型例题

典例一：与角平分线相结合（利用整体思想和设未知数简化思路）
例1 如图1，已知△ABC 的∠ABC 和∠ACB 的内角平分线BD 、CE 相交于点O ，求证：∠BOC 和∠A 的关系。

结论：
例2 如图2，已知∠ABC 和∠ACB 的外角平分线BO 、CO 相交于点O ，探究∠BOC 与∠A 的关系。

结论：
例3 如图3，已知△ABC 中，∠ABC 的内角平分线BO 和∠ACB 的外角平分线CO ，相交于点O ，探究∠O 与∠A 的关系。

结论：
O
例3变式:在例3的条件下，继续画∠OBC 的内角平分线和∠BCO 的外角平分线交于O 1, 则∠O n =_______.
典例二：凹四边形问题（多种证法开拓思维）
例1.试证明∠BOC=∠A+∠B+∠C
典例三：切割问题（利用邻补角和整体思想）例1.
O
O 1
......
变式1:如图，△ABC 中，∠1+∠2=250°，则∠C 的度数为_______.
变式2:如图，将三角形改为四边形，∠C=80°，则∠1+∠2=_______.
变式3:如图的四边形，∠C=80°，∠D=60°则∠1+∠2=_______.
变式3:如图的四边形，∠C=m °，∠D=n °则∠1+∠2=_______
典例四：8字型问题（多种证法开拓思维）
例1 如图所示,已知∠1=∠2,∠3=∠4,∠C=32°,∠D=28°,求∠P 的度数.
4
3P
2
1D
C
B
A
例2.
典例五：折叠型。

三角形的内、外角和三线综合练习题

三角形的内、外角和三线综合练习题三角形的内、外角和三线综合练习题一．解答题（共30小题）1．（2010•玉溪）平面内的两条直线有相交和平行两种位置关系（1）如图a，若AB∥CD，点P在AB、CD外部，则有∠B=∠BOD，又因∠BOD是△POD的外角，故∠BOD=∠BPD+∠D，得∠BPD=∠B﹣∠D．将点P移到AB、CD内部，如图b，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；（2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需证明）（3）根据（2）的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．2．（2006•浙江）已知：如图，AB∥CD，直线EF分别交AB、CD于点E、F，∠BEF的平分线与∠DFE的平分线相交于点P．求证：∠P=90°．3．（2000•内蒙古）如图，已知在三角形ABC中，∠C=∠ABC=2∠A，BD是AC边上的高，求∠DBC的度数．4．（2013•响水县一模）探究与发现：探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？已知：如图1，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？已知：如图2，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．探究三：若将△ADC改为任意四边形ABCD呢？已知：如图3，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．探究四：若将上题中的四边形ABCD改为六边形ABCDEF（图4）呢？请直接写出∠P与∠A+∠B+∠E+∠F的数量关系：_________．5．如图，△ABC中，∠A=40°，∠B=72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE交CE于F，求∠CDF的度数．6．如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC=60°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．（1）将图1中的三角板绕点O顺时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；（2）将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为_________秒（直接写出结果）；（3）将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究∠AOM与∠NOC之间的数量关系，并说明理由．7．如图，AD、BC交于O点，且∠A=∠B，∠C=∠D．求证：AB∥CD．8．如图，已知点A，D，B在同一直线上，∠1=∠2，∠3=∠E．求证：DE∥BC．9．如图，∠D=∠1，∠E=∠2，DC⊥EC．求证：AD∥BE．10．如图，若∠CAB=∠CED+∠CDE，求证：AB∥CD．11．直线AB、CD被直线EF所截，EF分别交AB、CD于M，N，∠EMB=50°，MG平分∠BMF，MG交CD于G．（1）如图1，若AB∥CD，求∠1的度数．（2）如图2，若∠MNC=140°，求∠1的度数．12．如图，四边形ABCD中，∠B=∠D=90°，AE平分∠BAD，若AE∥CF，∠BCF=60°，请你求出∠DCF的度数．并说明你的理由．13．已知AB∥CD，直线l与AB、CD分别交于点E、F，点P是直线CD上的一个动点（点P不与F重合），点M 在EF上，且∠FMP=∠FPM，（1）如图1，当点P在射线FC上移动时，若∠AEF=60°，则∠FPM=_________；假设∠AEF=a，则∠FPM= _________；（2）如图2，当点P在射线FD上移动时，猜想∠FPM与∠AEF有怎样的数量关系？请你说明理由．14．如图（1）直线GC∥HD，EF交CG、HD于A、B，三条直线把EF右侧的平面分成①、②、③三个区域，（规定：直线上各点不属于任何区域）．将一个透明的直角三角尺放置在该图中，使得30°角（即∠P）的两边分别经过点A、B，当点P落在某个区域时，连接PA、PB，得到∠PBD、∠PAC两个角．（1）如图（1），当点P落在第②区域时，求∠PAC+∠PBD的度数；（2）如图（2），当点P落在第③区域时，∠PAC﹣∠PBD=_________度（3）如图（3），当点P落在第①区域时，直接写出∠PAC、∠PBD之间的等量关系．15．如图，直线a∥b，直线AC分别交a、b于点B、点C，直线AD交a于点D．若∠1=20°，∠2=65°，求∠3的度数．16．（1）如图（1），AB∥CD，点P在AB、CD外部，若∠B=40°，∠D=15°，则∠BPD=_________．（2）如图（2），AB∥CD，点P在AB、CD内部，则∠B，∠BPD，∠D之间有何数量关系？证明你的结论；（3）在图（2）中，将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M，如图（3），若∠BPD=90°，∠BMD=40°，求∠B+∠D的度数．17．（2012•樊城区模拟）下面是有关三角形内外角平分线的探究，阅读后按要求作答：探究1：如图（1），在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现：∠BOC=90°+∠A（不要求证明）．探究2：如图（2）中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的数量关系？请说明理由．探究3：如图（3）中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的数量关系？（只写结论，不需证明）．结论：_________．18．（2011•宜兴市二模）操作示例如图1，△ABC中，AD为BC边上的中线，则S△ABD=S△ADC．实践探究（1）在图2中，E、F分别为矩形ABCD的边AD、BC的中点，则S阴和S矩形ABCD之间满足的关系式为_________（2）在图3中，E、F分别为平行四边形ABCD的边AD、BC的中点，则S阴和S平行四边形ABCD之间满足的关系式为_________；（3）在图4中，E、F分别为任意四边形ABCD的边AD、BC的中点，则S阴和S四边形ABCD之间满足的关系式为_________；解决问题：（4）在图5中，E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点，并且图中阴影部分的面积为20平方米，求图中四个小三角形的面积和，即S1+S2+S3+S4=_________．19．如图，在△BCD中，BE平分∠DBC交CD于F，延长BC至G，CE平分∠DCG，且EC、DB的延长线交于A 点，若∠A=33°，∠DFE=63°．（1）求证：∠DFE=∠A+∠D+∠E；（2）求∠E的度数；（3）若在上图中作∠CBE与∠GCE的平分线交于E1，作∠CBE1与∠GCE1的平分线交于E2，作∠CBE2与∠GCE2的平分线于E3，以此类推，∠CBE n与∠GCE n的平分线交于E n+l，请用含有n的式子表示∠E n+l的度数（直接写答案）．20．已知：△ABC中，AD⊥BC，AE平分∠BAC，请根据题中所给的条件，解答下列问题：（1）如图1，若∠BAD=60°，∠EAD=15°，求∠ACB的度数．（2）通过以上的计算你发现∠EAD和∠ACB﹣∠B之间的关系应为：_________．（3）在图2的△ABC中，∠ACB＞90°，那么（2）中的结论仍然成立吗？为什么？21．如图（甲），D是△ABC的边BC的延长线上一点．∠ABC、∠ACD的平分线相交于P1．（1）若∠ABC=80°，∠ACB=40°，则∠P1的度数为_________；（2）若∠A=α，则∠P1的度数为_________；（用含α的代数式表示）（3）如图（乙），∠A=α，∠ABC、∠ACD的平分线相交于P1，∠P1BC、∠P1CD的平分线相交于P2，∠P2BC、∠P2CD的平分线相交于P3依此类推，则∠Pn的度数为_________（用n与α的代数式表示）22．在△ABC中，∠C＞∠B，AE是△ABC中∠BAC的平分线；（1）若AD是△ABC的BC边上的高，且∠B=30°，∠C=70°（如图1），求∠EAD的度数；（2）若F是AE上一点，且FG⊥BC，垂足为G（如图2），求证：；（3）若F是AE延长线上一点，且FG⊥BC，G为垂足（如图3），②中结论是否依然成立？请给出你的结论，并说明理由．23．已知，如图，在△ABC中，AD平分∠BAC，DE，DF分别是△ADC的高和角平分线（∠C＞∠DAC），若∠B=80°，∠C=40°．（1）求∠DAE的度数；（2）试猜想∠EDF、∠C与∠DAC有何关系？并说明理由．24．如图，在△ABC中，已知∠ACB=67°，BE是AC上的高，CD是AB上的高，F是BE和CD的交点，∠DCB=45°，求∠ABE和∠BFC的度数．25．如图，已知△ABC中，∠B=40°，∠C=62°，AD是BC边上的高，AE是∠BAC的平分线．求：∠DAE的度数．（写出推导过程）26．已知△ABC中，∠BAC=90°，∠C=30°，点D为BC边上一点，连接AD，作DE⊥AB于点E，DF⊥AC于点F．（1）若AD为△ABC的角平分线（如图1），图中∠1、∠2有何数量关系？为什么？（2）若AD为△ABC的高（如图2），求图中∠1、∠2的度数．27．如图，（1）在△ABC中，∠A=52°，∠ABC与∠ACB的角平分线交于D1，∠ABD1与∠ACD1的角平分线交于点D2，依此类推，∠ABD4与∠ACD4的角平分线交于点D5，则∠BD5C的度数是_________．（2）在△ABC中，∠ABC与∠ACB的角平分线交于D1，∠ABD1与∠ACD1的角平分线交于点D2，∠ABD2与∠ACD2的角平分线交于点D3，若∠BD3C的度数是n°，则∠A的度数是_________（用含n的代数式表示）．28．已知△ABC．（1）若∠BAC=40°，画∠BAC和外角∠ACD的角平分线相交于O1点（如图①），求∠BO1C的度数；（2）在（1）的条件下，再画∠O1BC和∠O1CD的角平分线相交于O2点（如图②），求∠BO2C的度数；（3）若∠BAC=n°，按上述规律继续画下去，请直接写出∠BO2012C的度数．29．（1）如图1，在锐角△ABC中，BD、CE分别是AC、AB边上的高线，BD与CE相交于点P，若已知∠A=50°，∠BPC的度数为多少；（2）如图2，在钝角△ABC中，BD、CE分别是AC、AB边上的高线，BD与EC的延长线相交于点P，若已知∠A=50°，则∠BPC的度数为多少；（3）在△ABC中，若∠A=α，请你探索AB、AC边上的高线（或延长线）相交所成的∠BPC的度数．（可以用含α的代数式表示）30．如图（1），△ABC中，AD是角平分线，AE⊥BC于点E．（1）．若∠C=80°，∠B=50°，求∠DAE的度数．（2）．若∠C＞∠B，试说明∠DAE=（∠C﹣∠B）．（3）．如图（2）若将点A在AD 上移动到A´处，A´E⊥BC于点E．此时∠DAE变成∠DA´E，（2）中的结论还正确吗？为什么？三角形的内、外角和三线综合练习题参考答案与试题解析一．解答题（共30小题）1．（2010•玉溪）平面内的两条直线有相交和平行两种位置关系（1）如图a，若AB∥CD，点P在AB、CD外部，则有∠B=∠BOD，又因∠BOD是△POD的外角，故∠BOD=∠BPD+∠D，得∠BPD=∠B﹣∠D．将点P移到AB、CD内部，如图b，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；（2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需证明）（3）根据（2）的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．分析：（1）延长BP交CD于E，根据两直线平行，内错角相等，求出∠PED=∠B，再利用三角形的一个外角等于和它不相邻的两个内角的和即可说明不成立，应为∠BPD=∠B+∠D；（2）作射线QP，根据三角形的外角性质可得；（3）根据三角形的外角性质，把角转化到四边形中再求解．解答：解：（1）不成立．结论是∠BPD=∠B+∠D延长BP交CD于点E，∵AB∥CD∴∠B=∠BED又∵∠BPD=∠BED+∠D，∴∠BPD=∠B+∠D．（2）结论：∠BPD=∠BQD+∠B+∠D．（3）连接EG并延长，根据三角形的外角性质，∠AGB=∠A+∠B+∠E，又∵∠AGB=∠CGF，在四边形CDFG中，∠CGF+∠C+∠D+∠F=360°，∴∠A+∠B+∠C+∠D+∠E+∠F=360°．2．（2006•浙江）已知：如图，AB∥CD，直线EF分别交AB、CD于点E、F，∠BEF的平分线与∠DFE的平分线相交于点P．求证：∠P=90°．分析：由AB∥CD，可知∠BEF与∠DFE互补，由角平分线的性质可得∠PEF+∠PFE=90°，由三角形内角和定理可得∠P=90度．解答：证明：∵AB∥CD，∴∠BEF+∠DFE=180°．又∵∠BEF的平分线与∠DFE的平分线相交于点P，∴∠PEF=∠BEF，∠PFE=∠DEF，∴∠PEF+∠PFE=（∠BEF+∠DFE）=90°．∵∠PEF+∠PFE+∠P=180°，∴∠P=90°．3．（2000•内蒙古）如图，已知在三角形ABC中，∠C=∠ABC=2∠A，BD是AC边上的高，求∠DBC的度数．分析：根据三角形的内角和定理与∠C=∠ABC=2∠A，即可求得△ABC三个内角的度数，再根据直角三角形的两个锐角互余求得∠DBC的度数．解答：解：∵∠C=∠ABC=2∠A，∴∠C+∠ABC+∠A=5∠A=180°，∴∠A=36°．则∠C=∠ABC=2∠A=72°．又BD是AC边上的高，则∠DBC=90°﹣∠C=18°．4．（2013•响水县一模）探究与发现：探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？已知：如图1，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？已知：如图2，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．探究三：若将△ADC改为任意四边形ABCD呢？已知：如图3，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．探究四：若将上题中的四边形ABCD改为六边形ABCDEF（图4）呢？请直接写出∠P与∠A+∠B+∠E+∠F的数量关系：∠P=（∠A+∠B+∠E+∠F）﹣180°．分析：探究一：根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD，∠ECD=∠A+∠ADC，再根据三角形内角和定理整理即可得解；探究二：根据角平分线的定义可得∠PDC=∠ADC，∠PCD=∠ACD，然后根据三角形内角和定理列式整理即可得解；探究三：根据四边形的内角和定理表示出∠ADC+∠BCD，然后同理探究二解答即可；探究四：根据六边形的内角和公式表示出∠ADC+∠BCD，然后同理探究二解答即可．解答：解：探究一：∵∠FDC=∠A+∠ACD，∠ECD=∠A+∠ADC，∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A；探究二：∵DP、CP分别平分∠ADC和∠ACD，∴∠PDC=∠ADC，∠PCD=∠ACD，∴∠DPC=180°﹣∠PDC﹣∠PCD，=180°﹣∠ADC﹣∠ACD，=180°﹣（∠ADC+∠ACD），=180°﹣（180°﹣∠A），=90°+∠A；探究三：∵DP、CP分别平分∠ADC和∠BCD，∴∠PDC=∠ADC，∠PCD=∠BCD，∴∠DPC=180°﹣∠PDC﹣∠PCD，=180°﹣∠ADC﹣∠BCD，=180°﹣（∠ADC+∠BCD），=180°﹣（360°﹣∠A﹣∠B），=（∠A+∠B）；探究四：六边形ABCDEF的内角和为：（6﹣2）•180°=720°，∵DP、CP分别平分∠ADC和∠ACD，∴∠P=∠ADC，∠PCD=∠ACD，∴∠P=180°﹣∠PDC﹣∠PCD，=180°﹣∠ADC﹣∠ACD，=180°﹣（∠ADC+∠ACD），=180°﹣（720°﹣∠A﹣∠B﹣∠E﹣∠F），=（∠A+∠B+∠E+∠F）﹣180°，即∠P=（∠A+∠B+∠E+∠F）﹣180°．5．如图，△ABC中，∠A=40°，∠B=72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE交CE于F，求∠CDF的度数．分析：首先根据三角形的内角和定理求得∠ACB的度数，再根据CE平分∠ACB求得∠ACE的度数，则根据三角形的外角的性质就可求得∠CED=∠A+∠ACE，再结合CD⊥AB，DF⊥CE就可求解．解答：解：∵∠A=40°，∠B=72°，∴∠ACB=180°﹣40°﹣72°=68°，∵CE平分∠ACB，∴∠ACE=∠BCE=34°，∴∠CED=∠A+∠ACE=74°，∴∠CDE=90°，DF⊥CE，∴∠CDF+∠ECD=∠ECD+∠CED=90°，∴∠CDF=74°．6．如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC=60°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．（1）将图1中的三角板绕点O顺时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；（2）将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为12或30秒（直接写出结果）；（3）将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究∠AOM与∠NOC之间的数量关系，并说明理由．分析：（1）由角的平分线的定义和等角的余角相等求解；（2）由∠BOC=120°可得∠AOC=60°，则∠AON=30°或∠NOR=30°，即顺时针旋转300°或120°时ON平分∠AOC，据此求解；（3）因为∠MON=90°，∠AOC=60°，所以∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON，然后作差即可．解答：解：（1）已知∠AOC=60°，∴∠BOC=120°，又OM平分∠BOC，∠COM=∠BOC=60°，∴∠CON=∠COM+90°=150°；（2）延长NO，∵∠BOC=120°∴∠AOC=60°，当直线ON恰好平分锐角∠AOC，∴∠AOD=∠COD=30°，即顺时针旋转300°时NO延长线平分∠AOC，由题意得，10t=300°∴t=30，当NO平分∠AOC，∴∠NOR=30°，即顺时针旋转120°时NO平分∠AOC，∴10t=120°，∴t=12，∴t=12或30；（3）∵∠MON=90°，∠AOC=60°，∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON，∴∠AOM﹣∠NOC=（90°﹣∠AON）﹣（60°﹣∠AON）=30°，所以∠AOM与∠NOC之间的数量关系为：∠AOM﹣∠NOC=30°．7．如图，AD、BC交于O点，且∠A=∠B，∠C=∠D．求证：AB∥CD．分析：证两直线平行，需证得两直线的内错角相等．结合已知，可用△AOB和△COD的外角∠AOC为媒介，证得∠A=∠D或∠B=∠C，由此来证得AB∥CD．解答：证明：∵∠AOC=∠A+∠B，∠A=∠B，∴∠AOC=2∠B．∵∠AOC=∠C+∠D，∠C=∠D，∴∠AOC=2∠C．∴∠C=∠B．∴AB∥CD．8．如图，已知点A，D，B在同一直线上，∠1=∠2，∠3=∠E．求证：DE∥BC．分析：由∠1=∠2，∠AOE=∠COD可证得∠CDO=∠E；再由∠3=∠E得∠CDO=∠3，即得DE∥BC（内错角相等，两直线平行）．解答：证明：∵∠1=∠2，∠AOE=∠COD（对顶角相等），∴在△AOE和△COD中，∠CDO=∠E（三角形内角和定理）；∵∠3=∠E，∴∠CDO=∠3，∴DE∥BC（内错角相等，两直线平行）．9．如图，∠D=∠1，∠E=∠2，DC⊥EC．求证：AD∥BE．分析：根据DC⊥EC，得∠1+∠2=90°，再结合已知条件，得∠D+∠1+∠E+∠2=180°，利用三角形的内角和定理就可求得∠A+∠B的值，从而证明结论．解答：证明：∵DC⊥EC，∴∠1+∠2=90°，又∠D=∠1，∠E=∠2，∴∠D+∠1+∠E+∠2=180°．根据三角形的内角和定理，得∠A+∠B=180°，∴AD∥BE．10．如图，若∠CAB=∠CED+∠CDE，求证：AB∥CD．分析：利用三角形的内角和定理得∠C+∠CED+∠CDE=180°，已知∠CAB=∠CED+∠CDE，所以∠C+∠CAB=180°，根据同旁内角互补，两直线平行可证AB∥CD．解答：证明：在△ECD中∵∠C+∠CED+∠CDE=180°（三角形内角和定理），又∵∠CAB=∠CED+∠CDE（已知），∴∠C+∠CAB=180°（等量代换），∴AB∥CD（同旁内角互补，两直线平行）．11．直线AB、CD被直线EF所截，EF分别交AB、CD于M，N，∠EMB=50°，MG平分∠BMF，MG交CD于G．（1）如图1，若AB∥CD，求∠1的度数．（2）如图2，若∠MNC=140°，求∠1的度数．分析：（1）根据两角互补及角平分线的性质可求出∠BMG的度数，再根据平行线的性质即可求解；（2）先根据两角互补及角平分线的性质可求出∠NMG的度数，再由三角形内角与外角的性质及∠MNC=140°即可求出∠1的度数．解答：解：（1）∵∠BMF+∠EMB=180°，∴∠BMF=180°﹣∠EMB，∵∠EMB=50°，∴∠BMF=180°50°=130°，（2分）∵MG平分∠BMF，∴∠BMG=∠GMN=∠BMF=65°，（4分）∵AB∥CD，∴∠1=∠BMG=65°；（5分）（2）∵∠MNC=∠1+∠GMN，∴∠1=∠MNC﹣∠GMN，（7分）∵∠MNC=140°，∠GMN=65°，∴∠1=140°﹣65°=75°．（8分）12．如图，四边形ABCD中，∠B=∠D=90°，AE平分∠BAD，若AE∥CF，∠BCF=60°，请你求出∠DCF的度数．并说明你的理由．解答：解：∠DCF=60°，理由如下：∵∠B=90°∴∠1+∠BCF=90°∵∠BCF=60°∴∠1=30度．∵AE∥CF∴∠2=∠1=30度∵AE平分∠BAD∴∠3=∠2=30度又∵∠D=90°∴∠3+∠4=90°∴∠4=60°∵AE∥CF∴∠DCF=∠4=60°．13．已知AB∥CD，直线l与AB、CD分别交于点E、F，点P是直线CD上的一个动点（点P不与F重合），点M 在EF上，且∠FMP=∠FPM，（1）如图1，当点P在射线FC上移动时，若∠AEF=60°，则∠FPM=30°；假设∠AEF=a，则∠FPM=α；（2）如图2，当点P在射线FD上移动时，猜想∠FPM与∠AEF有怎样的数量关系？请你说明理由．分析：（1）根据两直线平行，同旁内角互补以及△PFM的内角和是180°填空；（2）根据两直线平行，内错角相等和三角形的内角和为180度，易得∠FPM=90°﹣∠AEF．解答：解：（1）∵AB∥CD，∴∠AEF+∠MFP=180°．∵∠MFP+∠FMP+∠FPM=180°，∴∠FMP+∠FPM=∠AEF；∵∠FMP=∠FPM，∴∠FPM=∠AEF；∴若∠AEF=60°，则∠FPM=30°；若∠AEF=a，则∠FPM=α；（2）∠FPM=90°﹣∠AEF．理由：∵AB∥CD，∴∠AEF=∠MFP（两直线平行，内错角相等）．∵∠MFP+∠FMP+∠FPM=180°，∴∠FMP+∠FPM=180°﹣∠MFP=180°﹣∠AEF；∵∠FMP=∠FPM，∴∠FPM=90°﹣∠AEF．14．如图（1）直线GC∥HD，EF交CG、HD于A、B，三条直线把EF右侧的平面分成①、②、③三个区域，（规定：直线上各点不属于任何区域）．将一个透明的直角三角尺放置在该图中，使得30°角（即∠P）的两边分别经过点A、B，当点P落在某个区域时，连接PA、PB，得到∠PBD、∠PAC两个角．（1）如图（1），当点P落在第②区域时，求∠PAC+∠PBD的度数；（2）如图（2），当点P落在第③区域时，∠PAC﹣∠PBD=30度（3）如图（3），当点P落在第①区域时，直接写出∠PAC、∠PBD之间的等量关系．分析：解答：（1）过点P作PQ∥GC，则由平行线的性质求出∠PAC+∠PBD=∠P，从而得出答案．（2）由GC∥HD，得∠EAC=∠EBD，再由外角的性质得出∠PAE=∠P+∠ABP，从而得出∠PAC=∠PBD+∠P；（3）由GC∥HD，得∠1=∠PBD，再由外角的性质得出∠1=∠P+∠CAP，从而得出∠PBD=∠PAC+∠P．解：（1）过点P作PQ∥GC，∴∠PAC=∠APQ，∠BPQ=∠PBD，∴∠PAC+∠PBD=∠APQ+∠QPB，即∠PAC+∠PBD=∠P，∵∠P=30°，∴∠PAC+∠PBD=30°．（2）∵GC∥HD，∴∠EAC=∠EBD，∵∠PAE=∠P+∠ABP，∴∠PAC=∠PBD+∠P，∴∠PAC﹣∠PBD=30°；（3）∵GC∥HD，∴∠1=∠PBD，∵∠1=∠P+∠CAP，∴∠PBD=∠PAC+∠P，即∠PBD﹣∠PAC=∠P．∴∠P=30°．15．如图，直线a∥b，直线AC分别交a、b于点B、点C，直线AD交a于点D．若∠1=20°，∠2=65°，求∠3的度数．分析：根据两直线a∥b推知，内错角∠2=∠4；然后由三角形的外角性质及等量代换求得∠3的度数即可．解答：解：∵a∥b，∴∠2=∠4（两直线平行，内错角相等），又∵∠4=∠1+∠3（外角定理），∠1=20°，∠2=65°，∴∠3=∠2﹣∠1=45°，即∠3=45°．16．（1）如图（1），AB∥CD，点P在AB、CD外部，若∠B=40°，∠D=15°，则∠BPD=25°．（2）如图（2），AB∥CD，点P在AB、CD内部，则∠B，∠BPD，∠D之间有何数量关系？证明你的结论；（3）在图（2）中，将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M，如图（3），若∠BPD=90°，∠BMD=40°，求∠B+∠D的度数．分析：（1）由AB∥CD，∠B=40°，根据两直线平行，内错角相等，即可求得∠BOD的度数，又由三角形外角的性质，可求得∠BPD的度数；（2）首先过点P作PE∥AB，由AB∥CD，可得AB∥PE∥CD，然后由两直线平行，内错角相等，即可证得∠BPD=∠1+∠2=∠B+∠D；（3）首先延长BP交CD于点E，利用三角形外角的性质，即可求得∠B+∠D的度数．解答：解：（1）∵AB∥CD，∠B=40°，∴∠BOD=∠B=40°，∴∠P=∠BOD﹣∠D=40°﹣15°=25°．故答案为：25°；（2）∠BPD=∠B+∠D．证明：过点P作PE∥AB，∵AB∥CD，∴AB∥PE∥CD，∴∠1=∠B，∠2=∠D，∴∠BPD=∠1+∠2=∠B+∠D．（3）延长BP交CD于点E，∵∠1=∠BMD+∠B，∠BPD=∠1+∠D，∴∠BPD=∠BMD+∠B+∠D，∵∠BPD=90°，∠BMD=40°，∴∠B+∠D=∠BPD﹣∠BMD=90°﹣40°=50°．17．（2012•樊城区模拟）下面是有关三角形内外角平分线的探究，阅读后按要求作答：探究1：如图（1），在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现：∠BOC=90°+∠A（不要求证明）．探究2：如图（2）中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的数量关系？请说明理由．探究3：如图（3）中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的数量关系？（只写结论，不需证明）．结论：∠BOC=90°﹣∠A．分析：（1）根据提供的信息，根据三角形的一个外角等于与它不相邻的两个内角的和，用∠A与∠1表示出∠2，再利用∠O与∠1表示出∠2，然后整理即可得到∠BOC与∠O的关系；（2）根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB，然后再根据三角形的内角和定理列式整理即可得解．解答：解：（1）探究2结论：∠BOC=∠A，理由如下：∵BO和CO分别是∠ABC和∠ACD的角平分线，∴∠1=∠ABC，∠2=∠ACD，又∵∠ACD是△ABC的一外角，∴∠ACD=∠A+∠ABC，∴∠2=（∠A+∠ABC）=∠A+∠1，∵∠2是△BOC的一外角，∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A；（2）探究3：∠OBC=（∠A+∠ACB），∠OCB=（∠A+∠ABC），∠BOC=180°﹣∠0BC﹣∠OCB，=180°﹣（∠A+∠ACB）﹣（∠A+∠ABC），=180°﹣∠A﹣（∠A+∠ABC+∠ACB），结论∠BOC=90°﹣∠A．18．（2011•宜兴市二模）操作示例如图1，△ABC中，AD为BC边上的中线，则S△ABD=S△ADC．实践探究（1）在图2中，E、F分别为矩形ABCD的边AD、BC的中点，则S阴和S矩形ABCD之间满足的关系式为；（2）在图3中，E、F分别为平行四边形ABCD的边AD、BC的中点，则S阴和S平行四边形ABCD之间满足的关系式为；（3）在图4中，E、F分别为任意四边形ABCD的边AD、BC的中点，则S阴和S四边形ABCD之间满足的关系式为；；解决问题：（4）在图5中，E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点，并且图中阴影部分的面积为20平方米，求图中四个小三角形的面积和，即S1+S2+S3+S4=20．分析：（1）利用E、F分别为矩形ABCD的边AD、BC的中点，分别求得S阴和S矩形ABCD即可．（2）利用E、F分别为平行四边形ABCD的边AD、BC的中点，分别求则S阴和S平行四边形ABCD即可．（3）利用E、F分别为任意四边形ABCD的边AD、BC的中点，分别求得则S阴和S四边形ABCD即可．（4）先设空白处面积分别为：x、y、m、n由上得，，分别求得S1、S2、S3、S4．然后S1+S2+S3+S4=S阴即可．解答：解：（1）由E、F分别为矩形ABCD的边AD、BC的中点，得S阴=BF•CD=BC•CD，S矩形ABCD=BC•CD，所以；（2）同理可得；；（3）同理可得；；（4）设空白处面积分别为：x、y、m、n（见右图），由上得，，∴S1+x+S2+S3+y+S4=．S1+m+S4+S2+n+S3=，∴（S1+x+S2+S3+y+S4）+（S1+m+S4+S2+n+S3）=S四边形ABCD．∴（S1+x+S2+S3+y+S4）+（S1+m+S4+S2+n+S3）=S1+x+S2+n+S3+y+S4+m+S阴∴S1+S2+S3+S4=S阴=20．故答案分别为：（1）；（2）；（3）；（4）20．19．如图，在△BCD中，BE平分∠DBC交CD于F，延长BC至G，CE平分∠DCG，且EC、DB的延长线交于A 点，若∠A=33°，∠DFE=63°．（1）求证：∠DFE=∠A+∠D+∠E；（2）求∠E的度数；（3）若在上图中作∠CBE与∠GCE的平分线交于E1，作∠CBE1与∠GCE1的平分线交于E2，作∠CBE2与∠GCE2的平分线于E3，以此类推，∠CBEn与∠GCEn的平分线交于En+l，请用含有n的式子表示∠En+l的度数（直接写答案）．分析：（1）根据三角形的一个外角等于和它不相邻的两个内角的和，得出∠DCE=∠A+∠D，∠DFE=∠DCE+∠E，将第一式代入第二式即可得证；（2）根据角平分线及三角形外角的性质得出∠ECG=∠DCG=（∠D+∠DBC），∠ECG=∠E+∠EBC=∠E+∠DBC，则∠D=2∠E，再利用上题结论∠DFE=∠A+∠D+∠E，将已知条件代入，即可求出∠E的度数；（3）先根据角平分线及三角形外角的性质得出∠E1=∠E，同理得出∠E2=∠E1，则∠E2=∠E=∠E，由此得出规律∠E n+l=∠E．解答：（1）证明：∵∠DCE=∠A+∠D，∠DFE=∠DCE+∠E，∴∠DFE=∠A+∠D+∠E；（2）解：∵∠DCG=∠D+∠DBC，CE平分∠DCG，∴∠ECG=∠DCG=（∠D+∠DBC），∵BE平分∠DBC，∴∠EBC=∠DBC，∵∠ECG=∠E+∠EBC=∠E+∠DBC，∴∠E+∠DBC=（∠D+∠DBC），∴∠E=∠D，∴∠D=2∠E．∵∠DFE=63°，∠A=33°，∠DFE=∠A+∠D+∠E，∴∠D+∠E=∠DEF﹣∠A=63°﹣33°=30°，∴2∠E+∠E=30°，∴∠E=10°；（3）∵∠ECG=∠E+∠EBC，CE1平分∠ECG，∴∠E1CG=∠ECG=（∠E+∠EBC）．∵BE1平分∠EBC，∴∠E1BC=∠EBC．∵∠E1CG=∠E1+∠E1BC=∠E1+∠EBC，∴∠E1+∠EBC=（∠E+∠EBC），∴∠E1=∠E．同理：∠E2=∠E1，∴∠E2=∠E=∠E，∴∠E n+l=∠E．20．已知：△ABC中，AD⊥BC，AE平分∠BAC，请根据题中所给的条件，解答下列问题：（1）如图1，若∠BAD=60°，∠EAD=15°，求∠ACB的度数．（2）通过以上的计算你发现∠EAD和∠ACB﹣∠B之间的关系应为：∠ACB﹣∠B=2∠EAD．（3）在图2的△ABC中，∠ACB＞90°，那么（2）中的结论仍然成立吗？为什么？分析：（1）先求出∠BAE=∠BAD﹣∠EAD=45°，再根据角平分线的定义，得出∠BAC=90°，则根据三角形内角和定理得出∠ACB=90°﹣∠B，故求出∠B的度数即可．而在直角△ABD中，∠B=90°﹣∠BAD=30°；（2）由（1）的计算发现∠EAD和∠ACB﹣∠B之间的关系应为：∠ACB﹣∠B=2∠EAD；（3）先根据三角形内角和定理及垂直的定义，得出∠ACB﹣∠B=∠BAD﹣∠CAD，再由角平分线的定义得出结论∠ACB﹣∠B=2∠EAD．解答：解：（1）∵∠BAD=60°，∠EAD=15°，∴∠BAE=∠BAD﹣∠EAD=45°，∵AE平分∠BAC，∴∠BAC=2∠BAE=90°．∵AD⊥BC，∠BAD=60°，∴∠B=30°，∴∠ACB=90°﹣30°=60°；（2）∵（1）中∠EAD=15°，∠ACB﹣∠B=60°﹣30°=30°，发现∠ACB﹣∠B=2∠EAD，∴推测∠ACB﹣∠B=2∠EAD；（3）在图2的△ABC中，∠ACB＞90°，那么（2）中的结论仍然成立．理由如下：∵在△ABC中，AD⊥BC，AE平分∠BAC，∴∠ADC=∠ADB=90°，∠BAE=∠CAE，∴∠ACB﹣∠B=90°﹣∠CAD﹣（90°﹣∠BAD）=∠BAD﹣∠CAD，又∵∠BAD=∠BAE+∠EAD，∠CAD=∠CAE﹣∠EAD，∴∠ACB﹣∠B=2∠EAD．21．如图（甲），D是△ABC的边BC的延长线上一点．∠ABC、∠ACD的平分线相交于P1．（1）若∠ABC=80°，∠ACB=40°，则∠P1的度数为30°；（2）若∠A=α，则∠P1的度数为α；（用含α的代数式表示）（3）如图（乙），∠A=α，∠ABC、∠ACD的平分线相交于P1，∠P1BC、∠P1CD的平分线相交于P2，∠P2BC、∠P2CD的平分线相交于P3依此类推，则∠Pn的度数为（）nα（用n与α的代数式表示）分析：由∠P1CD=∠P1+∠P1BC，∠ACD=∠ABC+∠A，而P1B、P1C分别平分∠ABC和∠ACD，得到∠ACD=2∠P1CD，∠ABC=2∠P1BC，于是有∠A=2∠P1，同理可得∠P1=2∠P2，即∠A=22∠P2，因此找出规律．解答：解：∵P1B、P1C分别平分∠ABC和∠ACD，∴∠ACD=2∠P1CD，∠ABC=2∠P1BC，而∠P1CD=∠P1+∠P1BC，∠ACD=∠ABC+∠A，∴∠A=2∠P1，∴∠P1=∠A，（1）∵∠ABC=80°，∠ACB=40°，∴∠A=60°，∴∠P1=30°；（2）∵∠A=α，∴∠P1的度数为α；（3）同理可得∠P1=2∠P2，即∠A=22∠P2，∴∠A=2n∠P n，∴∠Pn=（）nα．故答案为：30°，α，（）nα．22．在△ABC中，∠C＞∠B，AE是△ABC中∠BAC的平分线；（1）若AD是△ABC的BC边上的高，且∠B=30°，∠C=70°（如图1），求∠EAD的度数；（2）若F是AE上一点，且FG⊥BC，垂足为G（如图2），求证：；（3）若F是AE延长线上一点，且FG⊥BC，G为垂足（如图3），②中结论是否依然成立？请给出你的结论，并说明理由．分析：（1）根据三角形内角和定理得∠A=180°﹣30°﹣70°=80°，再根据角平分线定义得∠EAC=×80°=40°，由AD是△ABC的BC边上的高，得∠ADC=90°，计算出∠DAC=90°﹣70°=20°，则∠EAD=∠EAC﹣∠DAC=40°﹣20°=20°；（2）根据三角形内角和定理得∠A=180°﹣∠B﹣∠C，再根据角平分线定义得∠EAC=（180°﹣∠B﹣∠C）=90°﹣（∠B+∠C），而∠DAC=90°﹣∠C，可计算得∠EAD=∠EAC﹣∠DAC=90°﹣（∠B+∠C）﹣90°﹣∠C=（∠C﹣∠B），然后利用平行线的性质得到结论；（3）与（2）证明方法一样．解答：（1）解：∵∠B=30°，∠C=70°，∴∠A=180°﹣30°﹣70°=80°，∵AE是△ABC中∠BAC的平分线，∴∠EAC=×80°=40°，∵AD是△ABC的BC边上的高，∴∠ADC=90°，∴∠DAC=90°﹣70°=20°，∴∠EAD=∠EAC﹣∠DAC=40°﹣20°=20°；（2）证明：过A点作高AD，如图，∠A=180°﹣∠B﹣∠C，∵AE是△ABC中∠BAC的平分线，∴∠EAC=（180°﹣∠B﹣∠C）=90°﹣（∠B+∠C），而∠DAC=90°﹣∠C，∴∠EAD=∠EAC﹣∠DAC=90°﹣（∠B+∠C）﹣90°﹣∠C=（∠C﹣∠B），∵FG⊥BC，∴∠EFG=∠EAD，∴∠EFG=（∠C﹣∠B）；（3）②中结论依然成立．理由如下：过A点作高AD，如图，在（2）中得到∠EAD=（∠C﹣∠B），∵FG⊥BC，∴∠EFG=∠EAD，∴∠EFG=（∠C﹣∠B）．23．已知，如图，在△ABC中，AD平分∠BAC，DE，DF分别是△ADC的高和角平分线（∠C＞∠DAC），若∠B=80°，∠C=40°．（1）求∠DAE的度数；（2）试猜想∠EDF、∠C与∠DAC有何关系？并说明理由．分析：（1）先根据三角形内角和定理求出∠BAC的度数，再根据三角形的角平分线的定义即可求出∠DAE 的度数；（2）先根据三角形内角和定理及角平分线的定义求出∠CDF=（180°﹣∠DAC﹣∠C），再由直角三角形两锐角互余得出∠CDE=90°﹣∠C，则根据∠EDF=∠CDF﹣∠CDE即可得出∠EDF=（∠C﹣∠DAC）．解答：解：（1）∵在△ABC中，∠B=80°，∠C=40°，∴∠BAC=180°﹣80°﹣40°=60°，∵AD平分∠BAC，∴∠DAE=∠BAC=30°；（2）∠EDF=（∠C﹣∠DAC）．理由如下：在△DAC中，∵∠ADC+∠DAC+∠C=180°，∴∠ADC=180°﹣∠DAC﹣∠C，∵DF平分∠ADC，∴∠CDF=∠ADC=（180°﹣∠DAC﹣∠C），∵DE是△ADC的高，∴∠CDE=90°﹣∠C，∴∠EDF=∠CDF﹣∠CDE=（180°﹣∠DAC﹣∠C）﹣（90°﹣∠C）=（∠C﹣∠DAC）．故∠EDF=（∠C﹣∠DAC）．24．如图，在△ABC中，已知∠ACB=67°，BE是AC上的高，CD是AB上的高，F是BE和CD的交点，∠DCB=45°，求∠ABE和∠BFC的度数．分析：根据三角形高的定义得到∠CDB=90°，∠BEC=90°，先利用三角形内角和定理得∠DBC=180°﹣90°﹣45°=45°，∠EBC=180°﹣∠ECB﹣∠BEC=180°﹣67°﹣90°=23°，则∠ABE=∠ABC﹣∠EBC=45°﹣23°=22°，然后利用三角形外角性质可计算∠BFC=22°+90°=112°．解答：解：∵CD是AB上的高，∴∠CDB=90°，∵∠CDB+∠DBC+∠DCB=180°，∴∠DBC=180°﹣90°﹣45°=45°，∵BE是AC上的高，∴∠BEC=90°，∴∠EBC=180°﹣∠ECB﹣∠BEC=180°﹣67°﹣90°=23°，∴∠ABE=∠ABC﹣∠EBC=45°﹣23°=22°；∵∠BFC=∠FDB+∠DBF，∴∠BFC=22°+90°=112°．25．如图，已知△ABC中，∠B=40°，∠C=62°，AD是BC边上的高，AE是∠BAC的平分线．求：∠DAE的度数．（写出推导过程）分析：根据三角形的内角和定理，可求得∠BAC的度数，由AE是∠BAC的平分线，可得∠EAC的度数；在直角△ADC中，可求出∠DAC的度数，所以∠DAE=∠EAC﹣∠DAC，即可得出．解答：解：∵△ABC中，∠B=40°，∠C=62°，∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣62°=78°，∵AE是∠BAC的平分线，∴∠EAC=∠BAC=39°，∵AD是BC边上的高，∴在直角△ADC中，∠DAC=90°﹣∠C=90°﹣62°=28°，∴∠DAE=∠EAC﹣∠DAC=39°﹣28°=11°．26．已知△ABC中，∠BAC=90°，∠C=30°，点D为BC边上一点，连接AD，作DE⊥AB于点E，DF⊥AC于点F．（1）若AD为△ABC的角平分线（如图1），图中∠1、∠2有何数量关系？为什么？（2）若AD为△ABC的高（如图2），求图中∠1、∠2的度数．分析：（1）根据已知得出∠1=∠DAC，∠2=∠DAB，以及AD平分∠BAC，即可得出∠1=∠2；（2）首先得出DE∥AC，再利用∠1=∠ADB﹣∠BDE=30°，进而求出∠FDC=180°﹣∠DFC﹣∠C=60°，即可求出∠2=∠ADC﹣∠FDC的度数．解答：解：（1）∠1=∠2，理由如下：∵DE⊥AB，DF⊥AC，∴∠DEB=∠DFC=∠BAC=90°，∴DE∥AC，DF∥AB，∴∠1=∠DAC，∠2=∠DAB，∵AD平分∠BAC，∴∠DAC=∠DAB，∴∠1=∠2；（2）∵DE⊥AB，DF⊥AC，AD⊥BC，∴∠ADB=∠ADC=∠DEB=∠DFC=∠BAC=90°，∴DE∥AC，∴∠BDE=∠C=30°，∴∠1=∠ADB﹣∠BDE=30°，∵∠FDC=180°﹣∠DFC﹣∠C=60°，∴∠2=∠ADC﹣∠FDC=60°．27．如图，（1）在△ABC中，∠A=52°，∠ABC与∠ACB的角平分线交于D1，∠ABD1与∠ACD1的角平分线交于点D2，依此类推，∠ABD4与∠ACD4的角平分线交于点D5，则∠BD5C的度数是56°．（2）在△ABC中，∠ABC与∠ACB的角平分线交于D1，∠ABD1与∠ACD1的角平分线交于点D2，∠ABD2与∠ACD2的角平分线交于点D3，若∠BD3C的度数是n°，则∠A的度数是（用含n的代数式表示）．分析：（1）根据角平分线的性质可得到：∠ABD1=∠CBD1=∠ABC，∠ACD1=∠BCD1=∠ACB，再根据三角形的内角和定理可得：∠BD1C的度数，再根据∠ABD1与∠ACD1的角平分线交于点D2，可得∠D2BC=∠ABC，∠D2CB=∠ACB，进而求出∠BD2C=180°﹣（∠ABC+∠ACB），以此类推可得到：∠BD5C=180°﹣（∠ABC+∠ACB），再次利用三角形内角和代入∠ABC+∠ACB=180°﹣∠A，即可求出答案．（2）根据（1）中所求即可得出答案．解答：解：（1）∵∠A=52°，∴∠ABC+∠ACB=180°﹣52°=128°，又∠ABC与∠ACB的角平分线交于D1，∴∠ABD1=∠CBD1=∠ABC，∠ACD1=∠BCD1=∠ACB，∴∠CBD1+∠BCD1=（∠ABC+∠ACB）=×128°=64°，∴∠BD1C=180°﹣（∠ABC+∠ACB）=180°﹣64°=116°，同理∠BD2C=180°﹣（∠ABC+∠ACB）=180°﹣96°=84°，依此类推，∠BD5C=180°﹣（∠ABC+∠ACB）=180°﹣124°=56°．故答案为：56°；（2）由（1）可得：∠BD3C=180°﹣（∠ABC+∠ACB）=180°﹣（180°﹣∠A）=n°．解得：∠A=．故答案为：．28．已知△ABC．（1）若∠BAC=40°，画∠BAC和外角∠ACD的角平分线相交于O1点（如图①），求∠BO1C的度数；（2）在（1）的条件下，再画∠O1BC和∠O1CD的角平分线相交于O2点（如图②），求∠BO2C的度数；（3）若∠BAC=n°，按上述规律继续画下去，请直接写出∠BO2012C的度数．分析：由∠O1CD=∠O1+∠O1BC，∠ACD=∠ABC+∠A，而O1B、O1C分别平分∠ABC和∠ACD，得到∠ACD=2∠O1CD，∠ABC=2∠O1BC，于是有∠A=2∠O1，同理可得∠O1=2∠O2，即∠A=22∠O2，因此找出规律．解答：解：∵O1B、O1C分别平分∠ABC和∠ACD，∴∠ACD=2∠O1CD，∠ABC=2∠O1BC，而∠O1CD=∠O1+∠O1BC，∠ACD=∠ABC+∠A，∴∠A=2∠01=40°，∴∠O1=20°，同理可得∠O1=2∠O2，即∠A=22∠02=40°，∴∠O2=10°，∴∠A=2n∠A n，∴∠A n=n°×（）n．则∠BO2012C=0．29．（1）如图1，在锐角△ABC中，BD、CE分别是AC、AB边上的高线，BD与CE相交于点P，若已知∠A=50°，∠BPC的度数为多少；（2）如图2，在钝角△ABC中，BD、CE分别是AC、AB边上的高线，BD与EC的延长线相交于点P，若已知∠A=50°，则∠BPC的度数为多少；（3）在△ABC中，若∠A=α，请你探索AB、AC边上的高线（或延长线）相交所成的∠BPC的度数．（可以用含α的代数式表示）分析：（1）根据直角三角形两锐角互余求出∠ABD，再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解；（2）根据直角三角形两锐角互余可得∠A+∠ACE=90°，∠BPC+∠PCD=90°，再根据∠ACE和∠PCD是对顶角解答即可；。

三角形的外角性质专题精选习题

三角形一．选择题（共7小题）1．如图，已知BD是△ABC的中线，AB=5，BC=3，△ABD和△BCD的周长的差是（）A．2B．3C．6D．不能确定2．如图中，CD是△ABC的高的是（）A．B．C．D．3．如图，△ABC的角平分线AD，中线BE交于点O，则结论：①AO是△ABE的角平分线；②BO是△ABD的中线．其中（）A．①、②都正确B．①、②都不正确C．①正确②不正确D．①不正确，②正确4．下列说法：①三角形的高、中线、角平分线都是线段；②垂直于同一条直线的两条直线互相平行；③两条平行直线被第三条直线所截，同位角相等；④因为∠1=∠2，∠2=∠3，所以∠1=∠3．其中正确的是（）A．①③④B．②③④C．①②④D．③④5．直角三角形的三条角平分线交点在（）A．三角形外B．三角形内C．直角顶点处D．斜边上6．如图，AD是几个三角形的高？（）A．4B．5C．6D．77．在三边互不相等的三角形中，最长边的长为a，最长的中线的长为m，最长的高线的长为h，则（）A．a＞m＞h B．a＞h＞m C．m＞a＞h D．h＞m＞a二．填空题（共19小题）8．如图，在△ABC中，CD平分∠ACB，DE∥AC，DC∥EF，则与∠ACD相等角有_________个．9．如图所示，在△ABC中，BC边上的高是_________，AB边上的高是_________；在△BCE 中，BE边上的高是_________；EC边上的高是_________；在△ACD中，AC边上的高是_________；CD边上的高是_________．10．如图，在△ABC中，∠ACB=60°，∠BAC=75°，AD⊥BC于D，BE⊥AC于E，AD与BE交于H，则∠CHD=_________．11．（2006•威海）如图，△ABC面积为1，第一次操作：分别延长AB，BC，CA至点A1，B1，C1，使A1B=AB，B1C=BC，C1A=CA，顺次连接A1，B1，C1，得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2，B2，C2，得到△A2B2C2，…按此规律，要使得到的三角形的面积超过2006，最少经过_________次操作．12．（2012•呼和浩特）如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC=_________．13．（2011•徐州）如图AB∥CD，AB与DE交于点F，∠B=40°，∠D=70°，则∠E=_________．14．（2008•内江）在如图所示的四边形中，若去掉一个50°的角得到一个五边形，则∠1+∠2=_________度．15．（2006•吉林）如图，∠3=120°，则∠1﹣∠2=_________度．16．（2011•惠安县质检）将一副直角三角尺如图放置，已知AB∥DE，则∠AFC=_________度．17．如图，已知，∠1=∠2，∠3=∠4，∠B=66°，那么∠ADC=_________．18．如图所示，△ABC中，BD，CD分别平分∠ABC和外角∠ACE，若∠D﹦24°，则∠A﹦_________度．19．如图，∠A=α，∠B=40°，∠C=20°，∠O=4α，则α=_________度．20．如图是跷跷板示意图，支柱OC与地面垂直，点O是横板AB的中点，AB可以绕着点O上下转动，当A端落地时，∠OAC=20°，横板上下可转动的最大角度（即∠A′OA）是_________度．21．如图所示：∠1+∠2+∠3=_________度．22．如图，已知AC∥ED，∠C=28°，∠CBE=39°，则∠BED的度数是_________．23．如图，在△ABC中，∠ABC的外角平分线与∠ACB的外角平分线相交于点D，那么∠BDC与∠A 的数量关系是_________（直接写出结论）．24．如图所示，∠C的度数是_________．25．三角形三外角之比为3：4：5，则这个三角形最小内角为_________度．26．如图，在△ABC中，∠BAC=60°，线段BP、BE三等分∠ABC，线段CP、CE三等分∠ACB，那么∠BPE的度数是_________．三．解答题（共4小题）27．图①是一个三角形，分别连接这个三角形三边的中点得到图②；再分别连接图②中间小三角形三边的中点，得到图③．则图②有_________个三角形；图③有_________个三角形．28．如图，设n是大于1的自然数，从n×n的正方形的一个角上剪去一个1×1的方块将这个图形分成k 个面积都相等的三角形，试求k的最小值．29．如图，D、E分别是△ABC的AC、AB边上的点，BD、CE相交于点O，若S△OCD=2，S△OBE=3，S△OBC=4，求四边形ADOE的面积．30．一条直线截△ABC的边BC、CA、AB（或它们的延长线）于点D、E、F．求证：．。