【恒心】南京市、盐城市2014届高三年级第二次模拟考试(淮安三模)数学试题(含附加题)
【数学】江苏省南京市盐城市2014届高三模拟考试(理)

江苏省南京市盐城市2014届高三二模数学(理)试题一、填空题1.函数f(x)=ln x+1-x的定义域为.2.已知复数z1=-2+i,z2=a+2i(i为虚数单位,a∈R).若z1z2为实数,则a的值为.3.某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有.【解析】4.盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为.5.已知等差数列{a n }的公差d 不为0,且a 1,a 3,a 7成等比数列,则a 1d 的值为 .6.执行如图所示的流程图,则输出的k 的值为 .7.函数f (x )=A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0,0<φ<π)的图象如下图所示,则f (π3)的值为 .8.在平面直角坐标系xOy 中,双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线与抛物线y 2=4x 的准线相交于A ,B 两点.若△AOB 的面积为2,则双曲线的离心率为 .9.表面积为12π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为 .10.已知|OA →|=1,|OB →|=2,∠AOB =2π3,OC →=12OA →+14OB →,则OA →与OC →的夹角大小为 .11.在平面直角坐标系xOy 中,过点P (5,3)作直线l 与圆x 2+y 2=4相交于A ,B 两点,若OA⊥OB,则直线l的斜率为.12.已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),且.若直线y=kx与函数y=f(x)的图象恰有5个不同的公共点,则实数k的值为.考点:分段函数图像13.在△ABC中,点D在边BC上,且DC=2BD,AB∶AD∶AC=3∶k∶1,则实数k的取值范围为.14.设函数f(x)=ax+sin x+cos x.若函数f(x)的图象上存在不同的两点A,B,使得曲线y=f(x)在点A,B处的切线互相垂直,则实数a的取值范围为.二、解答题15.(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.(1)求证:AP∥平面BDE;(2)求证:BE⊥平面PAC.16.(本小题满分14分)在平面直角坐标系xOy 中,角α的顶点是坐标原点,始边为x 轴的正半轴,终边与单位圆O 交于点A (x 1 ,y 1 ),α∈(π4,π2).将角α终边绕原点按逆时针方向旋转π4,交单位圆于点B (x 2,y 2).(1)若x 1=35,求x 2;(2)过A ,B 作x 轴的垂线,垂足分别为C ,D ,记△AOC 及 △BOD 的面积分别为S 1,S 2,且S 1=43S 2,求tan α的值.17.(本小题满分14分)如图,经过村庄A 有两条夹角为60°的公路AB ,AC ,根据规划拟在两条公路之间的区域内建一工厂P ,分别在两条公路边上建两个仓库M 、N (异于村庄A ),要求PM =PN =MN =2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).解法五(变换法):。
11-江苏省南京市、淮安市、盐城市2014届高三第二次模拟考试报告
江苏省南京市、淮安市、盐城市2014届高三第二次模拟考试地理注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(综合题)两部分。
满分120分,考试用时100分钟。
2. 答题前,考生务必将自己的学校、班级、姓名写在密封线内。
[JZ]第Ⅰ卷(选择题共60分)一、选择题:共60分。
(一) 单项选择题:本大题共18小题,每小题2分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
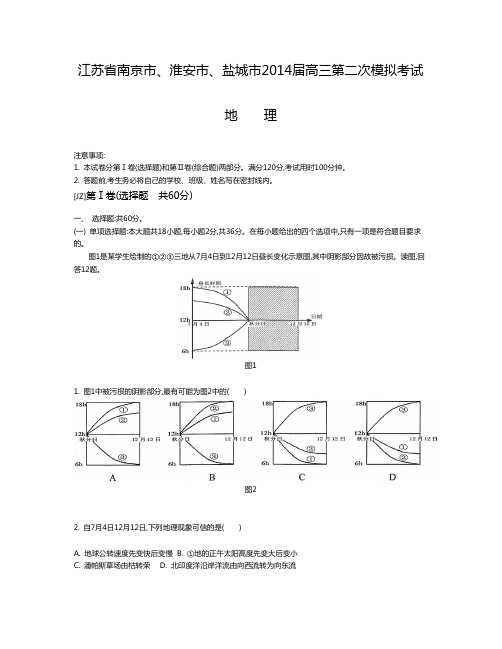
图1是某学生绘制的①②③三地从7月4日到12月12日昼长变化示意图,其中阴影部分因故被污损。
读图,回答12题。
图11. 图1中被污损的阴影部分,最有可能为图2中的( )图22. 自7月4日12月12日,下列地理现象可信的是( )A. 地球公转速度先变快后变慢B. ①地的正午太阳高度先变大后变小C. 潘帕斯草场由枯转荣D. 北印度洋沿岸洋流由向西流转为向东流图3图3为某山地等高线、等温线、雪线示意图。
读图,回答34题。
3. 该山地南坡属于( )A. 阳坡和背风坡B. 阴坡和背风坡C. 阴坡和迎风坡D. 阳坡和迎风坡4. 图中①②间分布最广的植被可能为( )A. 高山草甸B. 高寒荒漠C. 针阔混交林D. 高山针叶林位于澳大利亚西部沙漠中的波浪岩(图4),是一块巨大而完整的花岗岩体,大约在25亿年前形成。
经过日积月累的风雨冲刷和早晚剧烈的温差变化,渐渐地被侵蚀成波浪的形状。
读图,回答56题。
图4 图55. 图5为岩石圈物质循环示意图,上述波浪岩与图中数字表示的岩石类型一致的是( )A. ①B. ②C. ③D. ④6. 波浪岩的形成过程依次是( )A. 固结成岩—风化剥蚀—侵蚀搬运—地壳抬升B. 岩浆侵入—地壳抬升—风化剥蚀—侵蚀搬运C. 地壳抬升—侵蚀搬运—岩浆侵入—风化剥蚀D. 侵蚀搬运—岩浆侵入—地壳抬升—固结成岩图6为全球新能源分布示意图。
读图,回答78题。
图67. M表示的能源是( )A. 太阳能B. 潮汐能C. 风能D. 地热能8. 下列有关N能源的说法正确的是( )A. 一般位于板块交界处B. 近年来数量有减少趋势C. 主要分布在大气降水较多地区D. 对我国东部地区生产影响巨大图7是福建省2013年1月均温分布图(单位:℃)。
江苏省南京市、盐城市高三数学第二次模拟考试试题苏教版

南京市2014届高三年级第二次模拟考试 数 学 2014.03注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答题纸的密封线内.试题的答案写在答题..纸.上对应题目的答案空格内.考试结束后,交回答题纸. 参考公式:柱体的体积公式:V =Sh ,其中S 为柱体的底面积,h 为柱体的高.圆柱的侧面积公式:S 侧=2πRh ,其中R 为圆柱的底面半径,h 为圆柱的高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)1.函数f (x )=ln x +1-x 的定义域为 ▲ .2.已知复数z 1=-2+i ,z 2=a +2i(i 为虚数单位,a ∈R ).若z 1z 2为实数,则a 的值为 ▲ . 3.某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有 ▲ .4.盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为 ▲ .5.已知等差数列{a n }的公差d 不为0,且a 1,a 3,a 7成等比数列,则a 1d的值为6.执行如图所示的流程图,则输出的k 的值为 ▲ .7.函数f (x )=A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0,0<φ<π)的图象如下图所示,则f (π3)a(第3题图)(第6题图)的值为 ▲ .8.在平面直角坐标系xOy 中,双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线与抛物线y 2=4x 的准线相交于A ,B 两点.若△AOB 的面积为2,则双曲线的离心率为 ▲ .9.表面积为12π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为 ▲ .10.已知|OA →|=1,|OB →|=2,∠AOB =2π3,OC →=12OA →+14OB →,则OA →与OC →的夹角大小为 ▲ .11.在平面直角坐标系xOy 中,过点P (5,3)作直线l 与圆x 2+y 2=4相交于A ,B 两点,若OA ⊥OB ,则直线l 的斜率为 ▲ .12.已知f (x )是定义在R 上的奇函数,当0≤x ≤1时,f (x )=x 2,当x >1时,f (x +1)=f (x )+f (1),且. 若直线y =kx 与函数y =f (x )的图象恰有5个不同的公共点,则实数k 的值为 ▲ .13.在△ABC 中,点D 在边BC 上,且DC =2BD ,AB ∶AD ∶AC =3∶k ∶1,则实数k 的取值范围为 ▲ . 14.设函数f (x )=ax +sin x +cos x .若函数f (x )的图象上存在不同的两点A ,B ,使得曲线y =f (x )在点A ,B 处的切线互相垂直,则实数a 的取值范围为 ▲ .一、填空题:本大题共14小题,每小题5分,计70分.1.(0,1] 2.4 3.300 4.59 5.2 6.4 7.18. 5 9.12 10.60° 11.1或723 12.22-2 13.(53,73) 14.[-1,1]二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,平面PAB ⊥平面ABCD ,PA ⊥PB ,BP =BC ,E 为PC 的中点.(1)求证:AP ∥平面BDE ; (2)求证:BE ⊥平面PAC . 15.证:(1)设AC ∩BD =O ,连结OE .因为ABCD 为矩形,所以O 是AC 的中点.因为E 是PC 中点,所以OE ∥AP . …………………………………………4分 因为AP /⊂平面BDE ,OE ⊂平面BDE ,所以AP ∥平面BDE . …………………………………………6分 (2)因为平面PAB ⊥平面ABCD ,BC ⊥AB ,平面PAB ∩平面ABCD =AB ,所以BC ⊥平面PAB . ………………………………………8分 因为AP ⊂平面PAB ,所以BC ⊥PA .因为PB ⊥PA ,BC ∩PB =B ,BC ,PB ⊂平面PBC ,所以PA ⊥平面PBC . …………………………………………12分 因为BE ⊂平面PBC ,所以PA ⊥BE .因为BP =PC ,且E 为PC 中点,所以BE ⊥PC . 因为PA ∩PC =P ,PA ,PC ⊂平面PAC ,所以BE ⊥平面PAC . …………………………………………14分16.(本小题满分14分)在平面直角坐标系xOy 中,角α的顶点是坐标原点,始边为x 轴的正半轴,终边与单位圆O 交PBCDEA(第15题图)于点A (x 1 ,y 1 ),α∈(π4,π2).将角α终边绕原点按逆时针方向旋转π4,交单位圆于点B (x 2,y 2).(1)若x 1=35,求x 2;(2)过A ,B 作x 轴的垂线,垂足分别为C ,D ,记△AOC 及 △BOD 的面积分别为S 1,S 2,且S 1=43S 2,求tan α的值.16.解:(1)解法一:因为x 1=35,y 1>0,所以y 1=1-x 21=45.所以sin α=45,cos α=35.所以x 2=cos(α+π4)=cos αcos π4-sin αsin π4=-210. …………………………………6分解法二:因为x 1=35,y 1>0,所以y 1=1-x 21=45.A (35,45),则OA →=(35,45),…………2分OB →=(x 2,y 2), 因为OA →·OB →=|OA →||OB →|cos ∠AOB ,所以35x 2+45y 2= 2 2 ……4分又x 22+y 22=1,联立消去y 2得50 x 22-302x 2-7=0 解得x 2=-2 10或7210,又x 2<0,所以x 2=- 210. ………………………6分 解法三:因为x 1=35,y 1>0,所以y 1=1-x 21=45. 因此A (35,45),所以tan α=43.………2分所以tan(α+π4)=1+tan α1-tan α=-7,所以直线OB 的方程为y =-7x ……………4分由⎩⎨⎧y =-7x ,x 2+y 2=1.得x =± 2 10,又x 2<0,所以x 2=- 2 10. …………………6分(2)S 1=12sin αcos α=-14sin2α. …………………………………………8分因为α∈(π4,π2),所以α+π4∈(π2,3π4). 所以S 2=-12sin(α+π4)cos(α+π4)=-14sin(2α+π2)=-14cos2α. (10)分因为S 1=43S 2,所以sin2α=-43cos2α,即tan2α=-43. …………………………………12分所以2tan α1-tan 2α=-43,解得tan α=2或tan α=-12. 因为α∈(π4,π2),所以tan α=2.………14分17.(本小题满分14分)(第16题图)如图,经过村庄A 有两条夹角为60°的公路AB ,AC ,根据规划拟在两条公路之间的区域内建一工厂P ,分别在两条公路边上建两个仓库M 、N (异于村庄A ),要求PM =PN =MN =2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).解法一:设∠AMN =θ,在△AMN 中,MN sin60°=AMsin(120°-θ).因为MN =2,所以AM =433sin(120°-θ) . (2)分在△APM 中,cos ∠AMP =cos(60°+θ). …………………………………………6分AP 2=AM 2+MP 2-2 AM ·MP ·cos ∠AMP=163sin 2(120°-θ)+4-2×2×433sin(120°-θ) cos(60°+θ) ………………………………8分=163sin 2(θ+60°)-1633sin(θ+60°) cos(θ+60°)+4 =83[1-cos (2θ+120°)]-833 sin(2θ+120°)+4 =-83[3sin(2θ+120°)+cos (2θ+120°)]+203=203-163sin(2θ+150°),θ∈(0,120°). …………………………………………12分当且仅当2θ+150°=270°,即θ=60°时,AP 2取得最大值12,即AP 取得最大值2 3.答:设计∠AMN 为60 时,工厂产生的噪声对居民的影响最小.……………………………………14分 解法二(构造直角三角形): 设∠PMD =θ,在△PMD 中,∵PM =2,∴PD =2sin θ,MD =2cos θ. ……………2分 在△AMN 中,∠ANM =∠PMD =θ,∴MN sin60°=AMsin θ,AM =433sin θ,∴AD =433sin θ+2cos θ,(θ≥π2时,结论也正确).……………6分A PMNBC第17题图 D APMNBC(第17题图)AP 2=AD 2+PD 2=(433sin θ+2cos θ)2+(2sin θ)2=163sin 2θ+833sin θcos θ+4cos 2θ+4sin 2θ …………………………8分 =163·1-cos2θ2+433sin2θ+4=433sin2θ-83cos2θ+203=203+163sin(2θ-π6),θ∈(0,2π3). …………………………12分 当且仅当2θ-π6=π2,即θ=π3时,AP 2取得最大值12,即AP 取得最大值2 3.此时AM =AN =2,∠PAB =30° …………………………14分 解法三:设AM =x ,AN =y ,∠AMN =α.在△AMN 中,因为MN =2,∠MAN =60°, 所以MN 2=AM 2+AN 2-2 AM ·AN ·cos ∠MAN ,即x 2+y 2-2xy cos60°=x 2+y 2-xy =4. …………………………………………2分因为MN sin60°=AN sin α,即2sin60°=ysin α,所以sin α=34y ,cos α=x 2+4-y 22×2×x =x 2+(x 2-xy )4x =2x -y 4. …………………………………………6分cos ∠AMP =cos(α+60°)=12cos α-32sin α=12·2x -y 4-32·34y =x -2y4.……………………………8分在△AMP 中,AP 2=AM 2+PM 2-2 AM ·PM ·cos ∠AMP , 即AP 2=x 2+4-2×2×x ×x -2y4=x 2+4-x (x -2y )=4+2xy . (12)分因为x 2+y 2-xy =4,4+xy =x 2+y 2≥2xy ,即xy ≤4. 所以AP 2≤12,即AP ≤2 3.当且仅当x =y =2时,AP 取得最大值23.答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.………………………………14分 解法四(坐标法):以AB 所在的直线为x 轴,A 为坐标原点,建立直角坐标系. 设M (x 1,0),N (x 2,3x 2),P (x 0,y 0).∵MN =2,∴(x 1-x 2)2+3x 22=4. …………………………………………2分MN 的中点K (x 1+x 22,32x 2).∵△MNP 为正三角形,且MN =2.∴PK =3,PK ⊥MN . ∴PK 2=(x 0-x 1+x 22)2+(y 0-32x 2)2=3, k MN ·k PK =-1,即3x 2x 2-x 1·y 0-32x 2x 0-x 1+x 22=-1, …………………………………………6分∴y 0-32x 2=x 1-x 23x 2(x 0-x 1+x 22),∴(y 0-32x 2)2=(x 1-x 2)23x 22(x 0-x 1+x 22)2∴(1+(x 1-x 2)23x 22)(x 0-x 1+x 22)2=3,即43x 22(x 0-x 1+x 22)2=3,∴(x 0-x 1+x 22)2=94x 22.∵x 0-x 1+x 22>0 ∴x 0-x 1+x 22=32x 2,∴x 0=12x 1+2x 2,∴y 0=32x 1. …………………………………………8分∴AP 2=x 20+y 20=(2x 2+12x 1)2+34x 21=x 21+4x 22+2x 1x 2=4+4x 1x 2≤4+4×2=12, …………………………………………12分 即AP ≤23.答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.…………………………14分 解法五(变换法):以AB 所在的直线为x 轴,A 为坐标原点,建立直角坐标系. 设M (x 1,0),N (x 2,3x 2),P (x 0,y 0).∵MN =2,∴(x 1-x 2)2+3x 22=4.即x 21+4x 22=4+2x 1x 2∴4+2x 1x 2≥4x 1x 2,即x 1x 2≤2. …………………4分 ∵△MNP 为正三角形,且MN =2.∴PK =3,PK ⊥MN . MN →顺时针方向旋转60°后得到MP →.MP →=(x 0-x 1,y 0),MN →=(x 2-x 1, 3x 2). ∴⎣⎢⎢⎡⎦⎥⎥⎤12 32-32 12⎣⎢⎢⎡⎦⎥⎥⎤x 2-x 13x 2=⎣⎢⎡⎦⎥⎤x 0-x 1y 0,即x 0-x 1=12(x 2-x 1)+32x 2,y 0=-32(x 2-x 1)+32x 2.∴x 0=2x 2+12x 1,y 0=32x 1. …………………………………………8分∴AP 2=x 20+y 20=(2x 2+12x 1)2+34x 21=x 21+4x 22+2x 1x 2=4+4x 1x 2≤4+4×2=12, …………………………………………12分 即AP ≤23.答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.…………………………14分 解法六(几何法):由运动的相对性,可使△PMN 不动,点A 在运动.由于∠MAN =60°,∴点A 在以MN 为弦的一段圆弧(优弧)上,…………4分 设圆弧所在的圆的圆心为F ,半径为R ,由图形的几何性质知:AP 的最大值为PF +R . …………8分 在△AMN 中,由正弦定理知:MNsin60°=2R ,∴R =23, …………10分∴FM =FN =R =23,又PM =PN ,∴PF 是线段MN 的垂直平分线.设PF 与MN 交于E ,则FE 2=FM 2-ME 2=R 2-12=13.即FE =33,又PE =3. ……………………………12 ∴PF =43,∴AP 的最大值为PF +R =23.答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.…………………………14分 18. (本小题满分16分)在平面直角坐标系xOy 中,已知椭圆C ∶x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1,F 2,焦距为2,一条准线方程为x =2.P 为椭圆C 上一点,直线PF 1交椭圆C 于另一点Q . (1)求椭圆C 的方程;(2)若点P 的坐标为(0,b ),求过P ,Q ,F 2三点的圆的方程; (3)若F 1P →=λQF 1→,且λ∈[12,2],求OP →·OQ →的最大值.(1)解:由题意得⎩⎪⎨⎪⎧2c =2,a 2c=2, 解得c =1,a 2=2,所以b 2=a 2-c 2=1.所以椭圆的方程为x 22+y 2=1. …………………………………………2分 (2)因为P (0,1),F 1(-1,0),所以PF 1的方程为x -y +1=0.APMNBCFE由⎩⎪⎨⎪⎧x +y +1=0,x 22+y 2=1, 解得⎩⎨⎧x =0,y =1,或⎩⎨⎧x =-43,y =-13,所以点Q 的坐标为(-43,-13). ……………………4分 解法一:因为k PF 1·k PF 2=-1,所以△PQF 2为直角三角形. ……………………6分 因为QF 2的中点为(-16,-16),QF 2=523,所以圆的方程为(x +16)2+(y +16)2=2518. ……………………8分解法二:设过P ,Q ,F 2三点的圆为x 2+y 2+Dx +Ey +F =0, 则⎩⎨⎧1+E +F =0,1+D +F =0,179-43D -13E +F =0,解得⎩⎪⎨⎪⎧D =13,E =13,F =-43.所以圆的方程为x 2+y 2+13x +13y -43=0. …………………………………………8分(3)解法一:设P (x 1,y 1),Q (x 2,y 2),则F 1P →=(x 1+1,y 1),QF 1→=(-1-x 2,-y 2).因为F 1P →=λQF 1→,所以⎩⎨⎧x 1+1=λ(-1-x 2),y 1=-λy 2,即⎩⎨⎧x 1=-1-λ-λx 2,y 1=-λy 2,所以⎩⎪⎨⎪⎧(-1-λ-λx 2)22+λ2y 22=1,x 222+y 22=1,解得x 2=1-3λ2λ. …………………………………………12分所以OP →·OQ →=x 1x 2+y 1y 2=x 2(-1-λ-λx 2)-λy 22=-λ2x 22-(1+λ)x 2-λ =-λ2(1-3λ2λ)2-(1+λ)·1-3λ2λ-λ=74-58(λ+1λ) . …………………………………………14分 因为λ∈[12,2],所以λ+1λ≥2 λ·1λ=2,当且仅当λ=1λ,即λ=1时,取等号.所以OP →·OQ →≤12,即OP →·OQ →最大值为12. …………………………………………16分解法二:当PQ 斜率不存在时,在x 22+y 2=1中,令x =-1得y =± 2 2.所以11(1)(2OP OQ ⋅=-⨯-=,此时11,22λ⎡⎤=∈⎢⎥⎣⎦ (2)当PQ 斜率存在时,设为k ,则PQ 的方程是y =k (x +1),由⎩⎪⎨⎪⎧y =k (x +1),x 22+y 2=1.得(1+2k 2)x 2+4k 2x +2k 2-2=0, 韦达定理 22121222422==1212k k x x x x k k--+++,………………………………………4 设P (x 1,y 1),Q (x 2,y 2) ,则212121212(1)(1)OP OQ x x y y x x k x x ⋅=+=+++22212122222222222(1)()224(1)12122 61215122(12)2k x x k x x k k k k k k k k k k k =++++--=+++++-=⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯+=-<+分。
南京市盐城市届高三模拟考试数学试题及答案(理)

江苏省南京市盐城市2014届高三二模数学(理)试题一、填空题1.函数f(x)=ln x+1-x的定义域为.2.已知复数z1=-2+i,z2=a+2i(i为虚数单位,a∈R).若z1z2为实数,则a的值为.3.某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有.【解析】4.盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为.5.已知等差数列{a n }的公差d 不为0,且a 1,a 3,a 7成等比数列,则a 1d 的值为 .6.执行如图所示的流程图,则输出的k 的值为 .7.函数f (x )=A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0,0<φ<π)的图象如下图所示,则f (π3)的值为 .8.在平面直角坐标系xOy 中,双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线与抛物线y 2=4x 的准线相交于A ,B 两点.若△AOB 的面积为2,则双曲线的离心率为 .9.表面积为12π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为 .10.已知|OA →|=1,|OB →|=2,∠AOB =2π3,OC →=12OA →+14OB →,则OA →与OC →的夹角大小为 .11.在平面直角坐标系xOy 中,过点P (5,3)作直线l 与圆x 2+y 2=4相交于A ,B 两点,若OA⊥OB,则直线l的斜率为.12.已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),且.若直线y=kx与函数y=f(x)的图象恰有5个不同的公共点,则实数k的值为.考点:分段函数图像13.在△ABC中,点D在边BC上,且DC=2BD,AB∶AD∶AC=3∶k∶1,则实数k的取值范围为.14.设函数f(x)=ax+sin x+cos x.若函数f(x)的图象上存在不同的两点A,B,使得曲线y=f(x)在点A,B处的切线互相垂直,则实数a的取值范围为.二、解答题15.(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.(1)求证:AP∥平面BDE;(2)求证:BE⊥平面PAC.16.(本小题满分14分)在平面直角坐标系xOy 中,角α的顶点是坐标原点,始边为x 轴的正半轴,终边与单位圆O 交于点A (x 1 ,y 1 ),α∈(π4,π2).将角α终边绕原点按逆时针方向旋转π4,交单位圆于点B (x 2,y 2).(1)若x 1=35,求x 2;(2)过A ,B 作x 轴的垂线,垂足分别为C ,D ,记△AOC 及 △BOD 的面积分别为S 1,S 2,且S 1=43S 2,求tan α的值.17.(本小题满分14分)如图,经过村庄A 有两条夹角为60°的公路AB ,AC ,根据规划拟在两条公路之间的区域内建一工厂P ,分别在两条公路边上建两个仓库M 、N (异于村庄A ),要求PM =PN =MN =2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).解法五(变换法):答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.…………………14分 考点:利用正余弦定理解三角形 18.(本小题满分16分)在平面直角坐标系xOy 中,已知椭圆C ∶x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,焦距为2,一条准线方程为x =2.P 为椭圆C 上一点,直线PF 1交椭圆C 于另一点Q . (1)求椭圆C 的方程;(2)若点P 的坐标为(0,b ),求过P ,Q ,F 2三点的圆的方程; (3)若F 1P →=λQF 1→,且λ∈[12,2],求OP OQ 的最大值.解法二:当PQ斜率不存在时,19.(本小题满分16分)已知函数f (x )=ax +bx e x ,a ,b ∈R ,且a >0. (1)若a =2,b =1,求函数f (x )的极值; (2)设g (x )=a (x -1)e x -f (x ).① 当a =1时,对任意x ∈(0,+∞),都有g (x )≥1成立,求b 的最大值;② 设g′(x )为g (x )的导函数.若存在x >1,使g (x )+g′(x )=0成立,求ba 的取值范围.【解析】所以b ≤x 2-2x -xe x 在x ∈(0,+∞)上恒成立. …………………………8分 记h (x )=x 2-2x -xe x (x >0),则h ′(x )=(x -1)(2e x +1)e x.设u (x )=2x 3-3x 22x -1(x >1),则u ′(x )=8x [(x -34)2+316](2x -1)2.因为x >1,u ′(x )>0恒成立,所以u (x )在(1,+∞)是增函数,所以u (x )>u (1)=-1, 所以b a >-1,即ba 的取值范围为(-1,+∞). ………………………16分 解法二:因为g (x )=(ax -b x -2a )e x ,所以g ′(x )=(b x 2+ax -bx -a )e x .20. (本小题满分16分)已知数列{a n}的各项都为正数,且对任意n∈N*,a2n-1,a2n,a2n+1成等差数列,a2n,a2n+1,a2n+2成等比数列.(1)若a2=1,a5=3,求a1的值;(2)设a1<a2,求证:对任意n∈N*,且n≥2,都有a n+1a n<a2a1.a2n,a2n+1,a2n+2成等比数列”运用有两个方向,决定本题有两个解题方法.一是等量代换,求出数列通项公式后,比较大小.二是放缩,直接比较大小.由2a2n=a2n-1+a2n+1,①a 22n+1=a2n a2n+2.②;所以a 22n-1=又因为a 3a 2-a 2a 1=2a 2-a 1a 2-a 2a 1=2a 2a 1-a 12-a 22a 2a 1=-(a 1-a 2)2a 2a 1,21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共计20分.请在答.卷卡指定区域内.......作答.解答应写出文字说明、证明过程或演算步骤. 21.A .选修4—1:几何证明选讲如图,△ABC 为圆的内接三角形,AB =AC ,BD 为圆的弦,且BD ∥AC .过点A 作圆的切线与DB 的延长线交于点E ,AD 与BC 交于点F . (1)求证:四边形ACBE 为平行四边形; (2)若AE =6,BD =5,求线段CF 的长.21.B .选修4—2:矩阵与变换已知矩阵A =⎣⎢⎡⎦⎥⎤1 a -1 b 的一个特征值为2,其对应的一个特征向量为α=⎣⎢⎡⎦⎥⎤21.(1)求矩阵A ;(2)若A ⎣⎢⎡⎦⎥⎤x y =⎣⎢⎡⎦⎥⎤a b ,求x ,y 的值.【解析】21.C .选修4—4:坐标系与参数方程在极坐标系中,求曲线ρ=2cos θ关于直线θ=π4(ρ∈R )对称的曲线的极坐标方程.【解析】21. D .选修4—5:不等式选讲已知x ,y ∈R ,且|x +y |≤16,|x -y |≤14,求证:|x +5y |≤1. 【答案】详见解析 【解析】22.(本小题满分10分)某中学有4位学生申请A,B,C三所大学的自主招生.若每位学生只能申请其中一所大学,且申请其中任何一所大学是等可能的.(1)求恰有2人申请A大学的概率;(2)求被申请大学的个数X的概率分布列与数学期望E(X).23.(本小题满分10分)设f(n)是定义在N*上的增函数,f(4)=5,且满足:①任意n∈N*,f(n)∈Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).(1)求f(1),f(2),f(3)的值;(2)求f(n)的表达式.情形.因为f (2) f (k +12)=f (k +1)+f (k +12+2-1)=f (k +1)+f (k +32),。
江苏省南京市盐城市高三数学二模试题 文(含解析)苏教版

江苏省南京市盐城市2014届高三数学二模试题文(含解析)苏教版一、填空题1.【题文】函数f (x)=lnx+1-x的定义域为.【结束】2.【题文】已知复数z1=-2+i,z2=a+2i(i为虚数单位,a∈R).若z1z2为实数,则a的值为.【结束】3.【题文】某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有.【解析】【结束】4.【题文】盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为 .【结束】5.【题文】已知等差数列{an}的公差d 不为0,且a1,a3,a7成等比数列,则a1d的值为 .【结束】6.【题文】执行如图所示的流程图,则输出的k 的值为 .7.【题文】函数f(x)=Asin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0,0<φ<π)的图象如下图所示,则f(π3)的值为 .考点:三角函数解析式 【结束】8.【题文】在平面直角坐标系xOy 中,双曲线x2a2-y2b2=1(a >0,b >0)的两条渐近线与抛物线y2=4x 的准线相交于A ,B 两点.若△AOB 的面积为2,则双曲线的离心率为 .【结束】9.【题文】表面积为12π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为 .10.【题文】已知|OA →|=1,|OB →|=2,∠AOB =2π3,OC →=12OA →+14OB →,则OA →与OC →的夹角大小为 .【结束】11.【题文】在平面直角坐标系xOy 中,过点P(5,3)作直线l 与圆x2+y2=4相交于A ,B 两点,若OA ⊥OB ,则直线l 的斜率为 .【结束】12.【题文】已知f(x)是定义在R 上的奇函数,当0≤x ≤1时,f(x)=x2,当x >0时,f(x +1)=f(x)+f(1),且.若直线y =kx 与函数y =f(x)的图象恰有5个不同的公共点,则实数k 的值为 .02)2(2=++-x k x ,因为相切,所以,08)2(2=-+=∆k 又,0>k 所以.222-=k考点:分段函数图像 【结束】 13.【题文】在△ABC 中,点D 在边BC 上,且DC =2BD ,AB ∶AD ∶AC =3∶k ∶1,则实数k 的取值范围为 .【结束】 14.【题文】设函数f(x)=ax +sinx +cosx .若函数f(x)的图象上存在不同的两点A ,B ,使得曲线y =f(x)在点A ,B 处的切线互相垂直,则实数a 的取值范围为 .【结束】二、解答题15.【题文】(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB, BP=BC,E为PC的中点.(1)求证:AP∥平面BDE;(2)求证:BE⊥平面PAC.【结束】16.【题文】(本小题满分14分)在平面直角坐标系xOy 中,角α的顶点是坐标原点,始边为x 轴的正半轴,终边与单位圆O 交于点A(x1 ,y1 ),α∈(π4,π2).将角α终边绕原点按逆时针方向旋转π4,交单位圆于点B(x2,y2).(1)若x1=35,求x2;(2)过A ,B 作x 轴的垂线,垂足分别为C ,D ,记△AOC 及 △BOD 的面积分别为S1,S2,且S1=43S2,求tan α的值.解得x2=-210或7210,又x2<0,所以x2=-210.………………………6分【结束】17.【题文】(本小题满分14分)如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).∴PK2=(x0-x1+x22)2+(y0-32x2)2=3,解法五(变换法):【结束】18.【题文】(本小题满分16分)在平面直角坐标系xOy 中,已知椭圆C∶x2a2+y2b2=1(a >b >0)的左、右焦点分别为F1,F2,焦距为2,一条准线方程为x =2.P 为椭圆C 上一点,直线PF1交椭圆C 于另一点Q .(1)求椭圆C 的方程;(2)若点P 的坐标为(0,b),求过P ,Q ,F2三点的圆的方程;(3)若F1P →=λQF1→,且λ∈[12,2],求OP OQ ⋅的最大值.试题解析:(1)解:由题意得⎩⎪⎨⎪⎧2c =2,a2c =2, 解得c =1,a2=2,所以b2=a2-c2=1.【结束】19.【题文】(本小题满分16分)已知函数f(x)=ax +b xex ,a ,b ∈R ,且a >0. (1)若a =2,b =1,求函数f(x)的极值;(2)设g(x)=a(x -1)ex -f(x).① 当a =1时,对任意x ∈(0,+∞),都有g(x)≥1成立,求b 的最大值;② 设g′(x)为g(x)的导函数.若存在x >1,使g(x)+g′(x)=0成立,求b a的取值范围.当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数.整理得2ax3-3ax2-2bx+b=0.【结束】20.【题文】(本小题满分16分)已知数列{an}的各项都为正数,且对任意n∈N*,a2n -1,a2n ,a2n +1成等差数列,a2n ,a2n +1,a2n +2成等比数列.(1)若a2=1,a5=3,求a1的值;(2)设a1<a2,求证:对任意n∈N*,且n ≥2,都有an +1an <a2a1.a2n -2a2n ,n ≥2.③得:a2n -2a2n +a2na2n +2=2a2n ,即a2n -2 +a2n +2=2a2n .从而数列{a2n }是等差数列,所以a2n =a2 +(n -1)(a4-a2).由a4=(2a2-a1)2a2,可得a2n =[(a2-a1)n +a1]2a2.代入②解得解法二:因为a1,a2,a3成等差数列,a2,a3,a4成等比数列,a3,a4,a5成等差数列,所以a2n =a2 +(n -1)(a4-a2)=(a2-a1)n +a1a2.。
2014南京高三三模数学试题

南京市2014届高三年级第三次模拟考试数 学 2014.05注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答题纸内.试题的答案写在答题纸...上对应题目的答案空格内.考试结束后,交回答题纸.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)1.已知全集U =R ,集合A ={x |x ≤-2,x ∈R },B ={x |x <1,x ∈R },则(∁U A )∩B = ▲ . 2.已知(1+2i)2=a +b i(a ,b ∈R ,i 为虚数单位),则a +b = ▲ .3.某地区对两所高中学校进行学生体质状况抽测,甲校有学生800人,乙校有学生500人,现用分层抽样的方法在这1300名学生中抽取一个样本.已知在甲校抽取了48人,则在乙校应抽取学生人数为 ▲ .4.现有红心1,2,3和黑桃4,5共五张牌,从这五张牌中随机取2张牌,则所取2张牌均为红心的概率为 ▲ .5.执行右边的伪代码,输出的结果是 ▲ .6.已知抛物线y 2=2px 过点M (2,2),则点M 到抛物线焦点的距离为 ▲ . 7.已知tan α=-2,,且π2<α<π,则cos α+sin α= ▲ .8.已知m ,n 是不重合的两条直线,α,β是不重合的两个平面.下列命题: ①若α⊥β,m ⊥α,则m ∥β; ②若m ⊥α,m ⊥β,则α∥β; ③若m ∥α,m ⊥n ,则n ⊥α; ④若m ∥α,m β,则α∥β. 其中所有真命题的序号是 ▲ .(第5题图)9.将函数f (x )=sin(3x +π4)的图象向右平移π3个单位长度,得到函数y =g (x )的图象,则函数y =g (x )在[π3,2π3]上的最小值为 ▲ . 10.已知数列{a n }满足a n =a n -1-a n -2(n ≥3,n ∈N *),它的前n 项和为S n .若S 9=6,S 10=5,则a 1的值为 ▲ .11.已知函数f (x )=⎩⎨⎧x ,x ≥0,x 2,x <0,,则关于x 的不等式f (x 2)>f (3-2x )的解集是 ▲ .12.在R t △ABC 中,CA =CB =2,M ,N 是斜边AB 上的两个动点,且MN =2,则CM →·CN →的取值范围为 ▲ .13.在平面直角坐标系xOy 中,圆C 的方程为(x -1)2+y 2=4,P 为圆C 上一点.若存在一个定圆M ,过P 作圆M 的两条切线P A ,PB ,切点分别为A ,B ,当P 在圆C 上运动时,使得∠APB 恒为60︒,则圆M 的方程为 . 14.设二次函数f (x )=ax 2+bx +c (a ,b ,c 为常数)的导函数为f′(x ).对任意x ∈R ,不等式f (x )≥f′(x )恒成立,则b 2a 2+c2的最大值为 ▲ .二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且tan B tan A +1=2ca .(1)求B ;(2)若cos(C +π6)=13,求sin A 的值.16.(本小题满分14分)如图,在四棱锥P -ABCD 中,O 为AC 与BD 的交点,AB ⊥平面P AD ,△P AD 是正三角形, DC //AB ,DA =DC =2AB .(1)若点E 为棱P A 上一点,且OE ∥平面PBC ,求AEPE 的值;(2)求证:平面PBC ⊥平面PDC.PAB CDOE (第16题图)17.(本小题满分14分)某种树苗栽种时高度为A (A 为常数)米,栽种n 年后的高度记为f (n ).经研究发现f (n )近似地满足 f (n )=9A a +b t n ,其中t =2-23,a ,b 为常数,n ∈N ,f (0)=A .已知栽种3年后该树木的高度为栽种时高度的3倍.(1)栽种多少年后,该树木的高度是栽种时高度的8倍; (2)该树木在栽种后哪一年的增长高度最大.18.(本小题满分16分)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)过点P (-1,-1),c 为椭圆的半焦距,且c =2b .过点P 作两条互相垂直的直线l 1,l 2与椭圆C 分别交于另两点M ,N . (1)求椭圆C 的方程;(2)若直线l 1的斜率为-1,求△PMN 的面积; (3)若线段MN 的中点在x 轴上,求直线MN 的方程.19.(本小题满分16分)已知函数f (x )=ln x -mx (m ∈R ).(1)若曲线y =f (x )过点P (1,-1),求曲线y =f (x )在点P 处的切线方程; (2)求函数f (x )在区间[1,e]上的最大值;(3)若函数f (x )有两个不同的零点x 1,x 2,求证:x 1x 2>e 2.20.(本小题满分16分)已知a ,b 是不相等的正数,在a ,b 之间分别插入m 个正数a 1,a 2,…,a m 和正数b 1,b 2,…, b m ,使a ,a 1,a 2,…,a m ,b 是等差数列,a ,b 1,b 2,…,b m ,b 是等比数列. (1)若m =5,a 3b 3=54,求ba的值;(2)若b =λa (λ∈N *,λ≥2),如果存在n (n ∈N *,6≤n ≤m )使得a n -5=b n ,求λ的最小值及此时m 的值;(3)求证:a n >b n (n ∈N *,n ≤m ).。
2014江苏省南京市高三三模考试数学试题和答案
2014江苏省南京市高三三模考试数学试题和答案南京市2014届高三年级第三次模拟考试数学注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分。
本试卷满分为160分,考试时间为120分钟。
2.答题前,请务必将自己的姓名、学校、班级、学号写在答题纸内。
试题的答案写在答题纸上对应题目的答案空格内。
考试结束后,交回答题纸。
一、填空题(本大题共14小题,每小题5分,计70分。
不需写出解答过程,请把答案写在答题纸的指定位置上)1.已知全集U=R,集合A={x|x≤-2,x∈R},B={x|x<1,x∈R},则(∁U A)∩B= {-2.-1}。
2.已知(1+i)²=a+bi(a,b∈R,i为虚数单位),则a+b=2.3.某地区对XXX进行学生体质状况抽测,甲校有学生800人,乙校有学生500人,现用分层抽样的方法在这1300名学生中抽取一个样本。
已知在甲校抽取了48人,则在乙校应抽取学生人数为 30.4.现有红心1,2,3和黑桃4,5共五张牌,从这五张牌中随机取2张牌,则所取2张牌均为红心的概率为 3/10.5.执行右边的伪代码,输出的结果是 15.S←1I←3XXX≤200S←S×II←I+2EndWhilePrintI6.已知抛物线y²=2px过点M(2,2),则点M到抛物线焦点的距离为√2.7.已知tanα=-2,且-π/4<α<π/2,则cosα+sinα=-2√5/5.8.已知m,n是不重合的两条直线,α,β是不重合的两个平面。
下列命题:①若α⊥β,m⊥α,则m∥β;②若m⊥α,m⊥β,则α∥β;③若m∥α,XXX,则n⊥α;④若m∥α,m∥β,则α∥β。
其中所有真命题的序号是①、③。
9.将函数f(x)=sin(3x+π/3)的图象向右平移π/4个单位长度,得到函数y=g(x)的图象,则函数y=g(x)在[-π/4,5π/4]上的最小值为 -√3/2.10.已知数列{an}满足an=an-1-an-2(n≥3,n∈N*),它的前n项和为Sn。
江苏省南京市2014届高三第三次模拟考试数学试题
南京市2014届高三年级第三次模拟考试数 学 2014.05注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答题纸内.试题的答案写在答.题纸..上对应题目的答案空格内.考试结束后,交回答题纸. 一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)1.已知全集U =R ,集合A ={x |x ≤-2,x ∈R },B ={x |x <1,x ∈R },则(∁U A )∩B = ▲ . 2.已知(1+2i )2=a +b i(a ,b ∈R ,i 为虚数单位),则a +b = ▲ .3.某地区对两所高中学校进行学生体质状况抽测,甲校有学生800人,乙校有学生500人,现用分层抽样的方法在这1300名学生中抽取一个样本.已知在甲校抽取了48人,则在乙校应抽取学生人数为 ▲ .4.现有红心1,2,3和黑桃4,5共五张牌,从这五张牌中随机取2张牌,则所取2张牌均为红心的概率为 ▲ .5.执行右边的伪代码,输出的结果是 ▲ .6.已知抛物线y 2=2px 过点M (2,2),则点M 到抛物线焦点的距离为 ▲ . 7.已知tan α=-2,,且π2<α<π,则cos α+sin α= ▲ .8.已知m ,n 是不重合的两条直线,α,β是不重合的两个平面.下列命题: ①若α⊥β,m ⊥α,则m ∥β; ②若m ⊥α,m ⊥β,则α∥β; ③若m ∥α,m ⊥n ,则n ⊥α; ④若m ∥α,m β,则α∥β. 其中所有真命题的序号是 ▲ .(第5题图)9.将函数f (x )=sin(3x +π4)的图象向右平移π3个单位长度,得到函数y =g (x )的图象,则函数y=g (x )在[π3,2π3]上的最小值为 ▲ .10.已知数列{a n }满足a n =a n -1-a n -2(n ≥3,n ∈N *),它的前n 项和为S n .若S 9=6,S 10=5,则a 1的值为 ▲ .11.已知函数f (x )=⎩⎨⎧x ,x ≥0,x 2,x <0,,则关于x 的不等式f (x 2)>f (3-2x )的解集是 ▲ .12.在R t △ABC 中,CA =CB =2,M ,N 是斜边AB 上的两个动点,且MN =2,则CM →·CN →的取值范围为 ▲ .13.在平面直角坐标系xOy 中,圆C 的方程为(x -1)2+y 2=4,P 为圆C 上一点.若存在一个定圆M ,过P 作圆M 的两条切线PA ,PB ,切点分别为A ,B ,当P 在圆C 上运动时,使得∠APB 恒为60︒,则圆M 的方程为 . 14.设二次函数f (x )=ax 2+bx +c (a ,b ,c 为常数)的导函数为f′(x ).对任意x ∈R ,不等式f (x )≥f′(x )恒成立,则b 2a 2+c 2的最大值为 ▲ .二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且tan B tan A +1=2ca . (1)求B ;(2)若cos(C +π6)=13,求sin A 的值.16.(本小题满分14分)如图,在四棱锥P -ABCD 中,O 为AC 与BD 的交点,AB ⊥平面PAD ,△PAD 是正三角形, DC //AB ,DA =DC =2AB .(1)若点E 为棱PA 上一点,且OE ∥平面PBC ,求AEPE 的值; (2)求证:平面PBC ⊥平面PDC.PAB COE(第16题图)17.(本小题满分14分)某种树苗栽种时高度为A (A 为常数)米,栽种n 年后的高度记为f (n ).经研究发现f (n )近似地满足 f (n )=9Aa +b t n ,其中t =2-23,a ,b 为常数,n ∈N ,f (0)=A .已知栽种3年后该树木的高度为栽种时高度的3倍.(1)栽种多少年后,该树木的高度是栽种时高度的8倍; (2)该树木在栽种后哪一年的增长高度最大.18.(本小题满分16分)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)过点P (-1,-1),c 为椭圆的半焦距,且c =2b .过点P 作两条互相垂直的直线l 1,l 2与椭圆C 分别交于另两点M ,N . (1)求椭圆C 的方程;(2)若直线l 1的斜率为-1,求△PMN 的面积; (3)若线段MN 的中点在x 轴上,求直线MN 的方程.19.(本小题满分16分)已知函数f (x )=ln x -mx (m ∈R ).(1)若曲线y =f (x )过点P (1,-1),求曲线y =f (x )在点P 处的切线方程; (2)求函数f (x )在区间[1,e]上的最大值;(3)若函数f (x )有两个不同的零点x 1,x 2,求证:x 1x 2>e 2.20.(本小题满分16分)已知a ,b 是不相等的正数,在a ,b 之间分别插入m 个正数a 1,a 2,…,a m 和正数b 1,b 2,…,b m ,使a ,a 1,a 2,…,a m ,b 是等差数列,a ,b 1,b 2,…,b m ,b 是等比数列. (1)若m =5,a 3b 3=54,求ba 的值;(2)若b =λa (λ∈N *,λ≥2),如果存在n (n ∈N *,6≤n ≤m )使得a n -5=b n ,求λ的最小值及此时m 的值;(3)求证:a n >b n (n ∈N *,n ≤m ).南京市2014届高三年级第三次模拟考试数学附加题 2014.05注意事项:1.附加题供选修物理的考生使用. 2.本试卷共40分,考试时间30分钟.3.答题前,考生务必将自己的姓名、学校、班级、学号写在答题纸内.试题的答案写在答题纸...上对应题目的答案空格内.考试结束后,交回答题纸. 21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共计20分.请在答.卷.卡指定区域内......作答.解答应写出文字说明、证明过程或演算步骤. A .选修4—1:几何证明选讲已知圆O 的内接△ABC 中,D 为BC 上一点,且△ADC 为正三角形,点E 为BC 的延长线上一点,AE 为圆O 的切线,求证:CD 2=BD ·EC .B .选修4—2:矩阵与变换已知矩阵A =⎣⎢⎡⎦⎥⎤a k 0 1 (k ≠0)的一个特征向量为α=⎣⎢⎡⎦⎥⎤ k -1,A 的逆矩阵A -1对应的变换将点 (3,1)变为点(1,1).求实数a ,k 的值.C .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知M 是椭圆x 24+y 212=1上在第一象限的点,A (2,0),B (0,23)是椭圆两个顶点,求四边形OAMB 的面积的最大值.D .选修4—5:不等式选讲(第21题A 图)已知a ,b ,c ∈R ,a 2+2b 2+3c 2=6,求a +b +c 的最大值.【必做题】第22题、第23题,每题10分,共计20分.请在答.卷卡指定区域内.......作答.解答应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)如图,在正四棱锥P -ABCD 中,PA =AB =2,点M ,N 分别在线段PA 和BD 上,BN =13BD .(1)若PM =13PA ,求证:MN ⊥AD ;(2)若二面角M -BD -A 的大小为π4,求线段MN 的长度.23.(本小题满分10分)已知非空有限实数集S 的所有非空子集依次记为S 1,S 2,S 3,……,集合S k 中所有元素的平均值记为b k .将所有b k 组成数组T :b 1,b 2,b 3,……,数组T 中所有数的平均值记为m (T ). (1)若S={1,2},求m (T );(2)若S ={a 1,a 2,…,a n }(n ∈N *,n ≥2),求m (T ).南京市2014届高三年级第三次模拟考试数学参考答案 2014.05说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续C··PM ABDN (第22题图)部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.一、填空题:本大题共14小题,每小题5分,计70分.1.(-2,1) 2.-7 3.30 4.310 5.11 6.52 7.55 8.② 9.-22 10.1 11.(-∞,-3)∪(1,3) 12.[32,2] 13.(x -1)2+y 2=1 14.22-2 二、解答题:15.(本小题满分14分)解:(1)由tan B tan A +1=2c a 及正弦定理,得sin B cos A cos B sin A +1=2sin Csin A ,………………………………………2分所以sin B cos A +cos B sin A cos B sin A =2sin C sin A ,即sin(A +B )cos B sin A =2sin C sin A ,则sin C cos B sin A =2sin C sin A . 因为在△ABC 中,sin A ≠0,sin C ≠0, 所以cos B=12. ………………………………………5分因为B ∈(0,π),所以B =π3. ………………………………………7分(2)因为0<C <2π3,所以π6<C +π6<5π6.因为cos(C +π6)=13,所以sin(C +π6)=223. ………………………………………10分所以sin A =sin(B +C )=sin(C +π3)=sin[(C +π6)+π6] ………………………………………12分=sin(C +π6)cos π6+cos(C +π6)sin π6=26+16. ………………………………………14分16.(本小题满分14分)证 (1)因为OE ∥平面PBC ,OE ⊂平面PAC ,平面PAC ∩平面PBC =PC ,所以OE ∥PC ,所以AO ∶OC =AE ∶EP . ………………………………………3分因为DC //AB ,DC =2AB ,所以AO ∶OC =AB ∶DC =1∶2.所以AE PE =12. ………………………………………6分(2)法一:取PC 的中点F ,连结FB ,FD . 因为△PAD 是正三角形,DA =DC ,所以DP =DC .因为F 为PC 的中点,所以DF ⊥PC . ………………………………………8分因为AB ⊥平面PAD ,所以AB ⊥PA ,AB ⊥AD ,AB ⊥PD . 因为DC //AB ,所以DC ⊥DP ,DC ⊥DA .设AB =a ,在等腰直角三角形PCD 中,DF =PF =2a . 在Rt △PAB 中,PB =5a .在直角梯形ABCD 中,BD =BC =5a .因为BC =PB =5a ,点F 为PC 的中点,所以PC ⊥FB . 在Rt △PFB 中,FB =3a .在△FDB 中,由DF =2a ,FB =3a ,BD =5a ,可知DF 2+FB 2=BD 2,所以FB ⊥DF .………………………………………12分由DF ⊥PC ,DF ⊥FB ,PC ∩FB =F ,PC 、FB ⊂平面PBC ,所以DF ⊥平面PBC .又DF ⊂平面PCD ,所以平面PBC ⊥平面PDC . ………………………………………14分 法二:取PD ,PC 的中点,分别为M ,F ,连结AM ,FB ,MF , 所以MF ∥DC ,MF =12DC .因为DC //AB ,AB =12DC ,所以MF ∥AB ,MF =AB ,即四边形ABFM 为平行四边形,所以AM ∥BF . ………………………………………8分在正三角形PAD 中,M 为PD 中点,所以AM ⊥PD . 因为AB ⊥平面PAD ,所以AB ⊥AM .又因为DC //AB ,所以DC ⊥AM . 因为BF //AM ,所以BF ⊥PD ,BF ⊥CD .又因为PD ∩DC =D ,PD 、DC ⊂平面PCD ,所以BF ⊥平面PCD .……………………………12分因为BF ⊂平面PBC ,所以平面PBC ⊥平面PDC . ………………………………………14分17.(本小题满分14分)解:(1)由题意知f (0)=A ,f (3)=3A .所以⎩⎪⎨⎪⎧9Aa +b =A ,9A a +14b =3A ,解得a =1,b =8. ………………………………………4分 所以f (n )=9A1+8×tn ,其中t =2-23. 令f (n )=8A ,得9A 1+8×t n=8A ,解得t n =164, 即2-2n3=164,所以n =9.所以栽种9年后,该树木的高度是栽种时高度的8倍. ………………………………………6分 (2)由(1)知f (n )=9A1+8×t n .第n年的增长高度为△=f (n )-f (n -1)=9A1+8×t n-9A1+8×t n -1. ……………………………9分所以△=72At n -1(1-t )(1+8t n )(1+8t n -1)=72At n -1(1-t )1+8t n -1(t +1)+64t 2n -1=72A (1-t )1t n -1 +64t n+8(t +1) ………………………………………12分≤72A (1-t )264t n×1tn -1+8(t +1)=72A (1-t ) 8(1+t )2=9A (1-t )1+t . 当且仅当64t n=1tn -1,即2-2(2n -1)3=164时取等号,此时n =5.所以该树木栽种后第5年的增长高度最大. ………………………………………14分 18.(本小题满分16分)解:(1)由条件得1a 2+1b 2=1,且c 2=2b 2,所以a 2=3b 2,解得b 2=43,a 2=4.所以椭圆方程为:x 24+3y 24=1. ………………………………………3分 (2)设l 1方程为y +1=k (x +1),联立⎩⎨⎧y =kx +k -1,x 2+3y 2=4,消去y 得(1+3k 2)x 2+6k (k -1)x +3(k -1)2-4=0. 因为P 为(-1,1),解得M (-3k 2+6k +11+3k 2,3k 2+2k -11+3k 2).………………………………………5分当k ≠0时,用-1k代替k,得N(k 2-6k -3k 2+3,-k 2-2k +3k 2+3). ………………………………………7分将k =-1代入,得M (-2,0),N (1,1). 因为P (-1,-1),所以PM =2,PN =22, 所以△PMN的面积为12×2×22=2. ………………………………………9分(3)解法一:设M (x 1,y 1),N (x 2,y 2),则⎩⎨⎧x 12+3y 12=4,x 22+3y 22=4,两式相减得(x 1+x 2)(x 1-x 2)+3(y 1+y 2)(y 1-y 2)=0, 因为线段MN 的中点在x 轴上,所以y 1+y 2=0,从而可得(x 1+x 2)(x 1-x 2)=0.…………………12分若x 1+x 2=0,则N (-x 1,-y 1).因为PM ⊥PN ,所以PM →·PN →=0,得x 12+y 12=2.又因为x 12+3y 12=4,所以解得x 1=±1,所以M (-1,1),N (1,-1)或M (1,-1),N (-1, 1). 所以直线MN 的方程为y =-x . ………………………………………14分 若x 1-x 2=0,则N (x 1,-y 1),因为PM ⊥PN ,所以PM →·PN →=0,得y 12=(x 1+1)2+1. 又因为x 12+3y 12=4,所以解得x 1=-12或-1,经检验:x =-12满足条件,x =-1不满足条件. 综上,直线MN的方程为x +y =或x =-12. ………………………………………16分解法二:由(2)知,当k ≠0时,因为线段MN 的中点在x 轴上,所以3k 2+2k -11+3k 2=--k 2-2k +3k 2+3,化简得4k(k 2-4k-1)=,解得k=2±5. ………………………………………12分若k =2+5,则M (-12,52),N (-12,-52),此时直线MN 的方程为x =-12. 若k =2-5,则M (-12,-52),N (-12,52),此时直线MN 的方程为x =-12.…………14分当k =0时,M (1,-1),N (-1,1),满足题意,此时直线MN 的方程为x +y =0. 综上,直线MN的方程为x =-12或x +y =0. ………………………………………16分 19.(本小题满分16分)解:(1)因为点P (1,-1)在曲线y =f (x )上,所以-m =-1,解得m =1.因为f ′(x )=1x -1,所以切线的斜率为0,所以切线方程为y =-1.…………………………………3分 (2)因为f ′(x )=1x -m =1-mx x .①当m ≤0时, x ∈(1,e), f ′(x )>0,所以函数f (x )在(1,e )上单调递增,则f (x ) max =f (e )=1-me .②当1m ≥e ,即0<m ≤1e 时,x ∈(1,e),f ′(x )>0,所以函数f (x )在(1,e )上单调递增,则f (x )max =f(e )=1-me . ………………………………………5分③当1<1m <e ,即1e <m <1时,函数f (x )在 (1,1m )上单调递增,在(1m ,e )上单调递减,则f(x )max=f (1m)=-ln m -1. ………………………………………7分④当1m ≤1,即m ≥1时,x ∈(1,e), f ′(x )<0,函数f (x )在(1,e )上单调递减,则f (x ) max=f (1)=-m .………………………………………9分综上,①当m ≤1e 时,f (x )max =1-me ;②当1e <m <1时,f (x )max =-ln m -1; ③当m≥1时,f(x )max=-m . ………………………………………10分(3)不妨设x 1>x 2>0.因为f (x 1)=f (x 2)=0,所以ln x 1-mx 1=0,ln x 2-mx 2=0, 可得ln x 1+ln x 2=m (x 1+x 2),ln x 1-ln x 2=m (x 1-x 2).要证明x 1x 2>e 2,即证明ln x 1+ln x 2>2,也就是m (x 1+x 2)>2.因为m =ln x 1-ln x 2x 1-x 2,所以即证明ln x 1-ln x 2x 1-x 2>2x 1+x 2,即ln x 1x 2>2(x 1-x 2)x 1+x 2.………………………………………12分令x 1x 2=t ,则t >1,于是ln t >2(t -1)t +1.令ϕ(t )=ln t -2(t -1)t +1(t >1),则ϕ ′(t )=1t -4(t +1)2=(t -1)2t (t +1)2>0.故函数ϕ(t )在(1,+∞)上是增函数,所以ϕ(t )>ϕ(1)=0,即ln t >2(t -1)t +1成立.所以原不等式成立. ………………………………………16分 20.(本小题满分16分)解:(1)设等差数列的公差为d ,等比数列的公比为q ,则d =b -a6,q =6b a . a 3=a+3d=a +b 2,b 3=aq 3=ab . ………………………………………2分因为a 3b 3=54,所以2a -5ab +2b =0,解得ba =4或14. ………………………………………4分(2)因为λa =a +(m +1)d ,所以d =λ-1m +1a ,从而得a n =a +λ-1m +1a ×n .因为λa =a ×qm +1,所以q =λ1m +1,从而得b n =a ×λn m +1.因为a n -5=b n ,所以a +(λ-1)(n -5)m +1×a =a ×λnm +1.因为a >0,所以1+(λ-1)(n -5)m +1=λnm +1(*). ………………………………………6分因为λ,m ,n ∈N *,所以1+(λ-1)(n -5)m +1为有理数.要使(*)成立,则λn m +1必须为有理数.因为n ≤m ,所以n <m +1. 若λ=2,则λn m +1为无理数,不满足条件. 同理,λ=3不满足条件. ………………………………………8分当λ=4时,4n m +1=22n m +1.要使22nm +1为有理数,则2nm +1必须为整数.又因为n ≤m ,所以仅有2n =m +1满足条件. 所以1+3(n -5)m +1=2,从而解得n =15,m =29.综上,λ最小值为4,此时m 为29. ………………………………………10分(3)证法一:设c n >0,S n 为数列{c n }的前n 项的和. 先证:若{c n }为递增数列,则{S nn }为递增数列. 证明:当n ∈N *时,S n n <nb n +1n =b n +1.因为S n +1=S n +b n +1>S n +S n n =n +1n S n ,所以S n n <S n +1n +1,即数列{S nn }为递增数列.同理可证,若{c n }为递减数列,则{S nn }为递减数列. ………………………………………12分①当b >a 时,q >1.当n ∈N *,n ≤m 时,S m +1m +1>S nn .即aq (q m +1-1)q -1m +1>aq (q n -1)q -1n ,即aq m +1-a m +1>aq n -a n . 因为b =aq m +1,b n =aq n ,d =b -a m +1,所以d >b n -an ,即a +nd >b n ,即a n >b n . ②当b <a 时,0<q <1,当n ∈N *,n ≤m 时,S m +1m +1<S nn .即aq (q m +1-1)q -1m +1<aq (q n -1)q -1n . 因为0<q <1,所以aq m +1-a m +1>aq n -a n .以下同①.综上,a n>b n (n ∈N *,n ≤m ). ………………………………………16分证法二:设等差数列a ,a 1,a 2,…,a m ,b 的公差为d ,等比数列a ,b 1,b 2,…,b m ,b 的公比为q ,b =λa (λ>0,λ≠1).由题意,得d =λ-1m +1a ,q =aλ1m +1,所以a n =a +nd =a +λ-1m +1an ,b n =a λnm +1.要证a n >b n (n ∈N *,n ≤m ),只要证1+λ-1m +1n -λnm +1>0(λ>0,λ≠1,n ∈N *,n ≤m ).………………………………………12分构造函数f (x )=1+λ-1m +1x -λxm +1(λ>0,λ≠1,0<x <m +1),则f′(x )=λ-1m +1-1m +1λxm +1ln λ.令f′(x )=0,解得x 0=(m +1)log λλ-1ln λ.以下证明0<log λλ-1ln λ<1.不妨设λ>1,即证明1<λ-1ln λ<λ,即证明ln λ-λ+1<0,λln λ-λ+1>0. 设g (λ)=ln λ-λ+1,h (λ)=λln λ-λ+1(λ>1),则g′(λ)=1λ-1<0,h′(λ)=ln λ>0, 所以函数g (λ)=ln λ-λ+1(λ>1)为减函数,函数h (λ)=λln λ-λ+1(λ>1)为增函数. 所以g (λ)<g (1)=0,h (λ)>h (1)=0.所以1<λ-1lnλ<λ,从而0<logλλ-1lnλ<1,所以0<x0<m+1.………………………………………14分因为在(0,x0)上f′(x)>0,函数f(x)在(0,x0)上是增函数;因为在(x0,m+1)上f′(x)<0,函数f(x)在(x0,m+1)上是减函数.所以f(x)>min{f(0),f(m+1)}=0.所以a n>b n(n∈N*,n≤m).同理,当0<λ<1时,a n>b n(n∈N*,n≤m).………………………………………16分南京市2014届高三年级第三次模拟考试 数学附加题参考答案及评分标准 2014.05说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共计20分.请在答.卷.纸.指定区域内.....作答.解答应写出文字说明、证明过程或演算步骤. A .选修4—1:几何证明选讲 证:因为AE为圆O的切线,所以∠ABD=∠CAE . ………………………………………2分 因为△ACD 为等边三角形,所以∠ADC =∠ACD , 所以∠ADB=∠ECA,所以△ABD ∽△EAC . ………………………………………6分 所以ADBD=EC CA,即AD ·CA=BD ·EC . ………………………………………8分 因为△ACD 为等边三角形,所以AD =AC =CD , 所以CD 2=BD ·EC . ………………………………………10分 B .选修4—2:矩阵与变换解:设特征向量为α=⎣⎢⎡⎦⎥⎤k -1对应的特征值为λ,则⎣⎢⎡⎦⎥⎤a k 0 1 ⎣⎢⎡⎦⎥⎤ k -1=λ⎣⎢⎡⎦⎥⎤k -1,即⎩⎨⎧ak -k =λk , λ=1.因为k ≠0,所以a =2. ………………………………………5分因为A-1⎣⎡⎦⎤31=⎣⎡⎦⎤11,所以A ⎣⎡⎦⎤11=⎣⎡⎦⎤31,即⎣⎢⎡⎦⎥⎤2 k 0 1 ⎣⎡⎦⎤11=⎣⎡⎦⎤31,所以2+k =3,解得 k =1.综上,a =2,k =1. ………………………………………10分C .选修4—4:坐标系与参数方程 解:设M (2cos θ,23sin θ),θ∈(0,π2).由题知OA =2,OB =23, ………………………………………2分 所以四边形OAMB 的面积S =12×OA ×23sin θ+12×OB ×2cos θ =23sin θ+23cos θ=26sin(θ+π4). ………………………………………8分 所以当θ=π4时,四边形OAMB的面积的最大值为26. ………………………………………10分 D .选修4—5:不等式选讲解:由柯西不等式,得[a 2+(2b )2+(3c )2][12+(12)2+(13)2]≥(a +b +c )2.……………………………8分因为a 2+2b 2+3c 2=6,所以(a +b +c )2≤11, 所以-11≤a +b +c ≤11. 所以a +b +c的最大值为11,当且仅当a =2b =3c =61111. ………………………………10分 22.(本小题满分10分)证明:连接AC ,BD 交于点O ,以OA 为x 轴正方向,以OB 为y 轴正方向,OP 为z 轴建立空间直角坐标系.因为PA =AB =2,则A (1,0,0),B (0,1,0),D (0,-1,0),P (0,0,1). (1)由BN →=13BD →,得N (0,13,0),由PM →=13PA →,得M (13,0,23), 所以MN →=(-13,13,-23),AD →=(-1,-1,0).因为MN →·AD →=0.所以MN ⊥AD . ………………………………………4分(2)因为M 在PA 上,可设PM →=λPA →,得M (λ,0,1-λ). 所以BM →=(λ,-1,1-λ),BD →=(0,-2,0). 设平面MBD 的法向量n =(x ,y ,z ),由⎩⎪⎨⎪⎧n ·BD →=0,n ·BM →=0,得⎩⎨⎧-2y =0,λx -y +(1-λ)z =0,其中一组解为x =λ-1,y =0,z =λ,所以可取n =(λ-1,0,λ).………………………………8分因为平面ABD 的法向量为OP →=(0,0,1), 所以cos π4=|n ·OP →|n ||OP →||,即22=λ(λ-1)2+λ2,解得λ=12, 从而M (12,0,12),N (0,13,0), 所以MN=(12-0)2+(0-13)2+(12-0)2=226. ………………………………………10分 23.(本小题满分10分)解:(1)S ={1,2}的所有非空子集为:{1},{2},{1,2},所以数组T 为:1,2,32.因此m (T )=1+2+323=32. ………………………………………3分 (2)因为S ={a 1,a 2,…, a n },n ∈N *,n ≥2,所以m (T )=∑i =1na i +(12C 1n -1)∑i =1n a i +(13C 2n -1)∑i =1n a i +…+(1n C n -1n -1)∑i =1na i C n +C n +C n +…+C n=1+12C 1n -1+13C 2n -1+ (1)C n -1n -1C 1n +C 2n +C 3n +…+C nn∑i =1na i . ………………………………………6分又因为1k Ck -1n -1=1k ·(n -1)!(k -1) ! (n -k ) !=(n -1)!k ! (n -k ) !=1n ·n !(n -k ) ! k !=1nC kn ,……………………………8分所以m (T )=1n C 1n +1n C 2n +1n C 3n +…+1n C nn C 1n +C 2n +C 3n +…+C nn∑i =1n a i =1n ∑i =1na i .………………………………………10分。
南京市、盐城市2014届高三年级第二次模拟考试数学试题及答案
南京市2014届高三年级第二次模拟考试 数 学 2014.03 注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答题纸的密封线内.试题的答案写在答题纸上对应题目的答案空格内.考试结束后,交回答题纸. 参考公式:柱体的体积公式:V =Sh ,其中S 为柱体的底面积,h 为柱体的高.圆柱的侧面积公式:S 侧=2πRh ,其中R 为圆柱的底面半径,h 为圆柱的高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)1.函数f(x)=lnx +1-x 的定义域为 ▲ .2.已知复数z1=-2+i ,z2=a +2i(i 为虚数单位,a ∈R).若z1z2为实数,则a 的值为 ▲ .3.某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有 ▲ .4.盒中有3张分别标有1,2,3码,则两次抽取的卡片号码中至少有一个为偶数的概率为 5.已知等差数列{an}的公差d 不为0,且a1,a3,a76.执行如图所示的流程图,则输出的k 的值为 ▲ .7.函数f(x)=Asin (ωx +φ)(A ,ω,φ为常数,A >0,ω>0,0<φ8.在平面直角坐标系xOy 中,双曲线x2a2-y2b2=1(a >0,b A ,B 两点.若△AOB 的面积为2,则双曲线的离心率为 9.表面积为12π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为 ▲ .10.已知|OA →|=1,|OB →|=2,∠AOB =2π3,OC →=12OA →+14OB →,则OA →与OC →的夹角大小为 ▲ .11.在平面直角坐标系xOy 中,过点P(5,3)作直线l 与圆x2+y2=4相交于A ,B 两点,若OA ⊥OB ,则直线l 的斜率为 ▲ .12.已知f(x)是定义在R 上的奇函数,当0≤x ≤1时,f(x)=x2,当x >0时,f(x +1)=f(x)+f(1),且.a (第7题图)若直线y =kx 与函数y =f(x)的图象恰有5个不同的公共点,则实数k 的值为 ▲ . 13.在△ABC 中,点D 在边BC 上,且DC =2BD ,AB ∶AD ∶AC =3∶k ∶1,则实数k 的取值范围为 ▲ . 14.设函数f(x)=ax +sinx +cosx .若函数f(x)的图象上存在不同的两点A ,B ,使得曲线y =f(x)在点A ,B 处的切线互相垂直,则实数a 的取值范围为 ▲ .二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,平面PAB ⊥平面ABCD ,PA ⊥PB , BP =BC ,E 为PC 的中点.(1)求证:AP ∥平面BDE ; (2)求证:BE ⊥平面PAC .16.(本小题满分14分) 在平面直角坐标系xOy 中,角α的顶点是坐标原点,始边为x 轴的正半轴,终边与单位圆O 交 于点A(x1 ,y1 ),α∈(π4,π2).将角α终边绕原点按逆时针方向旋转π4,交单位圆于点B(x2,y2).(1)若x1=35,求x2;(2)过A ,B 作x 轴的垂线,垂足分别为C ,D ,记△AOC 及 △BOD 的面积分别为S1,S2,且S1=43S2,求tan α的值.17.(本小题满分14分)如图,经过村庄A 有两条夹角为60°的公路AB ,AC ,根据规划拟在两条公路之间的区域内建一工厂P ,分别在两条公路边上建两个仓库M 、N (异于村庄A),要求PM =PN =MN =2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).(第16题图) P NC PB C DE A (第15题图)18. (本小题满分16分)在平面直角坐标系xOy 中,已知椭圆C ∶x2a2+y2b2=1(a >b >0)的左、右焦点分别为F1,F2,焦距为2,一条准线方程为x =2.P 为椭圆C 上一点,直线PF1交椭圆C 于另一点Q . (1)求椭圆C 的方程;(2)若点P 的坐标为(0,b),求过P ,Q ,F2三点的圆的方程; (3)若F1P →=λQF1→,且λ∈[12,2],求OP →·OQ →的最大值.19.(本小题满分16分)已知函数f(x)=ax +bxex ,a ,b ∈R ,且a >0.(1)若a =2,b =1,求函数f(x)的极值; (2)设g(x)=a(x -1)ex -f(x).① 当a =1时,对任意x ∈(0,+∞),都有g(x)≥1成立,求b 的最大值;② 设g′(x)为g(x)的导函数.若存在x >1,使g(x)+g′(x)=0成立,求ba 的取值范围.20.(本小题满分16分)已知数列{an}的各项都为正数,且对任意n ∈N*,a2n -1,a2n ,a2n +1成等差数列, a2n ,a2n +1,a2n +2成等比数列. (1)若a2=1,a5=3,求a1的值;(2)设a1<a2,求证:对任意n ∈N*,且n ≥2,都有an +1an <a2a1.南京市2014届高三年级第二次模拟考试数学附加题 2014.03 注意事项:1.附加题供选修物理的考生使用.2.本试卷共40分,考试时间30分钟.3.答题前,考生务必将自己的姓名、学校、班级、学号写在答题纸的密封线内.试题的答案写在答题纸上对应题目的答案空格内.考试结束后,交回答题纸. 21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤. A .选修4—1:几何证明选讲如图,△ABC 为圆的内接三角形,AB =AC ,BD 为圆的弦,且BD ∥AC .过点A 作圆的切线与 DB 的延长线交于点E ,AD 与BC 交于点F . (1)求证:四边形ACBE 为平行四边形;(2)若AE =6,BD =5,求线段CF 的长.B .选修4—2:矩阵与变换已知矩阵A =⎣⎡⎦⎤1 a -1 b 的一个特征值为2,其对应的一个特征向量为α=⎣⎡⎦⎤21. (1)求矩阵A ;(2)若A ⎣⎡⎦⎤x y =⎣⎡⎦⎤ab ,求x ,y 的值.C .选修4—4:坐标系与参数方程在极坐标系中,求曲线ρ=2cosθ关于直线θ=π4(ρ∈R)对称的曲线的极坐标方程.D .选修4—5:不等式选讲已知x ,y ∈R ,且|x +y|≤16,|x -y|≤14,求证:|x +5y|≤1.【必做题】第22题、第23题,每题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)某中学有4位学生申请A ,B ,C 三所大学的自主招生.若每位学生只能申请其中一所大学,且申请其中任何一所大学是等可能的.(1)求恰有2人申请A 大学的概率;(2)求被申请大学的个数X 的概率分布列与数学期望E(X). 23.(本小题满分10分)设f(n)是定义在N*上的增函数,f(4)=5,且满足:①任意n ∈N*,f(n)∈Z ;②任意m ,n ∈N*,有f(m)f(n)=f(mn)+f(m +n -1).A EBC F D第21题A 图(1)求f(1),f(2),f(3)的值; (2)求f(n)的表达式.南京市2014届高三年级第二次模拟考试 数学参考答案 说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.一、填空题:本大题共14小题,每小题5分,计70分.1.(0,1] 2.4 3.300 4.59 5.2 6.4 7.18. 5 9.12 10.60° 11.1或723 12.22-2 13.(53,73) 14.[-1,1]二、解答题:15.证:(1)设AC ∩BD =O ,连结OE . 因为ABCD 为矩形,所以O 是AC 的中点.因为E 是PC 中点,所以OE ∥AP . …………………………………………4分 因为AP /⊂平面BDE ,OE ⊂平面BDE ,所以AP ∥平面BDE . …………………………………………6分 (2)因为平面PAB ⊥平面ABCD ,BC ⊥AB ,平面PAB ∩平面ABCD =AB ,所以BC ⊥平面PAB . …………………………………………8分 因为AP ⊂平面PAB ,所以BC ⊥PA .因为PB ⊥PA ,BC ∩PB =B ,BC ,PB ⊂平面PBC ,所以PA ⊥平面PBC . …………………………………………12分 因为BE ⊂平面PBC ,所以PA ⊥BE .因为BP =PC ,且E 为PC 中点,所以BE ⊥PC . 因为PA ∩PC =P ,PA ,PC ⊂平面PAC ,所以BE ⊥平面PAC . …………………………………………14分16.解:(1)因为x1=35,y1>0,所以y1=1-x 21=45.所以sin α=45,cos α=35. …………………………………………2分所以x2=cos(α+π4)=cos αcos π4-sin αsin π4=-210. …………………………………………6分(2)S1=12sin αcos α=-14sin2α.因为α∈(π4,π2),所以α+π4∈(π2,3π4).所以S2=-12sin (α+π4)cos (α+π4)=-14sin(2α+π2)=-14cos2α.…………………………………………8分因为S1=43S2,所以sin2α=-43cos2α,即tan2α=-43. (10)分所以2tanα1-tan2α=-43,解得tanα=2或tan α=-12.因为α∈(π4,π2),所以t anα=2. …………………………………………14分17.解法一:设∠AMN =θ,在△AMN 中,MN sin60°=AMsin(120°-θ).因为MN =2,所以AM =433sin(120°-θ) . ………………………………………2分在△APM 中,cos ∠AMP =cos(60°+θ). …………………………………………6分 AP2=AM2+MP2-2 AM·MP·cos ∠AMP =163sin2(120°-θ)+4-2×2×433 sin(120°-θ) cos(60°+θ) ………………………………8分 =163sin2(θ+60°)-1633sin(θ+60°) cos(θ+60°)+4 =83[1-cos (2θ+120°)]-833 sin(2θ+120°)+4 =-83[3sin(2θ+120°)+cos (2θ+120°)]+203=203-163sin(2θ+150°),θ∈(0,120°). …………………………………………12分 当且仅当2θ+150°=270°,即θ=60°时,AP2取得最大值12,即AP 取得最大值23.答:设计∠AMN 为60 时,工厂产生的噪声对居民的影响最小.……………………………………14分 解法二:设AM =x ,AN =y ,∠AMN =α. 在△AMN 中,因为MN =2,∠MAN =60°, 所以MN2=AM2+AN2-2 AM·AN·cos ∠MAN , 即x2+y2-2xycos60°=x2+y2-xy =4. …………………………………………2分 因为MN sin60°=AN sin α,即2sin60°=y sin α,所以sin α=34y ,cosα=x2+4-y22×2×x =x2+(x2-xy)4x =2x -y 4. …………………………………………6分cos ∠AMP =cos(α+60°)=12cos α-32sin α=12·2x -y 4-32·34y =x -2y4.……………………………8分在△AMP 中,AP2=AM2+PM2-2 AM·PM·cos ∠AMP ,即AP2=x2+4-2×2×x×x -2y4=x2+4-x(x -2y)=4+2xy .………………………………………12分因为x2+y2-xy =4,4+xy =x2+y2≥2xy ,即xy ≤4. 所以AP2≤12,即AP ≤23.当且仅当x =y =2时,AP 取得最大值23.答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.………………………………14分18.(1)解:由题意得⎩⎪⎨⎪⎧2c =2,a2c =2, 解得c =1,a2=2,所以b2=a2-c2=1.所以椭圆的方程为x22+y2=1. …………………………………………2分(2)因为P(0,1),F1(-1,0),所以PF1的方程为x -y +1=0.由⎩⎪⎨⎪⎧x +y +1=0,x22+y2=1, 解得⎩⎨⎧x =0,y =1,或⎩⎨⎧x =-43,y =-13,所以点Q 的坐标为(-43,-13). ……………………4分解法一:因为kPF 1·kPF 2=-1,所以△PQF2为直角三角形. ……………………6分 因为QF2的中点为(-16,-16),QF2=523,所以圆的方程为(x +16)2+(y +16)2=2518. ……………………8分解法二:设过P ,Q ,F2三点的圆为x2+y2+Dx +Ey +F =0,则⎩⎨⎧1+E +F =0,1+D +F =0,179-43D -13E +F =0, 解得⎩⎨⎧D =13,E =13,F =-43.所以圆的方程为x2+y2+13x +13y -43=0. …………………………………………8分(3)设P(x1,y1),Q(x2,y2),则F1P →=(x1+1,y1),QF1→=(-1-x2,-y2).因为F1P →=λQF1→,所以⎩⎨⎧x1+1=λ(-1-x2),y1=-λy2,即⎩⎨⎧x1=-1-λ-λx2,y1=-λy2,所以⎩⎪⎨⎪⎧(-1-λ-λx2)22+λ2y 22=1,x 222+y 22=1,解得x2=1-3λ2λ. …………………………………………12分所以OP →·OQ →=x1x2+y1y2=x2(-1-λ-λx2)-λy 22=-λ2x22-(1+λ)x2-λ =-λ2(1-3λ2λ)2-(1+λ)·1-3λ2λ-λ=74-58(λ+1λ) . …………………………………………14分因为λ∈[12,2],所以λ+1λ≥2 λ·1λ=2,当且仅当λ=1λ,即λ=1时,取等号.所以OP →·OQ →≤12,即OP →·OQ →最大值为12. …………………………………………16分19.解:(1)当a =2,b =1时,f (x)=(2+1x)ex ,定义域为(-∞,0)∪(0,+∞).所以f ′(x)=(x +1)(2x -1)x2ex . …………………………………………2分令f ′(x)=0,得x1=-1,x2=12,列表由表知f (x)的极大值是f (-1)=e -1,f (x)的极小值是f (12)=4e .……………………………………4分(2)① 因为g (x)=(ax -a)ex -f (x)=(ax -bx -2a)ex ,当a =1时,g (x)=(x -bx-2)ex .因为g (x)≥1在x ∈(0,+∞)上恒成立,所以b≤x2-2x -xex 在x ∈(0,+∞)上恒成立. …………………………………………8分记h(x)=x2-2x -xex (x >0),则h ′(x)=(x -1)(2ex +1)ex.当0<x <1时,h ′(x)<0,h(x)在(0,1)上是减函数;当x >1时,h ′(x)>0,h(x)在(1,+∞)上是增函数. 所以h(x)min =h(1)=-1-e -1.所以b 的最大值为-1-e -1. …………………………………………10分 ② 因为g (x)=(ax -b x -2a)ex ,所以g ′(x)=(b x2+ax -bx -a)ex .由g (x)+g ′(x)=0,得(ax -b x -2a)ex +(b x2+ax -bx-a)ex =0,整理得2ax3-3ax2-2bx +b =0.存在x >1,使g (x)+g ′(x)=0成立,等价于存在x >1,2ax3-3ax2-2bx +b =0成立. …………………………………………12分 因为a >0,所以b a =2x3-3x22x -1.设u(x)=2x3-3x22x -1(x >1),则u ′(x)=8x[(x -34)2+316](2x -1)2.因为x >1,u ′(x)>0恒成立,所以u(x)在(1,+∞)是增函数,所以u(x)>u(1)=-1,所以b a >-1,即ba 的取值范围为(-1,+∞). …………………………………………16分20.解:(1)因为a3,a4,a5成等差数列,设公差为d ,则a3=3-2d ,a4=3-d .因为a2,a3,a4成等比数列,所以a2=a 23a4=(3-2d)23-d . …………………………………………3分因为a2=1,所以(3-2d)2 3-d =1,解得d =2,或d =34.因为an >0,所以d =34.因为a1,a2,a3成等差数列,所以a1=2a2-a3=2-(3-2d)=12.…………………………………5分(2)证法一:因为a2n -1,a2n ,a2n +1成等差数列,a2n ,a2n +1,a2n +2成等比数列, 所以2a2n =a2n -1+a2n +1,① a 2 2n +1=a2na2n +2.② 所以a 2 2n -1=a2n -2a2n ,n ≥2.③所以a2n -2a2n +a2na2n +2=2a2n .因为an >0,所以a2n -2 +a2n +2=2a2n . …………………………………………7分 即数列{a2n }是等差数列.所以a2n =a2 +(n -1)(a4-a2).由a1,a2及a2n -1,a2n ,a2n +1是等差数列,a2n ,a2n +1,a2n +2是等比数列,可得a4=(2a2-a1)2a2.所以a2n =a2 +(n -1)(a4-a2)=(a2-a1)n +a1a2.所以a2n =[(a2-a1)n +a1]2a2.所以a2n +2=[(a2-a1)(n +1)+a1]2a2. (10)分从而a2n +1=a2na2n +2=[(a2-a1)n +a1][(a2-a1)(n +1)+a1]a2.所以a2n -1=[(a2-a1)(n -1)+a1][(a2-a1)n +a1]a2.①当n =2m ,m ∈N*时,an +1an -a2a1=[(a2-a1)m +a1][(a2-a1)(m +1)+a1]a2[(a2-a1)m +a1]2a2-a2a1=(a2-a1)(m +1)+a1(a2-a1)m +a1-a2a1=-m(a1-a2)2a1[(a2-a1)m +a1]<0. …………………………………………14分②当n =2m -1,m ∈N*,m ≥2时,an +1an -a2a1=[(a2-a1)m +a1]2a2[(a2-a1)(m -1)+a1][(a2-a1)m +a1]a2-a2a1=(a2-a1)m +a1(a2-a1)(m -1)+a1-a2a1=-(m -1)(a1-a2)2a1[(a2-a1)(m -1)+a1]<0.综上,对一切n ∈N*,n ≥2,有an +1an <a2a1. …………………………………………16分证法二:①若n 为奇数且n ≥3时,则an ,an +1,an +2成等差数列.因为an +2an +1-an +1an =an +2an -a2n +1an +1an =(2an +1-an)an -a2n +1an +1an =-(an +1-an)2an +1an ≤0,所以an +2an +1≤an +1an .②若n 为偶数且n ≥2时,则an ,an +1,an +2成等比数列,所以an +2an +1=an +1an .由①②可知,对任意n ≥2,n ∈N*,an +2an +1≤an +1an ≤…≤a3a2.又因为a3a2-a2a1=2a2-a1a2-a2a1=2a2a1-a12-a22a2a1=-(a1-a2)2a2a1,因为a1<a2,所以-(a1-a2)2a2a1<0,即a3a2<a2a1.综上,an +1an <a2a1.南京市2014届高三年级第二次模拟考试数学附加题参考答案及评分标准 2014.03说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,填空题不给中间分数.21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共计20分.请在答卷纸指定区域内作答.解答应写出文字说明、证明过程或演算步骤.A .选修4—1:几何证明选讲解:(1)因为AE 与圆相切于点A ,所以∠BAE =∠ACB .因为AB =AC ,所以∠ABC =∠ACB .所以∠ABC =∠BAE .所以AE ∥BC .因为BD ∥AC ,所以四边形ACBE 为平行四边形.…………………………………4分(2)因为AE 与圆相切于点A ,所以AE2=EB·(EB +BD),即62=EB·(EB +5),解得BE =4. 根据(1)有AC =BE =4,BC =AE =6.设CF =x ,由BD ∥AC ,得AC BD =CF BF ,即45=x 6-x ,解得x =83,即CF =83.………………………10分 B .选修4—2:矩阵与变换解:(1)由题意,得⎣⎡⎦⎤1 a -1 b ⎣⎡⎦⎤21=2⎣⎡⎦⎤21,即⎩⎨⎧2+a =4,-2+b =2,解得a =2,b =4.所以A =⎣⎡⎦⎤1 2-1 4. ………………………………………5分 (2)解法一:A ⎣⎡⎦⎤x y =⎣⎡⎦⎤a b ,即⎣⎡⎦⎤1 2-1 4 ⎣⎡⎦⎤x y =⎣⎡⎦⎤24, 所以⎩⎨⎧x +2y =2,-x +4y =4,解得⎩⎨⎧x =0,y =1.………………………………………10分 解法二:因为A =⎣⎡⎦⎤1 2-1 4,所以A -1=⎣⎢⎡⎦⎥⎤23 -13 16 16. ………………………………………7分 因为A ⎣⎡⎦⎤x y =⎣⎡⎦⎤a b ,所以⎣⎡⎦⎤x y =A -1⎣⎡⎦⎤a b =⎣⎢⎡⎦⎥⎤23 -13 16 16 ⎣⎡⎦⎤24=⎣⎡⎦⎤01. 所以⎩⎨⎧x =0,y =1. ………………………………………10分 C .选修4—4:坐标系与参数方程解法一:以极点为坐标原点,极轴为x 轴建立直角坐标系,则曲线ρ=2cosθ的直角坐标方程为 (x -1)2+y2=1,且圆心C 为(1,0).………………………4分直线θ=π4的直角坐标方程为y =x , 因为圆心C(1,0)关于y =x 的对称点为(0,1),所以圆心C 关于y =x 的对称曲线为x2+(y -1)2=1. ………………………………………8分所以曲线ρ=2cosθ关于直线θ=π4(ρR)对称的曲线的极坐标方程为ρ=2sinθ.…………………10分 解法二:设曲线ρ=2cosθ上任意一点为(ρ′,θ′),其关于直线θ=π4对称点为(ρ,θ), 则⎩⎪⎨⎪⎧ρ′=ρ,θ′=2k π+π2-θ. ………………………………………6分 将(ρ′,θ′)代入ρ=2cosθ,得ρ=2cos(π2-θ),即ρ=2sinθ. 所以曲线ρ=2cosθ关于直线θ=π4(ρ∈R)对称的曲线的极坐标方程为ρ=2sinθ.…………………10分 D .选修4—5:不等式选讲证: 因为|x +5y|=|3(x +y)-2(x -y)|. ………………………………………5分 由绝对值不等式性质,得|x +5y|=|3(x +y)-2(x -y)|≤|3(x +y)|+|2(x -y)|=3|x +y|+2|x -y|≤3×16+2×14=1. 即|x +5y|≤1. ………………………………………10分22.(本小题满分10分)解(1)记“恰有2人申请A 大学”为事件A ,P(A)=C42×2234=2481=827. 答:恰有2人申请A 大学的概率为827. ………………………………………4分 (2)X 的所有可能值为1,2,3.P(X =1)=334=127, P(X =2)=C43×A32+3×A3234=4281=1427, P(X =3)=C42×A3334=3681=49. X所以X 的数学期望E(X)=1×127+2×1427+3×49=6527. ………………………………………10分 23.解:(1)因为f(1)f(4)=f(4)+f(4),所以5 f(1)=10,则f(1)=2.……………………………………1分 因为f(n)是单调增函数,所以2=f(1)<f(2)<f(3)<f(4)=5.因为f(n)∈Z ,所以f(2)=3,f(3)=4. ………………………………………3分(2)解:由(1)可猜想f (n)=n+1.证明:因为f (n)单调递增,所以f (n+1)>f (n),又f(n)∈Z ,所以f (n+1)≥f (n)+1.首先证明:f (n)≥n+1.因为f (1)=2,所以n =1时,命题成立.假设n=k(k≥1)时命题成立,即f(k)≥k+1.则f(k+1)≥f (k)+1≥k+2,即n=k+1时,命题也成立.综上,f (n)≥n+1.………………………………………5分由已知可得f (2)f (n)=f (2n)+f (n+1),而f(2)=3,f (2n)≥2n+1,所以3 f (n)≥f (n+1)+2n+1,即f(n+1)≤3 f (n)-2n-1.下面证明:f (n)=n+1.因为f (1)=2,所以n=1时,命题成立.假设n=k(k≥1)时命题成立,即f(k)=k+1,则f(k+1)≤3f (k)-2k-1=3(k+1)-2k-1=k+2,又f(k+1)≥k+2,所以f(k+1)=k+2.即n=k+1时,命题也成立.所以f (n)=n+1 ………………………………………10分。
江苏省南京市盐城市高三数学二模试题(含解析)苏教版
江苏省南京市盐城市2014届高三数学二模试题(含解析)苏教版【名师综述】本试卷难度适中,既有知识点单一的题目(如第1到第7题),又有拉开档次的题目(如13,14),考查知识点和能力点基本到位。
其中,第13题将向量共线表示和三角形问题交汇在一起,试题的选拔性和交汇性极高。
建议考生:适当记忆一些结论,不仅能提高解题速度,而且能简缩思维,打开思路。
第12题,将函数奇偶性、分段函数解析式、类周期性及函数图像综合在一起,对学生思维能力要求较高。
建议考生:掌握函数要善于从图形分析,图像是函数的灵魂。
第14题内容鲜活,一改其常规面目,以导数为载体,将参数范围问题“隐身”于方程之中,“函数与方程”的思想完美体现!建议考生:掌握数学,需要从数学思想找源头,这样才能跳出题海,高瞻远瞩。
本套试题解答题题型中规中矩,是高考练兵的好素材。
【易错题解读】【理科试卷第6题】执行如图所示的流程图,则输出的k 的值为 .【纠错补练】若输入0,1,x y ==则如图伪代码程序输出的结果为 .Re ,32Print x yadx y While y y yEnd While +≤←【原创题解读】1.【理科试卷第 13 题】在△ABC 中,点D 在边BC 上,且DC =2BD ,AB ∶AD ∶AC =3∶k ∶1,则实数k 的取值范围为 .【举一反三】已知集合M={(,)|3x y x -≤y ≤1}x -,N={|P PA,(1,0),(1,0)}A B -,则表示M ∩N 的 图形面积等于 .【突出问题解读】【突出问题】方程的解的个数【解决方法】基础回顾:函数的零点与方程的解对应与转化关系方法技巧:利用变量分离,将方程有解问题转化为对应函数值域问题.强化训练:1. 已知函数()[]f x x x =-,其中[]x 表示不超过实数x 的最大整数.若关于x 的方程()f x kx k =+有三个不同的实根,则实数k 的取值范围是 ( )A .111[1,)(,]243-- B .111(1,][,)243-- C .111[,)(,1]342-- D .111(,][,1)342--2. 某同学为研究函数)10()1(11)(22≤≤-+++=x x x x f 的性质,构造了如右图所示的两个边长为1的正方形ABCD 和BEFC ,点P 是边BC 上的一个动点, 设CP x =,则()AP PF f x +=. 请你参考这些信息,推知函数()4()9g x f x =-的零点的个数是_______.3. 若方程()lg 2lg 1kx x =+仅有一个实根,那么k 的取值范围是____4. 设函数⎩⎨⎧<-≥⋅=0,2sin 20,2)(x x x x x f x ,则方程1)(2+=x x f 的实数解的个数为_________.5. 设定义域为R 的函数,0,20|,lg |)(2⎩⎨⎧≤-->=x x x x x x f 若关于x 的方程01)(2)(22=++x bf x f 有8个不同的 实数根,则实数b 的取值范围是_______.。
