3 同步发电机的基本方程
《电力系统分析理论》课件第6章 同步发电机的基本方程

第六章 同步发电机的基本方程
用傅里叶系数表示,取基波:
LabLba[m0 m2co2s(a300)] LbcLcb[m0 m2co2s(a900)] LcaLac[m0 m2co2s(a1500)]
d q
i 0
32cso1iansa
coas(120)
sina(120)
1
coas(120)
sina(120)
1
ia ib ic
2
2
2
或缩记为:
id0 qPaibc
(61)7
第六章 同步发电机的基本方程
利用逆变换,可以得到:
coas coas(120)
sina sina(120)
电流的正方向与磁链的正方向符
a
dy
+
a
+
D
Q
D
ω
fQ
c +D +x
合右手螺旋定则,定子各绕组中 b
D
c
电流的正方向与磁链的正方向符
+z
b
合右手螺旋定则
q
第六章 同步发电机的基本方程
➢ 感应电势:与电流正方向 一致
➢ 定子电流:中性点流向机 v f 端
➢ 定子电压:电流流出端为 正
➢ 转子电压:提供正向电流 的励磁电压是正的
vf
f
Rf
0
0
if
00
D Q
0
0 0
RD 0
0 RQ
iD iQ
v为各绕组端电i为 压各 ;绕组电流;
(61)
电力系统暂态分析第二章

&& &
&
U|0| jI|0|xqjId|0|(xdxq) EQ|0| jId(xd xq)
&& & EQ U|0| jI|0|xq
由于E q |0|
&
、jId|0| (xd xq )
&
均在q轴方向,所以E Q |0 |也必在q轴方
向,据此即可确定q轴方向。
d轴和q轴方向的确定
(3)空载电动势的确定
对于隐极机可以从正常运行时的电压和电流以及相角
求出 E q |0|
;对于凸极机需要知道I& d
|
0
、&
| I q |0
|
、U& d
|0
、| U& q
|0
才能求出
|
E
q
|0 |
,
即需要知道& +d、+q轴的方向,为确定+q轴的方amp;& & && & & E q |0 | U |0 | j I d |0 |x d j I q |0 |x q U |0 | j I d |0 |x q j I q |0 |x q j I d |0 |( x d x q )
交轴阻尼绕组:
发电机空载情况下突然三相短路定性分析
一、突然三相短路后的定子电流
1、短路前各相磁链
2、短路前瞬间各相磁链瞬时值
设短路发生时(t=0) 0,0 各相定子绕组磁链瞬时值
为:
3、短路后由励磁磁场在定子绕组产生的磁链
4、短路后定子电流在三相绕组中产生的磁链 5、短路后定子绕组总磁链
交流分量的幅值是衰减的,说明电势或阻抗是变化 的。
电力系统暂态分析第二章

虚构电势 EQ|0|。
& &&
&
&&
&
&
Eq|0| U |0| jI d|0| xd jI q|0| xq U |0| jI d|0| xq jI q|0| xq jI d|0| (xd xq )
&&
&
&
U |0| jI|0| xq jI d|0| (xd xq ) EQ|0| jI d (xd xq )
各相磁链波形图如下:
7、定子电流表达式及波形
各相短路电流的一般表达式,当 0 为任意角度时
二、突然短路后转子励磁绕组中的电流分量
1、强制励磁电流分量 i f |0| 2、非周期自由分量 i f 3、周期自由分量 i fp
三、突然短路后转子阻尼绕组的电流分量
1、d轴阻尼绕组 (1)非周期自由分量 (2)周期自由分量
交流分量的幅值是衰减的,说明电势或阻抗是变化 的。
励磁回路电流也含有衰减的交流分量和非周期分量, 说明定子短路过程中有一个复杂的电枢反应过程。
同步发电机三相短路电流
❖ 实际电机绕组中都存在电阻,因此所有绕组的磁链都随时间变化,形 成电磁暂态过程。 ❖ 周期分量,其幅值将从起始次暂态电流逐渐衰减至稳态值; ❖ 非周期分量和倍频周期分量,它们将逐渐衰减至零。 ❖ 短路电流计算一般指起始次暂态电流或稳态短路电流计算;而其它任 意时刻短路电流工频周期分量有效值计算工程上采用运算曲线方法。
四、发电机空载情况下短路电流的表达式
1、定子绕组阻抗变化过程 2、定子电流变化过程 3、短路周期电流电流表达式
X d X d X d
I I I
t
同步发电机电压方程相量图功率方程特性
电机学
1
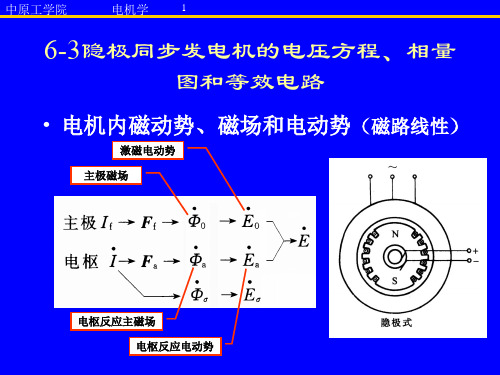
6-3隐极同步发电机的电压方程、相量
图和等效电路
• 电机内磁动势、磁场和电动势(磁路线性) 电机内磁动势、 磁路线性)
激磁电动势 主极磁场
电枢反应主磁场 电枢反应电动势
中原工学院
电机学
2
电路方程
• 初级电路 一相 初级电路(一相 一相) • 初级方程 • 激磁电动势大小
– 空载特性
中原工学院
电机学
7
凸极同步发电机分析方法
• 把电枢磁动势分解为: 把电枢磁动势分解为:
– 直轴磁动势
• 产生直轴磁场
– 交轴磁动势 交轴磁动势.
• 产生交轴磁场
• 可行分析
– 直轴的磁路随转子同步旋转,相对固定, 直轴的磁路随转子同步旋转,相对固定, 磁阻不变; 磁阻不变; – 交轴的磁路也随转子同步旋转,相对固定, 交轴的磁路也随转子同步旋转,相对固定, 磁阻不变。 磁阻不变。
• 运行特性:外特性,调整 外特性,
特性, 特性,效率特性
• 外特性
– n=同步转速,If和cosφ不 同步转速, 同步转速 不 变时, 变时,发电机端电压和电 枢电流之间的关系U=f(I) 枢电流之间的关系
• 电压调整率
中原工学院
电机学
23
6-7同步发电机的运行特性
• 调整特性 调整特性:
– n=同步转速,端电压=额 同步转速,端电压 额 同步转速 定电压, 定电压,cosφ=常数时的励 常数时的励 磁电流和电枢电流之间关 系,If=f(I)
中原工学院
电机学
10
直轴电枢反应电抗和 交轴电枢反应电抗
• 不计铁耗时,Ead滞后 d90o,Eaq滞后 q90o 不计铁耗时, 滞后I 滞后I
同步电机的基本方程

经过派克变换后,在d、q、0坐标系统中,发电机的磁链方程 组转化为线性代数方程组;
电压方程变为线性微分方程组,求解将大为简 化。
2020/1/8
28
7.2.3 同步电机派克方程式的标么制
定子侧基准值 发电机原始方程是针对三相电压、电流、磁链的瞬时值列写的。 通常分别选取定子额定相电压、定子额定相电流的幅值作为电 压与电流瞬时值的基准值
又相同的三个绕组,气隙中产生正弦分布的磁势。 4. 定子绕组沿定子均匀分布,转子恒速旋转时,转子绕组的磁
动势在定子绕组所感应的空载电势是时间的正弦函数。 5. 电机的定子和转子具有光滑的表面。(即不考虑定转子槽、
通风沟等)
2020/1/8
7
? 同步发电机各绕组轴线正方向示意图(凸极)
? 规定:定子各相的正值电 流产生该相的负值磁链。 转子各绕组电流产生的磁 通方向与参考方向相同时, 电流为正值。
?? ?
12
12
????ic ??
派克变 换矩阵
2020/1/8
24
举例:
?? ia ?? ?ib ? ?
I
m
?? ?
cos
cos
?? t
??
?
t
?
?
0
?
?
0?
120
?????
交流电流
?? ic ??
?? cos ?? t ? ? 0 ? 120 ????
派克变换
?? i d ?? ? iq ? ?
u d ? ? rs i d ? ?? d ? ?? q ?
u q ? ? rS i q ? ?? q ? ??
d
? ?
u o ? ? rS io ? ?? o
同步发电机转子运动方程

发电机组的转速是由作用在它转子上的转矩所决定的,作用在转子上的转矩主要包括原动机作用在转子上的机械转矩和发电机的电磁转矩两部分。
原动机的机械转矩是由发电厂动力部分(例如火电厂的锅炉和汽轮机)的运行状态决定,发电机的电磁转矩是由发电机及其连接的电力系统中的运行状态决定,在这些运行状态中如发生任意干扰都会使作用在转子上的转矩不平衡,也就会使转速发生变化。
因此要求系统在受到各种干扰后,发电机组经过一段过程的运动变化后仍能恢复同步运行,即δ角能达到一个稳态值。
能满足这一点,系统就是稳定的,否则就是不稳定的,而必须采取相应的措施以保证系统的稳定性。
一般将电力系统稳定性问题分为两大类,即静态稳定性和暂态稳定性。
所谓电力系统静态稳定性是指电力系统在某个运行状态下,突然受到任意小干扰后,能恢复到原来的(或是与原来的很接近)运行状态的能力。
这里所致的小干扰,是在这种干扰作用下,系统的状态变量的变化很小,因此允许将描述系统的状态方程线性化。
电力系统暂态稳定性是指电力系统在某个运行状态下,突然受到较大干扰后,能够过渡到一个新的稳态运行状态(或者回到原来运行状态)的能力。
由于受到的是大干扰,系统的状态方程不能线性化。
由于两种稳定性问题中受到的干扰的性质不同,因而分析的方法也不同。
电力系统的稳定性问题还可以根据需要按时间长短分为短期、中期和长期稳定,它们在分析时所用的系统元件的数学模型不同,例如长期稳定将计及锅炉的过程。
一:同步发电机转子运动方程同步发电机组转子的机械角加速度与作用在转子轴上的不平衡转矩之间的关系:T E d J M M M dtΩ=∆=- (1) 其中,Ω为转子机械角速度,/rad s ;J 为转子的转动惯量,2kg m ;M ∆为作用在转子轴上的不平衡转矩(略去风阻,摩擦等损耗即为原动机机械转矩T M 和发电机电磁转矩E M 之差),N m ;上式极为转子运动方程。
当转子以额定转速0Ω(即同步转速)旋转时,其动能为:2012K W J =Ω (2) 式中,K W 为转子在额定转速时的动能,J 。
第3章三相同步电机
cos ϕ N
f N 单位为Hz n N单位为r/min θN
• 额定励磁电流和电压 IfN 、UfN
3-2 同步发电机的磁场
一、空载运行 n s If I=0
1、空载磁场——主磁场
I f → F f → B0 → φ 0
→ 电枢齿 路径:气隙 →电枢齿 → 电枢轭 → 磁极 主磁通 → 极身 → 转子轭 作用:在三相绕组中感应 对称电动势
k w1 N 1φ a k w1 N 1 Fa Λa (k w1 N 1 ) 2 kIΛa La = = = = = k (k w1 N 1 ) 2 Λa I I I I
ψa
二、考虑磁路饱和时 非线性,迭加原理不适用
Ff & & → F → B →Φ → E Fa
& U
& IRa
3、等效电路
& & & & & & & & E0 =U + I Ra + jIXσ + jIXa =U + I Ra + jIXs
4、同步电抗
X s = X a + Xσ
a) 反映了Φa和Φσ的作用 b) 磁路不饱和时为常数 c)
∝ f X a = ωLa ∝ (k w1 N 1 ) 2 ∝ Λ 主磁路的磁导 a
& 图示瞬间,A相绕组电动势 E0 A 达正的最大值,方向从X入,A 出。
•从导体切割磁力线分析。
(交轴)
• 从磁通的变化来分析。 A相磁通为零,电动势滞后磁 通90度。
& & B相绕组 E0 B、C相绕组电动势 E0 C 滞后A相电动势120度和240度。
同步发电机基本方程为什么要进行派克变换
1 同步发电机基本方程为什么要进行派克变换?派克变换的物理意义是什么? 磁链方程式中出现变系数的主要原因:(1) 转子的旋转使定、转子绕组间产生相对运动,致使定、转子绕组间的互感系数发生相应的周期性变化。
(2) 转子在磁路上只是分别对于d 轴和q 轴对称而不是任意对称的,转子的旋转也导致定子各绕组的自感和互感的周期性变化。
①变换后的电感系数都变为常数,可以假想dd 绕组,qq 绕组是固定在转子上的,相对转子静止。
②派克变换阵对定子自感矩阵起到了对角化的作用,并消去了其中的角度变量。
Ld,Lq,L0 为其特征根。
③变换后定子和转子间的互感系数不对称,这是由于派克变换的矩阵不是正交矩阵。
④Ld 为直轴同步电感系数,其值相当于当励磁绕组开路,定子合成磁势产生单纯直轴磁场时,任意一相定子绕组的自感系数。
物理意义上理解,它将观察者的角度从静止的定子绕组转移到随转子一同旋转的转子上,从而使得定子绕组自、互感,定、转子绕组间互感变成常数,大大简化了同步电机的原始方程。
派克变换:将a 、b 、c 三相静止的绕组通过坐标变换等效为d 轴dd 绕组、q 轴qq 绕组,与转子一同旋转2 经Park 变换后,同步发电机的磁链方程是什么?电压方程是什么?⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡QD f q d QQa D Df Da fD f fa aQ q aD af d Q D f q d i i i i i i L m L L m L L mL m L m m L 0000230000230002300000000000ψψψψψψ 3 同步发电机稳态运行方程是什么?作出其相量图。
4短路的原因①绝缘材料的自然老化,设计、安装及维护不良所带来的设备缺陷发展成短路。
•②恶劣天气:雷击造成的闪络放电或避雷器动作,架空线路由于大风或导线覆冰引起电杆倒塌等。
同步发电机的数学模型课件资料
2.绕组的磁链方程(ψ=Li)
总磁链=本绕组电流产生ቤተ መጻሕፍቲ ባይዱ磁链+其它绕组电流产生的与本绕组交链的磁链
用矩阵形式表示为 a Laa Lab L L b ba bb c Lca Lcb f L fa L fb D LDa LDb L Q Qa LQb
二、电感系数
⒈
定子各相绕组的自感系数
以a相为例分析如下:
a相绕组电流 ia
正弦分布的磁势Fa
Fa cos (d轴分量) Fa waia
Fa sin (q轴分量)
α角为d轴与a相绕组轴线的夹角
如果用λad和λaq分别表示沿d轴和q轴方向 气隙磁通路径的磁导,则由定子磁势Fa 沿两个轴向产生的气隙磁通为
1.回路电势方程: 根据以上假定正方向,可得定转子各绕组的电势矩阵方程式为
va v b vc v f 0 0
a r 0 0 ia i b 0 r 0 0 b c 0 0 r ic if f rf D 0 rD iD i r Q Q Q
当α=90°或270°时, 互感系数Laf为零。
• 同理可得定子各相绕组与纵轴阻尼绕组 间的互感系数为
LbD LDb maf cos( 120) LcD LDc maf cos( 120) LaD LDa maD cos
由于转子横轴落后于纵轴90°,故定子各 相绕组与横轴阻尼绕组间的互感系数为
第二章2.4同步发电机及其基本方程
派克变换及d,q,0坐标系统
原始方程中的定子绕组方程取空间静止不 动,转子各绕组电量取随转子旋转的d.q 两相坐标系统列写。 Park变换是一种坐标变换,它将静止的定 子abc绕组变换到旋转的dq0坐标系统,变 换后定子dd、qq绕组中的等效磁势相对与 转子静止,磁路磁阻不变,相应的电感系 数也就变为常数。
LSR iabc LRR i fDQ
ψ dq 0 P 0 ψ abc P 0 LSS ψ = ψ = 0 U L RS fDQ 0 U fDQ P 0 LSS = 0 U LRS PLSS P 1 = LRS P 1
1
2.4同步发电机及其基本方程
本节知识点:
认识同步发电机的结构 同步电机的电势方程和磁链方程 同步发电机的基本方程 稳态运行模型及相关参数 暂态运行模型及相关参数 同步发电机的序参数
同步发电机的分类
1 隐极机 定子; 转子可以认为各向磁阻相同; 高速旋转的汽轮机。 2 凸轮机 定子同隐极机; 转子磁阻不再随意对称; 水轮机。
M af = maf cos α M bf = mbf cos( α 120 ) M cf = mcf cos( α + 120 )
定子和转子各相绕阻间的互感系数
定子绕组与直轴阻尼绕组间的互感系数
M aD = maD cos α M bD = mbD cos( α 120 ) M cD = mcD cos( α + 120 )
电磁基础
磁动势F = NI F l 磁通φ = ,其中Rm = 磁链ψ = Nφ = NI Rm s F 串联回路φ = Rm1 + Rm 2 E = j 4.44 fNφ
理想同步发电机
1、定子abc三相绕组结构完全相同,互相对称, 空间相隔120度电角度。 2、电机转子在结构上对于d轴与q轴完全对称。 3、定子、转子铁心同轴且表面光滑(忽略定、 转子上的齿槽),忽略齿谐波。 4、定子、转子绕组电流产生的磁动势在气隙中 是正弦分布的,忽略高次谐波。 5、磁路是线性的,无饱和,无磁滞和涡流损耗, 认为电机铁心部分导磁系数为常数,可应用迭 加原理。
